几何模型(小学奥数必会6大模型)
小学奥数-几何五大模型(等角模型)

小学奥数-几何五大模型(等角模型)
引言
在小学奥数研究中,几何是一个重要的内容。
而在几何学中,
等角模型是五大模型之一,它的认识对于学生的几何研究至关重要。
本文将介绍小学奥数中的几何五大模型之一——等角模型。
什么是等角模型
等角模型是指具有相等角度的模型,也即是说,模型的各个角
度都相等。
这个模型可以有不同的形状和大小,但其中的角度是相
等的。
等角模型的特点
等角模型具有以下几个特点:
1. 模型中的角度相等,这是等角模型最基本的特点。
2. 模型可以有不同的形状和大小,只要其中的角度相等即可。
3. 等角模型常常用于解决几何问题,通过对模型的认识和分析,可以帮助学生更好地解答相关问题。
等角模型的应用
等角模型在小学奥数中有着广泛的应用。
以下是等角模型的一
些应用场景:
1. 用于解决角度相等的问题:在解决一些与角度相关的问题时,可以通过等角模型的认识,找到其中的角度关系,从而解答问题。
2. 用于解决相似图形的问题:等角模型可以帮助学生理解相似
图形的概念和性质,从而在求解相似图形的问题时起到辅助作用。
3. 用于解决垂直角的问题:在解决垂直角相关问题时,等角模
型可以帮助学生理解垂直角的定义和性质,从而更好地解答问题。
总结
等角模型是小学奥数学习中的重要内容之一。
通过对等角模型
的认识和应用,可以帮助学生更好地理解几何学中的角度关系和性质,提高解决几何问题的能力。
小学奥数--几何模型分类总结汇总版(鸟头、燕尾、风筝、一般模型等)

目录目录 (1)模型一——《等积变换》 (2)一、知识点梳理 (2)二、例题精讲 (3)三、自我提升 (5)四、答案与解析 (7)模型二——《一半模型》 (11)一、知识点梳理 (11)二、例题精讲 (13)三、自我提升 (15)四、答案与解析 (16)模型三——《鸟头(共角)模型》 (19)一、知识点梳理 (19)二、例题精讲 (20)三、自我提升 (22)四、答案与解析 (24)模型四——《蝴蝶模型》 (25)一、知识点梳理 (25)二、例题精讲 (26)模型五——《沙漏模型》 (32)一、知识点梳理 (32)二、例题精讲 (32)三、自我提升 (35)四、答案与解析 (36)模型六——《燕尾模型》 (38)一、知识点梳理 (38)二、例题精讲 (39)三、自我提升 (41)四、答案与解析 (43)模块七——《长、正方体、圆柱、圆锥》 (45)一、知识点梳理 (45)二、例题精讲 (46)三、自我提升 (48)四、自我提升答案 (50)模型八——《圆、扇形》 (52)一、知识点梳理 (52)二、例题精讲 (53)三、自我提升 (55)四、答案与解析 (57)模型一——《等积变换》一、知识点梳理二、例题精讲三、自我提升四、答案与解析模型二——《一半模型》一、知识点梳理一半模型其实是等积变换模型的延伸,只是将三角形和平行四边形进行了整合与综合考查,但是学生往往遇到此类题目之后很难想到用等积变换,所以我们专门提炼出一半模型,帮助学生加深此部分知识点的理解,提高应用能力。
21b a ba ⨯⨯====⨯=∆∆∆∆BCP S BCD S BCF S BCE S ABCD S 口 平行四边形同理不规则图形ba 21b2b1a 21b2a 21b1a 21b2a 21b1a 21ba ⨯=+⨯=⨯⨯+⨯=+=⨯⨯=⨯=⨯=∆∆∆∆)(阴影;口BCE S ADE S BCE S ADE S ABCD S 拓展图形(比例应用)ba 41b2b1a 41b2221b1221b2221b1221b41b 221⨯=+⨯=⨯⨯+⨯⨯=+=⨯⨯=⨯⨯=⨯=⨯⨯==∆∆∆∆∆)(阴影;右图:左图:阴影a a BEG S AFG S aBEG S a AFG S a a BFE S常见图形的认识二、例题精讲例1如图所示,四边形ABCD与AEGF都是平行四边形,请你证明它们的面积相等.例2如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?例3如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例4图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.A BG CEFDHGFEDCBAGFED CBA例5正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?例6如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积例7 如图,有三个正方形的顶点D 、G 、K 恰好在同一条直线上,其中正方形GFEB 的边长为10厘米,求阴影部分的面积.E BA KEBA三、自我提升1、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.2、如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为 .3、长方形ABCD 的面积是2011平方厘米.梯形AFGE 的顶点F 在BC 上,D 是腰EG 的中点.试求梯形AFGE 的面积.G4AB CDEF A B C D E FG H4、已知正方形ABCD 边长为10,正方形BEFG 边长为6,求阴影部分的面积.5、右图中,ABCD 和CGEF 是两个正方形,AG 和CF 相交于H ,已知CH 等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积.6、如图,正方形ABCG 和正方形FCDE 并排放置,BE 与FC 相交于点H ,已知AB=6厘米,则阴影部分的面积是_________________平方厘米? 四、答案与解析1、【分析】如图所示,连接AD ,则BC 平行AD ,三角形ABC 和三角形BCD 等底等高,因此三角形ABCJIHGA BCD EF HG F E D C B A的面积就等于小正方形的面积的一半,据此即可得解.解:据分析可知:4×4÷2=8(平方厘米);答:三角形ABC的面积是8平方厘米.2、【分析】方法一:如图所示,连接AF和BD,则AF平行BD,三角形FAD与三角形FAB等底等高,即面积相同。
小学奥数几何五大模型.pdf
(4)相似模型
1、相似三角形:形状相同、大小不相等的两个三角形相似;
2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:
①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;
②相似三角形周长的比等于相似比;
③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型
结论:因为DE BC ∥,所以ADE ABC △∽△,则
①AD AE DE
==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;
E
D C B
A E D
C
B A
③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型
例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?
G
F
E D C
B
A。
小学奥数几何五大模型

在小学奥数知识体系中,几何五大模型是几何专题中非常重要的一块知识点,方法性很强,掌握了几何的五大模型,对于我们解决组合型直图形或者非规则图形是非常有帮助的,所以几何五大模型在小学几何体系中的重中之重!几何五大模型的难点在于我们要在掌握各个模型适用的题型、相应的方法、公式的基础上学会灵活运用,还有就是有时要根据题意同时运用多种模型,从而更好的解决问题!接下来e 度徐丽老师会针对几何五大模型进行解析,希望能帮助到各位家长。
它们包括:等积模型鸟头定理蝴蝶定理相似模型燕尾定理模型一三角形等积模型已经知道三角形面积的计算公式:三角形面积=底*高/2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小);如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论:①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.例题:【解析】图中阴影部分的面积等于长方形ABCD面积的一半,即4*3/2=6(平方厘米)。
图中的E、F、G分别是正方形ABCD三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?解析:如上图,把另外三个三等分点标出之后,正方形的3个边就都被分成了相等的三段。
小学奥数必学几何五大模型及例题解析

小学奥数必学几何五大模型及例题解析一、等积变换模型——很重要,小学常考⑴等底等高的两个三角形面积相等;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图右图12::S S a b =⑶夹在一组平行线之间的等积变形,如下图ACDBCD S S =△△;反之,如果ACDBCD S S =△△,则可知直线AB 平行于CD 。
⑷正方形的面积等于对角线长度平方的一半;⑸三角形面积等于与它等底等高的平行四边形面积的一半;经典例题:1S 2S 解析:连接CE ,如图。
AE=3AB,所以S △AEC =3S △ABC=3 所以 S △BCE =2又因为:BD=2BC,所以S △BDE =2 S △BCE =4点评:此题就是三角形等积变换模型的直接应用二、鸟头定理(共角定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△图1 图2此模型的结论可以用将来初中学到的正弦定理进行证明!因为S △ABC =AB ×ACsinA ,S △ADE =AD ×AEsinA所以:S △ABC :S △ADE= (AB ×ACsinA ):(AD ×AEsinA )=(AB ×AC ):(AD ×AE )经典例题:S △ADF :S △ABC=(AD ×AF ):(AB ×AC )=(2BD ×AF ):(3BD ×4AF )=1:6 S △BDE :S △ABC=(BD ×BE ):(AB ×BC )=(BD ×BE ):(3BD ×2BE )=1:6 S △CEF :S △ABC=(CE ×CF ):(CB ×CA )=(CE ×3AF ):(2CE ×4AF )=3:8 1-1/6-1/6-3/8=7/24 S △ABC =7÷7/24=24(平方厘米).点评:本题直接用到鸟头模型,先分别求出三个角上的三个三角形占S △ABC 的比例,再求出S △DEF 占S △ABC 的比例,就能直接求出S △ABC 的面积。
人教版六年级下册数学小升初奥数:几何五大模型模型(课件)

02 三角形:燕尾模型
A
O
B
D
A
F
E O
B D
S△ABD:S△ACD=BD:CD S△OBD:S△OC?B:D?:CD
C
S△ABO:S△CBO=AE:CE S△ACO:S△BCO=AF:BF S△ABO:S△ACO=BD:CD
C
02 三角形:燕尾模型
(1)
例、如图,已知 BD=DC,EC=2AE,三角形 是 30,求阴影部分面积?
01 长方形:一半模型(犬齿模型)
(1)
1 S阴影 2 S长方形
例 、(长郡系)如图,ABFE 和 CDEF 都是矩形,AB 的长是 4 厘米, BC 的长是 3 厘米,那么图中阴影部分的面积是多少平方厘米。
解题思路: 将大长方形分成若干个小长方形;
每个阴影面积都=对应长方形的一半; 全部阴影面积=长方形ABCD的一半; S阴影=3×4÷2=6cm2;
几何五大模型
二、鸟头(共角)定理模型
1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形; 2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点
则有:S△ABC:S△ADE=(AB×AC):(AD×AE)
ABC
的面积
1 G①
③ ②
③ ⑥③
解题思路: 构建完整燕尾模型,利用份数思维;
AE:CE=1:2
BD:CD=1:1
2
AE:CE=1:2
设S△AEF为1份,则S△CEF为2份 S△ABF:S△ACF=1:1,S△ABF为3份 S△ABF:S△CBF=1:2,S△CBF为6份
小学奥数-几何五大模型(相似模型)分解
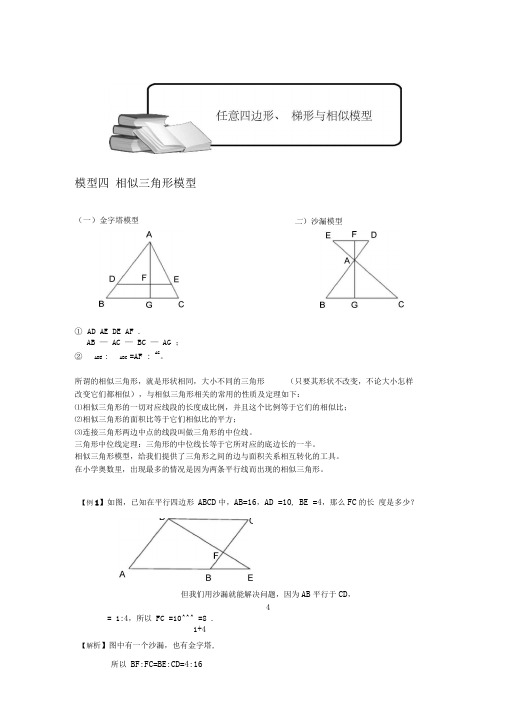
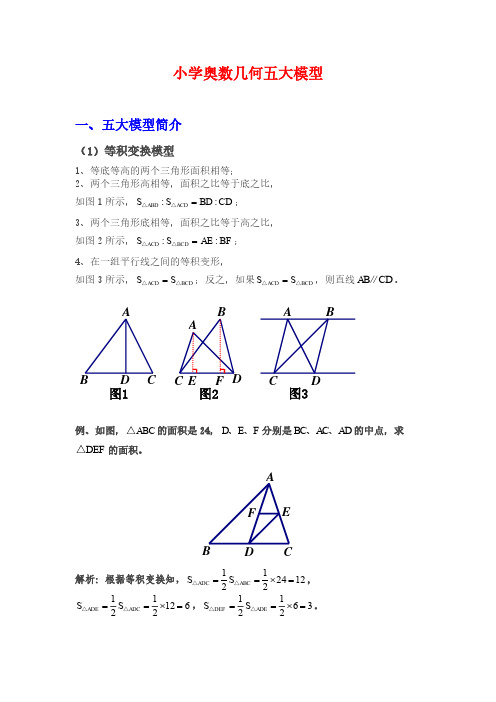
模型四 相似三角形模型(一)金字塔模型① AD AE DE AF .AB — AC — BC — AG ;②ADE :ABC=AF : AG。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。
相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。
在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。
【例1】如图,已知在平行四边形 ABCD 中,AB=16,AD =10, BE =4,那么FC 的长 度是多少?但我们用沙漏就能解决问题,因为AB 平行于CD ,4= 1:4,所以 FC =10^^^ =8 .1+4二)沙漏模型【解析】图中有一个沙漏,也有金字塔,进而有S四边形DEGF=3份 ,S 四边形FGCB =5份,所以ADE: S 四边形DEGF : S 四边形 FGCB =1: 3: 5如图,测量小玻璃管口径的量具 ABC , AB 的长为15厘米,AC 被分为60等份。
如果小玻璃管口 DE 正好对着量具上20等份处(DE 平行AB ),那么小玻璃管口径 DE 是多大?有一个金字塔模型, 所以DE:AB=DC:AC , DE :15 =40:60,所以DE=10厘米。
如图,DE 平行 BC ,若 AD: DB =2:3,那么 S AADE : S AECB =【解析】根据金 字塔 模 型 AD : AB = AE : AC = DE :BC =2: (2+3) =2:5,S A ADE: SA ABC =22 :52=4: 25 ,设SA ADE —4份则SA ABC=25 份,SABEC= 25 X 5 = 3份,所以& A D :SA毛 C 4【例4】如图,A ABC 中,DE , 贝U S A ADE : &边形DEGF :S四边形FGCB【解析】设S AADE =1份,根据面积比等于相似比的平方,所以SA ADE : SA AFG =AD: AF —1: 4,SA ADE : SA ABC =AD: AB =1: 9 ,因此S A AFG =4 份,S A ABC =9 份,【例2】 【解析】 【例3】FG ,BC 互相平行, AD = DF = FB ,2已知△ ABC 中,DE 平行 BC ,若 AD : DB =2:3,且 S 弟形DBCE 比 $△ ADE 大 8.5 cm2求 SA ABC 。
几何综合六种模型(学生版)

几何综合六种模型通用的解题思路:题型一:两垂一圆构造直角三角形模型平面内有两点A,B,再找一点C,使得ABC为直角三角形分类讨论:若∠A=90°,则点C在过点A且垂直于AB的直线上(除点A外);若∠B=90°,则点C在过点B且垂直于AB的直线上(除点B外);若∠C=90°,则点C在以AB为直径的圆上(除点A,B外).以上简称“两垂一圆”.“两垂一圆”上的点能构成直角三角形,但要除去A,B两点.题型二:两圆一中垂构造等腰三角形模型分类讨论:若AB=AC,则点C在以点A为圆心,线段AB的长为半径的圆上;若BA=BC,则点C在以点B为圆心,线段AB的长为半径的圆上;若CA=CB,则点C在线段AB的垂直平分线PQ上以上简称“两圆一中垂”“两圆一中垂”上的点能构成等腰三角形,但是要除去原有的点A,B,还要除去因共线无法构成三角形的点MN以及线段AB中点E(共除去5个点)需要注意细节题型三:胡不归模型【模型解读】一动点P在直线MN外的运动速度为V 1,在直线MN上运动的速度为V2,且V1<V2,A、B为定点,点C在直线MN上,确定点C的位置使ACV2+BCV1的值最小.(注意与阿氏圆模型的区分)1)ACV2+BCV1=1V1BC+V1V2AC,记k=V1V2,即求BC+kAC的最小值.2)构造射线AD使得sin∠DAN=k,CHAC=k,CH=kAC,将问题转化为求BC+CH最小值.3)过B点作BH⊥AD交MN于点C,交AD于H点,此时BC+CH取到最小值,即BC+kAC最小.【解题关键】在求形如“PA+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型.(若k>1,则提取系数,转化为小于1的形式解决即可)。
【最值原理】两点之间线段最短及垂线段最短。
题型四:阿氏圆模型【模型解读】如图1所示,⊙O的半径为r,点A、B都在⊙O外,P为⊙O上一动点,已知r=k·OB,连接PA、PB,则当“PA+k·PB”的值最小时,P点的位置如何确定?如图2,在线段OB上截取OC使OC=k·r,则可说明△BPO与△PCO相似,即k·PB=PC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模型一:等高模型定义:三角形面积的大小,取决于三角形底和高的乘积。
如果固定三角形的底(或高)不变,另一者变大(小)n 倍,三角形的面积也就变大(小)n 倍。
六种基本类型:两个三角形高相等,面积比等于底之比;两个三角形底相等,面积比等于高之比公式:DCBDS S ADC ABD =∆∆;FCEDS S ABC ABD =∆∆其中,BC=EF 且两三角形的高相等公式:1=∆∆DEFABCS S夹在一组平行线之间的等积变形公式:1==∆∆∆ABDABCBCD ACD S S等底等高的两个平行四边形面积相等(长方形和正方形可看作特殊的平行四边形)公式:1=CDEFABCDS S三角形面积等于与它等底等高的平行四边形面积的一半公式:ABCDEDC S S 21=∆两个平行四边形高相等,面积比等于他们底的比公式:EFABS S DEFG ABCD =例题:长方形ABCD 的面积为36cm 2,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?()5.135.418185.43681211836212136212121=-=-=∴=⨯=⨯⨯=+=++=⨯=++=++∴=++====∴===∴=∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆BEF BEF BEF DGH BFH BEH CDH BCH ABH DGH BFH BEH CDH BCH ABH ABCD CDH DGH BCH BFH ABH BEH CGHDGH CFH BFH BEHAEH S S BF BE S S S S S S S S S S S S S S S S S S S S S S S S S S S S EB AE HC BH 阴影阴影,,,,同理,、如图,连接模型二:相似模型定义:形状相同,大小不相同的两个三角形,一切对应线段的长度成比例的模型。
两种基本类型:(一)金字塔模型(二)沙漏模型①相似三角形的一切对应线段的长度成比例,并且这个比例等于他们的相似比;公式:AGAFBC DE AC AE AB AD ===②相似三角形的面积比等于他们相似比的平方;公式:22::AG AF S S ABC ADE =∆∆③连接三角形两边中点的线段叫做三角形的中位线。
(三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。
)公式:当DE 为中点时,BCDE 21=例题:如图,DE 平行BC ,且AD=2,AB=5,AE=4,求AC 的长.由金字塔模型得5:2:::===BC DE AC AE AB AD ,所以10524=⨯÷=AC模型三:鸟头模型(共角模型)定义:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比对应角(相等角或互补角)两夹边的乘积之比。
四种基本类型:公式:AEAD ADE S ⨯⨯=∆∆例题:如图,三角形ABC 的面积是1,延长BA 到D,使DB=AB;延长CA 到E,使EA=2AC;延长CB 至F,使FB=3BC,求三角形DEF 的面积?解:71612263218014212 1243 2213CACE 3BC CF 2AC AE =--+=--+==⨯=⨯⨯=︒=∠+∠⇒=+=+==⨯=⨯⨯==⨯=⨯⨯=====∠=∠⇒∠=∠⇒∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆ABC S DBF S CEF S ADE S DEF S BFBD BCBA ABC S DBF S DBF ABC DBF S ABC S ADE S CEF S S CB CA CFCE ABC S CEF S AC AB AE AD ABC S ADE S AD AB FCEBCA CEF S ABC S EAD BAC ADE S ABC S 与与与总模型四:风筝模型定义:两个共底的三角形,其面积之比等于其顶点到顶点连线与底边所在直线交点的线段长度之比。
两种基本类型:(同侧风筝模型、异侧风筝模型)公式:同侧风筝模型:ADCS ODCS AB OB ∆∆=异侧风筝模型:BCDS ABCS OD AO ∆∆=例题:如图,正方形ABCD 的面积为1,E、F 分别是BC 和DC 的中点,DE 与BF 相交于M 点,DE 与AF 相交于N 点,那么阴影三角形MFN 的面积是多少?图1图230121 151FAD 151 MFN 1513511FD FA FN FM FAD MFN 128141BEF BED MF DM 148121BEF BEA NF AN 111 1ED BC 1BED 11BEA 812121 2121BEF 81 2121 2121BEF 2 111=⨯===⨯⨯=⨯⨯========⨯⨯=⨯====⨯⨯=⨯==⨯⨯=⨯=====⇒=∆∆∆∆∆∆∆∆∆◊∆∆∆◊S S S S S S S S S ABCD S S BF EC S BF EC S EF BD EF AE AD CD BC AB ABCD S 通过鸟头模型得到:)(如图、连接)(如图、连接模型五:蝴蝶模型定义:1、任意四边形蝴蝶模型为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,可以了解四边形的内部的四个三角形的面积关系。
2、梯形的蝴蝶模型研究的是被梯形对角线分成的四块三角形面积之间的关系以及三角形面积比和线段比之间的相互转化。
公式:任意四边形:24313241::S S S S S S S S ⨯=⨯⇒=梯形:()。
长度之比的位置的转移线段两个模型的主要作用是模型,金字塔模型。
这其他平行线模型:沙漏思想。
例模型面积问题的重要面积问题,以及其他比这是解决梯形蝴蝶模型分的面积份数,数,进而表示出所有部出合适三角形的面积份设份数:按比例条件设小:中:大:总小:大中:大小:中的结论:梯形蝴蝶模型关于面积找到上底与下底之比为找平行线点是:梯形蝴蝶模型题目中重右”。
左下,或“上翅磅,面积乘积相等”型结论可记为:“两对任意四边形中的蝴蝶模总结:)之比为如下结论(上底与下底反复运用等高模型,有.5.4::::b :a 3.b :a 2 1.2.1::.3::::::::.2.1:2222222313432412142b a b ab a b a b a S S b a BC AD OD OB OC OA S S S S S S S S S S b a +====⨯=⨯=========例题:如图ABCD 和CEGF 是两个正方形,AG 和CF 相交于H,已知CH 等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积。
49.54.536AGEF 5.4)36(321213cmBC 21HF :CH FG :AC 6cm 36CGEF 18CGEF 21186121261212 362121621:31,2222222=++==-⨯⨯=⨯====⇒=====+==⨯===⨯=====⇒=◊∆◊◊∆∆∆∆∆∆∆∆∆S DF AD ADF S cm S cm S CFG S EFG S CFG S cm GFH S GHF S cm CHG S AHC S cm CHG S AHF S HF CH CF CH ACEG FG AC FG AC :由到如下结论由梯形蝴蝶模型可以得:由已知得:是梯形,四边形平行于则、如图,连接如图,梯形ABCD 中,AD 与BC 平行,AD=BE=EC,O 是AC 与BD 的交点,P 点是AE 与BD 的交点。
若已知三角形AOD 的面积为10,那么阴影部分(即四边形OPEC)的面积是多少?25530541:21:21://21:,21:602302021:21 //=-=-==⇒=⇒=⇒=∴====⇒==⇒==∴==∆∆◊∆∆∆∆◊∆∆∆∆APO AEC POEC AOP OCD AOP ADC ADEC ADC OCD OCD AOD S S S S S S AE P CD AP OD AO CD AE OD AO ADEC CPOD AO S S S S S S BC AD BC AD ECBE AD ADEC :中点为::由蝴蝶模型可得:为平行四边形四边形连接::由蝴蝶模型可得为平行四边形,四边形模型六:燕尾模型定义:燕尾定理:在三角形ABC 中,AD,BE,CF 相交于同一点O,有S△AOB∶S△AOC=BD∶CD S△AOB∶S△COB=AE∶CE S△BOC∶S△AOC=BF∶AF 因此图类似燕尾而得名。
公式:DBDA DGB S DGA S CGB S CGA S FCFA FGC S FGA S BGC S BGA S ECEB EGC S EGB S AGC S AGB S :::::::::======∆∆∆∆∆∆∆∆∆∆∆∆例题:如图,在三角形ABC 中,D 是BC 的中点,E 是AC 的三等分点,AE=2EC.三角形ABC 的面积是60平方厘米,那么三角形ABF的面积是多少平方厘米?224246041414121211:2:1:1:cm a ABF S a a a a a ABC S a BFC S BFD S a BFC S a ABF S aAFC S a ABF S EC AE FECS EFA S BFC S ABF S DC BD BFD S ABF S AC E BC D ====+++====⇒==⇒=======∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆∆设:由燕尾模型可得:的三等分点是中点,是。
