断裂力学——3裂纹尖端应力场和位移场计算
合集下载
三维有限单元法计算裂纹应力强度因子的方法一 四分之一点位移法.

两种基于三维有限单元法计算裂纹应力强度因子的方法。
根据线弹性断裂理论,裂纹尖端的位移场可表示为
n u = (式
1.1) z u = (式1.2) 0t u = (式1.3)
式中,n 和t 分别为裂纹前沿的法线方向和切线方向;z 为垂直于裂纹平面方向;μ为材料剪切模量。
1/4点位移法
根据式(式 1.2),若裂纹表面上(θ=180°)某一点的垂直于裂纹平面的位移已知,那么应力强度因子
K = (式1.4)
用从有限单元法求出的1/4点位移
()1/4z u 求应力强度因子的方法即为1/4点位
移法,即
K = (式1.5)
显然这一方法很简单,但要求裂纹尖端附近的应力应变场能较好地被模拟。
图1.1是典型的1/4点位移法的计算网格。
图1.1 典型的1/4点位移法的计算网格。
裂纹张开位移的计算
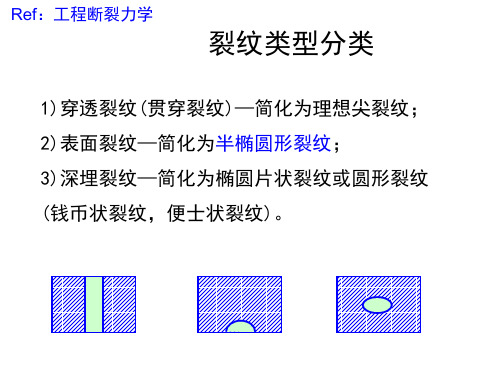
α的统计平均值为 7.644×10-6 K-1。 E的平均值 456GPa, Tm的平均值 2643℃, α·Tm· Tm的平均 值为9541MPa
LSGM结合很好:形成非晶了 熔点1700℃ 线膨胀系数略大于 YSZ
石英玻璃SiO2:CTE:0.5 Tm:1710℃ Tg:1194℃
Al2TiO5:CTE:0.8 Tm:1894℃
0.65
0.74
10-6
0.67
10-2
0.72
10-6
~0.5
103
0.75
10-5
0.67
10-6
0.58
10-1
0.3
108
0.3
107
SiO2
dT/dt(℃/s)
10-3
熔点时的粘度高,易形成玻璃,析晶阻力
结 论
较大, TM 时的璃。
Tg/TM 接近“ 2/3” 时,易形成玻璃,即三分 之二规则。
由Tg与TM作图知,易生成玻璃的组成在直线的上方。
此规则反映形成玻璃所需冷却速率大小。
熔点低的氧化物易于形成玻璃,易形成非晶的物质:键强高、 熔点低的离子共价混合物,如:SiO2、B2O3
B - O 键 能 4 9 8 kj/mol, 比 Si - O 键 能 444kj/mol 大,但因为 B2O3 玻璃的层状或链状 结构的特性,任何 [BO3]附近空间并不完全被 三角体所充填,而不同于[SiO4]。 B2O3玻璃的层之间是分子力,是一种弱键, 所以B2O3玻璃软化温度低(450℃),表面张力小, 化学稳定性差 ( 易在空气中潮解 ) ,热膨胀系数 高。
Tm/℃ E/GPa α/10-6K-1 α·Tm/% α·E·Tm/MPa α·E/(MPa/K) 3225 3067 2950 3245 3445 2982 2747 2648 2177 3036 3613 2204 3037 3985 2188 1810 2140 2517 2365 2776 2450 2760 1900 1900 2250 2050 1894 1867 2677 3300 2550 2827 2300 2700 560 470 590 540 400 510 510 430 460 630 580 480 680 560 540 400 670 540 770 720 441 480 330 210 350 400 13 205 190 240 390 320 175 205 7.8 8.3 9.4 5.9 7.2 7.2 7.6 7.3 9.2 8.0 7.2 10.1 8.2 7.1 10.5 11.7 8.6 7.8 7.8 3.8 4.5 5.3 5.4 2.5 5.7 8.4 0.8 9.0 11 9.3 9.0 13.0 9.1 10-12.4 2.52 2.45 2.77 1.64 2.41 2.14 2.09 1.93 2.00 2.43 2.60 2.23 2.49 2.83 2.30 2.12 1.84 1.96 1.84 1.05 1.10 1.46 1.03 0.48 1.28 1.72 0.15 1.68 2.94 3.07 2.30 3.68 2.645 2.7 14087 11532 16360 10338 9646 10943 10647 8312 9213 15300 15088 10685 16934 15844 12406 8471 12330 10602 14204 7595 4862 7021 3386 997.5 4489 6888 19 3444 5594 7366 8950 11760 4629 5535 4.368 3.901 5.546 3.186 2.880 3.672 3.876 3.139 4.232 5.040 4.176 4.848 5.576 3.976 5.670 4.680 5.762 4.212 6.006 2.736 1.984 2.544 1.782 0.525 1.995 3.360 0.010 1.845 2.090 2.232 3.510 4.160 2.012 2.050
断裂力学复习要点与习题解析

此时 K1 < ;设计可行。
若设计护板材料受拉伸a应力皆为600 是否可行?
4103
4103
2021/1/4
22
例题6:
某构件由高强度钢板焊成,探伤发现在焊缝中
心存在一个20长的中心穿透裂纹。 残余应力测试
发现在裂纹周围存在残余应力场如图。最大残余应
力位于裂纹中心,其值为
,假如裂纹面上
的残余应力为直线型分布,材料的
● 所有的应力强度因子K都可以表示成什么形式?
● 平面应力情况下 与厚度有什么关系
●什么是能量(应变能)释放率G?能量释放率G与应力强度因子K有什么关系?
● S准则是怎样描述的? 与 K1c,K2c,K3c 有什么关系?
2021/1/4
3
S 准则假设为:
S 1、裂纹沿S最小的方向扩展,即由 确定开裂方向: m in
x r 1 0.02 0.6s
Kr0.6s2(a)0.5sin1a x0 a230s(a)0.5
2021/1/4
19
例题3
一高强钢 在380 ºC 回火, 在600 ºC 回火,
,
s 1 8 0 0 M P a,K 1 c ,5 0 M P am
假设这样处理的无限大板存在 单边裂s 纹 ,1 设5 0 计0 工M 作P 应a 力,K 为1 c 6 0 M P am
计算上述两种处理可以容许的临界裂纹尺寸为多少? 解:
,
在600 ºC 回火,
,
假设这样处理的无限大板存在 中心裂纹s1 ,1 设8 计0 0 工M 作P 应a 力,为K 1 c 5 0 M P am
计算那种处理可以满足要求?
s 1 5 0 0 M P a,K 1 c 6 0 M P am
断裂力学第二讲断裂力学理论Fracture Mechanics

(1913), pp.219–230.
5
C. E. Inglis
Sir Charles Edward Inglis (31 July 1875-19 April 1952) was a British civil engineer. Inglis spent much of his life as a lecturer and academic at King's College Cambridge and made several important studies into the effects of vibration and defects on the strength of plate steel. Inglis served in the Royal Engineers during the First World War and invented a lightweight, reusable steel bridge - the precursor and inspiration for the Bailey bridge of the Second World War . His military service was rewarded with an appointment as an Officer of the Order of the British Empire
12
Griffith理论
一、动机 两个矛盾的事实
The stress needed to fracture bulk glass is around 100 MPa.
The theoretical stress needed for breaking atomic bonds is approximately 10,000 MPa
5
C. E. Inglis
Sir Charles Edward Inglis (31 July 1875-19 April 1952) was a British civil engineer. Inglis spent much of his life as a lecturer and academic at King's College Cambridge and made several important studies into the effects of vibration and defects on the strength of plate steel. Inglis served in the Royal Engineers during the First World War and invented a lightweight, reusable steel bridge - the precursor and inspiration for the Bailey bridge of the Second World War . His military service was rewarded with an appointment as an Officer of the Order of the British Empire
12
Griffith理论
一、动机 两个矛盾的事实
The stress needed to fracture bulk glass is around 100 MPa.
The theoretical stress needed for breaking atomic bonds is approximately 10,000 MPa
裂纹板尖端应力场
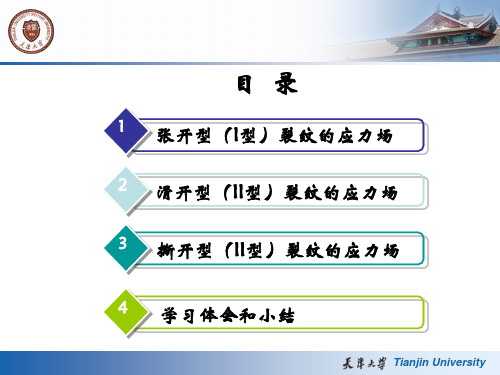
结构的几何参数、边界条件而变化);r<<a。
。
Tianjin University
I型裂纹尖端的应力场
对于I型应力场中的给定点(r,θ) ,其应力场方程
一般式可写成通式:
结论:
ij
KI
(2r)1/ 2
fij ( )
(1) ij1 r ,故当r→0时,ij ,称为应力具有 1 r 的
对无限大板,中心有一长为2a的裂纹尖端位移场:
u KII 4G
r
2
2k
3
sin
2
sin 3
2
KII
4G
r
2
2k
3 cos
2
cos
3
2
w 0(平面应变)
w
E
(
x
y
)dz(平面应力)
KII a
E
(
x
y
)dz(平面应力)
3
其中:k 1
平面应力
3 4 平面应变
Tianjin University
I型裂纹尖端的应力场
2.有限尖端半径的裂纹端部区域的应力场:
x y xy
KI
2
r
cos
2
1
sin
2
sin
3
2
奇异性。只要是I型裂纹问题裂尖区域的应力场都具有 相同的奇异性,它远比其它附加项要大得多。
(2)应力分量由两部分组成:一部分是关于场分布的描 述,它随点的坐标而变化,通过的奇异性及角分布函fij 数 来体现;另一部分是关于场强度的描述,由应力强度因
清华大学断裂力学讲义第三章线弹性断裂力学

在前面的平面问题求解中,需要确定两个解析函数(z)和(z) ,其实在对称和
反对称特例下,可利用Westergaard函数进一步简化为一个解析函数的求解。
以I型问题为例:
F Re zz zdz
12 x1,0=0 x1 , 利用了对称性
2F F,
Imzz z Imzz z 0
x2 0
12
x2
Re
Z
I
2u1 Re z
2u2 Im z
2u1
2
1
Re
ZI dz x2 ImZI Ax1
2u2
1 2
Im
ZI dz x2 ReZI Ax2
当 x2= 0时剪应力为零,这意味着裂纹面是主平面。
例:双轴载荷下含中心裂纹的无穷大板
自由裂纹表面:
i 0 22
u1
x1, 0
1 4
a2 x12
K II
lim
za
i
Z
II
z
2 z a
x1 a
III型裂纹的复变函数表示方法 为了统一
应力场 位移场
32 i 31 ZIII
u3 Im ZIII
III型中心裂纹承受远场均匀剪切
ZIII
z z2 a2
KIII a
u3
x1, 0
x2 0
zz z A A为实常数 x2 0
u v u v x y y x
解析延拓(定义见下页): z A zz
I型裂纹的Westergaard应力函数: ZI z 2z
附:解析延拓数学定理 若 f1 在 R1中解析, f2 在 R2 中解析,且 R1 R2 ,如果
f1 f2 in R1 R2
1
反对称特例下,可利用Westergaard函数进一步简化为一个解析函数的求解。
以I型问题为例:
F Re zz zdz
12 x1,0=0 x1 , 利用了对称性
2F F,
Imzz z Imzz z 0
x2 0
12
x2
Re
Z
I
2u1 Re z
2u2 Im z
2u1
2
1
Re
ZI dz x2 ImZI Ax1
2u2
1 2
Im
ZI dz x2 ReZI Ax2
当 x2= 0时剪应力为零,这意味着裂纹面是主平面。
例:双轴载荷下含中心裂纹的无穷大板
自由裂纹表面:
i 0 22
u1
x1, 0
1 4
a2 x12
K II
lim
za
i
Z
II
z
2 z a
x1 a
III型裂纹的复变函数表示方法 为了统一
应力场 位移场
32 i 31 ZIII
u3 Im ZIII
III型中心裂纹承受远场均匀剪切
ZIII
z z2 a2
KIII a
u3
x1, 0
x2 0
zz z A A为实常数 x2 0
u v u v x y y x
解析延拓(定义见下页): z A zz
I型裂纹的Westergaard应力函数: ZI z 2z
附:解析延拓数学定理 若 f1 在 R1中解析, f2 在 R2 中解析,且 R1 R2 ,如果
f1 f2 in R1 R2
1
断裂力学(2)

2 2 y 2 2 Re Z y Im Z x x
2 2
I xy (ReZ I y Im Z I ) xy xy
证明
满足必要条件:
2
2 0
证明: 先求
2 2 Re Z 2 ( y Im Z )
2 Im Z 2 Im Z Im Z Im Z y y 2 2 y y x y
Im Z y Im Z 2 y
2
2 因为 Z 解析,有 2
最后
2 2 2 2 Re Z 0
(2)几何方程
u x x v y y v u xy x y
1 x ( x y) E 1 y ( y x) E 2(1 ) xy xy E
(4)边界条件 应力边界条件 位移边界条件 混合边界条件
3). 应力函数(Airy function) :
(1)
Z Re Z Re Z x Re Z Re Z Re z z x z x
要求满足:
0
2 2
Re Z y Im Z
应力分量为:
2I 2 x 2 2 Re Z y Im Z y y
z 1, x z i y
Z f ( z)
z x iy
于是有:
Z Z z Z x z x z Z Z z Z i y z y z
Z 解析函数的导数 是唯一的,于是有: z
Z Z i y x
又:
Z f ( z ) Re Z i Im Z
裂纹板尖端应力场

E
( x y )dz (平面应力)
其中:
3 平面应力 k 1 3 4 平面应变
Tianjin University
K II a
III型裂纹尖端的应力场
由于裂纹面是 沿z方向错开,因 此平行于xy平面 的位移u=0, v=0,只有z方向 的位移w≠0,显 然这一问题不属 于平面问题,它 是反平面问题
ij
Tianjin University
I型裂纹尖端的应力场
KI u 4G KI 4G w r 3 2k 1 cos cos 2 2 2
Irwin推导出裂纹顶端附近(r,θ)处的位移为:
r 3 2k 1 sin sin 2 2 2 w 0(平面应变)
Tianjin University
II型裂纹尖端的应力场
对无限大板,中心有一长为2a的裂纹尖端位移场:
K II u 4G K II 4G w r 3 2k 3 sin sin 2 2 2
r 3 2k 3 cos cos 2 2 2 w 0(平面应变)
滑开型 (II型)
轮齿根部 裂纹
撕开型 (III型)
圆轴的环形 切槽裂纹
Tianjin University
I型裂纹尖端的应力场
1. 长为2a的“无限大”板的中心穿透裂纹
无限宽板的 中心裂纹
裂纹顶端附近的 应力场
Tianjin University
I型裂纹尖端的应力场
KI 3 cos 1 sin sin 2 2 2 2 r KI 3 y cos 1 sin sin 2 2 2 2 r KI 3 xy sin cos cos 2 2 2 2 r xz xz 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K I lim Z I 2 a
0
Z ( )
a
2a
K lim 2 Z ( ) a
0
l ( a) Z Ⅲ ( ) ( 2a)
KI lim 2 ZI ( ) l a
z
z 2 a2 a 2
2
z
z
z
0
只有实部且为一常数
z 0 Z II
lim Z ' ( z ) lim
z
z
z
a
2 3/2
x y 0
xy
在裂纹表面
y0
z
z a
2
x a 处
2
满足平板周围的边界条件 虚数
12
K lim 2 Z ( )
0
Ⅱ型裂纹求解
第三步:用 Z ( z) 求II型裂尖附近的应力场和位移场
应力强度因子是在裂尖时 0 存在极限,若考虑裂尖附近 的一个微小区域,则有:
K 2 Z ( )
Z ( ) K 2
若以极坐标表示复变量 则可得到
8
Ⅱ型裂纹求解
得到II型裂纹问题各应力分量表达式为
x 2 ImZ y Re Z ' y y Re Z '
‘ xy Re Z y Im Z
进而可得到位移分量
(1 ) u= 2(1 ) Im Z yReZ E (1 ) (1 2 )ReZ y Im Z v= E
断裂力学第三讲
Shanghai University
断裂力学 Fracture Mechanics
郭战胜 davidzsguo@ 办公地点:延长校区力学所317室 平时答疑:每周一:5-6节 晚修答疑:每周一:18:00-20:30 地点:HE108或HE104b
1
裂纹尖端附近的应力场和位移计算
这就是III型裂纹问题在裂纹 尖端附近的应力场表达式
20
Ⅲ型裂纹求解
Z III K III 2 r
cos i sin 2 2
Z III
1 K III K III 2r 2 d 2 K III cos i sin 2 2 2 2
3 xy cos sin cos 2 2 2 2 r KⅠ
用张量标记可缩写成
KI ij fij 2 r
4
xz yz 0
Ⅰ型裂纹求解
u 1 [(1 ) Re ZⅠ (1 ) y Im ZⅠ] E
1 v [2 Im ZⅠ (1 ) y Re ZⅠ] E
u
平面应力
1 [(1 2 ) Re ZⅠ y Im ZⅠ] E
v
1 [2(1 ) Im ZⅠ y Re ZⅠ] E
平面应变
KⅠ r 3 u [(2k 1) cos cos ] 4G 2 2 2
KⅠ r 3 v [(2k 1)sin sin ] 4G 2 2 2
13
Ⅱ型裂纹求解
把上面两式代入前面应力表达式中,应力和位移场得表达式
3 x sin (2 cos cos ) 2 2 2 2 r KⅡ
3 y cos sin cos 2 2 2 2 r KⅡ
xy
KⅡ
3 cos (1 sin sin ) 2 2 2 2 r
II Re Z II z y Im Z II z y
因为
Im Z z Re Z z Re Z z Re Z z Im Z z Re Z z y y x 2 II 所以 z y Re Z II 2 x 2 II 2 II z z Re Z II z y Im Z II 2 Im Z II z y Re Z II 2 xy y
非零应力分量 边界条件:
w Im Z Ⅲ yz G Re Z Ⅲ y y
y 0, x a, yz 0
z , xz 0, yz
17
Ⅲ型裂纹求解
选取函数 Z ( z ) Ⅲ
l z
z 2 a2
处,
满足边界条件
在裂纹表面
y0 x a
16
Ⅲ型裂纹求解
单元体的平衡方程:
xz yz 0 x y
w w 2 2 w0 2 x y
2 2
位移函数满足Laplace方程,所以为调和函数. 解析函数性质:任意解析函数的实部和虚部都是解析的.
w Im Z Ⅲ 1 w( x, y ) Im Z Ⅲ ( z ) xz G x x Im ZⅢ G
Z ( z )
x
x a
2 2
Re Z ( z) 0
y xy 0
满足裂纹表面处的边界条件
x 2 ImZ y Re Z '
y y Re Z '
‘ xy Re Z y Im Z
11
Ⅱ型裂纹求解
将坐标原点移到右裂尖,采用新坐标
3 4 k 3 1
平面应变 平面应力
w0
平面应变
w
E
( x y )dz
平面应力
5
Ⅰ型裂纹求解
需要注意的是,推导过程中,使用了
0 这个条件,所以
前面得到的应力场和位移场公式只适用于裂纹尖端附近区域,即要 求 ( +a) f ( ) 。对于稍远处,应该用 Z ( ) 所示的 ZI ( 2a)
xz yz 0
z 0
平面应力
z ( x y )
u
平面应变
KⅡ r 3 [(2k 3)sin sin ] 4G 2 2 2
v
KⅡ r 3 [(2k 2) cos cos ] 4G 2 2 2
3 平面应力 k 1 3 4 平面应变
14
Ⅲ型裂纹求解
对于I型和II型裂纹来说,是属于平面问题。但对于III型裂纹, 由于裂纹面是沿z方向错开,因此平行于xy平面的位移为零, 只有z方向的位移不等于零 对于此类反平面问题,前面给出的平面问题的基本方程已不 适用,因此不能沿用Airy应力函数求解,需要从弹性力学的 一般(空间)问题出发,推导公式。弹性力学一般问题的基 本方程,可以仿照平面问题的方法导出
KI lim 2 ZI ( )
0
用解析函数求解III型裂纹尖端 应力强度因子的定义式
Ⅲ型裂纹求解
应力强度因子是在裂尖时 0 存在极限,若考虑裂尖附近 的一个微小区域,则有:
KI 2 ZΙΙI ( )
Z ΙI ( ) K I 2
若以极坐标表示复变量 则可得到
re i r (cos i sin )
K y r sin 2 r sin cos Z ( ) (cos i sin ) 2 2 2 2 2 r 3 K II K II 3 K 3 3 II 2 2 Z II r cos i sin 2 2 2 2 2 2 r
2
3
Ⅰ型裂纹求解
x Re ZⅠ y Im ZⅠ y Re ZⅠ y Im ZⅠ
xy y Re ZⅠ
z 0
(平面应力)
z ( x y ) 2 Re ZⅠ (平面应变)
3 x cos (1 sin sin ) 2 2 2 2 r KⅠ 3 y cos (1 sin sin ) 2 2 2 2 r KⅠ
za a Z ( ) 2a
f ( ) 趋于常数,设: 当 0 ,
f ( )
K lim f ( ) lim Z ( ) 0 0 2 右裂尖附近, 在很小范围内时
用解析函数求解II型裂纹尖端 应力强度因子的定义式
平面应变
9
Ⅱ型裂纹求解
第二步:选II型裂纹的
边界条件:
Z ( z)
y xy 0
z y 0
选取
0 在 y ,
x a
处
xy 在 z 处
Z ( z )
能够满足全部边界条件。
z
z 2 a2
10
Ⅱ型裂纹求解
lim Z ( z ) lim
xz
cos i sin 2 2
re i r (cos i sin )
K III Z III 2 r
K III sin 2 2 r K III yz cos 2 2 r
K III cos 2 2 r K III Im Z III sin 2 2 r Re Z III
0
注意:以上三种类型求解方法,仅适用于含贯穿裂纹的无限大板在 载荷或位移对裂纹中点的坐标轴对称或反对称的情况。
22
值得指出的是,上述三种裂纹问题的应力场表达式,虽然是根 据无限大半具有中心穿透裂纹且在均匀外加应力作用下获得的。 进一步的分析表明,这些解具有普遍的意义,也就是说,对于 其他有限尺寸板的穿透裂纹(包括中心裂纹和边裂纹),在非 均匀受力条件下,裂纹尖端附近的应力场(更确切地说是应力 场的奇异项)表达式也是相同的,其不同之处仅仅是应力强度 因子的不同,因此,对于特定的含裂纹结构只需要确定相应的 应力强度因子就可以了。
