专科离散数学模拟试题
离散数学考试模拟试题及详细参考答案共四套

离散数学考试模拟试题及详细参考答案共四套a 离散模拟答案11命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.一、简答题(共6道题,共32分)1.求命题公式(P→(Q→R))(R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)d eb c图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)二、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→F)→C, B→(A∧S)B→Eb)x(P(x)→Q(x)), x(Q(x)∨R(x)),x R(x) x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠且B≠,关系R满足:<,>∈R,当且仅当< x1, x2>∈R1且∈R2。
离散数学模拟题及答案

一、填空1.不能再分解的命题称为____________,至少包含一个联结词的命题称为____________。
2.一个命题公式A(P, Q, R)为真的所有真值指派是000, 001, 010, 100,则其主析取范式是__________________,其主合取范式是_________________。
3.设A={a,b,c},B={b,c,d,e},C={b,c},则( A ⋃ ⊕=____________。
4.幂集P(P(∅)) =________________。
5.设A为任意集合,请填入适当运算符,使式子A________A=∅;A________A’=∅成立。
6.设A={0,1,2,3,6},R={〈x,y〉|x≠y∧(x,y∈A)∧y≡x(mod 3)},则D(R)=____________,R(R)=____________。
7.称集合S是给定非空集合A的覆盖:若S={S1,S2,…,S n},其中S i⊆A,S i≠Ø,i=1,2,…,n,且______ _____;进一步若_____ _______,则S是集合A的划分。
8.两个重言式的析取是____ ____式,一个重言式和一个永假式的合取式是式。
9.公式┐(P∨Q) ←→(P∧Q)的主析取范式是。
10. 已知Π={{a}{b,c}}是A={a,b,c}的一个划分,由Π决定的A上的一个等价关系是。
二、证明及求解1.求命题公式(P→Q)→(Q∨P)的主析取范式。
2.推理证明题1)⌝P∨Q,⌝Q∨R,R→S⇒P→S。
2) (∀x)(P(x)→Q(y)∧R(x)),(∃x)P(x)⇒Q(y)∧(∃x)(P(x)∧R(x))x)},S={〈x,y〉|x,y∈A∧(x=y+2)}。
3.设A={0,1,2,3},R={〈x,y〉|x,y∈A∧(y=x+1∨y=2试求R S R。
4.证明:R是传递的⇔R*R⊆R。
5.设R是A上的二元关系,S={<a, b>| 存在c∈A,使<a, c>∈R,且<c, b>∈R}。
离散数学试题与参考答案

离散数学试题与参考答案(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《离散数学》试题及答案一、选择题:本题共5小题,每小题3分,共15分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 命题公式Q Q P →∨)(为 ( )(A) 矛盾式 (B) 可满足式 (C) 重言式 (D) 合取范式2.设P 表示“天下大雨”, Q 表示“他在室内运动”,则命题“除非天下大雨,否则他不在室内运动”符号化为( )。
(A). P Q →; (B).P Q ∧; (C).P Q ⌝→⌝; (D).P Q ⌝∨.3.设集合A ={{1,2,3}, {4,5}, {6,7,8}},则下式为真的是( ) (A) 1A (B) {1,2, 3}A (C) {{4,5}}A (D) A4. 设A ={1,2},B ={a ,b ,c },C ={c ,d }, 则A ×(B C )= ( )(A) {<1,c >,<2,c >} (B) {<c ,1>,<2,c >} (C) {<c ,1><c ,2>,} (D) {<1,c >,<c ,2>} 5. 设G 如右图:那么G 不是( ). (A)哈密顿图; (B)完全图;(C)欧拉图; (D) 平面图.二、填空题:本大题共5小题,每小题4分,共20分。
把答案填在对应题号后的横线上。
6. 设集合A ={,{a }},则A 的幂集P (A )=7. 设集合A ={1,2,3,4 }, B ={6,8,12}, A 到B 的关系R =},,2,{B y A x x y y x ∈∈=><, 那么R -1=8. 在“同学,老乡,亲戚,朋友”四个关系中_______是等价关系. 9. 写出一个不含“→”的逻辑联结词的完备集 . 10.设X ={a ,b ,c },R 是X 上的二元关系,其关系矩阵为M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001001101,那么R 的关系图为三、证明题(共30分)11. (10分)已知A 、B 、C 是三个集合,证明A ∩(B ∪C)=(A ∩B)∪(A ∩C) 12. (10分)构造证明:(P (Q S))∧(R ∨P)∧Q R S13.(10分)证明(0,1)与[0,1),[0,1)与[0,1]等势。
《离散数学》考试试卷(试卷库20卷)及答案

《离散数学》考试试卷(试卷库20卷)及答案第 1 页/共 4 页《离散数学》考试试卷(试卷库20卷)试题总分: 100 分考试时限:120 分钟、选择题(每题2分,共20分)1. 设论域为全总个体域,M(x):x 是人,Mortal(x):x 是要死的,则“人总是要死的”谓词公式表示为( )(A ))()(x Mortal x M → (B ))()(x Mortal x M ∧(C )))()((x Mortal x M x →?(D )))()((x Mortal x M x ∧?2. 判断下列命题哪个正确?( )(A )若A∪B=A∪C,则B =C (B ){a,b}={b,a}(C )P(A∩B)≠P(A)∩P (B)(P(S)表示S 的幂集)(D )若A 为非空集,则A ≠A∪A 成立3. 集合},2{N n x x A n∈==对( )运算封闭(A )乘法(B )减法(C )加法(D )y x -4. 设≤><,N 是偏序格,其中N 是自然数集合,“≤”是普通的数间“小于等于”关系,则N b a ∈?,有=∨b a ( )(A )a(B )b(C )min(a ,b)(D ) max(a ,b)5. 有向图D=,则41v v 到长度为2的通路有( )条(A )0 (B )1 (C )2 (D )36. 设无向图G 有18条边且每个顶点的度数都是3,则图G 有( )个顶点(A )10 (B )4 (C )8 (D )127. 下面哪一种图不一定是树?()(A )无回路的连通图(B )有n 个结点n-1条边的连通图(C )每对结点间都有通路的图(D )连通但删去一条边则不连通的图 8. 设P :我将去镇上,Q :我有时间。
命题“我将去镇上,仅当我有时间”符号化为()(A )P →Q (B )Q →P (C )P Q (D )Q P ?∨? 9. 下列代数系统中,其中*是加法运算,()不是群。
离散数学模拟试卷和答案

北京语言大学网络教育学院《离散数学》模拟试卷一注意:1.试卷保密,考生不得将试卷带出考场或撕页,否则成绩作废。
请监考老师负责监督。
2.请各位考生注意考试纪律,考试作弊全部成绩以零分计算。
3.本试卷满分100分,答题时间为90分钟。
4.本试卷分为试题卷和答题卷,所有答案必须答在答题卷上,答在试题卷上不给分。
一、【单项选择题】(本大题共15小题,每小题3分,共45分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在答题卷相应题号处。
1、在由3个元素组成的集合上,可以有 ( ) 种不同的关系。
[A] 3[B] 8[C]9[D]272、设{}{}1,2,3,5,8,1,2,5,7A B A B ==-=,则( )。
[A] 3,8 [B]{}3 [C]{}8 [D]{}3,83、若X 是Y 的子集,则一定有( )。
[A]X 不属于Y [B]X ∈Y [C]X 真包含于 Y [D]X∩Y=X4、下列关系中是等价关系的是( )。
[A]不等关系 [B]空关系 [C]全关系 [D]偏序关系5、对于一个从集合A 到集合B 的映射,下列表述中错误的是( )。
[A]对A 的每个元素都要有象 [B] 对A 的每个元素都只有一个象 [C]对B 的每个元素都有原象 [D] 对B 的元素可以有不止一个原象6、设p:小李努力学习,q:小李取得好成绩,命题“除非小李努力学习,否则他不能取得好成绩”的符号化形式为( )。
[A]p→q [B]q→p [C]┐q→┐p [D]┐p→q7、设A={a,b,c},则A 到A 的双射共有( )。
[A]3个 [B]6个 [C]8个 [D]9个8、一个连通图G具有以下何种条件时,能一笔画出:即从某结点出发,经过图中每边仅一次回到该结点()。
[A] G没有奇数度结点 [B] G有1个奇数度结点[C] G有2个奇数度结点[D] G没有或有2个奇数度结点9、设〈G,*〉是群,且|G|>1,则下列命题不成立的是()。
《离散数学》模拟题02
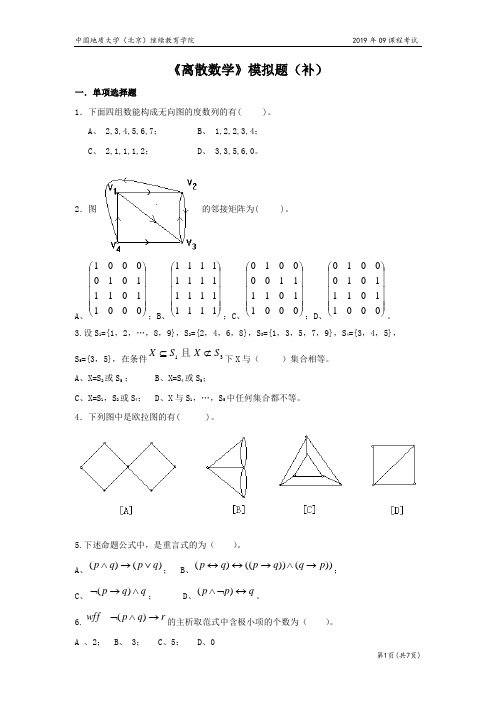
《离散数学》模拟题(补)一.单项选择题1.下面四组数能构成无向图的度数列的有( )。
A、 2,3,4,5,6,7;B、 1,2,2,3,4;C、 2,1,1,1,2;D、 3,3,5,6,0。
2.图的邻接矩阵为( )。
A、;B、;C、;D、。
3.设S1={1,2,…,8,9},S2={2,4,6,8},S3={1,3,5,7,9},S4={3,4,5},S5={3,5},在条件下X与()集合相等。
A、X=S2或S5 ;B、X=S4或S5;C、X=S1,S2或S4;D、X与S1,…,S5中任何集合都不等。
4.下列图中是欧拉图的有( )。
5.下述命题公式中,是重言式的为()。
A、;B、;C、;D、。
6.的主析取范式中含极小项的个数为()。
A 、2; B、 3; C、5; D、0⎪⎪⎪⎪⎪⎭⎫⎝⎛1111111⎪⎪⎪⎪⎪⎭⎫⎝⎛1111111111111111⎪⎪⎪⎪⎪⎭⎫⎝⎛1111111⎪⎪⎪⎪⎪⎭⎫⎝⎛111111131SXSX⊄⊆且)()(qpqp∨→∧))())(()(pqqpqp→∧→↔↔qqp∧→⌝)(qpp↔⌝∧)(rqpwff→∧⌝)(7.给定推理① P ② US ① ③ P ④ ES ③ ⑤ T ②④I ⑥ UG ⑤推理过程中错在( )。
A 、①->②;B 、②->③;C 、③->④;D 、④->⑤8.设S 1={1,2,…,8,9},S 2={2,4,6,8},S 3={1,3,5,7,9},S 4={3,4,5}, S 5={3,5},在条件下X 与( )集合相等。
A 、X=S 2或S 5 ;B 、X=S 4或S 5;C 、X=S 1,S 2或S 4;D 、X 与S 1,…,S 5中任何集合都不等。
9.设R 和S 是P 上的关系,P 是所有人的集合,,则表示关系 ( )。
A 、;B 、;C 、 ;D 、。
10.下面函数( )是单射而非满射。
A 、; B 、;C 、;D 、。
离散数学考试题及答案

离散数学考试题及答案一、选择题(每题5分,共20分)1. 下列哪个选项不是离散数学的研究对象?A. 图论B. 组合数学C. 微积分D. 逻辑学答案:C2. 在逻辑学中,下列哪个命题是真命题?A. 如果今天是周一,那么明天是周二。
B. 如果今天是周一,那么明天是周三。
C. 如果今天是周一,那么明天是周四。
D. 如果今天是周一,那么明天是周五。
答案:A3. 在集合论中,下列哪个符号表示集合的并集?A. ∩B. ∪C. ⊆D. ⊂答案:B4. 在图论中,下列哪个术语描述的是图中的顶点集合?A. 边B. 路径C. 子图D. 顶点答案:D二、填空题(每题5分,共20分)1. 如果一个集合A包含5个元素,那么它的子集个数是______。
答案:322. 在逻辑学中,如果命题P和命题Q都是真命题,那么复合命题“P且Q”的真值是______。
答案:真3. 在图论中,如果一个图的顶点数为n,那么它的最大边数是______。
答案:n(n-1)/24. 如果一个二叉树的深度为3,那么它最多包含______个节点。
答案:7三、简答题(每题10分,共30分)1. 请简述什么是图的连通性,并给出一个例子。
答案:图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如,在一个完全图K3中,任意两个顶点之间都可以通过一条边直接连接,因此它是连通的。
2. 解释什么是逻辑蕴含,并给出一个例子。
答案:逻辑蕴含是指如果一个命题P为真,则另一个命题Q也必须为真。
例如,命题P:“如果今天是周一”,命题Q:“明天是周二”。
如果今天是周一,那么根据逻辑蕴含,明天必须是周二。
3. 请描述什么是二叉搜索树,并给出它的一个性质。
答案:二叉搜索树是一种特殊的二叉树,其中每个节点的左子树只包含小于当前节点的数,右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题(每题15分,共30分)1. 给定一个集合A={1, 2, 3, 4, 5},请计算它的幂集,并列出所有元素。
网络学院《离散数学》模拟-答案

网络学院离散数学模拟试题1 考试时间120 分钟考试方式:开卷专业年级姓名学号一、选择填空题(每个空格3分,共30分)1.设A,B是集合,且φA,则_____必定成立。
D-B=A.A=B B.B⊆A C.A∩B=φD.A⊆B 2.{φ,{φ}}-φ=_____;CA. φ B. {φ} C. {φ,{φ}} D. {{φ}}3.设集合A={{0}},则P(A) =_____。
DA. P(P({0}))B. P({0})∪φC. P({0})∪{{0}}D. {φ,{{0}}}4.设有集合A={1,2,3,4},则从A到{0,1}的不同的函数有____个。
EA.0 B.1 C.4 D.12 E. 16 F. 24 G. 32 5.设G=(a)为12阶循环群,则G没有____阶子群。
EA.1 B.2 C.3 D.4 E. 5 F. 66.凡_____都满足消去律。
DA. 代数系统B. 半群C. 独异点D. 群7.从无向完全图K中至少删除____条边后,所得的图将成为平面图。
B5A.0 B.1 C.2 D.38.若无向图G是有99个结点,9个连通分量,则G中的边数必_____。
C A. ≤90 B. =90 C. ≥90 D. =100 E. ≥1009.下列句子中为命题的是_____。
AA.今天不是星期六。
B.考场内禁用手机!C.今天是周末吗?D.今天真冷呀!10. 任意两个不同极大项的析取式必为______。
AA. 永真公式B. 可满足公式C. 永假公式D. 等值公式二、求出谓词公式(,)(,,)u v F u v w G u v w ∃∃→∀的前束范式。
(10分)解:(,)(,,)u v F u v w G u v w ∃∃→∀ ⇔1111(,)(,,)u u F u v w G u v w ∃∃→∀ ⇔111(,)(,,)u v F u v w G u v w ⌝∃∃∨∀ ⇔1111(,)(,,)u y F u v w G u v w ∀∀⌝∨∀⇔1111(,)(,,)u v wF u vG u v w ∀∀∀⌝∨()三、用形式证明的方法证明下列论证的有效性:“本班有些同学是有经验的C++程序员,任何C++程序员都知道对象的概念。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专科《离散数学模拟》试题(一)
姓名______________ 学号______________ 成绩______________
一、填空(每小题5分,共25分)
1.设}41,,3|{≤≤∈==K N k k x x A ,则用列举法表示A =_____________________.
2.设}2,{φ=A ,则A 的幂集=A 2________________________.
3.设)}1,2(),2,4(),3,1{(=ρ是A 到B 的关系,则ρ的逆关系=ρ
~_______________.
4.下图G 的邻接矩阵
A =__________________________ 5.设}},3,2{,3,2{φ=A ,则=-}}3,2{{A
二、选择题(将正确答案的编号填入相应题目后面的括号中,每小题5分,共20分)
1.设集合}3,2,1{=A ,A 上的关系)}1,1(),1,2(),1,3(),3,2{(=ρ,则ρ是( ).
A .自反的
B .反对称的
C .可传递的
2.设有函数Z Z Z f →⨯:(Z 表示非负整数集),定义为y x y x f +=),(,则f 是( ).
A .满射
B .内射
C .双射
3.设}4,3,2,1{=A ,则A 的分划有( ).
A .}}3{},4,2{),1{(
B .}}4{},3,2{{
C .}}4{},3,2,1{{
4.设简单图G 所有结点的度之和为12,则G 一定有( ).
A .3条边
B .4条边
C .6条边
4
v 3v 2
v 1v
三、问答题(每小题6分,共42分)
1.下图G 是否二部图?若是,找出它的互补结点子集. 2.设有命题公式)(Q P P F →⌝∨=,问F
3.判断下图是否欧拉图,若是,找出一个欧拉回路. 4.设1ρ和2ρ是集合A 上的偏序关系,问1ρ-
5.判断下述命题公式的等值关系是否成立 P Q P Q P Q ∨⌝⇔→∧→)((
6.将下一命题符号化.分析到个体词、谓词和量词,使用全总个体域.
“有些大学生不钦佩任何运动员”
v 2v 1v 5
3v 5v
7.设有函数R R f →:和R R g →:(R 表示实数集),其中,14)(+=x x f 32)(2-=x x g .试求?)2(=gf
四、证明题(共13分)
1.设简单无向图G 有n 个结点,n+1条边,证明G 中至少有一上结点的度≥3. (7分)
2.用“形式证明”的方法证明
)(S R P →→、Q 、S R P Q →⇒∨⌝ (6分)
专科《离散数学模拟》试题(二)
姓名______________ 学号______________ 成绩______________
一、填空(每小题5分,共25分)
1.设a a A ,{=是小于15的正奇数},则A 的元素是________________________.
2.设}7,6,2,1{},7,5,3,1{},7,6,5,4,3,2,1{===B A V 则='-A B __________________.
3.设}},2{,1{φ=A ,则A 的幂集有元素_____________个.
4.设},,,{d c b a A =,A 上的关系)},(),,(),,(),,{(c d d b b a a a =ρ,则=2ρ_________.
5.设有函数B A f →:和函数A b g →:,且f g ⋅是A 上的恒等函数,则f 是____射,g 是______射.
二、选择题(将正确答案的编号填入相应题目后面的括号中)(每小题5分,共20分)
1.设有函数R R g R R f →→:,:(R 表示实数集),且2
)(,12)(x x g x x f =+=,则复合数函数f g ⋅是( )
A .满射
B .内射
C .双射
2.图G1是( )
A .欧拉图
B .哈米尔顿图
C .二部图
D .树 3.定义正整数集N 上的关系为:当且仅当“y x ≤
).
4v 3v 2v 1
v
A .自反的
B .对称的
C .反对称的
D .可传递的
4.设T 是一棵具有n 个结点m 条边)2(≥n 的树,则T ( ).
A .连通
B .包含有环
C .1-=n m
D .至少有两个度为1的结点.
三、问答题( )
1.以下图G2是否平面图,若是平面图,将图重画,使其边没有交叉.
2.以下两个谓词公式等值关系成立吗?
()())()((x xB x xA x B x A x ∀∨∀⇔∨∀ 3.设P 、Q 是命题变元,以下两命题公式等值关系成立吗?
Q P Q P Q ⌝⇔→∧→))(( 4v 3
v 2v 1v
4.设}2,1{=A ,在A 上可以定义多少个不同的偏序关系?
5.将下一命题符号化,分析到个体词,谓词和量词,使用全总个体域
“在北京工作的人未必都是北京人”
6.图),(3E V G =如下所示,试问G 有多少个分图?
v 8
7.设用G 是由5棵树构成的一个树林,G 有20个结点,问G 有多少条边?
四、证明题(共13分)
1.设ρ是集合A 上的等价关系,试证明ρρ
ρ=⋅~(7分) 2.设T 是一棵完全二元树,0n 表示树叶结点数,试证明边数)1(20-=n m (6分)
专科《离散数学模拟》试题(三)
姓名______________ 学号______________ 成绩______________
一、填空(每小题5分,共25分)
1.设A 和B 是两个有限集,若#A <#B ,则存在由A 到B 的______射.若#A >#B ,则存在由A 到B 的______射.
2.设G 是具有n 个结点,m 条边的连通图,则G 的生成树T 有_____个结点,____条边.
3.设有函数A A f →:,且A I f =2,则可以判定f 是_____射.
4.设T 是一棵完全二元树,有15个结点,其中8个树叶结点,则T 分枝结点数是______________,T 的所有结点度数之和是________________.
5.设}3,2,1,0{=A ,}7,6,4{=B ,}14,12,9,8{=C ,1ρ是由A 到B 的关系,2ρ是由B 到C 原关系,分别定义为)}14,7(),12,6(),12,4(),8,4{(1=ρ,则复合关系=⋅21ρρ________________________________________________.
二、选择题(将正确答案的编号填入相应题目后面的括号中)(每小题5分,共20分)
1.设有函数R R f →:,(R 表示实数集),x x f 2)(=,则f 是( ).
A .满射
B .内射
C .双射
2.设命题公式)(),(P Q P H Q P G ⌝→→=→⌝=,则G 与H 的关系是( ).
A .H G ⇒
B .G H ⇒
C .H G ⇔
3.设G 是具有n 个结点m 条边,K 个面的连通平面图,其中2≥m ,则有( )成立.
A .2=+-k m n
B .63-≤n m
C .1-=n m
D .42-=n m
4.设B A ,是两个集合,当( )时,有B B A = .
A .
B A =
B .B A ⊆
C .A B ⊆
D .φ=-B A 三、问答题
1.设}7,6,5,4{},4,3,2,1{==B A ,ρ是由A 到B 的关系,定义为)}7,2(),6,3(),5,4(),4,2{(=ρ,则ρ的定义域=?ρ的值域=?
2.设ρ是集合}6,5,4,3,2,1{=A 上的关系
)}6,6(),3,6(),1,6(),5,5(),2,5(),4,4(),6,3(),3,3(),1,3(),5,2(),2,2(),6,1(),3,1(),1,1{(=ρ
(1)画出ρ的关系图.
(2)ρ是否等价关系?若是,请写出ρ的所有等价类.
3.一个班有50个人,在第一次考试中有26人得优秀,在第二次考试中有21人得优秀,如果两次考试都得优秀的有14人,问两次考试都没有得优秀的有多少人?
4.一棵(无向)树有6个度为2的结点,4个度为3的结点,2个度为4的结点,其余是度为1的结点,问该树有几个度为1的结点.
5.设},{},,{c b B b a A ==,试求集合B A 22 .
6.将下一命题符号化,分析到个体词,谓词和量词,使用全总个体域
“所有的火车比所有的汽车跑得快”
7
四、证明题(共13分)
分)
1.如果小王是理科学生,则他的数学成绩很好.
是文科学生.
2.证明:
P
x
Q
x
x⇒
⌝
∀
x
-
∀
>
(x
(
)
(
)
)),
(
x
P
(
Q
)
(注:a是个体常元)(6分)。
