集美大学信号与系统2007级试卷A及评分

合集下载

-(1)信号与系统A卷答案(8K)

装订线2011—2012学年第一学期闽江学院考试试卷（参考答案与评分标准）考试课程：信号与系统试卷类别：A 卷☑ B 卷□ 考试形式：闭卷☑ 开卷□ 适用专业年级： 09电子信息工程（1）（2），09电子信息科学与技术，09电子科学与技术班级姓名学号一、选择题 12%，每题2分1、（ B ）已知f(t)的波形如下图。

问1(1)2f t -+在1t =时刻的取值为：A ．1B ．2C ．0D ．1/22、（ A ）以下描述系统的时域微分方程中，代表的系统为稳定系统的是： A ．''()'()2()2'()6()y t y t y t f t f t ++=+B ．''()'()2()2'()()y t y t y t f t f t --=+C ．''()3'()2()2'()6()y t y t y t f t f t -+=-D ．''()'()2()3()y t y t y t f t -+= 3、（ C ）已知信号()2cos()4k f k π=，经过由两个子系统1()()k h k a k ε=，2()()(1)h k k a k δδ=--级联组成的系统后，输出为：A ．()ka k εB ．()k δC ．2cos(4k π D ．1()(1)k k a k a k εε---4、（ D ）就连续性，周期性和关于纵轴的对称性而言，连续周期信号的幅度谱的特点是：A ．连续的，周期的，对称的B ．离散的，周期的，非对称的C ．连续的，非周期的，对称的D ．离散的，非周期的，对称的5、（ A ）序列和(1)k k δ∞=-∞-∑等于：A ．1B ．∞C ．(1)k ε-D ．(1)k k ε- 6、（ C ）若周期矩形脉冲信号的周期为2s ，幅度为1V ，则该信号的谱线间隔为：A ．1HzB ．2HzC ．0.5HzD ．4Hz二、填空题 20%，每题2分1、序列3()cos()cos()4436f k k k ππππ=+++的周期是 24 。

《信号与系统》期末试卷A卷与答案.pptx

2、（8 分）
0
y(t)
1 t2 2
Tt
1 T2
1
2 t Tt
2
3T2
2
2
0
t 0 0t T
T t 2T 2T t 3T 3T t
3、（3×4 分＝12 分）
j dX ( j / 2)
（1）
tx(2t) 2
d
(1t)x(1t) x(1t) tx(1t)
（2） X ( j)e j j d [X ( j)e j] jX ' ( j)e j d
（3）
t
dx(t) dt
X ( j)
dX ( j) d
第页 4共 6 页
学海无涯
4、（5 分）解 :
s2
1 2s 2
s2 2s 2
s2 2s 2
F (s) es 2(s 1) es (s 1)2 1
f (t) (t 1) 2e(t 1) cos(t 1)u(t 1)
学海无涯
《信号与系统》期末试卷 A 卷
班级：
学号：
姓名：
_ 成绩：
一．选择题（共 10 题，20 分）
j( 2 )n
j( 4 )n
1、 x[n] e 3 e 3 ，该序列是
A.非周期序列 B.周期 N 3
D。
C.周期 N 3/ 8
CDCC
D. 周期 N 24
2、一连续时间系统y(t)= x(sint)，该系统是
3
3
(b)若系统因果，则Re{s} 2，h(t) 1 e2tu(t)－1 et u(t) 4分
3
3
(c)若系统非稳定非因果，则Re{s} －1，h(t) 1 e2t u(t) 1 et u(t) 4分

信号与系统试题2007A、B卷答案

………………………………装………………………………订…………………………………线………………………………
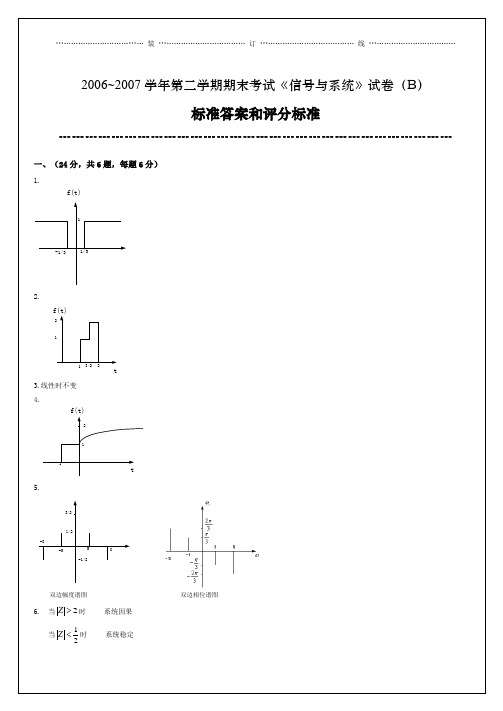
2006~2007学年第二学期期末考试《信号与系统》试卷（B）
标准答案和评分标准
﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉
一、（24分，共6题，每题6分）ຫໍສະໝຸດ 1.2.3.线性时不变
4.
（3分）
（3分）
九、（10分）
根据其S域电路图可得
（5分）
（5分）
标准答案和评分标准制定人：______________________________年月日
任课教师：______________________________________________年月日
系（教研室）主任：______________________________________年月日
………………………………装………………………………订…………………………………线………………………………
2006~2007学年第二学期期末考试《信号与系统》试卷（A）
标准答案和评分标准
﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉﹉
一、（24分，共6题，每题6分）
1.
2.
3.线性时不变
4.
5.
双边幅度谱图双边相位谱图
6.当时系统因果
当时系统稳定
二、（9分）
三、（9分）
1)（3分）
2)（3分）
3)（3分）
四、（10分）
解：对方程进行单边拉氏变换：
五、（共10分）
（8分）
y(t)的最小采样频率为2*1002=2004(rad/s)（2分）
六、（9分）
七、（9分）

信号与系统试题库及答案

信号与系统试题库及答案，共22页1.下列信号的分类方法不正确的是（ A ）：A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、因果信号与反因果信号2.下列说法正确的是（ D ）：A 、两个周期信号x(t)，y(t)的和x(t)+y(t)一定是周期信号。

B 、两个周期信号x(t)，y(t)的周期分别为2和，则其和信号x(t)+y(t) 是周期信号。

C 、两个周期信号x(t)，y(t)的周期分别为2和，其和信号x(t)+y(t)是周期信号。

D 、两个周期信号x(t)，y(t)的周期分别为2和3，其和信号x(t)+y(t)是周期信号。

3.下列说法不正确的是（ D ）。

A 、一般周期信号为功率信号。

B 、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t)是功率信号；D 、et 为能量信号;一、填空（每空1分，共15分）1、离散信号基本运算有；；；四种。

2、拉氏变换中初值定理、终值定理分别表示为)(lim )0(S SF f S ∞→=，； )(l i m )(0S SF f S →=∞ 。

3、连续系统的分析方法有时域分析法；频域分析法和复频域分析法。

这三种分析方法，其输入与输出表达式分别是 y(t)=h(t)*f(t); Y(jω)= H(jω)·. F(jω); Y(s)= H(s)·. F(s)集美大学2008—2009学年第2学期信号与系统试卷及答案一、判断题(共9分，每题1.5分，对的打“V ”，错的打“X ”)。

1、一个信号的脉冲持续时间越小，它的频带宽度也就越小。

（ × ）2、一个信号的脉冲幅度数值越大，它的频谱幅度也就越大。

（ V ）3、一个能量有限的连续时间信号，它一定是属于瞬态信号。

（ V ）4、一个功率有限的连续时间信号，它一定是属于周期信号。

（ × ）5、一个因果稳定的连续时间系统，它的零极点必然都位于S 左半平面。

信号与系统2006试卷A参考答案

栏姓名
息
班级
订
信
生
专业
考
学院装
P5
P6
G (ω)
A
A/2
A/2
−3ωm −ω m ωm 3ωm
ω
(4分,没标注扣2分)
信息工程
学号线
栏姓名
得
五、限选题（每题 10 分）
分
1、给定系统流图如图所示，列写状态方程与输出方程。指出 A B C D 。
e1(t)
8
1/s
4 7 7 -3
3 r(t) [通信、电子专业必做]
课程名称
适用学院、专业、
年级
备注
集美大学试卷纸
2007—2008 学年第 2 学期
信号与系统
试卷 A
卷别
信息工程学院 2006 级通信工程、电子信息工程、自动化
考试闭卷 ■ 方式开卷 □
参考答案及评分标准
5、已知系统函数
H (s)
=
(s
1 + 1)(s
+
2)
，起始条件为： y(0− )
= 1,
∴系统完全可控、完全可观的条件是a ≠ −1且b ≠ 0。
息
班级
订
信
生
专业
考
学院装
信息工程
P7
P8
f
(t)
=
3cos t
+
sin
⎛ ⎜⎝
5t
+
π 6
⎞ ⎟⎠
+
2
cos
⎛ ⎜⎝
8t
+
π 3
⎞ ⎟⎠
1.画出单边幅度频谱和相位谱； 2.画出双边幅度谱和相位谱。

信号与系统试卷及参考答案

试卷及答案信号与系统试卷〔1〕〔总分值：100分，所有答案一律写在答题纸上〕考试班级学号成绩考试日期：年月日，阅卷教师：考试时间120分钟，试卷题共2页一一线性非时变离散系统，具有一初始状态x(0)，当鼓励为时f(k)，响应为y(k)=((1/2)k+1)u(k)；假设初始状态不变，当鼓励为-f(k)时，响应y(k)=((-1/2)k-1)u(k)为；试求当初始状态2x(0)为，鼓励为4f(k)时，系统的响应？〔10分〕二绘出以下函数的图形〔1〕.一连续时间信号x(t)如下图，试概略画出信号y(t)=x(2-t/3)的波形图。

〔8分〕t(2). 试概略画出信号y(t)=u(t 2-4) 的波形图。

〔8分〕三计算以下函数(1). y(t)=⎰-44(t 2+3t+2)(δ(t)+2δ(t-2))dt 〔4分〕 (2). f(t)=e -2t u(t), h(t)= e -2t u(t), y(t)=f(t)*h (t) 〔8分〕(3). f(k)=1, k=0,1,2,3, h(k)=1, k=0,1,2,3, y(k)=f(k)*h (k) 〔8分〕〔4〕 f(t)=e -2t u(t), 求y(t)=[t f(2t)] 的富立叶变换〔8分〕〔5〕y’(t)+2y(t)=δ(t)+u(t), y(0)=0, 试求y(t)=? 〔8分〕〔6〕. y(k)-y(k-1)-2y(k-2)=u(k)+2u(k-2), y(-1)= 2,y(-2)= -1/2, 试求零输入响应y x (k)=? 零状态响应y f (k)=? 〔8分〕四一线性非时变因果系统，当鼓励为u(t)时，响应为)]2()([cos )(cos )(ππ---+=-t u t u t t tu e t g t ，求当鼓励f(t)=δ(t)时的响应)(t h 。

〔10分〕五某一子系统，当输入f(t)=e -t u(t)时，零状态响应y f (t) = (1/2 e -t - e -2t +1/2e -3t )u(t), 试求将两个这样的子系统串联时，总系统的冲激响应。

2007信号与系统A卷

命题人：胡异丁试卷分类（A 卷或B 卷） A五邑大学试卷学期： 2006 至 2007 学年度第 2 学期课程：信号与系统专业：班级：姓名：学号：（6分）已知信号()t f 的波形如图1所示，试画出()63+-t f 的波形。

图1（4分）求积分 dt e t t242)3(-⎰-δ求图2所示函数)(1t f 和)(2t f 的卷积积分)(*)()(21t f t f t f ，并画出)(t f 的波形。

图2求下列微分方程所描述系统的零输入响应、零状态响应和完全响应。

)(2)(')(4)('5)(''t x t x t y t y t y +=++，)()(t u t x =，2)0(=-y ，4)0('=-y（共16分）（1）求信号)(cos )(00t t t f -=ω的傅里叶变换，0ω为常数。

（5分）（2）求如图3所示信号的傅里叶变换。

（6分）图3（3）已知)()(ωF t f ↔，试用)(ωF 表示信号)63(-t f 的频谱。

（5分）（共16分）（1）求信号t et f t5cos )(4-=的单边拉普拉斯变换。

（5分）（2）求函数10732++s s 的拉普拉斯反变换。

（5分）（3）求函数s e s s s -+++84832的拉普拉斯反变换。

（6分）利用Mason 公式求图4所示系统的系统函数。

图4（10分）已知某反馈系统如图5所示，求该系统的系统函数)()()(12s V s V s H ，并判断K 满足什么条件时，系统是稳定的。

图5已知某系统的信号流图如图6所示，请列写该系统的状态方程和输出方程，并写成标准矩阵形式。

图6（8分）已知某系统的状态方程为()()⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎦⎤⎢⎢⎣⎡)()(0110)()(1012212121t x t x t t t t λλλλ 其中，⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-)()()()(21t u e t t x t x t δ，且⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--00)0()0(21λλ，试求解该状态方程。

集美大学信号与系统2007级试卷A及评分

态为 r (0− ) = 2,
班级
jImZ
Z－plane
H ( z) =
生
1 −2 1 z − 1.6 = (1 + ) ( z + 0.4) ( z + 0.7) z + 0.4 ( z + 0.7)
d （2）系统的零输入响应 rzi (t ) ；（3）系统的 r (0− ) = −4 ；求（1）系统的特征根； dt
9、当对某信号 f(t)进行左移成 f(t＋3)后，其幅度频谱（不变），相位频谱附加（3ω
− jωt0
3、一个能量有限的连续时间信号，它一定是属于瞬态信号。有限时长 4、一个功率有限的连续时间信号，它一定是属于周期信号。直流不是
（ V ）（ × ））。
学院
5、一个因果稳定的连续时间系统，它的零极点必然都位于 S 左半平面。非最小相位（ × ） 6、一个因果稳定的离散时间系统，它的每个极点的模必然都小于 1。单位圆内（ V ）
息
姓名
2、已知某离散时间系统的系统函数 H ( z ) = 型仿真方框图。
订
z − 1.6 ，画出（1）零极点图； 2）级联（ 2 z + 1.1z + 0.28
分
d2 d r (t ) + 30r (t ) = 3e(t ) ，若系统输入信号 e(t ) = u (t ), 和起始状 1、给定系统微分方程 2 r (t ) + 11 dt dt
E －2 -2-T -T -T+2 O f(t) 2 T-2 T T+2 t E
分
四、综合题（共 16 分，每小题 8 分）综合题
1、先绘制y(t)的波形，再利用频域卷积定理求如图所示的乘法系统的输出信号频谱Y(jω)。

A2007级试卷及答案

②随着 ω 的增大，由 0 变到 π ， B1 B2 越来越小， A1 A2 越来越大，则 H ( jω ) 越来越小； ③当 ω = π 时， A1 = 0.4, A2 = 1.4, B1 = 0, B2 = 1 ，则 H ( e jπ ) =
B1 B2 =0； A1 A2
④随着 ω 的继续增大，由 π 变到 2 π ， B1 B2 越来越大， A1 A2 越来越小，则 H ( jω ) 越来越大； ⑤当 ω = 2π 时， A1 = 1.6, A2 = 0.6, B1 = 2, B2 = 1 ，则 H ( e j 2π ) = 系统的幅频响应曲线如图所示。
r(t)=0
t +1/ 2
（3 分）
r(t)=
∫
0
1 1 1 τ dτ = (t + )2 2 4 2 1 3 3 τ dτ = t 2 − 2 4 16 1
2
t +1/ 2
(3) 1<t<3/2
r(t)=
t −1 2
∫
(4) 3/2<t<3 (5) 3<t
r(t)=
t −1
∫ 2 τ dτ = 4 (3 + 2t − t
1 3 F ( z) − 2 = + 2 z z −1 z − 3 1 3 − z z 2 + 2 （4分） F ( z) = z −1 z − 3
（1） z > 3
3 k 1 f ( k ) = − ε ( k ) + ⋅ ( 3) ε ( k ) 2 2
k
（Hale Waihona Puke 分）（2） z < 1
（1 分）（1 分）
（1 分）

集美大学信息工程学院微机与接口答案2008A

(3) WR =0, IO/ M =1
(4) WR =0, IO/ M =0
第 1 页共 7页
3.某计算机的字长是 16 位，它的存储器容量是 64KB，若按字编址那么它的最大
寻址范围是( 2 )。
(1)64K 字
(2)32K 字
(3)64KB
(4)32KB
4.某一 SRAM 芯片的容量是 512×8 位，除电源和接地线外，该芯片的其他引脚最
=（3.75+5）/（5+5）×256 =224 =0E0H
六、综合应用题(每小题 10 分，共 20 分)
得分评阅人 1.如图所示采用 8255A 作为打印机接口。PA 口作为向打印机输出的数据口，工作于方式 0，采用程序查询的控制方式。由 PC0 产生负脉冲选通信号，PC7 读取外没状态 BUSY，8255A 的端口地址为 90H～93H。写出从内存 2000H：3000H 开始取出 100 个数据送打印机的控制程序。
为低电平,则在 T3 与 T4 状态之间插入等待状态 TW。
2.在 8253 的方式控制字中,有一项计数锁存操作,其作用是暂停计数器的计数。（ × ）应改为：锁存计数器的当前值到锁存器，但不影响对计数器的计数工作。
3.8250 的溢出错误指示 CPU 还未取走前一个数据,接收移位寄存器又将接收到的一个新数据送至输入缓冲器。（ √ ）
4.在 8088 系统（最小组态）中,执行指令”MOV [2000H],AX”需 1 个总线周期。（ × ）应改为：需 2 个总线周期
5. DMA 控制器 8237A 现行字节数寄存器的值减到 0 时,终止计数。（ × ）应改为：DMA 控制器 8237A 现行字节数寄存器的值减到 0，再由 0 减到 0FFFFH

测控2007级《信号与系统》试题解答（A）

测控2007级《信号与系统》试题解答（A）测控2007级《信号与系统》试题解答一、选择题（每小题4分，共20分）1. 积分2'()()t e t t dt δδ∞--∞+等于(A) 1 ； (B) 2 ； (C) 3 ； (D) 4解：()'2'2'2200()()()()|213t t t t t e t t dt e t dt e t dt e e δδδδ∞∞∞----=-∞-∞-∞+=+=-+=+=??所以正确答案为（C ）。

2. 卷积()()222t u t u t *+--等于(A) 0 ； (B) 2 ； (C) 4 ； (D) 8解：()()()()2222222220t u t u t u u d d ττττττ∞-∞-*+--=+--==所以正确答案为（A ）。

3. 序列和[]sin 24n n n πδ∞=-∞-∑等于 (A) 1 ；(B) ∞ ； (C)[]2k δ- ； (D) []2u k -解：[]2sin 2sin 144n n n ππδ∞=-∞-==∑ 所以正确答案为（A ）。

4.卷积和等于(A)(B)； (C)(D) 1解：[][][]{}[][]23231u k k k u k u k δδ*---=---= 所以正确答案为（D ）。

5. 下列等式不成立的是(A) ()()()()0f t t f t δδ=； (B) ()()()()''0f t t f t δδ=；(C) ()()()f t t f t δ*=； (D) ()()()''f t t ft δ*=解：()()()()()()()()''''000f t t f t f t f t δδδδ=-+≠所以正确答案为（B ）。

二、（6分）试判断下列信号是否为周期信号。

若是，确定其基波周期。

① 2()sin ()6f t t π=-；② []2cos()sin()2cos()4826f k k k k ππππ=+-+ 解：① 21()sin ()1cos(2)623f t t t ππ??=-=--是周期信号。

信号与系统期末A卷答案及评分标准-12自动化

考试考查：考试
）补考（）重修（）
S 域的右半平面映射到 Z 域的单位圆内。（ × ）离散信号的频谱一定是连续的。（ × ）当系统是线性时不变时，其零状态响应是输入和冲激响应的卷积。（ √ ）卷积只适用于线性系统。（ √ ）当信号在�� < 0时，��(��) = 0，则该信号为因果信号。（ √ ）
时频变换
��(��) = ∫ ��(��)��
−∞
−��
�� ； ��(��) = ∫ ��(��)��
0−
解： ��(s) =
2 �� −4�� ⟷ ��(��) = 2�� −3(��−4) ��(�� − 4) �� + 3
∞
时延频谱搬移微分特性卷积微积分特性
��(�� ± ��0 ) ⟷ ��(��)�� ±��0 ； ��(�� ± ��0 ) ⟷ ��(��)�� ±��0 ； ��(�� − ��) ⟷ �� −�� (��) ��(��)�� ±��0 �� ⟷ ��(�� ∓ ��0 )； ��(��)�� ±��0 �� ⟷ ��(�� ∓ ��0 )； 1 ��(��)��(�� ) ⟷ [��(�� + �� ) + ��(�� − �� )] 2 (��) (��) �� ⟷ (��) ��(��)； �� (��) (��) ⟷ �� (��) �� ′ (��) = ��1′ (��) ∗ ��2 (��) = ��1 (��) ∗ ��2′ (��) �� (−1) (��) = �� 1

信号与系统期末A卷答案及评分标准-11电气

�� −1 �� 解： ��(��) = = �� −2 ⟷ ��(��) = 2��−2 ��(�� − 2) �� − 2 �� − 2
解： ��(��) = ∑ ��(��)��
��(��)�� ±��0�� ⟷ ��(�� ∓ ��0 )；
��(�� ± ��0 ) ⟷ ��(��)�� ±��0
�� 2. 计算积分式 ∫ (1 − ��)�� (�� − ) �� 的值。 2 0 �� 解： ∫ (1 − ��)�� (�� − ) �� = ∫ (1 − �� ) �� (�� − ) �� = ∫ �� (�� − ) �� = 1 2 2 2 2 0 0 0
(−1)
(��) =
(−1) (��) ∗ ��2 (��) �� 1
= ��1 (��) ∗
(−1) ��2 (��)
��(��) ∗ δ(�� − ��0 ) = ��(�� − ��0 ) ��(��)δ(�� − ��0 ) = ��(��0)δ(�� − ��0 ) �� ′ (��) = δ(��)

《信号和系统》试题(卷)与答案解析

i go2012年度教学质量综合评估测验卷《信号与系统》试题注：1、开课学院：信息工程学院学院。

命题组：电子信息教研组2、考试时间：120分钟，所有答案均写在答题纸上。

3、适用班级：信息工程学院通信工程专业及电子类专业。

4、在答题前，请在所发两张答题纸上认真填写所要求填写的个人信息。

卷面题型及分值：总分一二三四五六七八九十100202060一、选择题（每小题2分，共10小题。

每一小题仅有一个选项是正确的。

共计20分）1、下列说法不正确的是（）。

A 、一般周期信号为功率信号。

B 、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C 、ε(t )是功率信号；D 、e t 为能量信号2、下列关于冲激函数性质的表达式不正确的是（）。

A 、B 、)()0()()(t f t t f δδ=()t aat δδ1)(=C 、D 、)(d )(t tεττδ=⎰∞-)()-(t t δδ=3、，属于其极点的是（）。

)2)(1()2(2)(-++=s s s s s H A 、1 B 、2 C 、0 D 、-24、If f 1(t ) ←→F 1(jω)， f 2(t ) ←→F 2(jω) Then[ ]A 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) *b F 2(jω) ]B 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) - b F 2(jω) ]C 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) + b F 2(jω) ]D 、[a f 1(t ) + b f 2(t ) ] ←→ [a F 1(jω) /b F 2(jω) ]5、下列说法不正确的是（）。

A 、H(z)在单位圆内的极点所对应的响应序列为衰减的。

即当k→∞时，响应均趋于0。

B 、H(z)在单位圆上的一阶极点所对应的响应函数为稳态响应。

2006-2007信号与系统试题A卷答案及评分细则

西南科技大学2006——20007学年第2学期《信号与系统X 》期末考试试卷（A 卷）一、填空题（每空2分，共10分）1．6。

2．20071--z。

3．5}Re{,51->+s s 。

4．1<z 。

备注：其它表述正确，给满分。

5．πω8000max <。

二、判断题（每题2分，共10分）1．╳2．√3．√4．╳ 5．√三、证明题（5分）备注：其它解法，根据步骤与答案情况，给分。

证明： )()(ωj X t x F−→←∴)()(**ωj X t x F-−→←，)()(ωj X t x F-−→←-，)()(**ωj X t x F−→←---------（2分）又 )(t x 为实奇信号，即：)()()()(*t x t x t x t x --=--==*--------（1分）∴)()()()(**ωωωωj X j X j X j X -=--=-=即：)(ωj X 为虚奇信号。

--------（2分）四、绘图题（每小题6分，共18分）1．解： )1()1()(112--+=t x t x t x ---（2分）又系统为线性时不变系统，∴)1()1()(112--+=t y t y t y ---（2分）)(2t y 波形如右图所示。

---（2分）。

备注：若直接给结果图，正确给满分。

其它解法，根据步骤与答案情况，给分。

西南科技大学2006——20007学年第2学期《信号与系统X 》期末考试试卷（A 卷）2．解：根据卷积的微积分性质，有)(*)()(*)()(')1(t h t xt h t x t y -==---（2分）又 )1()1()('--+=t t t h δδ∴)1()1()]1()1([*)()()1()1()1(--+=--+=---t xt xt t t xt y δδ ---（2分） )()1(t x-、)('t h 、)(t y 的波形如图所示。

07信号与系统期末考试AB卷及答案

一、选择题（将唯一正确答案填入括号中，每题2分，共20分）1．图1是)(t f 的信号波形，则)1(--t f 的波形为：（ B ）2．请选出)2(2)1()()(-+--=t u t u t u t f 的波形图（ D ）3．直流信号E 和阶跃信号)(t u 的傅里叶变换是：（ C ）（A ）)(2w E δπ，)(w πδ （B ）)(w E δ，)(w πδ （C ）)(2w E δπ，jw w /1)(+πδ （D ）)(w E δ，jw w /1)(+πδ4．若一LTI 系统输入)(1t e ，输出为)(1t r ，输入)(2t e ，输出为)(2t r ，则输入为dtt de t ae )()(21-，输出为：（ D ）（A ）dt t dr t ar )()(21+ （B ）)()(21t r t r + （C ）)()(21t r t ar + （D ）dtt dr t ar )()(21- 5．已知)]3(/[)14()]([++=s s s t f L ，则)(t f 的初值)0(+f 为：（ A ）（A ）4 （B ）3 （C ）2 （D ）06．一LTI 无失真传输系统，它的幅度特性和相位特性要求为：（ D ）（A ）幅度特性为常数，相位特性无要求（B ）幅度特性和相位特性均无要求（C ）幅度特性无要求，相位特性的斜率为0t - （D ）幅度特性为常数，相位特性的斜率为0t -7．一理想低通滤波器的截止频率为c w ，下列信号经该滤波器滤波后信号不失真的是（c w w 32=）：（ B ）（A ）cos2wt (B) coswt (C) coswt+cos2wt (D) cos3wt0-11tf(t)(A)12021tf(t)(B)120-11tf(t)(C)1221tf(t)(D)1211t f(t)0-11t f(-t-1)0-11t f(-t-1)-2(A)(B)011t f(-t-1)(C)11tf(-t-1)2(D)图18．已知1)]([2-=z zn x Z ，（1>z ），则)](3[n x Z n 为：（ D ）（A ）12-z z，1>z （B ）932-z z ，1>z（C ）12-z z，3>z （D ）932-z z ，3>z9．9．已知某系统的单位样值响应)()8.1()(n u n h n =，则该系统的因果性和稳定性：（ B ）（A ）因果，稳定（B ）因果，不稳定（C ）非因果，稳定（D ）非因果，不稳定10．以下哪项陈述不是状态空间法分析系统的优点：（ A ）（A ）特别适用于单输入单输出系统的分析（B ）特别适用于多输入多输出系统的分析（C ）便于研究系统内部的一些物理量的变化规律（D ）适用于非线性时变系统的研究二、填空题：（每小题2分，共20分）11．dt t t t ejwt)]()([0--⎰∞∞--δδ 的结果为：（ 01j w t e - ）。

集美大学信号与系统历届期末考试试卷

学号栏息姓名
线 4、列出如图所示的差分方程，并指出其阶次。
（7 分）
班级
信
订
2 x[n] 1/Z 3 ∑ -4 1/Z y[n]
生考专业
5
1/Z
学院（系）
装
P5
5、某离散系统的差分方程为：
y[ n] + 0.2 y[ n − 1] − 0.24 y[ n − 2] = x[ n] + x[ n − 1]
考
学院（系）
装
7、一个频率为 f0 的余弦波，其幅度峰值按照周期为 T2 的正弦规律变化，（f0>>f2＝1/T2），这种信号称为：，余弦波称为：。 8、线性相位系统是指其相频特性为：系统后，信号的所有频率分量受到的时延，这种特点能使得信号经过，其大小与无关。
P1
9、一个连续信号经过理想采样后的幅度频谱如图所示，请标出原连续信号所具有的最高频率采样频率，奈奎斯特频率以及信号直流分量强度
，。
A 0 f （Hz）
10、两信号在时域里进行为。
或相乘，分别等效于频域里的相乘或
，后者相差一个比例系数
二、绘图与信号或系统表达 20％
1、绘出抽样信号
S a (t ) =
Sin ( t ) ，（－2π≤t≤2π）的大致图形，标出关键点坐标。（5 分） t
2、计算
g (ω ) =
∫
∞
−∞
P3
2、已知双脉冲信号 f（t）如图所示，写出表达式，并利用傅立叶变换的性质求其幅度频谱和相位频谱。（10 分） A
2 0 -B B T-B T T+B t
P4
3、因果周期矩形脉冲 p(t)如图所示，试先求出第一周期的拉氏变换，再求得信号 p(t)的 P(s)（8 分） p(t) E …… 0 T 2T 3T 4T 5T t

《信号与系统》试题及答案,DOC

2012年度教学质量综合评估测验卷《信号与系统》试题注：1、开课学院：信息工程学院学院。

命题组：电子信息教研组2、考试时间：120分钟，所有答案均写在答题纸上。

3、适用班级：信息工程学院通信工程专业及电子类专业。

4、在答题前，请在所发两张答题纸上认真填写所要求填写的个人3、)2)(1()(-+=s s s H ，属于其极点的是（）。

A 、1B 、2C 、0D 、-2 4、If f 1(t )←→F 1(j ω)，f 2(t )←→F 2(j ω)Then[] A 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)*b F 2(j ω)] B 、[a f 1(t )+b f 2(t )]←→[a F 1(j ω)-b F 2(j ω)]C、[a f1(t)+b f2(t)]←→[a F1(jω)+b F2(jω)]D、[a f1(t)+b f2(t)]←→[a F1(jω)/b F2(jω)]5、下列说法不正确的是（）。

A、H(z)在单位圆内的极点所对应的响应序列为衰减的。

即当k→∞时，响应均趋于0。

67A、f(t)=cos(2t)+cos(4t)B、f(t)=sin(2t)+sin(4t)C、f(t)=sin2(4t)D、f(t)=cos2(4t)+sin(2t)8、已知某LTI连续系统当激励为)(t f时，系统的冲击响应为)(t h，零状态响应为)(t y zs ，零输入响应为)(t y zi ，全响应为)(1t y 。

若初始状态不变时，而激励为)(2t f 时，系统的全响应)(3t y 为（）。

A 、)(2)(t y t y zs zi +B 、()2()zi y t f t +C 、)(4t y zsD 、)(4t y zi 9、设有一个离散反馈系统，其系统函数为：)1(2)(k z zz H --=，问若要使该系统稳定，常数应k 该满足的条件是（）。

A 17、已知)21(2323)(22<<+-+=z z z z z X ，则=)(n x 。

《信号与系统》试卷A答案

第二学期《信号与系统》A 卷答案及评分标准一、选择题(每题4分，共20分)1．D 2.D 3.C 4.C 5.A二、填空题（每题4分，共24分）1．-12．u(t)+u(t-1)+u(t-2)3．稳定4．jdF(w)/dw-2F(w)5．线性，非线性6．0.5n u(n)三、计算题（共56分）1．f(t)=Ecos(πτt),22t ττ-≤≤ F(w)=22()jwt f t e dt ττ--⎰=22cos()jwt E t e dt ττπτ--⎰=202cos()cos E t tdt τπωτ⎰ =20[cos()cos()]E t t dt τππωωττ++-⎰ =2222cos 2E πτωτπτω- 共6分，写出表达式给2分，写对傅立叶变换公式给2分，积分过程及结果2分。

2.f(t)= f 1(t)*f 2(t)=sintu(t)*u(t-1)=sin ()(1)u u t d ττττ∞-∞--⎰ =10sin t d ττ-⎰=10cos |t τ--=1-cos(t-1),t>1 共8分，写对两个函数的表达式分别各给2分，带入卷积公式正确得2分，积分过程2分，结果表达正确2分。

3. 当输入为f(t)时, r(t)=(2e -t +cos2t)u(t)=r zs (t)+r zi (t)（2分）当输入为3f(t)时, r(t)=(e -t +cos2t)u(t)=3 r zs (t)+ r zi (t)（2分）联立上面两式得，r zs (t)= - 0.5e -t u(t)（1分） r zi (t)=(2.5 e -t +cos2t)u(t)（1分）当输入为5f(t)时，r(t)=5 r zs (t)+ r zi (t)（1分）=(-2.5 e -t +2.5 e -t +cos2t)=cos2t u(t)（1分）4.解：（1）冲激相应应满足方程h ’’(t)+4h ’(t)+3h(t)=δ’(t)+2δ(t)。