2020年高考数学二轮复习第一部分专题二三角函数平面向量第二讲三角恒等变换与解三角形习题
高考数学二轮复习第一部分专题篇专题二三角函数、平面向量第二讲三角恒等变换与解三角形课件理

第二十七页,共46页。
考点(kǎo diǎn)二
试题 通解
优解
考点(kǎo diǎn)
由
正
、
余
弦
定
理
得
2sin C-sin sin B
B
=
a2+c2-b2 b2+c2-a2
=
acos bcos
B A
=
一
考点(kǎo diǎn)
sin sin
Acos Bcos
BA,所以
2sin
Ccos
A=sin(A+B)=sin
(2)由已知得21absin
C=3
2
3 .
又 C=π3,所以 ab=6.
由已知及余弦定理得 a2+b2-2abcos C=7,
故 a2+b2=13,从而(a+b)2=25.
所以△ABC 的周长为 5+ 7.
第九页,共46页。
考点三
三角(sānjiǎo)恒等变换与解三角(sānjiǎo)形的 综合问题
考点(kǎo diǎn)一
试题(shìt解í)析(jiě
考点一 考点二
考点三
利用同角三角函数的基本关系式求解. 因为 tan α=34,则 cos2 α+2sin 2α=coss2inα2+α4+sicnoαs2coαs α= 1ta+n24tαa+n 1α=1+3424+×134=6245.故选 A.
α)cos(2π+α)+ 22cos2(α+π)=( D )
A.-
2 3
C.-13
B.
2 3
1 D.3
第十五页,共46页。
考点(kǎo diǎn)一
试题
通解 优解
考点(kǎo diǎn) 因为 α 是第四象限角,tan α=- 22,故csions αα=- 22,由 sin2 α
(浙江专用)高考数学二轮复习专题一三角函数与平面向量第2讲三角恒等变换与解三角形课件

第2讲三角恒等变换与解三角形高考定位1 •三角函数的化简与求值是高考的命题热点,其中同角三角函数的基本关系、诱导公式是解决计算问题的工具,三角恒等变换是利用三角恒等式(两角和的核心;2•正弦定理与余弦定理以及解三角形问题是高考的必考内容,主要考查边、角、面积的计算及有关的范围问题.与差、二倍角的正弦、余弦、正切公式)进行变换, “角”的变换是三角恒等变换真题感晤丨考点整合:::::::• ■•••••••••••••••••■ ••••• ••••・••・•••••••• ••••••• • • ・• •罷瀧皐1明考向專蕊扣要点i真题感1.(2018-全国III卷)若sina=28 A97 B9解析cos 2a =1—73,贝0 cos 2a =(8D_9答案2.(2018-全国III卷)AABC的内角A,B, C的对边分别为a, b, c.若△ABC的面积为a2-}~b2— c2,则C=(仆兀B-3C'4r兀D6解析根据题意及三角形的面积公式知j^sin c =厂,所以sin C —/ + 方2 —c22ab= cos C,所以在△ 4BC中,答案C3.(2018•浙江卷)在厶ABC中,角4, B, C所对的边分别为©b, c.若a=^i, b = 2,4 = 60°,贝lj sin B= ________ , c= _________ .・2X迪r解析因为b = 2, A = 60°,所以由正弦定理得^=零. 由余弦定理t/2—Z?2+c2— 2£>ccos A 可得c2— 2c—3 = 0,所以c=3.答案卑34.(2017•浙江卷)已知△ ABC, AB=AC=4, BC=2.点。
为AB延长线上一点,BD = 2,连接CD 则△BDC的面积是__________ , cos ZBDC= ___________ ・解析依题意作出图形,如图所示,则sinZDBC=sinZABC.由题意知AB=AC=4, BC=BD=2,贝U sinZ4BC=乎,cosZABC=^.所以S^BDC —2 BCBD sinZDBC= | X2X2X .因为BD2+BC2-CD2CQ = {Td由余弦定理,得cosZBDC=4+10—4 ^JIQ 2X2XV1O= 4 ・答案V15 Vio2 4B\—~7Ccos DBC —cosZABC= 2BDBC1・三角函数公式(2) 诱导公式:对于“㊁土弘kEZ 的三角函数值”与“a 角的三角函数值” 面口诀记忆:奇变偶不变,符号看象限.(3) 两角和与差的正弦、余弦、正切公式:sin(a±0) = sin acos 〃土cos asin 0; cos(a 土〃)=cos acos P s in asin 〃; tan(a 土〃)(4) 二倍角 公式:sin 2a = 2sin acos a, cos la=cos 2a — sin 2a = 2cos 26z —1 = 1_____ b y考点整合⑴同角关系: sin 2a+cos 2a=l,a.cos a的关系可按下tan a 土tan卩1 tan atan B(5)辅助角公式:asin x~\~bcos x==^/u2+Z?2sin(x+^), 其中tan(p=^.2•正弦定理、余弦定理、三角形面积公式 (1) 正弦定理在厶ABC 中,聶=岛=蠢=2R(R 为AABC 的外接圆半径);(2)余弦定理在△佔c 中, a 1 = b 1-\-c 1— 2bccos A ;变形:b 2j rc 2- j 2 1 2 2 2 b 十 c —a~ ci —2bccos4, cos A — n 7(3)三角形面积公式1 7 1 1SgBc=fbsin C=~Z?csin A=^acsin B.变形:a = 2/?sin A, sinci : b : c=sinA : sin B : sin C等.I热点聚焦丨分类突破I■■■誥絃総研热点扭[析考法浚签瘗热点一三角恒等变换及应用【例1] (1)(2018-全国I卷)己知角a的顶点为坐标原点,始边与x轴的非负半轴重2合,终边上有两点A(l, a). B(2, b),且cos 2(z=j,贝\\\a~b\ = { ) 1A-5 D.1(2)若tan兀a = 2tanI 3兀cos a—而则一;一, sin<z_5A.lB.2C.3D.4(3)如图,圆O与兀轴的正半轴的交点为A,点C, B在圆O上,且点C位于第一象12 _丄、巨_13,\/3cos2|—sin|-cos^— j 的值为2解析⑴由题意知cos a>0•因为cos 2a = 2cos2a—1=~,所以、6 、5 …土*得Itan od=*~・由题意知Itan a\ =,所以1“一勿=晋.故选B.,ZAOC=a.若IBCI = 1,则限,点B的坐标为cos 心晋,sin 0 =/ \ JI sin a — sin 心2+1 —3 . 7t . 7t tan a = 2— 1 sin otcosc -cos asing --------------------------- 1 5 5 7i tan 5f 3旳 co r _w(713兀、 s 吨+「而 sin”+£ tan a 】 .7T 71 asing tang sin acos^+cos(3)由题意得\OC\ = \OB\ = \BC\ = \,从而AOBC 为等边三角形,所以sinZAOB = 513*答案(1)B (2)C ⑶备 sin 曾_彳=器所以羽cos?号一sin^cos*— 22« 3_ 厂 1+cos a sin a 吋3 1 . =p3・ 2 P 2探究提高1 •解决三角函数的化简求值问题的关键是把“所求角”用“已知角”表示(1)当已知角有两个时”“所求角”般表示为“两个已知角”的和或差的形式;⑵当“已知角”有一个时,此时应着眼于“所求角”的和或差的关系,然后应用诱导公式把"所求角”变成"已知角".2•求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解.【训练11 (1)(2018-全国II卷)已知sin a+cos 0= 1, cos oc+sin0=0,则sin(a+0)⑵(2017•北京卷)在平面直角坐标系兀Oy中,角u与角0均以S为始边,它们的终边关于y轴对称.若sin(/=*,则cos(or—〃)= ___________ .一 1 ] 4、疗71 兀(3)(2018-湖州质检)若cos(2a_0) = _盲,sin(a—20)=〒,Ov0v&vav刁贝!j a+0的值为解析(l)Tsin a + cos p= 1, cos a+sin0=0,sin2a + co邙+2sin acos①cos2a+sii?0+2cos asin £=0,②①②两式相加可得sin2a+cos2a+sin2^+cos2^+2(sin acos 0+cos asin 0)=1,/.sin(ot+^)1 =_2-(2)c t与0的终边关于y轴对称,贝lj a+p=Tt+2k7t,比丘乙:・B=Tt_aS ・7( 1) 7 /.cos(a—^) = cos( a — n + a — 2^)= — cos 2a=— (1 — 2sin^a) = — 11— 2X-| =—-,所以sin(2a—0)=p7・所以cos(a—20)=*所以cos(a +0) = cos[(2oc一0) —(a —20)] = cos(2«—”)・cos@ —2") + sin(2a —”)sin(a —X因为问+0罟,所以a + B =£. 答案(1)—£ (2)—£ (3)|热点二正、余弦定理的应用[考法1]三角形基本量的求解【例2—1】(2018-全国I卷)在平面四边形ABCD中,ZADC=90° , ZA=45° , AB =2, BD=5.⑴求cosZADB;(2)若DC=2d求BCRD A D C 2解⑴在△ABD中'由正弦定理得口二右而即而产sin為' 所以sinZADB=€・由题设知,ZADB<90°,、2(2)由题设及(1)知,cos ZBDC= sin ZADB =在△BCD 中,由余弦定理得、2BC 2=BD 2-hDC 2-2BDDCcosZBDC=25-h8-2X5X2\/2X^-=25. 所以BC=5.所以 cos ZADB=2=运 25— 5 •探究提高1•解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则考虑两个定理都有可能用到.2.关于解三角形问题,一般要用到三角形的内角和定理,正弦、余弦定理及有关三角形的性质,常见的三角恒等变换方法和原则都适用,同时要注意“三统一”,即“统—角、统一函数、统一结构"•[考法2]求解三角形中的最值问题【例2 — 2】(2018-绍兴质检)已知",b, c分别为ZVIBC的内角4, B, C的对边,且tzcos C+羽asin C—b—c = 0・⑴求4;(2)若ci = 2,求AABC面积的最大值.解(1)由cicos C+书asin C—b—c=0及正弦定理得sin Acos C+^/3sin Asin C—sin B —sin C=0・因为B=TI—A — Cy所以书sinAsin C—cos Asin C—sin C=0・易知sin C T^O,所以^/3sin A—cos A=l,所以sin A—=-又0<A<7i,所以A=^.(2)法一由⑴得B+C=y C=^—B (OVB<刽,由正弦定理得聶=盒二c 2 4 4 4 晶寸—卞 所以bpsinb c=^sm C. sin § v v v易知一£<23—£<¥,故当2E-*=号,即B=£时,S △初c 取得最大值,最大值为斗平A=|x^sin B X ^sin C sin |=^sin Bsin C=^ (2n }•sin B sin w B Id 丿¥血"cos B +^sin 2B =sin 2B~/3 , J3 2^3 3C0S 2B+ 3 = 3 / \ 7C 1 sin 2B —y + I 6丿 113・所以S^BC =法二由(1)知4=务又u = 2,由余弦定理得22= b2+c2-2bccos p即b2-\-c2~bc—4 Z?c+4 —Z?2+ c22Z?c bcW4,当且仅当b = c = 2时,等号成立.] 1 、厅、庁所以SgBc=qbcsin A=^X专bcW计X4=书,即当b = c = 2时,S^BC取得最大值, 最大值为也.探究提高求解三角形中的最值问题常用如下方法:(1)将要求的量转化为某一角的三角函数,借助于三角函数的值域求最值・(2)将要求的量转化为边的形式,借助于基本不等式求最值.[考法3]解三角形与三角函数的综合问题( \【例2 — 3】(2018-嘉兴、丽水高三测试)己知函数您)= cos 2x+中+羽(sinx+cosx)2.(1)求函数/(x)的最大值和最小正周期;(2)设△ABC的三边心b, c所对的角分别为力,B, C,若a = 2, 0=好/片+㊁戶好求b的值.] 、/3 ( Tt]解(1)因为—2COS 2%—专sin 2x+A/3(l+sin 2x) = sin 2x+g +书,所以/W的最大值为1+羽,最小正周期T=TI.z\ / \ / \ / \C(2)因为/ (才十qJ=sinl+C+gJ+^=cos C+& +羽=羽,所以cos| C+g =0 c=y由余弦定理c2=a+b2-2abcos C可得沪一2^ —3 = 0,因为b>0,所以b = 3.探究提高解三角形与三角函数的综合题,其中,解决与三角恒等变换有关的问题, 优先考虑角与角之间的关系;解决与三角形有关的问题,优先考虑正弦、余弦定理.【训练2】(2016-浙江卷)在△ABC中,内角儿B,C所对的边分别为心4 c.已矢口b+c = 2acos B.⑴证明:A = 2B;2(2)若△ABC的面积S=牛,求角A的大小.(1)证明由正弦定理得sin B+sin C=2sin Acos B,故2sin Acos B = sin B + sin(A+B) =sin B + sin Acos B + cos Asin B,于是sin B = sin(A-B).又儿Be(0, TC),故0<4—3<兀,所以或 3 =A—B,因此A=7t(舍去)或A = 2B,所以A = 2B・2 2(2)解由S=才得如bsin C=予,故有sin Bsin C=gsin 2B = sin Bcos B,因sinBHO,得sin C=cos B.又B, C£(O, TC),所以C=q土B. 当B+C=》时,A=|;当C~B=^时,A=中.综上,4=申或M纳总结丨思维升华I ■■■■課穩穩探规律瘗防失:误浚签瘗1 •对于三角函数的求值,需关注:(1)寻求角与角关系的特殊性,化非特殊角为特殊角,熟练准确地应用公式;I(2)注意切化弦、异角化同角、异名化同名、角的变换等常规技巧的运用;(3)对于条件求值问题,要认真寻找条件和结论的关系,寻找解题的突破口,对于很难入手的问题,可利用分析法.2.三角形中判断边、角关系的具体方法:(1)通过正弦定理实施边角转换;(2)通过余弦定理实施边角转换;(3)通过三角变换找出角之间的关系;(4)通过三角函数值符号的判断以及正、余弦函数的有界性进行讨论;(5)若涉及两个(或两个以上)三角形,这时需作出这些三角形,先解条件多的三角形,再逐步求出其他三角形的边和角,其中往往用到三角形内角和定理,有时需设岀未知量,从几个三角形中列岀方程(组)求解.3.解答与三角形面积有关的问题时,如已知某一内角的大小或三角函数值,就选择S= fabsinC来求面积,再利用正弦定理或余弦定理求出所需的边或角.。
高考数学二轮复习专题一三角函数与平面向量第2讲三角恒等变换

第2讲 三角恒等变换与解三角形[考情考向分析] 正弦定理、余弦定理以及解三角形问题是高考的必考内容,主要考查:1.边和角的计算.2.三角形形状的判断.3.面积的计算.4.有关参数的范围问题.由于此内容应用性较强,与实际问题结合起来进行命题将是今后高考的一个关注点,不可轻视.热点一 三角恒等变换例1 (1)若cos ⎝ ⎛⎭⎪⎫α+π3=45,则cos ⎝ ⎛⎭⎪⎫π3-2α=________.答案 -725解析 ∵cos ⎝⎛⎭⎪⎫α+π3=45, ∴cos ⎝ ⎛⎭⎪⎫α+π3=sin ⎣⎢⎡⎦⎥⎤π2-⎝⎛⎭⎪⎫α+π3=sin ⎝ ⎛⎭⎪⎫π6-α=45,∴cos ⎝ ⎛⎭⎪⎫π3-2α=1-2sin 2⎝ ⎛⎭⎪⎫π6-α=-725.(2)在平面直角坐标系xOy 中,以Ox 轴为始边作角α,角α+π4的终边经过点P (-2,1).①求cos α的值; ②求cos ⎝⎛⎭⎪⎫5π6-2α的值.解 ①由于角α+π4的终边经过点P (-2,1),故cos ⎝ ⎛⎭⎪⎫α+π4=-255,sin ⎝ ⎛⎭⎪⎫α+π4=55, ∴cos α=cos ⎝⎛⎭⎪⎫α+π4-π4=cos ⎝ ⎛⎭⎪⎫α+π4cos π4+sin ⎝ ⎛⎭⎪⎫α+π4sin π4=-1010.②sin α=sin ⎝⎛⎭⎪⎫α+π4-π4=sin ⎝ ⎛⎭⎪⎫α+π4cos π4-cos ⎝⎛⎭⎪⎫α+π4sin π4=31010,则sin 2α=2sin αcos α=-35,cos 2α=cos 2α-sin 2α=-45,cos ⎝⎛⎭⎪⎫5π6-2α=cos 5π6cos 2α+sin 5π6sin 2α=43-310.思维升华 (1)三角变换的关键在于对两角和与差的正弦、余弦、正切公式,二倍角公式,三角恒等变换公式的熟记和灵活应用,要善于观察各个角之间的联系,发现题目所给条件与恒等变换公式的联系,公式的使用过程要注意正确性,要特别注意公式中的符号和函数名的变换,防止出现“张冠李戴”的情况.(2)求角问题要注意角的范围,要根据已知条件将所求角的范围尽量缩小,避免产生增解. 跟踪演练1 (1)已知cos ⎝ ⎛⎭⎪⎫π2+α=3sin ⎝ ⎛⎭⎪⎫α+7π6,则tan ⎝ ⎛⎭⎪⎫π12+α=________.答案 23-4解析 ∵cos ⎝ ⎛⎭⎪⎫π2+α=3sin ⎝ ⎛⎭⎪⎫α+7π6,∴-sin α=-3sin ⎝⎛⎭⎪⎫α+π6,∴sin α=3sin ⎝ ⎛⎭⎪⎫α+π6=3sin αcos π6+3cos αsin π6 =332sin α+32cos α, ∴tan α=32-33,又tan π12=tan ⎝ ⎛⎭⎪⎫π3-π4=tanπ3-tan π41+tan π3tanπ4=3-11+3=2-3, ∴tan ⎝ ⎛⎭⎪⎫π12+α=tanπ12+tan α1-tan π12tan α=()2-3+32-331-()2-3×32-33=23-4.(2)(2018·江苏如东中学等五校联考)已知α∈⎝ ⎛⎭⎪⎫π3,5π6,且cos ⎝⎛⎭⎪⎫α-π3=35,则sin α的值是________. 答案4+3310解析 ∵α∈⎝ ⎛⎭⎪⎫π3,5π6,∴α-π3∈⎝ ⎛⎭⎪⎫0,π2,给合同角三角函数基本关系式有: sin ⎝⎛⎭⎪⎫α-π3=1-cos 2⎝⎛⎭⎪⎫α-π3=45,则sin α=sin ⎝⎛⎭⎪⎫α-π3+π3=sin ⎝ ⎛⎭⎪⎫α-π3cos π3+cos ⎝ ⎛⎭⎪⎫α-π3sin π3=45×12+35×32=4+3310. 热点二 正弦定理、余弦定理例2 (2018·江苏泰州中学调研)如图,在圆内接△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,满足a cos C +c cos A =2b cos B .(1)求B 的大小;(2)若点D 是劣弧AC 上一点,AB =3,BC =2,AD =1,求四边形ABCD 的面积. 解 (1)方法一 设外接圆的半径为R ,则a =2R sin A ,b =2R sin B ,c =2R sin C , 代入得2R sin A cos C +2R sin C cos A =2×2R sin B cos B , 即sin A cos C +sin C cos A =2sin B cos B , 所以sin B =2sin B cos B . 所以sin B ≠0,所以cos B =12.又B 是三角形的内角, 所以B =π3.方法二 根据余弦定理,得a ·a 2+b 2-c 22ab +c ·b 2+c 2-a 22bc=2b ·cos B ,化简得cos B =12.因为0<B <π,所以B =π3.(2)在△ABC 中,AC 2=AB 2+BC 2-2AB ·BC cos∠ABC =9+4-2×3×2×12=7,所以AC =7.因为A ,B ,C ,D 四点共圆,所以∠ADC =2π3.在△ACD 中,AC 2=AD 2+CD 2-2AD ·CD cos∠ADC ,代入得7=1+CD 2-2·CD ·⎝ ⎛⎭⎪⎫-12,所以CD 2+CD -6=0,解得CD =2或CD =-3(舍). 所以S ABCD =S △ABC +S △ACD=12AB ·BC sin∠ABC +12AD ·CD sin∠ADC =12×3×2×32+12×1×2×32=2 3. 思维升华 关于解三角形问题,一般要用到三角形的内角和定理,正弦、余弦定理及有关三角形的性质,常见的三角变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”,这是使问题获得解决的突破口.跟踪演练2 在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos A a +cos B b =23sin C 3a .(1)求角B 的大小; (2)已知a sin Csin A=4,△ABC 的面积为63,求边长b 的值. 解 (1)由已知得b cos A +a cos B =233b sin C ,由正弦定理得sin B cos A +cos B sin A =233sin B sin C ,∴sin(A +B )=233sin B sin C ,又在△ABC 中,sin(A +B )=sin C ≠0, ∴sin B =32,∵0<B <π2,∴B =π3. (2)由已知及正弦定理得c =4,又 S △ABC =63,B =π3,∴12ac sin B =63,得a =6,由余弦定理b 2=a 2+c 2-2ac cos B , 得 b =27.热点三 解三角形与三角函数的综合问题例3 (2018·江苏三校联考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,已知a 2-c 2=2b ,且sin A cos C =3cos A sin C . (1)求b 的值;(2)若B =π4,S 为△ABC 的面积,求S +82cos A cos C 的取值范围.解 (1)由正弦定理、余弦定理知sin A cos C =3cos A sin C 可等价变形为a ·a 2+b 2-c 22ab =3c ·b 2+c 2-a 22bc,化简得a 2-c 2=b 22.因为a 2-c 2=2b ,所以b =4或b =0(舍去).(2)由正弦定理b sin B =c sin C 得S =12bc sin A =12×4×4sinπ4sin A sin C =82sin A sin C ,所以S +82cos A cos C =82cos(A -C ) =82cos ⎝ ⎛⎭⎪⎫2A -3π4. 在△ABC 中,由⎩⎪⎨⎪⎧0<A <3π4,A >3π4-A ,得A ∈⎝⎛⎭⎪⎫3π8,3π4.所以2A -3π4∈⎝ ⎛⎭⎪⎫0,3π4,所以cos ⎝ ⎛⎭⎪⎫2A -3π4∈⎝ ⎛⎭⎪⎫-22,1, 所以S +82cos A cos C ∈(-8,82).思维升华 解三角形与三角函数的综合题,要优先考虑角的范围和角之间的关系;对最值或范围问题,可以转化为三角函数的值域来求解. 跟踪演练3 已知函数f (x )=2cos 2x +sin ⎝⎛⎭⎪⎫7π6-2x -1(x ∈R ). (1)求函数f (x )的最小正周期及单调递增区间;(2)在△ABC 中,三内角A ,B ,C 的对边分别为a ,b ,c ,已知f (A )=12,若b +c =2a ,且AB →·AC→=6,求a 的值. 解 (1)f (x )=sin ⎝⎛⎭⎪⎫7π6-2x +2cos 2x -1=-12cos 2x +32sin 2x +cos 2x=12cos 2x +32sin 2x =sin ⎝ ⎛⎭⎪⎫2x +π6.∴函数f (x )的最小正周期T =2π2=π.由2k π-π2≤2x +π6≤2k π+π2(k ∈Z ),可解得k π-π3≤x ≤k π+π6(k ∈Z ).∴f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z ).(2)由f (A )=sin ⎝⎛⎭⎪⎫2A +π6=12,可得2A +π6=π6+2k π或2A +π6=5π6+2k π(k ∈Z ).∵A ∈(0,π),∴A =π3,∵AB →·AC →=bc cos A =12bc =6,∴bc =12, 又∵2a =b +c ,∴cos A =12=(b +c )2-a 22bc -1=4a 2-a 224-1=a28-1,∴a =2 3.1.若△ABC 的内角满足sin A +2sin B =2sin C ,则cos C 的最小值是________. 答案6-24解析 由sin A +2sin B =2sin C , 结合正弦定理得a +2b =2c .由余弦定理得cos C =a 2+b 2-c 22ab=a 2+b 2-(a +2b )242ab =34a 2+12b 2-2ab22ab≥2⎝ ⎛⎭⎪⎫34a 2⎝ ⎛⎭⎪⎫12b 2-2ab22ab=6-24, ⎝ ⎛⎭⎪⎫当且仅当b 2=32a 2时,等号成立 故6-24≤cos C <1, 故cos C 的最小值为6-24. 2.(2018·全国Ⅲ改编)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若△ABC 的面积为a 2+b 2-c 24,则C =________. 答案π4解析 ∵S =12ab sin C =a 2+b 2-c 24=2ab cos C4=12ab cos C , ∴sin C =cos C ,即tan C =1. 又∵C ∈(0,π),∴C =π4.3.(2018·全国Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b sin C +c sin B =4a sinB sinC ,b 2+c 2-a 2=8,则△ABC 的面积为________.答案233解析 ∵b sin C +c sin B =4a sin B sin C , ∴由正弦定理得sin B sin C +sin C sin B =4sin A sin B sin C . 又sin B sin C >0,∴sin A =12.由余弦定理得cos A =b 2+c 2-a 22bc =82bc =4bc>0,∴cos A =32,bc =4cos A =833, ∴S △ABC =12bc sin A =12×833×12=233.4.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5cos C ,并且a =2,则△ABC 的面积为________. 答案52解析 因为0<A <π,cos A =23,所以sin A =1-cos 2A =53. 又由5cos C =sin B =sin(A +C ) =sin A cos C +cos A sin C =53cos C +23sin C 知,cos C >0, 并结合sin 2C +cos 2C =1,得sin C =56,cos C =16.于是sin B =5cos C =56.由a =2及正弦定理a sin A =csin C ,得c = 3.故△ABC 的面积S =12ac sin B =52.5.已知函数f (x )=3sin ωx ·cos ωx -cos 2ωx (ω>0)的最小正周期为2π3.(1)求ω的值;(2)在△ABC 中,sin B ,sin A ,sin C 成等比数列,求此时f (A )的值域. 解 (1)f (x )=32sin 2ωx -12(cos 2ωx +1) =sin ⎝⎛⎭⎪⎫2ωx -π6-12, 因为函数f (x )的最小正周期为T =2π2ω=2π3,所以ω=32.(2)由(1)知f (x )=sin ⎝ ⎛⎭⎪⎫3x -π6-12, 易得f (A )=sin ⎝⎛⎭⎪⎫3A -π6-12. 因为sin B ,sin A ,sin C 成等比数列,所以sin 2A =sin B sin C ,所以a 2=bc ,所以cos A =b 2+c 2-a 22bc =b 2+c 2-bc2bc≥2bc -bc 2bc =12(当且仅当b =c 时取等号). 因为0<A <π,所以0<A ≤π3,所以-π6<3A -π6≤5π6,所以-12<sin ⎝ ⎛⎭⎪⎫3A -π6≤1,所以-1<sin ⎝ ⎛⎭⎪⎫3A -π6-12≤12, 所以f (A )的值域为⎝⎛⎦⎥⎤-1,12.A 组 专题通关1.(2018·全国Ⅲ改编)若sin α=13,则cos 2α=________.答案 79解析 ∵sin α=13,∴cos 2α=1-2sin 2α=1-2×⎝ ⎛⎭⎪⎫132=79.2.tan 70°+tan 50°-3tan 70°tan 50°的值为________. 答案 - 3解析 因为tan 120°=tan 70°+tan 50°1-tan 70°tan 50°=-3,即tan 70°+tan 50°-3tan 70°tan 50°=- 3.3.(2018·江苏泰州中学调研)已知sin θ+2cos θ=0,则1+sin 2θcos 2θ=________. 答案 1解析 由题设可知sin θ=-2cos θ, 则原式=sin 2θ+cos 2θ+2sin θcos θcos 2θ =(4+1-4)cos 2θcos 2θ=1. 4.在△ABC 中,若原点到直线x sin A +y sin B +sin C =0的距离为1,则此三角形为________三角形.(填“直角”“锐角”“钝角”) 答案 直角 解析 由已知可得,|sin C |sin 2A +sin 2B=1,∴sin 2C =sin 2A +sin 2B ,∴c 2=a 2+b 2, 故△ABC 为直角三角形.5.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,a cos B +b cos A =2c cos C ,c =7,且△ABC 的面积为332,则△ABC 的周长为________.答案 5+7解析 在△ABC 中,a cos B +b cos A =2c cos C , 则sin A cos B +sin B cos A =2sin C cos C , 即sin(A +B )=2sin C cos C , ∵sin(A +B )=sin C ≠0, ∴cos C =12,∴C =π3,由余弦定理可得,a 2+b 2-c 2=ab , 即(a +b )2-3ab =c 2=7,又S =12ab sin C =34ab =332,∴ab =6,∴(a +b )2=7+3ab =25,a +b =5, ∴△ABC 的周长为a +b +c =5+7. 6.若sin 2α=55,sin(β-α)=1010,且α∈⎣⎢⎡⎦⎥⎤π4,π,β∈⎣⎢⎡⎦⎥⎤π,3π2,则α+β的值是________. 答案7π4解析 ∵sin 2α=55,α∈⎣⎢⎡⎦⎥⎤π4,π, ∴cos 2α=-255且α∈⎣⎢⎡⎦⎥⎤π4,π2,又∵sin(β-α)=1010,β∈⎣⎢⎡⎦⎥⎤π,3π2,∴cos(β-α)=-31010,∴sin(α+β)=sin[(β-α)+2α]=sin(β-α)cos 2α+cos(β-α)sin 2α =1010×⎝ ⎛⎭⎪⎫-255+⎝ ⎛⎭⎪⎫-31010×55=-22, cos(α+β)=cos[(β-α)+2α]=cos(β-α)cos 2α-sin(β-α)sin 2α=⎝ ⎛⎭⎪⎫-31010×⎝ ⎛⎭⎪⎫-255-1010×55=22, 又α+β∈⎣⎢⎡⎦⎥⎤5π4,2π,∴α+β=7π4. 7.设△ABC 内切圆与外接圆的半径分别为r 与R .且sin A ∶sin B ∶sin C =2∶3∶4,则cos C =________;当BC =1时,△ABC 的面积等于________.答案 -14 31516解析 ∵sin A ∶sin B ∶sin C =2∶3∶4,∴a ∶b ∶c =2∶3∶4.令a =2t ,b =3t ,c =4t (t >0),则cos C =4t 2+9t 2-16t 212t 2=-14, 又∵C ∈(0,π),∴sin C =154. 当BC =1时,AC =32, ∴S △ABC =12×1×32×154=31516. 8.如图,在△ABC 中,BC =2,∠ABC =π3,AC 的垂直平分线DE 与AB ,AC 分别交于D ,E 两点,且DE =62,则BE 2=________.答案 52+ 3 解析 如图,连结CD ,由题设,有∠BDC =2A ,所以CD sin π3=BC sin 2A =2sin 2A , 故CD =3sin 2A. 又DE =CD sin A =32cos A =62, 所以cos A =22,而A ∈(0,π),故A =π4, 因此△ADE 为等腰直角三角形,所以AE =DE =62. 在△ABC 中,∠ACB =5π12, 所以AB sin 5π12=2sin π4, 故AB =3+1,在△ABE 中,BE 2=(3+1)2+⎝ ⎛⎭⎪⎫622-2×(3+1)×62×22=52+ 3. 9.(2018·江苏)已知α,β为锐角,tan α=43,cos(α+β)=-55. (1)求cos 2α的值;(2)求tan(α-β)的值.解 (1)因为tan α=43,tan α=sin αcos α, 所以sin α=43cos α. 又因为sin 2α+cos 2α=1,所以cos 2α=925, 因此,cos 2α=2cos 2α-1=-725.(2)因为α,β为锐角,所以α+β∈(0,π).又因为cos(α+β)=-55,所以α+β∈⎝ ⎛⎭⎪⎫π2,π, 所以sin(α+β)=1-cos 2(α+β)=255, 因此tan(α+β)=-2. 因为tan α=43, 所以tan 2α=2tan α1-tan 2α=-247. 因此,tan(α-β)=tan[2α-(α+β)]=tan 2α-tan (α+β)1+tan 2αtan (α+β)=-211. 10.(2018·江苏扬州中学调研)已知△ABC 的三个内角A ,B ,C 所对的边分别为a ,b ,c ,向量m =(1,2),n =⎝⎛⎭⎪⎫cos 2A ,cos 2A 2,且m ·n =1. (1)求角A 的大小; (2)若b +c =2a =23,求sin ⎝⎛⎭⎪⎫B -π4的值. 解 (1)由题意得m ·n =cos 2A +2cos 2A 2=2cos 2A -1+cos A +1=2cos 2A +cos A , 又因为m ·n =1,所以2cos 2A +cos A =1, 解得cos A =12或cos A =-1, ∵0<A <π, ∴A =π3. (2)在△ABC 中,由余弦定理得(3)2=b 2+c 2-2bc ·12=b 2+c 2-bc ,① 又b +c =23,∴b =23-c , 代入①整理得c 2-23c +3=0,解得c =3,∴b =3,于是a =b =c =3,即△ABC 为等边三角形,∴B =π3, ∴sin ⎝ ⎛⎭⎪⎫B -π4=sin ⎝ ⎛⎭⎪⎫π3-π4=6-24. B 组 能力提高11.如图,在△ABC 中,D ,F 分别为BC ,AC 的中点,AD ⊥BF ,若sin 2C =716sin∠BAC ·sin∠ABC ,则cos C =________.答案 78解析 设BC =a ,AC =b ,AB =c ,由sin 2C =716sin∠BAC ·sin∠ABC 可得,c 2=716ab , 由AD ⊥BF 可得,AD →·BF →=AB →+AC →2·⎝ ⎛⎭⎪⎫12AC →-AB →=0, 整理可得,14AC →2-12AB →2-14AB →·AC →=0, 即14b 2-12c 2-14bc cos∠BAC =0, 即2b 2-4c 2-2bc cos∠BAC =0,2b 2-4c 2-(b 2+c 2-a 2)=0,即a 2+b 2-c 2=4c 2=74ab , 所以cos C =a 2+b 2-c 22ab =78. 12.(2018·北京)若△ABC 的面积为34(a 2+c 2-b 2),且C 为钝角,则B =________;c a的取值范围是________.答案 π3 (2,+∞) 解析 由余弦定理得cos B =a 2+c 2-b 22ac, ∴a 2+c 2-b 2=2ac cos B .又∵S =34(a 2+c 2-b 2), ∴12ac sin B =34×2ac cos B , ∴tan B =3,又B ∈(0,π),∴B =π3. 又∵C 为钝角,∴C =2π3-A >π2, ∴0<A <π6. 由正弦定理得c a =sin ⎝ ⎛⎭⎪⎫2π3-A sin A=32cos A +12sin A sin A =12+32·1tan A. ∵0<tan A <33,∴1tan A>3, ∴c a >12+32×3=2, 即c a >2. ∴c a 的取值范围是(2,+∞).13.在锐角△ABC 中,角A 所对的边为a ,△ABC 的面积S =a 24,给出以下结论: ①sin A =2sin B sin C ;②tan B +tan C =2tan B tan C ;③tan A +tan B +tan C =tan A tan B tan C ;④tan A tan B tan C 有最小值8.其中正确结论的个数为________.答案 4解析 由S =a 24=12ab sin C ,得a =2b sin C , 又a sin A =bsin B ,得sin A =2sin B sin C ,故①正确; 由sin A =2sin B sin C ,得sin(B +C )=sin B cos C +cos B sin C =2sin B sin C ,两边同时除以cos B cos C ,可得tan B +tan C =2tan B tan C ,故②正确;由tan(A +B )=tan A +tan B 1-tan A tan B,且tan(A +B )=tan(π-C )=-tan C ,所以tan A +tan B 1-tan A tan B=-tan C , 整理移项得tan A +tan B +tan C =tan A tan B tan C ,故③正确;由tan B +tan C =2tan B tan C ,tan A =-tan(B +C )=tan B +tan C tan B tan C -1, 且tan A ,tan B ,tan C 都是正数,得tan A tan B tan C =tan B +tan C tan B tan C -1·tan B tan C =2tan B tan C tan B tan C -1·tan B tan C =2(tan B tan C )2tan B tan C -1, 设m =tan B tan C -1,则m >0,tan A tan B tan C =2(m +1)2m=2⎝ ⎛⎭⎪⎫m +1m +4≥4+4m ·1m =8, 当且仅当m =tan B tan C -1=1,即tan B tan C =2时取“=”,此时tan B tan C =2,tan B +tan C =4,tan A =4,所以tan A tan B tan C 的最小值是8,故④正确.14.已知向量a =(2sin 2x ,2cos 2x ),b =(cos θ,sin θ)⎝⎛⎭⎪⎫|θ|<π2,若f (x )=a ·b ,且函数f (x )的图象关于直线x =π6对称. (1)求函数f (x )的解析式,并求f (x )的单调递减区间;(2)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若f (A )=2,且b =5,c =23,求△ABC 外接圆的面积.解 (1)f (x )=a ·b =2sin 2x cos θ+2cos 2x sin θ=2sin(2x +θ),∵函数f (x )的图象关于直线x =π6对称, ∴2×π6+θ=k π+π2,k ∈Z , ∴θ=k π+π6,k ∈Z , 又|θ|<π2,∴θ=π6.∴f (x )=2sin ⎝⎛⎭⎪⎫2x +π6. 由2k π+π2≤2x +π6≤2k π+3π2,k ∈Z , 得k π+π6≤x ≤k π+2π3,k ∈Z . ∴f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤k π+π6,k π+2π3,k ∈Z . (2)∵f (A )=2sin ⎝⎛⎭⎪⎫2A +π6=2, ∴sin ⎝⎛⎭⎪⎫2A +π6=1. ∵A ∈(0,π),∴2A +π6∈⎝ ⎛⎭⎪⎫π6,13π6, ∴2A +π6=π2,∴A =π6. 在△ABC 中,由余弦定理得a 2=b 2+c 2-2bc cos A=25+12-2×5×23cos π6=7, ∴a =7.设△ABC 外接圆的半径为R , 由正弦定理得a sin A =2R =712=27, ∴R =7,∴△ABC 外接圆的面积S =πR 2=7π. 精美句子1、善思则能“从无字句处读书”。
【高考推荐】2020-2021高考数学二轮复习专题二三角函数、平面向量第二讲三角恒等变换与解三角形教案理
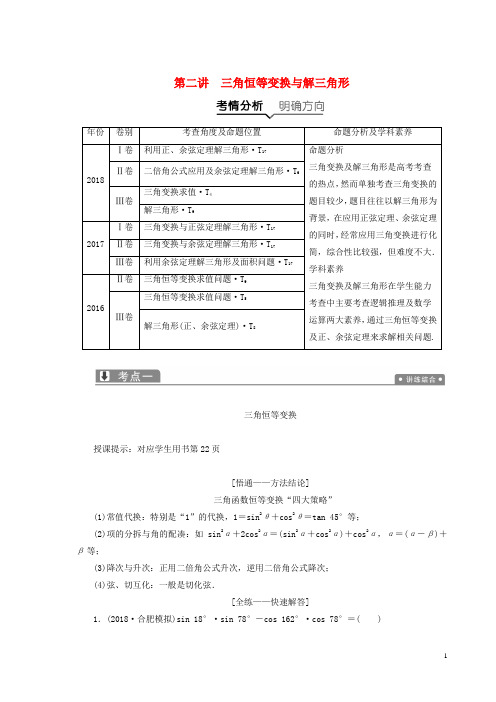
第二讲三角恒等变换与解三角形年份卷别考查角度及命题位置命题分析及学科素养2018Ⅰ卷利用正、余弦定理解三角形·T17命题分析三角变换及解三角形是高考考查的热点,然而单独考查三角变换的题目较少,题目往往以解三角形为背景,在应用正弦定理、余弦定理的同时,经常应用三角变换进行化简,综合性比较强,但难度不大.学科素养三角变换及解三角形在学生能力考查中主要考查逻辑推理及数学运算两大素养,通过三角恒等变换及正、余弦定理来求解相关问题.Ⅱ卷二倍角公式应用及余弦定理解三角形·T6Ⅲ卷三角变换求值·T4解三角形·T92017Ⅰ卷三角变换与正弦定理解三角形·T17Ⅱ卷三角变换与余弦定理解三角形·T17Ⅲ卷利用余弦定理解三角形及面积问题·T172016Ⅱ卷三角恒等变换求值问题·T9Ⅲ卷三角恒等变换求值问题·T5解三角形(正、余弦定理)·T8三角恒等变换授课提示:对应学生用书第22页[悟通——方法结论]三角函数恒等变换“四大策略”(1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等;(2)项的分拆与角的配凑:如sin2α+2cos2α=(sin2α+cos2α)+cos2α,α=(α-β)+β等;(3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次;(4)弦、切互化:一般是切化弦.[全练——快速解答]1.(2018·合肥模拟)sin 18°·sin 78°-cos 162°·cos 78°=( )A .-32 B .-12 C.32 D.12解析:sin 18°·sin 78°-cos 162°·cos 78°=sin 18°·sin 78°+cos 18°·cos 78°=cos(78°-18°)=cos 60°=12,故选D.答案:D2.(2018·高考全国卷Ⅲ)若sin α=13,则cos 2α=( )A.89B.79 C .-79D .-89解析:∵sin α=13,∴cos 2α=1-2sin 2α=1-2×⎝ ⎛⎭⎪⎫132=79.故选B. 答案:B3.(2018·沈阳模拟)已知tan θ=2,则sin θ+cos θsin θ+sin 2θ的值为( )A.195B.165C.2310D.1710解析:原式=sin θ+cos θsin θ+sin 2θ=sin θ+cos θsin θ+sin 2θsin 2θ+cos 2θ=tan θ+1tan θ+tan 2θtan 2θ+1,将tan θ=2代入,得原式=2310,故选C. 答案:C4.(2017·高考全国卷Ⅰ)已知α∈(0,π2),tan α=2,则cos(α-π4)=________.解析:∵α∈(0,π2),tan α=2,∴sin α=255,cos α=55,∴cos(α-π4)=cos αcosπ4+sin αsin π4=22×(255+55)=31010. 答案:31010三角函数式的化简方法及基本思路(1)化简方法弦切互化,异名化同名,异角化同角,降幂或升幂,“1”的代换,辅助角公式等. (2)化简基本思路“一角二名三结构”,即:一看“角”,这是最重要的一环,通过角之间的差别与联系,把角进行合理地拆分,从而正确使用公式;二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“切化弦”,关于sin α·cos α的齐次分式化切等;三看“结构特征”,分析结构特征,找到变形的方向,常见的有“遇到分式要通分”,“遇根式化被开方式为完全平方式”等.解三角形的基本问题及应用授课提示:对应学生用书第22页[悟通——方法结论] 正、余弦定理、三角形面积公式(1)a sin A =b sin B =c sin C =a +b +c sin A +sin B +sin C=2R (R 为△ABC 外接圆的半径). 变形:a =2R sin A ,b =2R sin B ,c =2R sin C ; sin A =a 2R ,sin B =b 2R ,sin C =c2R;a ∶b ∶c =sin A ∶sin B ∶sin C .(2)a 2=b 2+c 2-2bc cos A ,b 2=a 2+c 2-2ac cos B ,c 2=a 2+b 2-2ab cos C .推论:cos A =b 2+c 2-a 22bc ,cos B =a 2+c 2-b 22ac ,cos C =a 2+b 2-c 22ab.变形:b 2+c 2-a 2=2bc cos A ,a 2+c 2-b 2=2ac cos B ,a 2+b 2-c 2=2ab cos C . (3)S △ABC =12ab sin C =12ac sin B =12bc sin A .(1)(2017·高考全国卷Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin B+sin A (sin C -cos C )=0,a =2,c =2,则C =( )A.π12B.π6C.π4D.π3解析:因为sin B +sin A (sin C -cos C )=0,所以sin(A +C )+sin A sin C -sin A cos C =0,所以sin A cos C +cos A sin C +sin A sin C -sin A cos C =0,整理得sin C (sin A +cos A )=0,因为sin C ≠0,所以sin A +cos A =0,所以tan A =-1,因为A ∈(0,π),所以A =3π4,由正弦定理得sin C =c ·sin A a=2×222=12,又0<C <π4,所以C =π6. 答案:B(2)(2018·高考全国卷Ⅱ)在△ABC 中,cos C 2=55,BC =1,AC =5,则AB =( )A .4 2 B.30 C.29D .2 5解析:∵cos C 2=55,∴cos C =2cos 2C 2-1=2×⎝ ⎛⎭⎪⎫552-1=-35.在△ABC 中,由余弦定理,得AB 2=AC 2+BC 2-2AC ·BC ·cos C =52+12-2×5×1×⎝ ⎛⎭⎪⎫-35=32,∴AB =32=4 2. 故选A. 答案:A(3)(2018·福州模拟)如图,小明同学在山顶A 处观测到一辆汽车在一条水平的公路上沿直线匀速行驶,小明在A 处测得公路上B ,C 两点的俯角分别为30°,45°,且∠BAC =135°.若山高AD =100 m ,汽车从B 点到C 点历时14 s ,则这辆汽车的速度约为________m/s(精确到0.1).参考数据:2≈1.414,5≈2.236.解析:因为小明在A 处测得公路上B ,C 两点的俯角分别为30°,45°,所以∠BAD =60°,∠CAD =45°.设这辆汽车的速度为v m/s ,则BC =14v ,在Rt △ADB 中,AB =AD cos ∠BAD =ADcos 60°=200.在Rt △ADC 中,AC =AD cos ∠CAD =100cos 45°=100 2.在△ABC 中,由余弦定理,得BC 2=AC2+AB 2-2AC ·AB ·cos∠BAC ,所以(14v )2=(1002)2+2002-2×1002×200×cos 135°,所以v=50107≈22.6,所以这辆汽车的速度约为22.6 m/s.答案:22.61.解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理;如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理;以上特征都不明显时,则考虑两个定理都有可能用到.2.关于解三角形问题,一般要用到三角形的内角和定理,正弦、余弦定理及有关三角形的性质,常见的三角恒等变换方法和原则都适用,同时要注意“三统一”,即“统一角、统一函数、统一结构”.[练通——即学即用]1.(2018·南昌模拟)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,cos 2A =sin A ,bc =2,则△ABC 的面积为( )A.12B.14C .1D .2 解析:由cos 2A =sin A ,得1-2sin 2A =sin A ,解得sin A =12(负值舍去),由bc =2,可得△ABC 的面积S =12bc sin A =12×2×12=12.答案:A2.(2018·广州模拟)在△ABC 中,∠ACB =60°,BC >1,AC =AB +12,当△ABC 的周长最短时,BC 的长是________.解析:设AC =b ,AB =c ,BC =a ,△ABC 的周长为l , 由b =c +12,得l =a +b +c =a +2c +12.又cos 60°=a 2+b 2-c 22ab =12,即ab =a 2+b 2-c 2,得a ⎝ ⎛⎭⎪⎫c +12=a 2+⎝ ⎛⎭⎪⎫c +122-c 2,即c =a 2-12a +14a -1.l =a +2c +12=a +2a 2-a +12a -1+12=3⎣⎢⎡⎦⎥⎤(a -1)2+43()a -1+12a -1+12=3⎣⎢⎡⎦⎥⎤(a -1)+12(a -1)+43+12 ≥3⎣⎢⎡⎦⎥⎤2(a -1)×12(a -1)+43+12,当且仅当a -1=12(a -1)时,△ABC 的周长最短,此时a =1+22,即BC 的长是1+22. 答案:1+22解三角形的综合问题授课提示:对应学生用书第23页[悟通——方法结论] 三角形中的常用结论(1)A +B =π-C ,A +B 2=π2-C2. (2)在三角形中大边对大角,反之亦然.(3)任意两边之和大于第三边,任意两边之差小于第三边.(4)在△ABC 中,tan A +tan B +tan C =tan A ·tan B ·tan C (A ,B ,C ≠π2).(2017·高考全国卷Ⅱ)(12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知(1)求cos B ❷; (2)若a +c =6❸,△ABC 的面积为2❹,求b . [学审题]条件信息想到方法注意什么信息❶:两角和与半角的三角等式关系 三角形内角和定理及倍角公式 (1)三角形中的三角恒等关系式化简时,三角形内角和定理及倍角公式的正确使用 (2)转化与化归思想、整体代入思想在解题过程中的应用信息❷:求cos B 化已知条件为cos B 的关系式 信息❸:a +c =6 寻找平方后与余弦定理中a 2+c 2的关系式信息❹:三角形面积为2利用面积公式来求ac 的值[规范解答] (1)由题设及A +B +C =π得sin B =8sin 2B2,(2分)即sin B =4(1-cos B ), (3分) 故17cos 2B -32cos B +15=0, (4分) 解得cos B =1517,cos B =1(舍去).(6分) (2)由cos B =1517,得sin B =817,(7分) 故S △ABC =12ac sin B =417ac .(8分) 又S △ABC =2,则ac =172.(9分)由余弦定理及a +c =6得b 2=a 2+c 2-2ac cos B=(a +c )2-2ac (1+cos B ) (10分)=36-2×172×⎝ ⎛⎭⎪⎫1+1517=4. (11分) 所以b =2.(12分)1.与三角形面积有关的问题的解题模型2.学科素养:通过三角恒等变换与利用正、余弦定理着重考查逻辑推理与数学运算两大素养.[练通——即学即用](2018·长郡中学模拟)在锐角△ABC 中,a ,b ,c 分别为角A ,B ,C 的对边,且4sin A cos 2A -3cos(B +C )=sin 3A + 3.(1)求A 的大小;(2)若b =2,求△ABC 面积的取值范围.解析:(1)∵A +B +C =π,∴cos(B +C )=-cos A ①,∵3A =2A +A ,∴sin 3A =sin(2A +A )=sin 2A cos A +cos 2A sin A ②, 又sin 2A =2sin A cos A ③, cos 2A =2cos 2A -1 ④,将①②③④代入已知,得2sin 2A cos A +3cos A =sin 2A cos A +cos 2A sin A +3, 整理得sin A +3cos A =3,即sin ⎝⎛⎭⎪⎫A +π3=32,又A ∈⎝⎛⎭⎪⎫0,π2,∴A +π3=2π3,即A =π3.(2)由(1)得B +C =2π3,∴C =2π3-B ,∵△ABC 为锐角三角形, ∴2π3-B ∈⎝ ⎛⎭⎪⎫0,π2且B ∈⎝⎛⎭⎪⎫0,π2, 解得B ∈⎝ ⎛⎭⎪⎫π6,π2,在△ABC 中,由正弦定理得2sin B =c sin C,∴c =2sin C sin B =2sin ⎝ ⎛⎭⎪⎫2π3-B sin B =3tan B+1,又B ∈⎝⎛⎭⎪⎫π6,π2,∴1tan B ∈()0,3,∴c ∈(1,4),∵S △ABC =12bc sin A =32c ,∴S △ABC ∈⎝ ⎛⎭⎪⎫32,23.授课提示:对应学生用书第124页一、选择题1.(2018·合肥调研)已知x ∈()0,π,且cos ⎝ ⎛⎭⎪⎫2x -π2=sin 2x ,则tan ⎝ ⎛⎭⎪⎫x -π4等于( )A.13 B .-13 C .3 D .-3 解析:由cos ⎝ ⎛⎭⎪⎫2x -π2=sin 2x 得sin 2x =sin 2x ,∵x ∈(0,π),∴tan x =2,∴tan ⎝⎛⎭⎪⎫x -π4=tan x -11+tan x =13.答案:A2.(2018·成都模拟)已知sin α=1010,α∈⎝ ⎛⎭⎪⎫0,π2,则cos ⎝ ⎛⎭⎪⎫2α+π6的值为( )A.43-310 B.43+310 C.4-3310D.33-410解析:∵sin α=1010,α∈⎝⎛⎭⎪⎫0,π2,∴cos α=31010,sin 2α=2sin αcos α=2×1010×31010=610=35,cos 2α=1-2sin 2α=1-2×⎝⎛⎭⎪⎫10102=1-15=45, ∴cos ⎝ ⎛⎭⎪⎫2α+π6=45×32-35×12=43-310. 答案:A3.(2018·昆明三中、五溪一中联考)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若△ABC 的面积为S ,且2S =(a +b )2-c 2,则tan C 等于( )A.34 B.43 C .-43D .-34解析:因为2S =(a +b )2-c 2=a 2+b 2-c 2+2ab , 由面积公式与余弦定理,得ab sin C =2ab cos C +2ab , 即sin C -2cos C =2,所以(sin C -2cos C )2=4, sin 2C -4sin C cos C +4cos 2Csin 2C +cos 2C =4, 所以tan 2C -4tan C +4tan 2C +1=4, 解得tan C =-43或tan C =0(舍去).答案:C4.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若c b<cos A ,则△ABC 为( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .等边三角形解析:根据正弦定理得c b =sin Csin B<cos A ,即sin C <sin B cos A .∵A +B +C =π,∴sin C =sin(A +B )<sin B cos A , 整理得sin A cos B <0.又三角形中sin A >0,∴cos B <0,π2<B <π,∴△ABC 为钝角三角形. 答案:A5.如图,在△ABC 中,∠C =π3,BC =4,点D 在边AC 上,A D =D B ,D E ⊥AB ,E 为垂足.若DE =22,则cos A 等于( )A.223 B.24 C.64D.63解析:依题意得,BD =AD =DE sin A =22sin A ,∠BDC =∠ABD +∠A =2∠A .在△BCD 中,BCsin ∠BDC=BDsin C ,4sin 2A =22sin A ×23=423sin A ,即42sin A cos A =423sin A ,由此解得cos A =64. 答案:C6.(2018·高考全国卷Ⅰ)已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点A (1,a ),B (2,b ),且cos 2α=23,则|a -b |=( )A.15B.55C.255D .1解析:由cos 2α=23,得cos 2α-sin 2α=23,∴cos 2α-sin 2αcos 2α+sin 2α=23,即1-tan 2α1+tan 2α=23,∴tan α=±55,即b -a 2-1=±55, ∴|a -b |=55. 故选B. 答案:B7.(2018·武汉调研)如图,据气象部门预报,在距离某码头南偏东45°方向600 km 处的热带风暴中心正以20 km/h 的速度向正北方向移动,距风暴中心450 km 以内的地区都将受到影响,则该码头将受到热带风暴影响的时间为( )A .14 hB .15 hC .16 hD .17 h解析:记现在热带风暴中心的位置为点A ,t 小时后热带风暴中心到达B 点位置(图略),在△OAB 中,OA =600,AB =20t ,∠OAB =45°,根据余弦定理得6002+400t 2-2×20t×600×22≤4502,即4t 2-1202t +1 575≤0,解得302-152≤t≤302+152,所以Δt =302+152-302-152=15(h),故选B.答案:B8.(2018·武汉调研)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若a =2b sin C ,则 tan A +tan B +tan C 的最小值是( )A .4B .3 3C .8D .6 3解析:由a =2b sin C 得sin A =2sin B sin C ,∴sin(B +C )=sin B cos C +cos B sin C =2sin B sin C , 即tan B +tan C =2tan B tan C .又三角形中的三角恒等式tan A +tan B +tan C =tan A tan B tan C , ∴tan B tan C =tan Atan A -2,∴tan A tan B tan C =tan A ·tan Atan A -2,令tan A -2=t ,得tan A tan B tan C =(t +2)2t =t +4t+4≥8,当且仅当t =4t, 即t =2,tan A =4 时,取等号.答案:C 二、填空题9.(2018·广西三市一联)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,a sin B =2sin C ,cos C =13,△ABC 的面积为4,则c =________.解析:由a sin B =2sin C ,得ab =2c , 由cos C =13,得sin C =223,则S △ABC =12ab sin C =23c =4,解得c =6.答案:610.(2018·皖南八校联考)若α∈⎝ ⎛⎭⎪⎫0,π2,cos ⎝ ⎛⎭⎪⎫π4-α=22cos2α,则sin 2α=________.解析:由已知得22(cos α+sin α)=22(cos α-sin α)·(cos α+sin α),所以cos α+sin α=0或cos α-sin α=14,由cos α+sin α=0得tan α=-1,因为α∈⎝⎛⎭⎪⎫0,π2,所以cos α+sin α=0不满足条件;由cos α-sin α=14,两边平方得 1-sin 2α=116,所以sin 2α=1516.答案:151611.已知△ABC 中,AB +2AC =6,BC =4,D 为BC 的中点,则当AD 最小时,△ABC 的面积为________.解析:AC 2=AD 2+CD 2-2AD ·CD ·cos∠ADC , 且AB 2=AD 2+BD 2-2AD ·BD ·cos∠ADB , 即AC 2=AD 2+22-4AD ·cos∠ADC , 且(6-2AC )2=AD 2+22-4AD ·cos∠ADB , ∵∠ADB =π-∠ADC , ∴AC 2+(6-2AC )2=2AD 2+8,∴AD 2=3AC 2-122AC +282=3(AC -22)2+42,当AC =22时,AD 取最小值2, 此时cos ∠ACB =8+4-282=528,∴sin ∠ACB =148, ∴△ABC 的面积S =12AC ·BC ·sin∠ACB =7.答案:712.(2018·成都模拟)已知△ABC 中,AC =2,BC =6,△ABC 的面积为32.若线段BA 的延长线上存在点D ,使∠BDC =π4,则CD =________.解析:因为S △ABC =12AC ·BC ·sin∠BCA ,即32=12×2×6×sin∠BCA , 所以sin ∠BCA =12.因为∠BAC >∠BDC =π4,所以∠BCA =π6,所以cos ∠BCA =32.在△ABC 中,AB 2=AC 2+BC 2-2AC ·BC ·cos∠BCA=2+6-2×2×6×32=2, 所以AB =2,所以∠ABC =π6,在△BCD 中,BC sin ∠BDC =CDsin ∠DBC ,即622=CD12,解得CD = 3. 答案: 3 三、解答题13.(2018·武汉调研)在锐角△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,满足cos 2A -cos 2B +2cos ⎝⎛⎭⎪⎫π6-B ·cos ⎝ ⎛⎭⎪⎫π6+B =0.(1)求角A 的值;(2)若b =3且b ≤a ,求a 的取值范围.解析:(1)由cos 2A -cos 2B +2cos ⎝ ⎛⎭⎪⎫π6-B cos ⎝ ⎛⎭⎪⎫π6+B =0,得2sin 2B -2sin 2A +2⎝ ⎛⎭⎪⎫34cos 2B -14sin 2B =0,化简得sin A =32,又△ABC 为锐角三角形,故A =π3. (2)∵b =3≤a ,∴c ≥a ,∴π3≤C <π2,π6<B ≤π3,∴12<sin B ≤32. 由正弦定理a sin A =bsin B ,得a 32=3sin B ,∴a =32sin B ,由sin B ∈⎝ ⎛⎦⎥⎤12,32得a ∈[3,3).14.(2018·唐山模拟)在△ABC 中,AB =2AC =2,AD 是BC 边上的中线,记∠CAD =α,∠BAD =β.(1)求sin α∶sin β;(2)若tan α=sin ∠BAC ,求BC . 解析:(1)∵AD 为BC 边上的中线, ∴S △AC D =S △AB D ,∴12AC ·AD sin α=12AB ·AD sin β, ∴sin α∶sin β=AB ∶AC =2∶1. (2)∵tan α=sin ∠BAC =sin(α+β), ∴sin α=sin(α+β)cos α, ∴2sin β=sin(α+β)cos α,∴2sin[(α+β)-α]=sin(α+β)cos α, ∴sin(α+β)cos α=2cos(α+β)sin α, ∴sin(α+β)=2cos(α+β)tan α, 又tan α=sin ∠BAC =sin(α+β)≠0, ∴cos(α+β)=cos ∠BAC =12,在△ABC 中,BC 2=AB 2+AC 2-2AB ·AC cos ∠BAC =3, ∴BC = 3.15.(2018·广州模拟)已知a ,b ,c 是△ABC 中角A ,B ,C 的对边,且3cos B cos C +2=3sinB sinC +2cos 2A .(1)求角A 的大小;(2)若△ABC 的面积S =53,b =5,求sin B sin C 的值.解析:(1)由3cos B cos C +2=3sin B sin C +2cos 2A , 得3cos(B +C )+2=2cos 2A , 即2cos 2A +3cos A -2=0, 即(2cos A -1)(cos A +2)=0, 解得cos A =12或cos A =-2(舍去).因为0<A <π,所以A =π3.(2)由S =12bc sin A =34bc =53,得bc =20,因为b =5,所以c =4.由余弦定理a 2=b 2+c 2-2bc cos A ,得a 2=25+16-2×20×12=21,故a =21.根据正弦定理a sin A =b sin B =csin C,得sin B sin C =b a sin A ×c a sin A =57.16.(2018·山西八校联考)在△ABC 中,a ,b ,c 分别是内角A ,B ,C 的对边,且(a +c )2=b 2+3ac .(1)求角B 的大小;(2)若b =2,且sin B +sin(C -A )=2sin 2A ,求△ABC 的面积. 解析:(1)由(a +c )2=b 2+3ac ,整理得a 2+c 2-b 2=ac ,由余弦定理得cos B =a 2+c 2-b 22ac =ac 2ac =12,∵0<B <π, ∴B =π3.(2)在△ABC 中,A +B +C =π,即B =π-(A +C ),故sin B =sin(A +C ), 由已知sin B +sin(C -A )=2sin 2A 可得sin(A +C )+sin(C -A )=2sin 2A , ∴sin A cos C +cos A sin C +sin C cos A -cos C sin A =4sin A cos A , 整理得cos A sin C =2sin A cos A . 若cos A =0,则A =π2,由b =2,可得c =2tan B =233,此时△ABC 的面积S =12bc =233.若cos A ≠0,则sin C =2sin A , 由正弦定理可知,c =2a ,代入a 2+c 2-b 2=ac ,整理可得3a 2=4,解得a =233,∴c =433,此时△ABC 的面积S =12ac sin B =233.综上所述,△ABC 的面积为233.17.(2018·常德市模拟)已知函数f (x )=2sin ωx +m cos ωx (ω>0,m >0)的最小值为-2,且图象上相邻两个最高点的距离为π.(1)求ω和m 的值;(2)若f ⎝ ⎛⎭⎪⎫θ2=65,θ∈⎝ ⎛⎭⎪⎫π4,3π4,求f ⎝ ⎛⎭⎪⎫θ+π8的值.解析:(1)易知f (x )=2+m 2sin(ωx +φ)(φ为辅助角), ∴f (x )min =-2+m 2=-2,∴m = 2.由题意知函数f (x )的最小正周期为π,∴2πω=π,∴ω=2.(2)由(1)得f (x )=2sin 2x +2cos 2x =2sin ⎝⎛⎭⎪⎫2x +π4, ∴f ⎝ ⎛⎭⎪⎫θ2=2sin ⎝ ⎛⎭⎪⎫θ+π4=65,∴sin ⎝ ⎛⎭⎪⎫θ+π4=35.∵θ∈⎝⎛⎭⎪⎫π4,3π4,∴θ+π4∈⎝ ⎛⎭⎪⎫π2,π,∴cos ⎝⎛⎭⎪⎫θ+π4=-1-sin 2⎝⎛⎭⎪⎫θ+π4=-45,∴sin θ=sin ⎝ ⎛⎭⎪⎫θ+π4-π4=sin ⎝ ⎛⎭⎪⎫θ+π4cos π4-cos ⎝⎛⎭⎪⎫θ+π4sin π4=7210,∴f ⎝ ⎛⎭⎪⎫θ+π8=2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫θ+π8+π4 =2sin ⎝ ⎛⎭⎪⎫2θ+π2=2cos 2θ=2(1-2sin 2θ)=2⎣⎢⎡⎦⎥⎤1-2×⎝⎛⎭⎪⎫72102=-4825.。
高考数学二轮复习 第一部分 专题篇 专题二 三角函数、平面向量 第二讲 三角恒等变换与解三角形课件 文(1)

的关系式进行求解. cos2 θ-sin2 θ 1-tan2 θ ∵cos 2θ= 2 = , cos θ+sin2 θ 1+tan2 θ 1 1- 9 4 1 又∵tan θ=- ,∴cos 2θ= = . 3 1 5 1+ 9
考点二
考点三
考点一
试题
解析
考点一
考点二
考点三
π 3 2.(2016· 高考全国Ⅰ卷)已知 θ 是第四象限角,且 sinθ+ = , 4 5 4 π - 则 tanθ-4 =________. 3
考点一
试题
解析
考点一
考点二
考点三
π π π π 1 3.(2016· 合肥检测)已知 cos +α· cos -α=- ,α∈ , . 4 6 3 3 2
(1)求 sin 2α 的值; 1 (2)求 tan α- 的值. tan α
考点一
试题
π π π π π 1 1 (1)cos + α · cos - α=cos + α · sin + α= sin2α+ =- , 3 2 4 6 3 6 6
考点一
三角恒等变换
[经典结论· 全通关]
考点一
三角函数恒等变换“四大策略” (1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45° 等;
考点二
考点三
(2)项的分拆与角的配凑: 如 sin2α+2cos2α=(sin2α+cos2α)+cos2α, α=(α-β)+β 等; (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次; (4)弦、切互化:一般是切化弦.
考点二
考点三
考点三
试题
2020届高考数学二轮复习全程方略课件:专题二 三角函数与平面向量(2)三角恒等变换与解三角形 Wo

[变式训练] (2017·西安质检)如图,一辆汽车在一条 水平的公路上向正西行驶,到 A 处时测得公路北侧一山 顶 D 在西偏北 30°的方向上,行驶 600 m 后到达 B 处, 测得此山顶在西偏北 75°的方向上,仰角为 30°,则此 山的高度 CD=________m.
[变式训练] 设 f(x)=sin xcos x-cos2x+π4. (1)求 f(x)的单调区间; (2)在锐角△ABC 中,角 A,B,C 的对边分别为 a, b,c.若 fA2=0,a=1,求△ABC 面积的最大值. 解:(1)由题意知 f(x)= sin22x-1+cos22x+π2=
第二十七页,编辑于星期日:一点 五分。
sin22x-1-s2in
2x =sin
2x-12.
由-π2+2kπ≤2x≤π2+2kπ,k∈Z,
可得-π4+kπ≤x≤π4+kπ,k∈Z.
由π2+2kπ≤2x≤32π+2kπ,k∈Z,
可得π4+kπ≤x≤34π+kπ,k∈Z.
第二十八页,编辑于星期日:一点 五分。
所 以 f(x) 的
(k∈Z),单调递减区间是π4+kπ,34π+kπ(k∈Z).
(2)由
A
f
2
=sin
A-12=0,
得 sin A=12,
由题意知
A
为锐角,所以
cos
A=
3 2.
第二十九页,编辑于星期日:一点 五分。
由余弦定理 a2=b2+c2-2bccos A,
可得 1+ 3bc=b2+c2≥2bc,
即 bc≤2+ 3,且当 b=c 时等号成立.
因此12bcsin
2+ A≤ 4
3 .
2020高考数学二轮总复习第1部分层级2专题2三角函数与解三角形第2讲三角恒等变换与解三角形课件理

A.-12
B.12
C.-
3 2
D.
3 2
(3)(一题多解)(2019·福建省百校临考冲刺)若 α∈(0,π),且 3sin α+2cos α=2,则
tan α2=( )
A.
3 2
B.
3 4
C.2 3 3
D.4 3 3
1 [解析] (1)cossi2n15151°0-°ssinin22105°5°=sinc7o0s°3s1in0°20°=cosc2o0s°s5i0n°20°=2ssiinn4400°°=12. (2)解法一:因为 α 为锐角,β 为第二象限角,cos(α-β)>0,sin(α+β)>0, 所以 α-β 为第四象限角,α+β 为第二象限角, 因此 sin(α-β)=- 23,cos(α+β)=- 23, 所以 sin 2α=sin[(α-β)+(α+β)]=- 23×- 23+12×12=1. 因为 α 为锐角,所以 2α=π2, 所以 sin(3α-β)=sin(2α+α-β)=cos(α-β)=12,故选 B.
A.4 2
B. 30
C. 29
D.2 5
解析:选 A ∵cosC2= 55, ∴cos C=2cos2C2-1=2× 552-1=-35. 在△ABC 中,由余弦定理,得 AB2=AC2+BC2-2AC·BC·cos C=52+12-2×5×1×-35=32, ∴AB= 32=4 2.故选 A.
4.(2018·全国卷Ⅲ)△ABC 的内角 A,B,C 的对边分别为 a,b,c.若△ABC 的面积
2a,则ba=( )
边长,且直线 bx+ycos A+cos B=0 与 ax+ycos B+cos A=0 平行,则△ABC 一定是( )
高考数学二轮复习专题篇素养提升 专题1三角函数三角恒等变换与解三角形第2讲三角恒等变换与解三角形文理

②由 f(x)=12sin2x-π6= 63,
得 sin2x-π6= 33,
∵x∈0,π4,∴-π6≤2x-π6≤π3,
∴cos2x-π6=
6 3.
∴cos 2x=cos2x-π6+π6 =cos2x-π6× 23-sin2x-π6×21 = 36× 23- 33×12= 22- 63.
三角恒等变换的“四大策略” (1)常值代换:特别是“1”的代换, 1=sin2θ+cos2θ=tan 45°等. (2)项的拆分与角的配凑: 如sin2α+2cos2α=(sin2α+cos2α)+cos2α,α=(α-β)+β等. (3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次. (4)弦、切互化:一般是切化弦.
分值 10 12 10
年份 卷别 Ⅰ卷
2019 Ⅱ卷 Ⅲ卷 Ⅰ卷
2018 Ⅱ卷 Ⅲ卷
题号
考查角度
分值
17 正余弦定理
12
二倍角公式、基本关系式、余弦定理、
15
5
三角形面积公式
18
正余弦定理、三角形面积公式
12
17
正余弦定理、解三角形
12
二倍角、辅助角公式、基本关系式、
10、15 和的正弦公式、余弦定理
10°=
典例1
A.34
(1)(2020·全国Ⅱ卷模拟)cos2 40°+2sin 35°sin 55°sin
( A)
B.14
C.12+
3 2
D.3
3 4
(2)(2020·宜宾模拟)已知 α∈0,π2,且 3sin2α-5cos2α+sin 2α=0,则
sin 2α+cos 2α=
( A)
A.1
B.-2137
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲 三角恒等变换与解三角形[限时规范训练]一、选择题1.(2017·高考山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( ) A.π2 B.2π3C .πD .2π解析:y =3sin 2x +cos 2x =2sin ⎝ ⎛⎭⎪⎫2x +π6,T =2π2=π.故选C. 答案:C2.(2017·高考全国卷Ⅲ)已知sin α-cos α=43,则sin 2α=( )A .-79B .-29C.29D.79解析:∵sin α-cos α=43,∴(sin α-cos α)2=1-2sin αcos α=1-sin 2α=169,∴sin 2α=-79.故选A.答案:A3.已知α∈⎝ ⎛⎭⎪⎫π2,3π2,tan ⎝ ⎛⎭⎪⎫α-π4=-7,则sin α的值等于( )A.35 B .-35C.45D .-45解析:因为tan ⎝⎛⎭⎪⎫α-π4=-7,所以tan α-11+tan α=-7,得tan α=-34,即sin αcos α=-34.又α∈⎝ ⎛⎭⎪⎫π2,3π2,所以α∈⎝ ⎛⎭⎪⎫π2,π.又sin 2 α+cos 2 α=1,得sin α=35,故选A.答案:A4.在△ABC 中,cos 2A 2=b +c 2c(a ,b ,c 分别为角A ,B ,C 的对边),则△ABC 的形状为( )A .正三角形B .直角三角形C .等腰三角形或直角三角形D .等腰直角三角形解析:∵cos 2A 2=b +c 2c ,∴1+cos A 2=b +c 2c ,∴1+b 2+c 2-a 22bc =b +c c,化简得a 2+b 2=c 2.故△ABC 是直角三角形. 答案:B5.在△ABC 中,A =60°,若a ,b ,c 成等比数列,则b sin Bc=( ) A.12 B.32 C.22D.6+24解析:∵a ,b ,c 成等比数列,∴b 2=ac ,① 又A =60°,则由正弦定理得asin A =bsin B,即a =b sin A sin B ,代入①得,b 2=cb sin A sin B ,则b =c sin A sin B, 所以b sin Bc =sin A =sin 60°=32.故选B. 答案:B6.在锐角△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若sin A =223,a =2,S △ABC =2,则b 的值为( ) A. 3 B.322C .2 2D .2 3解析:由S △ABC =12bc sin A =12bc ×223=2,解得bc =3.因为A 为锐角,sin A =223,所以cosA =13,由余弦定理得a 2=b 2+c 2-2bc cos A ,代入数据解得b 2+c 2=6,则(b +c )2=12,b +c =23,所以b =c =3,故选A. 答案:A7.(2017·高考全国卷Ⅲ)函数f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6的最大值为( )A.65 B .1 C.35D.15解析:法一:∵f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6=15⎝ ⎛⎭⎪⎫12sin x +32cos x +32cos x +12sin x =110sin x +310cos x +32cos x +12sin x =35sin x +335cos x =65sin ⎝⎛⎭⎪⎫x +π3,∴当x =π6+2k π(k ∈Z)时,f (x )取得最大值65.故选A.法二:∵⎝ ⎛⎭⎪⎫x +π3+⎝ ⎛⎭⎪⎫π6-x =π2,∴f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6=15sin(x +π3)+cos(π6-x ) =15sin ⎝ ⎛⎭⎪⎫x +π3+sin ⎝ ⎛⎭⎪⎫x +π3=65sin ⎝⎛⎭⎪⎫x +π3≤65.∴f (x )max =65. 故选A.答案:A8.(2017·高考全国卷Ⅰ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知sin B +sin A (sin C -cos C )=0,a =2,c =2,则C =( ) A.π12 B.π6 C.π4D.π3解析:因为a =2,c =2,所以由正弦定理可知,2sin A =2sin C ,故sin A =2sin C .又B =π-(A +C ), 故sin B +sin A (sin C -cos C ) =sin(A +C )+sin A sin C -sin A cos C=sin A cos C +cos A sin C +sin A sin C -sin A cos C =(sin A +cos A )sin C =0.又C 为△ABC 的内角,故sin C ≠0, 则sin A +cos A =0,即tan A =-1. 又A ∈(0,π),所以A =3π4.从而sin C =12sin A =22×22=12. 由A =3π4知C 为锐角,故C =π6.故选B.答案:B 二、填空题9.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足b sin A =a cos B ,则角B 的大小为________.解析:∵b sin A =a cos B ,由正弦定理,得sin B sin A =sin A cosB. ∵sin A ≠0,∴sin B =cos B ,∵B 为△ABC 内角,∴B =π4.答案:π410.(2017·高考江苏卷)若tan ⎝⎛⎭⎪⎫α-π4=16,则tan α=________. 解析:法一:∵tan ⎝⎛⎭⎪⎫α-π4=tan α-tanπ41+tan αtanπ4=tan α-11+tan α=16,∴6tan α-6=1+tan α(tanα≠-1),∴tan α=75.法二:tan α=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π4+π4=tan ⎝ ⎛⎭⎪⎫α-π4+tan π41-tan ⎝ ⎛⎭⎪⎫α-π4tanπ4=16+11-16×1=75.答案:7511.(2017·高考北京卷)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若sin α=13,则cos(α-β)=________.解析:由题意知α+β=π+2k π(k ∈Z),∴β=π+2k π-α(k ∈Z), sin β=sin α,cos β=-cos α.又sin α=13,∴cos(α-β)=cos αcos β+sin αsin β=-cos 2α+sin 2α=2sin 2α-1=2×19-1=-79.答案:-7912.在△ABC 中,若C =60°,AB =2,则AC +BC 的取值范围为________.解析:设角A ,B ,C 的对边分别为a ,b ,c .由题意,得c =2.由余弦定理可得c 2=a 2+b 2-2ab cosC ,即4=a 2+b 2-ab =(a +b )2-3ab ≥14(a +b )2,得a +b ≤4.又由三角形的性质可得a +b >2,综上可得2<a +b ≤4. 答案:(2,4] 三、解答题13.(2016·高考山东卷)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知2(tan A +tan B )=tan A cos B +tan Bcos A. (1)证明:a +b =2c ; (2)求cos C 的最小值. 解析:(1)证明:由题意得2⎝⎛⎭⎪⎫sin A cos A +sin B cos B =sin A cos A cos B +sin B cos B cos A,∴2sin(A +B )=sin A +sinB. 又∵A +B =π-C ,∴sin(A +B )=sin ()π-C =sin C , ∴2sin C =sin A +sin B 由正弦定理得a +b =2c . (2)由(1)知c =a +b2,所以cos C =a 2+b 2-c22ab=a 2+b 2-⎝⎛⎭⎪⎫a +b 222ab =38⎝ ⎛⎭⎪⎫a b +b a -14≥12,当且仅当a =b 时,等号成立,故cos C 的最小值为12.14.(2016·高考四川卷)在△ABC 中,角A ,B ,C 所对的边分别是a ,b ,c ,且cos A a +cos B b =sin Cc.(1)证明:sin A sin B =sin C ; (2)若b 2+c 2-a 2=65bc ,求tanB.解析:(1)证明:根据正弦定理,可设a sin A =b sin B =csin C =k (k >0),则a =k sin A ,b =k sin B ,c =k sin C ,代入cos A a +cos B b =sin C c 中,有cos A k sin A +cos B k sin B =sin C k sin C ,变形可得sin A sin B =sin A cos B +cos A sin B =sin(A +B ). 在△ABC 中,由A +B +C =π, 有sin(A +B )=sin(π-C )=sin C , 所以sin A sin B =sin C .(2)由已知,b 2+c 2-a 2=65bc ,根据余弦定理,有cos A =b 2+c 2-a 22bc =35,所以sin A =1-cos 2A =45.由(1),知sin A sin B =sin A cos B +cos A sin B ,所以45sin B =45cos B +35sin B ,故tan B =sin Bcos B =4.15.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2sin C -sin B sin B =a 2+c 2-b2b 2+c 2-a 2.(1)求角A 的大小;(2)若a =3,sin C =2sin B ,求b ,c 的值. 解析:(1)由正、余弦定理得2sin C -sin B sin B =a cos B b cos A =sin A cos Bsin B cos A,所以2sin C cos A =sin(A +B )=sin C , 因为sin C ≠0,故cos A =12,所以A =π3.(2)由sin C =2sin B 得c =2b , 因为a =3,A =π3,所以由余弦定理得a 2=b 2+c 2-2bc cos A =b 2+c 2-bc =3b 2, 解得b =3,c =2 3.。
