生物统计学 第五章 卡方检验
合集下载
重庆大学生物统计学_第五章 卡方检验
卡方 (χ2) 分布的函数
( ) CHIDIST：自由度为n的卡方分布在x点处的单尾概率 P χ2 > x
CHIINV： 返回自由度为n的卡方分布的单尾概率函数的逆函 数• CHIDIST •
X•
需要计算分布的数字（X非负值） •
Degrees_freedom • 自由度 •
CHIINV • Probability • 卡方分布的单尾概率 • Degrees_freedom • 自由度 •
没有关联 • 2. 规定显著性水平 • 3. 根据无效假设计算出理论数 • 4. 根据规定的显著水平和自由度计算出卡方值，
再和计算的卡方值进行比较。 • 如果接受假设，则说明因子之间无相关联，
是相互独立的 • 如果拒绝假设，则说明因子之间的关联是显
著的，不独立 •
一、2X2列联表的独立性检验 •
设A、B是一个随机试验中的两个事件，其中A可能 出现r1、r2个结果，B可能出现c1、c2个结果，两 因子相互作用形成4个数，分别以O11、O12、O21、 O22表示，即 • 2X2列联表的一般形式 •
故应否定H0，接受HA，认为鲤鱼体色F2性状比不符合3:1比率
（4）推断：由CHIINV(0.025, 1)=6.63, 即 χ c 2 > χ0 2.05(1),即P<0.05
故应否定H0，接受HA，认为鲤鱼体色F2性状比不符合3:1比率
独立性检验 •
步骤： • 1. 提出无效假设，即认为所观测的各属性之间
故应否定H0，接受HA，认为吸烟与患气管病极显著相关
（4）推断：由CHIINV(0.025, 1)=6.63, 即 故应否定H0，接受HA，认为吸烟与患气管炎病密切相关
二、rXc列联表的独立性检验 •
《卡方检验正式》课件
卡方检验的结果可以直接解释为实际意义 ，例如，如果卡方值较大，则说明观察频 数与期望频数存在显著差异。
缺点
对数据要求高
卡方检验要求数据量较大，且各分类的期望频数不能太小，否则可能 导致结果不准确。
对离群值敏感
卡方检验对离群值比较敏感，离群值可能会对结果产生较大的影响。
无法处理缺失值
卡方检验无法处理含有缺失值的数据，如果数据中存在缺失值，需要 进行适当的处理。
案例二：市场研究中的卡方检验
总结词
市场研究中，卡方检验用于评估不同市 场细分或产品特征与消费者行为之间的 关联。
VS
详细描述
在市场研究中，卡方检验可以帮助研究者 了解消费者对不同品牌、产品或服务的偏 好。例如，通过比较不同年龄段消费者对 某品牌的选择比例，企业可以更好地制定 市场策略和产品定位。
案例三：社会调查中的卡方检验
小，表示两者之间的差异越小。通常根据卡方值的概率水平来判断差异
是否具有统计学显著性。
02
卡方检验的步骤
建立假设
假设1
观察频数与期望频数无显著差异
假设2
观察频数与期望频数有显著差异
收集数据
从样本数据中获取观察频数 确定期望频数，可以使用理论值或预期频数
制作交叉表
将收集到的数据整理成二维表格形式，行和列分别表示分类变量
卡方检验的基本思想
01
基于假设检验原理
卡方检验基于假设检验的原理，通过构建原假设和备择假设，利用观测
频数与期望频数的差异来评估原假设是否成立。
02
比较实际观测频数与期望频数
卡方检验的核心是比较实际观测频数与期望频数，通过卡方值的大小来
评估两者之间的差异程度。
03
生物统计学第五章 χ2检验
是指对样本的理论数先通过一定的理论分 布推算出来，然后用实际观测值与理论数相比 实际观测值与 布推算出来，然后用实际观测值 理论数相比 较，从而得出实际观测值与理论数之间是否吻 因此又叫吻合度检验。 合。因此又叫吻合度检验。
独立性检验
是指研究两个或两个以上 两个或两个以上的 是指研究两个或两个以上的计数资料或属 性资料之间是相互独立的或者是相互联系的假 性资料之间是相互独立的或者是相互联系的假 设检验， 设检验，通过假设所观测的各属性之间没有关 然后证明这种无关联的假设是否成立。 联，然后证明这种无关联的假设是否成立。
羔羊性别观察值与理论值
性别 公 母 合计 观察值（ ） 观察值（O） 428 448 876 理论值(E) 理论值 438 438 876 O-E -10 +10
0
由于差数之和正负相消，并不能反映实 由于差数之和正负相消， 际观测值与理论值相差的大小。 际观测值与理论值相差的大小。
为了避免正、负相抵消的问题， 为了避免正、负相抵消的问题，可将实际 观测值与理论值的差数平方后再相加， 观测值与理论值的差数平方后再相加，也就是 计算： 计算：
3.计算样本的χ 3.计算样本的χ2值 计算样本的
4.进行统计推断 4.进行统计推断 χ2 < χ2α χ2 > χ2α P > α P < α H0 H0 HA HA
χ2检验的注意事项
1、任何一组的理论次数Ei 都必须大于5，如果Ei 任何一组的理论次数E 都必须大于5 如果E ≤5， ≤5，则需要合并理论组或增大样本容量以满足 Ei ＞ 5 在自由度＝ 需进行连续性矫正， 2、在自由度＝1时，需进行连续性矫正，其矫正 的 χ 2c 为 ： χ2＝ ∑ （ Oi－Ei － 0.5 ）2 Ei
独立性检验
是指研究两个或两个以上 两个或两个以上的 是指研究两个或两个以上的计数资料或属 性资料之间是相互独立的或者是相互联系的假 性资料之间是相互独立的或者是相互联系的假 设检验， 设检验，通过假设所观测的各属性之间没有关 然后证明这种无关联的假设是否成立。 联，然后证明这种无关联的假设是否成立。
羔羊性别观察值与理论值
性别 公 母 合计 观察值（ ） 观察值（O） 428 448 876 理论值(E) 理论值 438 438 876 O-E -10 +10
0
由于差数之和正负相消，并不能反映实 由于差数之和正负相消， 际观测值与理论值相差的大小。 际观测值与理论值相差的大小。
为了避免正、负相抵消的问题， 为了避免正、负相抵消的问题，可将实际 观测值与理论值的差数平方后再相加， 观测值与理论值的差数平方后再相加，也就是 计算： 计算：
3.计算样本的χ 3.计算样本的χ2值 计算样本的
4.进行统计推断 4.进行统计推断 χ2 < χ2α χ2 > χ2α P > α P < α H0 H0 HA HA
χ2检验的注意事项
1、任何一组的理论次数Ei 都必须大于5，如果Ei 任何一组的理论次数E 都必须大于5 如果E ≤5， ≤5，则需要合并理论组或增大样本容量以满足 Ei ＞ 5 在自由度＝ 需进行连续性矫正， 2、在自由度＝1时，需进行连续性矫正，其矫正 的 χ 2c 为 ： χ2＝ ∑ （ Oi－Ei － 0.5 ）2 Ei
生物统计学第四版--教学大纲
课程简介《生物统计学》是运用数理统计的原理和方法来分析和解释生物界各种现象和试验调查资料的一门学科，是生物学各专业的专业基础课。
本门课程在第七学期进行，是在学生已学习了《高等数学》课程和《植物学》、《动物学》、《生理学》、《遗传学》等生物学各学科的基础知识的基础上开设本门课程。
本课程系统地介绍了生物统计学的基本原理和方法,在简要叙述了生物统计学的概念、产生、发展和作用、生物学研究中试验资料的整理、特征数的计算、概率和概率分布、抽样分布基础上，着重介绍了平均数和频率的假设检验、X 2检验、方差分析、直线回归与相关分析、可直线化的非线性回归分析、协方差分析、试验设计的原理和常用试验设计及其统计分析、多元回归与相关分析和多项式回归分析，同时简要介绍聚类分析、判别分析、主成分分析、因子分析、典型相关、时间序列分析等多元分析。
本课程的主要目的是培养学生具有生物学试验设计的能力和对试验资料进行统计分析处理的能力.一、教学环节和教学方法1教学环节本门课程为生物学的专业基础课，在第七学期进行。
学生已学习了《高等数学》课程和《植物学》、《动物学》、《生理学》、《遗传学》等生物学各学科的基础知识，在此基础上开设本门课程。
主要教学形式为课堂讲授，主要教学环节包括课堂讲授、辅导答疑、课外作业、习题讲解等。
2教学方法以课堂讲授为主,研制电子教案和多媒体幻灯片以及C A I课件,在教学方法和手段上采用现代教育技术.二、本课程的性质和任务《生物统计学》是运用数理统计的原理和方法来分析和解释生物界各种现象和试验调查资料的一门学科，是生物学各专业的专业基础课.随着生物学的不断发展，对生物体的研究和观察已不再局限于定性的描述，而是需要从大量调查和测定数据中，应用统计学方法，分析和解释其数量上的变化，以正确制定试验计划,科学地对试验结果进行分析，从而作出符合科学实际的推断。
《生物统计学》不仅提供如何正确地设计科学试验和收集数据的方法，而且也提供如何正确地整理、分析数据,得出客观、科学的结论的方法。
生物统计学—卡方检验
CHIINV Probability Degrees_freedom
卡方分布的单尾概率 自由度
精品课件
卡方检验基础
2检验是以2分布为基础的一种假设检验 方法，主要用于分类变量，根据样本数据推 断总体的分布与期望分布是否有显著差异， 或推断两个分类变量是否相关或相互独立。
精品课件
卡方检验基础
2值的计算：
其否定 2 区 2为 和 2 ： 2
1
2
2
精品课件
例：已知某农田受到重金属污染，经抽样测定铅浓度分别为:
4.2, 4.5, 3.6, 4.7, 4.0, 3.8, 3.7, 4.2 (ug/g),方差为
0.150, 试检验受到污染的农田铅浓度的方差是不是和正常 浓度铅浓度的方差（0.065）相同
分析：1）一个样本方差同质性检验
由于离散型资料的卡方检验只是近似地服
从连续型变量的卡方分布，所以在对离散型资料
进行卡方检验计算的时，结果常常偏低，特别是
当自由度df=1时，有较大偏差，为此需要进行矫
正：
k c2 i1
等
精品课件
卡方 (c2) 分布
总体
m
选择容量为n 的 简单随机样本 计算样本方差S2
计算卡方值
2 = (n-1)S2/σ2
计算出所有的
2值
精品课件
不同容0
2
卡方 (c2) 分布的特点
不同容量样本的抽样分布
1、 2分布是一个以自由度n为参数
的分布族，自由度n决定了分布的 形状，对于不同的n有不同的卡方 分布
如果样本确实是抽自由（P1， P2，…,Pk）代表的总体，Oi和Ei之间的差异就只
是随机误差，则Pearson统计量可视为服从卡方 分布
统计学卡方检验
个体化干预
根据分析结果，为患者提供个体化的干预措施，提高生存质量。
06
卡方检验注意事项及局限 性讨论
样本量要求及抽样方法选择
样本量要求
卡方检验对样本量有一定的要求，通常建议每个单元格的期望频数不小于5，以确保检验结果的稳定性和可靠性 。当样本量不足时，可能会导致检验效能降低，增加第二类错误的概率。
抽样方法选择
在进行卡方检验时，应选择合适的抽样方法。简单随机抽样是最常用的方法，但在某些情况下，如分层抽样或整 群抽样可能更适合。选择合适的抽样方法有助于提高检验的准确性和可靠性。
期望频数过低时处理策略
合并类别
当某个单元格的期望频数过低时，可以考虑 合并相邻的类别，以增加期望频数。合并类 别时应注意保持类别的逻辑性和实际意义。
适用范围及条件
适用范围
卡方检验适用于多个分类变量之间的独立性或相关性检验，如医学、社会科学等领域的调查研究。
条件
使用卡方检验需要满足一些前提条件，如样本量足够大、每个单元格的期望频数不宜过小等。此外， 对于有序分类变量或存在空单元格的情况，需要采用相应的处理方法或选择其他适合的统计方法。
02
卡方检验方法
统计学卡方检验
目录
• 卡方检验基本概念 • 卡方检验方法 • 数据准备与预处理 • 卡方检验实施步骤 • 卡方检验在医学领域应用举例 • 卡方检验注意事项及局限性讨论
01
卡方检验基本概念
定义与原理
01
02
定义
原理
卡方检验是一种基于卡方分布的假设检验方法，用于推断两个或多个 分类变量之间是否独立或相关。
确定分组界限
在确定分组界限时，可以采用等距分组、等频分组或 基于数据分布的分组方法。选择合适的分组界限有助 于保持各组之间的均衡性，减少信息损失。
根据分析结果，为患者提供个体化的干预措施，提高生存质量。
06
卡方检验注意事项及局限 性讨论
样本量要求及抽样方法选择
样本量要求
卡方检验对样本量有一定的要求，通常建议每个单元格的期望频数不小于5，以确保检验结果的稳定性和可靠性 。当样本量不足时，可能会导致检验效能降低，增加第二类错误的概率。
抽样方法选择
在进行卡方检验时，应选择合适的抽样方法。简单随机抽样是最常用的方法，但在某些情况下，如分层抽样或整 群抽样可能更适合。选择合适的抽样方法有助于提高检验的准确性和可靠性。
期望频数过低时处理策略
合并类别
当某个单元格的期望频数过低时，可以考虑 合并相邻的类别，以增加期望频数。合并类 别时应注意保持类别的逻辑性和实际意义。
适用范围及条件
适用范围
卡方检验适用于多个分类变量之间的独立性或相关性检验，如医学、社会科学等领域的调查研究。
条件
使用卡方检验需要满足一些前提条件，如样本量足够大、每个单元格的期望频数不宜过小等。此外， 对于有序分类变量或存在空单元格的情况，需要采用相应的处理方法或选择其他适合的统计方法。
02
卡方检验方法
统计学卡方检验
目录
• 卡方检验基本概念 • 卡方检验方法 • 数据准备与预处理 • 卡方检验实施步骤 • 卡方检验在医学领域应用举例 • 卡方检验注意事项及局限性讨论
01
卡方检验基本概念
定义与原理
01
02
定义
原理
卡方检验是一种基于卡方分布的假设检验方法，用于推断两个或多个 分类变量之间是否独立或相关。
确定分组界限
在确定分组界限时，可以采用等距分组、等频分组或 基于数据分布的分组方法。选择合适的分组界限有助 于保持各组之间的均衡性，减少信息损失。
生物统计学第五章 卡方检验
500
512
515
542
522
514
488
497
475
487
497
493 498 502 494 499 490
500
491 494 496 518 484 496
518
506 482 494 503 517 491
508
487 482 494 503 517 491
530
486 512 488 503 506 490
三、独立性检验
原理：通过观测数与理论数之间的一致性判断事件 之间的独立性，即判断两个事件是否是独立事件或 处理间差异是否显著。
方法：将数据列成列联表，也称列联表卡方检验。
一、2×2列联表卡方检验
（一）原理：例5 青霉素可以注射，也可以口服，每天给感冒患者 口服或注射 80 万单位的青霉素，调查两种给药方 式的药效，结果如下表所示，试分析青霉素的两 种给药方式的药用效果是否有差异？
0.302 0.061 0.155 0.121 0.09 1.539
10
总计
0
100
0
590
0.0051
1
题解
1、提出假设 H0：O-E=0；HA： O-E≠0 2、总体参数未知，需要由样本比例估计P=590/1000=0.59 3、计算理论值和卡方值，理论频率Pi按照二项分布公式计 算——n=10，0≤k ≤10，理论数Ei=NPi
10 ——
167.5～170.5 ——
1 100
0.01 1.00
0.009 1.00
0.9 100
（5）Oi与Ei进行比较，判断两者之间的不符合度，检验程序 如下：①零假设：H0：O-E=0；HA： O-E≠0 ②检验统计量：
卡方检验-适合性检验
本科学生实验报告学号姓名学院生命科学学院专业、班级生物科学15C班实验课程名称生物统计学<实验>指导教师及职称孟丽华开课时间2016 至2017 学年下学期填报时间2017 年 5 月26 日云南师范大学教务处编印的检验，而是对总体分布的假设检验。
适合性检验（吻合度检验）：是指对样本的理论数先通过一定的理论分布推算出来，然后用实际观测值与理论数相比较，从而得出实际观测值与理论数之间是否吻合。
因此又叫吻合度检验。
实验流程：（1）听老师讲解理论知识；（2）结合书上习题5.4进行练习，加强对知识的掌握：设置变量输入各组数据进行加权进行适合性检验4、实验方法步骤及注意事项：实验方法步骤：1、打开SPSS页面。
2、设置变量，将变量名分别设置为“类型”和“数量”，将Decimals改为0，在“类型”变量中，点击Values进行赋值，将“钩芒”赋值为1，“长芒”赋值为2，“短芒”赋值为3，设置好变量后，输入各组数据。
3、点击Date——Weight Cases…进行加权，在跳出的Weight Cases框中点二、输入各组数据三、进行加权四、进行适合性检验2、对实验现象、数据及观察结果的分析与讨论：（1）假设H0：大麦F2代芒性状表型的比率符合9：3：4的理论比率；H A：其比率不符合9：3：4的理论比率。
（2）选取显著水平为α=0.05。
（3）计算统计数χ2：采用χ2值计算简式可得χ2=1/n∑O i2/Pi－n=1/(348+115+157)×[3482/(9/16)+1152/(3/16)+1572/(4/16)]－(348+115+157)=0.041或利用SPSS软件进行计算。
（4）查χ2值表，df=2时，χ20.05=5.99，χ2<χ20.05,所以，接受H0，认为大麦F2代芒性状表型比率符合9：3：4的理论比例。
或由SPSS的计算结果可知：Asymp.sig.=0.980，因为0.980>0.05，所以接受H0，认为大麦F2代芒性状表型比率符合9：3：4的理论比例。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
独立性检验 料之间是相互独立的或者是相互联系的假设检
验，通过假设所观测的各属性之间没有关联， 然后证明这种无关联的假设是否成立。
同质性检验 在连续型资料的假设检验中，对一个样本方差
的同质性检验，也需进行χ2 检验。
第五章 第一节 χ2检验的原理与方法 第二节 适合性检验 第三节 独立性检验
➢ χ2检验就是统计样本的实际观测值与理论推算
离散型资料 总体分布未知
检验对象
总体参数或几个总体参 数之差
不是对总体参数而是对 总体分布的假设检验
χ2 检验的相关知识
三、χ2检验的用途 指对样本的理论数先通过一定的理论分布推算
适合性检验 出来，然后用实际观测值与理论数相比较，从
而得出实际观测值与理论数之间是否吻合。因 此又叫吻合度检验。 是指研究两个或两个以上的计数资料或属性资
（4）推断
确定自由度，df=(r-1)(c-1)，查临界值 表，进行推断。
给药方式 口服 注射 总数
给药方式与给药效果的2×2列联表
有效 58 64 122(C1)
无效 40 31 71(C2)
总数
98(R1) 95(R2) 193(T)
有效率 59.2％ 67.4％
1.H0 ：给药方式与给药效果相互独立。 HA ：给药方式与给药效果有关联。
进行计算：
2 1
n
Oi2 n pi
Oi －第 i 组的实际观测数 pi －第 i 组的理论比率 n－总次数
豌豆
F2代，共556粒
315
101 108
32
此结果是否符合自由组合规律
根据自由组合规律，理论分离比为：
黄圆：黄皱：绿圆：绿皱＝ 9 ：3 ：3 ：1 16 16 16 16
方法一
豌豆杂交实验F2分离结果
32
黄圆：黄皱：绿圆：绿皱＝ 9 ：3 ：3 ：1 16 16 16 16
2 1
n
Oi2 pi
n
1 556
3152 9
1012 3
1082 3
322 1
556
0.470
16 16 16 16
χ2 ＝0.016+0.101+0.135+0.218＝0.470
第五章 第一节 χ2检验的原理与方法 第二节 适合性检验 第三节 独立性检验
(Oi Ei )2 值越大，观测值与理论值相差也就
越大，反之越小。
Oi 9 Ei 6
Oi 49 Ei 46
将实际观测值与理论值的差数平方，即（O－E）
2，再用差数的平方除以相应的理论值，将之化
Байду номын сангаас
为相对数，从而来反映（O－E）2 的比重，最后
将各组求和，这个总和就是χ2 。
2
(Oi Ei )2 Ei
独立性检验 （independence test）
➢ 又叫列联表（contingency table）χ2检 验，它是研究两个或两个以上因子彼此之 间是独立还是相互影响的一类统计方法。
（一）2×2列联表的独立性检验
设A，B是一个随机试验中的两个事件，其中A可能出现r1 、 r2个结果，B可能出现c1、c2个结果，两因子相互作用形 成4格数，分别以O11 、O12 、O21 、O22表示，下表是2×2 列联表的一般形式
黄圆
黄皱
绿圆
绿皱
实际观测数O 理论频数P 理论数E O－E (O-E)2/E
315 9/16 312.75 2.25 0.016
101 3/16 104.25 -3.25 0.101
108 3/16 104.25 3.75 0.135
32 1/16 34.75 -2.75 0.218
(1) H0 ：豌豆F2分离符合9：3：3：1的自由组合规律； HA ：豌豆F2分离不符合9：3：3：1的自由组合规律；
第五章 χ2检验
χ2 检验的相关知识
一、χ2检验的定义
对样本的频数分布所来自的总体 分布是否服从某种理论分布或某 种假设分布所作的假设检验，即 根据样本的频数分布来推断总体 的分布。
χ2 检验的相关知识
二、χ2检验与连续型资料假设检验的区别
连续型资料假设检验 2检验
数据资料
连续型资料
所属总体 总体正态分布
两个比率比较的u (t) 检验，在观察例数 不足够大或拟对多个比率进行比较时，该 检验不适宜，因为直接对多个样本率作两 两间的u (t) 检验有可能加大第一类错误。
χ2检验的基本思想是检验实际频数与理论 频数的差别是否由抽样误差所此起的，也 是就是样本率（或样本构成比）来推断总 体率（或总体构成比）。
χ2检验的注意事项
由于检验的对象－次数资料是间断性的，而χ2分 布是连续型的，检验计算所得的χ2值只是近似地 服从χ2分布，所以应用连续型的χ2分布的概率检 验间断性资料所得的χ2值就有一定的偏差。
由次数资料算得的χ2均有偏大的趋势，即概率偏 低。当df=1，尤其是小样本时，必须作连续性矫正。
(2)取显著水平α ＝0.05 (3)计算统计数χ2值：
χ2 ＝0.016+0.101+0.135+0.218＝0.470
(4)查临界值表，进行推断：
df =4-1＝3
2 0.05
7.815
χ2＜ χ20.05
P＞0.05
接受H0 ，即豌豆F2分离符合9：3：3：1的自由组合规律。
方法二
315
101 108
2 A 3a 22 208 381 22 1.256
3n
3 289
2 A 3a 22 208 381 22 1.256
3n
3 289
(4)查值表，进行推断
df =1
2 0.05
3.84
P＞0.05
接受H0 ，即大豆花色F2分离符合3：1比率
对于资料组数多于两组的值，可通过下面简式
122(C1)
无效 40(36.05) 31(34.95)
71(C2)
总数
98(R1) 95(R2) 193(T)
给药方式 口服 注射 总数
有效 58(61.95) 64(60.05)
122(C1)
无效 40(36.05) 31(34.95)
71(C2)
总数
98(R1) 95(R2) 193(T)
红色理论数为： Ei ＝1602×1/4=400.5
2
2
( Oi Ei
0.5)2
(15031201.5 0.5)2 ( 99 400.5 0.5)2
301.63
i1
Ei
1201.5
400.5
（4）推断 查χ2值表，当df=1时，χ20.05 ＝3.84。 实得χ2c ＝301.63＞χ20.05
行 列
c1
c2
总和
r1
r2
总和
O11
O12
R1= O11 + O12
O21
O22
R2= O21 + O22
C1= O11 + O21 C1= O12 + O22
T
（１）假设 （2）水平
无效假设H0 ：事件A和事件B无关; HA ：事件A和事件B有关联关系。
确定显著水平α
（3）检验 依据H0 ，推算出理论数，计算χ2值
值之间的偏离程度。
➢ 实际观测值与理论推算值之间的偏离程度就决 定其χ2值的大小。
➢ 两值偏差越大， χ2值就越大，越不符合； ➢ 偏差越小，χ2值就越小，越趋于符合； ➢ 两值完全相等， χ2值就为0，表明理论值完全符
合。
876只羔羊性别调察
性别 观察值（O） 理论值(E)
O-E
公羊
428
母羊
448
可加性 非负值
随O和E而变化
χ2值与概率P成反比， χ2值越小，P值越大， 说明实际值与理论值之差越小，样本分布与假设的 理论分布越相一致;
χ2越大，P值越小，说明两者之差越大，样本 分布与假设理论分布越不一致。
1.提出无效假设H0
观测值与理论值的差异由抽样误差引起，即观 测值＝理论值。备择假设HA ：观测值与理论值 的差值不等于0，即观测值≠理论值
合计
876
438
-10
438
+10
876
0
要回答这个问题，首先需要确定一个统计量， 将其用来表示实际观测值与理论值偏离的程 度；然后判断这一偏离程度是否属于抽样误 差，即进行显著性检验。
判断实际观测值与理论值偏离的程度，最简 单的办法是求出实际观测值与理论值的差数。
876只羔羊性别调察
性别 观察值（O） 理论值(E)
O-E
公羊
428
母羊
448
合计
876
438
-10
438
+10
876
0
➢ 由于差数之和正负相消，并不能反映实际观测 值与理论值相差的大小。
为了避免正、负相抵消的问题，可将实际观测值 与理论值的差数平方后再相加，也就是计算：
∑（O－E）2
(Oi Ei )2 值越大，观测值与理论值相差也就
越大，反之越小。
即Eij＝Ri×Cj/T=行总数×列总数/总数
E11= R1 × C1/T=61.95 E21= R2 × C1/T=60.05
E12= R1 × C2/T=36.05 E22= R2 × C2/T=34.95
给药方式与给药效果的2×2列联表
给药方式 口服 注射 总数
有效 58(61.95) 64(60.05)
性别 公羊 母羊 合计
876只羔羊性别调察
观测值(O)
理论值(E) O E
428
验，通过假设所观测的各属性之间没有关联， 然后证明这种无关联的假设是否成立。
同质性检验 在连续型资料的假设检验中，对一个样本方差
的同质性检验，也需进行χ2 检验。
第五章 第一节 χ2检验的原理与方法 第二节 适合性检验 第三节 独立性检验
➢ χ2检验就是统计样本的实际观测值与理论推算
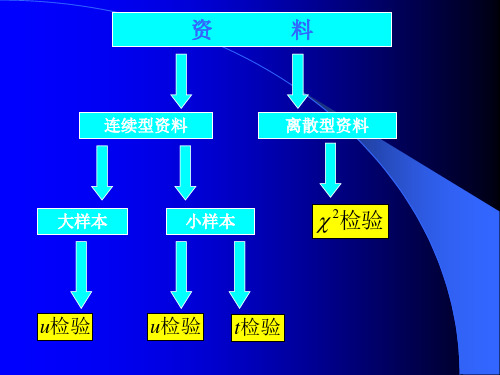
离散型资料 总体分布未知
检验对象
总体参数或几个总体参 数之差
不是对总体参数而是对 总体分布的假设检验
χ2 检验的相关知识
三、χ2检验的用途 指对样本的理论数先通过一定的理论分布推算
适合性检验 出来，然后用实际观测值与理论数相比较，从
而得出实际观测值与理论数之间是否吻合。因 此又叫吻合度检验。 是指研究两个或两个以上的计数资料或属性资
（4）推断
确定自由度，df=(r-1)(c-1)，查临界值 表，进行推断。
给药方式 口服 注射 总数
给药方式与给药效果的2×2列联表
有效 58 64 122(C1)
无效 40 31 71(C2)
总数
98(R1) 95(R2) 193(T)
有效率 59.2％ 67.4％
1.H0 ：给药方式与给药效果相互独立。 HA ：给药方式与给药效果有关联。
进行计算：
2 1
n
Oi2 n pi
Oi －第 i 组的实际观测数 pi －第 i 组的理论比率 n－总次数
豌豆
F2代，共556粒
315
101 108
32
此结果是否符合自由组合规律
根据自由组合规律，理论分离比为：
黄圆：黄皱：绿圆：绿皱＝ 9 ：3 ：3 ：1 16 16 16 16
方法一
豌豆杂交实验F2分离结果
32
黄圆：黄皱：绿圆：绿皱＝ 9 ：3 ：3 ：1 16 16 16 16
2 1
n
Oi2 pi
n
1 556
3152 9
1012 3
1082 3
322 1
556
0.470
16 16 16 16
χ2 ＝0.016+0.101+0.135+0.218＝0.470
第五章 第一节 χ2检验的原理与方法 第二节 适合性检验 第三节 独立性检验
(Oi Ei )2 值越大，观测值与理论值相差也就
越大，反之越小。
Oi 9 Ei 6
Oi 49 Ei 46
将实际观测值与理论值的差数平方，即（O－E）
2，再用差数的平方除以相应的理论值，将之化
Байду номын сангаас
为相对数，从而来反映（O－E）2 的比重，最后
将各组求和，这个总和就是χ2 。
2
(Oi Ei )2 Ei
独立性检验 （independence test）
➢ 又叫列联表（contingency table）χ2检 验，它是研究两个或两个以上因子彼此之 间是独立还是相互影响的一类统计方法。
（一）2×2列联表的独立性检验
设A，B是一个随机试验中的两个事件，其中A可能出现r1 、 r2个结果，B可能出现c1、c2个结果，两因子相互作用形 成4格数，分别以O11 、O12 、O21 、O22表示，下表是2×2 列联表的一般形式
黄圆
黄皱
绿圆
绿皱
实际观测数O 理论频数P 理论数E O－E (O-E)2/E
315 9/16 312.75 2.25 0.016
101 3/16 104.25 -3.25 0.101
108 3/16 104.25 3.75 0.135
32 1/16 34.75 -2.75 0.218
(1) H0 ：豌豆F2分离符合9：3：3：1的自由组合规律； HA ：豌豆F2分离不符合9：3：3：1的自由组合规律；
第五章 χ2检验
χ2 检验的相关知识
一、χ2检验的定义
对样本的频数分布所来自的总体 分布是否服从某种理论分布或某 种假设分布所作的假设检验，即 根据样本的频数分布来推断总体 的分布。
χ2 检验的相关知识
二、χ2检验与连续型资料假设检验的区别
连续型资料假设检验 2检验
数据资料
连续型资料
所属总体 总体正态分布
两个比率比较的u (t) 检验，在观察例数 不足够大或拟对多个比率进行比较时，该 检验不适宜，因为直接对多个样本率作两 两间的u (t) 检验有可能加大第一类错误。
χ2检验的基本思想是检验实际频数与理论 频数的差别是否由抽样误差所此起的，也 是就是样本率（或样本构成比）来推断总 体率（或总体构成比）。
χ2检验的注意事项
由于检验的对象－次数资料是间断性的，而χ2分 布是连续型的，检验计算所得的χ2值只是近似地 服从χ2分布，所以应用连续型的χ2分布的概率检 验间断性资料所得的χ2值就有一定的偏差。
由次数资料算得的χ2均有偏大的趋势，即概率偏 低。当df=1，尤其是小样本时，必须作连续性矫正。
(2)取显著水平α ＝0.05 (3)计算统计数χ2值：
χ2 ＝0.016+0.101+0.135+0.218＝0.470
(4)查临界值表，进行推断：
df =4-1＝3
2 0.05
7.815
χ2＜ χ20.05
P＞0.05
接受H0 ，即豌豆F2分离符合9：3：3：1的自由组合规律。
方法二
315
101 108
2 A 3a 22 208 381 22 1.256
3n
3 289
2 A 3a 22 208 381 22 1.256
3n
3 289
(4)查值表，进行推断
df =1
2 0.05
3.84
P＞0.05
接受H0 ，即大豆花色F2分离符合3：1比率
对于资料组数多于两组的值，可通过下面简式
122(C1)
无效 40(36.05) 31(34.95)
71(C2)
总数
98(R1) 95(R2) 193(T)
给药方式 口服 注射 总数
有效 58(61.95) 64(60.05)
122(C1)
无效 40(36.05) 31(34.95)
71(C2)
总数
98(R1) 95(R2) 193(T)
红色理论数为： Ei ＝1602×1/4=400.5
2
2
( Oi Ei
0.5)2
(15031201.5 0.5)2 ( 99 400.5 0.5)2
301.63
i1
Ei
1201.5
400.5
（4）推断 查χ2值表，当df=1时，χ20.05 ＝3.84。 实得χ2c ＝301.63＞χ20.05
行 列
c1
c2
总和
r1
r2
总和
O11
O12
R1= O11 + O12
O21
O22
R2= O21 + O22
C1= O11 + O21 C1= O12 + O22
T
（１）假设 （2）水平
无效假设H0 ：事件A和事件B无关; HA ：事件A和事件B有关联关系。
确定显著水平α
（3）检验 依据H0 ，推算出理论数，计算χ2值
值之间的偏离程度。
➢ 实际观测值与理论推算值之间的偏离程度就决 定其χ2值的大小。
➢ 两值偏差越大， χ2值就越大，越不符合； ➢ 偏差越小，χ2值就越小，越趋于符合； ➢ 两值完全相等， χ2值就为0，表明理论值完全符
合。
876只羔羊性别调察
性别 观察值（O） 理论值(E)
O-E
公羊
428
母羊
448
可加性 非负值
随O和E而变化
χ2值与概率P成反比， χ2值越小，P值越大， 说明实际值与理论值之差越小，样本分布与假设的 理论分布越相一致;
χ2越大，P值越小，说明两者之差越大，样本 分布与假设理论分布越不一致。
1.提出无效假设H0
观测值与理论值的差异由抽样误差引起，即观 测值＝理论值。备择假设HA ：观测值与理论值 的差值不等于0，即观测值≠理论值
合计
876
438
-10
438
+10
876
0
要回答这个问题，首先需要确定一个统计量， 将其用来表示实际观测值与理论值偏离的程 度；然后判断这一偏离程度是否属于抽样误 差，即进行显著性检验。
判断实际观测值与理论值偏离的程度，最简 单的办法是求出实际观测值与理论值的差数。
876只羔羊性别调察
性别 观察值（O） 理论值(E)
O-E
公羊
428
母羊
448
合计
876
438
-10
438
+10
876
0
➢ 由于差数之和正负相消，并不能反映实际观测 值与理论值相差的大小。
为了避免正、负相抵消的问题，可将实际观测值 与理论值的差数平方后再相加，也就是计算：
∑（O－E）2
(Oi Ei )2 值越大，观测值与理论值相差也就
越大，反之越小。
即Eij＝Ri×Cj/T=行总数×列总数/总数
E11= R1 × C1/T=61.95 E21= R2 × C1/T=60.05
E12= R1 × C2/T=36.05 E22= R2 × C2/T=34.95
给药方式与给药效果的2×2列联表
给药方式 口服 注射 总数
有效 58(61.95) 64(60.05)
性别 公羊 母羊 合计
876只羔羊性别调察
观测值(O)
理论值(E) O E
428