工程力学习题集
工程力学习题册

专业 学号 姓名 日期 成绩第一章 静力学基础一、是非判断题1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ) 1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( ) 1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( ) 1.4 力的可传性只适用于刚体,不适用于变形体。
( ) 1.5 两点受力的构件都是二力杆。
( ) 1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( ) 1.7 力的平行四边形法则只适用于刚体。
( ) 1.8 凡矢量都可以应用平行四边形法则合成。
( ) 1.9 只要物体平衡,都能应用加减平衡力系公理。
( ) 1.10 凡是平衡力系,它的作用效果都等于零。
( ) 1.11 合力总是比分力大。
( ) 1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( ) 1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ) 1.14 当软绳受两个等值反向的压力时,可以平衡。
( ) 1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ) 1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( )1.17 凡是两端用铰链连接的直杆都是二力杆。
( ) 1.18 如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、 BC 构件都不是二力构件。
( )二、填空题2.1如图所示,F 1在x 轴上的投影为 ;F 1在y 轴上的投影为 ;F 2在x 轴上的投影为 ;F 2在y 轴上的投影为 ;F 3在x 轴上的投影为 ;F 3在y 轴上的投影为 ;F 4在x 轴上的投影为 ;F 4在y 轴上的投影为 。
轴上的投影为 。
2.2将力F 沿x , y 方向分解,已知F = 100 N, F 在x 轴上的投影为86.6 N, 而沿x 方向的分力的大小为115.47 N , 则F 的y 方向分量与x 轴的夹角β为 ,F 在y 轴上的投影为 。
工程力学习题集(二)
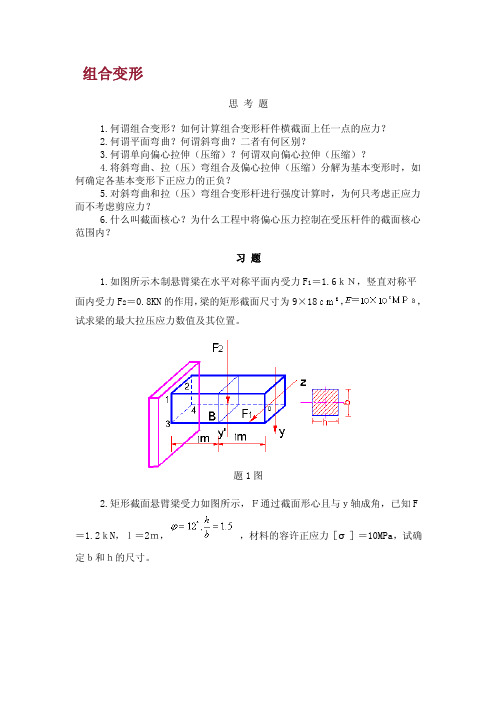
组合变形思考题1.何谓组合变形?如何计算组合变形杆件横截面上任一点的应力?2.何谓平面弯曲?何谓斜弯曲?二者有何区别?3.何谓单向偏心拉伸(压缩)?何谓双向偏心拉伸(压缩)?4.将斜弯曲、拉(压)弯组合及偏心拉伸(压缩)分解为基本变形时,如何确定各基本变形下正应力的正负?5.对斜弯曲和拉(压)弯组合变形杆进行强度计算时,为何只考虑正应力而不考虑剪应力?6.什么叫截面核心?为什么工程中将偏心压力控制在受压杆件的截面核心范围内?习题1.如图所示木制悬臂梁在水平对称平面内受力F1=1.6kN,竖直对称平面内受力F2=0.8KN的作用,梁的矩形截面尺寸为9×18,,试求梁的最大拉压应力数值及其位置。
题1图2.矩形截面悬臂梁受力如图所示,F通过截面形心且与y轴成角,已知F =1.2kN,l=2m,,材料的容许正应力[σ]=10MPa,试确定b和h的尺寸。
题2图3.承受均布荷载作用的矩形截面简支梁如图所示,q与y轴成角且通过形心,已知l=4m,b=10cm,h=15cm,材料的容许应力[σ]=10MPa,试求梁能承受的最大分布荷载。
题3图4.如图所示斜梁横截面为正方形,a=10cm,F=3kN作用在梁纵向对称平面内且为铅垂方向,试求斜梁最大拉压应力大小及其位置。
题4图5.柱截面为正方形,边长为a,顶端受轴向压力F作用,在右侧中部挖一个槽(如图),槽深。
求开槽前后柱内的最大压应力值。
题5图6.砖墙及其基础截面如图,设在1m长的墙上有偏心力F=40kN的作用,试求截面1-1和2-2上的应力分布图。
题6图7.矩形截面偏心受拉木杆,偏心力F=160kN,e=5cm,[σ]=10MPa,矩形截面宽度b=16cm,试确定木杆的截面高度h。
题7图8.一混凝土重力坝,坝高H=30m,底宽B=19m,受水压力和自重作用。
已知坝前水深H=30m,坝体材料容重,许用应力[]=10MPa,坝体底面不允许出现拉应力,试校核该截面正应力强度。
《工程力学》课后习题与答案全集

由 ,作出速度平行四边形,如图示:
即:
7.图示平行连杆机构中, mm, 。曲柄 以匀角速度 2rad/s绕 轴转动,通过连杆AB上的套筒C带动杆CD沿垂直于 的导轨运动。试示当 时杆CD的速度和加速度。
解:取CD杆上的点C为动点,AB杆为动系。对动点作速度分析和加速度分析,如图(a)、(b)所示。图中:
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
(d)由于不计杆重,杆AB在A、C两处受绳索作用的拉力 和 ,在B点受到支座反力 。 和 相交于O点,
根据三力平衡汇交定理,
可以判断 必沿通过
B、O两点的连线。
见图(d).
第二章力系的简化与平衡
思考题:1.√;2.×;3.×;4.×;5.√;6.×;7.×;8.×;9.√.
1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm,求此力系向O点简化的结果,并确定其合力位置。
则
(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
工程力学习题集

一、判断题1、力偶在任一轴上投影为零,故写投影平衡方程时不必考虑力偶。
()2、轴力的大小与杆件的横截面面积有关。
()3、轴力越大,杆件越容易被拉断,因此轴力的大小可以用来判断杆件的强度。
()4、平面图形对任一轴的惯性矩恒为正。
()5、弯曲应力有正应力和剪应力之分。
一般正应力由弯矩引起,剪应力由剪力引起。
()6、构件抵抗变形的能力称为刚度。
()7、作用力与反作用力是一组平衡力系。
()8、两个力在同一轴上的投影相等,此两力必相等。
()9、力偶对其作用面内任意点的力矩值恒等于此力偶的力偶矩,同时与力偶与矩心间的相对位置相关。
()10 、平面任意力系简化后,其主矢量与简化中心有关,主矩与简化中心无关。
()11、力系的合力一定比各分力大。
()12、平面汇交力系由多边形法则及的合力R,其作用点仍为各力的汇交点,其大小和方向与各力相加的次序无关。
()13、作用于物体上的力,均可平移到物体的任一点,但必须同时增加一个附加力偶。
()14、平面任意力系向任一点简化,其一般结果为一个主矢量和一个主矩。
()16、约束反力是被约束物体对其他物体的作用力。
()17、在拉(压)杆中,拉力最大的截面不一定是危险截面。
()18、平面弯曲梁的挠曲线必定是一条与外力作用面重合的平面曲线。
()19、两根材料、杆件长度和约束条件都相同的压杆,则其临界力也必定相同。
()20、主矢代表原力系对物体的平移作用。
()二、填空题1.工程实际中所使用的联接件其主要两种破坏形式为和。
2.实心圆杆扭转剪应力在横截面上的分布为,其中心应力为。
3.平面弯曲是。
4.内力图是指。
5.材料力学中变形固体的基本假设是,,和。
6.截面法的要点是(1);(2);(3)。
8.轴向拉伸(压缩)的强度条件是。
9. 强度是指的能力,刚度是指的能力,稳定性是指的能力。
10.力使物体产生的两种效应是效应和效应。
11.力偶对任意点之矩等于,力偶只能与平衡。
12.从拉压性能方面来说,低碳钢耐铸铁耐。
工程力学(机电一体化技术)_习题集(含答案)

《工程力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《工程力学》(编号为09004)共有单选题,填空题1,计算题,简答题,填空题2,填空题3等多种试题类型,其中,本习题集中有[填空题2,填空题3]等试题类型未进入。
一、单选题1.工程力学材料力学部分的基本研究对象是()A.刚体B.质点C.弹性变形体D.变形杆件2.工程力学静力学部分的基本研究对象是()A.刚体B.质点C.弹性变形体D.变形杆件3.两个力大小相等、方向相反、作用在两个相互作用物体的一条直线上,这是()。
A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性4.两个力大小相等、方向相反、作用在同一物体的一条直线上,这是()。
A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性5.两个力大小相等、方向相反、作用在同一物体的两条直线上称为()。
A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性6.刚体上作用着三个力并且保持平衡,则这三个力的作用线一定满足()。
A.共线B.共面C.共面且不平行D.共面且相交于同一点7.下列四图中矢量关系符合F4=F1+F2+F3的是图()。
F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D8.下列四图中矢量关系符合F2+F1=F4+F3的是图()。
F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D9.下列四图中矢量关系符合F3+F1=F4+F2的是图()。
F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D10.柔所约束的约束反力大小未知、作用点是柔索的联接点、方向在柔索的()方向。
A.垂直B.平行C.牵拉D.倾斜11.柔所约束的约束反力大小未知、作用点是柔索的联接点、方向在柔索的()方向。
A.垂直B.平行C.牵拉D.倾斜12.光滑铰链约束的约束反力大小和方向的特征是()A.一个大小方向均未知B.两个大小未知C.两个大小未知方向已知D.一个未知13.光滑铰链约束的约束反力大小和方向均未知,受力分析中常将其表达为()的力。
工程力学习题集

工程力学习题集2009年11月第一章习题1.1 画出图 1.1(a) ~ (f) 中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
1.2 画出图 1.2 所示各物体系中各物体的受力图。
未画重力的物体 , 质量均不计 , 所有接触处均为光滑接触。
1.4 如图 1.4 所示矩形搁板ABCD 可绕轴线AB 转动,M 、K 均为圆柱铰链 , 搁板用DE 杆支撑于水平位置,撑杆DE 两端均为铰链连接,搁板重为W ,试画出搁板的受力图。
1.5 图 1.5 所示为一水轮机简图,巳知使水轮机转动的力偶矩M z ,在锥齿轮B 处的力分解为三个分力:圆周力F t 、轴向力F a 、径向力F r ,试画出水轮机的受力图。
第二章习题2.1 已知图 2.1 中,F 1 = 150N ,F 2 = 200N 及F 3 = l00N 。
试用图解法及解析法求这四个力的合力。
2.2 起重用的吊环如题图 2.2 所示,侧臂AB 及AC 均由两片组成,吊环自重可以不计,起吊重物P =1200KN ,试求每片侧臂所受的力。
2.3 图示梁在A 端为固定铰支座,B 端为活动铰支座,P =20KN 。
试求在图示两种情形下A 和B 处的约束反力。
2.4 图示电动机重 W=5KN ,放在水平梁AC 的中间,A 和B 为固定铰链,C 为中间铰链,试求A 处的约束反力及杆BC 所受的力。
2.5 简易起重机用钢绳吊起重量G =2000N 的重物。
各杆的自重、滑轮的自重和尺寸都忽略不计,试求杆AB 和AC 受到的力。
假定A 、B 、C 三处可简化为铰链连接。
2.6 重为G =2KN 的球搁在光滑的斜面上,用一绳把它拉住。
巳知绳子与铅直墙壁的夹角为30 0 ,斜面与水平面的夹角为15° ,试求绳子的拉力和斜面对球的约束反力。
2.7 压榨机构如图所示,杆AB 、BC 自重不计,A 、B 、C 都可看作为铰链连接,油泵压力P =3KN ,方向水平。
《工程力学》课后习题与答案全集

工程力学习题答案第一章静力学基础知识思考题:1. X ;2. V ;3. V ;4. V ;5. K 6. K 7. V ;8. V习题一1•根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在 A B 、C 三处受力作用。
u由于力p和uuv R B 的作用线交于点Q 如图(a )所示,根据三力平衡汇交定理, 可以判断支座A 点的约束反力必沿 通过A 0两点的连线。
uP 3uvB 处受绳索作用的拉力uuv R B (b )同上。
由于力交于0点,根据三力平衡汇交定理, 可判断A 点的约束反力方向如 下图(b )所示。
的作用线 2.不计杆重,画出下列各图中 AB 杆的受力图。
uP 解:(a )取杆AB 和E 两处还受光滑接触面约束。
约束力UJVN E uuvuuN A 和 N E,在A的方向分别沿其接触表面的公法线, 外,在 并指向杆。
其中力uuvN A 与杆垂直,通过半圆槽的圆心 Q力 AB 杆受力图见下图(a )。
和C 对它作用的约束力 NBo------- r -------- —y —uuv N C铰销此两力的作用线必须通过(b )由于不计杆重,曲杆 BC 只在两端受 故曲杆BC 是二力构件或二力体,和 B 、C 两点的连线,且B O两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. V ;2.>;3. X ;4. K 5. V ;6.$7.>;8. x ;9. V .1.平面力系由三个力和两个力偶组成, 它们的大小和作用位置如图示,长度单位为cm 求此力系向O 点简化的结果,并确定其合力位置。
uvR R 解:设该力系主矢为 R ,其在两坐标轴上的投影分别为Rx、y。
由合力投影定理有:。
4.梁AB 的支承和荷载如图, 小为多少?解:梁受力如图所示:2. 位置:d M o /R 25000.232 火箭沿与水平面成F ,100 0.6100 80 2000 0.5 580m 23.2cm,位于O 点的右侧。
江苏师范大学工程力学习题集

B.F(a+b)cosα
C.F
D.F
2.某简支梁AB受载荷如图所示,现分别用RA、RB表示支座A、B处的约束反力,则它们的关系为( )。
A.RA<RB
B.RA>RB
C.RA=RB
D.无法比较
3.图示中四个力F1、F2、F3、F4对B点之矩是( )
A.mB(F1)=0
B.mB(F2)=F2l
13.图示构架,已知 ,不计各杆自重,试求 杆受力与铰链 处的约束力。
解答:选取构架整体为研究对象,作出其受力图。
取图示投影轴系,建立平衡方程
其中, , 。
联立上述平衡方程,解得 杆受力
(压)
铰链 处的约束力
14.已知重量为P的圆管用AB杆和绳BC固定在铅垂墙壁上,如图所示,AB杆与墙面间的夹角为α,求AB杆对圆管的支承力。
A.0.14kNB.0.265kN
C.0.213kND.0.237kN
6.图示ABC杆,固定端A的反力是( )
A.XA=P, YA=0B.YA=P, mA=Pa
C..XA=P, YA=0D.XA=P, YA=0,mA=Pa
7.构件在外力作用下平衡时,可以利用( )
A.平衡条件求出所有未知力B.平衡条件求出某些未知力
C.mB(F3)=F3lcos45°
D.mB(F4)=F4l
填空题
4.图示直角弯杆的A端作用一与水平线成60°夹角的力 ,弯杆的几何尺寸如图所示,
则力 对O点的矩MO( )=___Fa______。
5.直角弯杆OAB的AB段长度为1m,O端为光滑固定铰链支座,B端放置于倾角为30°的光滑斜面上。在弯杆上作用一力偶,其力偶矩的大小为M=100N·m,弯杆的自重不计,则支座O处约束力的大小为__100___N.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-8(a)、(c)、(d)、(e)、(g)、(h)1-8试画出下列系统中各指定物体的受力图。未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:
(1)选择研究对象(先画受力简单的物体),画出研究对象的轮廓形状;
(2)画出已知的主动力;
(3)在解除约束处按约束的性质画出约束力。
答案:略
(4)求拉力F的极值。
答案:F=sin(+m)G/cos(-m),当=m时,Fmin=Gsin(+m)
4-4砖夹的宽度为0.25m,曲杆AGB与GCED在G点铰接,尺寸如图示。设砖重G=120 N,提起砖的力作用在砖夹的中心线上,砖夹与砖之间的静摩擦系数fs=0.5,试求距离b为多大才能把砖夹起。
解题思路:
答案:yc=24cm
2-6(b)试求下列图形的形心。图中的长度单位为cm。
解题思路:
(1)设直角坐标系,把其中一根坐标轴设在图形的对称轴上;
(2)把图形分割成三个矩形,由式(2-20)求其重心坐标。
答案:xc=11cm
第三章
3-1(a)梁受荷载如图示,试求支座A、B的约束力。
解题思路:
(1)画出AB梁的受力图,B支座只有一个约束力,A支座可按“三力平衡汇交定理”画一个约束力,也可画两个相互垂直的约束分力;
解题思路:
(1)6根杆均为二力杆,用空间力系中对轴之矩求解比较方便;
(2)对力F作用线取矩,可求出杆2受力为零;
(3)对杆3轴线取矩,可求出杆4受力为零;
(4)如此类推。
答案:F1=F5=-F,F3=F,F2=F4=F6=0
3-10水平传动轴如图所示。r1=20 cm,r2=25 cm,a=b=50 cm,c=100 cm,C轮上的皮带是水平的,其拉力FT1=2Ft1=5 kN,D轮上的皮带与铅垂线成角=300。其拉力为FT2=2Ft2。试求平衡时FT2和Ft2的值及轴承A和B的约束力。
(4)由式(3-1)求支座A的约束力。
答案:FAx=qatan/8(),FAy=7qa/8(),MA=3qa2/4,
FNC=qa/8cos,FBx=qatan/8,FBy=3qa/8
3-3如图所示的压路机碾子重为20 kN,半径R=40 cm。如用一通过其中心O的水平力F将碾子拉过高h=8cm的石坎,试求此水平力的大小。不计摩擦。又问:力F的方向如何,才能最省力?
解题思路:
(1)AB、BC、CD、CE四杆均为二力杆;
(2)取B铰为研究对象,画受力图;
(3)由式(3-4)求杆BC的受力;
(4)取C铰为研究对象,画受力图;
(5)由式(3-4)求杆CE的受力。
答案:
3-6在图示结构中,各构件的自重略去不计,在构件AB上作用一矩为Me的力偶。试求A和C支座的约束力。
解题思路:
(1)画出碾子的受力图,依题意,A点的约束力为零;
(2)由式(3-4)求水平力的大小;
(3)画出力的三角形,依题意,力F与OB线垂直时最省力。
答案:F=15 kN,Fmin=12 kN,方向于OB垂直
3-4图示结构由AB、BC、CD、CE四杆铰接而成,已知力F1处于铅垂方向,力F2沿水平方向。试求杆CE所受的力。
2-5一平行力系由5个力组成,力的大小和作用线的位置如图所示,图中小方格的边长为10mm。试求此平行力系的合力。
解题思路:
思路一:
(1)把各力平移至O点,由式(2-10)、(2-11)、(2-12)求主矢的大小和方向;
(2)由式(2-14)、(2-15)求主矩的大小和转向;
(3)主矢和主矩垂直,可由式(2-8)求合力作用线到简化中心O的距离,并图示此合力。
解题思路:
(1)DE为二力杆,取CD杆连同滑轮为研究对象,由式(3-1)求D、C支座的约束力;
(2)取ABC为研究对象,由式(3-1)求A支座的约束力和约束力偶。
答案:FNE= F,FAx=F-6qa,FAy=2F(),MA=5F a+18qa2
3-9图示6根杆支撑一水平板,在板角处受铅垂力F作用,不计杆和板的重量,试求各杆的内力。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D对调,试分析对轴的受力是否有利。
解题思路:
(1)由式(6-1)求A、B、C、D轮上的扭转外力偶矩;
(2)分别列出AB、BC、CD三段的扭矩方程;
(3)按扭矩方程作出扭矩图;
(4)若将轮C与轮D对调,分析最大扭矩值并判断是否有利。
答案:(1)T1=955N.m,T2=1671N.m,T1=-1194N.m
(2)由式(3-4)或(3-1)求支座A、B的约束力。
答案:FAx=3 F /4(),FAy= F /4(),FNB=F /2( )
3-1(b)梁受荷载如图示,试求支座A、B的约束力。
解题思路:
(1)画出AB梁的受力图,B支座只有一个约束力,A支座有两个相互垂直的约束分力;
(2)由式(3-1)求支座A、B的约束力。
解题思路:略
答案:(f)FNmax=2FP;
(g)FNmax=FP+Alg。
6-5(a)、(c)试作图示各杆的扭矩图,并确定最大扭矩Tmax。
解题思路:略
答案:(a)Tmax=2Me;(c)Tmax=30kN.m。
6-6图示一传动轴,转速n=200 r/min,轮C为主动轮,输入功率P=60 kW,轮A、B、C均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)分析GCED部分的受力,D点有向下的摩擦力;
(2)由式(4-1)求D点正压力与摩擦力的关系;
(3)由式(3-1),对G点取矩,求距离b。
答案:
4-5制动装置如图所示。已知制动杆与轮间的静摩擦系数为fs,物块的重量为G,求制动时所需加的力F的最小值。
解题思路:
(1)分析轮的受力,轮与制动杆接触处有向上的摩擦力,由式(4-1)求正压力与摩擦力的关系,用式(3-1),对O点取矩,求摩擦力与G的关系;
(b)FSmax=qa,Mmax=qa2;
(d)FSmax=3Me/2l,Mmax=Me;
(e)FSmax=5qa/3,Mmax=8qa2/9;
(f)FSmax=qa,Mmax=qa2;
(g)FSmax=FP,Mmax=3FPa;
(h)FSmax=5ql/8,Mmax=3ql2/16;
(k)FSmax=3qa/2,Mmax=qa2;
(2)分析制动杆的受力,由式(3-1),对A点取矩,求力F的最小值。
答案:
第六章
6-1(a)、(d)试求图示各杆1-1、2-2及3-3截面上的轴力,并作轴力图。
解题思路:略
答案:(a)FN1=-30kN,FN2=0kN,FN3=60kN;
(d)FN1=20kN,FN2=5kN,FN3=15kN。
6-2(f)、(g)试作图示各杆的轴力图,并确定最大轴力FNmax。
(2)不利。
6-9(a)、(e)、(h)、(i)试列出图示各梁的剪力方程和弯矩方程。作剪力图和弯矩图,并确定Fsmax及Mmax值。
解题思路:略
答案:(a)FSmax=2ql,Mmax=3ql2/2;
(e)FSmax=2FP,Mmax=FPa;
(h)FSmax=3qa/8,Mmax=9qa2/128;
答案:FAx=0,FAy=5qa/4-F/2-m/2a,FNB=-qa/4+3F/2+m/2a
3-2(a)结构受荷载如图示,试求A、B、C处的约束力。
解题思路:
(1)分析BC部分的受力,画受力图;
(2)由式(3-1)求支座B、C的约束力;
(3)分析AB部分的受力,画受力图,注意固定端A处有两个约束力和一个约束力偶;
解题思路:
(1)由式(1-13)求力在直角坐标轴上的投影;
(2)由式(1-14)求合力的大小;
(3)由式(1-15)求合力的方向。
答案:FR=161.2N ,(FR,Fi)=29.70
1-3试计算下列各图中的力F对点O之矩。
解题思路:
各小题均由式(1-16)求力矩。
答案:略
1-4如图所示的挡土墙重G1=75 kN,铅直土压力G2=120 kN,水平土压力Fp=90 kN。试求三力对前趾A点之矩的和,并判断挡土墙是否会倾倒。
(2)由式(1-25)求力对三个坐标轴之矩;
(3)由式(1-26)求力对坐标原点之矩。
答案:Mx=0, , ,
1-7试画出下列各图中物体A,构件AB的受力图。未画重力的物体重量不计,所有接触面均为光滑接触。
解题思路:
(1)画出研究对象的轮廓形状;
(2)画出已知的主动力;
(3)在解除约束处按约束的性质画出约束力。
解题思路:
(1)由式(1-16)求三力对前趾A点之矩的代数和;
(2)若其值为负(顺时针转),则挡土墙不会翻倒。
答案:MA=-180kN.m,不会倾倒。
1-5如图所示,边长为a的正六面体上沿对角线AH作用一力F。试求力F在三个坐标轴上的投影,力F对三个坐标轴之矩以及对点O之矩矢。
解题思路:
(1)由式(1-13)、(1-14)、(1-15)求合力的大小和方向;
1-1五个力作用于一点O,如图示。图中方格的边长为10mm。试求此力系的合力。
解题思路:
(1)由式(1-13)求合力在直角坐标轴上的投影;
(2)由式(1-14)求合力的大小;
(3)由式(1-15)求合力的方向。
答案:FR=669.5N ,(FR,i)=34.90
1-2如图示平面上的三个力F1=100N,F2=50N,F3=50N,三力作用线均过A点,尺寸如图。试求此力系的合力。
(l)FSmax=qa,Mmax=qa2/2;
思路二:
(1)由式(2-16)求平行力系合力的大小;
(2)由式(2-17)求平行力系合力的作用点坐标。
