第5节波导管
声学波导管

声学波导管食不厌精 脍不厌细1、恒定截面波导内的声传播1.1、矩形波导管1.2 、圆柱形波导管设有一半径为a 的圆柱形管,一端延伸到无限远。
圆柱形管的声波方程应以柱坐标系来描述。
设管的径向坐标为r ,极角为θ,管轴用z 来表示。
直角坐标与柱坐标之间有如下关系⎪⎩⎪⎨⎧===z z r y r x θθsin cos 而柱坐标系的拉普拉斯算符可表示为2222221)(1zr r r r r ∂∂+∂∂+∂∂∂∂=∇θ (1-2-1) 于是三维声波动方程就可变换为:2222222211)(1t p c z p p r r p r r r ∂∂=∂∂+∂∂+∂∂∂∂θ (1-2-2) 根据分离变量法,令解,)()()(),,,(t j e z Z r R t z r p ωθθΘ=将其代入(1-2-2)式可得如下三个常微分方程⎪⎪⎪⎩⎪⎪⎪⎨⎧=-++=Θ+Θ=+0)(10022222222222R r m k dr dR r drR d m d d Z k dz Zd r z θ (1-2-3) 其中.22222r z k k ck +==ω (1-2-4)由于圆柱管道向无限远处延伸,对于Z 的方程可取行波解:;)(z jk z z e A z Z -= (1-2-5)对于Θ的方程可取解为),cos()(m m A ϕθθθ+=Θ (1-2-6) 因为)2()(πθθ+Θ=Θ的关系应该满足,所以式中m 一定要为正整数。
对于R 的方程我们作一适当变换,令x r k r =,则方程就化为0)1(12222=-++R xm dx dR x dx R d . (1-2-7) 这是一个标准的m 解贝塞尔方程,其一般解可表示为),()()(r k N B r k J A r k R r m r r m r r += (1-2-8) 这里)(r k J r m 与)(r k N r m 分别代表宗量为)(r k r 的m 阶柱贝塞尔函数与柱诺伊曼函数。
《电动力学》第29讲§5.4波导管、谐振腔

k 2 i
k i i
2
山东大学物理学院 宗福建
13
四、趋肤效应和穿透深度
E E0e zei( zt )
2
波幅降至原值1/e的传播距离称为穿透深度δ。由上式
1 2
山东大学物理学院 宗福建
14
五、导体表面上的反射 反射系数R定义为反射能流与入射能流值比。由上式得
山东大学物理学院 宗福建
33
§4.4 谐振腔、波导管
三、谐振腔
腔内电磁波的电场和磁场任一直角分量都满足亥
姆霍兹方程。设 u(x,y,z) 为 E 或 H 的任一直角分
量,有
2u k 2u 0
用分离变量法,令
u(x, y, z) X (x)Y ( y)Z(z)
山东大学物理学院 宗福建
34
解 设两导体板与y轴垂直。边界 条件为在两导体平面上,
Ex Ez 0 H y 0
若沿z轴传播的平面电磁波的电 场沿y轴方向偏振,则此平面波 满足导体上的边界条件,因此 可以在导体板之间传播。
山东大学物理学院 宗福建
29
§4.4 谐振腔、波导管
二、理想导体边界条件
例 证明两平行无穷大导体平面之间可以传播一种偏振 的TEM电磁波。
36
§4.4 谐振腔、波导管
山东大学物理学院 宗福建
22
§4.4 谐振腔、波导管
二、理想导体边界条件 在第二节中我们阐明在一定频率的电磁波情形,两不同介
质(包括导体)界面上的边值关系可以归结为
n n
(E2 (H2
E1) 0 H1) α
nn((DB22
D1) B1)
电动力学教学大纲

XX《电动力学》教学大纲课程编号: 3407课程名称:电动力学英文名称:学分/学时:4/64课程性质: 必修适用专业: 应用物理建议开设学期:5先修课程: 电磁学,数学物理方法,场论与复变函数开课单位:物理与光电工程学院一、课程的教学目标与任务(1)理解电磁运动的基本规律,理解电磁场基本性质;(2)获得分析和处理一些电磁基本规律问题的能力;(3)通过学习狭义相对论理论,掌握相对论的时空观及有关的基本理论;(4)为后续课程的学习和独力解决实际问题打下必要的基础。
二、课程具体内容及基本要求(一)引言(4学时)1。
基本要求了解《电动力学》的主要内容、熟悉研究对象等电磁场理论的史2.重点、难点掌握数学知识补充(矢量分析和算符运算)3。
作业及课外学习要求:课后及课本XX中的补充内容,掌握基本的矢量分析及算符运算法则(二)第一章电磁现象的普遍规律(8学时)1.基本要求第一节电荷和电场一、库仑定律(电荷连续分布带电体的电场)二、高斯定理,静电场的散度(矢量场的两个基本性质)三、静电场的旋度第二节电流和磁场一、电荷守恒定律(微分形式和积分形式)二、用毕—萨定律证明磁场旋度和散度公式第三节麦克斯韦方程组一、电磁感应定律二、位移电流三、麦克斯韦方程组四、洛伦兹力公式第四节介质的电磁性质一、极化和磁化的物理图象及描述二、极化强度的散度和磁化强度的旋度三、物质方程四、介质中的方程第五节电磁场的边值关系一、方程的积分形式二、法向分量的跃变三、切向分量的跃变第六节电磁场的能量和能流一、场和电荷系统的能量转化和守恒定律的一般形式二、电磁场能量密度和能流密度表示式三、电磁能量的传输2.重点、难点本章重点:方程及其物理根据,电磁场的边值关系,电磁场能量.难点:电磁场的矢量运算,电磁场及边值关系的物理图像。
3.作业及课外学习要求:课后题的部分内容,掌握电磁场的基本边值关系及方程.(三)第二章静电场(13学时)1.基本要求第一节静电场的标势及其微分方程一、静电场的标势二、静电势的微分方程和边值关系三、静电场的能量第二节唯一性定理一、静电问题的唯一性定理二、有导体存在时的唯一性定理第三节拉普拉斯方程分离变量法一、分离变量法二、边界条件的使用第四节电像法一、电像法的物理原理二、电像法的适用区域第五节格林函数法(选讲)一、点电荷密度二、格林函数三、格林公式和边值问题的解第六节电多极矩一、电势的多极展开二、电多极矩三、电荷体系在外电场中的能量2。
电动力学 波导管
x ez E sin 2 d k
2 0 2
(W / m2 )
(3) y=0板:
s ey H
ex
d
i
y 0
E0 cos
x eikz e k E sin x eikz z d 0 d
s (t ) Re[s eit ]
A1 = 0
ik z a x x H z H 0 cos Hx H 0 sin a a i a x Ey H 0 sin Ex Ez H y 0 a
A2
i a
H0
TE10模电磁场结构立体图
TE10 波 的 场 结 构
nH
TE10模的壁电流分布
E y A2 sin k x x cos k y ye
Ez A3 sin k x x sin k y ye
ik z z
ik z z
m n kx , ky , m, n 0, 1, 2 a b
由于 E 0,因此kx A1 k y A2 ikz A3 = 0
令u x,y 是E x,y , B的任意一直角分量.
u x,y X x Y y C1cosk x x D1sink x x C2cosk y y D2 sink y y
ikz z cos k x sin k ye 利用边界条件得: Ex A 1 x y
ez k E sin (
2 0 2
x
d
) cos 2 (t kz )
2 x 2 ex E0 sin sin 2(t kz ) (W / m2 ) 4 d d
1 S Re[ E H ] 2
第5节波导管
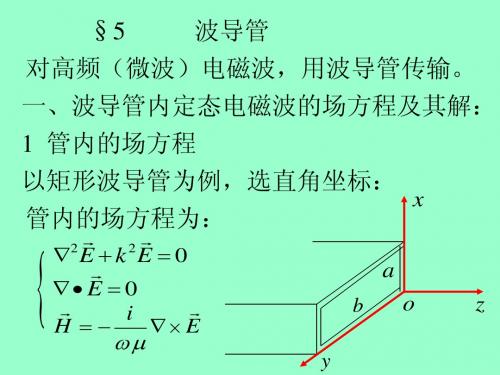
必须是实数
截止频率
其中:fC (1,0)
C (1,0)
1
2a 0 0 C 2a f C (1,0)
频率不得小于此频率
波长不得大于此波长
3 电磁波的纵波成分:
i ( k3 z t )
利用: 得到:
H H ( x, y)ei ( k3 z t ) E E( x, y)e E i0 H H i0 E E E E i0 H1 3 2 3 ik3 E2 y z y E3 E3 E1 i0 H 2 ik3 E1 z x x H3 E H 2 i0 E1 3 ik3 H 2 y z y H 3 H 3 H1 i0 H 2 ik3 H1 z x x
对直角坐标的三个分量:
2 E1 k 2 E1 0 2 E2 k 2 E2 0 E3 k E3 0
2 2
求解第一个方程:
E1 ( x, y, z) X ( x)Y ( y)Z ( z)
分离变量的方程:
2 2 X k 1 X 0 2 x 2 2 Y k 2Y 0 2 y 2 2 Z k 3Z 0 2 z
因为管内磁场重要,换系数表示:
ia E2 ( R, t ) H 0 sin
ik3 a i ( k3 z t ) H 1 ( R, t ) H 0 sin xe a H 3 ( R, t ) H 0 cos xei ( k3 z t ) a i A2 其中: H 0 a
a i H 3 ( R, t ) A2 cos xei ( k z t ) a a E2 ( R, t ) A2 sin xei ( k z t )
波 导 管

4.
H
的解由
H
i
E
确定
(1)当 E 为横波(横电波,即 TE
由上式得出 H z 0 ,所以 E
、波H)不Ez能同0
时为横波;
(2)当H为横波,H z 0 ,Ez 0,横磁波(TM波)
(3)不同的(m, n),有不同的TE 和TM( TEmn ,TM mn)
机动 目录 上页 下页 返回 结束
机动 目录 上页 下页 返回 结束
二.矩形波导中的电磁波
1.矩形波导管
y
r
四个壁构成的金属管,x 0,a b
k
四个面为
问题归结为:
yቤተ መጻሕፍቲ ባይዱ
0,b
z
ax
2E
1
2E
0
c 2 t 2
( E 0)
或
2E k 2E 0 ( E 0)
x
0 a
, Ey 0 ,
Ez
0
, Ex x
0
y
0 b
, Ex 0 ,
不能同时为零
E 0 k x A1 k y A2 ik z A3 0
Ex E y Ez
A1
cos
mx
a
sin
ny
b
eik z z
A2
sin
mx
a
cos
ny
b
eik z z
A3
sin
mx
a
sin
ny
b
eik z z
m a
A1
n b
A2
ikz
A3
0
其余两个常数 Ai 由激发源功率确定 。
k 2Ex
r )i
电磁场理论课件 4-5 波导管

Ex x
x0
0
z
Ex x
Akx C sin kx y ei(kzzt) 0
A
Ex A1 cos kx x sin ky yei(kzzt)
=
0
ax
相似地: Ey A2 sin kx x cos ky yei(kzzt)
x 0, Ez 0 B 0
y 0, Ez 0 D 0
2
2
2
E Ex Ey
TM11 : Ez A3 sin kx x sin k y yei(kz zt)
Hz 0
Ey Ex 0 kx A1 k y A2 0
x y
k x A1 k y A2 ik z A3 0
Ez 0 kx A1 k y A2 0
在波导管的横截面上,场是谐变的。其分布情况直接取 决于m和n这两个常数的值。不同的m和n的组合对应不同的场 结构。我们称之为不同的波型或模式,一组(m,n)的值组成 一个模式,TM波记为TMmn,TE波记为TEmn。在实际问题 中,我们总是选定一个模式来传递电磁波的。
c.10 c.01
1 ; a 1 ; b
c.11
1 2 1 2 ; a b
其中,对于TE10 波(又称为主波),通常对于矩形 波导总是取a>b,于是 fc,10 给出矩形波导中的最小 截止频率。凡是频率比截止频率 fc,10 小的电磁波不 能在波导内传输。和 fc,10 对应的波长为
复习
1. 理想导体边界条件 Et 0
En 0 n
2.谐振腔内的波型 E x,t E x ei t
E
x
E
y
E
z
A1
cos
m
L1
A2
波导管资料

截止波导管在工程实践中,屏蔽体的总体屏蔽效能是由屏蔽体中最薄弱的环节决定的,要使屏蔽体的屏蔽效能达到一个特定值,则屏蔽体上全部都要达到这个值。
因此,屏蔽系统的各个组成部分,其屏蔽性能与各个组成部分的匹配就很重要了。
屏蔽体上的电磁屏蔽薄弱环节是由于各种原因需要保留的孔洞和不同部分的连接而形成的缝隙。
解决这种缝隙的方法就是截止波导。
如图1所示,波导是简单的管状金属结构并呈现高通滤波器的特性。
波导允许截止频率以上的信号通过,而截止频率以下的信号则被阻止或衰减,这与高通滤波器的频率特性相似。
利用这个特性,可以设计成使干扰信号的频率落在波导的截止区内,这样波导起到了电磁屏蔽的作用。
这种波导称为截止波导。
图1 截止频率波导的截止频率可用下列公式计算:◆对于圆形截面的波导fcutoff=6900/D (2-6)式中,D为圆形波导直径(单位为英寸,1英寸=2.54厘米);fcutoff为截止频率(单位为MHz)。
◆对于矩形截面的波导fcutoff=5900/L (2-7)式中,L为矩形截面的对角线长度(单位为英寸);fcutoff为截止频率(单位为MHz)。
要保证波导对电磁波有较大的衰减,应使波导的截止频率为要屏蔽的电磁波频率的5倍以上。
当满足这个条件时,长度为Γ的波导对电磁波的衰减S为:◆对于圆形截面的波导衰减S=32T/D(dB)(2-8)式中,D为圆形波导直径(单位为英寸);T为长度(单位为英寸)。
◆对于矩形截面的波导衰减S=21T/L(dB)(2-9)式中,L为矩形截面对角线长度(单位为英寸);T为波导长度(单位为英寸)。
当需要在屏蔽体上开孔,而孔洞又会导致其电磁屏蔽效能达不到屏蔽要求时,则利用截止波导管的深度提供的额外的损耗就可以增加屏蔽效能。
设计截止波导管的步骤如图2所示。
使用截止波导管的关键是确保波导管工作在截止区,因此首先要根据干扰的最高频率来确定截止波导管的截止频率。
截止频率应是最高干扰频率的5倍以上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用边界条件定 E1 y b 0 确定
E1 x x a 0
k1 , k2 , k3
k2 n k1 m b a
确定
2 2 k3 k 2 k12 k2 ( ) 2 (n ) 2 (m ) 2 C b a k1 A1 k2 A2 ik3 A3 0 腔内场满足 E 0
a
xe i ( k3 z t )
电力线分布:平行于 y 的力线,在 x 方向 形成驻波,沿 z 方向传播。 磁力线分布:平行 x0 z 坐标面,在 x 方向 形成驻波,沿 z 轴方向传播。
管壁电流:
n ( H 2 H1 ) H 2 H , H1 0 n H
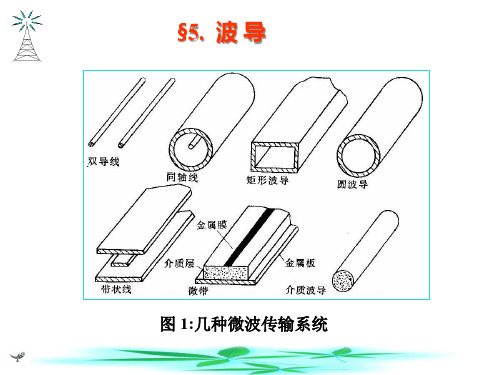
§5 波导管 对高频(微波)电磁波,用波导管传输。 一、波导管内定态电磁波的场方程及其解: 1 管内的场方程 以矩形波导管为例,选直角坐标: x 管内的场方程为:
2 Ek E 0 E 0 i H E
2
a
b
y
o
z
边界条件: Et 0
En 0 n
利用边界条件定系数:
E1
y 0
0
确定
0
C2 0 D1 0
E1
x x 0
确定
E1 ( x, y, z, t ) A1 cosk1 x sin k2 yei ( k3 z t ) E2 ( x, y, z, t ) A2 sin k1 x cosk2 yei ( k3 z t )
a i H 3 ( R, t ) A2 cos xei ( k z t ) a a E2 ( R, t ) A2 sin xei ( k z t )
3
k3 H 1 ( R, t ) A2 sin
xei ( k3 z t )
a
3
1 k32 )
i(
2
C2
讨论:1)波导管内一定存在纵波成分。 2)波分类: E3 0 横电波 TE H 3 0 横磁波 TM
举例: TE01
4
E3 0
H3 0
m0
n 1
TE01波的电磁场和管壁电流:
TE01 波的场 i ( k3 z t ) E1 (R, t ) A 0 1 cosk1 x sin k2 ye E2 ( R, t ) A2 sin k1x cosk2 yei ( k3 z t ) E3 (R, t ) A3 sin k1x sin k2 yei ( k3 z t ) 0 k1 , k 2 0 E1 0 a i ( k3 z t ) E2 ( R, t ) A2 sin xe ey a i H ( R, t ) E ( R, t )
因为管内磁场重要,换系数表示:
ia E2 ( R, t ) H 0 sin
ik3 a i ( k3 z t ) H 1 ( R, t ) H 0 sin xe a H 3 ( R, t ) H 0 cos xei ( k3 z t ) a i A2 其中: H 0 a
对直角坐标的三个分量:
2 E1 k 2 E1 0 2 E2 k 2 E2 0 E3 k E3 0
2 2
求解第一个方程:
E1 ( x, y, z) X ( x)Y ( y)Z ( z)
分离变量的方程:
2 2 X k 1 X 0 2 x 2 2 Y k 2Y 0 2 y 2 2 Z k 3Z 0 2 z
2
必须是实数
截止频率
其中:fC (1,0)
C (1,0)
1
2a 0 0 C 2a f C (1,0)
频率不得小于此频率
波长不得大于此波长
3 电磁波的纵波成分:
i ( k3 z t )
利用: 得到:
H H ( x, y)ei ( k3 z t ) E E( x, y)e E i0 H H i0 E E E E i0 H1 3 2 3 ik3 E2 y z y E3 E3 E1 i0 H 2 ik3 E1 z x x H3 E H 2 i0 E1 3 ik3 H 2 y z y H 3 H 3 H1 i0 H 2 ik3 H1 z x x
对 E3
E3 ( x, y, z, t ) (C'1 cosk1x D'1 sin k1x)(C'2 cosk2 y D'2 sin k2 y)C'3 eik3z
E3 x0 0
E3
y 0
0
确定 确定
C '1 0 C '2 0
E3 ( x, y, z, t ) A3 sin k1x sin k2 yei (k3z t )
分析 1)波沿 z 方向传播,行波波速由 k3 算出。 2)振幅随 x, y 变化,为驻波形式。 3)腔内的电磁波不是横波。
要求波导管满足频率要求: 1)保证波能沿 z 方向传播能量。 2)保证 x, y 方向形成驻波,满足谐振要求 2 截止频率:
m 2 n 2 k3 ( ) ( ) ( ) C a b m 2 n 2 ( ) ( ) 即: C a b m 2 n 2 C ( ) ( ) a b 0 0 1 m 2 n 2 fC ( ) ( ) a b 2 0 0
ቤተ መጻሕፍቲ ባይዱ果:
E1 i( E2 H1 H2
1
2 k 3 ) 2 C 1
2
(0 (0
H 3
E3 k3 ) y x
i(
2 k 3 ) 2 C 1
2
H 3
E3 k3 ) x y
i(
2
C2
2 k3 )
H 3 E3 ( k3 0 ) y y H 3 E ( k3 0 3 ) x y
解为:X ( x) C1 cosk1x D1 sin k1x
Y ( y) C2 cosk2 y D2 sin k2 y
Z ( z) C3eik3 z
组合后:
E1 ( x, y, z) (C1 cosk1x D1 sin k1x)(C2 cosk2 y D2 sin k2 y)C3eik3z
