波导管壁电流
微波技术与天线总复习题及其答案

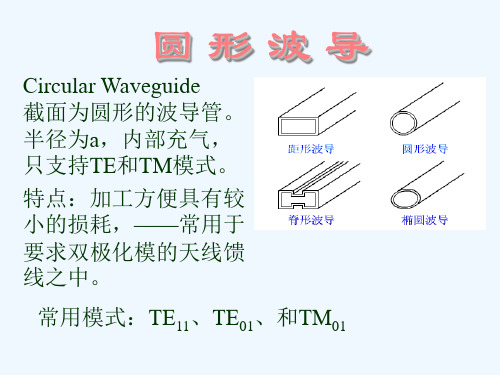
微波技术与天线基础总复习题一、填空题1、微波是一般指频率从 至 范围内的电磁波,其相应的波长从 至 。
并划为 四个波段;从电子学和物理学的观点看,微波有 、 、 、 、 等重要特点。
2、无耗传输线上的三种工作状态分别为: 、 、 。
3、传输线几个重要的参数:(1) 波阻抗: ;介质的固有波阻抗为 。
(2) 特性阻抗: ,或 ,Z 0=++I U 其表达式为Z 0= ,是一个复数; 其倒数为传输线的 .(3) 输入阻抗(分布参数阻抗): ,即Z in (d)= 。
传输线输入阻抗的特点是: a) b) c) d)(4) 传播常数:(5) 反射系数:(6) 驻波系数:(7) 无耗线在行波状态的条件是: ;工作在驻波状态的条件是: ;工作在行驻波状态的条件是: 。
4、负载获得最大输出功率时,负载Z 0与源阻抗Z g 间关系: 。
5、负载获得最大输出功率时,负载与源阻抗间关系: 。
6、史密斯圆图是求街均匀传输线有关 和 问题的一类曲线坐标图,图上有两组坐标线,即归一化阻抗或导纳的 的等值线簇与反射系数的 等值线簇,所有这些等值线都是圆或圆弧,故也称阻抗圆图或导纳圆图。
阻抗圆图上的等值线分别标有 ,而 和 ,并没有在圆图上表示出来。
导纳圆图可以通过对 旋转180°得到。
阻抗圆图的实轴左半部和右半部的刻度分别表示 或 和 或 。
圆图上的电刻度表示 ,图上0~180°是表示 。
7、阻抗匹配是使微波电路或系统无反射运载行波或尽量接近行波的技术措施,阻抗匹配主要包括三个方面的问题,它们是:(1);(2);(3)。
8、矩形波导的的主模是模,导模传输条件是,其中截止频率为,TE10模矩形波导的等效阻抗为,矩形波导保证只传输主模的条件是。
9、矩形波导的管壁电流的特点是:(1)、(2)、(3)。
10、模式简并现象是指,主模也称基模,其定义是。
单模波导是指;多模传输是。
11、圆波导中的主模为,轴对称模为,低损耗模为。
规则金属波导2

规则波导中导波场求解的一般步骤是: (1)结合具体波导边界条件求解波动方程。
E Ez 2 z V xy + k c = 0, H z H z ∂2 ∂2 2 V xy = 2 + 2 ∂x ∂y
2
解出纵向场分量Ez和Hz。求解方法通常用分离变 量法。边界条件要求在波导内壁表面电场的切线 分量和磁场的法线分量为零。
ωµ π π j (ωt − βz ) E y = − j k 2 a H 0 sin a x e c β π π j (ωt − βz ) H x = j 2 H 0 sin x e kc a ⋯ (16 ) a π H z = H 0 cos x e j (ωt − βz ) a E = E = H = 0 z y x
求出横向场分量。 3、1 矩形波导 矩形波导是横截面为矩形的空心金属管。 如图所示,a,b分别表示内壁的宽边和窄边 尺寸(a>b),波导内充有空气,管壁材料 通常用铜,也有铝、金、银等其它金属材 料。
矩形波导不能传输TEM波,但能传输横电波 (记TE或H)或横磁波(TM或E)。要得到 波导中TE波或TM波的电磁场分布情况,就 得求解纵向分量的波动方程。 1、矩形波导的模式及其场分量:(分离变 量法求解)
规则金属波导
金属波导即封闭的空心金属波导管。早在 1933年人们就在实验中发现空心金属管可以用来 传输能量。金属波导是厘米波段最常用的传输线, 包括矩形波导、圆形波导和同轴波导(通常称为 同轴线)。所谓“规则波导”是指无限长直波导, 其截面形状和尺寸、波导管壁的结构以及波导内 媒质分布情况沿其轴线方向(纵向)都是不变的。 这种规则波导的基本理论问题主要包括两部分, 即波导中的模式及其场结构问题(即所谓横向问 题)与这些模式沿波导轴向传输的基本特性问题 (即所谓纵向问题)。
电动力学课件 4.5 波导

Ex ( A sin k x x B cos k x x)(C sin k y y D cos k y y )ei ( kz z t ) i ( k z z t ) E ( A sin k x B cos k x )( C sin k y D cos k y ) e y x x y y i ( k z z t ) E ( A sin k x B cos k x )( C sin k y D cos k y ) e x x y y z
d 2Y 2 k yY 0 2 dy
X ( x) A sin k x x B cos k x x Y ( y ) C sin k y y D cos k y y
u ( x , y ) X ( x )Y ( y )
这里的 A、 B、C、 D、kx、ky都是待定常数。至此得到沿 z 轴方向传播的电磁波电场的三个分量为:
E
k
H
TE
k
z kz
TE波和 TM波是相对于叠加波的传播方向而言的
10
c) 截止频率
2 2
kx
m a
n m n 2 2 2 2 2 ky kz k k x k y kz k b a b 其中波数 k取决于波源的频率ω和波导内介质的性质,即
k
2 若电磁场的激发频率ω足够小,以致于 k 2 k x2 k y ,则 kz是
纯虚数, k z i ,显然由因子 e 能在该波导内传播。
i ( k z z t )
e z e i t 看到,这不再
是行波,而是场随着z的增加而指数衰减,所以此时电磁场不
2 2 2 2 ( 2 2 )u ( x , y ) ( k k z )u ( x , y ) 0 x y
电磁场与微波技术实验2矩形波导仿真与分析

实验二 矩形波导仿真与分析一、实验目的:1、 熟悉HFSS 软件的使用;2、 掌握导波场分析和求解方法,矩形波导高次模的基本设计方法;3、 利用HFSS 软件进行电磁场分析,掌握导模场结构和管壁电流结构规律和特点。
二、预习要求1、 导波原理。
2、 矩形波导模式基本结构,及其基本电磁场分析和理论。
3、 HFSS 软件基本使用方法。
三、实验原理由于矩形波导的四壁都是导体,根据边界条件波导中不可能传输TEM 模,只能传输TE 或TM 模。
这里只分析TE 模(Ez=0)对于TE 模只要解Hz 的波动方程。
即采用分离变量,并带入边界条件解上式,得出TE 模的横向分量的复振幅分别为(1)矩形波导中传输模式的纵向传输特性①截止特性波导中波在传输方向的波数β由式9 给出222000220z z c z H H k H x y ∂∂++=∂∂式7000220002200020002()cos()sin()()sin()cos()()sin()cos()()cos()sin()z x c c z y c c y x H c x y H c H n m n E j j H x y k y k b a b H m m n E j j H x y k x k a a b E m m n H j H x y Z k a a b E n m n H j H x y Z k b a b ωμωμπππωμωμπππβπππβπππ∂⎧==⎪∂⎪⎪∂==-⎪∂⎪⎨⎪=-=⎪⎪⎪==⎪⎩式822222c c k k ππβλλ=-=-式9式中k 为自由空间中同频率的电磁波的波数。
要使波导中存在导波,则β必须为实数,即k 2>k 2c 或λ<λc(f >f c ) 式10如果上式不满足,则电磁波不能在波导内传输,称为截止。
故k c 称为截止波数。
矩形波导中TE 10模的截止波长最长,故称它为最低模式,其余模式均称为高次模。
由于TE 10模的截止波长最长且等于2a,用它来传输可以保证单模传输。
圆形波导的理论分析和特性
传播常数: mn k k 截至波长: cmn 截至频率 2 a u 'mn v
u 'mn k a
2
2
3.2 18
3.2 19 3.2 20
f cmn
cmn
u 'mn 2 a
其中贝塞尔函数最小根u11'=1.841对应TE11模。 c=3.41a;次低模为根u01=3.832, c=1.64a
圆形波导分析 – TM modes.(续四)
波导阻抗: Z TM Ef Er Hf H r w k
2 2 cmn 2
3.2 25
2
传播常数: mn k k 截至波长: cmn 截至频率 2 a u mn v
u mn k a
m 0 n 1
u m n co s m f j ( w t z ) jw m a 2 E mn J m ( r) e 2 si n m f u mn r a co s m f j ( w t z ) jw a ' u mn E mn J m ( r) e sin m f u mn a
3.2 26
3.2 27 3.2 28
f cmn
cmn
u mn 2 a
其中贝塞尔函数最小根 u01=2.405对应TM01模。 c=2.62a
圆形波导的特性
圆形波导模的传输条件是c> 或fc<f;传输特性 与矩形波导类似,为高通器件。 圆形波导存在两种模式简并现象: TE0n与TMm0的模兼并; 另一种是m非零的TEmn与TMmn模的极化简并。 圆形波导的基模—— 主模为TE11,其截止波长最长(TE11=3.41a) 次模为TM01,其截止波长最长(TM01=2.62a)
矩形波导 PPT

m 场量沿x轴[0,a]出现的半周期(半个纯驻波)的数目;
n 场量沿y轴[0,b]出现的半周期的数目。
④j 相位关系 Ey-Hx、Ex-Hy
z轴有功率传输
Ez-Hx、Ez-Hy
x、y轴无功率传输
所以行波状态下,沿波导纵向(z轴)传输有功功率、横向(x、
y轴)无功功率。
2) 场结构
为了能形象和直观的了解场的分布(场结构),可以 利用电力线和磁力线来描绘它。电力线和磁力线遵循 的规律:
力线上某点的切线方向
该点处场的方向
力线的疏密程度
场的强弱
电力线 发自正电荷、止于负电荷,也可以环绕着交变磁场构 成闭合曲线,电力线之间不能相交。在波导壁的内表面(假设为 理想导体)电场的切向分量为零,只有法向分量(垂直分量), 即在波导内壁处电力线垂直边壁。
磁力线 总是闭合曲线,或者围绕载流导体,或者围绕交变电 场而闭合,磁力线之间不能相交,在波导壁的内表面上只能存在 磁场的切向分量,法向分量为零。
3)相速和群速
TMmn和TEmn波型的相速和群速表示式相同:
vp
v
1(/c)2
vg v 1-c2
4)波型阻抗
TMmn和TEmn波型阻抗为:
ZTE
1
1c2
g
ZTM
1c2
g
5)尺寸选择——矩形波导的工作波型图
基于前面的定义,根据波导横截面尺寸、工作波长、 截止波长之间关系,构成矩形波导工作波型图。根据不 同要求,可利用波型图对波导的横截面尺寸和波导波长 作出选择。
TE0n和TEm0是非简并模;其余的TEmn和TMmn都存在简并模: 若a=b, 则TEmn 、TEnm、TMmn和TMnm是简并模;若a=2b,则TE01与TE20,TE02和 TE40,TE50、TE32和TM32是简并模。
谢处方《电磁场与电磁波》(第4版)课后习题-第7章 导行电磁波【圣才出品】

第7章 导行电磁波(一)思考题7.1 什么是导波系统?什么是均匀导波系统?答:导波系统是指引导电磁波沿一定方向传播的装置。
均匀导波系统是指在任何垂直于电磁波传播方向的横截面上,导波装置具有相同的截面形状和截面面积及介质特性。
7.2 写出均匀导波系统中的纵向场分量与横向场分量的关系。
答:均匀导波系统中纵向场分量与横向场分量的关系:7.3 写出矩形波导中纵向场分量Ez 、H z 满足的方程和边界条件。
答:矩形波导中E z 满足下面的波动方程和边界条件:H z 满足下面的波动方程和边界条件:7.4 沿均匀波导传播的波有哪三种基本模式?答:横电磁波(TEM),横磁波(TM),横电波(TE)。
7.5 波阻抗的定义是什么?答:波阻抗在数值上等于与传播方向垂直的横截面内,相互垂直的电场与磁场分量之比。
7.6 试叙述均匀导波系统中的TEM波、TM波和TE波的传播特性。
答:在均匀导波系统中,(1)TEM波的传播特性:传播常数相速度波阻抗(2)TM波的传播特性:E z满足标量波动方程其传播条件f>f c(或λ<λc)传播常数波导波长相速度波阻抗(3)TE波的传播特性H z满足标量波动方程,其传播条件,传播常数,波导波长,相速度和TM波的形式相同。
波阻抗7.7 写出a×b矩形波导中TM波和TE波的截止波数、截止频率、相位常数、波导波长、相速度、波阻抗及传播条件。
答:a×b矩形波导中TM波和TE波截止波数截止频率相位常数波导波长相速度波阻抗传播条件f>f c(或λ<λc)7.8 矩形波导中的波是否存在色散?答:矩形波导中的波存在色散。
7.9 试说明为什么单导体的空心或填充电介质的波导管不能传播TEM波。
答:如果空心或填充电介质的波导管内存在TEM波,则磁场矢量应在横截面内,磁力线在横截面内形成闭合曲线,沿闭合磁力线的磁场积分应等于与之交链即轴向的电流,波导管不存在轴向的传导电流,因此必要求有轴向位移电流,这就要求存在轴向电场,而TEM波在传播方向上不存在电磁场。
08传输线-矩形波导

截止波长 c 2a
波导波长 g
1 2a
2
传播常数 =
2
g
2
1 2a
2
波阻抗 10
0
1 2a
2
相速
vp
v 1 2a
2
群速
vg v பைடு நூலகம் 2a
波阻抗 TE模
E y k Ex (3.86) Hy Hx
ZTM
TM模
ZTM Ey Ex (3.104) Hy H x k
其中,η为自由空间对应介质的波阻抗
截止波数
kc 2 k x 2 k y 2 ( m 2 n 2 ) ( ) a b
的半驻波数。即 ——m代表在x坐标方向场的半驻波数 ——n代表在y坐标方向场的半驻波数
TE10模
TE01模
TE11模
TM11模
矩形波导中高次模的力线图可以根据波指数的意义,由前
面提到的四个基本模式组合而成。
TE20模
TE21模
TM21模
截止模 ——截止模是指传播常数为纯实数,在波导中不能传播 的模式。 ——截止模的传播特性
a A10 b Re (3.92) 2 4
3 2
•
导体损耗
Rs Pl 2
•
c
J s dl (3.93)
2
介质损耗(小损耗)
d
k 2 tan 2
NP / m (3.29)
•
损耗功率Pl
Pl Rs
b y0
