振动与波波动光学练习题
大学物理 振动与波、波动光学练习题

06振动与波、波动光学练习题 一、选择题 1 一物体作简谐振动,振动方程为)4cos(πω+=t A y在4T t =(T 为周期)时刻,物体的加速度为 [ ]2222321)(,321)(,221)(,221)(ωωωωA D A C A B A A -- 2 两个质点各自作简谐振动,它们的振幅相同、周期相同,第一个质点的振动方程为)cos(1αω+=t A y 。
当第一个质点从相对平衡位置的正位移处回到平衡位置时,第二个质点正在最大位移处,则第二个质点的振动方程为 [ ])cos()(),23cos()()2cos()(),2cos()(2222παωπαωπαωπαω++=-+=-+=++=t A y D t A y C t A y B t A y A 3一质点沿y 轴作简谐振动,振动方程为)SI (),32cos(1042παπ++⨯=-t y ,从t = 0时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为[ ]s 61)(s,31)(s,21)(s,41)(s,81)(E D C B A 4 已知两个简谐振动曲线如图所示,1x 相位比2x 的相位 [ ]ππππ超前,落后,超前,落后)()(2)(2)(D C B A5题图 7题图5 一质点作简谐振动,周期为T 。
质点由平衡位置向X 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为 [ ],8)(6)(12)(4)(T D T C T B T A ,,, 6 在下面几种说法中,正确的说法是: [ ](A )波源不动时,波源的振动周期与波动的周期在数值上是不同的,(B )波源振动的速度与波速相同,(C) 在波传播方向上的任一质点的振动相位总是比波源的相位滞后,(D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前。
7一平面简谐波,沿X 轴负方向传播,角频率为ω,波速为u 。
设4T t =时刻的波形如图所示,则该波的表达式为: [ ]])(cos[)(),(cos )(]21)(cos[)(),(cos )(πωωπωω++=+=+-=-=ux t A y D u x t A y G u x t A y B ux t A y A 8 当机械波在媒质中传播时,一媒质质元的最大变形量发生在 [ ](A)媒质质元离开其平衡位置最大位移处,(B )媒质质元离开其平衡位置)2/2(A 处,(C )媒质质元在其平衡位置处,(D )媒质质元离开其平衡位置A/2处(A 是振动振幅)。
波动和波动光学复习题ans

一选择题:1. 频率为100Hz ,传播速度为300m/s 的平面简谐波,波线上两点振动的位相差为3/π,则两点相距为(A) 2m; (B) 2.19m; (C) 0.5m; (D) 28.6m. [ ]2. 一平面简谐波以速度u 沿X 轴正方向传播,在t t '=时波形曲线如图所示,则坐标原点的振动方程为(A) ⎥⎦⎤⎢⎣⎡+'-=2)(cos πt t bu a y ; (B) ⎥⎦⎤⎢⎣⎡-'-=2)(2cos ππt t b u a y ; (C) ⎥⎦⎤⎢⎣⎡+'+=2)(cos ππt t b u a y ; (D) ⎥⎦⎤⎢⎣⎡-'-=2)(cos ππt t bua y .[ ]3. 图a 表示0=t 时的余弦波的波形图,波沿X 轴正向传播;图b 为一余弦振动的曲线,则图a 中所表示的x=0处振动的初位相与图b 所表示的振动的初位相 (A) 均为零; (B) 均为2/π; (C) 均为2/π-;(D) 依次分别为2/π与2/π-; (E) 依次分别为2/π-与2/π. [ ]4. 一简谐波沿X 轴的正方向传播,4/T t =时的波形曲线如图所示。
若振动以余弦函数表示,且此题各点振动的初相取π-到π之间的值,则(A) O 点的初位相为00=φ; (B) 3点的初位相为2/3πφ-=; (C) 2点的初位相为πφ=2; (D) 1点的初位相为2/1πφ-=.[ ]5. 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成热能 (B) 它的势能转换成动能(C) 它从相邻的一段质元获得能量,其能量逐渐增大。
(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小。
[ ]6. 如图所示,1S 和2S 为两相干波源,它们的振动方向均垂直于图面,发出波长为λ的简谐波,P 点是两列波相遇区域中的一点,已知λ21=P S ,λ2.22=P S ,已知两列波在P 点发生相消干涉。
大学物理习题及解答(振动与波、波动光学)

1. 有一弹簧,当其下端挂一质量为m 的物体时,伸长量为9.8 ⨯10-2 m 。
假如使物体上下振动,且规定向下为正方向。
〔1〕t =0时,物体在平衡位置上方8.0 ⨯10-2 m处,由静止开始向下运动,求运动方程。
〔2〕t = 0时,物体在平衡位置并以0.60m/s 的速度向上运动,求运动方程。
题1分析:求运动方程,也就是要确定振动的三个特征物理量A 、ω,和ϕ。
其中振动的角频率是由弹簧振子系统的固有性质〔振子质量m 与弹簧劲度系数k 〕决定的,即m k /=ω,k 可根据物体受力平衡时弹簧的伸长来计算;振幅A 和初相ϕ需要根据初始条件确定。
解:物体受力平衡时,弹性力F 与重力P 的大小相等,即F = mg 。
而此时弹簧的伸长量m l 2108.9-⨯=∆。
如此弹簧的劲度系数l mg l F k ∆=∆=//。
系统作简谐运动的角频率为1s 10//-=∆==l g m k ω〔1〕设系统平衡时,物体所在处为坐标原点,向下为x 轴正向。
由初始条件t = 0时,m x 210100.8-⨯=,010=v 可得振幅m 100.8)/(2210102-⨯=+=ωv x A ;应用旋转矢量法可确定初相πϕ=1。
如此运动方程为])s 10cos[()m 100.8(121π+⨯=--t x〔2〕t = 0时,020=x ,120s m 6.0-⋅=v ,同理可得m 100.6)/(22202022-⨯=+=ωv x A ,2/2πϕ=;如此运动方程为]5.0)s 10cos[()m 100.6(122π+⨯=--t x2.某振动质点的x -t 曲线如下列图,试求:〔1〕运动方程;〔2〕点P 对应的相位;〔3〕到达点P 相应位置所需要的时间。
题2分析:由运动方程画振动曲线和由振动曲线求运动方程是振动中常见的两类问题。
此题就是要通过x -t 图线确定振动的三个特征量量A 、ω,和0ϕ,从而写出运动方程。
曲线最大幅值即为振幅A ;而ω、0ϕ通常可通过旋转矢量法或解析法解出,一般采用旋转矢量法比拟方便。
高考物理总复习专题练习:振动和波

高考物理复习振动和波专题训练及其答案一、单项选择题1.如图所示为一列简谐横波t时刻的图象,已知波速为0.2m/s,以下说法正确的是()A.经过0.5s,质点a、b、c通过的路程均为75cmB.若从t时刻起质点a比质点b先回到平衡位置,则波沿x轴正方向传播C.图示时刻质点a、b、c所受的回复力大小之比为2∶1∶3D.振源的振动频率为0.4Hz2.一列向右传播的简谐横波在某一时刻的波形如图所示,该时刻,两个质量相同的质点P、Q 到平衡位置的距离相等。
关于P、Q两个质点,以下说法正确的是()A.P较Q先回到平衡位置B.再经14周期,两个质点到平衡位置的距离相等C.两个质点在任意时刻的动量相同D.两个质点在任意时刻的加速度相同3.图为一列简谐波在0=t时刻的波形图,此时质点Q正处于加速运动过程中,且质点N在1st=时第一次到达波峰。
则下列判断正确的是()A.此时质点P也处于加速运动过程B.该波沿x轴负方向传播C.从0=t时刻起,质点P比质点Q晚回到平衡位置D.在0=t时刻,质点N的振动速度大小为1m/s4.如图所示为一列机械波在t=0时刻传播的波形图,此刻图中P点速度沿y轴正方向,t=2s 时刻,图中Q点刚好在x轴上。
则下列说法正确的是()A.该机械波沿x轴正方向传播B.该机械波周期不可能是8s3C.无论周期是多少,当Q点在x轴时,P点一定离x轴最远D.P点振幅是10cm5.如图所示是沿x轴传播的一列简谐横波在t=0时刻的波形图,已知波的传播速度为16.0m/s,从此时起,图中的P质点比Q质点先经过平衡位置.那么下列说法中正确的是()A.这列波一定沿x轴正向传播B.这列波的频率是3.2HzC.t=0.25s时Q质点的速度和加速度都沿y轴负向D.t=0.25s时P质点的速度和加速度都沿y轴负向6.如图(a)所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图(b)为xy 平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图(b)上x=0.4m处的Q点的说法正确的是().A.t=0时,速度最大,其大小为0.1m/s,方向沿y轴正方向B.t=0到t=5s内,通过的路程为20cmC.t=2s时,运动到x=0.2m处D.t=3s时,加速度最大,且方向向下7.一列简谐横波在某时刻的波形图如图所示,已知图中质点b的起振时刻比质点a延迟了0.5s,b和c之间的距离是5m,以下说法正确的是()A.此列波的波长为2.5mB.此列波的频率为2HzC.此列波的波速为2.5m/sD.此列波的传播方向为沿x轴正方向传播8.P、Q、M是某弹性绳上的三个质点,沿绳建立x坐标轴。
大学物理-波动光学习题(包括振动、波动、波的干涉、光的干涉、光的衍射、光的偏振)
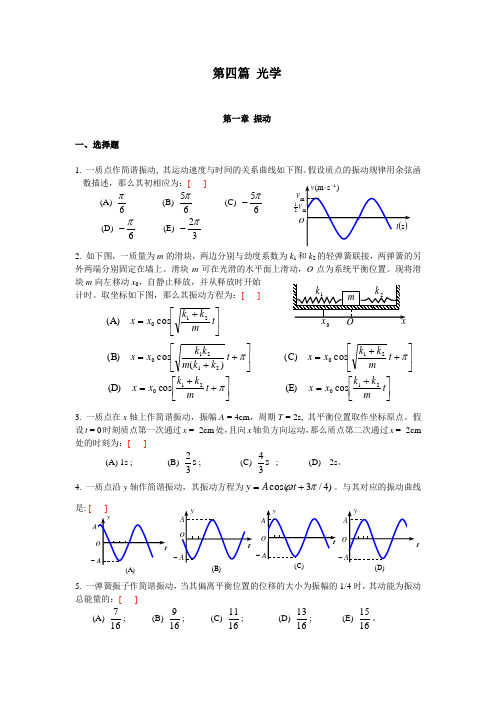
第四篇 光学第一章 振动一、选择题1. 一质点作简谐振动, 其运动速度与时间的关系曲线如下图。
假设质点的振动规律用余弦函数描述,那么其初相应为:[ ] (A)6π (B) 65π (C) 65π- (D) 6π- (E) 32π-2. 如下图,一质量为m 的滑块,两边分别与劲度系数为k 1和k 2的轻弹簧联接,两弹簧的另外两端分别固定在墙上。
滑块m 可在光滑的水平面上滑动,O 点为系统平衡位置。
现将滑块m 向左移动x0,自静止释放,并从释放时开始计时。
取坐标如下图,那么其振动方程为:[ ] ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos(A)⎥⎦⎤⎢⎣⎡++=πt k k m k k x x )(cos (B)21210⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (C)⎥⎦⎤⎢⎣⎡++=πt m k k x x 210cos (D) ⎥⎦⎤⎢⎣⎡+=t m k k x x 210cos (E)3. 一质点在x 轴上作简谐振动,振幅A = 4cm ,周期T = 2s, 其平衡位置取作坐标原点。
假设t = 0时刻质点第一次通过x = -2cm 处,且向x 轴负方向运动,那么质点第二次通过x = -2cm 处的时刻为:[ ](A) 1s ; (B)s 32; (C) s 34; (D) 2s 。
4. 一质点沿y 轴作简谐振动,其振动方程为)4/3cos(πω+=t A y 。
与其对应的振动曲线是: [ ]5. 一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的:[ ](A)167; (B) 169; (C) 1611; (D) 1613; (E) 1615。
(A)-(B)(C)(D)-06. 图中所画的是两个简谐振动的振动曲线,假设 这两个简谐振动可叠加,那么合成的余弦振动 的初相为: [ ] π21(A) π(B) π23(C) 0(D)二、填空题1. 一简谐振动的表达式为)3cos(ϕ+=t A x ,0=t 时的初位移为0.04m, s -1,那么振幅A = ,初相位 =2. 两个弹簧振子的的周期都是0.4s, 设开始时第一个振子从平衡位置向负方向运动,经过0.5s 后,第二个振子才从正方向的端点开始运动,那么这两振动的相位差为 。
机械振动机械波练习题和光学部分练习题

⎨ 0.2 c os(10t一、填空题1. 一 质 点 做 简 谐 振 动 的 振 动 方 程 为x = 0.5 cos ⎛πt + π⎫ (SI ),则该质点振动的振幅7. 已知一水平弹簧振子做简谐振动的振幅为 A ,弹簧劲度系数为 k , 则该谐振子系统的总能量E = ,以平衡位置为坐标原点,当弹簧振3 ⎪ ⎝ ⎭A = m , 周期 T = s , 初相子 运 动 到x = A 2处 时 的 系 统 的 势 能ϕ0 =,t = 1s 时的相位ϕ= ,t = 0时刻该质点的位置坐标 x 0 = m ,速度方向沿 x 轴(选填“正向”或“负向”)。
E P = ,此时系统的动能 E k = , 当弹簧振子处于 x = 处时,系统的动能和势能相等。
8. 两同方向同频率简谐振动的合成,已知振动方程2. 一个沿 x 轴做简谐振动的弹簧振子,其振动方程⎧π 用余弦函数表示,t = 0 时质点过平衡位置向负向振⎪x 1 = 3cos(2πt + 3)cm动,则该振动的初相ϕ= 。
初相在(-π,π]分别为⎨ ⎪x ⎪⎩2 = 4 cos(2πt + 7π )cm3 ,则合振动的振内取值) 3. 一个沿 x 轴做简谐振动的弹簧振子,振幅为 A , 其振动方程用余弦函数表示,t = 0 时质点过 x = A 2 幅为cm ,合振动的初相ϕ0 =(初相在(-π,π] 内取值)。
9. 两同方向同频率简谐振动的合成,已知振动方程向正向振动,则该振动的初相ϕ0 =。
(初相 ⎧x = 3cos(πt - π在(-π,π] 内取值)1分别为 )cm 6 5π,则合振动的振幅 ⎪x = 4 c os(πt + )cm 4. 一质点作简谐振动(用余弦函数表达),若将振动速度处于正最大值的某时刻取做t = 0 ,则该振动初相φ0 =(初相在(-π,π] 内取值)5. 一水平弹簧振子做简谐振动, 已知振动周期T = 3s ,则质点从平衡位置振动到振幅一半位置处所需的最短时间为s 。
物体的振动和波动练习题

物体的振动和波动练习题一、选择题1. 下列哪个不属于机械振动的基本特征?A. 振幅B. 周期C. 频率D. 波长2. 以下哪种波不需要介质传播?A. 机械波B. 横波C. 纵波D. 都需要介质传播3. 以下哪个现象不属于机械波传播中的失能?A. 反射B. 折射C. 干涉D. 散射4. 把频率为30Hz的振动用电路方式表示,需要设备的最小档位是A. 10sB. 1sC. 1msD. 1us5. 振幅越大,波的能量传播速度越快,这一说法A. 对B. 错6. 当一个横波传播时,传播介质上的每一个质点的振动方向A. 垂直于波的传播方向B. 与波的传播方向相同C. 与波的传播方向相反D. 与波的振动方向相同7. 下列不属于机械波的是A. 音波B. 光波C. 水波D. 地震波8. 声音能传播的介质是A. 真空B. 水C. 铁D. 木头9. 长度为0.1m的弦上传播的频率为500Hz的波,其波长为A. 10cmB. 20cmC. 40cmD. 50cm10. 一个在弹簧中传播的波,它所具有的振动特点可以用频率 f 表示。
当频率 f 增大时,振动速度将A. 不变B. 增大C. 减小D. 变为零二、填空题1. 机械波在介质中的传播速度与_________、_________有关。
2. 波长和_________成反比。
3. 波的频率和振动的_________有关。
4. 当光束从水中垂直射入空气时,光的_________发生折射。
5. 在两根相互平行的弹簧上各拧一节,右手拇指指向电流的方向,右手四指的弯曲方向表示_________。
三、简答题1. 请简要说明机械波和电磁波的区别。
2. 请解释频率和周期的概念,并写出它们的单位。
3. 什么是衰减? 请说明衰减对波传播的影响。
4. 什么是驻波? 它是如何形成的?5. 请举例说明机械波的反射和折射现象。
四、计算题1. 一支弦上传播的横波的振动频率为100Hz,波长为0.5m。
高考物理学科复习题七鸭部分第14讲振动与波动光练习含解析12

振动与波动 光1.(1)如图所示,一束复色光射到三棱镜上,从三棱镜另一面射出两单色光A 、B ,两种色光中折射率较小的是________;如果增大入射角,则先发生全反射的是________;如果A 、B 两种光使用同一装置做双缝干涉实验,条纹间距较大的是________.(2)一列简谐波沿x 轴正方向传播,该波在t =1.0 s 时的图象如图甲所示,介质中质点P 的振动图象如图乙所示.求:①该列简谐波的波速v ;②在0~10 s 时间内质点M 的路程s 和位移.解析:(1)由题图可知,B 光折射率较大,B 光的频率大,A 光折射率较小,A 光的频率小.由于B 光的折射率较大,B 光的全反射临界角较小,如果增大入射角,则B 光先发生全反射.在同种介质中,A 光的波长比B 光的波长长,如果A 、B 两种光使用同一装置做双缝干涉实验,根据Δx =l dλ知,条纹间距较大的是A 光.(2)①由题图甲得波长λ=4 m 由题图乙得周期T =1.0 s 波速v =λT=4 m/s.②由题图乙可知质点P 从t =0.5 s 开始振动 该波由质点P 传播到质点M 所需时间t =x v=5 s 所以在0~10 s 时间内质点M 振动了Δt =4.5 s 因为n =ΔtT=4.5路程s =4A ×n =4×0.2×4.5 m=3.6 m 0~10 s 时间内质点M 的位移为0 答案:(1)A 光 B 光 A 光 (2)①4 m/s ②3.6 m 02.(1)(多选)某同学漂浮在海面上,虽然水面波正平稳地以1.8 m/s 的速率向着海滩传播,但他并不向海滩靠近.该同学发现从第1个波峰到第10个波峰通过身下的时间间隔为15 s .下列说法正确的是( )A .水面波是一种机械波B .该水面波的频率为6 HzC .该水面波的波长为3 mD .水面波没有将该同学推向岸边,是因为波传播时能量不会传递出去E .水面波没有将该同学推向岸边,是因为波传播时振动的质点并不随波迁移 (2)如图所示,ABCD 是一玻璃砖的截面图,一束光与AB 面成30°角从AB 边上的E 点射入玻璃砖中,折射后经玻璃砖的BC 边反射后,从CD 边上的F 点垂直于CD 边射出.已知∠B =90°,∠C =60°,EB =10cm. BC =30 cm.真空中的光速c =3×108m/s ,求:①玻璃砖的折射率;②光在玻璃砖中从E 到F 所用的时间.(结果保留两位有效数字)解析:(1)水面波是机械振动在水面上传播,是一种典型的机械波,A 对;从第一个波峰到第十个波峰中经历了九个波形,时间间隔为15 s ,所以其振动周期为T =159 s =53s ,频率为0.6 Hz.B 错;其波长λ=vT =1.8 m/s×53 s =3 m ,C 对;波中的质点都上下振动,不随波迁移,但是能量随着波的传播而传递出去,D 错,E 对.(2)①光在玻璃砖中传播光路如图所示,由几何关系可得i =60°.γ=∠BQE =∠CQF =30° 由折射定律n =sin isin γ得n = 3②由n =c v,得v =3×108m/s 由几何关系得EQ =2EB =20 cmQF =QC cos 30°=(BC -BQ )cos 30°=(153-15) cm t =EQ +QF v≈1.8×10-9 s答案:(1)ACE (2)① 3 ②1.8×10-9s3.(1)(多选)由波源S 形成的简谐横波在均匀介质中向左、右传播.波源振动的频率为20 Hz ,波速为16 m/s.已知介质中P 、Q 两质点位于波源S 的两侧,且P 、Q 和S 的平衡位置在一条直线上,P 、Q 的平衡位置到S 的平衡位置之间的距离分别为15.8 m 、14.6 m .P 、Q 开始振动后,下列判断正确的是( )A .P 、Q 两质点运动的方向始终相同B .P 、Q 两质点运动的方向始终相反C .当S 恰好通过平衡位置时,P 、Q 两点也正好通过平衡位置D .当S 恰好通过平衡位置向上运动时,P 在波峰E .当S 恰好通过平衡位置向下运动时,Q 在波峰(2)如图,玻璃球冠的折射率为3,其底面镀银,底面的半径是球半径的32倍;在过球心O 且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M 点,该光线的延长线恰好过底面边缘上的A 点,求该光线从球面射出的方向相对于其初始入射方向的偏角.解析:(1)简谐横波的波长λ=v f =1620m =0.8 m .P 、Q 两质点距离波源S 的距离PS =15.8 m =19λ+34λ,SQ =14.6 m =18λ+14λ.因此P 、Q 两质点运动的方向始终相反,说法A 错误,说法B 正确.当S 恰好通过平衡位置向上运动时,P 在波峰的位置,Q 在波谷的位置.当S 恰好通过平衡位置向下运动时,P 在波谷的位置,Q 在波峰的位置.说法C 错误,说法D 、E 正确.(2)设球半径为R ,球冠底面中心为O ′,连接OO ′,则OO ′⊥AB .令∠OAO ′=α,有 cos α=O ′A OA =32RR①即α=30°② 由题意知MA ⊥AB 所以∠OAM =60°③设图中N 点为光线在球冠内底面上的反射点,所研究的光线的光路图如图所示.设光线在M 点的入射角为i ,折射角为γ,在N 点的入射角为i ′,反射角为i ″,玻璃的折射率为n .由于△OAM 为等边三角形,有i =60°④由折射定律有sin i =n sin γ⑤ 代入题给条件n =3得γ=30°⑥作底面在N 点的法线NE ,由NE ∥AM ,有i ′=30°⑦ 根据反射定律,有i ″=30°⑧ 连接ON ,由几何关系知△MAN ≌△MON , 故有∠MNO =60°⑨ 由⑦⑨式得∠ENO =30°⑩于是∠ENO 为反射角,NO 为反射光线.这一反射光线经球面再次折射后不改变方向.所以,射出玻璃球冠的光线相对于入射光线的偏角β为β=180°-∠ENO =150°答案:(1)BDE (2)150°4.(1)(多选)如图所示,等边三角形AOB 为透明柱状介质的横截面.一束单色光PQ 平行于角平分线OM 射向OA ,在界面OA 发生折射,折射光线平行于OB 且恰好射到M 点(不考虑反射光线).则( )A .透明柱状介质对单色光PQ 的折射率为 3B .从AMB 面出射的光线与入射光线PQ 的偏向角为60°C .保持入射点Q 不变,减小入射角,一直有光线从AMB 面射出D .保持入射光PQ 的方向不变,增大入射光的频率,出射点将在M 点下方E .增大入射光PQ 的频率,光在该介质中的传播速度不变(2) 如图所示,虚线是一列简谐横波在t =0时刻的波形,实线是这列波在t =1 s 时刻的波形.①若波沿x 轴正方向传播,则从t =1 s 时刻开始,x =3 m 处的质点第一次回到平衡位置需要的时间最长为多少?②若波速大小为75 m/s ,则波的传播方向如何? 解析:(1)入射角i =60 °,折射角γ=30 °,n =sin isin γ=3,由光路可逆性可知光从M 点折射时,折射角为60 °,由几何关系可知此出射光线与入射光线PQ 的偏向角为60 °,选项A 、B 正确;入射点Q 不变,减小入射角,则折射角减小,射到AB 面的入射角增大,可能发生全反射,选项C 错误;增大入射光频率,则从Q 点折射时的折射角变小,出射点将在M 点下方,选项D 正确;增大入射光频率,由n =c v,可知光在介质中传播速度减小,选项E 错误.(2)①由图象可知,波长λ=8 m当波沿x 轴正方向传播时,波在Δt =1 s 内传播距离为 Δs =(8n +5) m ,其中n =0,1,2,…v =ΔsΔt=(8n +5) m/s ,其中n =0,1,2,… 从t =1 s 时刻开始,平衡位置在x =3 m 处的质点第一次回到平衡位置需要的时间,即为波沿x 轴传播1 m 距离需要的时间,最长时间t max =Δx v min =15s =0.2 s. ②当波沿x 轴负方向传播时,波在Δt =1 s 内传播距离为s =(8n +3) m ,其中n =0,1,2,…若波速大小为75 m/s ,则1 s 内波传播的距离s =vt =75×1 m=75 m因为s =75 m =(9×8+3) m ,所以波沿x 轴负方向传播. 答案:(1)ABD (2)①0.2 s ②x 轴负方向5.(1)一列沿x 轴正方向传播的简谐波,在t =0时刻的波形图如图所示,已知这列波在P 出现两次波峰的最短时间是0.4 s ,根据以上可知:这列波的波速是__________ m/s ;再经过________ s 质点R 才能第一次到达波峰;这段时间里R 通过的路程为________ cm.(2)如图所示,一透明球体置于空气中,球半径R =10 cm ,折射率n =2,MN 是一条通过球心的直线,单色细光束AB 平行于MN 射向球体,B 为入射点,AB 与MN 间距为5 2 cm ,CD 为出射光线,真空中光速c =3×108 m/s.①补全光路并求出光从B 点传到C 点的时间; ②求CD 与MN 所成的角α.解析:(1)依题,P 点两次出现波峰的最短时间是0.4 s ,所以这列波的周期T =0.4 s .由波速公式得v =λT =40.4m/s =10 m/s由t =0时刻到R 第一次出现波峰,波移动的距离s =7 m则t =s v =710s =0.7 s在上述时间内,R 实际振动时间t 1=0.3 s 因此R 通过的路程为s =3A =6 cm.(2)①连接BC ,光路图如图所示;在B 点光线的入射角、折射角分别标为i 、r ,sin i =5210=22,所以i =45°.由折射率定律,在B 点有n =sin isin r可得sin r =12故r =30°.又BC =2R cos r ,v =c n所以t =BC v =BCn c =63×10-9s.②由几何关系可知∠COP =15°,∠OCP =135°,所以α=30°. 答案:(1)10 0.7 6 (2)①光路图见解析 63×10-9s ②30°高中物理 第一章 单元高考过关[时间:45分钟 满分:100分]一、选择题(每小题5分,共50分)2017年清明小长假,人们纷纷走出户外祭扫、踏青、赏花、观光……全国大江南北掀起了节日旅游热,显示了中国传统文化的魅力。
