matlab实验四
实验4 matlab gui设计

实验四 MATLAB GUI设计一.预备知识点1. 图形用户界面(GUI)是用户与计算机程序之间的交互方式,是用户与计算机进行信息交流的方式。
计算机在屏幕显示图形和文本,若有扬声器还可产生声音。
用户通过输入设备,如:键盘、鼠标、跟踪球、绘制板或麦克风,与计算机通讯。
用户界面设定了如何观看和如何感知计算机、操作系统或应用程序。
通常,多是根据悦目的结构和用户界面功能的有效性来选择计算机或程序。
图形用户界面或GUI是包含图形对象,如:窗口、图标、菜单和文本的用户界面。
以某种方式选择或激活这些对象,通常引起动作或发生变化。
最常见的激活方法是用鼠标或其它点击设备去控制屏幕上的鼠标指针的运动。
按下鼠标按钮,标志着对象的选择或其它动作。
2.对“句柄图形”的理解是设计和实现GUI的先决条件。
由图形命令生成的每一事物是一个图形对象。
图形对象不仅包括uimenu和uicontrol对象,而且还包括图形、坐标轴和他们的子对象。
让我们从另一个角度来看这一层次结构。
计算机的屏幕本身是根结点,图形是根对象的子对象,坐标轴,uimenu ,uicontrol是图形的子对象。
根可以包括多个图形,每个图形含有一组或多组坐标轴以及其子对象,每个图形也可以有一个或多个与坐标轴无关的uimenu和uicontrol。
虽然uicontrol对象无子对象结点,但他们确实具有多种类型。
uimenu对象常将其它的uimenu对象作为其子对象。
3. MATLAB的图形用户界面设计实际上是一种面向对象的设计方法。
假设想建立一个图形界面来显示和处理二维图形的颜色、线型及数据点的图标。
要求其基本功能是:(1)建立一个主坐标系,用来显示要绘制的二维图形;(2)建立一个列表框,允许用户选择不同的着色方法;(3)建立一组按扭,用于处理二维图形线型和数据点的图标;(4)为图形界面加入菜单项,用于决定坐标轴是否显示及坐标轴上是否需要网格;(A)最初图形界面的设想如下图所示:(B)根据上面的设想,下面我们就来制作它的图形用户界面:首先,我们先来看其图形窗口的设置。
实验四 Matlab编程

实验四Matlab编程【实验目的】1、了解Matlab运行方式2、熟悉Matlab程序流程与结构3、会编写简单的Matlab程序4、掌握M文件编辑器及程序的调试工具【实验内容】1、关系运算与逻辑运算2、m函数文件(function file)和m命令文件(script file)以及m文件的调试3、分支结构和循环结构4、相关语句或函数5、根据要求,完成实验报告中的内容【实验指导】1)关系运算与逻辑运算关系运算符>(大于) <(小于) >=(大于等于) <=(小于等于) ==(等于) ~=(不等于) 逻辑运算符& (与) |(或) ~(非) xor(异或)% 逻辑结果以“1”或者“非零数字”表示真, 以“0”表示假。
测试函数2)m函数文件(function file)基本数学函数自定义函数:以m文件形式出现✓格式:function [y1, y2, ..., yn]=fun_name(x1, x2, ..., xn)✓说明:◆函数名必须符合Matlab变量命名规则。
◆m文件名必须与函数名相同。
◆输出参数只有一个或者没有时,可以省略方括号。
◆输入参数可为0、1、2、...个,但不能省略圆括号。
◆M函数文件第一行必须以funtion开头。
◆函数有自已的工作空间,它与Matlab系统本身的工作空间是分开的。
◆当m文件到终点或者遇到return时结束调用。
◆函数可以调用其他函数,也可以调用自己。
◆一个m文件中可以定义多个函数,第一个出现的为主函数,其他的为子函数。
注意文件名与主函数名相同,子函数只能被主函数调用,而不能被该m文件外的函数或者m文件调用。
✓调用:[y1, y2, ..., yn]=fun_name(x1, x2, ..., xn)3)m命令文件(script file)该文件仅是一连串Matlab指令的集合,执行时按顺序执行。
它没有输入参数与输出参数,中间可以调用函数。
实验四MATLAB数值计算与符号计算

实验四 MATLAB数值计算与符号计算一、实验目的1.掌握数据插值和曲线拟合的方法2.掌握求数值导数和数值积分的方法3.掌握代数方程数值求解的方法4.掌握常微分方程数值求解的方法5.掌握求解优化问题的方法6.掌握求符号极限、导数和积分的方法7.掌握代数方程符号求解的方法8.掌握常微分方程符号求解的方法二、实验原理1.数据插值a) 一维数据插值 Y1=interp1(X,Y,X1,’method’)b) 二维数据插值 Z1=interp2(X,Y,Z,X1,Y1,’method’)2.曲线拟合[P,S]=polyfit(X,Y,m)3.符号对象的建立(1)符号量名=sym(符号字符串):建立单个的符号变量或常量;(2)syms arg1 arg2,…,argn:建立n个符号变量或常量。
4.基本符号运算(1)基本四则运算:+,-,*,\,^(2)分子与分母的提取:[n,d]=numden(s)(3)因式分解与展开:factor(s),expand(s)(4)化简:simplify, simple(s)5.符号函数及其应用(1)求极限:limit(f,x,a)(2)求导数:diff(f,x,a);(3)求积分:int(f,v)三、实验内容1.按下表用3次样条方法插值计算0~900范围内整数点的正弦值和0~750范围内整数点的正切值,然后用5次多项式拟合方法计算相同的函数值,并将两种计算结果进行比较。
x2=0:75;y1=sin(pi.*x1./180);y2=tan(pi.*x2./180);;a=interp1(x1,y1,45,'cublic')b=interp1(x1,y1,45,'cublic')p1=polyfit(x1,y1,5)p2=polyfit(x2,y2,5)c1=polyval(p1,x1);c2=polyval(p2,x2);subplot(2,1,1);plot(x1,c1,':o',x1,y1,'r');subplot(2,1,2);plot(x2,c2,':o',x2,y2,'r');10203040506070802.(1)求函数33()sin cos f x x x =+在点,,,6432x ππππ=的数值导数。
MATLAB实验四_求微分方程的解

参数说明
[T,Y] = solver(odefun,tspan,y0)
odefun 为显式常微分方程,可以用命令 inline 定义,或 在函数文件中定义,然后通过函数句柄调用。
dy 2 2 y 2 x 2x 求初值问题 的数值解,求解范 例: dx 围为 [0,0.5] y( 0 ) 1
dsolve的输出个数只能为一个 或 与方程个数相等。
只有很少一部分微分方程(组)能求出解析解。 大部分微分方程(组)只能利用数值方法求数值解。
Matlab函数数值求解
[T,Y] = solver(odefun,tspan,y0)
其中 y0 为初值条件,tspan为求解区间;Matlab在数值求解 时自动对求解区间进行分割,T (列向量) 中返回的是分割点 的值(自变量),Y (数组) 中返回的是这些分割点上的近似解, 其列数等于因变量的个数。
数学实验
实验四
求微分方程的解
问题背景和实验目的
自牛顿发明微积分以来,微分方程在描述事物运 动规律上已发挥了重要的作用。实际应用问题通过 数学建模所得到的方程,绝大多数是微分方程。 由于实际应用的需要,人们必须求解微分方程。 然而能够求得解析解的微分方程十分有限,绝大多 数微分方程需要利用数值方法来近似求解。 本实验主要研究如何用 Matlab 来计算微分方程 (组)的数值解,并重点介绍一个求解微分方程的 基本数值解法--Euler折线法。
Runge-Kutta 方法
Euler 法与 R-K法误差比较
Matlab 解初值问题
用 Maltab自带函数 解初值问题 求解析解:dsolve 求数值解:
ode45、ode23、 ode113、ode23t、ode15s、 ode23s、ode23tb
Matlab实验四拟合

解法 2.用多项式拟合的命令
1)输入以下命令:
x=0:0.1:1;
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
A=polyfit(x,y,2)
z=polyval(A,x);
plot(x,y,'k+',x,z,'r')
%作出数据点和拟合曲线的图形
r1 (xn ) ... rm (xn ) nm
则线性方程组可表示为: RT Ra RT y
由于当 r1(x), r2 (x), rm (x) 线性无关时,R 列满秩,RT R 可逆所以上述 方程组有唯一解:a (RT R)1 * RT y (称为该线性方程组的最小二乘
意义下的解)。此即线性最小二乘拟合所得系数。
(4)[x, options]=lsqcurvefit (‘fun’,x0,xdata,ydata,…); (5)[x,options,funval]=lsqcurvefit(‘fun’,x0,xdata,ydata,…)
; (6) [x,options,funval,Jacob] = lsqcurvefit (‘fun’,x0,xdata,
用作线性最小二乘拟合的误差也可以考虑以下两种形式:
n
1.最小平方误差: J (a1, a2 ,...am ) ( ( yi f (xi ))2 ) i 1
2.最大偏差: J (a1, a2 ,...am ) max yi f (xi ) 1in
(二)基函数组的选取
线性最小二乘拟合 f(x)=a1r1(x)+ …+amrm(x)中函数
该问题即求解最优化问题:
(打印)实验四 MATLAB 高级图形绘制
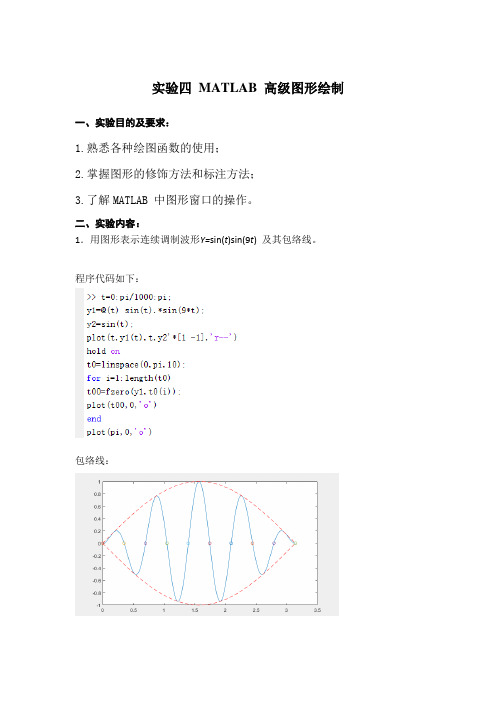
实验四MATLAB 高级图形绘制一、实验目的及要求:1.熟悉各种绘图函数的使用;2.掌握图形的修饰方法和标注方法;3.了解MATLAB 中图形窗口的操作。
二、实验内容:1.用图形表示连续调制波形Y=sin(t)sin(9t)及其包络线。
程序代码如下:包络线:2.x=[-2π,2π],y1=sinx、y2=cosx、y3=sin2x、y4=cos 2x①用MATLAB语言分四个区域分别绘制的曲线,并且对图形标题及横纵坐标轴进行标注。
程序:结果:②另建一个窗口,不分区,用不同颜色、线型绘出四条曲线,并标注图例注解。
程序:结果:③绘制三维曲线:⎪⎩⎪⎨⎧=≤≤==)cos()sin()200()cos()sin(t t t z t t y t x π程序:结果:3.绘制极坐标曲线ρ=asin(b+nθ),并分析参数a、b、n对曲线形状的影响。
(1)a=1;b=1;n=1(2)a=10;b=1;n=1(3)a=10;b=10;n=1 (4)a=10;b=10;n=10参数a、b、n对曲线形状的影响:由上面绘制的图形可知:a决定图形的大小,当a为整数时,图形半径大小就是a;b决定图形的旋转角度,图形的形状及大小不变;n决定图形的扇叶数,当n 为奇数时,扇叶数为n,当n为偶数时,扇叶数为2n。
三、结论本次实验用到了曲线绘图、三位曲线绘图的知识,与老师上课的内容一致,让我学的matlab绘图的知识得到了巩固,我还学会了如何使用title、subplot、plot、axis等函数。
在做实验的过程复习了hold on指令是覆盖函数继续绘图的意思。
实验四 MATLAB的绘图

西安邮电大学《Matlab程序设计基础》课内实验报告题目:实验四MATLAB的绘图院系名称:计算机学院专业名称:计算机科学与技术班级:计科1502班内序号:05141107(29)学生姓名:赵阳指导教师:张老师实验四MATLAB的绘图一、实验目的:掌握基本的绘图函数plot。
二、实验内容:1、在同一坐标系下绘制下面三个函数在[0,4pi]的图象。
代码如下:t=0:pi/100:4*pi;y1=t;y2=sqrt(t);y3=4*pi*exp(-0.1*t).*sin(t);plot(t,y1,t,y2,t,y3)2、编写程序,选择合适的步距,绘制下面函数在区间[-6,6]中的图象。
代码如下:x=linspace(-6,6,100);y=[];for x0=xif x0<=0y=[y,sin(x0)];elseif x0<=3y=[y,x0];elsey=[y,-x0+6];endendplot(x,y)3、用compass函数画下面相量图ua=1;ub=cos(-2*pi/3)+sin(-2*pi/3)*i;uc=cos(2*pi/3)+sin(2*pi/3)*i;compass([ua,ub,uc,ua-ub,ub-uc,uc-ua])代码如下:ua=1;ub=cos(-2*pi/3)+sin(-2*pi/3)*i;uc=cos(2*pi/3)+sin(2*pi/3)*i;compass([ua,ub,uc,ua-ub,ub-uc,uc-ua])4、三维空间曲线绘制z=0:0.1:4*pi;x=cos(z);y=sin(z);plot3(x,y,z)代码如下:z=0:0.1:4*pi;x=cos(z);y=sin(z);plot3(x,y,z)5、用mesh或surf函数,绘制下面方程所表示的三维空间曲面,x和y的取值范围设为[-3,3]。
代码如下:[x,y]=meshgrid(-3:0.5:3);z=-x^2/10+y^2/10;mesh(x,y,z)三、思考题在同一坐标系下,用不同颜色和线型绘制以下两个函数在tÎ[-2p,2p]范围内的图象。
matlab实验4_循环结构程序设计_参考解答

高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
clear all; close all; clc; y=0; n=1; while y<3
y=y+1/(2*n-1); n=n+1; end n=n-1; y=y-1/(2*n-1) n=n-1
运行结果:
y= 2.9944
x1=a/(b+x0); y=abs(x1-x0); x0=x1;
MATLAB 语言
3
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
n=n+1; end x1 r1=(-b+sqrt(b^2+4*a))/2 r2=(-b-sqrt(b^2+4*a))/2
clear all; close all; clc; prime=[]; for n=2:49
x=n*(n+1)-1; signx=0; for k=2:sqrt(x)
MATLAB 语言
5
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
根据
π2 6
=1 12
+
1 22
+1 32
+"+
1 n2
,求 π 的近似值。当
n
分别取
100、1000、10000
时,
结果是多少?
要求:分别用循环结构和向量运算(使用 sum 函数)来实现。 答:程序设计:
(1) 循环结构
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab实验四
实验目的
(1) 利用计算机完成控制系统的根轨迹作图。
(2) 了解控制系统根轨迹作图的一般规律。
(3) 利用根轨迹进行系统分析。
实验步骤
(1)运行matlab 。
(2)练习根轨迹的相关函数。
rlocus(sys) rlocus(sys,k) r=rlocus(sys)
[r,k]=rlocus(sys) (3)实验内容
1)给定如下系统的开环传递函数,作出它们的根轨迹,并完成给定要求。
()()()21++=
s s s k
s G
要求:准确记录根轨迹的起点、终点和根轨迹的条数。
确定根轨迹的分离点与相应的根轨迹增益。
确定临界稳定时根轨迹增益k 。
(1) num=[1];
den=conv([1 0],conv([1 1],[1 2])); sys=tf(num,den); rlocus(sys)
-6
-5-4-3-2-1012
-4-3
-2
-1
1
2
3
4R oot Locus
R eal Axis
I m a g i n a r y A x i s
、-1、0终点为无穷远∞。
(2) num=[1];
den=conv([1 0],conv([1 1],[1 2])); sys=tf(num,den); rlocus(sys);
[kd,pd]=rlocfind(sys)
Select a point in the graphics window selected_point = -0.4207 - 0.0000i kd =
0.3849 pd =
-2.1547 -0.4247 -0.4207
-6
-5-4-3-2-1012
-4-3
-2
-1
1
2
3
4
Root Locus
Real Axis
I m a g i n a r y A x i s
(3) num=[1];
den=conv([1 0],conv([1 1],[1 2])); sys=tf(num,den); rlocus(sys);
[k,p]=rlocfind(sys)
Select a point in the graphics window selected_point = 0.0153 - 1.4136i k =
6.0566 p =
-3.0051 0.0026 + 1.4197i 0.0026 - 1.4197i
-6
-5-4-3-2-1012
-4-3
-2
-1
12
3
4
Root Locus
Real Axis
I m a g i n a r y A x i s
()()()()164112
++-+=s s s s s k s G 要求:确定根轨迹与虚轴交点并确定系统稳定的根轨迹增益k 。
num=[1 1];
den=conv([1 0],conv([1 -1],[1 4 16])); sys=tf(num,den); rlocus(sys);
-10
-8-6-4
-2024
-8-6
-4
-2
2
4
6
8Root Locus
Real Axis
I m a g i n a r y A x i s
系统稳定的根轨迹增益k 范围为:23 <k<36.3
()()()23++=
s s s k s G 要求:确定系统具有最大超调量时Mp,max 时的根轨迹增益,作时域仿真验证。
确定系统阶跃响应无超调量时的根轨迹增益取值范围,并作时域仿真验证。
num=[1 3];
den=conv([1 0],[1 2]); sys=tf(num,den); rlocus(sys);
此时系统的最大超调量Mp,max=1.17,根轨迹增益为2 以1.96作时域仿真验证
num1=[1.96 6]; den1=[1 4 6]; step(num1,den1)
00.51 1.52 2.53
0.2
0.4
0.6
0.8
1
1.2
1.4
Step Response
Tim e (sec)
A m p l i t u d e
如图可以看出超调量为0的区域取增益为0.4作时域仿真验证
num1=[0.4 1.2]; den1=[1 2.4 1.2]; step(num1,den1)
012345678
0.10.20.30.40.50.6
0.70.80.91Step Response
Tim e (sec)
A m p l i t u d e
实验要求:
记录给定系统与显示的根轨迹图;
完成上述各要求,分析闭环极点在s平面上的位置与系统动态性能的关系。
实验心得:。
