青岛版八年级上册数学《第5章 几何证明初步》单元测试卷(有答案)
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

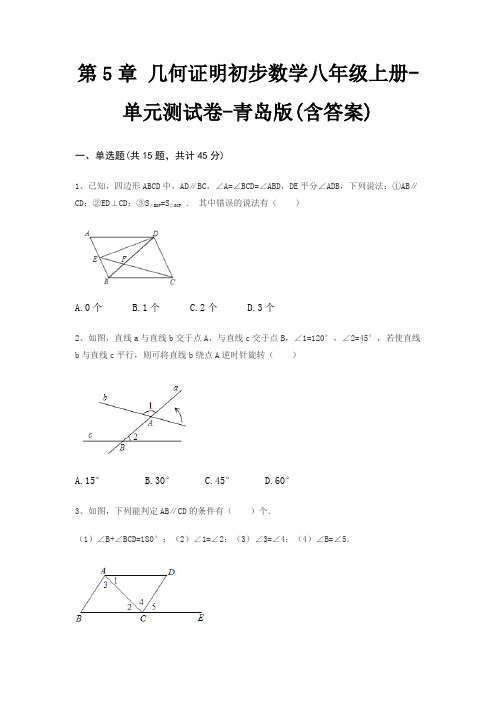
第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,点在的延长线上,下列条件中能判断的是()A. B. C. D.2、如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是()A.不变B.一直变大C.先减小后增大D.先增大后减小3、如图,用尺规作出了BF∥OA,作图痕迹中,弧MN是()A.以B为圆心,OD长为半径的弧B.以C为圆心,CD长为半径的弧 C.以E为圆心,DC长为半径的弧 D.以E为圆心,OD长为半径的弧4、已知一个等腰三角形两个内角度数之比为1:4,则这个等腰三角形顶角度数为()A.75°B.90°C.105°D.120°或20°5、三角形的内角和等于()A. B. C. D.6、下列说法不能推出△ABC是直角三角形的是()A. B. C.∠A=∠B=∠C D.∠A=2∠B=2∠C7、下列命题中是真命题的是()A.相等的两个角是对顶角B.两条直线被第三条直线所截,同位角相等 C.在同一平面内,如a∥b,b∥c,则a∥c D.若a>b,则﹣a>﹣b8、如图,下列能判定AB∥CD的条件的个数()(1 )∠B=∠BCD;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1B.2C.3D.49、下列说法中正确的是A.过一点有且仅有一条直线与已知直线平行B.若,则点C是线段AB的中点C.两点之间的所有连线中,线段最短D.相等的角是对顶角10、如图所示,一张△ABC纸片,点D,E分别在线段AC,AB上,将△ADE沿着DE折叠,A 与A′重合,若∠A=α,则∠1+∠2=()A.αB.2αC.180°﹣αD.180°﹣2α11、如图,ΔABC与ΔA’B’C’关于直线l对称,则∠B的度数为()A.30°B.50°C.90°D.100°12、如图,已知直线AB∥CD,∠C=125°,∠A=45°,那么∠E的大小为()A.70B.80C.90D.10013、如图,AB∥CD,则∠1.∠2.∠3.∠4的关系是( )A.∠1-∠2+∠3+∠4=180°B.∠1+∠2+∠3=∠4C.∠1+∠2-∠3+∠4=180°D.∠2+∠3+∠4 -∠1=180°14、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是()A.1B.C.2D.415、下列条件中能得到互相平行的直线的是()A.互为邻补角的角平分线所在的直线B.对顶角的平分线所在的直线 C.两条平行线的一对内错角的平分线所在的直线 D.两条平行线的一对同旁内角的平分线所在的直线二、填空题(共10题,共计30分)16、如图,在△ABC中,∠ABC和∠ACB的角平分线交于点O,BO的延长线交于AC于点D,若∠DOC=40°,则∠A=________。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图所示,直线a、b被直线c所截,现给出下列四种条件:①∠2=∠6;②∠2=∠8;③∠1+∠4=180°;④∠3=∠8,其中能判断是a∥b的条件的序号是()A.①②B.①③C.①④D.③④2、如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=38°时,∠1=()A.52°B.38°C.42°D.60°3、下列选项中,哪个不可以得到?()A. B. C. D.4、如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=()A.10°B.20°C.30°D.40°5、如图,已知A点坐标为(5,0),直线与y轴交于点B,连接AB,若∠a=75°,则b的值为 ( )A.3B.C.D.6、若一个角的两边分别平行于另一个角的两边,那么这两个角为()A.相等B.互补C.相等或互补D.以上结论都不对7、如图,的度数为().A. B. C. D.8、如图,在中,,,点、在上,将、分别沿、翻折,点、分别落在点、的位置,再将、分别沿、翻折,点与点恰好重合于点,则的度数是()A.90°B.120°C.135°D.150°9、如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,则下列结论不正确的是()A.∠CAD=∠BADB.BD=CDC.AE=EDD.DE=DB10、如图,已知a∥b,∠2=50°,∠3=100°,则∠1的度数为()A.80°B.70°C.60°D.50°11、如图,点C在AD上,CA=CB,∠A=20°,则∠BCD=( )A.20°B.40°C.50°D.140°12、如图,在△ABC 中,AB=AC,BO、CO 分别平分∠ABC,∠ACB,DE 经过点 O,且 DE ∥BC,DE 分别交 AB,AC 于 D,E,则图中等腰三角形的个数为( )A.2B.3C.4D.513、在△ABC中,∠A=2∠B=75°,则∠C等于()A.30°B.67.5°C.105°D.135°14、等腰三角形的一个内角为50°,则另外两个角的度数分别为()A.65°,65B.50°,80°C.65°,65°或50°,80° D.50°,50°15、如图,∠A、∠1、∠2的大小关系是()A.∠A>∠1>∠2B.∠2>∠1>∠AC.∠A>∠2>∠1D.∠2>∠A>∠1二、填空题(共10题,共计30分)16、如图,现将一块含有60°角的三角板的顶点放在直尺的一边上,若∠1=∠2,那么∠1的度数为________.17、如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为________.18、如图,∠1+∠2+∠3+∠4+∠5+∠6+∠7=________.19、如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为________.20、如图,∠ACD是△ABC的外角,CE∥AB,∠ACB=75°,∠ECD=45°,则∠A的度数为________.21、将一张矩形纸条与一块三角板如图放置,若∠1=36°,则∠2=________.22、如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=________°.23、如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别落在D′,C′的位置上,ED′与BC交于G点,若∠EFG=56°,则∠AEG=________.24、如图,把一张长方形纸条ABCD沿AF折叠.已知∠ADB=25°,AE∥BD,则∠BAF=________.25、如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=________°.三、解答题(共5题,共计25分)26、如图,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度数.27、如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.28、如图,在△ABC中,已知∠ABC=30°,点D在BC上,点E在AC上,∠BAD=∠EBC,AD 交BE于F.(1)求的度数;(2)若EG∥AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.29、如图是A,B,C三个岛的平面图,C岛在A岛的北偏东32°方向,B岛在A岛的北偏东66°方向,C岛在B岛的北偏西44°方向.求C岛看A、B两岛的视角∠ACB的度数?30、如图,在△ABC中,AB=AC,点D,点E分别是BC,AC上一点,且DE⊥AD.若∠BAD =55°,∠B=50°,求∠DEC的度数.参考答案一、单选题(共15题,共计45分)2、A3、C4、A5、C6、C7、A8、B9、D10、D11、B12、D13、B14、C15、B二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)
第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、已知,四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③S△EDF=S△BCF.其中错误的说法有()A.0个B.1个C.2个D.3个2、如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15°B.30°C.45°D.60°3、如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1B.2C.3D.44、如图,A,B,C,D是⊙O上四个点,且弧AB=弧BC=弧CD,BA和CD的延长线相交于P,∠P=40°,则∠ACD的度数是()A.15°B.20°C.40°D.50°5、下列说法中错误的是()A.在中,若,则是直角三角形B.在中,若,则是直角三角形 C.在中,若,,的度数比是7:3:4,则是直角三角形 D.在中,若三边长,则是直角三角形6、下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角;③过一点有且仅有一条直线与已知直线平行;④长方体是四棱柱;其中正确的有()A.1个B.2个C.3个D.4个7、如图,在中,,点在上,以点为圆心,为半径作,点恰好在上,是的切线,则的度数是()A.35°B.30°C.25°D.20°8、已知直线a∥b,将一副三角板按如图所示放置在两条平行线之间,则∠1的度数是A.45°B.60°C.75°D.80°9、如图,已知AB∥DE ,∠ABC=70°,∠CDE=140°,则∠BCD的值为()A.20°B.30°C.40°D.70°10、关于三角形,下列说法错误的是()A.三角形具有稳定性B.三角形任意两边之和大于第三边C.三角形的内角和是180°D.钝角三角形一定不是等腰三角形11、如图,在条件:①∠5=∠6,②∠7=∠2,③∠3+∠8=180°,④∠3=∠2,⑤∠4+∠1=180°中,能判定a∥b的条件有()A.4个B.3个C.2个D.1个12、如图,在四边形ABCD中,∠A+∠D=α,∠ABC的平分线与∠BCD的平分线交于点P,则∠P=()A.90°﹣αB.90°+ αC.D.360°﹣α13、如图,直线c与直线a、b相交,且a∥b,则下列结论:①∠1=∠2;②∠1=∠3;③∠3=∠2中正确的个数为()A.0B.1C.2D.314、如图,AB∥CD,CB平分∠ECD交AB于点B,若∠ECD=60°,则∠B的度数为()A.25°B.30°C.35°D.40°15、如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=,∠ACB=,则()A. B. C.D.二、填空题(共10题,共计30分)16、“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA、OB组成.两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E在槽中滑动,若∠BDE=84°.则∠CDE是________ °.17、如图,中,,与分别是与的平分线,,.则的周长是________.18、如图,AB∥CD,∠1=64°,FG平分∠EFD,则∠2=________度.19、如图,直线AB、CD相交于点E,DF∥AB.若∠D=65°,则∠AEC=________20、如图,l∥m,等边△ABC的顶点B在直线m上,∠1=20°,则∠2的度数为________.21、如图,平分,,,则________.22、如图,,若和分别垂直平分和,则是________ 度.23、如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G=________.24、好久未见的A,B,C,D,E五位同学欢聚一堂,他们相互握手一次,中途统计各位同学握手次数为:A同学握手4次,B同学握手3次,C同学握手2次,D同学握手1次,那么此时E同学握手________次.25、如图,AB∥CD,E是BC延长线上一点,若∠B=50°,∠D=20°,则∠E的度数为________.三、解答题(共5题,共计25分)26、如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.27、如图,已知∠1=∠2,再添上什么条件可使AB∥CD成立?并就你添上的条件证明AB∥CD.28、上午8时,一条船从海岛A出发,以15n mile/h(海里/时,1 n mile/h=1852m)的速度向正北航行,10时到达海岛B处.从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°.求从海岛B到灯塔C的距离.29、如图,∠CAB=100°,∠ABF=130°,AC∥MD,BF∥ME,求∠DME的度数.30、如图,已知∠EFC+∠BDC=180°,∠DEF=∠B,试判断DE与BC的位置关系,并说明理由.参考答案一、单选题(共15题,共计45分)1、A2、A3、C4、A5、D6、B7、C8、C9、B10、D11、A12、C13、D14、B15、A二、填空题(共10题,共计30分)16、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人”;乙说:“两项都参加的人数小于5人” .对于甲、乙两人的说法,有下列四个命题,其中真命题的是()A.若甲对,则乙对B..若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对2、下列说法正确的是()A.经验、观察或实验完全可以判断一个数学结论的正确与否B.推理是科学家的事,与我们没有多大的关系C.对于自然数n,n 2+n+37一定是质数D.有10个苹果,将它放进9个筐中,则至少有一个筐中的苹果不少于2个3、在锐角三角形中,∠A>∠B>∠C,则下列结论中错误的是()A.∠A>60°B.∠B>45°C.∠C<60°D.∠B+∠C<90°4、如图,点E在BC的延长线上,下列条件不能判定AB∥CD的是()A.∠3=∠4B.∠B=∠DCEC.∠4=∠2D.∠D+∠DAB=180°5、如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为()A.50°B.40°C.30°D.20°6、等腰三角形的顶角为150°,则它的底角为()A.30°B.15°C.30°或15°D.50°7、如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=()A.110°B.120°C.125°D.135°8、如图,直线AB∥CD,直线EF分别与AB,CD交于点E,F,EG平分∠BEF,交CD于点G,若∠1=70°,则∠2的度数是()A.60°B.55°C.50°D.45°9、如图,直线∥,点在上,且.若,那么等于()A. B.50° C. D.10、如图,已知△ABC平移后得到△DEF,则以下说法中,错误的是()A. AC= DF;B. BC∥EF;C.平移的距离是BD;D.平移的距离是AD.11、如图,若直线a∥b,AC⊥AB,∠1=34°,则∠2的度数为()A.34°B.56°C.66°D.146°12、如图,AB=AC,AD=AE,∠A=105°,∠D=25°,则∠ABE等于()A.65°B.60°C.55°D.50°13、两条直线被第三条直线所截,那么下面说法正确的上是()A.同位角相等B.内错角相等C.同旁内角互补D.以上都不对14、如图,直线a,b被直线c所截,当a∥b时,下列说法正确的是()A.一定有∠1=∠2B.一定有∠1+∠2=90°C.一定有∠1+∠2=100°D.一定有∠1+∠2=180°15、如图,在△ABC中,∠BAC、∠BCA的平分线相交于点I,若∠B=35°,BC=AI+AC,则∠BAC的度数为()A.60°B.70°C.80°D.90°二、填空题(共10题,共计30分)16、若等腰三角形的一个内角为50°,则它的顶角为 ________ .17、如图,把沿线段折叠,使点落在点处,,若∠A+∠B=110°,则=________.18、如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以点A为圆心、AC的长为半径画弧,交AB边于点D,则弧CD的长等于________.(结果保留π)19、如图,∠A=12°,∠ABC=90°,∠ACB=∠DCE,∠ADC=∠EDF,∠CED=∠FEG,则∠F=________°.20、已知直线a∥b,若∠1=40°50′,则∠2=________.21、如下图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=________22、如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF=________.23、如图,在矩形ABCD中,AB=9,,点P是边BC上的动点(点P不与点B,点C重合),过点P作直线PQ∥BD,交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点,则∠CQP=________.24、如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD.求证:∠C=∠D.证明:∵∠A=∠AOC,∠B=∠BOD(已知)又∠AOC=∠BOD(________)∴∠A=∠B(________)∴AC∥BD(________)∴∠C=∠D(________)25、如图,在△ABC中,∠A=60°,若剪去∠A得到四边形BCDE,则∠1+∠2=________度.三、解答题(共5题,共计25分)26、在△ABC中,∠A=38°,∠B=70°,CD⊥AB于点D,CE平分∠ACB,DP⊥CE于点P,求∠CDP的度数.27、如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD相交于D,试说明∠A=2∠D的理由.28、请将下面的说理过程和理由补充完整.如图,点B,E,C,F在一条直线上,BE=CF,AB∥DE,AB=DE,说明AC=DF.解:∵BE=CF,(已知)∴BE+EC=CF+ ▲.(等式的性质)即 BC= ▲.∵AB∥DE,(已知)∴∠B= ▲.(▲)又∵AB=DE,(已知)∴△ABC≌△DEF.(▲)∴AC=DF.(▲)29、如图,DB是△ABC的高,AE是角平分线,∠BAE=26°,求∠BFE的度数.30、已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.参考答案一、单选题(共15题,共计45分)2、D3、D4、A5、C6、B7、D8、B9、C10、C11、B12、D13、D14、D15、B二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、28、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠EDF的度数为()A.50°B.40°C.80°D.60°2、如图,AB∥CD,若∠2是∠1的两倍,则∠2等于()A.60°B.90°C.120°D.150°3、如图,连接正十边形的对角线 AC 与 BD 交于点 E,则∠AED 的度数是()A.126°B.116°C.120°D.110°4、如图,在中,,,是的平分线,经过A,D两点的圆的圆心O恰好落在上,分别与、相交于点E、F.若圆半径为2.则阴影部分面积().A. B. C. D.5、如图,△ABC中,∠A=36°,∠B=60°,EF∥BC,FG平分∠AFE,则AFG的度数为()A.36°B.37°C.42°D.47°6、下列结论中,错误结论有();①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360º;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在中,若,则为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个A.6个B.5个C.4个D.3个7、△ABC中,∠A,∠B,∠C的对边分别为a,b,c,下列命题中的假命题是()A.若∠A=∠C-∠B,则∠C=90ºB.若∠C=90º,则C.若∠A=30º,∠B=60º,则AB=2BCD.若,则∠C=90º8、如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是()A.0B.C.D.19、若等腰中有一个内角为,则这个等腰三角形的一个底角的度数为()A. B. C. 或 D. 或10、如图,在中,,,则的度数是()A. B. C. D.11、如图,AE‖BD,∠1=120°,∠2=40°,则∠C的度数是()A.10°B.20°C.30°D.40°12、在△ABC中,∠B和∠C的平分线交于点I,边AB和AC的垂直平分线交于点O,若∠BIC=90°+ θ,则∠BOC=()A.90°﹣θB.2θC.180°﹣θD.以上答案都不对13、在如图,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:∵∠1=∠2(已知),∴AC∥DF(A.同位角相等,两直线平行),∴∠3=∠5(B.内错角相等,两直线平行).又∵∠3=∠4(已知)∴∠5=∠4(C.等量代换),∴BC∥EF(D.内错角相等,两直线平行).上述过程中判定依据错误的是()A.AB.BC.CD.D14、如图,在等边三角形的内部,作,两两相交于三点(三点不重合).设,则下列关系正确的是()A. B. C.D.15、如图,下列条件中能判定的是()A. B. C. D.二、填空题(共10题,共计30分)16、如图,这是生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片合部分都是直角,刀片的上,下是平行的动刀片时会形成∠1和∠2,则∠1+∠2=________.17、如图,l∥m,∠1=120°,∠A=55°,则∠ACB的大小是________ .18、推理填空:如图,,,将说明成立的理由填写完整.解:因为(已知),所以(________)又因为(已知),所以(等量代换),所以________(同位角相等,两直线平行),所以(________)19、如图,在中,平分,的中垂线交于点,交于点,连接,.若,则的度数为________;20、已知,如图.AD∥BE,∠1=∠2,求证:∠A=∠E,请完成解答过程.证明:∵AD∥BE(已知)∴∠A=∠________(________)又∵∠1=∠2(已知)∴AC∥________(________)∴∠3=∠________(两直线平行,内错角相等)∴∠A=∠E(等量代换)21、如图,直线l∥m,点A在直线l上,点c在直线m上,且有AB⊥BC,∠1=40°,则∠2=________度.22、如图,直线、被直线所截,若,,则________.23、如图,已知,如果,那么的度数为________.24、如图,在△ABC中,AB、AC的垂直平分线l1、l2相交于点O,若∠BAC等于82°,则∠OBC=________°.25、如图所示,直线,直线分别与相交于点小宇同学利用尺规按以下步骤作图:①以点为圆心,以任意长为半径作弧交于点,交于点;②分别以为圆心,以大于长为半径作弧,两弧在内交于点;③作射线交于点.若,则的度数为________三、解答题(共5题,共计25分)26、如图在四边形ABCD中,∠B=∠D=90°,AE、CF分别平分∠BAD和∠BCD.试问直线AE、CF的位置关系如何?请说明你的理由.27、推理填空:如图,E点为DF上的点,B为AC上的点,,那么,请完成它成立的理由解:又)( ) ( ) ( )( )( )( )( )28、如图所示,直线 a 、 b 被 c 、 d 所截,且 c⊥a,c⊥b,∠1=70°,求∠2的度数.29、如图,△ABC中,∠A=90°,D为AC上一点,E为BC上一点,点A和点E关于BD对称,点B和点C关于DE对称.求∠ABC和∠C的度数.30、根据题意结合图形填空:已知:如图,AD⊥BC于D,EG⊥BC与G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.答:是,理由如下:∵AD⊥BC,EG⊥BC(▲_)∴∠4=∠5=90°(_▲)∴AD∥EG(▲_)∴∠1=∠E(▲)∠2=∠3(▲_)∵∠E=∠3(▲)∴▲(等量代换)∴AD是∠BAC的平分线(▲)参考答案一、单选题(共15题,共计45分)1、A2、C3、A4、C5、C6、C7、D8、D9、D10、B11、B12、B13、B14、B15、C二、填空题(共10题,共计30分)16、17、18、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、下列说法正确的是()A.“任意画一个三角形,其内角和为360°”是随机事件.B.某种彩票的中奖率是,说明每买100张彩票,一定有1张中奖.C.“篮球队员在罚球线上投篮一次,投中”为随机事件.D.投掷一枚质地均匀的硬币100次,正面向上的次数一定是50次.2、如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为()A.30°B.34°C.36°D.40°3、如图,已知AB∥CD,∠EBA=45°,∠E+∠D的度数为()A.30°B.60°C.90°D.45°4、如图,∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于()A.2B.3C.4D.55、如图所示,已知l1∥l2,直线l与l1、l2分别相交于C、D两点,把一块含有30°角的三角板按如图位置摆放.若∠1=130°,则∠2=()A.60°B.50°C.30°D.20°6、如图,AB∥CD,∠D=30°,∠E=35°,则∠B的度数为()A.60°B.65°C.70°D.75°7、如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是()A.①②③B.①②④C.①③④D.①②③④8、如图,将三角尺的直角顶点放在直尺的一边,∠1=30°,∠2=70°,则∠3等于()A.20°B.30°C.40°D.50°9、如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是()A.30°B.20°C.15°D.14°10、下列命题是真命题的是()A.内错角相等B.过一点有且只有一条直线与已知直线垂直C.同位角相等,两直线平行D.一个角的补角大于这个角11、如图,,,,则的度数为()A. B. C. D.12、下列命题为真命题的是()A.三角形的一个外角大于任何一个和它不相邻的内角B.两直线被第三条直线所截,同位角相等C.垂直于同一直线的两直线互相垂直D.三角形的外角和为13、如图,直线m∥n,若∠1=30°,∠2=58°,则∠BAC的度数为()A.12°B.28°C.29°D.30°14、将—副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,直线a、b被直线c所截,,若∠2=50º,则∠1等于( )A.120 ºB.130 ºC.140 ºD.150 º2、如图,将直尺与含角的直角三角板放在一起,若,则的度数是()A. B. C. D.3、甲、乙、丙三位同学进行立定跳远比赛,每人轮流跳一次称为一轮,每轮按名次从高到低分别得3分、2分、1分(没有并列名次),他们一共进行了五轮比赛,结果甲共得14分;乙第一轮得3分,第二轮得1分,且总分最低.那么丙得到的分数是( )A.8分B.9分C.10分D.11分4、如图,把矩形ABCD沿EF对折,若,则等于()A.115°B.130°C.120°D.65°5、小亮为宣传“两会”,设计了形状如图所示的彩旗,图中∠ACB=90°,∠D=15°,点A在CD上,AD=AB,BC=2dm,则AD的长为()A.3dmB.4dmC.5dmD.6dm6、在△ABC中,已知∠A=∠B= ∠C,则三角形是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形7、如图,已知∠1 = 70º,如果CD∥BE,那么∠B的度数为()A.70ºB.100ºC.110ºD.120º8、如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=85°,则∠2的度数为()A.24°B.25°C.30°D.35°9、如图,直线,,,则的度数是()A. B. C. D.10、如图,在正方形的外侧,作等边三角形,则为()A.45°B.25°C.30°D.40°11、如图,直线,则的度数是().A.38°B.48°C.42°D.39°12、如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为()A.6B.7C.8D.913、如图,在矩形ABCD中,点E在AD上,且EC平分∠BED,AB=1,∠ABE=45°,则BC的长为()A. B.1.5 C. D.214、下列说法:①有理数的绝对值一定是正数;②两点之间的所有连线中,线段最短;③相等的角是对顶角;④过一点有且仅有一条直线与已知直线垂直;⑤不相交的两条直线叫做平行线,其中正确的有()A.1个B.2个C.3个D.4个15、O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E 点,若BC=10cm,那么△ODE的周长为()A.8cmB.9cmC.10cmD.11cm二、填空题(共10题,共计30分)16、如图,在与中,AB、EF相交于点D,点F在边BC上,,,.下列结论:①;②;③中,正确的是________.(填序号)17、如图,直线EF分别与直线AB、CD相交于点P和点Q,已知:AB∥CD,∠1=∠2,求证:PG∥QH。
第5章 几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)

第5章几何证明初步数学八年级上册-单元测试卷-青岛版(含答案)一、单选题(共15题,共计45分)1、如图,在的边上取一点使,作于,作交于点,则与的关系是()A. B. C.D.2、如图,已知AB∥CD,∠DFE=130°,则∠ABE的度数为()A.40°B.50°C.60°D.130°3、如图,直线,若,,则的度数为()A. B. C. D.4、如图,已知AB∥EF,CD⊥BC,∠B=x°,∠D=y°,∠E=z°,则()A.x+y-z=90B.x-y+z=0C.x+y+z=180D.y+z- x =905、下列说法中正确的个数有()①三角形的三条高都在三角形内,且相交于一点;②三角形的中线都是过顶点平分对边的直线;③在△ABC中,若∠A=∠B=∠C,则△ABC一定是直角三角形;④三角形的一个外角大于与它不相邻的每个内角;A.0个B.1个C.2个D.3个6、下列四种说法:①三角形三个内角的和为360°;②三角形一个外角大于它的任何一个内角;③三角形一个外角等于它任意两个内角的和;④三角形的外角和等于360°. 其中正确说法的个数为()A.0B.1C.2D.37、如图,∠1=60º,∠2=60º,∠3=57º,则∠4=57º,下面是A,B,C,D四个同学的推理过程,你认为推理正确的是()A.因为∠1=60º=∠2,所以a∥b,所以∠4=∠3=57ºB.因为∠4=57º=∠3,所以a∥b,故∠1=∠2=60ºC.因为∠2=∠5,又∠1=60º,∠2=60º,故∠1=∠5=60º,所以a∥b,所以∠4=∠3=57ºD.因为∠1=60º,∠2=60º,∠3=57º,所以∠1=∠3=∠2-∠4=60º-57º=3º,8、如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )A.90°B.135°C.270°D.315°9、一副三角板如图放置,点D在CB的延长线上,EF∥CD,∠C=∠EDF=90°,∠A=45°,∠EFD=30°,则∠DFB=( )A.15°B.20°C.25°D.30°10、下列语句中:①一条直线有且只有一条垂线;②不相等的两个角一定不是对顶角;③两条不相交的直线叫做平行线;④若两个角的一对边在同一直线上,另一对边互相平行,则这两个角相等;⑤不在同一直线上的四个点可画6条直线;⑥如果两个角是邻补角,那么这两个角的平分线组成的图形是直角.其中错误的有()A.2个B.3个C.4个D.5个11、如图,在△ABC中,BE平分∠ABC交AC于点E,CD⊥AC交AB于点D,∠BCD=∠A,则∠BEA的度数( )A.155°B.135°C.108°D.100°12、如图,直线,点A在直线上,以点A为圆心,适当长度为半径画弧,分别交直线、于B、C两点,连结AC、BC.若,则的大小为()A. B. C. D.13、如图,已知AB∥CD,∠1=62°,则∠2的度数是()A.28°B.62°C.108°D.118°14、如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为()A.15°B.20°C.25°D.30°15、如图所示,△ABC 中, AB=AC,过AC上一点作DE⊥AC,EF⊥BC,若∠BDE=140°,则∠DEF=()A.60°B.65°C.70°D.75°二、填空题(共10题,共计30分)16、如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=________度.17、如图,已知直线AB∥CD,FH平分∠EFD,FG⊥FH,∠AEF=62°,则∠GFC=________度.18、如图,∠AOB=40°,OP平分∠AOB,点C为射线OP上一点,作CD⊥OA于点D,在∠POB的内部作CE∥OB,则∠DCE=________度.19、如图,AB∥CD,AD与BC交于点O,OP平分∠BOD,交CO的延长线于P,若∠A=100º,∠B=30º,则∠P的度数是________20、如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=________ 度.21、如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,则∠P的度数为________.22、如图,直线a,b被直线c,d所截.若,,,则的度数为________度.23、若一个等腰三角形的顶角等于40°,则它的底角等于________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020-2021学年青岛新版八年级上册数学《第5章几何证明初步》单元测试卷一.选择题1.下列语句中,不是命题的是()A.延长线段AB到CB.自然数都是整数C.有两条边相等的三角形是等腰三角形D.平行于同一条直线的两条直线平行2.如图,能推出AD∥BC的条件是()A.∠1=∠4B.∠1=∠B C.∠2=∠3D.∠2=∠43.下列说法不正确的是()A.若两相等的角有一边平行,则另一边也互相平行B.两条直线相交,所成的两组对顶角的平分线互相垂直C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直D.在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直4.下列说法中,正确的个数有()个①平面内,过一点作一条直线的平行线,只能作一条;②平面内,过一点与一条已知直线垂直的直线只有一条;③直线外一点与直线上各点连接的所有线段中,垂线段最短④两点之间的距离是指连接两点的线段.A.1B.2C.3D.45.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E、G为垂足,则下列说法中错误的是()A.CE∥FGB.CE=FGC.A、B两点的距离就是线段AB的长D.直线a、b间的距离就是线段CD的长6.三角形的三个内角中,最小的角不大于()A.50°B.30°C.60°D.90°7.△ABC的三个内角∠A、∠B、∠C,满足3∠A>5∠B,3∠C≤2∠B,则△ABC的形状是()A.钝角三角形B.直角三角形C.锐角三角形D.不能确定8.在A,B,C三个盒子中分别装有红、黄、蓝颜色的小球中的一种,将它们分别给甲、乙、丙三个人.已知甲没有得到A盒;乙没有得到B盒,也没有得到黄球;A盒中没有装红球,B盒中装着蓝球.则丙得到的盒子编号和小球的颜色分别是()A.A,黄B.B,蓝C.C,红D.C,黄9.5个选手P,Q,R,S,T举行一场赛跑.P胜Q,P胜R,Q胜S,并且T在P之后,Q 之前跑完全程.谁不可能得第三名()A.P与Q B.P与R C.P与S D.P与T10.如果l1∥l2,l2∥l3,l3∥l4,那么l1与l4的关系是()A.平行B.相交C.重合D.不能确定二.填空题11.如图,如果∠B=∠1=∠2=50°,那么∠D=.12.填空完成推理过程:如图,∵AB∥EF(已知)∴∠A+=180°()∵DE∥BC(已知)∴∠DEF=()∠ADE=()13.命题“和为180°的两个角互为补角”的逆命题是,这个逆命题是命题(填“真”或“假”).14.四个空矿泉水瓶可以换一瓶矿泉水,现拿16个空矿泉水瓶,最多能喝瓶矿泉水.15.在同一平面内,经过不在直线上的一点作已知直线的平行线只有一条..(判断对错)16.直线l同侧有A、B、C三点,如果A、B两点确定的直线l1,与B、C两点确定的直线l2都与直线l平行,则A、B、C三点的位置关系是,理论依据是.17.如图,∠ABC=90°,AB=10cm,∠D+∠C=180°,则AD与BC的距离是.18.已知三角形的一个内角是40°,则当此三角形的另外两个角中有一个角等于时,这个三角形是等腰三角形.19.反证法是证明方法,它是从命题的结论出发,经过得出,从而证明命题成立.20.如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是.三.解答题21.下面的句子哪些是命题,哪些不是命题,为什么?(1)我是中国人;(2)你吃饭了吗?(3)对顶角相等;(4)内错角相等;(5)延长线段AB;(6)明天可能下雨;(7)若a2>b2,则a>b.22.有红、黄、蓝三个箱子,一个苹果放入其中某个箱子内,并且(1)红箱子盖上写着:“苹果在这个箱子里”(2)黄箱子盖上写着:“苹果不在这个箱子里”(3)蓝箱子盖上写着:“苹果不在红箱子里”已知(1)、(2)、(3)中只有一句是真的,问苹果在哪个箱子里?23.用标有1克,2克,6克的砝码各一个,在一架无刻度的天平上称量重物.如果天平两端均可放置砝码,那么可以称出的不同克数的质量共有多少种?24.用反证法证明:(1)已知:a<|a|,求证:a必为负数.(2)求证:形如4n+3的整数k(n为整数)不能化为两个整数的平方和.25.如图,M,N,T和P,Q,R分别在同一直线上,MR分别与PN,QT交于点E,F,且∠MEN=∠RFQ,∠P=∠T.求证:∠M=∠R.26.(1)如图1,AP,BP分别平分∠CAD,∠CBD,则有∠P=(∠C+∠D),请说明理由.(2)如图2,AP,BP分别平分∠CAD的补角∠CAM和∠CBD.请直接写出∠P与∠C,∠D的关系,不必说明理由.27.如图,a∥b,c,d是截线,已知∠1=80°,∠5=105°,求∠2,∠3,∠4的度数.参考答案与试题解析一.选择题1.解:自然数也是整数,有两条边相等的三角形是等腰三角形,平行于同一条直线的两条直线平行都是命题,对情况作出了判断.故B,C,D错误.延长线段AB到C,只是陈述,不是命题.故选A.2.解:根据图示知,只有∠2与∠3的内错角,所以根据∠2=∠3可以推知AD∥BC.故选:C.3.解:A、若两相等的角有一边平行,则另一边也互相平行或者相交,所以说法错误;B、两条直线相交,所成的两组对顶角的平分线互相垂直,说法正确;C、两条平行线被第三条直线所截,同旁内角的平分线互相垂直,说法正确;D、在同一个平面内,经过直线外一点,有且只有一条直线与这条直线垂直,说法正确;故选:A.4.解:①平面内,过直线外一点作一条直线的平行线,只能作一条,故①错误;②平面内,过一点与一条已知直线垂直的直线只有一条,故②正确;③直线外一点与直线上各点连接的所有线段中,垂线段最短,故③正确;④两点之间的距离是指连接两点的线段的长度,故④错误.故选:B.5.解:A、∵CE⊥b,FG⊥b,∴FG∥EC,故此选项正确,不符合题意;B、∵a∥b,FG∥EC,∴四边形FGEC是平行四边形,∴FG=EC,故此选项正确,不符合题意;C、A、B两点的距离就是线段AB的长,此选项正确,不符合题意;D、直线a、b间的距离就是线段CE的长,故此选项错误,符合题意.故选:D.6.解:∵180°÷3=60°,∴三角形的三个角中至少有一个角不大于60°.故选:C.7.解:∵3∠A>5∠B,3∠C≤2∠B,得∠B<∠A,∠C≤∠B∴∠C<∠A∴∠B+∠C<∠A∵∠A+∠B+∠C=180°,∴2(∠B+∠C)<180°,∴∠B+∠C<90°,∴﹣(∠B+∠C)>﹣90°,∴180°﹣(∠B+∠C)>180°﹣90°=90°即∠A>90°.∴△ABC是钝角三角形,故选:A.8.解:已知A盒中没有装红球,而B盒中装着蓝球,则A盒装的是黄球,C盒装的是红球;由于乙没有得到B盒,也没有得到黄球,因此乙得到的是C盒;由于甲没有得到A盒,因此丙得到的是A盒,装的是黄球.故选A.9.解:为了叙述方便,P胜Q暂写成P>Q;由题意,知:P>Q,P>R,Q>S,P>T>Q;综合上述三种情况可得出P是第一名,且T>Q>S,由于R的位置不确定,因此本题可分四种情况:①P>R>T>Q>S时,第三名是T;②P>T>R>Q>S时,第三名是R;③P>T>Q>R>S时,第三名是Q;④P>T>Q>S>R时,第三名是Q;因此不可能是第三名的只有P和S,故选C.10.解:∵l1∥l2,l2∥l3,l3∥l4,∴l1∥l4或l1与l4重合.故选:D.二.填空题11.解:∵∠B=∠2=50°,∴AD∥BC,∴∠D=∠1,∵∠1=50°,∴∠D=50°.故答案为:50°.12.解:∵AB∥EF(已知)∴∠A+∠AEF=180°(两直线平行,同旁内角互补),∵DE∥BC(已知),∴∠DEF=∠CFE(两直线平行,内错角相等),∠ADE=∠B(两直线平行,同位角相等).故答案为:∠AEF;(两直线平行,同旁内角互补);∠CFE;(两直线平行,内错角相等);∠B;(两直线平行,同位角相等).13.解:“和为180°的两个角互为补角”的逆命题是互为补角的两个角和为180°,这个逆命题为真命题,故答案为:互为补角的两个角和为180°;真.14.解:16个空瓶可换16÷4=4瓶矿泉水;4瓶矿泉水喝完后又可得到4个空瓶子,可换4÷4=1瓶矿泉水;因此最多可以喝矿泉水4+1=5瓶.故答案为:5.15.解:∵过直线外以点作已知直线的平行线,有且只有一条,∴在同一平面内,经过不在直线上的一点作已知直线的平行线只有一条正确.故答案为:√.16.解:A、B、C三点的位置关系是:在同一直线上,理论依据是:在同一平面内,经过直线外一点有且只有一条直线与已知直线平行.故答案为:在同一直线上;在同一平面内,经过直线外一点有且只有一条直线与已知直线平行.17.解:∵∠D+∠C=180°,∴AD∥BC,∵∠ABC=90°,∴∠BAD=90°,∵AB=10cm,∴AD与BC的距离是:10cm.故答案为:10cm.18.解:∵三角形有两个角相等,且其中的一个内角是40°,∴分两种情况:第一种情况是:这两个相等的角是40°.∵三角形内角和是180°,∴第三个角是:180°﹣40°﹣40°=100°.第二种情况是:一个角是40°,另外两个角相等.∵三角形内角和是180°,∴另外两个角是:(180°﹣40°)÷2=140°÷2=70°.由上可得,当此三角形的另外两个角中有一个角等于100°或70°时,这个三角形是等腰三角形.故答案为:100°或70°.19.解:根据反证法证明的步骤:从命题的结论反面出发,经过推理论证得出矛盾,从而证明命题成立.故答案为:间接,反面,推理论证,矛盾.20.解:∵管道拐弯前后的方向保持不变,∴管道的两个拐角∠α=∠β.故答案为:内错角相等,两直线平行.三.解答题21.解:(1)、(3)、(4)、(7)是命题;(2)为问句,(5)为描叙句,(6)是猜测,它们都没有进行判断,所以它们都不是命题.22.解:若苹果在红箱子里⇒(1)(2)正确(3)错误若苹果在黄箱子里⇒(1)(2)错误(3)正确若苹果在蓝箱子里⇒(1)错(2)(3)正确故苹果在黄箱子里.23.解:①当天平的一端放1个砝码,另一端不放砝码时,可以称量重物的克数有1克,2克,6克;②当天平的一端放2个砝码,另一端不放砝码时,可以称量重物的克数有3克,7克,8克;③当天平的一端放3个砝码时,可以称量重物的克数有9克;④当天平的一端放1个砝码,另一端也放1个砝码时,可以称量重物的克数有1克,4克,5克;⑤当天平的一端放1个砝码,另一端放2个砝码时,可以称量重物的克数有3克,5克,7克.去掉重复的克数后,可称重物的克数共有9种.24.证明:(1)假设a≥0,则|a|=a,这与已知|a|>a相矛盾,因此假设不成立,所以a必为负数;(2)假设4n+3的整数部分k能化成两个整数的平方和,不妨设这两个整数为α,β,则4n+3=α2+β2,因为(n+2)2+(﹣n2﹣1)≠α2+β2,所以假设不成立,故4n+3的整数k不能化为两个整数的平方和.25.证明:∵∠MEN=∠PEF,∠MEN=∠RFQ,∴∠PEF=∠RFQ,∴PN∥QT,∴∠P=∠TQR.∵∠P=∠T,∴∠T=∠TQR,∴PR∥MT,∴∠M=∠R.26.(1)解:∵AP、BP分别平分∠CAD、∠CBD,∴∠DAP=∠CAP=∠CAD,∠CBP=∠DBP=∠CBD,∵∠AEB是△ADE和△BEP的外角,∴∠AEB=∠D+∠DAP=∠DBP+∠P,∴∠D+∠CAD=∠CBD+∠P,∴∠CAD﹣∠CBD=∠P﹣∠D,∵∠AFB是△BCF和△AFP的外角,∴∠AFB=∠CAP+∠P=∠CBP+∠C,∴∠CAD+∠P=∠CBD+∠C,∴∠CAD﹣∠CBD=∠C﹣∠P,∵∠CAD﹣∠CBD=∠P﹣∠D,∴∠C﹣∠P=∠P﹣∠D,∴∠P=(∠C+∠D),J.(2)如图2中,作AJ平分∠DAC交BP的延长线于∵PA平分CAM,AJ平分∠DAC,∴∠PAJ=(∠CAM+∠DAC)=90°∴∠APB=90°+∠J =90°+(∠C+∠D).27.解:∵a∥b,c,d是截线,∴∠2=∠1=80°,∠3+∠5=180°,∠3=∠4,∴∠3=180°﹣105°=75°,∴∠4=75°,即∠2,∠3,∠4的度数分别为80°,75°,75°.。
