平行线的判定习题精选
(完整版)平行线的判定习题
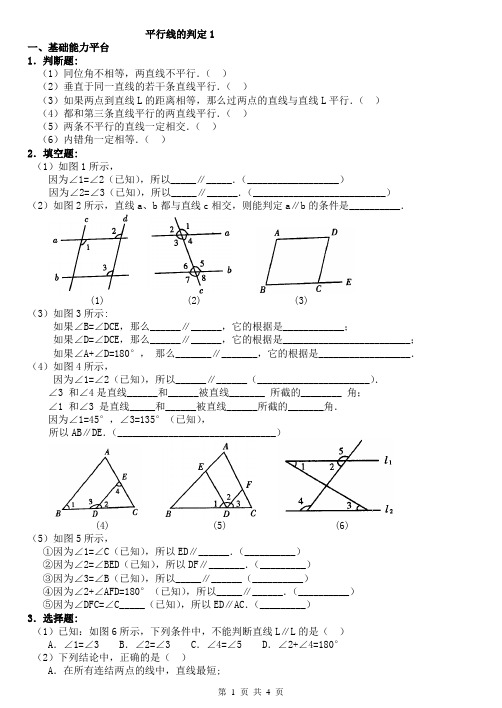
平行线的判定1一、基础能力平台1.判断题:(1)同位角不相等,两直线不平行.()(2)垂直于同一直线的若干条直线平行.()(3)如果两点到直线L的距离相等,那么过两点的直线与直线L平行.()(4)都和第三条直线平行的两直线平行.()(5)两条不平行的直线一定相交.()(6)内错角一定相等.()2.填空题:(1)如图1所示,因为∠1=∠2(已知),所以_____∥_____.(__________________)因为∠2=∠3(已知),所以_____∥______.(__________________________)(2)如图2所示,直线a、b都与直线c相交,则能判定a∥b的条件是__________.(1) (2) (3)(3)如图3所示:如果∠B=∠DCE,那么______∥______,它的根据是____________;•如果∠D=∠DCE,那么______∥______,它的根据是_________________________;如果∠A+∠D=180°,•那么_______∥_______,它的根据是__________________.(4)如图4所示,因为∠1=∠2(已知),所以______∥______(______________________).∠3•和∠4是直线______和______被直线_______•所截的________•角;•∠1•和∠3•是直线_____和______被直线______所截的_______角.因为∠1=45°,∠3=135°(已知),所以AB∥DE.(_______________________________)(4) (5) (6)(5)如图5所示,①因为∠1=∠C(已知),所以ED∥______.(__________)②因为∠2=∠BED(已知),所以DF∥_______.(_________)③因为∠3=∠B(已知),所以_____∥______(__________)④因为∠2+∠AFD=180°(已知),所以_____∥______.(__________)⑤因为∠DFC=∠C_____(已知),所以ED∥AC.(_________)3.选择题:(1)已知:如图6所示,下列条件中,不能判断直线L∥L的是()A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°(2)下列结论中,正确的是()A.在所有连结两点的线中,直线最短;B.经过两点有且只有一条直线;C.内错角互补,两直线平行;D.没有公共点的两条线段一定平行(3)已知a⊥b,b⊥c,则直线a与直线c的关系为()A.相交 B.垂直 C.平行 D.以上都不对(4)已知a∥b,c∥b,则直线a和c的关系是()A.相交 B.垂直 C.平行 D.相交或平行(5)两条直线被第三条直线所截,有一对同旁内角互补,•则这一对同旁内角的角平分线()A.互相垂直 B.互相平行C.相交但不垂直 D.不能确定(6)在同一平面内不相邻的两个直角,如果它们有一条边在同一条直线上,•那么另一条边相互() A.平行 B.垂直 C.平行或垂直 D.平行或垂直或在同一条直线上4.填写理由:(1)如图7所示,因为∠A=_____(已知),所以AC∥DE(________________________).因为∠A+_____=•180°(已知),所以AB∥FD(___________________________).(7) (8) (9)(2)如图8所示,因为AC平分∠DAB(已知),所以∠1=∠3(__________________).又因为∠1=∠2(已知),所以∠2=∠3(_____________________________).所以DC∥AB(___________________________________).(3)如图9所示,C、D、E在一条直线上.因为∠1=130°(已知),所以∠2=50°(_________).又因为∠A=50°(已知),所以∠2=∠A(_________).所以AB∥CD(____________).二、拓展延伸训练1.如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB、CD的位置关系如何?2.如图所示,ADB 是一条直线,∠ADE=∠ABC ,且DG 、BF 分别是∠ADE 和∠ABC•的平分线,那么DG 与BF 平行吗?为什么?平行线的判定21.如图,直线AB 、CD 相交与点E ,要使DF ∥AB .若需要图中与∠D 相等的角有( )A .4个B .3个C .2个D .1个2.如图,直线a ,b 被c 所截,若∠1=32°,要使a ∥b ,则∠2的大小为( )A .32°B .148°C .52°D .128°3.如图,把一块直角三角板的直角顶点放在直线b 上,如果∠2=62°,要使a //b ,那么∠1的度数是( )A .28°B .52°C .62°D .68°二、填空题4.如图,∠2=150°,当∠1=_______时,a ∥b .5.如图, 点B 、C 、D 在同一条直线上,∠ACB =90°,若∠A =54°,∠ECD =36°,则CE _________ AB .6.如图, AE 平分∠BAC 交BD 于点E ,若2122∠=︒,要使AC ∥BD ,则1∠= .8765cb a3412三、解答题7.如图,直线l 与直线a 、b 分别交于点A 、B ,若∠1 = 60°,∠2=120°,试说明a ∥b .1.如图1所示,下列条件中,能判断AB∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2;C.∠3=∠4D.∠BAC=∠ACD34DCBA21FE D CBA(1) (2) (3)2.如图2所示,如果∠D=∠EFC,那么( )A.AD∥BCB.EF∥BCC.AB∥DCD.AD∥EF 3.下列说法错误的是( )A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行 4.如图3,直线a,b 被直线c 所截,现给出下列四个条件:①∠1=∠-5; ②∠1=∠7; ③∠2+∠3=180°; ④∠4=∠7.其中能说明a∥b 的条件序号为( ) A.①② B.①③ C.①④ D.③④ 5.如左图,BE 是AB 的延长线。
平行线的性质判定专项练习40题

平行线的判定专项练习1.已知:如图,BE平分∠ABC,∠1=∠2.求证:BC∥DE.2.如图所示,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,试说明BF∥CE.3.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3,求证:BE∥DF.4.如图,OP平分∠MON,A、B分别在OP、OM上,∠BOA=∠BAO,那么AB平行于ON吗?若平行,请写出证明过程;若不平行,请说明理由.5.已知,如图B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,求证:DE∥BC.6.如图,直线AB、CD与直线EF相交于E、F,已知:∠1=105°,∠2=75°,求证:AB∥CD.7.如图,∠D=∠A,∠B=∠FCB,求证:ED∥CF.8.已知∠1的度数是它补角的3倍,∠2等于45°,那么AB∥CD吗?为什么?9.如图,已知AC∥ED,EB平分∠AED,∠1=∠2,求证:AE∥BD.10.如图,AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,求证:AE∥BF.11.如图,在△ABC中,点D在AB上,∠ACD=∠A,∠BDC的平分线交BC于点E.求证:DE∥AC.12.如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.13.如图所示所示,已知BE是∠B的平分线,交AC于E,其中∠1=∠2,那么DE∥BC吗?为什么?14.如图,已知∠C=∠D,DB∥EC.AC与DF平行吗?试说明你的理由.15.如图,直线AB,CD被EF所截,∠3=∠4,∠1=∠2,EG⊥FG.求证:AB∥CD.16.如图,已知AB∥CD,∠1=∠2,求证:BE∥CF.17.已知∠BAD=∠DCB,∠1=∠3,求证:AD∥BC.18.如图,AD是三角形ABC的角平分线,DE∥CA,并且交AB与点E,∠1=∠2,DF与AB是否平行?为什么?19.如图,∠D=∠1,∠E=∠2,DC⊥EC.求证:AD∥BE.20.如图,已知:∠C=∠DAE,∠B=∠D,那么AB平行于DF吗?请说明理由.21.如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断DE、BF是否平行,并说明理由.22.如图,CD⊥AB,GF⊥AB,∠1=∠2.试说明DE∥BC.23.如图所示,∠CAD=∠ACB,∠D=90°,EF⊥CD.试说明:∠AEF=∠B.24.已知:如图所示,C,P,D三点在同一条直线上,∠BAP+∠APD=180°,∠E=∠F,求证:∠1=∠2.25.已知:如图,∠1=∠2,∠A=∠F,则∠C与∠D相等吗?试说明理由.26.如图,已知DE平分∠BDF,AF平分∠BAC,且∠1=∠2.求证(1)DF∥AC;(2)DE∥AF.27.如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,试说明BE∥DF.28.如图,在四边形ABCD中,∠A=∠C=90°,∠1=∠2,∠3=∠4,求证:BE∥DF.29.如图,AB与CD相交于点O,并且∠A=∠1,试问∠2与∠B满足什么关系时,AC∥BD?说明理由.30.如图所示,已知:∠1=∠2,∠E=∠F.试说明AB∥CD.31.如图,AD平分∠BAC,EF平分∠DEC,且∠1=∠2,试说明DE与AB的位置关系.32.如图,已知B、C、D三点在同一条直线上,∠B=∠1,∠2=∠E,试说明AD∥CE.33.已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.34.如图,已知∠1=∠2,∠C=∠CDO,求证:CD∥OP.35.如图所示,∠ABC=∠BCD,BE、CF分别平分∠ABC和∠BCD,请你说出BE与CF的位置关系,并说出你的理由.36.如图,已知∠1=∠A,∠2=∠B,那么MN与EF平行吗?如果平行,请说明理由.37.如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于38.如图,AD⊥BC于点D,EF⊥BC于点F,EF交AB于点G,交CA的延长线于点E,且∠1=∠2.AD平分∠BAC吗?说说你的理由.39.如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.求∠PAG的度数.40.已知AB∥CD,分别探讨下列四个图形中∠APC和∠PAB、∠PCD的关系.(只要求直接写出),并请你从所得四个关系中任意选出一个说明理由12 AB CDFGE。
平行线的判定练习题(有答案)

平行线的判定练习题(有答案)平行线的判定专项练习60题(有答案)1.已知:如图,BE平分∠ABC,∠1=∠2.求证:BC∥DE.2.如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.3.如图所示,AB⊥BC,BC⊥CD,BF和CE是射线,并且∠1=∠2,试说明BF∥CE.4.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3,求证:BE∥DF.5.如图,OP平分∠MON,A、B分别在OP、OM上,∠BOA=∠BAO,那么AB平行于ON吗?若平行,请写出证明过程;若不平行,请说明理由.6.已知:如图,∠1=∠2,∠A=∠C.求证:AE∥BC.平行线的判定--- 第 1 页共 1 页7.已知,如图B、D、A在一直线上,且∠D=∠E,∠ABE=∠D+∠E,BC是∠ABE的平分线,求证:DE∥BC.8.如图,已知∠AEC=∠A+∠C,试说明:AB∥CD.9.如图,已知AC∥ED,EB平分∠AED,∠1=∠2,求证:AE∥BD.10.如图,直线AB、CD与直线EF相交于E、F,已知:∠1=105°,∠2=75°,求证:AB∥CD.11.如图,∠D=∠A,∠B=∠FCB,求证:ED∥CF.12.如图,已知AB⊥BC,CD⊥BC,∠1=∠2,求证:EB∥FC.平行线的判定---第 2 页共 2 页13.如图所示所示,已知BE是∠B的平分线,交AC于E,其中∠1=∠2,那么DE∥BC吗?为什么?14.如图,已知∠C=∠D,DB∥EC.AC与DF平行吗?试说明你的理由.15.如图,AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,求证:AE∥BF.16.如图,已知AB∥CD,∠1=∠2,求证:BE∥CF.17.已知∠BAD=∠DCB,∠1=∠3,求证:AD∥BC.18.如图,AD是三角形ABC的角平分线,DE∥CA,并且交AB与点E,∠1=∠2,DF与AB是否平行?为什么?平行线的判定---第 3 页共 3 页19.如图,已知:∠C=∠DAE,∠B=∠D,那么AB平行于DF吗?请说明理由.20.如图,已知点B在AC上,BD⊥BE,∠1+∠C=90°,问射线CF与BD平行吗?说明理由.21.已知∠1的度数是它补角的3倍,∠2等于45°,那么AB∥CD吗?为什么?22.已知:如图,BDE是一条直线,∠ABD=∠CDE,BF平分∠ABD,DG平分∠CDE,求证:BF∥DG.23.如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断DE、BF是否平行,并说明理由.24.如图,若∠CAB=∠CED+∠CDE,求证:AB∥CD.25.如图,CD⊥AB,GF⊥AB,∠1=∠2.试说明DE∥BC.平行线的判定---第 4 页共 4 页26.如图所示,∠CAD=∠ACB,∠D=90°,EF⊥CD.试说明:∠AEF=∠B.27.已知:如图所示,C,P,D三点在同一条直线上,∠BAP+∠APD=180°,∠E=∠F,求证:∠1=∠2.28.如图,∠D=∠1,∠E=∠2,DC⊥EC.求证:AD∥BE.29.如图,在四边形ABCD中,∠A=∠C,BE平分∠ABC,DF平分∠ADC,试说明BE∥DF.30.已知:如图,∠1=∠2,∠A=∠F,则∠C与∠D相等吗?试说明理由.31.如图,在四边形ABCD中,∠A=∠C=90°,∠1=∠2,∠3=∠4,求证:BE∥DF.平行线的判定---第 5 页共 5 页平行线测姓名:一、选择题1.下列命题中,不正确的是____ [ ]A.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行B.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行C.两条直线被第三条直线所截,那么这两条直线平行D.如果两条直线都和第三条直线平行,那么这两条直线也互相平行2.如图,可以得到DE∥BC的条件是______ [ ](2题)(5题)(3题)(7题) (8题)A.∠ACB=∠BAC B.∠ABC+∠BAE=180° C.∠ACB+∠BAD=180°D.∠ACB=∠BAD3.如图,直线a、b被直线c所截,现给出下列四个条件: (1)∠1=∠2(2)∠3=∠6(3)∠4+∠7=180° (4)∠5+∠8=180°,其中能判定a∥b的条件是_________[ ]A.(1)(3) B.(2)(4)C.(1)(3)(4) D.(1)(2)(3)(4)4.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是________[ ]A.第一次向右拐40°,第二次向左拐40° B.第一次向右拐50°,第二次向左拐130°C.第一次向右拐50°,第二次向右拐130° D.第一次向左拐50°,第二次向左拐130°5.如图,如果∠1=∠2,那么下面结论正确的是_________.[ ]A.AD∥BC B.AB∥CD C.∠3=∠4 D.∠A=∠C6.同一平面内有四条直线a、b、c、d,若a∥b,a⊥c,b⊥d,则直线c、d的位置关系为()A.互相垂直 B.互相平行 C.相交 D.无法确定7.如图,在平行四边形ABCD中,下列各式不一定正确的是()A.∠1+∠2=180° B.∠2+∠3=180° C.∠3+∠4=180° D.∠2+∠4=180°8.如图,AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC的度数为()A.30° B.60° C.90° D.120°二、填空题 9.如图,由下列条件可判定哪两条直线平行,并说明根据.(1)∠1=∠2,.(2)∠A=∠3,.(3)∠ABC+∠C=180°.10.如果两条直线被第三条直线所截,一组同旁内角的度数之比为3∶2,差为36°,那么这两条直线的位置关系是________.11.同垂直于一条直线的两条直线_______.同一平面内,不重合的两直线的位置关系是。
平行线的判定定理习题答案.doc
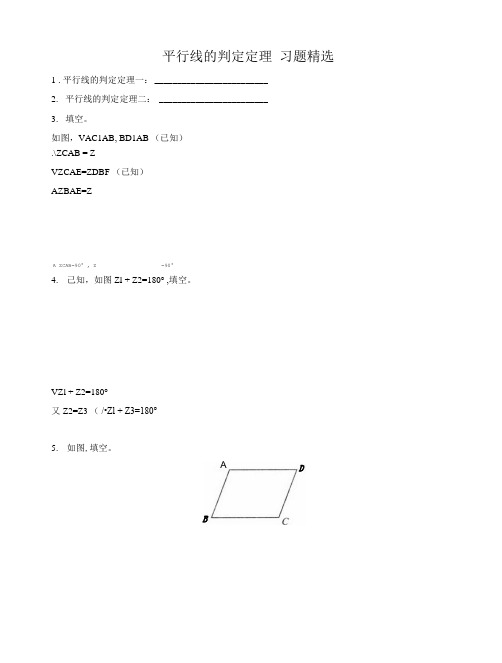
平行线的判定定理习题精选1 .平行线的判定定理一:_________________________2.平行线的判定定理二: ________________________3.填空。
如图,VAC1AB, BD1AB (已知).\ZCAB = ZVZCAE=ZDBF (已知)AZBAE=ZA ZCAB=90° , Z =90°4.己知,如图Zl + Z2=180° ,填空。
VZl + Z2=180°又Z2=Z3 (/•Zl + Z3=180°5.如图,填空。
A DB10.如图,已知:ZAOE+ZBEF=180° , ZAOE+ZCDE= 180° ,求证:CD 〃BE 。
(1) ZA 与 互补,贝(2) ZA 与 互补,贝6.下列命题中,不正确的是(A .如果两条直线都和第三条宜线平行,那么两条直线也互相平行B. 两条直线被第三条直线所截,如果同位角相等,那么两直线平C. 两条直线被第三条直线所截,如果内错角互补,那么两直线必平D. 两条直线被第三条直线所截,如果两直线不平行,那么内错伯必不相如图,直线a 、b 被直线c 所截,给出下列条件,①Z1 = Z2,②匕3=匕6,③Z4+Z7=180° + Z8=180°其中能判断a//b 的是(7. A. ①③ B.②④AB 〃8.已知: 如图, Z1 = ZA, Z2= ZC,求证: 9. 如图, 已知: Zl + Z2=180°11.如图,已知:13.已知:如图,14.已知:如图: 求证:GH〃MN。
ZA=Z1, ZC=Z2o 求证:求证:AB〃CD。
AB±BC, Zl + Z2=90° , Z2=Z3o 求证:BE〃DF。
ZAHF+ZFMD=180°, GH 平分ZAHM, MN 平分ZDMHo12.如图,巳知: Zl = ZC+ZEo 求证:ACz/BDoD答案1.内错角相等,两宜线平行2.同旁内角互补,两直线平行3.略4.略5.(1) ZD CD 同旁内角互补两直线平行(2) ZB BC 同旁内角互补,两直线平行6. C7. D8.VZ1 = ZA, Z2=ZC, XZ1 = Z2 (对顶角相等),AZA=ZC (等量代换),AAB/7CD (内错角相等,两直线平行)。
平行线的判定精选习题

平行线的判定精选习题1、(1999•西安)下列命题中,不正确的是()A、如果两条直线都和第三条直线平行,那么这两条直线也互相平行B、两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行C、两条直线被第三条直线所截,那么这两条直线平行D、两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行2、(1999•烟台)下列命题中,正确的是()A、同位角相等B、同旁内角相等的两直线平行C、同旁内角互补D、平行于同一条直线的两直线平行3、(2006•苏州)如图,给出了过直线外一点画已知直线的平行线的方法,其依据是()A、同位角相等,两直线平行B、内错角相等,两直线平行C、同旁内角互补,两直线平行D、两直线平行,同位角相等4、(2007•新疆)如图,已知∠1=70°,要使AB∥CD,则须具备另一个条件()A、∠2=70°B、∠2=100°C 、∠2=110°D、∠3=110°5、(2006•宜昌)如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB、AC、AE、ED、EC、DB中,相互平行的线段有()A、4组B、3组C、2组D、1组6、(2005•双柏县)如图,∠1=∠2,则下列结论一定成立的是()A、AB∥CDB、AD∥BCC、∠B=∠DD、∠3=∠47、(2004•淄博)如图,下列条件中,不能判断直线l1∥l2的是()A、∠1=∠3B、∠2=∠3C、∠4=∠5D、∠2+∠4=180°8、如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A、1B、2C、3D、49、如图,在下列结论给出的条件中,不能判定AB∥DF的是()A、∠2+∠A=180B、∠3=∠AC、∠1=∠4D、∠B=∠FDC10、(2003•河北)某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是()A、第一次左拐30°,第二次右拐30°B、第一次右拐50°,第二次左拐130°C、第一次右拐50°,第二次右拐130°D、第一次向左拐50°,第二次向左拐120°11、如图,点E在CD延长线上,下列条件中不能判定AB∥CD的是()A、∠1=∠2B、∠3=∠4C、∠5=∠BD、∠B+∠BDC=180°12.如图③因为∠1=∠2,所以______∥_______( ).因为∠2=∠3,所以________∥________()。
平行线的判定专项练习60题(有答案)
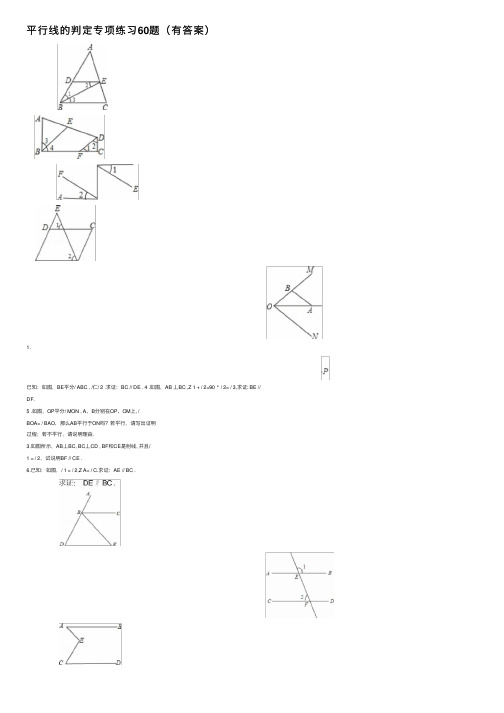
平⾏线的判定专项练习60题(有答案)1.已知:如图,BE平分/ ABC , /仁/ 2 .求证:BC // DE . 4 .如图,AB 丄BC ,Z 1 + / 2=90 ° / 2= / 3,求证: BE // DF.5 .如图,OP平分/ MON , A、B分别在OP、OM上, /BOA= / BAO,那么AB平⾏于ON吗?若平⾏,请写出证明过程;若不平⾏,请说明理由.3.如图所⽰,AB丄BC, BC丄CD , BF和CE是射线, 并且/1 = / 2,试说明BF // CE .6.已知:如图,/ 1 = / 2,Z A= / C.求证:AE // BC .7.已知,如图B、D、A在⼀直线上,且/ D= / E,/ ABE= / D+ / E, BC 是/ ABE 的平分线,10.如图,直线AB、CD与直线EF相交于E、F,已知: / 仁105 ° / 2=75 ° 求证:AB // CD .&如图,已知/ AEC= / A+ / C,试说明:AB // CD . 11.如图,/ D= / A,/ B= / FCB,求证:ED // CF.9.如图,已知AC // ED, EB 平分/ AED,/ 1 = / 2, 求证:AE // BD .12 .如图,已知AB丄BC , CD丄BC ,Z 1= / 2,求证:114.如图,已知/ C=Z D , DB // EC . AC 与DF 平⾏吗? 试说明你的理由.17 .已知/ BAD= / DCB ,/ 1 = / 3,求证:AD // BC .B C15.如图,AC 丄 AE , BD 丄 BF ,/ 仁35° / 2=35° 求证:AE // BF .18 .如图,AD 是三⾓形 ABC 的⾓平分线,DE // CA , 并且交AB 与点E ,/仁/ 2, DF 与AB 是否平⾏?为什么?13 ?如图所⽰所⽰,已知 BE 是/ B 的平分线,交 AC 于E ,其中/ 1 = / 2,那么DE // BC 吗?为什么?16.如图,已知 AB // CD ,/ 1 = / 2,求证: BE // CF.19.如图,已知:/ C= / DAE ,/ B=/ D ,那么 AB 平⾏于DF 吗?请说明理由.20 .如图,已知点B 在AC 上,BD 丄BE ,/ 1 + / C=90 ° 问射线CF 与BD 平⾏吗?说明理由.23.如图,四边形 ABCD 中,/ A= / C=90 ° BF 、DE 分别平分/ ABC 、/ ADC .判断DE 、BF 是否平⾏,并说明理由.21.已知/ 1的度数是它补⾓的 3倍,/ 2等于45°那么AB // CD 吗?为什么?AB // CD .⼖BDE 是⼀条直线,/ ABD= / CDE , DG平分/ CDE ,求证:BF // DG .24.如图,若/ CAB= / CED+ / CDE ,求证:22.已知:如图, BF 平分/ ABD ,25. 如图,CD 丄AB ,GF丄AB,/ 1 = / 2 .试说明DE //BC .28.如图,/ D= / 1, Z E=Z 2, DC丄EC.求证:AD // BE.26. ⼥⼝图所⽰,Z CAD= Z ACB , Z D=90 ° EF± CD .试说明:Z AEF= Z B .29.如图,在四边形ABCD中,Z A= Z C, BE平分Z ABC,DF 平分Z ADC,试说明BE // DF.27. 已知:如图所⽰,C, P, D三点在同⼀条直线上,Z BAP+ Z APD=180 ° Z E= Z F,求证:Z 1 = Z 2.30.已知:如图,Z 1 = Z 2,Z A= Z F,则Z C与Z D相等吗?试说明理由.31.如图,在四边形 ABCD 中,/ A= / C=90 ° / 1= / 2 / 3= / 4,求证:BE // DF .3C BCC BD334 .如图,已知/ 1 = / 2,/ C= / CDO ,求证:CD // OP .32.如图,已知/ 仁/2 求证:a // b35.如图,已知 DE 平分/ BDF , AF 平分/ BAC ,且 / 仁 / 2.求证(1) DF // AC ; (2) DE // AF .33.如图,DE 丄AO 于E , BO 丄AO 于O , FC 丄AB 于 C ,Z 仁/ 2,找出图中互相平⾏的线,并加以说明.36.如图,AD 平分/ BAC , EF 平分/ DEC ,且/ 1 = / 2 试说明DE 与AB 的位置关系.OO B37. 如图,在△ ABC中,点D在AB上,/ ACD= / A , /BDC的平分线交BC于点E.40.如图,直线AB、CD被直线EF所截,/ 1+ / 4=180° 求证:AB // CD .38. 如图,AB与CD相交于点0,并且/ A= / 1,试问 / 2与/B满⾜什么关系时,AC // BD ?说明理由.41 ?如图所⽰,已知:/ 1 = / 2,/ E= / F.试说明AB // CD .39. 如图,已知/ 1 = / A,/ 2= / B,那么MN 与EF平⾏吗?如果平⾏,请说明理由.42 .如图,已知EF 丄CD 于F,/ GEF=25 ° / 1=65° 则AB 与CD平⾏吗?请说明理由.求证:DE // AC .。
平行线判定练习题
平行线判定练习题题目一:判断下列直线是否平行。
1. 直线AB:y = 2x + 3直线CD:y = 2x - 12. 直线EF:2x + 3y = 6直线GH:6x + 9y = 183. 直线IJ:3x - 4y = 12直线KL:6x - 8y = 24题目二:判断下列线段是否平行。
1. 线段AB:A(1, 2), B(3, 4)线段CD:C(-1, 0), D(1, 2)2. 线段EF:E(-3, 4), F(-1, 2)线段GH:G(2, 3), H(4, 1)3. 线段IJ:I(0, 0), J(3, 0)线段KL:K(1, 1), L(4, 1)解答:题目一:1. 直线AB:y = 2x + 3直线CD:y = 2x - 1两条直线的斜率都是2,且斜率相等,因此直线AB与直线CD平行。
2. 直线EF:2x + 3y = 6直线GH:6x + 9y = 18将两条直线转化为斜截式形式:直线EF:y = (-2/3)x + 2直线GH:y = (-2/3)x + 2两条直线具有相同的斜率 (-2/3),且截距也相同,因此直线EF与直线GH平行。
3. 直线IJ:3x - 4y = 12直线KL:6x - 8y = 24将两条直线转化为斜截式形式:直线IJ:y = (3/4)x - 3直线KL:y = (3/4)x - 3两条直线具有相同的斜率 (3/4),且截距也相同,因此直线IJ与直线KL平行。
题目二:1. 线段AB:A(1, 2), B(3, 4)线段CD:C(-1, 0), D(1, 2)计算线段AB的斜率:斜率m = (y2 - y1) / (x2 - x1)= (4 - 2) / (3 - 1)= 2 / 2= 1计算线段CD的斜率:斜率m = (y2 - y1) / (x2 - x1)= (2 - 0) / (1 - (-1))= 2 / 2= 1两条线段的斜率相等,并且不共线,因此线段AB与线段CD平行。
平行线的判定练习题(有答案)
亲爱的朋友,很高兴能在此相遇!欢迎您阅读文档平行线的判定练习题(有答案),这篇文档是由我们精心收集整理的新文档。
相信您通过阅读这篇文档,一定会有所收获。
假若亲能将此文档收藏或者转发,将是我们莫大的荣幸,更是我们继续前行的动力。
平行线的判定练习题(有答案)篇一:(913)平行线的判定专项练习60题(有答案)ok 平行线的判定专项练习60 题(有答案)1. 已知:如图,BE平分/ ABC /仁/2.求证:BC// DE2. 如图,已知/ A=Z F,Z C=Z D,试说明BD// CE3. 如图所示,AB丄BC BCLCD BF和CE是射线,并且/仁/2, 试说明BF/ CE.4 .如图,AB丄BC / 1+Z 2=90°, / 2=2 3,求证:BE// DF.5 .如图,OP平分/ MONAB 分别在OROMk, 2 BOA2 BAO 那么AB平行于ON吗?若平行,请写出证明过程;若不平行,请说明理由.6. 已知:如图,2 1=2 2,2 A=2 C.求证:AE// BC 平行线的判定--- 第1 页共1 页7.已知,如图B、D、A 在一直线上, 且2 D=2 E,2 ABE=2 D+2 E,BC是2 ABE的平分线,-1-求证:DE/ BC.8 .如图,已知/ AEC h A+Z G 试说明:AB// CD9. 如图,已知AC// ED EB平分Z AED Z 1=Z2,求证:AE// BD10. 如图,直线AB. CD与直线EF相交于E、F,已知:Z仁105° Z 2=75°,求证:AB/ CD.11. 如图,Z D=Z A Z B=Z FCB 求证:ED// CF.12. 如图,已知AB丄BC CDLBC Z 仁Z 2,求证:EB// FC.平行线的判定---第2 页共2 页13. 如图所示所示,已知BE是ZB的平分线,交AC于E, 其中Z 1=Z 2,那么DE// BC吗?为什么?14. 如图,已知Z C=Z D DB// EC AC与DF平行吗?试说明你的理由.15. 如图,ACLAE BDLBF,Z 1=35°,Z 2=35°,求证:AE/ BF.16.如图,已知AB/ CD,Z 1=Z 2,求证:BE/ CF.17. 已知Z BAD Z DCB Z 仁Z3,求证:AD// BC18. 如图,AD是三角形ABC的角平分线,DE//CA并且交AB 与点E,Z仁Z2, DF与AB是否平行?为什么?平行线的判定---第 3 页共3 页19. 如图,已知:/ C=Z DAE / B=/ D 那么AB平行于DF 吗?请说明理由.20. 如图,已知点B在AC上,BDLBE / 1+Z C=90,问射线CF与BD平行吗?说明理由.21. 已知/I的度数是它补角的3倍,/2等于45°,那么AB// CD 吗?为什么?22. 已知:如图,BDE是一条直线,/ ABD/ CDE BF平分 / ABD DG平分/ CDE 求证:BF// DG23. 如图,四边形ABCD中, / A=/ C=90 , BF、DE分别平分/ ABC / ADC判断DE BF是否平行,并说明理由.24 .如图,若/ CAB/ CED/ CDE 求证:AB// CD25. 如图,CDLAB GFLAB / 仁/2.试说明DE// BC 平行线的判定---第 4 页共4 页26. 如图所示,/ CAD/ ACB / D=90 , EF± CD 试说明: / AEF=/ B.27.已知:如图所示,C,P,D 三点在同一条直线上,/ BAP/ APD=180,/ E=/ F,求证:/ 仁/ 2.28. 如图,/ D=/ 1,/ E=/2, DCLEC 求证:AD// BE29. 如图,在四边形ABCD中, / A=/ C BE平分/ ABC DF平分/ ADC试说明BE// DF.30. 已知:如图,/仁/2, /A=Z F,则/C与/D相等吗? 试说明理由.31. 如图,在四边形ABCD中,/ A=Z C=90°,/仁/2, / 3=2 4,求证:BE// DF.平行线的判定---第5 页共5 页篇二:七年级平行线的判定与性质练习题带答案平行线测试题姓名:一、选择题1 .下列命题中,不正确的是______ []A. 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行B. 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行C. 两条直线被第三条直线所截,那么这两条直线平行D. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行2. ___________________________________ 如图,可以得到DE// BC的条件是__________________________ [](2题)(5题)(3题)(7 题)(8题)A.2ACB=2BACB.2ABC+2BAE=180°C.2ACB+2BAD=180°D.Z ACB h BAD3.如图,直线a、b 被直线c 所截,现给出下列四个条件:⑴/ 仁/ 2(2) / 3二/ 6(3) / 4+Z 7=180° (4) / 5+Z 8=180°, 其中能判定a//b 的条件是________ []A .(1)(3)B .(2)(4)C .(1)(3)(4)D .(1)(2)(3)(4) 4.一辆汽车在笔直的公路上行驶,两次拐弯后,行驶的方向与原来的方向相同,这两次拐弯的角度可能是______________ []A .第一次向右拐40°,第二次向左拐40° B.第一次向右拐50°,第二次向左拐130°C.第一次向右拐50°,第二次向右拐130°D.第一次向左拐50°,第二次向左拐130°5. _____________________________________________ 如图,如果/仁/2,那么下面结论正确的是_________________ .[]A. AD// BCB AB// CDC / 3=Z 4D. / A=ZC6. 同一平面内有四条直线a、b、c、d,若a / b, a丄c, b±d, 则直线c、d 的位置关系为()A 互相垂直B 互相平行C 相交D 无法确定7. 如图,在平行四边形ABCD中,下列各式不一定正确的是()A . / 1+Z 2=180°B . / 2+Z 3=180° C. / 3+Z 4=180° D. / 2+Z 4=1808 .如图,AD// BC / B=30°, DB平分/ ADE 则/ DEC 的度数为()A.30°B.60°C.90°D.120°二、填空题9.如图,由下列条件可判定哪两条直线平行,并说明根据.⑴/ 仁/ 2, (2) / A=Z 3,.(3) / ABC y C=180 .10.如果两条直线被第三条直线所截, 一组同旁内角的度数之比为3 : 2,差为36°,那么这两条直线的位置关系是________________ 11.同垂直于一条直线的两条直线_________ .同一平面内, 不重合的两直线的位置关系是。
(完整版)平行线的判定习题(含答案)(最新整理)
2019年4月16日初中数学作业学校:___________姓名:___________班级:___________考号:___________一、单选题1.如右图所示,在下列条件中,不能判断l1∥l2的是()A.∠1=∠3B.∠2=∠3C.∠4+∠5=180°D.∠2+∠4=180°【答案】B【解析】【分析】直接利用平行线的判定方法分别分析得出答案.【详解】解:A、∠1=∠3根据内错角相等,两直线平行能判定l1∥l2,故此选项不符合题意;B. ∠2=∠3无法判定l1∥l2,故此选项符合题意;C. ∠4+∠5=180°, ∠2=∠5,所以∠4+∠2=180°, 根据同旁内角互补,两直线平行能判定l1∥l2,故此选项不符合题意;D. ∠2+∠4=180°,能判定l1∥l2,故此选项不符合题意;故选:B.【点睛】本题考查平行线的判定,正确掌握判定方法是解题关键.2.如图,直线a,b被直线c所截,下列条件能判断a//b的是( ).A.∠1=∠2B.∠1=∠4C.∠3+∠4=180°D.∠2+∠4=180°【答案】B【解析】【分析】根据平行线的判定定理,同位角相等,两直线平行即可解题.【详解】解:A. ∠1=∠2是对顶角,无法判断,B. ∠1=∠4,根据同位角相等,两直线平行即可判定a//b,正确,C. ∠3+∠4=180°,邻补角互补无法判断平行,D. ∠2+∠4=180°,内错角不是互补的,错误,故选B.【点睛】本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理是解题关键.3.如图,下列条件:①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.能判定AB∥EF的有( )A.1个B.2个C.3个D.4个【答案】C【解析】【分析】根据平行线的判定定理对各小题进行逐一判断即可.【详解】解:①∵∠B+∠BFE=180°,∴AB∥EF,故本小题正确;②∵∠1=∠2,∴DE∥BC,故本小题错误;③∵∠3=∠4,∴AB∥EF,故本小题正确;④∵∠B=∠5,∴AB∥EF,故本小题正确.故选:C.【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.4.如图,下列条件中,不能判断直线的是()∠1=∠3∠2=∠3∠4=∠5A.B.C.D.∠2+∠4=180°【答案】B【解析】【分析】根据同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行对各选项进行判断.【详解】当∠1=∠3时,a∥b;当∠4=∠5时,a∥b;当∠2+∠4=180°时,a∥b.故选:B.【点睛】本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.5.如图,点E在AD延长线上,下列条件中不能判定BC∥AD的是( )∠1=∠2∠C=∠CDEA.B.∠3=∠4∠C+∠ADC=180∘C.D.【答案】A【解析】【分析】分别利用同旁内角互补两直线平行,内错角相等两直线平行进行判断,即可得出答案.【详解】解:A、∵∠1=∠2,∴AB∥CD,本选项符合题意;B、∵∠C=∠CDE,∴BC∥AD,本选项不合题意;C、∵∠3=∠4,∴BC∥AD,本选项不合题意;D、∵∠C+∠ADC=180°,∴AD∥BC,本选项不符合题意.故选:A.【点睛】此题考查了平行线的判定,平行线的判定方法有:同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行,熟练掌握平行线的判定是解本题的关键.6.如图,下列条件中能得到AB∥CD的是( )∠1=∠2∠2=∠3∠1=∠4∠3=∠4 A.B.C.D.【答案】C【解析】【分析】根据平行线的判定定理对各选项进行逐一判断即可.【详解】A、因为∠1=∠2,不能得出AB∥CD,错误;B、∵∠2=∠3,∴AD∥BC,错误;C、∵∠1=∠4,∴AB∥CD,正确;D、因为∠3=∠4,不能得出AB∥CD,错误;故选C.【点睛】本题考查的是平行线的判定,熟知平行线的判定定理是解答此题的关键.7.下列说法错误的是( )A.在同一平面内,不相交的两条线段必然平行B.在同一平面内,不相交的两条直线必然平行C.在同一平面内,不平行的两条线段延长后必然相交D.在同一平面内,两条直线没有公共点,那么两条直线平行【答案】A【解析】【分析】根据两条直线的位置关系直接可以找出错误的选项.【详解】在同一平面内,不相交的两条直线必然平行; 在同一平面内,不平行的两条线段延长后必然相交; 在同一平面内,两条直线没有公共点,那么两条直线平行;只有A选项中,在同一平面内,不相交的两条线段不一定平行,故A错误.故选A.【点睛】此题重点考察学生对两直线的位置关系的理解,掌握两直线的位置关系是解题的关键. 8.同一平面内的两条线段,下列说法正确的是( )A.一定平行B.一定相交C.可以既不平行又不相交D.不平行就相交【答案】C【解析】【分析】根据线段有固定长度这一特点来解题即可.【详解】同一平面内的两条线段,可以出现相交,平行,也可以出现既不平行也不相交的状态.故选C【点睛】此题重点考察学生对两条线段位置关系的理解,抓住线段有固定长度是解题的关键. 9.在同一平面内,两条不重合直线的位置关系可能是( )A.垂直或平行B.垂直或相交C.平行或相交D.平行、垂直或相交【答案】C【解析】【分析】根据前提条件结合直线的位置关系直接可以得到答案.【详解】在同一平面内,两条不重合的直线的位置关系只有两种:平行或相交.故选C【点睛】此题重点考察学生对两直线位置关系的理解,掌握两直线的位置关系是解题的关键. 10.如图,已知点E在BC的延长线上,则下列条件中不能判断AB∥CD的是( )A.∠B=∠DCE B.∠BAD+∠D=180°C.∠1=∠4D.∠2=∠3【答案】D【解析】【分析】根据平行线的判定定理即可直接作出判断.【详解】A、根据同位角相等,两直线平行即可证得,故选项错误;B、根据同旁内角互补,两直线平行,即可证得,故选项错误;C、根据内错角相等,两直线平行即可证得,故选项错误;D、∠2和∠3是AD和BC被AC所截形成的角,因而不能证明AB∥CD,故选项正确.故选:D.【点睛】本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.11.如图,下列判定两直线平行错误的是()A.若∠D=∠3,则BE∥DF B.若∠B=∠2,则AB∥CDC.若∠1+∠D=,则BE∥DF D.若∠1+∠B=,则AB∥CD18001800【答案】A【解析】【分析】根据平行线的判定逐一判断即可.【详解】A. ∠D和∠3是一组同旁内角,根据“同旁内角互补,两直线平行”,可得本选项错误;B. ∠B和∠2是一组同位角角,根据“同位角相等,两直线平行”,可得本选项正确;C. 因为∠1 = ∠3,若∠1+∠D=,则∠3+∠D=,根据“同旁内角互补,两直线18001800平行”,可得本选项正确;D. ∠1和∠B,是一组同旁内角,根据“同旁内角互补,两直线平行”,可得本选项正确.故选:A.【点睛】本题考查平行线的判定方法;熟练掌握平行线的判定方法,并能进行推理论证是解题关键.12.如图,已知CD、BF相交于点O,∠D=,下面判定两直线平行正确的是650()A.当∠C=时,AB∥CD B.当∠A=时,AC∥DE6501150C.当∠E=时,CD∥EF D.当∠BOC=时,BF∥DE12501150【答案】D【解析】选项A中,∠C和∠D是直线AC、DE被DC所截形成的内错角,内错角相等,判定两直线平行;选项B中,不符合三线八角构不成平行;选项C中,∠E和∠D是直线DC、EF被DE所截形成的同旁内角,因为同旁内角不互补,所以两直线不平行;选项D中,∠BOC的对顶角和∠D是直线BF、DE被DC所截形成的同旁内角,同旁内角互补,判定两直线平行【详解】解:A、错误,因为∠C=∠D,所以AC∥DE;B、错误,不符合三线八角构不成平行;C、错误,因为∠C+∠D≠180°,所以CD不平行于EF;D、正确,因为∠DOF=∠BOC=140°,所以∠DOF+∠D=180°,所以BF∥DE.故选:D.【点睛】本题考查平行线的判定,解题关键是在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.13.如图,下列条件中,能判断FB∥CE的是()A.∠F+∠C=B.∠ABF=∠C C.∠F=∠C D.∠A=∠D1800【答案】B【解析】【分析】分析四个选项,看哪个选项的条件满足平行线的判定定理,由此即可得出结论.【详解】解:A、∠F+∠C=180°,不能得出FB∥CE,A不可以;B、∠ABF=∠C,同位角相等,两直线平行,B可以;C、∠F=∠C,不能得出FB∥CE,C不可以;D、∠A=∠D,内错角相等,两直线平行,但得出的是DF∥AC,D不可以.【点睛】本题考查平行线的判定定理,解题的关键是牢记平行线的判定定理.本题属于基础题,难度不大,解决该题型题目时,寻找相等或互补的角去证明直线平行.14.如图,一根直尺EF压在三角板的角∠BAC上,欲使CB∥EF,则应使∠ENB的度300数为()A.B.C.D.1000110012001300【答案】C【解析】【分析】根据平行线的判定方法即可解答.【详解】解:因为三角板含有30°的角,所以∠B=60°,当∠ENB+∠B=180°时,根据“同旁内角互补,两直线平行”,可使CB∥EF,此时∠ENB=180°-∠B=180°-60°=.1200故选:C.【点睛】本题考查平行线的判定方法,解题关键是熟练掌握判定方法,根据题目要求选择简单方法.15.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=69°,若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )A.69°B.49°C.31°D.21°【答案】D【解析】先根据b⊥c得出∠2的度数,再由平行线的判定定理即可得出结论.【详解】∵b⊥c,∴∠2=90°.∵∠1=69°,a∥b,∴直线b绕着点A顺时针旋转的度数=90°﹣69°=21°,故选D.【点睛】本题考查了垂直的定义,平行线的判定,熟练掌握和正确运用相关知识是解题的关键. 16.如图是小敏作“过已知直线外一点画这条直线的平行线”,从图中可知,小敏画平行线的依据是( )①两直线平行,同位角相等②两直线平行,内错角相等③同位角相等,两直线平行④内错角相等,两直线平行A.①②B.②③C.③④D.①④【答案】C【解析】【分析】①②为平行线的性质,③④为平行线的判定定理.【详解】解:根据平行线的判定与性质可知,①②为平行线的性质,③④为平行线的判定定理,∴小敏是依据③④画平行线的.故选:C.【点睛】本题主要考查平行线的判定与性质,解此题的关键在于熟记平行线的判定定理与性质的区别.17.如图,下列结论:若,则∥;若,则∥;若①∠1=∠3AB CD②∠2=∠4AB CD③∠ADC=∠5,则AD//BC;若∠DAB+∠ABC=180°,则AD//BC,其中正确的个数是④()A.1个B.2个C.3个D.4个【答案】C【解析】【分析】根据内错角相等,两直线平行可以对①②③进行判断,根据同旁内角互补,两直线平行可以对④进行判断,由此即可得答案.【详解】①若∠1=∠3,则AB∥CD,正确;②若∠2=∠4,则AD∥BC,故②错误;③若∠ADC=∠5,则AD//BC,正确;④若∠DAB+∠ABC=180°,则AD//BC,正确,故选C.【点睛】本题考查了平行线的判定,熟练掌握平行线的判定定理是解题的关键.18.如图,下列推理正确的是( )A.∵∠1=∠2,∴AD∥BC B.∵∠3=∠4,∴AB∥CDC.∵∠3=∠5,∴AB∥DC D.∵∠3=∠5,∴AD∥BC【答案】C【解析】【分析】利用平行线的判定方法判断即可得到结果.【详解】∵∠3=∠5,∴AB∥DC(同位角相等,两直线平行).故选C.【点睛】此题考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.二、解答题∠AED=∠C∠1=∠B EF//AB19.如图,,,说明:.【答案】见解析.【解析】【分析】先由同位角相等,得出两直线平行,再根据两直线平行,得出内错角相等,最后根据同位角相等,得出两直线平行即可.【详解】∠AED=∠C∵(已知)DE//BC∴(同位角相等,两直线平行)∠1=∠EFC又∵(两直线平行,内错角相等)∠B=∠EFC∴(等量代换)EF//AB∴(同位角相等,两直线平行)【点睛】本题主要考查了平行线的判定与性质,解题时注意:两直线平行,内错角相等;同位角相等,两直线平行.20.如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于E.(1)求证:AD∥BC;(2)若∠ADB=36°,求∠EFC的度数.【答案】(1)证明见解析;(2)36°.【解析】【分析】(1)求出∠ABC+∠A=180°,根据平行线的判定推出即可;(2)根据平行线的性质求出∠DBC,根据垂直推出BD∥EF,根据平行线的性质即可求出∠EFC.【详解】(1)证明:∵∠ABC=180°-∠A,∴∠ABC+∠A=180°,∴AD∥BC;(2)∵AD∥BC,∠ADB=36°,∴∠DBC=∠ADB=36°,∵BD⊥CD,EF⊥CD,∴BD∥EF,∴∠DBC=∠EFC=36°【点睛】本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.21.平面上有6条直线,共有12个不同的交点,画出它们可能的位置关系(画三种图形).【答案】详见解析.【解析】【分析】从平行线的角度考虑,先考虑只有二条直线平行,再考虑三条平行,作出草图即可看出.【详解】如下图.【点睛】本题考查平行线与相交线的综合运用.没有明确平面上六条不重合直线的位置关系,需要运用分类讨论思想.22.如图,根据要求填空.(1)过A作AE∥BC,交______于点E;(2)过B作BF∥AD,交______于点F;(3)过C作CG∥AD,交__________于点G;(4)过D作DH∥BC,交BA的__________于点H.【答案】(1)DC;(2)DC;(3)AB;(4)延长线.【解析】【分析】根据要求,直接进行作图就可以解决.【详解】(1)过A作AE∥BC,交DC于点E;(2)过B作BF∥AD,交DC于点F;(3)过C作CG∥AD,交AB的延长线于点G;(4)过D作DH∥BC,交BA的延长线于点H.【点睛】本题主要考查平行线的作法以及几何语言的准确性.23.探索与发现:(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.【答案】(1)a1⊥a3,理由详见解析;(2)a1∥a4;(3)a1⊥a2 011.【解析】【分析】(1)根据两直线平行,同位角相等得出相等的角,再根据垂直的定义解答;(2)根据(1)中结论即可判定垂直;(3)根据规律发现,与脚码是偶数的直线互相平行,与脚码是奇数的直线互相垂直,根据此规律即可判断.【详解】(1)a1⊥a3.理由如下:如图1,∵a1⊥a2,∴∠1=90°,∵a2∥a3,∴∠2=∠1=90°,∴a1⊥a3;(2)同(1)的解法,如图2,直线a1与a4的位置关系是:a1∥a4;(3)直线a1与a3的位置关系是:a1⊥a2⊥a3,直线a1与a4的位置关系是:a1∥a4∥a5,以四次为一个循环,⊥,⊥,∥,∥以此类推,a1∥a2009,a1⊥a2010,所以直线a1与a2011的位置关系是:a1⊥a2011.【点睛】本题考查了平行公理的推导,作出图形更有利于规律的发现以及规律的推导.三、填空题24.已知,如图,要使得AB∥CD,你认为应该添加的一个条件是________【答案】∠ECD=∠A(答案不唯一).【解析】【分析】根据平行线的判定定理,即可直接写出条件.【详解】添加的条件是:∠ECD=∠A(答案不唯一).故答案为:∠ECD=∠A.【点睛】本题考查了平行线的判定定理,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养学生“执果索因”的思维方式与能力.25.在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则______.【答案】a∥b【解析】【分析】根据平行线的判定解答即可.【详解】在同一平面内,三条不同的直线a、b、c,若a⊥c,b⊥c,则a∥b.故答案为:a∥b.【点睛】本题考查了平行线的判定与性质,在同一平面内,垂直于同一直线的两直线平行的性质,是基础题,熟记平行线的判定是解题的关键.126.设a、b、c为平面上三条不同直线,(1)若a∥b,b∥c,则a与c的位置关系是________;(2)若a⊥b,b⊥c,则a与c的位置关系是________.【答案】a∥c;a∥c.【解析】【分析】(1)根据两条直线的位置关系直接写出答案.(2)根据垂线的性质去解答即可.【详解】设a、b、c为平面上三条不同直线,(1)若a∥b,b∥c,则a与c的位置关是a∥c,(2)若a⊥b,b⊥c,则a与c的位置关系是a∥c.故答案为(1). a∥c (2). a∥c【点睛】此题重点考察学生对两直线的位置关系和垂线性质的理解,掌握两直线的位置和垂线的性质是解题的关键.27.如图,某工件要求AB∥ED,质检员小李量得∠ABC=146°,∠BCD=60°,∠EDC=154°,则此工件________.(填“合格”或“不合格”)【答案】合格【解析】【分析】作CF∥AB,由平行线的性质得出∠ABC+∠1=180°,求出∠1,得出∠2,由∠2+∠EDC=180°,得出CF∥ED,证出AB∥ED,即可得出结论.【详解】作CF∥AB,如图所示:则∠ABC+∠1=180°,∴∠1=180°-146°=34°,∴∠2=∠BCD-∠1=60°-34°=26°,∵∠2+∠EDC=26°+154°=180°,∴CF∥ED,∴AB∥ED;故答案为:合格.【点睛】本题考查了平行线的性质与判定;熟练掌握平行线的判定与性质,并能进行推理论证是解决问题的关键28.如图,EN⊥CD,点M在AB上,∠MEN=156°,当∠BME=________°时,AB∥C D.【答案】66.【解析】【分析】过点E作EF∥AB,由平行线的性质可得∠BME=MEF,利用平行线的判定定理和性质定理可得∠NEF=90°,易得∠BME.【详解】过点E作EF∥AB,∴∠BME=MEF,∵AB∥CD,∴EF∥CD,∵EN⊥CD,∴EN⊥EF,∴∠NEF=90°,∵∠MEN=156°,∴∠MEF+90°=156°,∴∠MEF=∠BME=156°-90°=66°.故答案为:66.【点睛】本题主要考查了平行线的判定定理及性质定理,综合运用定理是解答此题的关键.29.如图,已知CD⊥DA,DA⊥AB,∠1=∠2. 试说明DF∥AE. 请你完成下列填空,把解答过程补充完整.解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°( ).∴∠CDA=∠DAB(等量代换).又∠1=∠2,从而∠CDA-∠1=∠DAB-________(等式的性质).即∠3=_______.∴DF∥AE( ).【答案】垂直的定义;∠2;∠4;内错角相等,两直线平行【解析】【分析】(1)根据垂直的定义填空;(2)根据等式的性质进行填空;(3)根据图象中角的位置关系进行解答;(4)根据平行线的判定定理进行解答即可.【详解】解:∵CD⊥DA,DA⊥AB,∴∠CDA=90°,∠DAB=90°(垂直的定义),∴∠CDA=∠DAB(等量代换),又∠1=∠2,从而∠CDA-∠1=∠DAB-∠2 (等式的性质).即∠3=∠4,∴DF∥AE(内错角相等,两直线平行).故答案为:垂直的定义;∠2;∠4;内错角相等,两直线平行.【点睛】本题主要考查了平行线的判定定理等知识点,解此题的关键在于熟记书本中基本的知识点.30.如图,当∠1=∠__时,AB∥DC.【答案】4【解析】【分析】当∠1=∠4 时,根据内错角相等,两直线平行可以判定AB∥DC.【详解】∵∠1=∠4,∴AB∥DC(内错角相等,两直线平行).【点睛】此题主要考查了平行线的判定,内错角相等,两直线平行.。
(完整版)平行线的判定习题
平行线的判定1一、基础能力平台1.判断题:(1)同位角不相等,两直线不平行.( )(2)垂直于同一直线的若干条直线平行.( )(3)如果两点到直线L的距离相等,那么过两点的直线与直线L平行.( )(4)都和第三条直线平行的两直线平行.( )(5)两条不平行的直线一定相交.( )(6)内错角一定相等.()2.填空题:(1)如图1所示,因为∠1=∠2(已知),所以_____∥_____.(__________________)因为∠2=∠3(已知),所以_____∥______.(__________________________)(2)如图2所示,直线a、b都与直线c相交,则能判定a∥b的条件是__________.(1) (2) (3)(3)如图3所示:如果∠B=∠DCE,那么______∥______,它的根据是____________;•如果∠D=∠DCE,那么______∥______,它的根据是_________________________;如果∠A+∠D=180°,•那么_______∥_______,它的根据是__________________.(4)如图4所示,因为∠1=∠2(已知),所以______∥______(______________________).∠3•和∠4是直线______和______被直线_______•所截的________•角;•∠1•和∠3•是直线_____和______被直线______所截的_______角.因为∠1=45°,∠3=135°(已知),所以AB∥DE.(_______________________________)(4)(5) (6)(5)如图5所示,①因为∠1=∠C(已知),所以ED∥______.(__________)②因为∠2=∠BED(已知),所以DF∥_______.(_________)③因为∠3=∠B(已知),所以_____∥______(__________)④因为∠2+∠AFD=180°(已知),所以_____∥______.(__________)⑤因为∠DFC=∠C_____(已知),所以ED∥AC.(_________)3.选择题:(1)已知:如图6所示,下列条件中,不能判断直线L∥L的是( )A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°(2)下列结论中,正确的是()A.在所有连结两点的线中,直线最短;B.经过两点有且只有一条直线;C.内错角互补,两直线平行;D.没有公共点的两条线段一定平行(3)已知a⊥b,b⊥c,则直线a与直线c的关系为( )A.相交 B.垂直 C.平行 D.以上都不对(4)已知a∥b,c∥b,则直线a和c的关系是()A.相交 B.垂直 C.平行 D.相交或平行(5)两条直线被第三条直线所截,有一对同旁内角互补,•则这一对同旁内角的角平分线()A.互相垂直 B.互相平行C.相交但不垂直 D.不能确定(6)在同一平面内不相邻的两个直角,如果它们有一条边在同一条直线上,•那么另一条边相互( )A.平行 B.垂直 C.平行或垂直 D.平行或垂直或在同一条直线上4.填写理由:(1)如图7所示,因为∠A=_____(已知),所以AC∥DE(________________________).因为∠A+_____=•180°(已知),所以AB∥FD(___________________________).(7) (8)(9)(2)如图8所示,因为AC平分∠DAB(已知),所以∠1=∠3(__________________).又因为∠1=∠2(已知),所以∠2=∠3(_____________________________).所以DC∥AB(___________________________________).(3)如图9所示,C、D、E在一条直线上.因为∠1=130°(已知),所以∠2=50°(_________).又因为∠A=50°(已知),所以∠2=∠A(_________).所以AB∥CD(____________).二、拓展延伸训练1.如图所示,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,那么直线AB、CD的位置关系如何?2.如图所示,ADB是一条直线,∠ADE=∠ABC,且DG、BF分别是∠ADE和∠ABC•的平分线,那么DG与BF 平行吗?为什么?8765c ba3412平行线的判定21.如图,直线AB 、CD 相交与点E ,要使DF ∥AB .若需要图中与∠D 相等的角有( )A .4个B .3个C .2个D .1个2.如图,直线a ,b 被c 所截,若∠1=32°,要使a ∥b ,则∠2的大小为( )A .32°B .148°C .52°D .128°3.如图,把一块直角三角板的直角顶点放在直线b 上,如果∠2=62°,要使a //b ,那么∠1的度数是( ) A .28° B .52° C .62° D .68°二、填空题4.如图,∠2=150°,当∠1=_______时,a ∥b .5.如图, 点B 、C 、D 在同一条直线上,∠ACB =90°,若∠A =54°,∠ECD =36°,则CE _________ AB . 6.如图, AE 平分∠BAC 交BD 于点E ,若2122∠=︒,要使AC ∥BD ,则1∠= .三、解答题7.如图,直线l 与直线a 、b 分别交于点A 、B ,若∠1 = 60°,∠2=120°,试说明a ∥b .1.如图1所示,下列条件中,能判断AB∥CD 的是( )A.∠BAD=∠BCDB.∠1=∠2; C 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线的判定习题精选
一.判断题:
1.两条直线被第三条直线所截,只要同旁内角相等,则两条直线一定平行。
( )
2.如图①,如果直线1l ⊥OB ,直线2l ⊥OA ,那么1l 与 2l 一定相交。
( )
3.如图②,∵∠GMB=∠HND (已知)∴AB ∥CD (同位角相等,两直线平行)( )
二.填空题:
1.如图③ ∵∠1=∠2,∴_______∥________( )。
∵∠2=∠3,∴_______∥________( )。
2.如图④ ∵∠1=∠2,∴_______∥________( )。
∵∠3=∠4,∴_______∥________( )。
3.如图⑤ ∠B=∠D=∠E ,那么图形中的平行线有________________________________。
4.如图⑥ ∵ AB ⊥BD ,CD ⊥BD (已知)
∴ AB ∥CD ( )
又∵ ∠1+∠2 = 180(已知)
∴ AB ∥EF ( )
∴ CD ∥EF ( )
三.选择题:
1.如图⑦,∠D=∠EFC ,那么( )
A .AD ∥BC
B .AB ∥CD
C .EF ∥BC
D .AD ∥EF
2.如图⑧,判定AB ∥CE 的理由是( )
A .∠B=∠ACE
B .∠A=∠ECD
C .∠B=∠ACB
D .∠A=∠ACE
3.如图⑨,下列推理错误的是( )
A .∵∠1=∠3,∴a ∥b
B .∵∠1=∠2,∴a ∥b
C .∵∠1=∠2,∴c ∥d
D .∵∠1=∠2,∴c ∥d
4.如图,直线a 、b 被直线c 所截,给出下列条件,①∠1=∠2,②∠3=∠6, ③∠4+∠7=180°,④∠5+∠8=180°其中能判断a ∥b 的是( )
A .①③
B .②④
C .①③④
D .①②③④
四.完成推理,填写推理依据:
1.如图⑩ ∵∠B=∠_______,∴ AB ∥CD ( ) ∵∠BGC=∠_______,∴ CD ∥EF ( )
∵AB ∥CD ,CD ∥EF , ∴ AB ∥_______( )
2.如图⑾ 填空:
(1)∵∠2=∠3(已知)∴ AB__________( )
(2)∵∠1=∠A(已知)∴__________()
(3)∵∠1=∠D(已知)∴__________()
(4)∵_______=∠F(已知)∴AC∥DF()
3.填空。
如图,∵AC⊥AB,BD⊥AB(已知)
∴∠CAB=90°,∠______=90°()∴∠CAB=∠______()
∵∠CAE=∠DBF(已知)∴∠BAE=∠______ ()
∴_____∥_____()
4.已知,如图∠1+∠2=180°,填空。
∵∠1+∠2=180°()∠2=∠3()
∴∠1+∠3=180°()
∴_________()
五.证明题
1.已知:如图⑿,CE平分∠ACD,∠1=∠B,求证:AB∥CE
2.如图:∠1=︒
53,试说明直线AB与CD,BC与DE
53,∠2=︒
127,∠3=︒
的位置关系。
3.如图:已知∠A=∠D,∠B=∠FCB,能否确定ED与CF的位置关系,请说明理由。
4.已知:如图,,,且.
求证:EC∥DF.
5.如图,已知:∠AOE+∠BEF=180°,∠AOE+∠CDE=180°,
求证:CD∥BE。
