理论力学思考题
理论力学思考题习题答案

第一章 质点力学矿山升降机作加速度运动时,其变加速度可用下式表示:⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 :由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 由加速度的微分形式我们可知dtdv a =代入得 dt T t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫⎝⎛-=002sin 1π 可得 :D T t c T ct v ++=2cos 2ππ(D 为常数)代入初始条件:0=t 时,0=v , 故c T D π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππ 又因为dtds v =所以 =ds dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ 对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ 直线FM 在一给定的椭圆平面内以匀角速ω绕其焦点F 转动。
求此直线与椭圆的焦点M 的速度。
已知以焦点为坐标原点的椭圆的极坐标方程为()θcos 112e e a r +-=式中a 为椭圆的半长轴,e 为偏心率,常数。
解:以焦点F 为坐标原点题1.8.1图则M 点坐标 ⎩⎨⎧==θθsin cos r y r x 对y x ,两式分别求导⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos r r yr r x 故()()22222cos sin sin cos θθθθθθ r r r r y xv ++-=+=222ωr r+= 如图所示的椭圆的极坐标表示法为()θcos 112e e a r +-=对r 求导可得(利用ωθ= ) 又因为()()221cos 111ea e e a r -+-=θ即 ()rer e a --=21cos θ所以()()2222222221211cos 1sin e r e ar r ea --+--=-=θθ故有 ()2222224222sin 1ωθωr e a r e v +-=()2224221e a r e -=ω()()]1211[2222222e r e ar r e a --+--22ωr +()()⎥⎦⎤⎢⎣⎡--+-⋅-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω即 ()r a r br v -=2ω(其中()b a e b ,1222-=为椭圆的半短轴)质点作平面运动,其速率保持为常数。
理论力学思考题习题答案

第一章 质点力学矿山升降机作加速度运动时,其变加速度可用下式表示:⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 式中c 及T 为常数,试求运动开始t 秒后升降机的速度及其所走过的路程。
已知升降机的初速度为零。
解 :由题可知,变加速度表示为⎪⎭⎫ ⎝⎛-=T t c a 2sin1π 由加速度的微分形式我们可知dtdv a =代入得 dt T t c dv ⎪⎭⎫ ⎝⎛-=2sin 1π 对等式两边同时积分dt T t c dv t v⎰⎰⎪⎭⎫⎝⎛-=002sin 1π 可得 :D T t c T ct v ++=2cos 2ππ(D 为常数)代入初始条件:0=t 时,0=v , 故c T D π2-=即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=12cos 2T t T t c v ππ 又因为dtds v =所以 =ds dt T t T t c ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+12cos 2ππ 对等式两边同时积分,可得:⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛-+=t T t T T t c s 2sin 22212πππ 直线FM 在一给定的椭圆平面内以匀角速ω绕其焦点F 转动。
求此直线与椭圆的焦点M 的速度。
已知以焦点为坐标原点的椭圆的极坐标方程为()θcos 112e e a r +-=式中a 为椭圆的半长轴,e 为偏心率,常数。
解:以焦点F 为坐标原点题1.8.1图则M 点坐标 ⎩⎨⎧==θθsin cos r y r x 对y x ,两式分别求导⎪⎩⎪⎨⎧+=-=θθθθθθcos sin sin cos r r yr r x 故()()22222cos sin sin cos θθθθθθ r r r r y xv ++-=+=222ωr r+= 如图所示的椭圆的极坐标表示法为()θcos 112e e a r +-=对r 求导可得(利用ωθ= ) 又因为()()221cos 111ea e e a r -+-=θ即 ()rer e a --=21cos θ所以()()2222222221211cos 1sin e r e ar r ea --+--=-=θθ故有 ()2222224222sin 1ωθωr e a r e v +-=()2224221e a r e -=ω()()]1211[2222222e r e ar r e a --+--22ωr +()()⎥⎦⎤⎢⎣⎡--+-⋅-=2222222221121e e ar r r e e a r ω()r r a b r -=2222ω即 ()r a r br v -=2ω(其中()b a e b ,1222-=为椭圆的半短轴)质点作平面运动,其速率保持为常数。
西南大学《理论力学》复习思考题及答案

西南大学《理论力学》复习思考题及答案(0123)《理论力学》复习思考题一、单项选择题1.某质点在运动过程中,其所属的状态参量位移、速度、加速度和外力中,方向一定相同的是:()A.加速度与外力;B.位移与加速度;C.速度与加速度;D.位移与速度。
2.下面关于内禀方程和密切面的表述中,正确的是()A.密切面是轨道的切线和轨道曲线上任意点所组成的平面;B.加速度矢量a全部位于密切面内;C.切向加速度在密切面内,法向加速度为主法线方向,并与密切面垂直;D.加速度和主动力在副法线方向上的分量均等于零。
3.选出正确的表述:()A.牛顿运动定律能成立的参照系叫惯性参照系;B.牛顿运动定律不能成立的参照系叫非惯性参照系;C.对于非惯性参照系,只要加上适当的惯性力,牛顿运动定律就“仍然”可以成立;D.以上三种表述均正确。
4.研究有心力问题,采用哪一种坐标系最简单?()A.直角坐标系;B.自然坐标系;C.平面极坐标系;D.球面坐标系。
5.下列表述中正确的是:()A.对质心的动量矩定理和对固定点的动量矩定理在形式上都是相同的;B.对质心的动量矩定理和对其它任意点的动量矩定理在形式上都是相同的;C.对除了质心和固定点的其它任意点的动量矩定理和对固定点的动量矩定理在形式上都是相同的;D.以上表述均错误。
6.下列表述中正确的是:()A.质点组的动量定理中内力不起作用;B.质点组的动量矩定理中内力不起作用;C.质点组的动能定理中内力不起作用;D.以上表述均错误。
7.下列有关刚体的描述中,错误的是()A.刚体就是一种特殊的质点组;B.刚体内部任意两质点间距离不因力的作用而发生改变;C.刚体是一种理想化模型;D.刚体的形状不变,但大小可以改变。
8.下列关于地球自转所产生的影响中,错误的是:()A.落体偏东;B.右岸冲刷;C.傅科摆的进动;D.在南半球,低压区形成左旋的气旋,高压区形成右旋的气旋。
9.下列说法中,正确的是:()A.摩擦力的虚功总为零。
理论力学第三章思考题

第三章思考题3.1刚体一般是由n (n 是一个很大得数目)个质点组成。
为什么刚体的独立变量却不是3n 而是6或者更少?3.2何谓物体的重心?他和重心是不是 总是重合在一起的? 3.3试讨论图形的几何中心,质心和重心重合在一起的条件。
3.4简化中心改变时,主矢和主矩是不是也随着改变?如果要改变,会不会影响刚体的运动? 3.5已知一匀质棒,当它绕过其一端并垂直于棒的轴转动时,转动惯量为231ml ,m 为棒的质量,l 为棒长。
问此棒绕通过离棒端为l 41且与上述轴线平行的另一轴线转动时,转动惯量是不是等于224131⎪⎭⎫ ⎝⎛+l m ml ?为什么?3.6如果两条平行线中没有一条是通过质心的,那么平行轴定理式(3.5.12)能否应用?如不能,可否加以修改后再用?3.7在平面平行运动中,基点既然可以任意选择,你觉得选择那些特殊点作为基点比较好?好处在哪里?又在(3.7.1)及(3.7.4)两式中,哪些量与基点有关?哪些量与基点无关? 3.8转动瞬心在无穷远处,意味着什么?3.9刚体做平面平行运动时,能否对转动瞬心应用动量矩定理写出它的动力学方程?为什么?3.10当圆柱体以匀加速度自斜面滚下时,为什么用机械能守恒定律不能求出圆柱体和斜面之间的反作用力?此时摩擦阻力所做的功为什么不列入?是不是我们必须假定没有摩擦力?没有摩擦力,圆柱体能不能滚?3.11圆柱体沿斜面无滑动滚下时,它的线加速度与圆柱体的转动惯量有关,这是为什么?但圆柱体沿斜面既滚且滑向下运动时,它的线加速度则与转动惯量无关?这又是为什么? 3.12刚体做怎样的运动时,刚体内任一点的线速度才可以写为r ω⨯?这时r 是不是等于该质点到转动轴的垂直距离?为什么?3.13刚体绕固定点转动时,r ω⨯dtd 为什么叫转动加速度而不叫切向加速度?又()r ωω⨯⨯为什么叫向轴加速度而不叫向心加速度?3.14在欧勒动力学方程中,既然坐标轴是固定在刚体上,随着刚体一起转动,为什么我们还可以用这种坐标系来研究刚体的运动?3.15欧勒动力学方程中的第二项()21I I -y x ωω等是怎样产生的?它的物理意义又是什么?第三章思考题解答3.1 答:确定一质点在空间中得位置需要3个独立变量,只要确定了不共线三点的位置刚体的位置也就确定了,故须九个独立变量,但刚体不变形,此三点中人二点的连线长度不变,即有三个约束方程,所以确定刚体的一般运动不需3n 个独立变量,有6个独立变量就够了.若刚体作定点转动,只要定出任一点相对定点的运动刚体的运动就确定了,只需3个独立变量;确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量,确定任一点在平面上的位置需二个独立变量,共需三个独立变量;知道了定轴转动刚体绕转动轴的转角,刚体的位置也就定了,只需一个独立变量;刚体的平动可用一个点的运动代表其运动,故需三个独立变量。
理论力学思考题(二)

理论力学思考题(二)一、单项选择题1、空间的两个力F 1与F 2对某定点O 的力矩矢相等,下述说法正确的是 。
A 、这两个力的作用线必平行; B 、这两个力必在同一平面上;C 、这两个力的大小与O 点到各力作用线的距离成反比。
2、重P 的物块放在圆形曲面上,如图所示,接触面的摩擦系数为ƒS 。
为使物快保持平衡,在其上加一水平方向的力F ,当α〈arctan ƒS 时, 下述说法正确的是 。
A 、F 可指向左,也可指向右; B 、F 必须指向左; C 、F 必须指向右。
3、点的下述运动不可能的是 。
A 、 加速度越来越大,而速度大小不变; B 、加速度越来越小,而速度越来越大; C 、加速度越来越大,而速度越来越小; D 、速度越来越大,而全加速度大小为零。
4、圆盘以匀角速度ω饶定轴O 转动,动点M 相对圆盘以匀速v r 沿圆盘直径运动,如图所示。
当动点M 到达圆盘中心O 位置时,科氏加速度a c 正确的是 。
A 、c a =0B 、c a =2ωv r ,方向垂直向上C 、c a =2ωv r ,方向垂直向下5、半径为R 的圆柱在水平面上连滚带滑的向前运动,图示瞬时A 为圆柱的最高点,如图所示。
下述结果正确的是 。
A、圆柱顶点A 的速度为:2A c v v =;B、A 点的切向加速度为:A c a a R τε=+;C、A 点的法向加速度为:2n A a R ω=. 6、两个质点,质量相同,初始速度的大小和方向也完全相同,以后任何瞬时的速度大小都相同。
下述说法正确的是 。
A 、任何瞬时,这两个质点的切向加速度大小必相同;B 、任何瞬时,这两个质点受力大小一定相同;C 、这两个质点的运动方程一定相同。
7、图示球M 重P ,由两根无重杆AM 及BM 支撑,且AM=BM 。
在静止状态 下,两杆内力大小相等。
现系统以角速度ω饶铅直轴AB 旋转,如图所示。
下列各说法正确的是 。
A 、两杆内力大小相等,即AM BM F F =;B 、AM BM F F >;C 、AM BM F F <。
理论力学思考题答案

第一章思考题解答1.1答:平均速度是运动质点在某一时间间隔内位矢大小和方向改变的平均快慢速度,其方向沿位移的方向即沿对应的轨迹割线方向;瞬时速度是运动质点在某时刻或某未知位矢和方向变化的快慢程度其方向沿该时刻质点所在点轨迹的切线方向。
在的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.2答:质点运动时,径向速度和横向速度的大小、方向都改变,而中的只反映了本身大小的改变,中的只是本身大小的改变。
事实上,横向速度方向的改变会引起径向速度大小大改变,就是反映这种改变的加速度分量;经向速度的方向改变也引起的大小改变,另一个即为反映这种改变的加速度分量,故,。
这表示质点的径向与横向运动在相互影响,它们一起才能完整地描述质点的运动变化情况1.3答:内禀方程中,是由于速度方向的改变产生的,在空间曲线中,由于恒位于密切面内,速度总是沿轨迹的切线方向,而垂直于指向曲线凹陷一方,故总是沿助法线方向。
质点沿空间曲线运动时, z何与牛顿运动定律不矛盾。
因质点除受作用力,还受到被动的约反作用力,二者在副法线方向的分量成平衡力,故符合牛顿运动率。
有人会问:约束反作用力靠谁施加,当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。
有人也许还会问:某时刻若大小不等,就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同,质点的位置也在改变,副法线在空间中方位也不再是原来所在的方位,又有了新的副法线,在新的副法线上仍满足。
这反映了牛顿定律得瞬时性和矢量性,也反映了自然坐标系的方向虽质点的运动而变。
1.4答:质点在直线运动中只有,质点的匀速曲线运动中只有;质点作变速运动时即有。
理论力学思考题
理论⼒学思考题第⼀章静⼒学公理和物体的受⼒分析1-1 说明下列式⼦与⽂字的意义和区别:(1) F1 = F2(2) F1 = F2(3) ⼒F1等效于⼒F2 。
答:(1)若F1 = F2 ,则⼀般只说明这两个⼒⼤⼩相等,⽅向相同。
(2)若F1 = F2 ,则⼀般只说明两个⼒⼤⼩相等,⽅向是否相同,难以判定。
(3)⼒F1等效于⼒F2 ,则说明两个⼒⼤⼩相等,⽅向、作⽤效果均相同。
1-2 试区别F R = F1 + F2和F R = F1 + F2两个等式代表的意义。
答:前者为两个⽮量相加,后者为两个代数量相加。
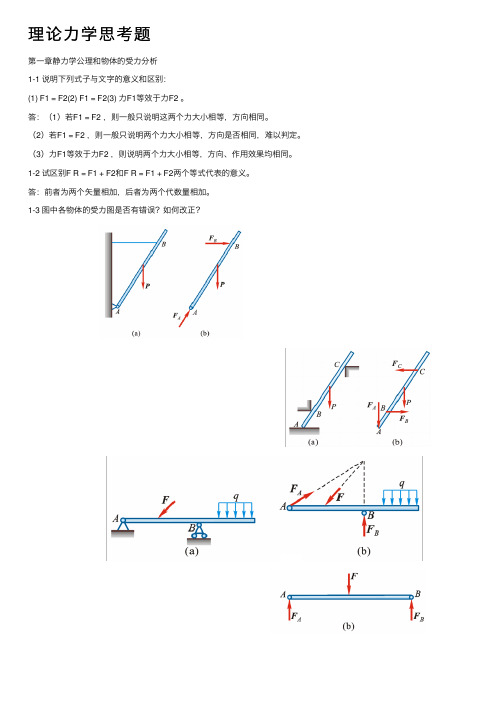
1-3 图中各物体的受⼒图是否有错误?如何改正?(1)(2)(3)(4)答:(1)B处应为拉⼒,A处⼒的⽅向不对;(2)C、B处⼒⽅向不对,A处⼒的指向反了;(3)A处⼒的⽅向不对,本题不属于三⼒汇交问题;(4)A、B处⼒的⽅向不对。
(受⼒图略)1-4 刚体上A点受⼒F作⽤,如图所⽰,问能否在B点加⼀个⼒使刚体平衡?为什么?答:不能;因为⼒F的作⽤线不沿AB连线,若在B点加和⼒F等值反向的⼒会组成⼀⼒偶。
1-5 如图所⽰结构,若⼒F作⽤在B点,系统能否平衡?若⼒F仍作⽤在B点,但可以任意改变⼒F的⽅向,F在什么⽅向上结构能平衡?答:不能平衡;若F沿着AB的⽅向,则结构能平衡。
1-6 将如下问题抽象为⼒学模型,充分发挥你们的想象、分析和抽象能⼒,试画出它们的⼒学简图和受⼒图。
(1)⽤两根细绳将⽇光灯吊挂在天花板上;(2)⽔⾯上的⼀块浮冰;(3)⼀本打开的书静⽌放于桌⾯上;(4)⼀个⼈坐在⼀只⾜球上。
答:略。
(课后练习)1-7 如图所⽰,⼒F作⽤于三铰拱的铰链C处的销钉上,所有物体重量不计。
(1)试分别画出左、右两拱和销钉C的受⼒图;(2)若销钉C属于AC,分别画出左、右两拱的受⼒图;(3)若销钉C属于BC,分别画出左、右两拱的受⼒图。
提⽰:单独画销钉受⼒图,⼒F 作⽤在销钉上;若销钉属于AC ,则⼒F 作⽤在AC 上。
理论力学思考题

1.1答:平均速度是运动质点在某一时间间隔tt t ∆+→内位矢大小和方向改变的平均快慢速度,其方向沿位移的方向即沿t ∆对应的轨迹割线方向;瞬时速度是运动质点在某时刻或某未知位矢和方向变化的快慢程度其方向沿该时刻质点所在点轨迹的切线方向。
在0→∆t 的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.3答:内禀方程中,na 是由于速度方向的改变产生的,在空间曲线中,由于a 恒位于密切面内,速度v 总是沿轨迹的切线方向,而n a 垂直于v 指向曲线凹陷一方,故na 总是沿助法线方向。
质点沿空间曲线运动时,0,0≠=bb F a z 何与牛顿运动定律不矛盾。
因质点除受作用力F ,还受到被动的约反作用力R ,二者在副法线方向的分量成平衡力0=+b b R F ,故0=b a 符合牛顿运动率。
有人会问:约束反作用力靠谁施加,当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。
有人也许还会问:某时刻若bb R F 与大小不等,ba 就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同,质点的位置也在改变,副法线在空间中方位也不再是原来b a 所在的方位,又有了新的副法线,在新的副法线上仍满足00==+b b b a R F 即。
这反映了牛顿定律得瞬时性和矢量性,也反映了自然坐标系的方向虽质点的运动而变。
1.4答:质点在直线运动中只有n a a 而无τ,质点的匀速曲线运动中只有τa a n 而无;质点作变速运动时即有n t a a 又有。
1.9答:不一定一致,因为是改变物体运动速度的外因,而不是产生速度的原因,加速度的方向与合外力的方向一致。
外力不但改变速度的大小还改变速度的方向,在曲线运动中外力与速度的方向肯定不一致,只是在加速度直线运动二者的方向一致。
1.10答:当速度与物体受的合外力同一方位线且力矢的方位线不变时,物体作直线运动。
在曲线运动中若初速度方向与力的方向不一致,物体沿出速度的方向减速运动,以后各时刻既可沿初速度方向运动,也可沿力的方向运动,如以一定初速度上抛的物体,开始时及上升过程中初速度的方向运动,到达最高点下落过程中沿力的方向运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章静力学公理和物体的受力分析1-1 说明下列式子与文字的意义和区别:(1) F1 = F2(2) F1 = F2(3) 力F1等效于力F2 。
答:(1)若F1 = F2 ,则一般只说明这两个力大小相等,方向相同。
(2)若F1 = F2 ,则一般只说明两个力大小相等,方向是否相同,难以判定。
(3)力F1等效于力F2 ,则说明两个力大小相等,方向、作用效果均相同。
1-2 试区别F R = F1 + F2和F R = F1 + F2两个等式代表的意义。
答:前者为两个矢量相加,后者为两个代数量相加。
1-3 图中各物体的受力图是否有错误?如何改正?(1)(2)(3)(4)答:(1)B处应为拉力,A处力的方向不对;(2)C、B处力方向不对,A处力的指向反了;(3)A处力的方向不对,本题不属于三力汇交问题;(4)A、B处力的方向不对。
(受力图略)1-4 刚体上A点受力F作用,如图所示,问能否在B点加一个力使刚体平衡?为什么?答:不能;因为力F的作用线不沿AB连线,若在B点加和力F等值反向的力会组成一力偶。
1-5 如图所示结构,若力F作用在B点,系统能否平衡?若力F仍作用在B点,但可以任意改变力F的方向,F在什么方向上结构能平衡?答:不能平衡;若F沿着AB的方向,则结构能平衡。
1-6 将如下问题抽象为力学模型,充分发挥你们的想象、分析和抽象能力,试画出它们的力学简图和受力图。
(1)用两根细绳将日光灯吊挂在天花板上;(2)水面上的一块浮冰;(3)一本打开的书静止放于桌面上;(4)一个人坐在一只足球上。
答:略。
(课后练习)1-7 如图所示,力F作用于三铰拱的铰链C处的销钉上,所有物体重量不计。
(1)试分别画出左、右两拱和销钉C的受力图;(2)若销钉C属于AC,分别画出左、右两拱的受力图;(3)若销钉C属于BC,分别画出左、右两拱的受力图。
提示:单独画销钉受力图,力F 作用在销钉上;若销钉属于AC ,则力F 作用在AC 上。
(此作为课堂练习)第二章 平面力系2-1 输电线跨度l 相同,电线下垂量h 越小,电线越易于拉断,为什么?答:根据电线所受力的三角形可得结论。
由图可知:2sin 2sinT W h F l αα==、 ∵ h 越小 → α 越小 → sinα 越小;则:F T 越大 → 电线越易于拉断。
2-2 图示三种结构,构件自重不计,忽略摩擦,θ=60º。
如B 处作用相同的作用力F ,问铰链A 处的约束力是否相同?答:不同(自己作出各受力图)。
2-3 如图所示,力或力偶对点A 的矩都相等,它们引起的支座约束力是否相等?答:只有图(a )和图(b )中B 处的约束力相同,其余都不同。
2-4 从力偶理论知道,一力不能与力偶平衡。
但是为什么螺旋压榨机上,力偶似乎可以用被压榨物体的反抗力F N 来平衡(如图所示)?为什么如图所示的轮子上的力偶M 似乎与重物的力P 相平衡?这种说法错在哪里?答:图(a)中力偶由螺杆上的摩擦力和法向力的水平分力形W αh 2αTF TF W成的力偶平衡,螺杆上的摩擦力与法向力的铅直方向的分力与F N 平衡;图(b)中重力P 与O 处的约束力构成力偶与M 平衡。
2-5 某平面力系向A 、B 两点简化的主矩皆为零,此力系最终的简化结果可能是一个力吗?可能是一个力偶吗?可能平衡吗?答:可能是作用线过A 、B 两点的一个力或平衡,不可能是一个力偶。
2-6 平面汇交力系向汇交点以外一点简化,其结果可能是一个力吗?可能是一个力偶吗?可能是一个力和一个力偶吗?答:可能是一个力(作用线过汇交点);不可能是一个力偶;可能是一个力(作用线不过汇交点)和一个力偶。
2-7 某平面力系向平面内任意一点简化的结果都相同,此力系简化的最终结果可能是什么? 答:可能是一个力偶或平衡。
2-8 某平面任意力系向A 点简化得一个力()0RA RA F F ''≠及一个矩为()0A A M M ≠的力偶,B 为平面内另一点,问:(1)向B 点简化仅得一力偶,是否可能?(2)向B 点简化仅得一力,是否可能?(3)向B 点简化得RARB A B F F M M ''=≠,,是否可能? (4)向B 点简化得RARB A B F F M M ''==,,是否可能? (5)向B 点简化得RARB A B F F M M ''≠=,,是否可能? (6)向B 点简化得RARB A B F F M M ''≠≠,,是否可能? 答:(1)不可能;(2)可能;(3)可能;(4)可能(AB ∥RA F '的作用线时);(5)不可能;(6)不可能。
2-9 图中OABC 为正方形,边长为a 。
已知某平面任意力系向A 点简化得一主矢(大小为RA F ')及一主矩(大小、方向均未知),又已知该力系向B 点简化得一合力,合力指向O 点。
给出该力系向C 点简化的主矢(大小、方向)及主矩(大小、转向)。
答:主矢:RC RA F F ''=、平行于BO ,主矩:22C RA M aF '=、顺时针。
2-10在上题中,若某平面任意力系满足=0=0y B F M ∑∑、 ,则(判断正误):A .必有=0A M ∑; C .可能有=00x O F M ≠∑∑、 ;B .必有=0C M ∑;D .可能有0=0x O F M ≠∑∑、 。
答:正确:B ;不正确:A 、C 、D 。
(∵题设条件说明该力系的合力过B 点且∥x 轴)2-11 不计图示各构件自重,忽略摩擦。
画出刚体ABC 的受力图,各铰链均需画出确切的约束力方向,不得以两个分力代替。
图中DE ∥FG 。
提示:左段OA 部分相当一个二力构件,A 处约束力应沿OA ,从右段可以判别B 处约束力应平行于DE 。
(受力图略)第三章 空间力系3-1 在正方体的顶角A 和B 处,分别作用力F 1 和F 2,如图所示。
求此两力在x 、y 、z 轴上的投影和对x 、y 、z 轴的矩;试将图中的力F 1 和F 2向点O 简化,并用解析式计算其大小和方向。
答:设正方体的棱长为a ,则由题图可知:111111333333x y z F F F F F F =-=-=、、, ()()()1111133033x y z M F aF M F aF M F ==-=、、; 2222222022x y z F F F F F ===、、, ()()()2222222022x y z M F aF M F M F aF ===-、、; 向O 点简化的主矢:1211232332R F F F i F j F F k ⎛⎫⎛⎫'=-+-++ ⎪ ⎪⎝⎭⎝⎭v v v v 主矩:12123232O M F F ai Faj F ak ⎛⎫=+-- ⎪⎝⎭v v v 3-2 图示正方体上A 点作用一个力F ,沿棱方向,问:(1) 能否在B 点加一个不为零的力,使力系向A 点简化的主矩为零?(2) 能否在B 点加一个不为零的力,使力系向B 点简化的主矩为零?(3) 能否在B 、C 两处各加一个不为零的力,使力系平衡?(4) 能否在B 处加一个力螺旋,使力系平衡?(5) 能否在B 、C 两处各加一个力偶,使力系平衡?(6) 能否在B 处加一个力,在C 处加一个力偶,使力系平衡?答:(1)能;(2)不能;(3)不能;(4)不能;(5)不能;(6)能。
3-3 图示为一边长为a 的正方体,已知某力系向B 点简化得到一合力,向C '点简化也得一合力。
问:(1)力系向A 点和A '点简化所得主矩是否相等?(2)力系向A 点和O '点简化所得主矩是否相等?答:(1)不等;(2)相等。
(题设条件说明该力系的合力过B C '点)3-4 在上题图中,已知空间力系向B '点简化得一主矢(其大小为F )及一主矩(大小、方向均未知),又已知该力系向A 点简化为一合力,合力方向指向O 点。
试:(1) 用矢量的解析表达式给出力系向B '点简化的主矩;(2) 用矢量的解析表达式给出力系向C 点简化的主矢和主矩。
答:(1)()B M Fa j k '=-v v v ;(2)RC CF Fi M Fak '=-=-v v v v ,。
3-5 (1)空间力系中各力的作用线平行于某一固定平面;(2)空间力系中各力的作用线分别汇交于两个固定点。
试分析这两种力系最多能有几个独立的平衡方程。
答:各为5个。
3-6 传动轴用两个止推轴承支持,每个轴承有三个未知力,共6个未知量。
而空间任意力系的平衡方程恰好有6个,是否为静定问题?答:为超静定问题。
3-7 空间任意力系总可以由两个力来平衡,为什么?答:空间任意力系简化的最终结果为合力、合力偶、力螺旋、平衡四种情况,分别考虑两个力能否与一个力、一个力偶、力螺旋(力螺旋可以看成空间不确定的两个力)、平衡四种情况平衡。
3-8 某一空间力系对不共线的三点主矩都为零,问此力系是否一定平衡?答:一定平衡。
3-9 空间任意力系向两个不同的点简化,试问下述情况是否可能?(1) 主矢相等,主矩相等; (2) 主矢不相等,主矩相等;(3) 主矢相等,主矩不相等; (4) 主矢、主矩都不相等。
答:(2)(4)可能;(1)(3)不可能。
3-10 一均质等截面直杆的重心在哪里?若把它弯成半圆形,重心位置是否改变?答:在杆正中间。
改变。
第四章 摩擦4-1已知一物块重P = 100 N ,用水平力F = 500 N 的力压在一铅直表面上,如图所示,其摩擦因数f s = 0.3,问此时物块所受的摩擦力等于多少?答:摩擦力为100N 。
4-2 如图所示,试比较用同样材料、在相同的光洁度和相同的胶带压力F 作用下,平胶带与三角胶带所能传递的最大拉力。
答:三角带传递的拉力大。
取平胶带与三角带横截面分析正压力(如右下图所示),可见三角带的正压力大于平胶带的正压力。
∵ 接触面处的正压力分别为:平胶带:N F F =,三角带:2sin N F F θ=; ∴ 它们所能传递的最大拉力分别为:平胶带:max T s F f F =,,三角带:max sin s T f F F θ=,; 而 sin 1θ<,因此,三角带传递的拉力大。
4-3 为什么传动螺纹多用方牙螺纹(如丝杠)?而锁紧螺纹多用三角螺纹(如螺钉)?答:参考上题分析可知,在相同外力(力偶或轴向力)作用下,方牙螺纹产生的摩擦力较小,而三角螺纹产生的摩擦力较大,这正好符合传动与锁紧的要求。
4-4 如图所示,砂石与胶带间的静摩擦因数f s = 0.5,试问输送带的最大倾角θ为多大?答:arctan0.526.56θ≈︒<4-5 物块重P ,一力F 作用在摩擦角之外,如左下图所示。
