第六章图与网络分析
合集下载
运筹学课件 第六章图与网络分析(清华大学出版社)
w(P ) = min w(P) 0
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
P
路P0的权称为从vs到vt的距离,记为:d( vs,vt )
OR3 12
– 最短路算法
Dijkstra算法 :有向图 ,wij≥0 一般结论:
vs到 j的 短 v 最 路
vs ,...,vi ,...,vj ⇒ vs ,...,vi
vs到 i的 短 v 最 路
OR3 17
4 )
标号的点,考察弧( v 4 为刚得到 P 标号的点,考察弧( v 4 , v 6),( v 4 , v 7)的端点 v 6,v 7: T ( v ) = min [T ( v ), P ( v ) + l ] = min [13 , 9 + 9 ] = 13 46 6 6 4 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 , 9 + 7 ] = 14 47 7 7 4 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 13 。 6 6 此时 P 标号的点集 S = { , , , v , v , v } v1 v 2 v 3 5 4 6 。 6 7)v 为刚得到 P 标号的点,考察弧( 标号的点,考察弧( v 6 , v 7),( v 6 , v 8)的端点 v 7, 8: v 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [14 ,13 + 5 ] = 14 67 7 7 6 T ( v ) = min [T ( v ), P ( v ) + l ] = min [+ ∞ ,13 + 4 ] = 17 68 8 8 6 标号, 最小, 比较所有 T 标号, T ( v ) 最小,所以令 P ( v ) = 14 。 7 7 此时 P 标号的点集 S = { , , , v , v , v , v } v1 v 2 v 3 5 4 6 7 。 7
运筹学(第6章 图与网络分析)

a1 (v1) 赵
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈
定义: 图中的点用v表示,边用e表示。对每条边可用它
所连接的点表示,记作:e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后,可用图来表示相遇情况,如 下图所示。
运动员 A
B C
D
E
F G
H
例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系,那么只用两点之间的联线就很难刻画他们之间的关 系了,这是我们引入一个带箭头的联线,称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj],称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点,反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联,称点vi和vj相邻;若边ei和
e5
e7
(v2)钱
a2 a3 a4 a14 a15
a8 a9
a7 (v4) 李
(v3)孙
a5 (v5) 周 a6 a10 (v6)吴
图6-3
a12 a11 a13
(v7)陈
定义: 图中的点用v表示,边用e表示。对每条边可用它
所连接的点表示,记作:e1=[v1,v1]; e2=[v1,v2];
树是图论中结构最简单但又十分重要的图。在自然和社会领 域应用极为广泛。 例6.2 乒乓求单打比赛抽签后,可用图来表示相遇情况,如 下图所示。
运动员 A
B C
D
E
F G
H
例6.3 某企业的组织机构图也可用树图表示。
厂长
人事科
财务科
总工 程师
生产副 厂长
经营副 厂长
开发科
技术科
生产科
设备科
供应科
动力科
e2
(v1) 赵
e1
e3
e4 孙(v3) 李(v4)
周(v5)
图6-2
e5 吴(v6) 陈(v7)
(v2)钱
如果我们把上面例子中的“相互认识”关系改为“认识” 的关系,那么只用两点之间的联线就很难刻画他们之间的关 系了,这是我们引入一个带箭头的联线,称为弧。图6-3就是 一个反映这七人“认识”关系的图。相互认识用两条反向的 弧表示。
端点,关联边,相邻 若有边e可表示为e=[vi,vj],称vi和
e2 v2 e6 e1 e4 v1 e3 v3 e8
vj是边e的端点,反之称边e为点vi
或vj的关联边。若点vi、vj与同一条 边关联,称点vi和vj相邻;若边ei和
e5
e7
第6章 图与网络分析――基础知识PPT课件

D
E
F
甲
√
√
√
乙
√
√
√
丙
√
√
丁
√
√
戊
√
√
√
己
√
√
√
将研究对象用点表示。对象与对象之间用边表示。依题意,找出不相邻的顺序。
B
C
ACBFED
A
D
36
F
E
类型2. 求最小部分树。避圈法和破圈法
基本定理:图中任一个点i,若j是与i相邻点 中距离最短的,则边[i,j]一定含在该图的 最小部分树内。
推论:把图的所有点分成集合V和它的补集两 个集合,则两集合之间连线的最短边一定 包含在最小部分树内。
A
7
2 2
S
5
B
5
D
5
T
1
1
4
3
7
C
E
4
39
[例2]如图6-2,SABCDET代表村镇,它们中间 连线表明各村镇间现有道路交通情况,连线旁 数字代表道路的长度。现要求沿图中道路架设 电线,使上述村镇全部通上电,应如何架设使 总的长度为最短。
A
7
2 2
S
5
B
5
D
5
T
1
1
4
3
7
C
E
4
40
[例2]如图6-2,SABCDET代表村镇,它们中间 连线表明各村镇间现有道路交通情况,连线旁 数字代表道路的长度。现要求沿图中道路架设 电线,使上述村镇全部通上电,应如何架设使 总的长度为最短。
点边交替序列,点边均不重 复。
点边交替序列,起点和终点 不重复。 点边交替序列,起点和终点 重复。
图与网络分析

end;
例 1 中 1 到 7 点的最短路是 1-2-5-7
查伴随矩阵 E 的第一行
1234567
10020255 19
hw
小结
• 最短路有广泛的应用 (P176案例) • 最短路的多种形式:无向图,有向图无循环圈,有向
图,混合图,无负边权,有负边权,有负回路,k-最 短路等 • 当存在负权值边时,Floyd算法比Dijkstra算法效率高, 且程序极简单。但Dijkstra算法灵活 • 若图是前向的,则Dijkstra算法也可以求两点间最长路 • 一般情况下,两点间最长路是 NP-complete,但最短 路是 P算法 • 两点间k-最短路:分为边不相交的和边相交的 求边不相交的k-最短路非常容易:先求最短路,将该 最短路中的边从网路删去,再用Dijkstra算法可求次最 短路,以此类推
hw
6.1.4 链,圈,路径,回路,连通图
• 走过图中所有边且每条边仅走一次的闭行走称为欧拉 回路
定理 2:偶图一定存在欧拉回路(一笔画定理) 6.1.4 连通图,子图,成分
• 设有两个图 G1(V1, E1), G2(V2, E2), 若V2 V1, E2 E1, 则 G2 是 G1 的子图
• 无向图中,若任意两点间至少存在一条路径,则称为 连通图(connected graph),否则为非连通图( disconnected graph);非连通图中的每个连通子图称为成分 (component)
线表示实体间的关联
A
A D
C
C
D
B
B
2
hw
6.1 图与网络的基本概念
6.1.1图与网络 • 节点 (Vertex)
– 物理实体、事物、概念 – 一般用 vi 表示
第六章_图与网络分析

T (e ) :割集{ S 1 , S 2 } ,其中 S 1 , S 2 为 e 的两个连通分支的点集合
1 2
3 4 5
右图的关联矩阵是
2
1 1 1 0 0 0 2 1 0 1 1 0 3 0 1 1 0 1 4 0 0 0 1 1
1
4
3
邻接矩阵示例
图(7)的邻接矩阵是
1 2 3 4 5 1 0 2 1 3 1 4 1 5 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0
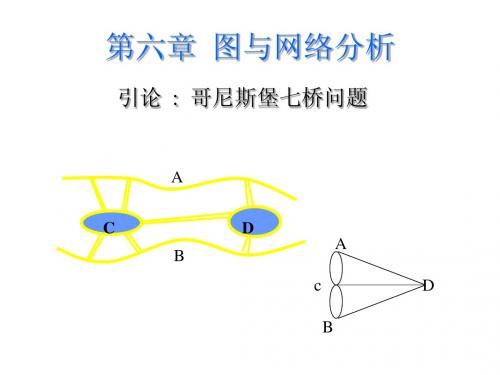
斯堡城有一条普雷格尔河,河中有两个
岛屿,河的两岸和岛屿之间有七座桥相 互连接,如下图所示。
当地的居民热衷 于这样一个问题,一 个漫步者如何能够走 过这七座桥,并且每 座桥只能走过一次, 最终回到原出发地。 尽管试验者很多, 但是都没有成功。
A
D
C B
为了寻找答案,1736年欧 拉把陆地缩为一点,把桥作为 连接点的边,将这个问题抽象 成图形的一笔画问题。即能否 从某一点开始不重复地一笔画 出这个图形,最终回到原点。 欧拉在他的论文中证明了这是 不可能的,因为这个图形中每 一个顶点都与奇数条边相连接 ,不可能将它一笔画出,这就 是古典图论中的第一个著名问 题。
随着科学技术的进步,特别是电子计
算机技术的发展,图论的理论获得了更进
一步的发展,应用更加广泛。如果将复杂
的工程系统和管理问题用图的理论加以描
述,可以解决许多工程项目和管理决策的 最优问题。因此,图论越来越受到工程技 术人员和经营管理人员的重视。
1736年瑞士科学家欧拉发表了关于 图论方面的第一篇科学论文,解决了著 名的哥尼斯堡七座桥问题。德国的哥尼
A
D
1 2
3 4 5
右图的关联矩阵是
2
1 1 1 0 0 0 2 1 0 1 1 0 3 0 1 1 0 1 4 0 0 0 1 1
1
4
3
邻接矩阵示例
图(7)的邻接矩阵是
1 2 3 4 5 1 0 2 1 3 1 4 1 5 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0
斯堡城有一条普雷格尔河,河中有两个
岛屿,河的两岸和岛屿之间有七座桥相 互连接,如下图所示。
当地的居民热衷 于这样一个问题,一 个漫步者如何能够走 过这七座桥,并且每 座桥只能走过一次, 最终回到原出发地。 尽管试验者很多, 但是都没有成功。
A
D
C B
为了寻找答案,1736年欧 拉把陆地缩为一点,把桥作为 连接点的边,将这个问题抽象 成图形的一笔画问题。即能否 从某一点开始不重复地一笔画 出这个图形,最终回到原点。 欧拉在他的论文中证明了这是 不可能的,因为这个图形中每 一个顶点都与奇数条边相连接 ,不可能将它一笔画出,这就 是古典图论中的第一个著名问 题。
随着科学技术的进步,特别是电子计
算机技术的发展,图论的理论获得了更进
一步的发展,应用更加广泛。如果将复杂
的工程系统和管理问题用图的理论加以描
述,可以解决许多工程项目和管理决策的 最优问题。因此,图论越来越受到工程技 术人员和经营管理人员的重视。
1736年瑞士科学家欧拉发表了关于 图论方面的第一篇科学论文,解决了著 名的哥尼斯堡七座桥问题。德国的哥尼
A
D
第6章 图与网络分析

为了区别起见。把两点之间的不带箭头的连线称 为边,带箭头的连线称为弧。 用图来描述事物间的联系,不仅直观清晰,便于 统观全局,而且网络图的画法简便,不必拘泥于 比例和曲直。总之,这里所讲的图是反映对象之 间关系的一种工具。
29
2013-2-14
无向图
由点和边组成的图称为无向图。
无向图可表示为一个有序二元组(V,E),记为 G=(V,E),其中 V =(v1,v2,…….vp)是 p 个点的集合,E={e1,e2,……eq}是 q 条边的集 合,并且 ei 是一个无序二元组,记为 ei=[vi,vj]=[vj,vi], vi,vj∈V。
2013-2-14 31
环、多重边、简单图、多重图
一条边的两个端点如果相同,称此边 为环(自回路) 。如上图中的 e1。 两个点之间多于一条边的,称为多重 边。如上图中的 e4,e5。 不含环和多重边的图称为简单图,含 有多重边的图称为多重图。
2013-2-14 32
点的次
以点 v 为端点的边数叫做点 v 的次, 记作 d(v)。 如上图中, 1)=4, 2)=4。 d(v d(v 若 V=(v1,v2,…….vp),则称{ d(v1),d(v2),…….d(vp)}为图 G 的次序列。 次为 1 的点称为悬挂点,连接悬挂点的边称为悬挂边。次为 0 的点称为 孤立点。 次为奇数的点称为奇点,次为偶数的点称为偶点。 定理 1 任何图 G=(V,E)中,所有点的次数之和等于边数的 2 倍。即
运筹学 Operations Research
高 谦
烟台大学文经学院 基础教学部
2013-2-14 1
引言 图论是专门研究图的理论的一门数学 分支,属于离散数学范畴,与运筹学有 交叉,它有200多年历史,大体可划分 为三个阶段: 第一阶段是从十八世纪中叶到十九世纪 中叶,处于萌芽阶段,多数问题围绕游 戏而产生,最有代表性的工作是所谓的 Euler七桥问题,即一笔画问题。
29
2013-2-14
无向图
由点和边组成的图称为无向图。
无向图可表示为一个有序二元组(V,E),记为 G=(V,E),其中 V =(v1,v2,…….vp)是 p 个点的集合,E={e1,e2,……eq}是 q 条边的集 合,并且 ei 是一个无序二元组,记为 ei=[vi,vj]=[vj,vi], vi,vj∈V。
2013-2-14 31
环、多重边、简单图、多重图
一条边的两个端点如果相同,称此边 为环(自回路) 。如上图中的 e1。 两个点之间多于一条边的,称为多重 边。如上图中的 e4,e5。 不含环和多重边的图称为简单图,含 有多重边的图称为多重图。
2013-2-14 32
点的次
以点 v 为端点的边数叫做点 v 的次, 记作 d(v)。 如上图中, 1)=4, 2)=4。 d(v d(v 若 V=(v1,v2,…….vp),则称{ d(v1),d(v2),…….d(vp)}为图 G 的次序列。 次为 1 的点称为悬挂点,连接悬挂点的边称为悬挂边。次为 0 的点称为 孤立点。 次为奇数的点称为奇点,次为偶数的点称为偶点。 定理 1 任何图 G=(V,E)中,所有点的次数之和等于边数的 2 倍。即
运筹学 Operations Research
高 谦
烟台大学文经学院 基础教学部
2013-2-14 1
引言 图论是专门研究图的理论的一门数学 分支,属于离散数学范畴,与运筹学有 交叉,它有200多年历史,大体可划分 为三个阶段: 第一阶段是从十八世纪中叶到十九世纪 中叶,处于萌芽阶段,多数问题围绕游 戏而产生,最有代表性的工作是所谓的 Euler七桥问题,即一笔画问题。
运筹学第6章 图与网络

也就是说| V1 |必为偶数。
定理6.2有学者也称作定理6.1的推论。根据定理6.2,握手定理也可以 表述为,在任何集体聚会中,握过奇次手的人数一定是偶数个。
12 该课件的所有权属于熊义杰
另外,现实中不存在面数为奇数且每个面的边数也是奇数的多面 体,如表面为正三角形的多面体有4个面,表面为正五边形的多面体有 12个面等等,也可以用这一定理予以证明。因为在任意的一个多面体 中, 当且仅当两个面有公共边时,相应的两顶点间才会有一条边,即 任意多面体中的一个边总关联着两个面。所以,以多面体的面数为顶
v j V2
(m为G中的边数)
因式中 2m 是偶数, d (v j ) 是偶数,所以 d (vi ) 也必为偶数
v j V2
vi V1
( 两个同奇同偶数的和差必为偶数 ), 同时,由于 d (vi ) 中的每个加数 d (vi )
均为奇数,因而 d (vi ) 为偶数就表明, d (vi ) 必然是偶数个加数的和 ,
图论、算法图论、极值图论、网络图论、代数图论、随机图论、 模糊图论、超图论等等。由于现代科技尤其是大型计算机的迅 猛发展,使图论的用武之地大大拓展,无论是数学、物理、化 学、天文、地理、生物等基础科学,还是信息、交通、战争、 经济乃至社会科学的众多问题.都可以应用图论方法子以解决。
1976年,世界上发生了不少大事,其中一件是美国数学家 Appel和Haken在Koch的协作之下,用计算机证明了图论难题— —四色猜想(4CC):任何地图,用四种颜色,可以把每国领土染 上一种颜色,并使相邻国家异色。4CC的提法和内容十分简朴, 以至于可以随便向一个人(哪怕他目不识丁)在几分钟之内讲清 楚。1852年英国的一个大学生格思里(Guthrie)向他的老师德·摩 根(De Morgan)请教这个问题,德·摩根是当时十分有名的数学家, 他不能判断这个猜想是否成立,于是这个问题很快有数学界流 传开来。1879年伦敦数学会会员Kemple声称,证明了4CC成立, 且发表了论文。10年后,Heawood指出了Kemple的证明中
运筹学第六章图与网络分析a管理精品资料

min T (v j) T ( v j) ,L ( v i) d ij j
3. 在与固定标号点相邻的临时标号点中选取 具有最小标号的点vi给予固定标号,即:
L(vi)=min{ T(vj) } 返回第2步。 4. 当vn得到固定标号时,计算结束。 注: 固定标号L(vi)表示v1到vi的最短距离, 临时标号T(vj)表示v1到vi距离的上界。
能一笔画的图一定是欧拉圈或含有欧拉链。 定理:连通的多重图G是欧拉图的充要条件是G 中无奇点。 推论:连通的多重图G有欧拉链的充要条件是G 中恰有两个奇点。
第二节 树图和图的最小部分树
树图:无圈的连通图称为树图,记为T(V,E)。 2-1 树的性质 性质1:任何树中必存在至少两个次为1的点(悬 挂点)。
若一个简单图中任意两点之间均有边相连,
则称该图为完全图。
对含有n个顶点的完全图,其边数有
Cn2
1n(n1) 2
条。
如果图的顶点能分成两个互不相交的非空
集合V1和V2 ,使在同一集合中任意两个顶点 都不相邻,则称该图为偶图(或二分图)。
若偶图的顶点集合V1、V2之间的每一对不 同顶点之间都有一条边相连,则称该图为完全 偶图。在完全偶图中, V1若有m个顶点, V2 有n个顶点,则其边数共有m×n条。
临时标号
v2(5) v3(2) v4(∞) v5(∞) v6(∞) v7(∞) v2(5) v4(9) v5(∞) v6(6) v7(∞) v4(7) v5(12) v6(6) v7(∞) v4(7) v5(7) v7(12)
v5(7) v7(12)
v7(10)
❖ Dijkstra 算 法 仅 适 合 于 所 有 的 权
Hale Waihona Puke 3-2 求任意两点间最短距离的矩阵算法(Floyd) 设邻接矩阵为D,计算D1=D+D, D2= D1 +D ,
3. 在与固定标号点相邻的临时标号点中选取 具有最小标号的点vi给予固定标号,即:
L(vi)=min{ T(vj) } 返回第2步。 4. 当vn得到固定标号时,计算结束。 注: 固定标号L(vi)表示v1到vi的最短距离, 临时标号T(vj)表示v1到vi距离的上界。
能一笔画的图一定是欧拉圈或含有欧拉链。 定理:连通的多重图G是欧拉图的充要条件是G 中无奇点。 推论:连通的多重图G有欧拉链的充要条件是G 中恰有两个奇点。
第二节 树图和图的最小部分树
树图:无圈的连通图称为树图,记为T(V,E)。 2-1 树的性质 性质1:任何树中必存在至少两个次为1的点(悬 挂点)。
若一个简单图中任意两点之间均有边相连,
则称该图为完全图。
对含有n个顶点的完全图,其边数有
Cn2
1n(n1) 2
条。
如果图的顶点能分成两个互不相交的非空
集合V1和V2 ,使在同一集合中任意两个顶点 都不相邻,则称该图为偶图(或二分图)。
若偶图的顶点集合V1、V2之间的每一对不 同顶点之间都有一条边相连,则称该图为完全 偶图。在完全偶图中, V1若有m个顶点, V2 有n个顶点,则其边数共有m×n条。
临时标号
v2(5) v3(2) v4(∞) v5(∞) v6(∞) v7(∞) v2(5) v4(9) v5(∞) v6(6) v7(∞) v4(7) v5(12) v6(6) v7(∞) v4(7) v5(7) v7(12)
v5(7) v7(12)
v7(10)
❖ Dijkstra 算 法 仅 适 合 于 所 有 的 权
Hale Waihona Puke 3-2 求任意两点间最短距离的矩阵算法(Floyd) 设邻接矩阵为D,计算D1=D+D, D2= D1 +D ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e3
v3
若链中所有的顶点也互不相同,这样的链称为路.
e4
v4
起点和终点重合的链称为圈. 起点和终点重合的路称为回路.
若图中的每一对顶点之间至少存在一条链, 称这 样的图为连通图, 否则称该图是不连通的. 第10页
完全图,偶图
任意两点之间均有边相连的简单图, 称为完全图. K n
K2
K3
K4
2 | E | Cn
第20页
6.2树图和图的最小部分树问题 Minimal tree problem 6.2.1树的概念
若图中的每一对顶点之间至少存在一条链, 称这样的图 为连通图. 树图(简称树Tree): 无圈的连通的图,记作T(V, E)
组织机构、家谱、学科分支、因特网络、通讯网络及高压线路 网络等都能表达成一个树图 。
第13页
有向图 G : (V,E),记为 G=(V,E)
G 的点集合: V {v1 , v2 ,...,vn } G 的弧集合: E {eij } 且 eij 是一个有序二元组 (vi , v j ) ,记
为 eij (vi , v j ) 。下图就是一个有向图,简记 G 。 若 eij (vi , v j ) ,则称 eij 从 v i 连向 v j ,点 v i 称为 eij 的尾,v j 称为 eij 的头。 v i 称为 v j 的前继, v j 称为 v i 的后继。 基本图:去掉有向图的每条弧上的方向所得到的无向图。
有向图 G (V , E ) 的关联矩阵:一个 | V | | E | 阶矩阵
B (bik ) ,
1, 当 弧ek以 点i为 尾 其中 bik 1, 当 弧ek以 点i为 头 0, 否 则
第17页
右图的关联矩阵是
1 1 2 1 3 0 4 0 5 0
A (aij ) ,其中
1, 当点i与点j邻接 aij 0, 否则
有向图 G (V , E ) 的邻接矩阵:一个 | V | | V | 阶矩 阵 A (aij ) ,其中
1, 当有弧从i连向j aij 0, 否则
第19页
1
2
2
3
1
4
4
5
3
图1
图2
图(1)的邻接矩阵是
1 2 2 3 3 4 4 5 5 1 1 0 2 1 3 1 4 1 5 0 1 0 1 0 1 1 1 0 1 1 1 0 1 0 1 0 1 1 1 0
图(2)的邻接矩阵是 1 2 3 4
1 0 2 1 3 0 4 0 1 0 1 0 1 1 0 1 0 1 0 0
e4
e6
v4
第 8页
e2 V2 V3 e3 e6 v1 e7 V4
例如: V=(v1, v2, v3,v4, v5, v6 ), E= ( e1, e2, e3, e4, e5, e6, e7 , )
e1
e4
V5
V6
e5
第 9页
次,奇点,偶点,孤立点 与点v相关联的边的数目称为点v的次(度或线度),记作d(v)
5 4 3
v3
5 8
2
7
v5
1 6
v2
v4
图6-1
v6
在一个连通图G中, 取部分边连接G的所 有点组成的树称为G 的部分树或支撑树 (Spanning Tree )。 图6-2是图6-1的 部分树。
v1
4
v3
2
7
v5
1
v2
3
v4
图 6- 2
v6
第22页
§6.2.2树图的性质
悬挂点
悬挂边
性质1 任何树图中必存在次为1的点. 证明:用反证法. 假设树图中不存在次为1的点.
济南 郑州
徐州 南京
武汉
第 3页
例,有甲,乙,丙,丁,戊五个球队,它们之间比赛的情况,也 可以用图表示出来。已知甲队和其它各队都比赛过一次,乙 队和甲丙队比赛过,丙队和乙,丁队比赛过,丁队和丙,戊队 比赛过,戊队和甲,丁队比赛过。 为了反映这个情况,可以用点v1, v2, v3, v4, v5分别代 表这五个队,某两个队之间比赛过,就在这两个队所相应的 点之间联一条线,这条线不过其它的点,如图所示
V5
v1 V2 V3
V4
V1
V2
V3
图5
V4
V5
第 4页
图4
v1
8 4
v3 5
7
v5
5
v2 3
8
v4
2 6
1
v6
运筹学中研究的图具有下列特征: (1)用点表示研究对象,用边(有方向或无方向)表示对 象之间某种关系。 (2)强调点与点之间的关联关系,不讲究图的比例大小与 形状。 (3)每条边上都赋有一个权,其图称为赋权图(网络)。实际 中权可以代表两点之间的距离、费用、利润、时间、容量等不 同的含义。 (4)建立一个网络模型,求最大值或最小值。 第 5页
若边e=[vi,vj],称vi和vj是边e的端点; 边e为点vi或vj的关联边; 若点vi、vj与同一条边关联,称点vi和vj 相邻(邻接); 若边ei和ej具有共同的端点,称边ei和ej相邻; 环,多重边,简单图: 若边e的两个端点相重合,称该边为环;
e1 e2 v2 v1 e5 e3
若两顶点之间至少有两条边,称为具有多重边; v3 无环、无多重边的图称作简单图。
G的部分树(或支撑树): 若G1是G的部分图又是树图. 树枝: 树图的各条边. 将网络图G边上的权看作两点间的长度(距离、费用、 时间),定义G的部分树T的长度等于T中每条边的长 度之和,记为C(T)。 G的所有部分树中长度最小的部 分树称为最小部分树,最小支撑树,或简称为最小树。
第21页
v1 8
v2 v4
v5
v1 v3
第23页
性质2 具有n个顶点的树图的边数恰好为n-1条. 证明:用归纳法.
当n=2和n=3时, 上述性质显然成立. 假设当n=k-1时, 上述性质也成立. 当n=k时, 因树中至少有一个悬挂点,将此悬挂点及 关联的悬挂边从树图中拿掉. 根据前述,剩下的图仍为树图,故此时图中有k-1个 点,据假定应有k-2条边. 再把拿掉的悬挂点及悬挂边放回去,说明树图中含 有k个点时,边数为k-1条.
若图的顶点能分成两个互不相交的非空集合V1和V2,使在同 一集合中任意两个顶点均不相邻,称 这样的图为偶图(二分图). 若偶图的顶点集合V1和V2之间的每对不同顶点都有边相连, 称 这样的图为完全偶图.
Km,n
| E | m n
K3, 2
简单图G的补图 :与G有相同顶点集合的简单图,且补图中的两 个点相邻当且仅当它们在G中不相邻
又连通图中不存在孤立点,故树图中所有顶点的次≥2. 不妨设d(v1)=2, 既v1有两条关联边, 设关联边的其他两个端点为v2 , v3,而d(v2 )≥2, d(v3) ≥2, 又可知与v2 , v3关联的边的其他端点v4 , v5,同样d(v4 )≥2, d(v5) ≥2,可继续一直往下推。 而图的顶点的总数是有限的,故最后 必然回到前面的某一顶点,于是在图中出 现了圈,这与树的定义产生了矛盾.
1 1 1 1 0 0 0 0 2 1 0 1 1 1 1 0 3 0 1 0 1 0 1 1 4 0 0 0 0 1 0 1
e1
1
2
e5 e4 e7
第18页
4
e3 e2
e6
3
邻接矩阵
简单图 G (V , E ) 的邻接矩阵:一个 | V | | V | 阶矩阵
第11页
子图,部分图
设G=(V,E)是一个图, 并设V V 和E E , 如果对E 中
任意的一条边eij [vi , v j ], 都有 vi V , v j V , 则称G [V , E ] 是G的一个子图. 若V V , E E , 则称 G 是G的一个部分图.
n1
n2
n4
n3
第14页
网 络
设G是一个图(有向图),若对G的每条边(弧) 都赋予一个实数,称为这条边(弧)的权,则 G连同它 边(弧)上的权称为一个(有向)网络或赋权(有向) 图,记为G=(V,E,W).
A 2 C
8 5
B
2
3 7
D
1
1Байду номын сангаас
4 2
4
3 2
5
4 4
3
2
第15页
无向完全图:在无向图中,如果任意两个顶点之间 存在边。 有向完全图:在有向图中,如果任意两顶点之间都 有存在方向互为相反的两条弧。
0 2
1
含有n个顶点的无向完全图有多少条边? n(n-1)/2
含有n个顶点的有向完全图有多少条弧? n(n-1)
第16页
关联矩阵
简单图 G (V , E ) 的关联矩阵:一个 | V | | E | 阶矩阵
B (bik ) ,
其中
1, 当点i与边ek 关联 bik 0, 否则
图的意义
因此,可以说图是反映对象之间关系的一种工 具,在一般情况下,图中点的相对位置如何,点与点 之间联线的长短曲直,对于反映对象之间的关系, 并不是重要的。 如上例,可以用如图4所示的图去反映五个球队 的比赛情况,这与图5没有本质的区别,所以,图论 中的图与几何图,工程图等是不同的.
第 6页
§6.1 图的基本概念
运筹学中研究的图是生活中各类图的抽象概括, 它表明一些研究对象和这些对象之间的相互关系。 用点表示研究对象,用边表示这些对象之间的联 系,则图G可定义为点和边的集合,记为
G {V , E }
式中V是点的集合,E是边的集合。
