最小二乘法处理复摆实验数据
北京大学复摆实验报告

1.28140 1.27314 1.26429 1.25752 1.25029 1.24472 1.23855 1.23435 1.23137 1.23021 1.22986 1.23189 1.23572 1.24205 1.25219 1.26689 1.28497 1.30712 1.33931 1.37785 1.43054 1.49646 1.58282 1.70131 1.866637 2.05579 2.43580
2. 将复摆安装到支架上,利用铅直线调整铁架下部支脚螺钉,使复摆在垂直平面内 摆动,且尽可能使平衡位置在光电门中央;
3. 利用复摆上位置不同的小孔作为刀口悬挂点,记下此点到零刻度线(即质心)的 距离hi,用光电计时器记录此时复摆运动20个周期的时间20Ti,列表记录数据;
4. 数据处理
1) 作T 2h ∼ h2图,用线性拟合法求重力加速度g 2) 用公式求g 3) 作T ∼ h图,求出复摆对于任意悬挂点的等值摆长,从而求出g
g11 = 4π2/k1 = 4π2/4.063 = 9.718m · s−2
(25)
右半部分如Figure 6所示:
斜率k2 = 4.028s2/m, 截距b1 = 0.1420s2m, 相关系数R22 = 0.999996 计算得:
g12 = 4π2/k1 = 4π2/4.028 = 9.802m · s−2
RG = h0
也是图中两条曲线的极小值之间的距离,且h1 + h2 = EF = 2RG. 取一周期为T值 (H点 ) 处 引 一 直 线MN平 行 于 横 轴 , 交 两 条 对 称 曲 线 于A,B,C,D四 点 , 把 这 四 点 分 成A,C和B,D两组,在摆杆上每一组中两点都位于质心G(Figure 3所示)的两旁,并与
数据的处理最小二乘法

P(KN)
20.00 18.00 16.00 14.00
2.标实验点:
12.00
实验点可用“ ”、 10.00
“ ”、“ ”等符号标 8.00
出(同一坐标系下不同曲
线用不同的符号)。
6.00
4.00
3. 连成图线:
2.00
用直尺、曲线板等把 点连成直线、光滑曲线。
0 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 f(mm)
板等连接。要尽可能使所描绘的曲线通 过较多的测量点。
•
(5)注解和说明:
•
在图纸上要写明图线的名称、作图
者姓名、日期以及必要的简单说明(如实验
条件:温度、压力等)。
• 直线图解法首先是求出斜率和截距,进 而得出完整的线性方程。其步骤如下:
• 选点 求斜率 求截距
1. 标明坐标轴:
用粗实线画坐标轴, 用箭头标轴方向,标坐标 轴的名称或符号、单位, 再按顺序标出坐标轴整分
误差的产生和消除
• 方法误差:(比较严重的)原因:分析与操作方 法本身造成的。
• 例:重量分析中的沉淀的溶解或吸附杂质。 • 仪器的操作不当等。
• 消除方法:作对照试验,用已知的标准 试样进行多次测定。
• 通过校正系数校正试样的分析结果。
校正系数
标准试样标准值 标准试样测定值
分析结果 试样测定值 校正系数
系统误差的性质可归纳为如下三点:
• 重现性 • 单向性 • 数值基本恒定 • 系统误差可以校正。可用一定的方法消除。
偶然误差的性质:
• 误差的大小、正负都是不固定的。 • 偶然误差不可测误差。 • 在消除系统误差后,在同样条件下多次测定,可
组合测量的最小二乘法处理实验报告 牟

求解过程
实验分析与思考题解答:
1、 把普通万用表测得的三个电阻的值,经过最小二乘处理后其精度提高了吗? 答:提高了,不然也不会怎么复杂的去求残余平方和的最小值了。其实就是通过数学的求导 方法求出了残余平方最小值从而修正了测量数据。
2、 组合测量的最小二处理有什么实际意义? 答:当独立测量次数增多后,通过最小二乘处理,可以减小随机误差的影响,提高测量结果的精确度。
ai1ai2 0 0 0 1 0 1 2
ai1ai3 0 0 0 0 0 1 1
ai2ai3 0 0 0 0 1 1 2
li1ai1 L1 0 0 L4 0 L6 L1+L4+L6
liai2 0 L2 0 L4 L5 L6 L2+L4+L5+L6
liai3 0 0 L3 0 L5 L6 L3+L5+L6
组合测量的最小二乘法处理实验报告
实验工作者:牟彪 学号:200906090109 实验日期:2013.4.3
实验名称:
组合测量的最小二乘法处理
实验目的:
根据随机误差的理论,当独立测量次数增多后,通过最小二乘处理,可以减小随机误差的影 响,提高测量结果的精确度。组合测量的最小二乘处理,是可以在一定程度上改善由于仪器测量 精度不够好引起的测量精度问题的。因此,在实际的工程测量时间工作中,掌握这种方法具有重 要的实际意义。 本实验通过对一组物理量采用组合测量方法来获取测量结果, 以达到进一步理解组合测量方 法的原理、掌握组合测量的基本思想,学会组合测量数据的处理方法。
组合测量的最小二乘处理, 是可以在一定程度上改善由于仪器测量精度不够好引起的测量精度问题的。 因此,在实际的工程测量时间工作中,掌握这种方法具有重要的实际意义。
实验报告_复摆实验
1.764
1.764
1.764
4
1.774
1.774
1.774
6
1.537
1.533
1.535
6
1.527
1.527
1.527
8
1.379
1.389
1.384
8
1.406
1.406
1.406
10
1.301
1.306
1.304
10
1.317
1.317
1.317
12
1.265
1.269
1.267
12
1.262
姓名
学号
院系
时间
地点
【实验题目】复摆实验
【实验记录】
1.复摆中心G的位置:0刻度处
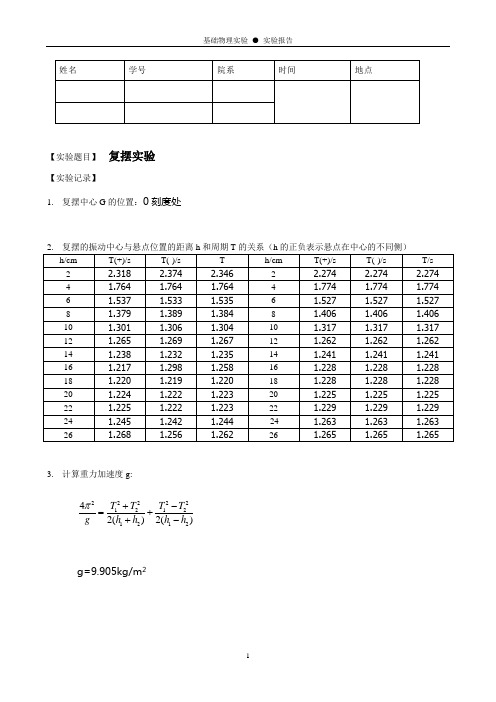
2.复摆的振动中心与悬点位置的距离h和周期T的关系(h的正负表示悬点在中心的不T(-)/s
T
h/cm
T(+)/s
T(-)/s
T/s
2
2.318
2.374
2.346
2
2.274
2.274
2.274
1.262
1.262
14
1.238
1.232
1.235
14
1.241
1.241
1.241
16
1.217
1.298
1.258
16
1.228
1.228
1.228
18
1.220
1.219
1.220
18
1.228
1.228
1.228
20
1.224
1.222
1.223
数值分析曲线拟合的最小二乘法实验报告

数值分析曲线拟合的最小二乘法实验报告数值分析曲线拟合的最小二乘法实验报告篇一:数值分析设计曲线拟合的最小二乘法曲线拟合的最小二乘法一、目的和意义在科学实验的统计方法研究中,往往要从一组实验数据?xi,yi??i?0,1,2,?,m?中,寻找自变量x与因变量y之间的函数关系y?F?x?。
由于观测数据往往不准确,因此不要求y?F?x?经过所有点?xi,yi?,而只要求在给定点xi上误差而只要求所在所有给定点xi上的误差?i?F(xi)?yi ?i?0,1,2,?,m?按某种标准最小。
若记????0,?1,?2,?,?m?,就是要求向量?的范数如果用最大范数,计算上困难较大,通常采用欧式范数?最小。
2T 作为误差度量的标准。
F?x?的函数类型往往与实验的物理背景以及数据的实际分布有关,它一般含有某些待定参数。
如果F?x?是所有待定参数的线性函数,那么相应的问题称为线性最小二乘问题,否则称为非线性最小二乘问题。
最小二乘法还是实验数据参数估计的重要工具。
这是因为这种方法比其他方法更容易理解,即使在其他方法失效的情况下,用最小二乘法还能提供解答,而且从统计学的观点分析,用该方法求得各项估计具有最优统计特征,因此这一方法也是系统识别的重要基础。
线性最小二乘问题可以借助多元微分学知识通过求解法方程组得到解答。
用最小二乘法求拟合曲线时,首先要确定S?x?的形式。
这不单纯是数学问题,还与所研究问题的运动规律以及所得观测数据?xi,yi?有关;通常要从问题的运动规律以及给定数据描图,确定S?x?的形式,并通过实际计算选出较好的结果。
为了使问题的提法更有一般性,通常把最小二乘法中的? 22 都考虑为加权平方和22 ? ????xi???S?xi??f?xi??? i?0 m 2 这里??xi??0是?a,b?上的加权函数,它表示不同点?xi,f?xi?处的数据比重不同。
?二、计算方法在某冶炼过程中,根据统计数据的含碳量与时间关系,试求含碳量y与时间t的拟合曲线。
复摆实验报告

【实验题目】复摆实验【实验记录】1. 复摆中心g的位置:0刻度处3. 计算重力加速度g:4?2t12?t22t12?t22??g2(h1?h2)2(h1?h2)g=9.905kg/m2 14. 作t-h图5. 利用mgt2h?4?2ig?4?2mh2,作t2h~h2关系图,考察其线形关系,由最小二乘法计算g和复摆对重心的转动惯量ig。
ig=0.002536kg*m*m 【结论与讨论】误差分析:1 在实验中,复摆的摆动不能很好的控制在同一平面摆动。
2 实验前没有很好的调节复摆对称。
3 复摆摆动可能幅度过大。
结论:利用复摆可以测量重力加速度,同时还可以由这个方法衍生开来测量不规则物体的转动惯量。
成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇二:实验报告_复摆实验【实验题目】复摆实验【实验记录】1. 复摆中心g的位置:3. 计算重力加速度g:4?2t12?t22t12?t22??= g2(h1?h2)2(h1?h2)g= 14. 作t-h图5. 利用mgth?4?ig?4?mh,作th~h关系图,考察其线形关系,由最小二乘法计222222算g和复摆对重心的转动惯量ig。
【结论与讨论】成绩(满分30分):????????? 指导教师签名:??????????????????? 日期:???????????????????2篇三:复摆振动研究.实验报告复摆振动的研究姓名:黄青中学号:200902050238 摘要:了解用复摆物理模型来测量物体的转动惯量。
通过观测复摆的振动,测定复摆振动的一些参量(重力加速度g,回转半径r,转动惯量ig)。
分析复摆的振动,研究振动周期与质心到支点距离的关系。
复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。
通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。
大学物理实验 常用的数据处理方法
1.7 常用的数据处理方法实验数据及其处理方法是分析和讨论实验结果的依据。
在物理实验中常用的数据处理方法有列表法、作图法、逐差法和最小二乘法(直线拟合)等。
1.7.1 列表法在记录和处理数据时,常常将所得数据列成表。
数据列表后,可以简单明确、形式紧凑地表示出有关物理量之间的对应关系;便于随时检查结果是否合理,及时发现问题,减少和避免错误;有助于找出有关物理量之间规律性的联系,进而求出经验公式等。
列表的要求是:(1)要写出所列表的名称,列表要简单明了,便于看出有关量之间的关系,便于处理数据。
(2)列表要标明符号所代表物理量的意义(特别是自定的符号),并写明单位。
单位及量值的数量级写在该符号的标题栏中,不要重复记在各个数值上。
(3)列表的形式不限,根据具体情况,决定列出哪些项目。
有些个别的或与其他项目联系不大的数据可以不列入表内。
列入表中的除原始数据外,计算过程中的一些中间结果和最后结果也可以列入表中。
(4)表中所列数据要正确反映测量结果的有效数字。
列表举例如表1-2所示。
表1-2铜丝电阻与温度关系1.7.2 作图法作图法是将两列数据之间的关系用图线表示出来。
用作图法处理实验数据是数据处理的常用方法之一,它能直观地显示物理量之间的对应关系,揭示物理量之间的联系。
1.作图规则为了使图线能够清楚地反映出物理现象的变化规律,并能比较准确地确定有关物理量的量值或求出有关常数,在作图时必须遵守以下规则。
(1)作图必须用坐标纸。
当决定了作图的参量以后,根据情况选用直角坐标纸、极坐标纸或其他坐标纸。
(2)坐标纸的大小及坐标轴的比例,要根据测得值的有效数字和结果的需要来定。
原则上讲,数据中的可靠数字在图中应为可靠的。
我们常以坐标纸中小格对应可靠数字最后一位的一个单位,有时对应比例也适当放大些,但对应比例的选择要有利于标实验点和读数。
最小坐标值不必都从零开始,以便做出的图线大体上能充满全图,使布局美观、合理。
(3)标明坐标轴。
实验十三复摆实验实验实验报告

M (h − h′) = mh
化简得
h′ M − m = = 98.8% h m
由于小刀口质量对重心位置改变的影响小于 2%,其对实验结果的测量产生的 影响很小,在精度不高的实验中可以忽略不计。
20T(s) 25.1014 24.9162 24.6173 24.5552 24.3776 24.2379 24.0708 23.9831 23.8758 23.7983 23.7448 23.7388 23.7625 23.8433 23.9861 24.1568 24.3954 24.8841 25.4196 26.0742 26.9978 28.1755 29.8452 31.8723 34.9437 39.5663
h2/cm2
201.07 174.24 148.35 125.44 103.63 84.64 66.91
T2h/cm·s2
20.36 19.30 18.26 17.29 16.40 15.68 14.77
h2/cm2
51.84 38.19 27.04 17.47 10.24
T2h/cm·s2
14.57 13.72 13.26 12.88 12.40
注:记 0 点左侧为负,右侧为正。 复摆质量 M = 412.80g;小刀口质量 m = 5.15g 1、对数据进行最小二乘法处理有:
表 13-2 悬点在 0 点右侧时 h2 与 T2h 数据表
h2/cm2
793.55 739.84 685.39 635.04 584.67 538.24 491.95
̇̇ 则 由于 β = θ ̇̇ + mgh sin θ = 0 Iθ
在摆角很小 ≤ 5� 时, sin θ ≈ θ , (13.3)式化为 (13.3)
