ArcGis中三参数和七参数转换
三参数与七参数的区别

参数问题一直是测量方面最大的问题,我简单的解释一下,首先说七参,就是两个空间坐标系之间的旋转,平移和缩放,这三步就会产生必须的七个参数,平移有三个变量Dx,Dy,DZ;旋转有三个变量,再加上一个尺度缩放,这样就可以把一个空间坐标系转变成需要的目标坐标系了,这就是七参的作用。
如果说你要转换的坐标系XYZ三个方向上是重合的,那么我们仅通过平移就可以实现目标,平移只需要三个参数,并且现在的坐标比例大多数都是一致的,缩放比默认为一,这样就产生了三参数,三参就是七参的特例,旋转为零,尺度缩放为一。
四参是应用在两个平面之间转换的,还没有形成统一的标准,说的有点乱,如果还是不明白可以给我留言。
希望有帮助。
1.2四参数操作:设置→求转换参数(控制点坐标库)四参数是同一个椭球内不同坐标系之间进行转换的参数。
在工程之星软件中的四参数指的是在投影设置下选定的椭球内GPS坐标系和施工测量坐标系之间的转换参数。
工程之星提供的四参数的计算方式有两种,一种是利用“工具/参数计算/计算四参数”来计算,另一种是用“控制点坐标库”计算。
需要特别注意的是参予计算的控制点原则上至少要用两个或两个以上的点,控制点等级的高低和分布直接决定了四参数的控制范围。
经验上四参数理想的控制范围一般都在5-7公里以内。
四参数的四个基本项分别是:X平移、Y平移、旋转角和比例。
从参数来看,这里没有高程改正,所以建议采用“控制点坐标库”来求取参数,而根据已知点个数的不同所求取的参数也会不同,具体有以下几种。
1.2.1四参数+校正参数:所需已知点个数:2个1.2.2四参数+高程拟合GPS的高程系统为大地高(椭球高),而测量中常用的高程为正常高。
所以GPS测得的高程需要改正才能使用,高程拟合参数就是完成这种拟和的参数。
计算高程拟和参数时,参予计算的公共控制点数目不同时计算拟和所采用的模型也不一样,达到的效果自然也不一样。
高程拟后有三种拟合方式:a.高程加权平均:所需已知点个数:3个b.高程平面拟合:所需已知点个数:4 ~ 6个c.高程曲面拟合:所需已知点个数:7个以上二、七参数操作:工具→参数计算→计算七参数所需已知点个数:3个或3个以上七参数的应用范围较大(一般大于50平方公里),计算时用户需要知道三个已知点的地方坐标和WGS-84坐标,即WGS-84坐标转换到地方坐标的七个转换参数。
aricgis投影转换的要领
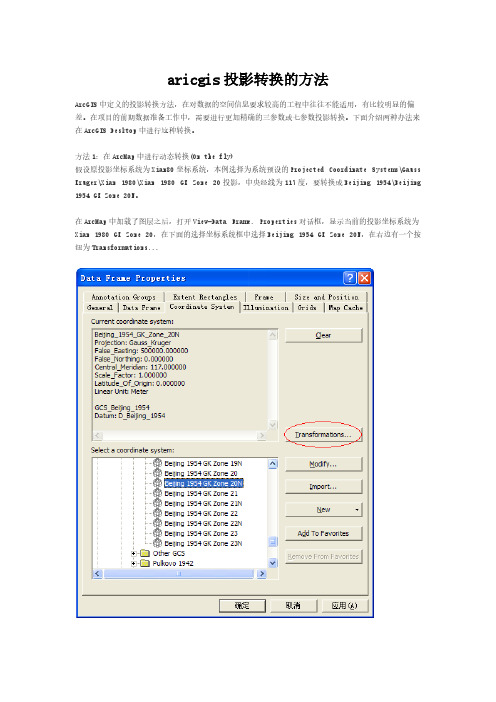
aricgis投影转换的方法ArcGIS中定义的投影转换方法,在对数据的空间信息要求较高的工程中往往不能适用,有比较明显的偏差。
在项目的前期数据准备工作中,需要进行更加精确的三参数或七参数投影转换。
下面介绍两种办法来在ArcGIS Desktop中进行这种转换。
方法1:在ArcMap中进行动态转换(On the fly)假设原投影坐标系统为Xian80坐标系统,本例选择为系统预设的Projected Coordinate Systems\Gauss Kruger\Xian 1980\Xian 1980 GK Zone 20投影,中央经线为117度,要转换成Beijing 1954\Beijing 1954 GK Zone 20N。
在ArcMap中加载了图层之后,打开View-Data Frame. Properties对话框,显示当前的投影坐标系统为Xian 1980 GK Zone 20,在下面的选择坐标系统框中选择Beijing 1954 GK Zone 20N,在右边有一个按钮为Transformations...点击打开一个投影转换对话框,可以在对话框中看到Convert from和Into表明了我们想从什么坐标系统转换到什么坐标系统。
在下方的using下拉框右边,点击New...,新建一个投影转换公式,在Method下拉框中可以选择一系列转换方法,其中有一些是三参数的,有一些是七参数的,然后在参数表中输入各个转换参数。
输入完毕以后,点击OK,回到之前的投影转换对话框,再点击OK,就完成了对当前地图的动态投影转换。
这时还没有对图层文件本身的投影进行转换,要转换图层文件本身的投影,再使用数据导出,导出时选择投影为当前地图的投影即可。
方法2:对于有大量图层需要进行投影转换时,这种手工操作的办法显得比较繁琐,每次都需要设置参数。
可以只定义一次投影转换公式,而在此后的转换中引用此投影转换公式即可。
常用的七参数转换法和四参数转换法以及涉及到的基本测量学知识

常⽤的七参数转换法和四参数转换法以及涉及到的基本测量学知识原⽂:1.背景在了解这两种转换⽅法时,我们有必要先了解⼀些与此相关的基本知识。
我们有三种常⽤的⽅式来表⽰空间坐标,分别是:经纬度和⾼层、平⾯坐标和⾼层以及空间直⾓坐标。
2.经纬度坐标系(⼤地坐标系)这⾥我⾸先要强调:天⽂坐标表⽰的经纬度和⼤地坐标系表⽰的经纬度是不同的。
所以,同⼀个经纬度数值,在BJ54和WGS84下表⽰的是不同的位置,⽽以下我说的经纬度均指⼤地坐标系下的经纬度。
⼤地坐标系是⼤地测量中以参考椭球⾯为基准⾯建⽴起来的坐标系。
下⾯我跟⼤家⼤致谈谈其中涉及到的两个重要概念。
2.1⼤地⽔准⾯和⼤地球体地球表⾯本⾝是⼀个起伏不平、⼗分不规则的表⾯,这些⾼低不平的表⾯⽆法⽤数学公式表达,也⽆法进⾏运算,所以在量测和制图时,我们必须找⼀个规则的曲⾯来代替地球的⾃然表⾯。
当海洋静⽌时,它的⾃由⽔⾯必定与该⾯上各点的重⼒⽅向(铅垂直⽅向)成正交,我们把这个⾯叫做⽔准⾯。
但是,地球上的⽔准⾯有⽆数个,我们把其中与静⽌的平均海⽔⾯相重合的⽔准⾯设想成⼀个可以将地球进⾏包裹的闭合曲⾯,这个⽔准⾯就是⼤地⽔准⾯。
⽽被⼤地⽔准⾯包裹所形成的球体即为⼤地球体。
2.2地球椭球体由于地球体内部质量分布的不均匀,引起重⼒⽅向的变化,这个处处与重⼒⽅向成正交的⼤地⽔准⾯边成为了⼀个⼗分不规则的也不能⽤数学来表⽰的曲⾯。
不过虽然⼤地⽔准⾯的形状⼗分的不规则,但它已经是⼀个很接近于绕⾃转轴(短轴)旋转的椭球体了。
所以在测量和制图中就⽤旋转椭球来代替⼤地球体,这个旋转球体通常称地球椭球体,简称椭球体。
2.3常⽤⼤地坐标系不同坐标系,其椭球体的长半径,短半径和扁率是不同的。
⽐如我们常⽤的四种坐标系所对应的椭球体,它们的椭球体参数就各不相同:BJ54坐标系:属参⼼坐标系,长轴6378245m,短轴6356863,扁率1/298.3。
XIAN80坐标系:属参⼼坐标系,长轴6378140m,短轴6356755,扁率1/298.25722101。
ARCGIS中坐标转换及地理坐标、投影坐标定义

ARCGIS中坐标转换及地理坐标、投影坐标定义1、动态投影(ArcMap)所谓动态投影指,ArcMap中的Data 的空间参考或是说坐标系统是默认为第一加载到当前工作区的那个文件的坐标系统,后加入的数据,如果和当前工作区坐标系统不相同,则ArcMap会自动做投影变换,把后加入的数据投影变换到当前坐标系统下显示!但此时数据文件所存储的数据并没有改变,只是显示形态上的变化!因此叫动态投影!表现这一点最明显的例子就是,在Export Data 时,会让你选择是按this layer's source data(数据源的坐标系统导出),还是按照the Data (当前数据框架的坐标系统)导出数据!2、坐标系统描述(ArcCatalog)大家都知道在ArcCatalog中可以一个数据的坐标系统说明!即在数据上鼠标右键->Properties->XY Coordinate System选项卡,这里可以通过modify,Select、Import方式来为数据选择坐标系统!但有许多人认为在这里改完了,数据本身就发生改变了!但不是这样的!这里缩写的信息都对应到该数据的.aux 文件!如果你去把该文件删除了,重新查看该文件属性时,照样会显示Unknown!这里改的仅仅是对数据的一个描述而已,就好比你入学时填写的基本资料登记卡,我改了说明但并没有改变你这个人本身!因此数据文件中所存储的数据的坐标值并没有真正的投影变换到你想要更改到的坐标系统下!但数据的这个描述也是非常重要的,如果你拿到一个数据,从ArcMap下所显示的坐标来看,像是投影坐标系统下的平面坐标,但不知道是基于什么投影的!因此你就无法在做对数据的进一不处理!比如:投影变换操作!因为你不知道要从哪个投影开始变换!因此大家要更正一下对 ArcCatalog中数据属性中关于坐标系统描述的认识!3、投影变换(ArcToolBox)上面说了这么多,要真正的改变数据怎么办,也就是做投影变换!在ArcToolBox->Data Management Tools->Projections and Transformations下做!在这个工具集下有这么几个工具最常用:1、Define Projection2、Feature->Project3、Raster->Project Raster4、Create Custom Geographic Transformation当数据没有任何空间参考时,显示为Unknown!时就要先利用Define Projection来给数据定义一个Coordinate System,然后在利用Feature->Project或Raster->Project Raster工具来对数据进行投影变换!由于我国经常使用的投影坐标系统为北京54,西安80!由这两个坐标系统变换到其他坐标系统下时,通常需要提供一个Geographic Transformation,因为Datum 已经改变了!这里就用到我们说常说的转换3参数、转换7参数了!而我们国家的转换参数是保密的!因此可以自己计算或在购买数据时向国家测绘部门索要!知道转换参数后,可以利用Create Custom Geographic Transformation工具定义一个地理变换方法,变换方法可以根据3参数或7参数选择基于GEOCENTRIC_TRANSLATION和 COORDINATE_方法!这样就完成了数据的投影变换!数据本身坐标发生了变化!当然这种投影变换工作也可以在ArcMap中通过改变Data 的Coordinate System来实现,只是要在做完之后在按照Data 的坐标系统导出数据即可!方法一:在Arcmap中转换:1、加载要转换的数据,右下角为经纬度2、点击视图——数据框属性——坐标系统3、导入或选择正确的坐标系,确定。
使用ArcGIS实现WGS84经纬度坐标到北京54高斯投影坐标的转换

使用ArcGIS实现WGS84经纬度坐标到北京54高斯投影坐标的转换【摘要】本文针对从事测绘工作者普遍遇到的坐标转换问题,简要介绍ArcGIS实现WGS84经纬度坐标到北京54高斯投影坐标转换原理和步骤。
【关键词】ArcGIS 坐标转换投影变换1坐标转换简介坐标系统之间的坐标转换既包括不同的参心坐标之间的转换,或者不同的地心坐标系之间的转换,也包括参心坐标系与地心坐标系之间的转换以及相同坐标系的直角坐标与大地坐标之间的坐标转换,还有大地坐标与高斯平面坐标之间的转换。
在两个空间角直坐标系中,假设其分别为O--XYZ和O--XYZ,如果两个坐标系的原点相同,通过三次旋转,就可以使两个坐标系重合;如果两个直角坐标系的原点不在同一个位置,通过坐标轴的平移和旋转可以取得一致;如果两个坐标系的尺度也不尽一致,就需要再增加一个尺度变化参数;而对于大地坐标和高斯投影平面坐标之间的转换,则需要通过高斯投影正算和高斯投影反算,通过使用中央子午线的经度和不同的参考椭球以及不同的投影面的选择来实现坐标的转换。
如何使用ArcGIS实现WGS84经纬度坐标到BJ54高斯投影坐标的转换?这是很多从事GIS工作或者测绘工作者普遍遇到的问题。
本文目的在于帮助用户解决这个问题。
我们通常说的WGS-84坐标是指经纬度这种坐标表示方法,北京54坐标通常是指经过高斯投影的平面直角坐标这种坐标表示方法。
为什么要进行坐标转换?我们先来看两组参数,如表1所示:表1 BJ54与WGS84基准参数很显然,WGS84与BJ54是两种不同的大地基准面,不同的参考椭球体,因而两种地图下,同一个点的坐标是不同的,无论是三度带六度带坐标还是经纬度坐标都是不同的。
当要把GPS接收到的点(WGS84坐标系统的)叠加到BJ54坐标系统的底图上,那就会发现这些GPS点不能准确的在它该在的地方,即“与实际地点发生了偏移”。
这就要求把这些GPS点从WGS84的坐标系统转换成BJ54的坐标系统了。
七参数转换求解范文

七参数转换求解范文七参数转换是一种用于将一个坐标系转换为另一个坐标系的数学方法。
该方法通常用于大地测量学和地理信息系统中,以实现不同坐标系统之间的转换。
七参数包括三个平移参数(ΔX、ΔY、ΔZ)、三个旋转参数(ω、φ、κ)以及一个尺度参数(s)。
最小二乘法是一种数学优化方法,用于拟合一个数学模型与实际观测数据之间的差异。
在七参数转换中,最小二乘法可用于确定平移参数、旋转参数和尺度参数的最佳数值。
最小二乘法的基本原理是将观测数据的残差的平方和最小化。
残差是指每个观测点的预测值与实际值之间的差异。
通过最小化残差的平方和,可以得到使模型最优的参数。
求解七参数转换的步骤如下:1.收集已知坐标点的变换关系数据,并确定参考坐标系和目标坐标系之间的转换关系。
2.利用最小二乘法,建立七参数转换模型。
模型可以表示为:X'=s(RΔX)+XY'=s(RΔY)+YZ'=s(RΔZ)+Z其中,(X,Y,Z)为目标坐标系中的点的坐标,(X',Y',Z')为参考坐标系中的点的坐标,R为旋转矩阵,s为尺度参数,ΔX、ΔY、ΔZ为平移参数。
3.利用已知坐标点的变换关系数据,求解七个参数的最佳数值。
最小二乘法求解参数的数值可以通过矩阵运算得到。
4.将求得的七个参数代入七参数转换模型中,即可将目标坐标系中的点的坐标转换为参考坐标系中的点的坐标。
在实际应用中,由于测量误差和观测数据的不确定性,七参数转换的求解可能存在一定的误差。
因此,在进行七参数转换时,需要对测量数据进行精确控制,并对求解结果进行误差分析。
此外,也可以采用多个已知坐标点的变换关系数据进行求解,以提高转换的准确性。
总之,七参数转换是一种常用的坐标转换方法,可以实现不同坐标系统之间的转换。
通过最小二乘法,可以求解七个参数的最佳数值,从而实现坐标转换。
在实际应用中,需要对测量数据进行精确控制,并对求解结果进行误差分析,以保证转换的准确性。
利用七参数进行坐标转换公式

利用七参数进行坐标转换公式
坐标转换是指将一种坐标系中的坐标转换为另一种坐标系中的
坐标。
在测量、地图制图和地理信息系统等领域中,常常需要进行坐标转换。
常用的坐标转换方法有七参数法、四参数法和三参数法等。
七参数法是较为精确的坐标转换方法,适用于大范围、大量数据的坐标转换。
七参数法基于地球的旋转和形状变化,通过旋转角、旋转轴、比例因子和三个方向的平移量来描述坐标系之间的差异。
假设已知两种坐标系的某一点的坐标(X,Y,Z),且已知它们之间的七参数,可以通过以下公式进行坐标转换:
X1 = s*(X - Z*y + Y*z) + Tx
Y1 = s*(Y + Z*x - X*z) + Ty
Z1 = s*(Z - Y*x + X*y) + Tz
其中,s为比例因子,Tx、Ty、Tz分别为三个方向的平移量,x、y、z为旋转轴的方向余弦值。
需要注意的是,七参数法所描述的坐标系之间的差异是三维的,因此在进行坐标转换时,需要考虑高程的变化。
如果只需要进行水平坐标的转换,可以采用四参数法或三参数法。
总之,选择合适的坐标转换方法和参数,可以提高坐标转换的精度和效率,为地理空间信息的采集、存储和处理提供基础支撑。
- 1 -。
七参数转换法推导公式

七参数转换法推导公式七参数转换法是一种地理坐标系转换的方法,用于将一个坐标系中的坐标转换到另一个坐标系中。
它通过七个参数来描述两个坐标系之间的差异,从而实现坐标的转换。
下面将对七参数转换法的原理进行推导,并给出相应的公式。
我们假设有两个坐标系,分别为坐标系A和坐标系B。
其中,坐标系A的原点为(Xa, Ya, Za),坐标系B的原点为(Xb, Yb, Zb)。
我们需要将坐标系A中的点(Pa, Qa, Ra)转换到坐标系B中,得到坐标(Pb, Qb, Rb)。
根据七参数转换法的原理,我们知道坐标系A和坐标系B之间的差异主要包括平移、旋转和尺度变换。
下面对这三个差异分别进行推导。
1. 平移差异假设坐标系A和坐标系B之间的平移差异为(dx, dy, dz),则坐标系A中的点(Pa, Qa, Ra)经过平移变换后得到坐标系B中的点(Pb', Qb', Rb'),其中:Pb' = Pa + dxQb' = Qa + dyRb' = Ra + dz2. 旋转差异假设坐标系A和坐标系B之间的旋转差异为(ωx, ωy, ωz),其中ωx表示绕x轴旋转的角度,ωy表示绕y轴旋转的角度,ωz表示绕z轴旋转的角度。
我们可以通过旋转矩阵来描述旋转变换。
假设旋转矩阵为R,则坐标系A中的点(Pa, Qa, Ra)经过旋转变换后得到坐标系B中的点(Pb'', Qb'', Rb''),其中:Pb'' = R11 * Pa + R12 * Qa + R13 * RaQb'' = R21 * Pa + R22 * Qa + R23 * RaRb'' = R31 * Pa + R32 * Qa + R33 * Ra3. 尺度变换差异假设坐标系A和坐标系B之间的尺度变换差异为(m, n, p),其中m 表示x轴的尺度变换比例,n表示y轴的尺度变换比例,p表示z轴的尺度变换比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在ArcGIS Desktop中进行三参数或七参数精确投影转换ArcGIS中定义的投影转换方法,在对数据的空间信息要求较高的工程中往往不能适用,有比较明显的偏差。
在项目的前期数据准备工作中,需要进行更加精确的三参数或七参数投影转换。
下面介绍两种办法来在ArcGIS Desktop中进行这种转换。
方法1:在ArcMap 中进行动态转换(On the fly) 假设原投影坐标系统为Xian80坐标系统,本例选择为系统预设的Projected Coordinate Systems\Gauss Kruger\Xian 1980\Xian 1980 GK Zone 20投影,中央经线为117度,要转换成Beijing 1954\Beijing 1954 GK Zone 20N。
在ArcMap中加载了图层之后,打开View-Data Frame Properties对话框,显示当前的投影坐标系统为Xian 1980 GK Zone 20,在下面的选择坐标系统框中选择Beijing 1954 GK Zone 20N,在右边有一个按钮为Transformations...
点击打开一个投影转换对话框,可以在对话框中看到Convert from和Into表明了我们想从什么坐标系统转换到什么坐标系统。
在下方的using下拉框右边,点击New...,新建一个投影转换公式,在Method下拉框中可以选择一系列转换方法,其中有一些是三参数的,有一些是七参数的,然后在参数表中输入各个转换参数。
输入完毕以后,点击OK,回到之前的投影转换对话框,再点击OK,就完成了对当前地图的动态投影转换。
这时还没有对图层文件本身的投影进行转换,要转换图层文件本身的投影,再使用数据导出,导出时选择投影为当前地图的投影即可。
方法2:对于有大量图层需要进行投影转换时,这种手工操作的办法显得比较繁琐,每次都需要设置参数。
可以只定义一次投影转换公式,而在此后的转换中引用此投影转换公式即可。
这种方法需要在ArcTools中进行操作。
在Data Management Tools\Projections and Tranformations\下,有Create Custom Geographic Transformation 命令。
打开这个命令,选择输入和输出的投影,可以是系统自带的也可以是自己设置的,选择转换方法,与方法1种介绍的类似,可选择三参数或者七参数,然后输入各个参数指。
通过为这个投影转换公式指定一个名称,可以在以后的操作中直接引用此公式而不用重复输入各个参数了。
点击OK生成这个投影转换公式。
在方法一里面,我们是动态的改变了地图的投影,然后通过数据导出的办法将要转换投影的图层重新生成的。
在这里,我们可以直接使用Data Management Tools\Projections and Tranformations\下的Project命令,生成转换后的图层文件,Project命令分别位于Feature和Raster目录下,分别针对于矢量和栅格数据。
在这个命
令中,在指定了输入的图层后,Input Coordinate System自动的识别出了输入的投影,需要用户指定输出的投影,如果两者与之前定义投影转换公式的输入和输入投影的话,在下面的Geographic Transformation下拉框中会出现之前定义的公式名称,直接选择即
可使用。
点击OK以后就可以直接生成这个图层文件而不需要进一步的操作了。
