大学数学竞赛课件页PPT文档
合集下载
数学趣味竞赛ppt课件

28
17 如果有一个人要坐船带一条狼,一只羊和一捆白菜过河.但是每次只能带一样东西过去.如 果人不在,狼就会吃羊,狼不在, 羊就会吃菜.请问你该如何安排这个人过河?
29
18计算: 1、9+99+999+9999 2、103+104+105+106+107+108+109
30
19、一本书的页号为1至n。把这本书的各页号累加的时候,有一个页号被错误的多加了一 次,结果,所得的错误的和数为2005。那么被多加一次的页一定是52。为什么?
20
9、6棵树栽3行每行栽3棵,如何栽??
21
10、汉字中为什么会有大写数字?() A. 大写数字是古代固有的 B. 防止贪官涂改账册 C. 正式严谨场合需用大写
22
11世界无烟日是每年的几月几日? () A.4月7日
B.5月31日 C.6月26日 D.7月26日
23
12.具有“眼睛维生素”称号的是( ) A、维生素A
68
第一轮比赛结束后要淘汰 4支队伍哦~~~
抢
风
答
险
题
题
第
二观 轮众
抢
答
题
2
第一轮 : 抢答题 抢答规则: 1、 等主持人读完题说“开始”后才开始抢答,否则视做自动放弃本轮题.如遇此情况,
在主持人再次说开始后再抢答。 2、 抢答方法:举手。由竞赛现场工作人员统一结果后,宣布抢到回答权的小组。答对一
题加10分,答错扣10分。 3、 作答的参赛者限时10秒内作答,否则按作答错误处理。
55
D组: 3. 老王一天要刮四五十次脸,脸上却仍有胡子。这是什么原因?(脑筋急转弯) 4.2010年上海世博会的主题是什么? 返回选题
17 如果有一个人要坐船带一条狼,一只羊和一捆白菜过河.但是每次只能带一样东西过去.如 果人不在,狼就会吃羊,狼不在, 羊就会吃菜.请问你该如何安排这个人过河?
29
18计算: 1、9+99+999+9999 2、103+104+105+106+107+108+109
30
19、一本书的页号为1至n。把这本书的各页号累加的时候,有一个页号被错误的多加了一 次,结果,所得的错误的和数为2005。那么被多加一次的页一定是52。为什么?
20
9、6棵树栽3行每行栽3棵,如何栽??
21
10、汉字中为什么会有大写数字?() A. 大写数字是古代固有的 B. 防止贪官涂改账册 C. 正式严谨场合需用大写
22
11世界无烟日是每年的几月几日? () A.4月7日
B.5月31日 C.6月26日 D.7月26日
23
12.具有“眼睛维生素”称号的是( ) A、维生素A
68
第一轮比赛结束后要淘汰 4支队伍哦~~~
抢
风
答
险
题
题
第
二观 轮众
抢
答
题
2
第一轮 : 抢答题 抢答规则: 1、 等主持人读完题说“开始”后才开始抢答,否则视做自动放弃本轮题.如遇此情况,
在主持人再次说开始后再抢答。 2、 抢答方法:举手。由竞赛现场工作人员统一结果后,宣布抢到回答权的小组。答对一
题加10分,答错扣10分。 3、 作答的参赛者限时10秒内作答,否则按作答错误处理。
55
D组: 3. 老王一天要刮四五十次脸,脸上却仍有胡子。这是什么原因?(脑筋急转弯) 4.2010年上海世博会的主题是什么? 返回选题
大学数学竞赛课件.ppt

100!
湘潭大学数学与计算科学学院 王文强 上一页 下一页
2
二、分段函数在分段点处的可导性
例1 设 f ( x) x x( x 2) ,求 f ( x).
解 先去掉绝对值
x2 ( x 2), x 0
f ( x) x2 ( x 2),0 x 2,
x
2
(
x
2),
x
2
当x 0时, f(0) f(0) 0, f (0) 0;
lim
x2
f ( x) f (2) x2
x2 ( x 2)
lim
4.
x2 x 2
f(2) f(2), f ( x)在x 2处不可导.
3x2 4x, x 2,或x 0 f ( x) 0, x 0,
3 x2 4 x,0 x 2,
湘潭大学数学与计算科学学院 王文强 上一页 下一页
e (arctan x ) 2 1 x2
x0 1.
故所求切线方程为 y x.
2
lim nf ( ) lim 2
n
n n
ቤተ መጻሕፍቲ ባይዱ
f (2) n 2
f (0)
2 f (0) 2
n 湘潭大学数学与计算科学学院 王文强 上一页 下一页
11
例 2 已知曲线的极坐标方程r 1 cos ,求曲线上 对应于 处的切线与法线的直角坐标方程。
x
sin x
湘潭大学数学与计算科学学院 王文强 上一页 下一页
10
四、求切线方程和法线方程
例 1 已知两曲线 y f ( x)与 y arctan x et2dt 在点(0,0) 0
处的切线相同,写出此切线方程,并求lim nf ( 2 ).
n
湘潭大学数学与计算科学学院 王文强 上一页 下一页
2
二、分段函数在分段点处的可导性
例1 设 f ( x) x x( x 2) ,求 f ( x).
解 先去掉绝对值
x2 ( x 2), x 0
f ( x) x2 ( x 2),0 x 2,
x
2
(
x
2),
x
2
当x 0时, f(0) f(0) 0, f (0) 0;
lim
x2
f ( x) f (2) x2
x2 ( x 2)
lim
4.
x2 x 2
f(2) f(2), f ( x)在x 2处不可导.
3x2 4x, x 2,或x 0 f ( x) 0, x 0,
3 x2 4 x,0 x 2,
湘潭大学数学与计算科学学院 王文强 上一页 下一页
e (arctan x ) 2 1 x2
x0 1.
故所求切线方程为 y x.
2
lim nf ( ) lim 2
n
n n
ቤተ መጻሕፍቲ ባይዱ
f (2) n 2
f (0)
2 f (0) 2
n 湘潭大学数学与计算科学学院 王文强 上一页 下一页
11
例 2 已知曲线的极坐标方程r 1 cos ,求曲线上 对应于 处的切线与法线的直角坐标方程。
x
sin x
湘潭大学数学与计算科学学院 王文强 上一页 下一页
10
四、求切线方程和法线方程
例 1 已知两曲线 y f ( x)与 y arctan x et2dt 在点(0,0) 0
处的切线相同,写出此切线方程,并求lim nf ( 2 ).
n
全国大学生数学竞赛辅导ppt

2 0 2
2.设y y ( x)由方程xe f ( y ) e y ln 29确定, 其中f具有二阶导数且f 1,
d y ___ . 2 dx
2
3.设s 0, 求I n e x dx, (n 1,2,).
sx n 0
Page 10
4.求最小实数c, 使得满足 | f ( x) | dx 1的连续的
Page 11
f ( x) 6. f ( x)连续,g ( x) f ( xt )dx且 lim A, A 0 x 0 x 为常数,求g ( x)并讨论g ( x)在x 0处的连续性.
1
1 7.求方程x sin 2 x 501的近似解, (精确 x 到0.001).
x x
存在一点 x0使得f ( x0 ) 0. 证明:f ( x) 0在(,)恰有两实根。
11.设f ( x)在x 1点附近有定义,且在x 1 点可导,并已知f (1) 0, f (1) 2, f (sin 2 x cos x) 求 lim . 2 x 0 x x tan x
Page 15
14.设f ( x)在 x 0的某邻域内有二阶连续导数 且f (0), f (0), f (0)均不为零, 证明:存在唯一一组实数 k1 , k2 , k3 , k1 f (h) k2 f (2h) k3 f (3h) f (0) 使得 lim 0. 2 h 0 h
0
1
函数f ( x)都有 f ( x )dx c.
0
1
x 2t t 2 5.设函数y f ( x)由参数方程 (t 1)所 y (t ) d2y 3 确定,且 2 , 其中 (t )具有二阶导数, dx 4(1 t ) t2 3 u 2 曲线y (t )与y e du 在t 1处相切,求 1 2e 函数 (t ).
2.设y y ( x)由方程xe f ( y ) e y ln 29确定, 其中f具有二阶导数且f 1,
d y ___ . 2 dx
2
3.设s 0, 求I n e x dx, (n 1,2,).
sx n 0
Page 10
4.求最小实数c, 使得满足 | f ( x) | dx 1的连续的
Page 11
f ( x) 6. f ( x)连续,g ( x) f ( xt )dx且 lim A, A 0 x 0 x 为常数,求g ( x)并讨论g ( x)在x 0处的连续性.
1
1 7.求方程x sin 2 x 501的近似解, (精确 x 到0.001).
x x
存在一点 x0使得f ( x0 ) 0. 证明:f ( x) 0在(,)恰有两实根。
11.设f ( x)在x 1点附近有定义,且在x 1 点可导,并已知f (1) 0, f (1) 2, f (sin 2 x cos x) 求 lim . 2 x 0 x x tan x
Page 15
14.设f ( x)在 x 0的某邻域内有二阶连续导数 且f (0), f (0), f (0)均不为零, 证明:存在唯一一组实数 k1 , k2 , k3 , k1 f (h) k2 f (2h) k3 f (3h) f (0) 使得 lim 0. 2 h 0 h
0
1
函数f ( x)都有 f ( x )dx c.
0
1
x 2t t 2 5.设函数y f ( x)由参数方程 (t 1)所 y (t ) d2y 3 确定,且 2 , 其中 (t )具有二阶导数, dx 4(1 t ) t2 3 u 2 曲线y (t )与y e du 在t 1处相切,求 1 2e 函数 (t ).
大学数学导数名师公开课获奖课件百校联赛一等奖课件

x) x
u( x0 )
v( x0
x)
lim
x
0
u(
x0
)
v( x0
x) x
v( x0 )
u( x0 ) v( x0 ) u( x0 ) v( x0 ) .
注意: (uv)× uv ,千万不要把导数乘积公式 (2)
记错了.
前页 后页 返回
例1 求 f ( x) a0 xn a1xn1 an1x an 的导数.
前页 后页 返回
解 (i) y arcsin x, x (1, 1 ) 是 x sin y 在 (π 2,π 2 ) 上旳反函数,故 (arcsin x) 1 1 1 , x (1, 1).
(sin y) cos y 1 x2 同理, (arccos x) 1 , x (1, 1) .
y x ln .
前页 后页 返回
定理5.7 若函数 u( x),v( x) 在点 x0 可导, v( x0 ) 0 ,
则
f ( x) u( x) v( x)
在点 x0 也可导,且
u( x)
v(
x)
x x0
u(
x0
)v(
x0 v
)
2
u( ( x0 )
x0
)v(
x0
)
.
(4)
前页 后页 返回
d y d y du , dx du d x
若将
其中 y f (u),u ( x) , 这么就轻易了解 “链”
旳
前页 后页 返回
意义了.
在链式法则中一定要区别 f ( ( x)) f (u) | u ( x) 与 ( f ( ( x))) f ( ( x))( x) 的不同含义.
大学生数学竞赛二重积分.ppt)
f ( x, y)dy
0 1 x
1
2 d
1 f ( cos , sin )d .
0
sin cos
例3. 计算二重积分
x 2 y 2 4 dxdy, D : x 2 y 2 9. y
D
x2 y2 9
D D1 D2 ,
D1 : x 2 y 2 4 ;
D2
D1
xo2 y2 4
于坐标轴的直线网来划分
D
区域 D.
则面积元素为d dxdy 0
x
故二重积分可写为
f x, yd f x, ydxdy
D
D
三、二重积分的性质
(二重积分与定积分有类似的性质)
性质1 当k为常数时,
kf ( x, y)d k f ( x, y)d .
D
D
性质2
[ f ( x, y) g( x, y)]d
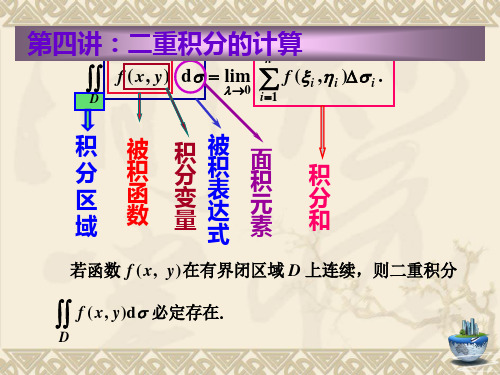
第四讲:二重积分的计算
n
D
f (x, y)
d lim
0
f (i ,i ) i .
i 1
积 分 区 域
被 积 函 数
积 分 变 量
被 积 表 达 式
面 积 元 素
积 分 和
若函数 f ( x, y)在有界闭区域 D 上连续,则二重积分
f ( x, y)d 必定存在.
D
y 在直角坐标系下用平行
直角坐标与极坐标的相互转化公式
x r cos y r sin
x2 y2 r2
dx dy rdrd
将直角坐标系下的二重积分转化为极坐
标系下的二次积分
⑴写出已知 X 型区域:D x, y a x b,1 x y 2 x
⑵将第二个不等式改成等式y=1 x,y=2 x画出两条曲线
0 1 x
1
2 d
1 f ( cos , sin )d .
0
sin cos
例3. 计算二重积分
x 2 y 2 4 dxdy, D : x 2 y 2 9. y
D
x2 y2 9
D D1 D2 ,
D1 : x 2 y 2 4 ;
D2
D1
xo2 y2 4
于坐标轴的直线网来划分
D
区域 D.
则面积元素为d dxdy 0
x
故二重积分可写为
f x, yd f x, ydxdy
D
D
三、二重积分的性质
(二重积分与定积分有类似的性质)
性质1 当k为常数时,
kf ( x, y)d k f ( x, y)d .
D
D
性质2
[ f ( x, y) g( x, y)]d
第四讲:二重积分的计算
n
D
f (x, y)
d lim
0
f (i ,i ) i .
i 1
积 分 区 域
被 积 函 数
积 分 变 量
被 积 表 达 式
面 积 元 素
积 分 和
若函数 f ( x, y)在有界闭区域 D 上连续,则二重积分
f ( x, y)d 必定存在.
D
y 在直角坐标系下用平行
直角坐标与极坐标的相互转化公式
x r cos y r sin
x2 y2 r2
dx dy rdrd
将直角坐标系下的二重积分转化为极坐
标系下的二次积分
⑴写出已知 X 型区域:D x, y a x b,1 x y 2 x
⑵将第二个不等式改成等式y=1 x,y=2 x画出两条曲线
《高等数学竞赛讲座》课件

V. 总结
总结竞赛内容和要点: 总结竞赛中涉及的各个数学领域的知识点和解题技巧。
鼓励学生参加竞赛的积极性和热情: 引导学生重视高等数学竞赛,激发他们的 兴趣和热情。
提高学生数学素养和竞赛水平的建议和指导: 给出一些建议和指导,Байду номын сангаас助学生 提高数学素养和竞赛水平。
III. 解题技巧
常用方法和技巧: 学习解题技巧,如逆向思维、数学归纳法和构造法等,以提 高解题效率。
常见易错点: 分析竞赛中出现的典型错误,帮助同学们避免常见的陷阱。
优秀解题方法分享: 分享一些优秀同学的解题思路和方法,启发大家寻找更多 解题思路。
IV. 答疑解惑
对于难题的解释和讲解: 解释高难度题目的解题思路和方法,帮助同学们理解和掌握。 对于同学提出的问题进行回答和解决: 回答同学们在竞赛准备中遇到的疑惑和困惑,帮助他们解决问题。
例题1:极限计算: 分析极限的定义、运用不同的极限性质,解答复杂的极限计算题目。 例题2:方程求解: 利用数学方法解决各类方程,包括多项式方程、三角方程和指数方程。 例题3:向量运算: 讨论向量的性质和运算法则,解决与向量相关的几何和代数问题。 例题4:微分方程: 掌握微分方程的基本概念和解题方法,分析各种类型的微分方程。 例题5:不等式证明: 运用数学推理和逻辑推断,证明各类数学不等式。
《高等数学竞赛讲座》 PPT课件
I. 竞赛内容
概述: 高等数学竞赛是一个充满挑战和乐趣的比赛,涉及各个数学领域的题目。
题型:题目覆盖了极限计算、方程求解、向量运算、微分方程以及不等式证明 等多个方面。 评分方法:通过对答案的正确性、解题过程的完整性以及解题思路的独特性进 行评分。
II. 案例分析
全国大学生数学建模竞赛简介PPT课件

194
35
225
39
224
38
262
46
223
43
队数
总数
中国
211
4
235
6
260
21
292
26
259
40
315
84
320
84
393
115
409
107
472
138
479
155
美国大学生数学建模竞赛
• 1985年开始举办数学建模竞赛(MCM), 1989年我国 (我校)学生开始参加。
• 1999年开始增办交叉学科竞赛(ICM).
竞赛宗旨
竞赛事项
❖ 答卷按省(市、自治区)和全国两级评奖; ❖ 每年赛题、优秀答卷及获奖名单刊登于次年
“工程数学学报”第1期; ❖ 全国组委会网址:
竞赛的社会影响不断扩大
❖ 99年的竞赛命名为“99’创维杯全国大学生数学建 模竞赛”;
❖ 2000年的竞赛命名为“2000网易杯全国大学生数 学建模竞赛”;
❖ A,C 为连续型题目; B,D为离散型题目
评奖标准
❖ 假设的合理性、建模的创造性、结果的正确 性和文字表述的清晰程度。
竞赛意义
大学阶段难得的一次近似于“真刀真枪” 的训练,模拟了毕业后工作时的情况,既丰 富、活跃了广大同学的课外生活,也为优秀 学生脱颖而出创造了条件.
竞赛意义
❖ 数学建模竞赛培养学生创新精神,提高 学生综合素质;
年 2000 2001 2002 2003 2004 2005
参赛国数 9 11 11 8 9 9
参赛总队数 495 579 628 638 742 808
大学生数学竞赛 74页PPT文档

《高等代数与空间解析几何》辅导
课堂要求:
1、不迟到、不早退。有事要请假,不无故缺课; 2、上课要带笔记本和草稿纸; 3、注意力集中,认真听课,不讲小话。带有手机的要关闭; 4、勤于思考,积极回答老师提出的问题; 5、课后要-10月20日进行培训,时间约为2个月,总培 训时数为54学时(讲课48学时,测试两次6学时)。 培训分为两个阶段: 第一阶段:2009年8月24日-9月20日。第一阶段培训结束后进 行一次综合测试,选拔参加全国赛的选手。 第二阶段:2009年9月22日-10月20日主要针对参加全国大学 生数学竞赛的选手进行强化培训。 2、培训课程
林群院士在谈到教改动态时说,微积分的发展可分为以下几代,第 一代是牛顿积分,其特点是说不清楚,行之有效。第二代是柯西积分, 其特点是说得清楚,学生知其然,不知其所以然。这就是现在我们的 微积分教学,教师在教学时可以清楚地说明微积分的理论,使用各种 方法去解决问题,学生在课堂上也可以听得明白,但一到考试时学生 就糊涂,不知道要用什么方法来解决问题。现在需要发展第三代微积 分。所谓第三代微积分,本质上还是柯西积分,但需要换一种观念, 力求让学生学习轻松,这就是要求多题一解,使学生不但在课堂上可 以听明白,而且在考试时也能应付自如。
§5 线性空间
§6 线性变换
则
§7 λ-矩阵
§8 欧氏空间
是正交变换.
§9 双线性函数与二次型
记为 T
B=
则
令
根据正交化做法, 存在上三角矩阵, 使 这时
§10 矢量及其线性运算
§11 曲面与曲线
法向量是(1,2,3), 即是这个平面与垂线
本次竞赛的目的
北航高宗升教授在谈到竞赛目的时说,竞赛目的有二个,一是提 高、促进大学数学教学改革。二是发现人才。关于人才,高宗升教 授特别说明,这是指具有数学思想、能够用数学思想去解释实际问 题,用发散思维去考虑实际问题的人才。他还举了一个例子,在莫 斯科数学竞赛中,有这样一个题目,给出19个ε-δ的表述,要求学 生对每一种表述是从哪个方面去解释ε-δ进行说明,并对每一种表 述构造出一个函数。高宗升教授特别说明,对于这样的题目,如果 学生不具备数学思想,不能用发散思维去考虑问题,将无法完成这 种题目。
课堂要求:
1、不迟到、不早退。有事要请假,不无故缺课; 2、上课要带笔记本和草稿纸; 3、注意力集中,认真听课,不讲小话。带有手机的要关闭; 4、勤于思考,积极回答老师提出的问题; 5、课后要-10月20日进行培训,时间约为2个月,总培 训时数为54学时(讲课48学时,测试两次6学时)。 培训分为两个阶段: 第一阶段:2009年8月24日-9月20日。第一阶段培训结束后进 行一次综合测试,选拔参加全国赛的选手。 第二阶段:2009年9月22日-10月20日主要针对参加全国大学 生数学竞赛的选手进行强化培训。 2、培训课程
林群院士在谈到教改动态时说,微积分的发展可分为以下几代,第 一代是牛顿积分,其特点是说不清楚,行之有效。第二代是柯西积分, 其特点是说得清楚,学生知其然,不知其所以然。这就是现在我们的 微积分教学,教师在教学时可以清楚地说明微积分的理论,使用各种 方法去解决问题,学生在课堂上也可以听得明白,但一到考试时学生 就糊涂,不知道要用什么方法来解决问题。现在需要发展第三代微积 分。所谓第三代微积分,本质上还是柯西积分,但需要换一种观念, 力求让学生学习轻松,这就是要求多题一解,使学生不但在课堂上可 以听明白,而且在考试时也能应付自如。
§5 线性空间
§6 线性变换
则
§7 λ-矩阵
§8 欧氏空间
是正交变换.
§9 双线性函数与二次型
记为 T
B=
则
令
根据正交化做法, 存在上三角矩阵, 使 这时
§10 矢量及其线性运算
§11 曲面与曲线
法向量是(1,2,3), 即是这个平面与垂线
本次竞赛的目的
北航高宗升教授在谈到竞赛目的时说,竞赛目的有二个,一是提 高、促进大学数学教学改革。二是发现人才。关于人才,高宗升教 授特别说明,这是指具有数学思想、能够用数学思想去解释实际问 题,用发散思维去考虑实际问题的人才。他还举了一个例子,在莫 斯科数学竞赛中,有这样一个题目,给出19个ε-δ的表述,要求学 生对每一种表述是从哪个方面去解释ε-δ进行说明,并对每一种表 述构造出一个函数。高宗升教授特别说明,对于这样的题目,如果 学生不具备数学思想,不能用发散思维去考虑问题,将无法完成这 种题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1 设
x1
2, x2
2
1 x1
,
, xn1
2
1 xn
,
.
求证
lim
n
xn
存在,并求其值.
分析 给定数列的奇数项子列单调增加有上界,偶数项子列单 调减少有下界,因此两子列均收敛 . 对于这种数列仍可应用 单调有界准则.
湘潭大学数学与计算科学学院 王文强 上一页 下一页
11
1
1
x 12 ,x 22x 1, ,x n 12x n, .
解 首先易见 2xn3, 又计算可得
1 x n 2 x nx n 1 x n 1(x n 1 x n 1 ),n 2 ,3 , ,
x3x10, x4x20,
因此 xn2 xn与 xn1 xn1异号,子列{ x2n }单调 减少有下界 2,子列{ x2n1}单调增加有上界 3,
f2(x)ln (xx21)是奇函数,
f2 ( x ) ln ( x x 2 1 )
(x2 1) x2 ln
x x2 1
湘潭大学数学与计算科学学院 王文强 上一页 下一页
2
f2 ( x ) ln ( x x 2 1 ) ln (x x 2 1 x )2 x 1 2 ln 1 ln (x x 2 1 ) f 2 (x ) .
湘潭大学数学与计算科学学院 王文强 上一页 下一页
7
即
f1[g1(x)] 当xb,g1(x)a时,
f[g(x)]f1[g2(x)] f2[g1(x)]
当xb,g2(x)a时, 当xb,g1(x)a时,
f2[g2(x)] 当xb,g2(x)a时.
例 3 设函数 D( x) 01,,x0为为有无理理数数,则 D[D( x)] __1___.
所以两子列均收敛,然后由递推式
湘潭大学数学与计算科学学院 王文强 上一页 下一页
12
x2n12x1 2n21x2 2n x2 1n1,
两端取极限得
由此得到
ln i m x 2n 1ln i m x 2n12,
lni m xn 1 2.
湘潭大学数学与计算科学学院 王文强 上一页 下一页
因此 x (exex)ln (xx21)是奇函数。
于是
I 1 x [ x 5 ( e x e x ) ln ( x x 2 1 ) ] d x . 1
1x6dx021x6dx2.
1
0
7
湘潭大学数学与计算科学学院 王文强 上一页 下一页
3
例 2 设F( x) f ( x),则下列结论正确的是( A ) (A)若 f ( x)为奇函数,则F ( x)为偶函数。 (B)若 f ( x)为偶函数,则F ( x)为奇函数。 (C)若 f ( x)为周期函数,则F ( x)为周期函数。 (D)若 f ( x)为单调函数,则F ( x)为单调函数。 解 (B)不成立,反例 f(x)x2,F(x)x31
例 1 已知
f
(
x)
f1( x) f2 ( x)
求 f [g( x)]
xa xa
和
g(
x)
g1 ( g2 (
x) x)
xb ,
xb
湘潭大学数学与计算科学学院 王文强 上一页 下一页
6
例 1 已知
f
(
x)
f1( x) f2 ( x)
求 f [g( x)]
xa xa
1.1 函数
湘潭大学数学与计算科学学院 王文强 上一页 下一页
1
一、有关函数的四种性质
(奇偶性、单调性、周期性、有界性)
例1 求 I 1 x [ x 5 ( e x e x ) ln ( x x 2 1 ) ] d x . 1
解 f1(x)exex是奇函数, f 1 ( x ) e x e x f 1 ( x ) ,
x
F (x)F (0)0 f(t)dt
x
F(0)0 f(u)d(u)
x
F(0)0 f(u)du F(x).
所以,F ( x)为偶函数。
湘潭大学数学与计算科学学院 王文强 上一页 下一页
5
二、有关复合函数 1. 已知 f ( x), g( x)求 f [g( x)] 2. 已知 f [g( x)]和 g( x),求 f ( x)
3 (C)不成立,反例 f ( x ) c o s x 1 , F ( x ) s i n x x
(D)不成立,反例 f ( x ) 2 x ,F ( x ) x 2 在 ( , ) 内
(A)成立。 湘潭大学数学与计算科学学院 王文强 上一页 下一页
4
x
证明 F (x)F (0)0f(t)dt,f为奇函数,
f(x)f(1)
xlnt dt
1
ln 2 t
x 1 ln 2 x .
1t
2
2
1
所以
f (x) 1ln2 x. 2
湘潭大学数学与计算科学学院 王文强 上一页 下一页
9
1.2 极限
湘潭大学数学与计算科学学院 王文强 上一页 下一页
10
一、数列与函数极限的存在准则
(1)夹逼准则; (2)单调有界收敛准则
和
g(
x)
g1 ( g2 (
x) x)
xb ,
xb
解 当 x b , g 1 (x ) a 时 , f[g(x)]f1[g1(x)],
当 x b , g 2 (x ) a 时 , f[g(x)]f1[g2(x)], 当 x b , g 1 (x ) a 时 , f[g(x)]f2[g1(x)], 当 x b , g 2 (x ) a 时 , f[g(x)]f2[g2(m n
xn
a,
则lim 1 n n
分析 函数D(x)的函数值是有理数1或0,所以D[D(x)]1.
湘潭大学数学与计算科学学院 王文强 上一页 下一页
8
例 2 已知 f (ex ) xe x ,且 f (1) 0,求 f ( x).
解 令 e x t, 则 xlnt. 因此
于是
f(ex)f(t)lnt. t
