2014大学物理作业下作业和附加题
东北大学的大学的物理附加地的题目标准详解第4,14,5章作业标准详解.doc

实用标准文案第 4章刚体的转动作业一、教材:选择填空题 1~4;计算题: 13, 27,31二、附加题(一)、选择题1、有两个半径相同,质量相等的细圆环 A 和 B . A 环的质量分布均匀, B 环的质量分布不均匀.它们对通过环心并与环面垂直的轴的转动惯量分别为J A和J B,则J A和J B的关系为[C]A、J A J BB、J A J BC、J A J BD、无法确定2、假设卫星环绕地球中心作圆周运动,则在运动过程中,卫星对地球中心的[ A ]A、角动量守恒,动能也守恒; B 、角动量守恒,动能不守恒C、角动量不守恒,动能守恒; D 、角动量不守恒,动量也不守恒E、角动量守恒,动量也守恒3、花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为 J0,角速度为0 .然后她将两臂收回,使转动惯量减少为 1 J 0 .此时她转动的角速度变为[ D ]3A、1B 、1C、3 0 D、3 03 0 3 04、如图所示,一静止的均匀细棒,长为L 、质量为 M ,可绕通过棒的端点且垂直于棒长的光滑固定轴 O 在水平面内转动,转动惯量为 1 ML2.一质量为 m 、速率为3 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为1v, O2 俯视图则此时棒的角速度为[ B ]A、mvB 、 3mv C、5mv D、7mvML 2ML 3ML 4ML(二)、计算题1、质量分别为 m和 2m,半径分别为 r 和 2r 的两个均质圆盘,同轴地粘在一起,可绕通过盘心且垂直于盘面的水平1v 2v实用标准文案光滑轴转动,在大小盘边缘都绕有细绳,绳下端都挂一质量为 m 的重物,盘绳无相对滑动,如图所示,求: 1) 圆盘对水平光滑轴的转动惯量;2) 圆盘的角加速度。
解:( 1) J 1 mr 2 1 2m 2r 29mr22 22(2)T 2 mg ma 2mg T 1 ma 1T 2 2r T 2 r Ja 1 a 2 2g2rr19r2、一根长为 l ,质量为 M 的均质细杆,其一端挂在一个光滑的水平轴上,静止在竖直位置。
大学物理作业标准答案(下)
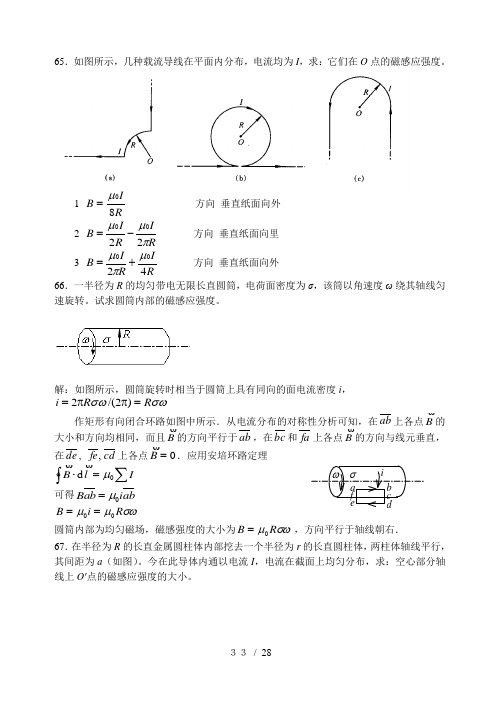
65.如图所示,几种载流导线在平面内分布,电流均为I ,求:它们在O 点的磁感应强度。
1 RIB 80μ=方向 垂直纸面向外2 R I R I B πμμ2200-= 方向 垂直纸面向里 3 RI R I B 4200μπμ+= 方向 垂直纸面向外 66.一半径为R 的均匀带电无限长直圆筒,电荷面密度为σ,该筒以角速度ω绕其轴线匀速旋转。
试求圆筒内部的磁感应强度。
解:如图所示,圆筒旋转时相当于圆筒上具有同向的面电流密度i , σωσωR R i =ππ=)2/(2作矩形有向闭合环路如图中所示.从电流分布的对称性分析可知,在ab 上各点B的大小和方向均相同,而且B 的方向平行于ab ,在bc 和fa 上各点B的方向与线元垂直,在de , cd fe ,上各点0=B.应用安培环路定理 ∑⎰⋅=I l B 0d μ可得ab i ab B 0μ=σωμμR i B 00==圆筒内部为均匀磁场,磁感强度的大小为σωμR B 0=,方向平行于轴线朝右.67.在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体,两柱体轴线平行,其间距为a (如图)。
今在此导体内通以电流I ,电流在截面上均匀分布,求:空心部分轴线上O '点的磁感应强度的大小。
解:)(22r R IJ -=π10121r J B ⨯=μ20221r k J B ⨯-=μj Ja O O k J r r J B B 021********21)(21μμμ=⨯=-⨯=+=r R Ia)(2220-=πμ68.一无限长圆柱形铜导体,半径为R ,通以均匀分布的I 今取一矩形平面S (长为L ,宽为2R ),位置如图,求:通过该矩形平面的磁通量。
解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定律可得:)(220R r r R IB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr rL RI Rd 2020⎰π=μπ=40LIμ在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为)(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r IL R Rd 220⎰π=μ2ln 20π=ILμ 穿过整个矩形平面的磁通量21ΦΦΦ+=π=40LIμ2ln 20π+ILμ69.如图所示,载有电流I 1和I 2的无限长直导线相互平行,相距3r ,今有载有电流I 3的导线MN = r 水平放置,其两端M 、N 分别与I 1、I 2距离均为r ,三导线共面,求:导线MN 所受的磁场力的大小与方向。
大学物理上册作业题

大学物理上册作业题(总17页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2014 ~2015学年第二学期 大学物理作业题第1章 质点运动学 作业一、教材:选择题1 ~ 4;计算题:9,13,14,17 二、附加题 (一)、选择题1、某物体的运动规律为d v /dt=-kv 2t ,式中的k 为大于零的常量.当t=0时,初速为v 0,则速度v 与时间t 的函数关系是[ ]A 、0221v kt v +=;B 、0221v kt v +-=;C 、02121v kt v +=;D 、02121v kt v +-=2、某质点作直线运动的运动学方程为x =3t-5t 3+6(SI),则该质点作[ ] A 、匀加速直线运动,加速度沿x 轴正方向 B 、匀加速直线运动,加速度沿x 轴负方向 C 、变加速直线运动,加速度沿x 轴正方向 D 、变加速直线运动,加速度沿x 轴负方向3、一质点在t=0时刻从原点出发,以速度v 0沿x 轴运动,其加速度与速度的关系为a =-kv 2,k 为正常数。
这个质点的速度v 与所经路程x 的关系是[ ] A 、kxe v v -=0;B 、)21(200v x v v -=;C 、201x v v -= ;D 、条件不足不能确定4、一质点在平面上运动,已知质点位置矢量的表示式为 j bt i at r 22+=(其中a 、b 为常量), 则该质点作[ ]A 、匀速直线运动B 、变速直线运动C 、抛物线运动D 、一般曲线运动(二)、计算题1一质点在一平面内做运动,其运动方程为: 2=+-r t ti t j()5(10)(SI)试求:(1)质点的轨道方程 (2)质点从t=0到t=5s这段时间的平均速度 (3)质点在第5s末的速度; (4)质点的加速度;2、已知质点沿x轴运动,其加速度和坐标的关系为a = 2+6x2 (SI),且质点在x= 0 处的速率为10m/s,求该质点的速度v与坐标x的关系。
大学物理作业2014(下)

大学物理作业2014(下)9-1一个沿x 轴作简谐振动的弹簧振子,振幅为A ,频率为υ,其振动方程用余弦函数表示。
若0t =时质点的状态分别是:(1)过平衡位置向正方向运动;(2)过平衡位置向负方向运动;(3) 过2A x =处向负方向运动;(4)过x =其相应的位置,并写出振动方程。
分析:根据旋转矢量法画出质点在x 轴的位置,计算出初相位,再写出振动方程。
解:根据已知条件,设振动方程为)2cos(?πν+=t A x(1)0=t 时,0=x ,0υ>,由图(1)得2π-=,振动方程为 c o s (2)2x A t ππν=- (2) 0=t 时,0=x ,0υ<,由图(2)得2π=,振动方程为 c o s (2)2x A t ππν=+ (3) 0=t 时,2A =x ,0υ<,由图(3)得3π?=,振动方程为 c o s (2)3x A t ππν=+ (4) 0=t 时,A 22=x ,0υ>,由图(4)得4π?-=,振动方程为 c o s (2)4x A t ππν=- 9-4一质点同时参与两个同方向同频率的简谐振动,它们的方程分别为:110cos 24x t π??=+ ??cm ,226cos 23x t π??=+cm ,求其合振动方程。
解:合振幅为912432120610A A 2A A A 2212212221.)cos()cos(=-++=-++=ππ??cm初相位11221122sin sin tan cos cos A A A A +=+326410326410ππππcoscos sinsin++==3.013 得21.255rad φπ==因此,合振动方程为2π图(1)图(2)4π图(4) 解8-1图图(3)212.9cos(2)5x t π=+9-5一弹簧振子作简谐振动,振幅A =0.20m ,如果弹簧的劲度系数k =2.0N/m ,所系物体的质量m =0.5kg ,(1) 当动能和势能相等时,物体的位移是多少?(2) 设t =0时,物体正在最大位移处,则达到动能和势能相等处所需的时间是多少(在一个周期内) ?分析:根据简谐振动的动能、势能计算公式求解。
大学物理下册练习与答案

I电磁学DC7・ 1 |如图所示,一电子经过Uo = 1 >10 7m / s o(1) 欲使这电子沿半圆自A 至C 运动,试求所需的磁场 大小和方向;(2) 求电子自A 运动到C 所需的时间。
9解:(1)电子所受洛仑兹力提供向心力 evoB = m —Rmv o 9.1 lx 10~ x IX 10 ?3_得出 B 二 = _i9= 1./10 TeR 1 .6X 10 - x 0 .05磁场方向应该垂直纸面向里。
(2) 所需的时间为 t =# =药-=兀0. 05 = 1 .6 X 10 rs22 vo l x 107血工地2.0怡2的一个正电子,射入磁感应强度B 二0.1T 的匀强磁场中,其速 度矢量与B 成89角,路径成螺旋线,其轴在B 的方向。
试求这螺旋线运动的周 期T 、螺距h 和半径r o解:正电子的速率为I /XX X X - v ==1 ------- 2~~10 ' 110 19 = 2 .6x 10 7 m/s* m *9.1 1X 10做螺旋运动的周期为2 Jim 2 K X 9.1 丈 1(T 31T = ---------- = -------------- --- --------- = 3 ,6X 10 SeB 1 .6X 10一 X 0.1螺距为 h = vcos 89 °T =2.6 * 10 7 X cos 89 0 :<3. 6 X 10 10 = 1 .6^ lO^m317ZX _X X X_丰径为 r = mv sin 89 = 9.11 ~F02 .6⑴ TO Sih 89 = 1 .5 ^103 Hlx — xeBL6 10'0.1磁力A 点时,具有速率V0 /0 10cmA h -----------------DC7・3加1图所示,一铜片厚为d二1.0mm,放在B=1.5T的磁场中,磁场方向与铜片表面垂直。
已知铜片里每立方厘米有8.4^ 1022个自由电子,每个电子的电荷C - = -1.6 19T,当铜片中有I=200A的电流流通时,(1)求铜片两侧的电势差Uaa' ;(2)铜片宽度b对Uaa,有无影响?为什么?/// B i ////Z/-------- 28 — = -2.23 X 10_ V,8/ 10X「1.6 ¥o f X 1 .0 X 10一负号表示『侧电势高。
大学物理(下)练习题及答案

xyoa•••a-(0,)P y qq-大学物理(下)练习题第三编 电场和磁场 第八章 真空中的静电场1.如图所示,在点((,0)a 处放置一个点电荷q +,在点(,0)a -处放置另一点电荷q -。
P 点在y 轴上,其坐标为(0,)y ,当y a ?时,该点场强的大小为(A) 204q y πε; (B) 202q y πε;(C)302qa y πε; (D)304qa y πε.[ ]2.将一细玻璃棒弯成半径为R 的半圆形,其上半部均匀分布有电量Q +, 下半部均匀分布有电量Q -,如图所示。
求圆心o 处的电场强度。
3.带电圆环的半径为R ,电荷线密度0cos λλφ=,式中00λ>,且为常数。
求圆心O 处的电场强度。
4.一均匀带电圆环的半径为R ,带电量为Q ,其轴线上任一点P 到圆心的距离为a 。
求P 点的场强。
5.关于高斯定理有下面几种说法,正确的是(A) 如果高斯面上E r处处为零,那么则该面内必无电荷;(B) 如果高斯面内无电荷,那么高斯面上E r处处为零;(C) 如果高斯面上E r处处不为零,那么高斯面内必有电荷;(D) 如果高斯面内有净电荷,那么通过高斯面的电通量必不为零; (E) 高斯定理仅适用于具有高度对称性的电场。
[ ]6.点电荷Q 被闭合曲面S 所包围,从无穷远处引入另一点电荷q 至曲面S 外一点,如图所示,则引入前后(A) 通过曲面S 的电通量不变,曲面上各点场强不变;(B) 通过曲面S 的电通量变化,曲面上各点场强不变;(C) 通过曲面S 的电通量变化,曲面上各点场强变化;(D) 通过曲面S 的电通量不变,曲面上各点场强变化。
[ ]7.如果将带电量为q 的点电荷置于立方体的一个顶角上,则通过与它不相邻的每个侧面的电场强度通量为xq g S Q g(A)06q ε; (B) 012q ε; (C) 024q ε; (D) 048q ε. [ ]8.如图所示,A 、B 为真空中两个平行的“无限大”均匀带电平面,A 面上的电荷面密度721.7718A C m σ--=-⨯⋅,B 面上的电荷面密度723.5418B C m σ--=⨯⋅。
东北大学大学物理附加题答案第4,14,5章作业答案-推荐下载

在水平面内转动。今有一质量为 1 m 、速率为 v 的子弹在水平面内沿棒的垂直方 2
向射向棒的中点,子弹穿出时速率减为 1 v ,当棒转动后,设棒上单位长度受到 2
的阻力正比于该点的速率(比例系数为 k)试求:(1)子弹穿出时,棒的角速
度0 为多少?(2)当棒以 转动时,受到的阻力矩 M f 为多大?(3)棒从
以速度v0从杆的中点穿过,穿出速度为v, 求:1)杆开始转动时的角速度;
2)杆的最大摆角。
解:(1)碰撞前后角动量守恒
mv0
l 2
3m v0 v
2Ml
1 3
Ml 2
(2)碰撞后机械能守恒
1 J2 Mg l 1 cos
2
arccos 1
2
mv
3m2 v0 v2
匀速直线运动的乙测得时间间隔为 5 s,则乙相对于甲的运动速度是( c 表示真空
0
变为
1 2
0
时,经历的时间为多少?
解:(1)以子弹和棒组成的系统为研究对象。取子弹和棒碰撞中间的任一状态分析受力,
子弹与棒之间的碰撞力 f 、 f ' 是内力。一对相互作用力对同一转轴来说,其力矩之和为
零。因此,可以认为棒和子弹组成的系统对转轴的合外力矩为零,则系统对转轴的角动量
守恒。
mv 2
J 1 mL2 3
L 2
解上述两式得: 0
m 2
v 2
L 2
J0
3v 8L
(2)设在离转轴距离为 l 得取一微元 dl ,则该微元所受的阻力为: df kvdl kldl
该微元所受的阻力对转轴的力矩为:
(配合教材下册)大学物理学课后作业与自测题参考答案与部分解析

x+R, R
令dФ=0,得Ф最大时 x=1( 5-1)R.
dx
2
24-4 答案 μ0 ·I2(R+d)(1+π)-RI1,方向⊙
2π
R(R+d)
解析 圆电流产生的磁场 B1=μ20RI2,方向⊙,长直导线电流的磁场 B2=2μπ0IR2,方向⊙,导体管电流
第 1 页(共 15 页)
产 生 的 磁 场 , B3 = μ0I1 , 方 向 , 所 以 , 圆 心 O 点 处 的 磁 感 强 度 B = B1 + B2 - B3 = 2π(d+R)
B=2Sρgtan α≈9.35×10-3 T. I
26-4 答案 πkωBR5,方向在纸面内且垂直 B 向上 5
解析 在圆盘上取一个半径为 r、宽度为 dr 的圆环,其环上电荷为 dq=σ2πrdr,圆环以角速度ω旋 转,其圆电流为 dI=σrωdr,其磁矩大小为 dm=πr2dI=πr2(kr)ωrdr,则圆环上电流所受的磁力矩为
28-4 答案 0.01 T
28-4
解析
εi=|ddФt |,i=Rεi=R1|ddФt |,而
i=dq,得 dt
dq=idt=1|dФ|, R
Q dq =1
0
R
0
dФ,Q=1Ф, R
Ф=RQ=π×10-5 Wb,因为Ф=πr2B,所以 B=0.01 T.
答案 -μ0Ivln a+b,方向为 N→M,μ0Ivln a+b
dM=Bdm=πkωr4dr,所以,圆盘所受总磁力矩 M= dM = R πkωr4dr=πkωBR5,M 的方向在纸面
0
5
内且垂直 B 向上.
26-5 答案 (1)πa2BI0sin2 ωt;(2)1BI0ωπa2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9章 振动 作 业一、教材:选择填空题 1~5;计算题:13,14,18 二、附加题 (一)、选择题1、一沿x 轴作简谐振动的弹簧振子,振幅为A ,周期为T ,振动方程用余弦函数表示,如果该振子的初相为π34,则t =0时,质点的位置在: (A)过A x 21=处,向负方向运动; (B) 过A x 21=处,向正方向运动; (C) 过A x 21-=处,向负方向运动; (D) 过A x 21-=处,向正方向运动。
2、一质点作简谐振动,振动方程为:x =A cos(ωt +φ )在t=T/2(T 为周期)时刻,质点的速度为:(A) sin A ωϕ-. (B) sin A ωϕ. (C) cos A ωϕ-. (D) cos A ωϕ.3、一质点沿x 轴做简谐运动,振动方程为:21410cos(2)3x t ππ-=⨯+。
从t = 0时刻起,到x =-2cm 处,且向x 轴正方向运动的最短时间间隔为: (A) 1s 8. (B) 1s 4. (C) 1s 2. (D) 1s 3. (E) 1s 6.(二)、计算题1、一物体沿x 轴做简谐运动,振幅A = 0.12m ,周期T = 2s .当t = 0时,物体的位移x 0= 0.06m ,且向x 轴正向运动.求:(1)此简谐运动的运动方程;(2)t = T /4时物体的位置、速度和加速度;2、一物体沿x 轴做简谐运动,振幅A = 10.0cm ,周期T = 2.0s .当t = 0时,物体的位移x 0= -5cm ,且向x 轴负方向运动.求:(1)简谐运动方程;(2)t = 0.5s 时,物体的位移;(3)何时物体第一次运动到x = 5cm 处?(4)再经过多少时间物体第二次运动到x = 5cm 处?3、若简谐振动方程为m ]4/20cos[1.0ππ+=t x ,求: (1)振幅、频率、角频率、周期和初相; (2)t =2s 时的位移、速度和加速度.4、如图所示,质量为10g 的子弹以1000m .s -1 的速度射入木块并嵌在木块中,并使弹簧压缩从而作简谐振动,若木块质量为4.99kg ,弹簧的劲度系数31810N m -⨯⋅,求振动的振幅。
5、一物体沿x 轴作简谐振动,振幅为0.06m ,周期为2.0s ,当t =0时位移为0.03m ,且向轴正方向运动,求:(1)t =0.5s 时,物体的位移、速度和加速度;(2)物体从m 03.0-x =处向x 轴负方向运动开始,到达平衡位置.至少需要多少时间?第10章 波动 作 业一、教材:选择填空题 1~5;计算题:12,13,14, 21,30 二、附加题 (一)、选择题1、一平面简谐波的波动方程为y = 0.1cos(3πt -πx+π) (SI). t = 0时的波形曲线如图所示,则:(A) O 点的振幅为-0.1m (B) 波长为3m (C) a 、b 两点间相位差为π/2 .(D) 波速为9m/s 。
2、某平面简谐波在t = 0.25s 时波形如图所示,则该波的波函数为: (A) y = 0.5cos[4π (t -x /8)-π/2] (cm) . (B) y = 0.5cos[4π (t + x /8) + π/2] (cm) . (C) y = 0.5cos[4π (t + x /8)-π/2] (cm) . (D) y = 0.5cos[4π (t -x /8) + π/2] (cm) .3、一平面简谐波在0=t 时刻的波形曲线如图所示 ,则O 点的振动初位相为:πππ23)(;)(;21)(;0)(D C B A4、一平面简谐波 ,其振幅为A ,频率为v ,波沿x 轴正方向传播 ,设t t =0时刻波形如图所示 ,则x=0处质点振动方程为:;])(2cos[)(;]2)(2cos[)(];2)(2cos[)(;]2)(2cos[)(0000ππππππππ+-=--=+-=++=t t v A y D t t v A y C t t v A y B t t v A y A5、关于产生驻波的条件,以下说法正确的是: (A) 任何两列波叠加都会产生驻波; (B) 任何两列相干波叠加都能产生驻波; (C) 两列振幅相同的相干波叠加能产生驻波;(D) 两列振幅相同,在同一直线上沿相反方向传播的相干波叠加才能产生驻波.(二) 计算题1、如图所示 ,一平面简谐波沿Ox 轴传播 ,波动方程为])(2cos[ϕλπ+-=x vt A y ,求:1)P2)该质点的速度表达式与加速度表达式 。
2、一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.求:(1)P 点的振动表达式;(2)波动方程;)3(选择题)4(选择题3、 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m)的振动方程为0.03cos(4)2A y t ππ=-(m)求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程。
4、如图,一平面波在介质中以波速u=20m/s 沿x 轴负方向传播,已知A 点的振动方程为y=3×10-2cos4πt (SI)。
(1)以A 点为坐标原点写出波方程;(2)以距A 点5m 处的B 点为坐标原点,写出波方程。
5、一行波在媒质中传播,波速v =103m/s ,振幅为41.010m -⨯,频率为103Hz ,若该媒质密度为3800kg/m ρ=,试求:(1)波的平均能流密度;(2) 一分钟内,通过波传播方向上面积42410m S -=⨯的总能量是多少? (提示:(1)2212I A ρω=v (2)E=I t S )6、火车以u =30m/s 的速度行驶,汽笛的频率为0ν=650Hz.在铁路近旁的公路上坐在汽车里的人在下列情况听到火车鸣笛的声音频率分别是多少? (1)汽车静止;(2)汽车以v =45km/h 的速度与火车同向行驶.(设空气中声速为v =340m/s )第11章 光学 作 业一、教材:选择填空题 1~6;计算题:12,14,21,22,25(问题(1)、(2)),26,32 二、附加题 (一)、选择题1、 一束波长为λ的单色光由空气入射到折射率为n 的透明薄膜上, 要使透射光得到加强, 则薄膜的最小厚度应为:u题图4(A) λ/2 (B) λ/2n (C) λ/4 (D) λ/4n2、波长λ = 500nm 的单色光垂直照射到宽度b = 0.25 mm 的单缝上,单缝后面放置一凸透镜,在凸透镜的焦面上放置一屏幕,用以观测衍射条纹,今测得屏幕上中央条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为d = 12 mm , 则凸透镜的焦距为(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m3、一束由自然光和线偏光组成的复合光通过一偏振片,当偏振片转动时,最强的透射光是最弱的透射光光强的16倍,则在入射光中,自然光的强度I 1和偏振光的强度I 2之比I 1:I 2为(A) 2:15 (B) 15:2 (C) 1:15 (D) 15:1(二)、计算题1、如图所示,一束平行光线以入射角θ射入折射率为n 、置于空气中的透明圆柱棒的端面,试求:光线在圆柱棒内发生全反射时,折射率n 应满足的条件。
2、如图所示,一玻璃棒(n=1.5)长50cm ,两端面均为半球面,半径分别为5cm 和10cm ,一小物高0.1cm ,垂直位于左端球面顶点之前20cm 处的轴线上。
问:(1) 小物经玻璃棒成像在何处?(2)整个玻璃棒的横向放大率为多少?3、一竖立玻璃板的折射率为1.5,厚度为10cm ,观察者在玻璃板后10cm 处沿板的法向方向观察置于同一法线上10cm 处的一个小物体时,它的像距离观察者有多远?4、在双缝干涉实验中,单色光源S 到两缝S 1、S 2的距离分别为l 1、l 2,并且λλ,321=-l l 为入射光的波长,双缝之间的距离为d ,双缝到屏幕的距离为D ,如图,求:(1) 零级明纹到屏幕中央O 点的距离;(2) 相邻明条纹间的距离。
5、在杨氏双缝实验中,设两缝之间的距离为0.2mm .在距双缝1m 远的屏上观察干涉条纹,若入射光是波长为400nm 至760nm 的白光,问屏上离零级明纹20mm 处,哪些波长的光最大限度地加强?6、波长为λ的单色光垂直照射到折射率为n 2的劈形膜上,如图所示,图中n 1<n 2<n 3,观察反射光形成的干涉条纹;(1) 从劈形膜顶部O 开始向右数起,第五条暗纹中心所对应的薄膜厚度e 5是多少? (2) 相邻的二明纹所对应的薄膜厚度之差是多少?7、某种单色平行光垂直入射在单缝上,单缝宽b =0.15mm ;缝后放一个焦距f = 400 mm 的凸透镜,在透镜的焦平面上,测得中央明条纹两侧第三级暗条纹之间的距离为8.0mm ,求入射光的波长。
8、用一束含有两种波长的平行光垂直入射在光栅上,其中λ1=600 nm ,λ2=400nm ,实验发现距中央明纹5cm 处λ1光的第k 级主极大和λ2光的第(k +1)级主极大相重合,设放置在光栅与屏幕之间的透镜的焦距f = 50cm ,试求:(1)上述k =?(2)光栅常数题图63O第12章气体动理论作业一、教材:选择填空题1,2,4 计算题:14,16,20,21二、附加题(一)、选择题1、某种理想气体,体积为V,压强为p,绝对温度为T,每个分子的质量为m,R 为普通气体常数,N0为阿伏伽德罗常数,则该气体的分子数密度n为(A) pN0/(RT). (B) pN0/(RTV). (C) pmN0/(RT). (D)mN0/(RTV).2、若理想气体的体积为V,压强为p,温度为T,一个分子的质量为m,k为玻耳兹曼常量,R为摩尔气体常量,则该理想气体的分子数为:(A)pV/m. (B) pV/ (kT) . (C) pV /(RT) . (D) pV/(mT) .3、两瓶质量密度相等的氮气和氧气(氮气和氧气视为理想气体),若它们的方均根速率也相等,则有:(A) 它们的压强p和温度T都相等.(B) 它们的压强p和温度T都都不等.(C) 压强p相等,氧气的温度比氮气的高.(D) 温度T相等, 氧气的压强比氮气的高.(二)、计算题1、一容器中储有氧气,测得其压强为1atm,温度为300K。
试求:(1)单位体积内的氧分子数;(2)氧气的密度;(3)氧分子的质量;(4) 氧分子的平均平动动能。
2、一瓶氢气和一瓶氧气温度相同.若氢气分子的平均平动动能为6.21×10-21J,求: (1) 氧气分子的平均平动动能和方均根速率; (2) 氧气的温度。
