2018届高三数学第49练三视图与直观图练习
高三数学空间几何体的三视图与直观图试题答案及解析
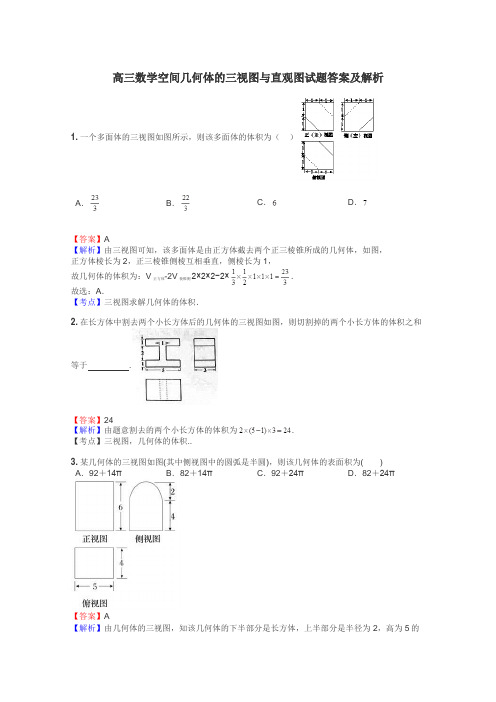
高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示,则该多面体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该多面体是由正方体截去两个正三棱锥所成的几何体,如图,正方体棱长为2,正三棱锥侧棱互相垂直,侧棱长为1,故几何体的体积为:V正方体-2V棱锥侧2×2×2−2×.故选:A.【考点】三视图求解几何体的体积.2.在长方体中割去两个小长方体后的几何体的三视图如图,则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图,几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图,知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.长方体中EH=4,HG=4,GK=5,所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π,选A.4.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示,则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示,故其俯视图应为C.6.某几何体的三视图如图所示,则该几何体的体积为A.12B.18C.24D.30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分,其直观图如上图所示,其中,侧面是矩形,其余两个侧面是直角梯形,由于,平面平面,所以平面,所以几何体的体积为:故选C.【考点】1、空间几何体的三视图;2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和侧视图可知,该几何体不可能是圆柱,排除选项C;又由俯视图可知,该几何体不可能是棱柱或棱台,排除选项A、B.故选D.9.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为()A.2B.C.2D.4【答案】A【解析】由题意可知,该三棱柱的侧视图应为矩形,如图所示.在该矩形中,MM1=CC1=2,CM=C1M1=·AB=.所以侧视图的面积为S=2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥,假设一条直角的棱长为x,则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.(2012•广东)某几何体的三视图如图所示,它的体积为()A.12πB.45πC.57πD.81π【答案】C【解析】由三视图可知,此组合体上部是一个母线长为5,底面圆半径是3的圆锥,下部是一个高为5,底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。
高三数学空间几何体的三视图与直观图试题答案及解析
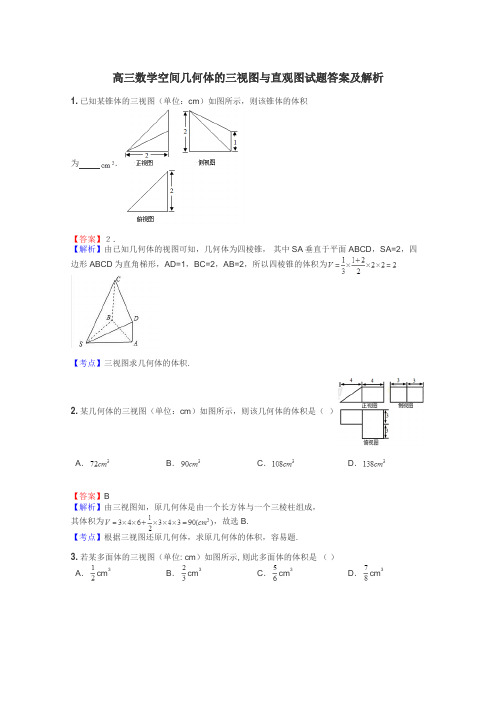
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为.【答案】2.【解析】由已知几何体的视图可知,几何体为四棱锥,其中SA垂直于平面ABCD,SA=2,四边形ABCD为直角梯形,AD=1,BC=2,AB=2,所以四棱锥的体积为【考点】三视图求几何体的体积.2.某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.B.C.D.【答案】B【解析】由三视图知,原几何体是由一个长方体与一个三棱柱组成,其体积为,故选B.【考点】根据三视图还原几何体,求原几何体的体积,容易题.3.若某多面体的三视图(单位: cm)如图所示, 则此多面体的体积是()A.cm3B.cm3C.cm3D.cm3【答案】C【解析】由三视图可得,该几何体相当于一个正方体切去一个三个侧棱长为1的三棱锥.所以该几何体的体积为.故选C.【考点】1.三视图.2.空间想象力.3.几何体的体积.4. (2014·孝感模拟)一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )A.16πB.14πC.12πD.8π【答案】A【解析】由三视图可知,该几何体是球挖去半球.其中两个半圆的面积为π×22=4π.个球的表面积为×4π×22=12π,所以这个几何体的表面积是12π+4π=16π.5.如图,某几何体的三视图都是等腰直角三角形,则几何体的体积是()A.8B.7C.9D.6【答案】C【解析】由三视图可知,几何体是底面为等腰直角三角形,有一侧棱与底面垂直(垂足在非直角处)的三棱锥,其底面面积为×6×3=9,三棱锥的高为3,所以三棱锥的体积=×9×3=9.6.已知某几何体的三视图(如图),正视图和侧视图均为两个相等的等边三角形,府视图为正方形,则几何体的体积为()A.B.4C.9D.9【答案】C【解析】由三视图可知,几何体由两个同底之正四棱锥组成所以其体积为V=2××32×3×=9 7.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.8.如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为()A.1B.2C.3D.4【答案】B【解析】由题意,棱锥的高为,底面面积为,∴.【考点】三视图,体积.9.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为()A.1B.C.D.【答案】C【解析】这是由两个三棱锥拼成的几何体,其体积为.选C.【考点】三视图及几何体的体积.10.―个几何体的三视图如图所示(单位:),则该几何体的体积为.【答案】18+9【解析】由三视图可知,此几何体为两个相切的球上方放了一个长方体组成的组合体,所以其体积为:V=3×6×1+2××=18+911.一个空间几何体的三视图如图所示,该几何体的表面积为__________.【答案】152【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,腰长为5.棱柱的高为8.因此表面积为【考点】三视图12.某三棱锥的三视图如图所示,则这个三棱锥的体积为;表面积为.【答案】;.【解析】由三视图知几何体如下图,为一个三棱锥,且三棱锥的一个侧面与底面垂直,底面三角形的一条边长为,该边上的高为,∴几何体的体积.它的表面积为.【考点】由三视图求面积、体积.13.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是_______.【答案】【解析】由题意可得该几何体是一个三棱锥,体积.【考点】1.三视图的知识.2.立几中的线面关系.3.三棱锥的体积公式.14.一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是【答案】【解析】由三视图,可知该几何体是三棱锥,并且侧棱,,,则该三棱锥的高是,底面三角形是直角三角形,所以这个几何体的体积==.【考点】由三视图求几何体的体积.15.一个几何体的三视图如图所示,则该机合体的体积为( )A.B.C.D.【答案】B【解析】分析可得该几何体是底面为菱形的四棱锥,则高底面面积,所以.故选B【考点】三视图四棱锥体积16.一个几何体的三视图如图所示,则该几何体的体积是【答案】【解析】通过三视图的观察可得,该几何体是一个四棱柱,底面是一个直角梯形,其上下底分别为2,3,梯形的高为2.四棱柱的高为2.所以几何体的体积为.【考点】1.三视图的知识.2.几何体的体积.3.空间想象力.17.某长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.4C.6D.8【答案】D【解析】割补可得其体积为2×2×2=8.18.某几何体的三视图如图所示,则该几何体的体积是________.【答案】16π-16【解析】由三视图知,该几何体是由一个底面半径为2,高为4的圆柱内挖去一个底面边长为2,高为4的正四棱柱后剩下的部分,∴V=(π×22-22)×4=16π-16.19.已知正方体ABCD-A1B1C1D1,M为棱A1B1的中点,N为棱A1D1的中点.如图是该正方体被M,N,A所确定的平面和N,D,C1所确定的平面截去两个角后所得的几何体,则这个几何体的正视图为().【答案】B【解析】对于选项A,由于只是截去了两个角,此切割不可能使得正视图成为梯形.故A不对;对于B,正视图是正方形符合题意,线段AM的影子是一个实线段,相对面上的线段DC1的投影是正方形的对角线,由于从正面看不到,故应作成虚线,故选项B正确;对于C,正视图是正方形,符合题意,有两条实线存在于正面不符合实物图的结构,故不对;对于D,正视图是正方形,符合题意,其中的两条实线符合俯视图的特征,故D不对.20.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,则该棱柱的体积为()A.B.C.D.6【答案】B【解析】由三视图知该直三棱柱高为4,底面正三角形的高为3,所以正三角形边长为6,所以V=×36×4=36.故选B.【考点】1.三视图;2.柱体体积计算.21.某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为的扇形,则该几何体的体积为()A.B.C.D.【答案】D【解析】由题意知道,该几何体体积是圆柱体积的,即.【考点】1、三视图;2、几何体体积.22.右图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )A.B.C.D.【答案】B【解析】由三视图可得该几何体是一个圆台,其两底直径分别为2和4,母线长为4,所以该几何体的侧面积是,选B..【考点】三视图,圆台的侧面积.23.如图是一个组合几何体的三视图,则该几何体的体积是 .A.B.C.D.【答案】A【解析】由三视图还原可知该几何体是一个组合体,下面是一个半径为4,高为8的圆柱,,上面是一个三棱柱,故所求体积为.【考点】三视图,圆柱、三棱柱的体积公式.24.已知一个几何体的三视图如图所示,则该几何体的体积为___________【答案】【解析】该几何体为圆柱中挖去半个球而得的组合体,其体积为.【考点】三视图.25.一个几何体的三视图如图所示(单位长度:),俯视图中圆与四边形相切,且该几何体的体积为,则该几何体的高为 .【答案】【解析】由如图所示的几何体的三视图知:这个几何体是一个半径为的球和一个直四棱柱的结合体,且这个直四棱柱的底面是对角线分别为和的棱形,这个直四棱柱的高为,∴这个几何体的体积:V=,解得h=.【考点】1.三视图;2.几何体的面积和体积26.一个几何体的三视图如图所示,则该几何体的直观图可以是()【答案】D【解析】通过三视图的俯视图可知,该几何体是由两个旋转体组成,故选D.【考点】1.三视图的应用.27.如图为一个几何体的三视图正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图所示,则该几何体的表面积为()A.B.C.D.【答案】D【解析】由三视图可知,这是一个由半个圆柱和一个三棱柱构成的组合体,这个组合体仍为一个柱体。
高三数学空间几何体的三视图与直观图试题

高三数学空间几何体的三视图与直观图试题1.某几何体三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】B【解析】由三视图知:几何体是正方体切去两个圆柱,正方体的棱长为2,切去的圆柱的底面半径为1,高为2,∴几何体的体积V=23﹣2××π×12×2=8﹣π.【考点】1、三视图;2、空间几何体的体积.2.如图是一个几何体的三视图,则该几何体的表面积是____________【答案】28+12【解析】这是一个侧放的直三棱柱,底面是等腰直角三角形,侧棱长为6故表面积为2×(×2×2)+(2+2+2)×6=28+12.【考点】三视图,几何体的表面积.3.如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2 的等腰三角腰形,则该几何体的体积是()A.B.C.D.4【答案】A【解析】由条件知几何体是三棱柱切掉一个三棱锥形成几何体,由已知柱体的高为2,所以.【考点】三视图.4.若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2,高为2的全等的等腰三角形,所以每条侧棱长都等于,所以四条侧棱长之和为.【考点】三视图.5.某几何体的三视图如图所示,则这个几何体的体积为()A.4B.C.D.8【答案】B【解析】由三视图可知,该几何体可分为一个三棱锥和一个四棱锥,其体积V=V四棱锥+V三棱锥=×2×2×4+××2×2×2=,故选B.6.如图是正方体截去阴影部分所得的几何体,则该几何体的侧视图是()【答案】C【解析】此几何体侧视图是从左边向右边看,故C符合题意.7.下列四个几何体中,每个几何体的三视图中有且仅有两个视图相同的是()A.①②B.①③C.③④D.②④【答案】D【解析】图①的三种视图均相同;图②的正视图与侧视图相同;图③的三种视图均不相同;图④的正视图与侧视图相同.故选D.8.如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.B.C.D.【答案】C【解析】因为加工前的零件半径为3,高为6,所以体积,又因为加工后的零件,左半部为小圆柱,半径为2,高4,右半部为大圆柱,半径为3,高为2,所以体积,所以削掉部分的体积与原体积之比为,故选C.【考点】本小题主要考查立体几何中的三视图,考查同学们的空间想象能力.9.已知一棱锥的三视图如图2所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为 .【答案】.【解析】作出其直观图如下图所示,结合三视图可知,该几何体是一个四棱锥,且其底面是一个直角梯形,其面积为,高为,因此,该几何体的体积为.【考点】1.三视图;2.空间几何体的体积10.(2011•浙江)若某几何体的三视图如图所示,则这个几何体的直观图可以是()A.B.C.D.【答案】D【解析】由已知中三视图的上部分有两个矩形,一个三角形故该几何体上部分是一个三棱柱下部分是三个矩形故该几何体下部分是一个四棱柱故选D11.图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.【答案】16【解析】从三视图可知,这是一个四棱锥,.【考点】三视图.12.某多面体的三视图(单位:cm)如图所示,则此多面体的体积是()A.B.C.D.【答案】D【解析】由三视图不难知道,此多面体为如所示的一个正方体截去一个三棱柱所得到的多面体,所以其体积为.13.已知几何体由正方体和直三棱柱组成,其三视图和直观图(单位:cm)如图所示.设两条异面直线和所成的角为,求的值.【答案】【解析】几何体由正方体和直三棱柱组成,求两条异面直线和所成的角. 由三视图和直观图可得线段的数量,异面直线和所成的角转化为.在通过解三角形即求得的余弦值,及为所求的结论.试题解析:由,且,可知,故为异面直线、所成的角(或其补角).由题设知,,取中点,则,且,.由余弦定理,得.【考点】异面直线所成的角.2.解三角形的知识.3.空间想象力.14.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【答案】C【解析】由三视图可知,该几何体是一个直四棱柱,且其底面是一个直角梯形,上底长为,下底长为,高为,因此该四棱柱的底面积,且四棱柱的高为,因此四棱柱的体积,故选C.【考点】1.三视图;2.空间几何体的体积15.一个空间几何体的三视图如图所示,则这个几何体的体积为;表面积为.【答案】;【解析】由三视图知几何体如下图,为一个直三棱柱,且三棱柱的一个侧面与另一个侧面垂直,,∴几何体的体积.它的表面积为.【考点】由三视图求面积、体积.16.已知三棱锥的底面是边长为的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为()A.B.C.D.【答案】D【解析】俯视图的高为,此即侧视图的底,侧视图的高即为正视图的高,所以其面积为.【考点】三视图.17.某三棱锥的主视图与俯视图如图所示,则其左视图的面积为A.B.C.D.【答案】A【解析】由主视图与俯视图可得三棱锥的一个侧面与底面垂直,其侧视图是等腰直角三角形,且直角边长为,所以侧视图的面积为,选.【考点】三视图18.如图是某几何体的三视图,其中正视图和侧视图是半径为1的半圆,俯视图是个圆,则该几何体的全面积是()A.πB.2πC.3πD.4π【答案】C【解析】由三视图知几何体的直观图是半个球,全面积为S=×4π×12+π×12=3π.19.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是 .【答案】.【解析】由正视图知,该四棱锥的高,底面菱形的两条对角线的长度分别为和,且两条对角线相互垂直平分,彼此分成四个全等的直角三角形,且直角三角形的两条直角边的长度分别为和,因此其底面积,故该四棱锥的体积.【考点】1.三视图;2.锥体的体积20.一空间几何体的三视图如图所示,该几何体的体积为16π+,则图中x的值为________.【答案】3【解析】由三视图可知,该几何体下面是圆柱,上面是四棱锥.圆柱的体积为4π×4=16π.四棱锥的底面积为×4×4=8,所以四棱锥的体积为×8×h=,所以16π+=16π+,所以四棱锥的高h=.所以x2=h2+22=5+4=9,即x=3.21.已知某几何体的三视图如右图所示,其中,主(正)视图,左(侧)视图均是由直角三角形与半圆构成,俯视图由圆与内接直角三角形构成,根据图中的数据可得此几何体的体积为( )A.B.C.D.【答案】A【解析】由三视图可得该几何体的上部分是一个三棱锥,下部分是半球,所以根据三视图中的数据可得.选A.【考点】三视图,几何体的体积.22.个几何体的三视图如图所示,则该几何体的体积为( )A.4B.C.8D.【答案】C【解析】有三视图可以看出,该几何体是一个三棱锥,它的体积为.【考点】三视图,几何体的体积.23.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 cm.【答案】【解析】由三视图可知,该几何体是半个圆锥.其体积为.【考点】1、三视图;2、几何体的体积.24.某路口的机动车隔离墩的三视图如右图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸(单位:)可求得隔离墩的体积为 ______.【答案】【解析】由三视图可知,隔离墩的体积等于一个圆柱和半个球体的体积之和,圆柱底面圆和球的半径都是,圆柱的高是,所以体积.【考点】三视图,几何体体积的计算.25.某几何体的三视图如图所示,其正视图,侧视图,俯视图均为全等的正方形,则该几何体的体积为()A.B.C.D.【答案】A【解析】该几何体是有两个全等的正四棱锥组成,故体积为.【考点】三视图下空间几何体的体积计算.26.一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可为()(A)(B)(C)(D)【答案】A【解析】由题意可知:该四面体为正四面体,其中一个顶点在坐标原点,另外三个顶点分别在三个坐标平面内,所以以zOx平面为投影面,则得到的正视图可以为选项A.【考点】本小题主要考查立体几何中三视图的有关知识,考查同学们的空间想象能力,属中档题.27.将一些棱长为1的正方体放在的平面上如图1所示,其正视图,侧视图如下所示.若摆放的正方体的个数的最大值和最小值分别为,则A.5B.6C.8D.9【答案】C【解析】最大值,最小值,所以8.故选C。
2018届高考数学二轮复习 空间几何体的结构、三视图与直观图专题

空间几何体的结构、三视图与直观图专题[基础达标](30分钟55分)一、选择题(每小题5分,共30分)1.如图,在下列几何体中是棱柱的有()A.1个B.2个C.3个D.4个C【解析】由棱柱的概念和题图可知,①③④为棱柱.2.连接正方体相邻各面的中心(所谓中心是指各面所在正方形的两条对角线的交点),所得的一个几何体是() A.四面体B.六面体C.八面体D.十面体C【解析】如图,正方体ABCD-A1B1C1D1,O1,O2,O3,O4,O5,O6分别是各表面的中心.由点O1,O2,O3,O4,O5,O6组成了一个八面体.3面的面积是()A.8B.10C.62D.82B【解析】将三视图还原成几何体的直观图,如图所示.由三视图可知,四面体的四个面都是直角三角形,面积分别为6,8,10,62,故面积最大的是10.4.将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的侧(左)视图为()B【解析】由侧(左)视图的规则可得该几何体的侧(左)视图如B项所示.5根据图中标出的尺寸,可得这个几何体最长的棱长是()A.2B.5C.22D.23C【解析】根据几何体的三视图,得该几何体为底面是等腰三角形,且侧面SBC 垂直于底面ABC的三棱锥,如图所示.三棱锥的高SD=2,底面三角形边长BC=2,高AD=2,故该三棱锥的最长棱是SA= SD2+AD2=22+22=2.6.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正(主)视图的面积不可能等于()A.1B.2C.2-12D.2+12C【解析】由题意知,正(主)视图的最大面积是对角面的面积,为2,最小面积为1,而2-12<1,故该正方体的正(主)视图的面积不可能为2-12.二、填空题(每小题5分,共15分)7(主)视图与俯视图如图所示,则它的侧(左)视图的面积为.34【解析】由题意可得该三棱锥的底面三角形的边长均为1,三棱锥高为3,故它的侧(左)视图的面积为12×32×3=34.8.如图,△A'B'C'是水平放置的△ABC的直观图,则在△ABC的三边及中线AD中,最长的线段是.AC【解析】△ABC是角B为直角顶点的直角三角形,AD是直角边BC上的中线,所以最长的线段为AC.9.用一个平面去截几何体,如果截面是三角形,那么这个几何体可能是(填序号).①棱柱②棱锥③棱台④圆柱⑤圆锥⑥圆台⑦球.①②③⑤【解析】通过画图,易知①②③⑤都能被截得到三角形的截面,而④⑥⑦不论如何去截,都得不到截面是三角形.三、解答题(共10分)10.(10分)某几何体的三视图如图所示,画出该几何体的直观图.【解析】该几何体类似棱台,先画底面矩形和中心轴,然后上底面矩形,连线即成.画法:如图,先画轴,依次画x',y',z'轴,三轴相交于点O',使∠x'O'y'=45°,∠x'O'z'=90°.在z'轴上取O'O″=8 cm,再画x″,y″轴.在坐标系x'O'y'中作直观图ABCD,使得AD=20 cm,AB=8 cm;在坐标系x″O″y″中作直观图A'B'C'D',使得A'D'=12 cm,A'B'=4 cm.连接AA',BB',CC',DD',即得到所求直观图.[高考冲关](15分钟25分)1.(5分ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的三视图是(用①②③④⑤⑥代表图形) ()A.③④⑤B.④⑤⑥C.①②③D.①②⑥C【解析】该四面体的正(主)视图是①,侧(左)视图是②,俯视图是③.2.(5分中,面积最大的侧面的面积为()A.22B.52C.62D.3B【解析】由三视图可知,该几何体的直观图如图所示,平面AED⊥平面BCDE,四棱锥A-BCDE的高为1,四边形BCDE是边长为1的正方形,则S△AED=12×1×1=12,S△ABC=S△ABE=12×1×=22,S△ACD=12×1×=52.3.(5分)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的侧面积是.3154【解析】由题意知,球心是底面三角形的中心,球的半径,就是三棱锥的高.由已知球的半径为1,设底面三角形的边长为a,有23×32a=1,得a=3,三棱锥侧面的高h=12+122=52,则该正三棱锥的侧面积S=3×12×3×52=315 4.4.(5分)如图,在六面体PABCQ中,QA=QB=QC=AB=CB=CA=2PA=2PB=2PC=2,设O1为正三棱锥P-ABC外接球的球心,O2为正四面体Q-ABC内切球的球心,则O1O2等于.0【解析】将该六面体放入一棱长为2正方体中,如图.正三棱锥P-ABC外接球的球心O1为正方体的体对角线PQ的中点,正四面体Q-ABC的内切球的球心O2也为PQ的中点,所以O1O2=0.5.(5分)已知某四棱锥,底面是边长为2的正方形,且俯视图如图所示,关于该四棱锥的下列结论中:①四棱锥中至少有两组侧面互相垂直;②四棱锥的侧面中可能存在三个直角三角形;③四棱锥中不可能存在四组互相垂直的侧面;④四棱锥的四个侧面不可能都是等腰三角形.所有正确结论的序号是.①②③【解析】由俯视图可知,四棱锥的顶点在底面上的射影落在正方形的一边上,如图所示,则可知平面PBC⊥平面PAB,平面PAD⊥平面PAB,故①正确;当PA⊥PB时,四棱锥的侧面中存在三个直角三角形,故②正确;显然△PCD 不能是直角三角形,故四棱锥中不可能存在四组互相垂直的侧面,故③正确;当PA=PB=AB时,四棱锥的四个侧面都是等腰三角形,故④错误.。
2018年高考数学总复习空间几何体的直观图与三视图

第二节空间几何体的直观图与三视图考纲解读1. 认识柱、锥、台、球及其简单组合体的机构特征,并能运用这些特征描述现实生活中简单物体的结构。
2. 能画出简单空间图形(长方体、圆柱、圆锥、棱柱、棱锥等及其及其简易组合)的三视图,能识别三视图,能所表示的立体模型,并会用斜二测画法画出它们的直观图•3. 会用平行投影,画出简单空间图形的三视图与直视图,了解空间图形的不同表示形式•4. 会画某些建筑物的三视图与直视图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).命题趋势探究高考中对本节内容的考查,可以分为以下两类•(1) 柱、锥、台、球的定义和相关性质是基础,以它们为载体考查线线、线面、面面间的关系是中点。
(2) 三视图为新课标新增内容,所以高考会加大对其考查的粒度.在高考中,主要考查三视图和直观图,特别是通过三视图确定原几何体的相关量.多以选择填空题为主,也不排除通过三视图来还原几何体的直观图的解答题,侧重于考查考生对基础知识的掌握以及应用所学知识解决问题的能力知识精讲一、空间几何体的直观图1. 斜二测画法斜二测画法的主要步骤如下:(1) 建立直角坐标系.在已知水平放置的平面图形中取互相垂直的Ox,Oy,建立直角坐标系.(2) 画出斜坐标系.在画直观图的纸上(平面上)画出对应图形.在已知图形平行于X 轴的线段,在直观图中画成平行于O'x',O'y:使.x'O'y' = 45:(或135),它们确定的平面表示水平平面.(3) 画出对应图形.在已知图形平行于x轴的线段,在直观图中画成平行于X'轴的线段,且长度保持不变;在已知图形平行于y轴的线段,在直观图中画成平行于y'轴,且长度变为原来的一般.可简化为“横不变,纵减半”.(4) 擦去辅助线.图画好后,要擦去x'轴、y'轴及为画图添加的辅助线(虚线).被挡住的棱画虚线.注:直观图和平面图形的面积比为.2:4.2. 平行投影与中心投影平行投影的投影线是互相平行的,中心投影的投影线相交于一点.二、空间几何体的三视图1.三视图的概念将几何体由前至后、由左至右、由上至下分别作正投影得到的三个投影图依次叫做该几何体的正(主)视图、左(侧)视图、俯视图,统称三视图•它们依次反应了几何体的高度与长度、高度与宽度、长度与宽度•2•作、看三视图的三原则(1)位置原则:度量原则长对正、高平齐、宽相等即正俯同长、正侧同高、俯侧同宽虚实原则轮廓线、现则实、隐则虚俯视图几何体上下方向投影所得到的投影图反映几何体的长度和宽度口诀正侧同高正府同长府侧同宽或长对正、高平齐、宽相等三、常见几何体的直观图与三视图常见几何体的直观图与三视图如表8-3所示•几何休正(主》祖怕删(左[挽團A. 0B.1C.2D. 3⑵如图8-10 所示丄O'A'B'是L OAB 水平放置的直观图,贝也OAB 的面积为()正三 楼台1F.P M转台iE A Kft题型归纳及思路提示 题型 斜二测画法与直观图思路提示注意用斜二测画法画直观图时水平方向与竖直方向长度的不同 应关系例下列叙述中正确的个数是① 相等的角在直观图中仍相等它们与实物图的对② 长度相等的线段,在直观图中长度仍相等;③ 若两条线段平行,在直观图中对应的线段仍平行④若两条线段垂直则在直观图中对应的线段也互相垂直 圜锚的3亍觇图是2亍 等樓-旳形和1亍阖正屋台及風台的正視图、 侧视圈均为梯够•册视图 为环彬4图 8-10A.6B. 3 2C.6.2D. 12解析⑴ ①因为.xOy=90”的直观图为.x'Oy'=45;或135 ,故①不正确;② 因为y 方向的线段的直观图在 y'方向的长度减半,故②不正确; ③ 因为所有x 方向的线段的直观图方向不变 ,所以y 方向的线段的直观图均在原有基础上旋转45:,故方向统一,故③正确.④ 由③中叙述知,④不正确.故选B.⑵ S O 'A'B‘=?O'A' O'B'sin 45①SOAB=#OA||OB sin90②42.① 十②得一=血业廻=丄丄三=返SOAB|OA||OB|si n90, 2 1 14而 S o'A'B'二13 4sin45’ =3“2,所以 3、、2' 2 S OAB ,即 S OAB =12 . 24故选D.SO 'A'BS OAB 4 -评注(1) ”斜”指的是在直观图中,x',y'轴的夹角为45 , “二测”指的是“平行关系不变”,以及“长度纵变横不变”(2) 直观图中保持不变的有线段的同向性与同向线段长之比直观图与原图的面积关变式1已知正L ABC的边长为a ,以它的一边为x轴,对应的高为y轴,画出它的水4平放置的直观图LA'B'C',则L A'B'C'的面积为().图 8-12B.D.耳216变式2利用斜二测画法 该平面图形的面积为(一个平面图形的直观图时边长为的正方形,如图8-11所示,则A. ,3B.2C.D. 4题型 思路提示已知直观图描绘三视图的原则是 :先看俯视图,观察几何体的摆放姿态长,侧视图与俯视图同宽•直视图=• 三视图再看正视图与侧视图同高,正视图与俯视图同例8.8正三棱柱ABC-ABQ ,如图8-12所示,以面BCC 1B 1为正前方画出的三视图正IA图1 图]分析先看俯视图,垂点法,把C 1,C 投影到底面图 8-13S 8-14变式2将正方体(如图1 所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的左 视图为().解析 由垂点法,把C,C i 分别投影到底面如图8-13所示,所以俯视图中间必有线段变式1如图8-14 所示,3AA' =3BB'二 CC'二 AB2().L ABC 为正三角形则多面体ABC-AA'// BB'// CC'_ 平面 ABC 且 B C 的正视图(也称主视图)是左视题型 思路提示由三视图想象出直观图必须与实物图对应 ,先看俯视图,根据三视图的形状并结合表8-1,定几何体的形状,由口诀 “正侧同高,正俯同长,俯侧同宽”定几何体的相关数据 例8.9 若某空间几何体的三视图如图 8-16所示,则该几何体的体积是()1 2 A. - B.C. 1D. 233分析 三视图为2个矩形和1个三角形,知该几何体是三棱柱.解析先看俯视图,定底面,再由正视图为矩形,侧视图为三角形知该几何体为直三棱柱 然后由口诀知数据,如图8-17 所示,所以以侧面为底得体积 V 二11 .2= 1 .2故选C.变式2如图8-19 所示,是长和宽分别相等的两个矩形,给定下列三个命题① 存在三棱柱,其正视图、俯视图如图8-19所示;C变式3已知棱长为1的正方体的俯视图是一个面积为 面积面积不可能等于()1的正方形,则该正方体的正视图的A. 1B.、2 C ..2-1 2D..2 12直视图=• 直观图简单几何体的基本量的计算俯视图 图 8-16图 8-17变式1如图8-18所示,是一个几何体的三视图 ,若其体积为3 3 ,则a =②存在四棱柱,其正视图、俯视图如图8-19 所示;③存在圆柱,其正视图、俯视图如图8-19 所示. 其中真命题的个数是()A. 3B. 2C. 1D. 0例8.10如图8-20 所示,一个空间几何体的正视图和侧视图都是低为 1,高为2的矩形,俯视图是一个圆,那么该几何体的表面积为().一个正三棱柱的侧棱长和底面边长相等,体积为2\ 3,它的三视图中的俯视图如图8-24 所示,左视图是一个矩形,则这个矩形的面积是正视图俯视图图 8-18俯视图 图 8-19A.2 二B.C.D.分析 解析 由三视图是 由三视图是 22个矩形和 2个矩形和 1个圆, 1个圆, 可知该几何体为圆柱.可知该几何体是圆柱,如图8-21 所示,再由口诀知 数据,所以几何体的表面积乐=2兀卩12丿 15“22二 .故选 2 2B.止视图侧视图俯视图侧视图变式1 A. 变式2 8-208-22某个几何体的三视图如图2、・3cm 3 B. 、3cm 38-22所示,C.若一个正三棱柱的正视图如图俯视图图 8-22则该几何体的体积是( ).3 3 3,3、3cm D.cm 428-23所示,则其侧面积等于变式3 正视图23解析由三视图知该几何体的直观图如图 上底面是长为4,宽为2的矩形;两个梯形侧面垂直于底面为 4;另外两个侧面是矩形,宽为4, 长为、.42 1 ^17,S 表二422 1 7 2= 4示.8故选卩. 变式1如图8-28所示,某几何体的正视图是平行四边形 几何体的体积为(). ,侧视图和俯视图都是矩形 ,则该A. 6、、3B. 9 3C. 12.3D.18. 3正视图俯视图图 8-25变式4 例 8.11一个几何体的三视图如图 一个空间几何体的三视图如图 8-25 所示,则该几何体的体积为 .8-26所示,则该几何体的表面积为(). A. 48 B.32 8、17C.48 8、17D. 807 1丄1俯视图图 8-268-27 所示,该几何体的下底面是边长为,上低长为2,下底长为 4的正方形,4,高4侧视图+正视图图 8-2720 = 1 -563 1 2即 h = 4(cm)变式2 一个几何体的三视图如图8-29所示,则该几何体的体积是变式3 (2012 辽宁理13) 一个几何体的三视图如图 8-30 所示, 则该几何体的表面积为贝H h 二cm.解析 先看俯视图知底面为直角三角形 ,再结合正视图和侧视图均为直角三角形 ,知其中一条侧棱垂直于底面,如图8-32 所示,再根据口诀知数据,所以体积啊理It1J J -4 4■ ■玄 同Cl0.62.4 0.6俯视图图 8-29侧视图11俯视图图 S-30图 8-31例8.12如图8-31所示,3个直角三角形是一个体积为20cm 3的几何体的三视图3A. 8B.38、23C.D.4,2 3变式3若几何体的三视图如图B.-2图 8-34C.8-35 2 3所示, D.则该几何体的体积是().5 6H a11侧视图8-35例8.13一个几何体的三视图及其尺寸 则该几何体的侧面积为cm(单位:cm )如图8-36 所示,2变式2若几何体的三视图如图 8-34 所示,其中正视图、侧视图为正方形, 俯视图是腰长为2的等腰直角三角形,则该几何体的体积是(图 8-32变式1某四面体的三视图如图8-33所示,A. 8B.6、、2 C. 10 D.俯视图侧视图图 S-33该四面体四个面的面积中最大的是().侧视图俯视图正视图 俯视图分析 由三视图是2个三角形和1个矩形,可知该几何体是正四棱锥. 解析 先看俯视图定底面一一正四棱锥的底面,再结合正视图和俯视图,将中心0 “拔地而起”得直观图,如图8-37所示,再由口诀知数据,且可知斜高h' = 5 ,所以几何体1 2的侧面积S 侧二4 8 5 = 80 cm 2 .2变式1某四棱锥的三视图如图 8-38 所示,该四棱锥的表面积是().变式2 一个棱锥的三视图如图8-39 所示,则这个棱锥的体积为变式3 一个五面体的三视图,其正视图与侧视图是等腰直角三角形 ,俯视图为直角梯形,部分边长如图8-40A. 32B.16 16、2 C. 48 D.16 3^ 2*K\33 \♦ 1 \ 乂 * \1 *4* 3 *正视图侧视图主视團图 8-38图 8-39—8 - 正视图8侧视图图 S-378-40所示,则此五面体的体积为正视图题型 直视图= 简单组合体的基本量的计算思路提示先根据三视图想象出几何的构造部分,一般考虑的是球、柱、锥、台体的组合体或其一 部分• 例8.14 如图8-41所示是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 ()•A. 9 二B. 10二C. 11二D. 12二分析先看俯视图定底面•解析 先看俯视图为圆,再结合正视图和侧视图有上、 下两部分,可知该几何体下面是圆柱上 面 是 球 , 如 图 8-42 所 示 , 所 以故选D.评注求几何体的表面积,通常将所给几何体分成基本的球、 柱、锥、台,再将它们的表面 积求和或作差,求体积也是同样的道理.图 441图 S-42变式1 一个几何体的三视图如图 则该几何体的体积为m变式2 一空间几何体的三视图如图8-44所示,则该几何体的体积为().A. 2兀 +2廳B. 4兀 +2巧C.2兀十2^3D4兀 33S 表-4二R 2 2二 R 2 2二 Rh =4 • : i2 2 22+ 2兀乂一;<3=4兀+2兀+6兀=1勿8-43所示(单位:m ),例8.15若某几何体的三视图(单位:cm )如图8-47 所示,则此几何体的体积是cm3.分析先看俯视图定底面——正四棱台的底面 ,再看正视图和侧视图是等腰梯形,属组合体.ffi 8-43w俯视图图 8-44变式3某几何体的三视图如图8-45所示,则它的体积是( 2兀 兀A. 8B. 8C. 8-2::D.33).2二3上面是矩形,下面俯视图正视图 侧视图变式4 一个几何体的三视图如图8-46 所示,则该几何体的体积为 俯观图俯视图 图 8-45图 8-46俯视图图 8-47 图 8-48解析先看俯视图定底面 是正四棱柱,下半部分是正四棱台,如图8-49所示,再结合“正侧同高,正俯同长, 侧 同宽” 知数据, 所 以 几何体 的 体2 1 2 23 V=4 2 4 4 8 8 3 =32 112 = 144cm . 变式1 一个几何体的三视图(单位:cm )如图8-49所示,侧该几何体的表面积是( A.280 B.292 C.360 D.372 变式2 某几何体的三视图(单位:cm )如图8-50所示,侧此几何体的体积是 正四棱台的底面 ,再由正视图和俯视图知该几何体上半部分 cm). k —6正视图 侧视图2 2 6 1 2 正视图側视图图 8-49俯觇图图 8-50变式3 一个几何体的三视图如图8-51所示(单位:m ),则该几何体的体积为例8.16 一个几何体的三视图及长度数据如图 8-52所示,则该几何体的表面积与体积分别为( )•1 俯视图图 8-52分析 先看俯视图定底面,再结合正视图和侧视图•解析 解法一:先看俯视图知底面为正方形,再结合正视图和侧视图知该集合 体如图8-53(a )所示,所以表面积S 表 =12 + 12+2 (1+2) 1 ;+1 2+ 2 1=7+ 2,把侧 面作底知其体积v1 1 =3.故选C2 2解法二:先把侧视图分割,如图8-53 (b )所示,贝U 结合俯视图和正视图知几何 体下半部分是正方体,上半部分是三棱柱(平放)如图 8-53 (c )所示,所以隹=5 12+1+2 丄 + .2 =7 .2, V =12 1 12 =-.故选 C2 2 2D. 8+ . 2 ,21B. 8+血,3 C 7+适」21变式1 (2012湖北理4)已知某几何体的三视图如图 8-54所示,则该几何体的体积为().图 8-54例8.17如图8-55所示为由长方体木块堆成的几何体的三视图,则组成此几何 体的长方体木块的块数为( ).图 8-55C. 10二D. 6二侧视图1 1(a )(b)(c)图 S-53A.竺B. 3 二42A.3块 B4块 C5块 D.6块分析 先看俯视图,从下往上“拔地而起” •解析 先看俯视图定底,再结合正视图和侧视图,从下往上堆积可知其直观图, 如图8-56所示.故选B.图 8-568-57所示,则正视图俯视图图 8-57 题型110 部分三视图=其余三视图思路提示 有三视图还原几何体,画出直观图,再画其三视图 .例8.18 一个长方体去掉一个小长方体,所得几何体的正视图与侧视图如图 8-58所示,则该集合体的俯视图为().正视图侧视图 图 S-5S变式1用单位立方体搭一个几何体,使其主视图和俯视图如图该几何体体积的最小值与最大值分别为( ).I)解析 因为该几何体是一个大长方体去掉一个小长方体,结合正视图及侧视图 中线段均为实线,所以“缺口”就在前面的左上方,所以俯视图“缺口”必在左 下方且为实线.故选D.变式1如图8-59所示,某几何体的正视图与侧视图都是边长为 1的正方形, 且体积为1,该几何体的俯视图可以是().2 图 8-60变式3 ( 2012湖南理3)某几何体的正视图和侧视图均如图 8-61所示,则该几何体的俯视图不可能是().图S-59 入 B.变式2 在一个几何体的三视图中,正视图和俯视图如图 8-60所示,则相应的A最有效训练题32 (限时45分钟)1.用斜二测画法画一个水平放置的平面图形的直观图为如图8-62所示的一个正方形,则原来的图形是()D.M, N,顶点A,D,G的两个截面截去两个角后所得2.如图8-63所示是一个正方体被过棱中点图8-61A B C D3. 如图8-64所示,矩形是水平放置的一个平面图形的直观图,其中,则原图形是A.正方体B.矩形C.菱形D. 一般的平行四边形图8-644. 某几何体的三视图如图8-65所示,它的体积为().A.12 二B.45 二C.57 二D. 81 二俯视图图8-655. 某三棱锥的三视图如图8-66所示,该三棱锥的表面积是(A.28+ 6 5B.30+ 6 5C.56+ 12 5D.60+12.5().4C3 D.4 1367主视图A.1B.2 ” I * * ] *正(G 视图侧(左)视图:cm ),则它的左视图的面积为俯视图图 8-666. 一个四棱锥的底面为正方形,三视图如图 8-67所示,这个四棱锥的体积是().7.若正三棱锥的主视图与俯视图如图 8-68所示(单位 2 cm .斗 1 >俯视图图 8-688. 一多面体的三视图如图 8-69所示,则其体积为 —4 +侧(左)视图正(主)视图9. 已知某几何体的三视图如图 8-70所示,则该几何体的体积为正视閹 侧观图图8 7010. 已知△ ABC 的平面直观图△ ABC '是边长为a 的正三角形,则△ ABC 的面积为 .11. 某高速公路收费站入口处的安全标示墩如图8-71 ( a )所示.墩的上半部分是正三棱锥 P- EFGH 下半部分是长方体 ABCD- EFGH 图8-71 ( b )、图8-71 ( c )分别是该标示墩的正(主)视图和俯视图.(1)请画出该安全标示墩的侧(左)视图;(2 )求安全标示墩的体积;(3)证明:直线 BD 丄平面PEG60cm0) (b) (c)图8-7112. 如图8-72所示是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图8-72所示.櫥探图图8-7 21(1 )求出该几何体的体积;(2 )若N是BC的中点,求证:AN//平面CME;(3)求证:平面BDE X平面BCD。
高三数学空间几何体的三视图与直观图试题
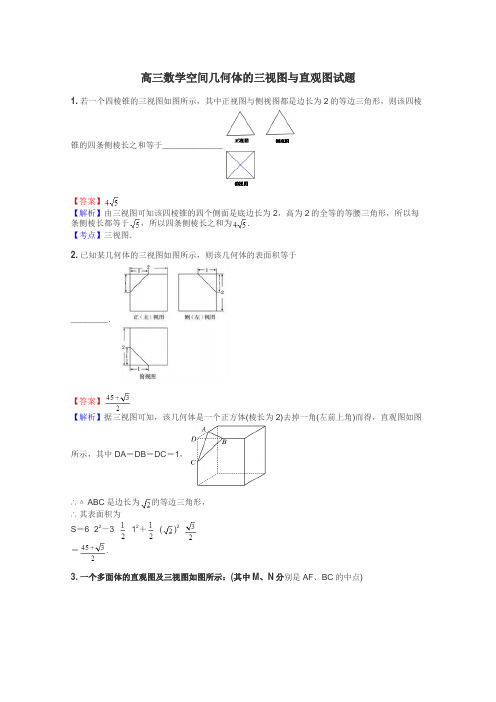
高三数学空间几何体的三视图与直观图试题1.若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2,高为2的全等的等腰三角形,所以每条侧棱长都等于,所以四条侧棱长之和为.【考点】三视图.2.已知某几何体的三视图如图所示,则该几何体的表面积等于________.【答案】【解析】据三视图可知,该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得,直观图如图所示,其中DA=DB=DC=1,∴△ABC是边长为的等边三角形,∴其表面积为S=6×22-3××12+×()2×=.3.一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.【答案】(1)见解析(2)【解析】解:由三视图可知,AB=BC=BF=2,DE=CF=2,∠CBF=.(1)证明:取BF的中点G,连接MG、NG,由M、N分别为AF、BC的中点可得,NG∥CF,MG∥EF,∴平面MNG∥平面CDEF,又MN⊂平面MNG,∴MN∥平面CDEF.(2)取DE的中点H.∵AD=AE,∴AH⊥DE,在直三棱柱ADE-BCF中,平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE.∴AH⊥平面CDEF.∴多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=.S矩形=DE·EF=4,CDEF∴棱锥A-CDEF的体积为V=·S·AH=×4×=.矩形CDEF4.一个几何体的主视图和俯视图如图所示,主视图是边长为的正三角形,俯视图是边长为的正六边形,则该几何体左视图的面积是【答案】【解析】左视图的面积为.【考点】三视图.5.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.6.三棱柱的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)⑴当x=4时,求几何体的侧面积和体积⑵当x取何值时,直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。
高三数学空间几何体的三视图与直观图试题
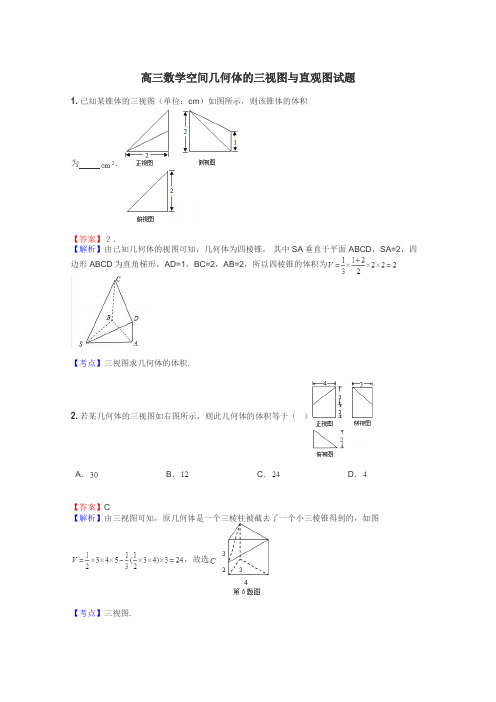
高三数学空间几何体的三视图与直观图试题1.已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为.【答案】2.【解析】由已知几何体的视图可知,几何体为四棱锥,其中SA垂直于平面ABCD,SA=2,四边形ABCD为直角梯形,AD=1,BC=2,AB=2,所以四棱锥的体积为【考点】三视图求几何体的体积.2.若某几何体的三视图如右图所示,则此几何体的体积等于()A.B.C.D.【答案】C【解析】由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,如图,故选【考点】三视图.3.如图是一个几何体的三视图,则该几何体的体积是____________【答案】12【解析】该几何体是一个直三棱柱,底面是等腰直角三角形体积为=12【考点】三视图,几何体的体积.4.下列四个几何体中,每个几何体的三视图中有且仅有两个视图相同的是()A.①②B.①③C.③④D.②④【答案】D【解析】图①的三种视图均相同;图②的正视图与侧视图相同;图③的三种视图均不相同;图④的正视图与侧视图相同.故选D.5.已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为()A.24-B.24-C.24-πD.24-【答案】A【解析】本题主要考查由三视图还原几何体并且求几何体的体积,意在考查考生的空间想象能力以及运算求解能力.由三视图知该几何体是一个长方体截去一个半圆柱,长方体的长,宽,高分别是4,3,2,∴长方体的体积是4×3×2=24,截去的半圆柱的底面圆的半径是1,高是3,∴半圆柱的体积是×π×1×3=,∴所求的几何体的体积是24-,故选A.6.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为()A.B.C.D.【答案】D【解析】由三视图可得,该几何体由一个半圆锥和一个四棱锥组成,半圆锥的底面半径为1,侧视图是一个边长为2的等边三角形,故圆锥的高为,则此半圆锥的体积为××π×1×=,四棱锥的体积为×2×2×=,这个几何体的体积为+=.7.如图所示是某几何体的三视图,则该几何体的表面积是()A.B.C.D.【答案】B【解析】由三视图知,几何体为底面半径为1,高为3的圆柱挖去一个与圆柱同底,高为2的圆锥,所以几何体的表面积故选【考点】几何体的三视图;几何体的表面积.8.如图,三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥底面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形,底宽为原底等边三角形的高,侧视图的高为侧棱长,所以侧视图的面积为,故选B.【考点】三视图9.(2013•湖北)一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有()A.V1<V2<V4<V3B.V1<V3<V2<V4C.V2<V1<V3<V4D.V2<V3<V1<V4【答案】C【解析】由题意以及三视图可知,该几何体从上到下由:圆台、圆柱、正四棱柱、正四棱台组成,体积分别记λ为V1==.V2=12×π×2=2π,V3=2×2×2=8V4==;∵,∴V2<V1<V3<V4故选C.10..已知某几何体的三视图如图所示,其中俯视图是圆,且该几何体的体积为;直径为2的球的体积为.则( )A.B.C.D.【答案】B【解析】由题意,该几何体是一个圆柱挖去一个圆锥得到的几何体,,,∴.选B.【考点】三视图,体积.11.一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图如图所示,则该几何体的侧视图可以为()A. B. C. D.【答案】B【解析】如图几何体:由正视图,俯视图得到的几何体如图所示,为长方体切去一个角的几何体,它的侧视图为B.【考点】三视图12.已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示.(1)画出该三棱锥的直观图.(2)求出侧视图的面积.【答案】(1)见解析 (2)6【解析】(1)如图所示.(2)根据三视图间的关系可得BC=2,∴侧视图中VA==2,∴S=×2×2=6.△VBC13.一个四棱锥的底面为菱形,其三视图如图所示,则这个四棱锥的体积是 .【答案】.【解析】由正视图知,该四棱锥的高,底面菱形的两条对角线的长度分别为和,且两条对角线相互垂直平分,彼此分成四个全等的直角三角形,且直角三角形的两条直角边的长度分别为和,因此其底面积,故该四棱锥的体积.【考点】1.三视图;2.锥体的体积14.某四棱锥的三视图如图所示,则该四棱锥的体积是()A.5B.2C.D.【答案】C【解析】该四棱锥的底面为一直角梯形,高为2,所以V=××(2+3)××2=15.如图所示的是一几何体的三视图,则该几何体的体积是________.【答案】【解析】由三视图可知该几何体是一个正方体去掉一角,其直观图如图所示,其中正方体的棱长为1,所以正方体的体积为1.去掉的三棱锥的体积为××1×1×1=,所以该几何体的体积为1-=.16.三视图如右图的几何体的全面积是()A.B.C.D.【答案】A【解析】由三视图可知该几何体是有一条侧棱垂直于底面的四棱锥.其中底面ABCD是边长为1的正方形,高为1,参考下图四棱锥,计算其全面积为,故选A.【考点】三视图,几何体的全面积.17.一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为的圆,且这个几何体是球体的一部分,则这个几何体的表面积为________________.【答案】.【解析】由三视图知,该几何体是一个球体中切去部分所形成的几何体,该几何体的表面由两个球的大圆的一半和原来球的表面的组成,故该几何体的表面积.【考点】1.三视图;2.空间几何体的表面积18.某几何体的三视图如右图(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A.B.C.D.【答案】A【解析】由三视图可知,几何体是长方体上放一个半圆柱,所以.【考点】1.三视图还原几何体;2.组合体的表面积.19.一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为()A.9B.10C.11D.【答案】C【解析】由三视图可知该几何体是在底面为边长是2的正方形,高是3的直三棱柱的基础上,截去一个底面积为,高为3的三棱锥形成的,所以.【考点】三视图.20.已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为( ) A.4πB.12πC.D.【答案】D【解析】由三棱柱的主视图和俯视图可知,三棱柱的侧棱长为4,底面边长为,过点向底面作垂线,垂足为D,易知AD=2,则外接球的球心O在PD上,设球的半径为,则,在三角形ADP中,,有,解得,所以.【考点】三视图、球的表面积公式.21.如图是一个几何体的三视图,正视图、侧视图是半径为的半圆,俯视图是半径为的圆,若该几何体的表面积为,则 ______.【答案】【解析】由三视图可知该几何体是一个半球,则该半球的表面积,故求得.【考点】本题主要考查立体几何三视图,常见几何题的体积求法.22.一个几何体的三视图如图所示,则该几何体的体积为【答案】【解析】根据题意,可知该几何体为四棱柱,底面是直角梯形,上底为4,下底为5,柱体的高为4,则可知该几何体的体积为,故可知答案为54。
高三数学空间几何体的三视图与直观图试题答案及解析
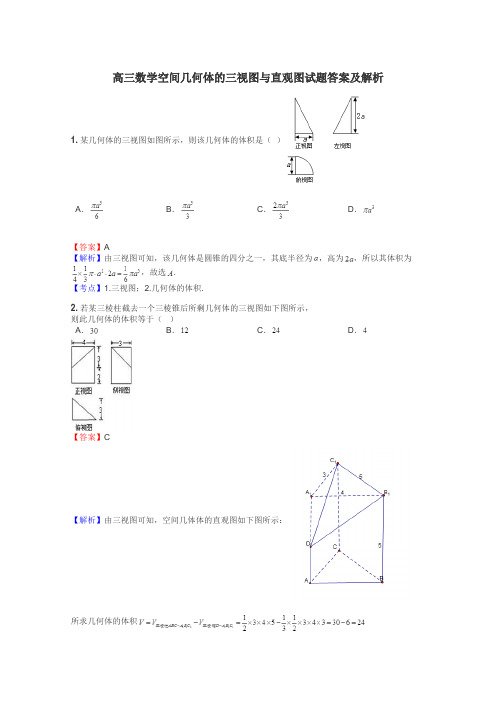
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是圆锥的四分之一,其底半径为,高为,所以其体积为,故选.【考点】1.三视图;2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,则此几何体的体积等于()A.B.C.D.【答案】C【解析】由三视图可知,空间几体体的直观图如下图所示:所求几何体的体积故选C.【考点】1、三视图;2、空间几何体的体积.3.如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为A.πB.2πC.3πD.4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥,且底面是边长为1的正方形,垂直于底面的侧棱长也为1,因此,该几何体可以补形为一个棱长为1的正方体,其外接球就是这个正方体的外接球,直径为正方体的对角线长,即2R=,故R=故外接球表面积为:4πR2=3π.【考点】三视图,几何体的外接球及其表面积4.如图所示,一个三棱锥的三视图是三个直角三角形(单位: cm),则该三棱锥的外接球的表面积为________cm2.【答案】29π【解析】从三棱锥的三视图可知,三棱锥有两侧面与底面垂直,把三棱锥补成长,宽,高分别为4,2,3的长方体,设外接球的半径为R,由42+22+32=4R2得,S=4πR2=29π(cm2).球5.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.2C.D.8【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形,正方形的边长为2.HD=3,BF =1,将相同的两个几何体放在一起,构成一个高为4的长方体,所以该几何体的体积为×2×2×4=8.6.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.7.一个几何体的三视图如图所示,已知这个几何体的体积为,= .【答案】【解析】由三视图知,原几何体是一个四棱锥,底面是面积为的矩形,高为,所以,解得.【考点】三视图,空间几何体的体积.8.如图,水平放置的正三棱柱的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为.【答案】【解析】左视图为一个矩形,长宽分别为,因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为() A.B.C.D.【答案】B【解析】依题意得,该正三棱柱的底面正三角形的边长为2,侧棱长为1.设该正三棱柱的外接球半径为R,易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×=,所以R2=+=,则该球的表面积为4πR2=.10.图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.【答案】16【解析】从三视图可知,这是一个四棱锥,.【考点】三视图.11.如图所示,一个空间几何体的正视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的体积为 ( )A.B.C.D.【答案】B【解析】几何体是圆柱,.【考点】三视图,圆柱的体积.12.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )A.1B.C.D.【答案】B【解析】由三视图可知,此几何体为三棱锥,如图,其中正视图为,是边长为2的正三角形,,且,底面为等腰直角三角形,,所以体积为,故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.【答案】C【解析】由题意知,正视图的最大面积为对角面的面积,最小面积为,而,故选C.【考点】三视图.14.已知某几何体的三视图如右图所示,其中俯视图是圆,且该几何体的体积为;直径为2的球的体积为.则()A.B.C.D.【答案】C【解析】由题意,该几何体是一个圆柱挖去一个圆锥得到的几何体,,,∴.选B.【考点】三视图,体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()A.B.C.D.【答案】B【解析】过B作BD⊥AC于点D,则BD=2,CD=2,所以BC=,因为SC⊥平面ABC,所以SC⊥BC,所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是由一个半圆柱和一个三棱锥拼接而成,且半圆柱的底面是半径为的半圆,高为,其底面积为,故其体积为,三棱锥的底面是一个直角三角形,三棱锥的高也为,其底面积为,故其体积为,所以该几何体的体积为,故选A.【考点】1.三视图;2.组合体的体积17.右图为某几何体的三视图,则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1,高为1的圆柱与半径为1的四分之一的球的组合体,所以体积为【考点】三视图18.一个空间几何体的三视图如图所示,该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的主视图与俯视图如右上图所示,则二面角 C-AB-D的正切值为.【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C-AB-D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形,则原△ABC 的面积为()A.a2B.a2C.a2D.a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶,则易知S= ( a)2,∴S=a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD =AD =2EC =2.(1)请画出该几何体的三视图; (2)求四棱锥B-CEPD 的体积.【答案】(1)见解析 (2)2【解析】解:(1)该组合体的三视图如图所示.(2)∵PD ⊥平面ABCD , PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形,∴BC ⊥CD ,且BC =DC =AD =2. 又∵平面PDCE∩平面ABCD =CD , BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ,DC ⊂平面ABCD , ∴PD ⊥DC.又∵EC ∥PD ,PD =2,EC =1,∴四边形PDCE 为一个直角梯形,其面积: S 梯形PDCE = (PD +EC)·DC =×3×2=3, ∴四棱锥B-CEPD 的体积V B-CEPD =S 梯形PDCE ·BC =×3×2=2.23. 某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π【答案】A【解析】将三视图还原成直观图为:上面是一个正四棱柱,下面是半个圆柱体.所以V=2×2×4+×22×π×4=16+8π.24.某几何体的三视图如图所示,则其体积为________.【答案】【解析】由三视图还原几何体为半个圆锥,高为2,底面半圆的半径r=1.∴体积V=×(π×12×2)=.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).(1)求四棱锥P-ABCD的体积;(2)若G为BC上的动点,求证:AE⊥PG.【答案】(1)(2)见解析【解析】(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4 ,BE=2 ,AB=4.∴VP-ABCD =PA·S四边形ABCD=×4 ×4×4=.(2)∵=,∠EBA=∠BAP=90°,∴△EBA∽△BAP,∴∠BEA=∠PBA.∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,∴AE⊥平面PBC.∵PG⊂平面PBC,∴AE⊥PG.26.如图所示,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为________.【答案】9【解析】由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S=×6×3=9,∴V=Sh=×9×3=9.27.某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第49练 三视图与直观图
1.一个多面体的三视图如图所示,则该多面体的体积为( )
A.23
3 B.476
C .6
D .7
2.(2017·兰州诊断考试)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )
A .2 B.9
2 C.32 D .3
3.(2017·太原调研)一个几何体的三视图如图所示(单位:cm),则该几何体的体积为( )
A.⎝
⎛⎭⎪⎫32+π4cm 3 B.⎝
⎛⎭⎪⎫32+π2cm 3
C.⎝
⎛⎭⎪⎫41+π4cm 3 D.⎝
⎛⎭⎪⎫41+π2cm 3 4.(2016·北京)某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A.16
B.13
C.12
D .1
5.如图,某直观图中,A ′C ′∥y ′轴,B ′C ′∥x ′轴,则该直观图所表示的平面图形是( )
A .正三角形
B .锐角三角形
C .钝角三角形
D .直角三角形
6.(2016·郑州模拟)某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy 的最大值为( )
A.32 B.327
C.64 D.647
7.某几何体的直观图如图所示,则该几何体的正视图和侧视图可能正确的是( )
8.(2017·郑州月考)如图,某几何体的正视图和俯视图都是矩形,侧视图是平行四边形,则该几何体的表面积为( )
A .15+3 3
B .9 3
C .30+6 3
D .18 3
二、填空题
9.如图,矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,其中O ′A ′=6,O ′C ′=2,则原图形OABC 的面积为________.
10.(2016·河北衡水中学四调)一个几何体的正视图和侧视图都是边长为1的正方形,且体积为12,则这个几何体的俯视图可能是下列图形中的________.(填入所有可能的图形前的编
号)
①锐角三角形;②直角三角形;③钝角三角形;④四边形;⑤扇形;⑥圆.
11.如图,△O ′A ′B ′是△OAB 的水平放置的直观图,其中O ′A ′=O ′B ′=2,则△OAB 的面积是________.
12.下列说法正确的是________.
①相等的线段在直观图中仍然相等;
②若两条线段平行,则在直观图中对应的两条线段仍然平行;
③两个全等三角形的直观图一定也全等;
④两个图形的直观图是全等的三角形,则这两个图形一定是全等三角形.
答案精析
1.A [该几何体是正方体去掉两个角所形成的多面体,其体积为V =2×2×2-2×13×
1
2×1×1×1=23
3
.]
2.D [由三视图知,该几何体是四棱锥,底面是一个直角梯形,底面积S =1
2×(1+2)×2
=3,高h =x ,所以其体积V =13Sh =1
3
×3x =3,解得x =3,故选D.]
3.C [根据给定的三视图可知,该几何体对应的直观图是两个长方体和一个圆柱的组合体,∴所求几何体的体积V =4×4×2+π×⎝ ⎛⎭⎪⎫122×1+3×3×1=⎝ ⎛⎭⎪⎫41+π4cm 3.]
4.A [由三视图知,三棱锥如图所示:由侧视图得高h =1,
又底面积S =12×1×1=1
2.
所以体积V =13Sh =1
6
.]
5.D [由直观图中,A ′C ′∥y ′轴,B ′C ′∥x ′轴,还原后原图AC ∥y 轴,BC ∥x 轴.直观图还原为平面图是直角三角形.故选D.]
6.C [依题意,题中的几何体是三棱锥P -ABC (如图所示), 其中△ABC 是直角三角形,AB ⊥BC ,PA ⊥平面ABC ,
BC =27,PA 2+y 2=102,(27)2+PA 2=x 2,
因此xy =x 102
-[x 2
-(27)2
]=x 128-x 2
≤x 2+(128-x 2)
2
=64,当且仅当x 2=128-x 2
,
即x =8时取等号,因此xy 的最大值是64.]
7.A [由几何体的直观图,可知该几何体可以看作由正方体ABCD -A 1B 1C 1D 1割掉四个角后所得的几何体ABCD -MNPQ ,如图所示,该几何体的正视图就是其在正方体的平面CDD 1C 1上的投影,显然为正方形CDD 1C 1与△CDQ 的组合;该几何体的侧视图就是其在平面BCC 1B 1上的投影,显然为正方形BCC 1B 1和△BCP 的组合.综上,只有A 选项正确.]
8.C [题图中所示的三视图对应的直观图是四棱柱,其底面边长为2+22
-(3)2
=3,侧视图的高为3,其表面积为2×3×3+2×3×2+2×3×3=30+6 3.] 9.24 2
解析 因为矩形O ′A ′B ′C ′是水平放置的一个平面图形的直观图,所以根据画直观图的基本原理知原图形是底边长为6的平行四边形,其高是2×
O ′C ′
cos
π4
=42,因此面积是
6×42=242,故答案为24 2. 10.②
解析 若俯视图是四边形,则此四边形也是边长为1的正方形,即几何体是棱长为1的正方体,其体积为1,不合题意;若俯视图是扇形或圆,则体积值中含π,所以俯视图不会是扇形或圆;若俯视图是锐角三角形或钝角三角形,则在正视图或侧视图正方形中还有一条竖直的实线或虚线,所以俯视图不会是锐角三角形或钝角三角形;若俯视图是腰长为1的等腰直角三角形,则此几何体体积为12×1×1×1=1
2,且满足正视图和侧视图都是边长为1的正方
形.故这个几何体的俯视图可能是②. 11.4
解析 在Rt △OAB 中,OA =2,OB =4,△OAB 的面积是S =1
2×2×4=4.
12.②
解析 用斜二测画法画水平放置的平面图形的直观图时,原图中的平行线在直观图中仍是平行线.。
