四年级奥数变化规律(一)解读
四年级奥数:第9讲 变化规律(一)

第9講變化規律(一)一、知識要點和、差的規律見下表(m≠0)二、精講精練【例題1】兩個數相加,一個加數增加9,另一個加數減少9,和是否發生變化?練習1:1.兩個數相加,一個數減8,另一個數加8,和是否變化?2.兩個數相加,一個數加3.另一個數也加3.和起什麼變化?【例題2】兩個數相加,如果一個加數增加10,要使和增加6,那麼另一個加數應有什麼變化?練習2:1.兩個數相加,如果一個加數增加8,要使和增加15,另一個加數應有什麼變化?2.兩個數相加,如果一個加數增加8,要使和減少15,另一個加數應有什麼變化?【例題3】兩數相減,如果被減數增加8,減數也增加8,差是否起變化?練習3:1.兩數相減,被減數減少6,減數也減少6,差是否起變化?2.兩數相減,被減數增加12.減數減少12.差起什麼變化?【例題4】兩數相乘,如果一個因數擴大8倍,另一個因數縮小2倍,積將有什麼變化?練習4:1.兩數相乘,如果一個因數縮小4倍,另一個因數擴大4倍,積是否起變化?2.兩數相乘,如果一個因數擴大3倍,另一個因數縮小12倍,積將有什麼變化?【例題5】兩數相除,如果被除數擴大4倍,除數縮小2倍,商將怎樣變化?練習5:1.兩數相除,被除數擴大30倍,除數縮小5倍,商將怎樣變化?2.兩數相除,被除數縮小12倍,除數縮小2倍,商將怎樣變化?三、課後作業1.兩個數相加,一個數減6,另一個數減2.和起什麼變化?2.兩個數相加,如果一個加數減少8,要使和減少8,另一個加數應有什麼變化?3.兩數相減,被減數減少10,減數增加10,差起什麼變化?4.兩數相乘,如果一個因數擴大3倍,另一個因數擴大6倍,積將有什麼變化?5.兩數相除,除數擴大6倍,要使商擴大3倍,被除數應怎樣變化?。
四年级奥数数字变换与规律的奥妙探索与应用

四年级奥数数字变换与规律的奥妙探索与应用数字变换与规律是奥数中一个重要的题型,通过探索数字的规律并应用到实际问题中,可以培养学生的逻辑思维和分析能力。
本文将从四年级的角度出发,对数字变换与规律的奥妙进行探索和应用。
一、数字的顺序变换在数字的顺序变换中,学生需要观察一组数字的排列顺序,找出其中的规律,并根据规律将数字进行变换。
以简单的例子来说明如何进行顺序变换。
例1:给定一组数字:2,4,6,8,10,...观察这组数字,我们可以发现每个数字都是前一个数字加上2,因此可以将规律表示为“每个数字是前一个数字加2”。
根据这个规律,我们可以继续写下去:12,14,16,18,20,...同样的方法可以应用到其他的数字序列中,通过发现规律,我们可以进行数字的顺序变换。
二、数字的排列组合在数字的排列组合中,学生需要观察给定的数字,并找出它们之间的关系,然后进行排列组合。
以下是一个例子来说明该过程。
例2:给定一组数字:1,2,3,4观察这组数字,我们可以发现每个数字都能和其他数字进行组合,而且每个数字只能出现一次。
因此我们可以列出所有的排列组合:1,2,3,41,2,4,31,3,2,41,3,4,21,4,2,31,4,3,22,1,3,42,1,4,32,3,1,42,3,4,12,4,1,32,4,3,13,1,2,43,1,4,23,2,1,43,2,4,13,4,1,23,4,2,14,1,2,34,1,3,24,2,1,34,2,3,14,3,1,24,3,2,1通过数字排列组合的训练,可以培养学生的思维灵活性和观察能力。
三、数字的奇偶变换数字的奇偶变换是另一类常见的数字变换题型。
学生需要观察给定的数字,然后按照一定的规则进行奇偶变换。
以下是一个例子。
例3:给定一组数字:1,2,3,4,5,6,7,8,9,10观察这组数字,我们可以发现规律:奇数变换为偶数,偶数变换为奇数。
根据这个规律,我们可以进行奇偶变换:1(奇)变为2(偶)2(偶)变为1(奇)3(奇)变为4(偶)4(偶)变为3(奇)5(奇)变为6(偶)6(偶)变为5(奇)7(奇)变为8(偶)8(偶)变为7(奇)9(奇)变为10(偶)10(偶)变为9(奇)通过这样的训练,学生可以培养对数字奇偶关系的敏感度,并能够准确地进行奇偶变换。
四年级数学奥数讲义+练习-第1讲 找规律(一)(全国通用版,含答案)

奥数已经成为现在孩子学习的加强工具。
一种思维方式的训练,一种让孩子学以致用,举一反三的法宝,一种可以扩宽孩子思维的奥秘兵器。
老师经常对学生们说,养成好的学习品质,拥有好的学习方法比学习知识自己重要得多,它是学好知识的前提。
学习奥数更是如此。
奥数题对学生们的要求是非常严格的,你既要注意到思维有广度有深度,在做题时还要加倍小心。
有些题往往是一字之差,谬之千里。
习惯的养成不是一朝一夕之功。
要养成好的学习习惯,首先,需要学生对这个问题有个正确的认识,有些家长往往错误地认为。
只要是标题问题理解了,出点小错不妨。
这样做的结果,往往助长了学生粗心大意之习气。
而在奥数题中,一点小错,往往是致命的。
学生做题出错了,我们应把它做为一个好的教育学生的契机,引导学生找出错误原因并不停积累,是知识方面的,要牢记。
是习惯方面的,要改正。
相信久而久之,好的习惯必能养成。
第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26(2)3,6,9,12,(),18,21(3)33,28,23,(),13,(),3(4)55,49,43,(),31,(),19(5)3,6,12,(),48,(),192(6)2,6,18,(),162,()(7)128,64,32,(),8,(),2(8)19,3,17,3,15,3,(),(),11,3..【答案】(1)18(2)15(3)18,8(4)37,25(5)24,96(6)54,486(7)16,4(8)13,3【例题2】先找出下列数排列的规律,然后在括号里填上适当的数。
四年级奥数数与形中的奥妙规律

四年级奥数数与形中的奥妙规律四年级奥数中的数与形的奥妙规律奥数(奥林匹克数学竞赛)作为一种具有挑战性和启发性的数学活动,被广泛应用于学生的数学学习中。
在四年级,奥数中的数与形的奥妙规律成为了学生们学习的重点之一。
通过数与形的结合,孩子们在进行数学推理和思维训练的同时,也能够培养他们的观察力和创造力。
本文将探讨四年级奥数中的数与形之间的奥妙规律。
一、数与形的关系数与形是数学中两个重要的概念,它们之间存在着密切的联系。
数是通过计数和比较来表示事物的数量,而形则是描述事物的形状和结构。
在奥数中,数与形的关系体现在数学问题中的模式和规律中。
1.1 数量与图形的对应关系在四年级的奥数中,孩子们需要掌握数量与图形的对应关系。
这种对应关系可以通过图形的形状和数量之间的关系进行描述。
例如,当某个图形中的小正方形数量与该图形的边长之间存在着一定的规律时,孩子们就可以通过计数的方式来确定图形中正方形的个数,从而通过图形推理出数的规律。
1.2 数量与排列的关系除了图形与数量之间的对应关系外,数与形还可以通过排列的方式进行关联。
排列指的是将不同的元素按照一定的规则进行组合和排列。
在奥数中,孩子们需要通过掌握排列规律,来解决与数与形相关的问题。
例如,给定一组数字,求出其中能够组成的所有三位数,要求不重复使用数字且不能以0开头。
通过排列的方法,孩子们可以将这个问题转化为一道有序排列的问题,从而得到所有可能的三位数。
二、奥数中的数与形之间的奥妙规律在四年级的奥数中,数与形之间存在着许多奥妙的规律。
这些规律的发现和应用可以帮助学生们提高他们的数学思维和解决问题的能力。
以下是一些常见的奥数规律:2.1 斐波那契数列与黄金分割斐波那契数列是一个非常有趣的数列。
它的规律是前两项之和等于后一项,即1,1,2,3,5,8,13...。
孩子们可以通过观察数列中相邻两项的比值,发现这个比值逐渐趋近于一个特殊的数值——黄金分割。
黄金分割是指一条线段分为两部分,较大部分与整体之比等于较小部分与较大部分之比。
四年级奥数思维训练专题-规律

四年级奥数思维训练专题-规律(一)专题简析:在进行加、减、乘、除四则运算是时一个数不变,另一个数发生改变,结果也会发生相应变化,抓住变化规律解题,会让我们的计算更轻松。
例1:两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?分析:一个加数增加9,假如另一个加数不变,和就增加9;一个加数不变,另一个加数减少9,和就减少9。
相当于和先增加9,又减少9,所以和不发生变化。
试一试1:两个数相加,一个数减6,另一个数减2,和起什么变化?例2:两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?分析:一个加数增加10,和就增加10。
现在“要使和增加6”,另一个加数应减少10-6=4。
试一试2:两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?例3:两数相减,如果被减数增加8,减数也增加8,差是否起变化?分析:被减数增加8,差就增加8;减数增加8,差就减少8。
差先增加8,接着又减少8,所以不发生变化。
试一试3:两数相减,被减数增加12,减数减少12,差起什么变化?例4:两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?分析:一个因数扩大8倍,积将扩大8倍;另一个因数缩小2倍,积将缩小2倍。
积先扩大8倍又缩小2倍,因此,积扩大:8÷2=4倍。
试一试4:两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?例5:两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?分析:被除数扩大4倍,商就扩大4倍;除数缩小2倍,商就扩大2倍。
商先扩大4倍,接着又扩大2倍,商将扩大4×2=8倍。
试一试5:两数相除,被除数缩小12倍,除数缩小2倍,商将怎样变化?专题十变化规律(二)专题简析:前面,我们学习了和、差、积、商的变化规律。
现在,我们利用这些规律来解决一些较简单的问题。
例1:两数相减,被减数减少8,要使差减少12,减数应有什么变化?分析:被减数减少8,假如减数不变,差也减少8;现在要使差减少12,减数应增加12-8=4。
四年级奥数数字规律的奇妙特性

四年级奥数数字规律的奇妙特性奥数(奥林匹克数学竞赛)作为一种智力竞赛项目,旨在培养学生的逻辑推理能力和数学思维能力。
其中,数字规律是奥数的一个重要内容,它涉及到数学中数字的变化和特性。
在四年级的奥数学习中,数字规律的奇妙特性给孩子们带来了很多的乐趣和启发。
本文将从数列规律、数字排列规律和数独规律三个方面,介绍四年级奥数数字规律的奇妙特性。
一、数列规律数列是一系列按照特定规则排列的数字组合。
在解题过程中,孩子们需要观察数字之间的变化,找出规律并运用规律进行推理。
1. 等差数列规律等差数列是指数字之间的差值是恒定的数列。
例如,1、4、7、10、13就是一个等差数列,公差为3。
对于四年级的学生来说,最常见的等差数列规律就是2、4、6、8、10……,这是一个公差为2的等差数列。
通过观察等差数列的规律,孩子们可以预测下一个数字是多少,从而提高他们的数学推理能力。
2. 斐波那契数列规律斐波那契数列是指从第三个数字开始,每个数字都是前两个数字之和的数列。
例如,1、1、2、3、5、8就是一个斐波那契数列。
通过观察斐波那契数列的规律,孩子们可以发现每个数字都是前两个数字之和,这种规律在生活中的很多场景中都有应用,例如花瓶里的花朵数目、兔子繁殖等。
3. 平方数列规律平方数列是指数字之间是平方关系的数列。
例如,1、4、9、16、25就是一个平方数列。
通过观察平方数列的规律,孩子们可以发现每个数字都是前一个数字的平方,这有助于提高他们的计算能力和数学思维能力。
二、数字排列规律数字排列是指将一组数字按照特定的规则进行排列组合,形成一个新的数字序列。
1. 阶乘规律阶乘是指从1到某个正整数之间所有整数的乘积。
例如,4的阶乘表示为4!,等于1 × 2 × 3 × 4 = 24。
通过观察阶乘的规律,孩子们可以发现阶乘的结果会随着数字的增大而迅速增加,这是一种非常有趣的数字现象。
2. 递增/递减规律递增或递减规律是指数字排列中的数值按照一定的增加或减少顺序排列。
(完整版)小学四年级奥数变化规律(一)

第九周变化规律(一)例 1:两个数相加,一个加数增添 9,另一个加数减少 9,和能否发生变化?剖析与解答:一个加数增添 9,若是另一个加数不变,和就增添9;若是一个加数不变,另一个加数减少 9,和就减少 9;和先增加 9,接着又减少9,所以不发生变化。
练习一1,两个数相加,一个数减8,另一个数加 8,和能否变化?2,两个数相加,一个数加 3,另一个数也加 3,和起什么变化?3,两个数相加,一个数减6,另一个数减 2,和起什么变化?例 2:两个数相加,假如一个加数增添 10,要使和增添 6,那么另一个加数应有什么变化?剖析与解答:一个加数增添 10,若是另一个加数不变,和就增添10。
此刻要使和增添6,那么另一个加数应减少10-6=4。
练习二1,两个数相加,假如一个加数增添8,要使和增添15,另一个加数应有什么变化?2,两个数相加,假如一个加数增添8,要使和减少15,另一个加数应有什么变化?3,两个数相加,假如一个加数减少8,要使和减少 8,另一个加数应有什么变化?例 3:两数相减,假如被减数增添 8,减数也增添 8,差能否起变化?剖析与解答:被减数增添 8,若是减数不变,差就增添 8;若是被减数不变,减数增添 8,差就减少 8。
两个数的差先增添 8,接着又减少 8,所以不起什么变化。
练习三1,两数相减,被减数减少6,减数也减少 6,差能否起变化?2,两数相减,被减数增添12,减数减少 12,差起什么变化?3,两数相减,被减数减少10,减数增添 10,差起什么变化?例 4:两数相乘,假如一个因数扩大 8 倍,另一个因数减小 2 倍,积将有什么变化?剖析与解答:假如一个因数扩大 8 倍,另一个因数不变,积将扩大8 倍;假如一个因数不变,另一个因数减小 2 倍,积将减小 2 倍。
积先扩大8 倍又减小 2 倍,所以,积扩大了8÷2=4 倍。
练习四1,两数相乘,假如一个因数减小 4 倍,另一个因数扩大 4 倍,和能否起变化?2,两数相乘,假如一个因数扩大 3 倍,另一个因数减小12 倍,积将有什么变化?3,两数相乘,假如一个因数扩大 3 倍,另一个因数扩大 6 倍,积将有什么变化?例 5:两数相除,假如被除数扩大 4 倍,除数减小 2 倍,商将如何变化?剖析与解答:假如被除数扩大 4 倍,除数不变,商就扩大 4 倍;如果被除数不变,除数减小 2 倍,商就扩大 2 倍。
小学四年级奥数第9讲 变化规律(一)(含答案分析)
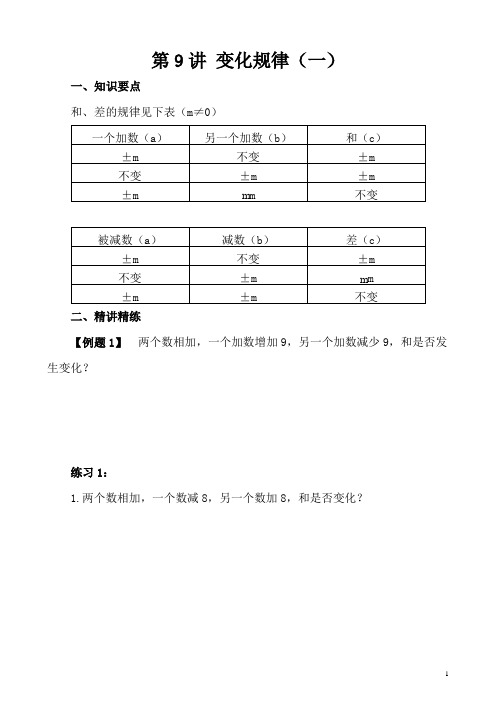
第9讲变化规律(一)一、知识要点和、差的规律见下表(m≠0)二、精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?练习1:1.两个数相加,一个数减8,另一个数加8,和是否变化?2.两个数相加,一个数加3.另一个数也加3.和起什么变化?【例题2】两个数相加,如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化?练习2:1.两个数相加,如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加,如果一个加数增加8,要使和减少15,另一个加数应有什么变化?【例题3】两数相减,如果被减数增加8,减数也增加8,差是否起变化?练习3:1.两数相减,被减数减少6,减数也减少6,差是否起变化?2.两数相减,被减数增加12.减数减少12.差起什么变化?【例题4】两数相乘,如果一个因数扩大8倍,另一个因数缩小2倍,积将有什么变化?练习4:1.两数相乘,如果一个因数缩小4倍,另一个因数扩大4倍,积是否起变化?2.两数相乘,如果一个因数扩大3倍,另一个因数缩小12倍,积将有什么变化?【例题5】两数相除,如果被除数扩大4倍,除数缩小2倍,商将怎样变化?练习5:1.两数相除,被除数扩大30倍,除数缩小5倍,商将怎样变化?2.两数相除,被除数缩小12倍,除数缩小2倍,商将怎样变化?三、课后作业1.两个数相加,一个数减6,另一个数减2.和起什么变化?2.两个数相加,如果一个加数减少8,要使和减少8,另一个加数应有什么变化?3.两数相减,被减数减少10,减数增加10,差起什么变化?4.两数相乘,如果一个因数扩大3倍,另一个因数扩大6倍,积将有什么变化?5.两数相除,除数扩大6倍,要使商扩大3倍,被除数应怎样变化?第9讲变化规律(一)一、知识要点和、差的规律见下表(m≠0)二、精讲精练【例题1】两个数相加,一个加数增加9,另一个加数减少9,和是否发生变化?【思路导航】一个加数增加9,假如另一个加数不变,和就增加9;假如一个加数不变,另一个加数减少9,和就减少9;和先增加9,接着又减少9,所以不发生变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习五
1、在一个减法算式里,被减数、减数与差的和是 120,而差是减数的3倍。如果差不变,被减数减 少5,减数应变为多少?
2、在一个减法算式里,被减数、减数与差的和是 90,而差是减数的2倍。如果被减数不变,差增加 7,减数应变为多少?
3、在一个减法算式里,被减数、减数与差的和是 180,而差比减数少8。如果被减数不变,减数减 少16,差应变为多少?
• 分析与解答:被减数增加8,假如减数不变,差就增加8; 假如被减数不变,减数增加8,差就减少8。两个数的差 先增加8,接着又减少8,所以不起什么变化。
练习三
1,两数相减,被减数减少6,减数也减少6,差是否起变 化?
2,两数相减,被减数增加12,减数减少12,差起什么变 化?
3,两数相减,被减数减少10
1,两个数相加,如果一个加数增加8,要使和增加15,另一 个加数应有什么变化?
2,两个数相加,如果一个加数增加8,要使和减少15,另一 个加数应有什么变化?
3,两个数相加,如果一个加数减少8,要使和减少8,另一 个加数应有什么变化?
例3:两数相减,如果被减数增加8,减数 也增加8,差是否起变化?
练习一
1、两个数相加,一个数减8,另一个数加8,和是否变 化?
2、两个数相加,一个数加3,另一个数也加3,和起什 么变化?
3、两个数相加,一个数减6,另一个数减2,和起什么 变化?
例2:两个数相加,如果一个加数增加10,要 使和增加6,那么另一个加数应有什么变化?
• 分析与解答:一个加数增加10,假如另一个 加数不变,和就增加10。现在要使和增加6, 那么另一个加数应减少10-6=4。
3,两数相减,减数减少9,要使差增加16,被减数应有 什么变化?
例5:被减数、减数、差相加得2076,差是减 数的一半。如果被减数不变,差增加42,减 数应变为多少?
思路导航: 减数与差的和即是被减数。2076里有2个被减数,被减 数等于2076÷2=1038.差是减数的一半,也就是说减 数是差的2倍,差应为1038÷(2+1)=346,减数为 346×2=692。被减数不变,差增加42,减数应减少42, 所以减数应变为692-42=650.
例4:两数相减,被减数减少8,要使 差减少12,减数应有什么变化?
• 分析与解答:被减数减少8,假如减数不变,差也减 少8;现在要使差减少12,减数应增加12-8=4。
练习四
1,两数相减,如果被减数增加6,要使差增加15,减数 应有什么变化?
2,两数相减,如果被减数增加20,要使差减少12,减数 应有什么变化?
变化规律(一)
主讲:雷老师
和、差的变化规律
一个加数 (a)
±m
不变
另一个加 数 (b)
不变
±m
和(c)
±m ±m
±m
-
不变
+m
被减数(a) 减数(b) 差(c)
±m
不变
±m
不变
±m ±m
±m - +m
不变
例1:两个数相加,一个加数增加9,另一个 加数减少9,和是否发生变化?
• 分析与解答:一个加数增加9,假如另一个加数不变,和 就增加9;假如一个加数不变,另一个加数减少9,和就 减少9;和先增加9,接着又减少9,所以不发生变化。
