第1章 机器人数学基础(2)(1)
合集下载
第一章机器人运动学(1)解析

点的齐次坐标(补充)
一般来说,n维空间的齐次坐标表示是一个(n+1)维空间 实体。有一个特定的投影附加于n维空间,也可以把它看作 一个附加于每个矢量的特定坐标—比例系数。
v
ai
bj
ck
式中i, j, k为x, y, z 轴上的单位矢量,
列矩阵 x
a= x
, b= y
规定,一般情况:41列阵[a b c w]T 中 w 为 零,且满足 a2 + b2 + c2 = 1,则[a b c 0]T 中 的 a、 图1.2 坐标轴的方向表示 b、c 表示某轴的方向; w不为零,则[a b c w]T 表 示空间某点的位置。
图示的矢量 u 的方向用可表达为: u = [a b c 0]T
B A
R
A B
R
1
A B
R
T
坐标变换
2)平ቤተ መጻሕፍቲ ባይዱ坐标变换 坐标系{A}和{B}
具有相同的方位,但 原点不重合.则点P在 两个坐标系中的位置 矢量满足下式:
A P B P A PB0
Robotics 数学基础
坐标变换
3).复合变换 一般情况原点既
不重和,方位也不同. 这时有:
A
P
A B
RB
矩阵描述.
二、齐次坐标表示
将一个 n 维空间的点用 n+1 维坐标表示,则该 n+1 维坐标即为 n 维坐标的齐次坐标。记为:
P = [a b c w]T
w 称为该齐次坐标中的比例因子,当取w=1 时, 其表示方法称为齐次坐标的规格化形式,即:
P = [PX PY PZ 1]T
当 w 不为1时,则相当于将该列阵中各元素同时 乘以一个非零的比例因子w,仍表示同一点P,即: a = wPX;b = wPY;c = wPZ。
工业机器人技术基础第1章 工业机器人概论
法国
英国 意大利、瑞典等
注重机器人基础研究
二十世纪70年代末开始研究,但 中途限制发展 发展迅速
中国
70年代萌芽期,80年代的开发期 和90年代后的应用期。
靠后
沈阳新松、 清华、哈工 大
国际上的工业机器人公司主要分为日系和欧系。
日系有:安川、OTC、松下、 发那科 (FANUC)和安川电机 (Yaskawa)。 欧系有:德国的KUKA、CLOOS、瑞典的ABB、意大利的COMAU,英国的
第一,创新能力较弱,核心技术和核心关键部件受制于人,尤其是高精度的减速器长
期需要进口,缺乏自主研发产品,影响总体机器人产业发展。 第二,产业规模小,市场满足率低,相关基础设施服务体系建设明显滞后。中国工业
机器人企业虽然形成了自己的部分品牌,但不能与国际知名品牌形成有力竞争。
第三,行业归口,产业规划需要进一步明确。 随着工业机器人的应用越来越广泛,我国也在积极推动我国机器人产业的发展。 尤其是进入“十三.五”以来,国家出台的《机器人产业发展规划(2016-2020)》对机 器人产业进行了全面规划,要求行业、企业搞好系列化、通用化、模块化设计,积极 推进工业机器人产业化进程。
工业机器人技术基础
目 录
第一章 工业机器人概论
第二章 工业机器人的数学基础
第三章 工业机器人的机械系统 第四章 工业机器人的动力系统 第五章 工业机器人的感知系统 第六章 工业机器人的控制系统
第七章 工业机器人编程与调试
第1章 工业机器人概论
工业机器人技术基础
主要内容
1.1 工业机器人定义及其发展(了解) 1.2 工业机器人基本组成及技术参数(掌握)
第1章 工业机器人概论
工业机器人技术基础
工业机器人运动学-1数学基础

则可得到如图1.8所示的点向量n.变换过程如下
1 00 4 2
6
0 1 0 -3 7
4
n = Trans <4, -3, 7> w = 0 0 1 7 3 = 10
0 00 1 1
1
z
z
•n
•v
0
2
y
2
w•
u•
•w
x
-7
•v
图1.7 Rot ( z, 90°) Rot ( y, 90°)
0•
•
7
y
x
已知两个向量
a = ax i + ay j + az k
b = bx i + by j + bz k
〔1.1〕
向量的点积是标量.用" ·"来定义向量点积,即
a ·b = ax bx + ay by + az bz
〔1.2 〕
向量的叉积是一个垂直于由叉积的两个向量构成的平面的向量.用"×" 表示叉积,即
1.2.1 点向量〔Point vectors〕 点向量描述空间的一个点在某个坐标系的空间位
置.同一个点在不同坐标系的描述及位置向量的值也不同.如图 1.1中,点p在E坐标系上表示为 Ev,在H坐标系上表示为 Hu,且v ≠ u.一个点向量可表示为
v = ai + bj + ck 通常用一个〔n + 1〕维列矩阵表示,即除 x、y、 z 三个方向上的分量外,再加一个比例因子 w ,即
01
0 001
1
0
0
1
如果按着逆序旋转,首先绕y轴旋转90°,然后再绕z轴旋转90°,其结果为
机器人学基础(全套课件470P)

机器人学基础
Fundamentals of Robotics
智能科学基础系列课0
Fundamentals of Robotics
1
Ch. 1 Introduction 第1章 绪 论
Ch. 1 Introduction
2
Contents
Course Schedule Top 10 Robotics News of 2008 Development of Robotics Structure, Feature, and Classification of
讲授
2 讲授
2 课堂 报告
2 实验
9
教学进度安排(3)
月 日 周次 4 20 8
教学内容 机器人编程
教学 时数
2
教学 课外 备 方式 时数 注
讲授 2
4 23 8
机器人编程训练
2 训练
4 27 9 综合实验:智能机器人的路 2 综合
径规划与行为决策实验
实验
4 30 9
机器人应用
2 讲授
5 4 10
Ch. 1 Introduction
17
2 Robot ride on a wheelbarrow
➢ In September 2008 Japanese Murata Manufacturing Institute launched a new type of robot riding on a wheelbarrow, named "seiko". This new type of robot can maintain its balance through a series of sensors and gyroscopes, and easy to complete riding of a wheelbarrow.
Fundamentals of Robotics
智能科学基础系列课0
Fundamentals of Robotics
1
Ch. 1 Introduction 第1章 绪 论
Ch. 1 Introduction
2
Contents
Course Schedule Top 10 Robotics News of 2008 Development of Robotics Structure, Feature, and Classification of
讲授
2 讲授
2 课堂 报告
2 实验
9
教学进度安排(3)
月 日 周次 4 20 8
教学内容 机器人编程
教学 时数
2
教学 课外 备 方式 时数 注
讲授 2
4 23 8
机器人编程训练
2 训练
4 27 9 综合实验:智能机器人的路 2 综合
径规划与行为决策实验
实验
4 30 9
机器人应用
2 讲授
5 4 10
Ch. 1 Introduction
17
2 Robot ride on a wheelbarrow
➢ In September 2008 Japanese Murata Manufacturing Institute launched a new type of robot riding on a wheelbarrow, named "seiko". This new type of robot can maintain its balance through a series of sensors and gyroscopes, and easy to complete riding of a wheelbarrow.
工业机器人技术基础-第2版-课件--第1章-工业机器人概论-
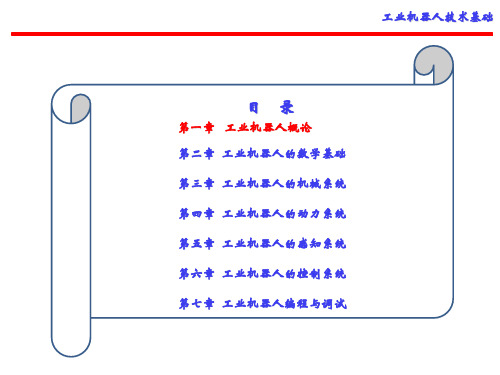
实际作业tact time最大缩 监视ROBOT的姿势、负荷, 设置面积A4尺寸,重量约
特
短15%幅度。附加功能:附 依据实际调整伺服增益/滤
加轴控制、追踪机能、
波。
8kg的新设计小型控制器。 搭载独自开发的5节闭连结
点 Ethernet等提升目标。
冲突检知机能,支持原点 机构及64bitCPU;
参 最大合成速度:5.5m/s 数 最大可搬重量:3.5kg
随着工业机器人的应用越来越广泛,我国也在积极推动我国机器人产业的发展。尤其是进入 “十三.五”以来,国家出台的《机器人产业发展规划(2016-2020)》对机器人产业进行了全面 规划,要求行业、企业搞好系列化、通用化、模块化设计,积极推进工业机器人产业化进程。
第1章 工业机器人概论
工业机器人技术基础
第1章 工业机器人概论
工业机器人技术基础
工业机器人在我国发展概况
中国的机器人产业应走什么道路,如何建立自己的发展模式,确实值得探讨。中国工程院在 2003年12月完成并公开的《我国制造业焊接生产现状与发展战略研究总结报告》中认为,我国应 从“美国模式”着手,在条件成熟后逐步向“日本模式”靠近。
目前,我国基本掌握了工业机器人的结构设计和制造、控制系统硬件和软件、运动学和轨迹规划等技术, 形成了机器人部分关键元器件的规模化生产能力。一些公司开发出的喷漆、弧焊、点焊、装配、搬运等机器人 已经在多家企业的自动化生产线上获得规模应用,弧焊机器人也已广泛应用在汽车制造厂的焊装线上。总体来 看,在技术开发和工程应用水平与国外相比还有一定的差距。主要表现在以下几个方面:
迅猛。由此可见,未来工业机器人的应用依托汽车产业,并迅速向各行业延伸。对于
机器人行业来讲,这是一个非常积极的信号。
工业机器人的数学基础

则称矩阵 A 和矩阵 B 相等,记为 A B 。需要注意的是,不是同型的矩阵是不能进
行相等比较的,同型矩阵之间不能比较大小。
12)负矩阵
对于矩阵 A (aij )mn ,每个元素取相反数,得到的矩阵称为 A 的负矩阵, 记为 A ,即
a11
A
a21
am1
a12 a22
am2
a1n
a2n
amn
1.2 矩阵的运算
1.矩阵的加法
设同型矩阵 A (aij )mn , B (bij )mn , A 与 B 的对应元素相加,称为矩 阵 A 与 B 的加法或和,记为 C (cij )mn ,即
a11 b11
C
A
B
a21
b21
am1 bm1
a12 b12 a22 b22
2.数与矩阵相乘
数 k 与矩阵 A (aij )mn 的乘积,称为数乘,记为 kA ,规定为
ka11
kAmn
ka21
kam1
ka12 ka22
kam2
ka1n
ka2n
kamn
矩阵数乘满足以下性质:
(1)分配律: k(A B) kA kB,(k l)A kA lA 。 (2)结合律: (kl)A k(lA) 。 (3)1A A,0A O 。
a1n
a2n
amn
称为 m 行 n 列矩阵,简称 m n 矩阵。通常用大写字母 A,B ,C , 表示矩阵, aij 表示矩阵中第 i 行、第 j 列的元素,这个元素可以是实数,也可以是虚数。 一个 m n 矩阵可以简记为 A Amn (aij )mn 。
将矩阵 A (aij )mn 的行与列依次互换得到的矩阵称为矩阵 A 的转置矩阵,简称转置,记为
行相等比较的,同型矩阵之间不能比较大小。
12)负矩阵
对于矩阵 A (aij )mn ,每个元素取相反数,得到的矩阵称为 A 的负矩阵, 记为 A ,即
a11
A
a21
am1
a12 a22
am2
a1n
a2n
amn
1.2 矩阵的运算
1.矩阵的加法
设同型矩阵 A (aij )mn , B (bij )mn , A 与 B 的对应元素相加,称为矩 阵 A 与 B 的加法或和,记为 C (cij )mn ,即
a11 b11
C
A
B
a21
b21
am1 bm1
a12 b12 a22 b22
2.数与矩阵相乘
数 k 与矩阵 A (aij )mn 的乘积,称为数乘,记为 kA ,规定为
ka11
kAmn
ka21
kam1
ka12 ka22
kam2
ka1n
ka2n
kamn
矩阵数乘满足以下性质:
(1)分配律: k(A B) kA kB,(k l)A kA lA 。 (2)结合律: (kl)A k(lA) 。 (3)1A A,0A O 。
a1n
a2n
amn
称为 m 行 n 列矩阵,简称 m n 矩阵。通常用大写字母 A,B ,C , 表示矩阵, aij 表示矩阵中第 i 行、第 j 列的元素,这个元素可以是实数,也可以是虚数。 一个 m n 矩阵可以简记为 A Amn (aij )mn 。
将矩阵 A (aij )mn 的行与列依次互换得到的矩阵称为矩阵 A 的转置矩阵,简称转置,记为
机器人的数学基础齐次变换矩阵及其运算
• (-1,2,2)平移后到{A’};动坐标系{A}相对于自身坐标系(即动系)的 X、Y、Z轴分别作(-1,2,2)平移后到{A’’}。已知A,写出坐标系{A’} 、 {0 1 1 1
0
0
0 1
0 1 0 0
A' 1 0 0 3 0 0 1 3
0
0
0 1
W Rot(Y,90)Rot(Z,90)U
0 0 1 0 0 1 0 0 7
0
1
0
0
1
0
0
0
3
1 0 0 0 0 0 1 0 2
0
0
0
1 0
0
0
1
1
上海电机学院 机械学院
• 平移变换和旋转变换可以组合在一个齐次变换中。上例 中点U若还要作4i-3j+7k的平移,则只要左乘上平移变换 算子即可得到最后的列阵表达式。
z' z
x' cos sin 0 0 x
y'
sin
cos
0
0
y
z' 0
0 1 0 z
1
0
0
0
1
1
记为: a′=Rot(z, θ)a
上海电机学院 机
械学院
旋转算子
绕Z轴旋转算子内容为:
cos sin 0 0
Rot(z,
)
sin
0
cos
0
0 0 1 0
0
0 0 1
同理,绕x轴、Y轴旋转算子内容为:
B C
R
0
B
pC 1
0
复合变换可解释为:
(1)CAT 和 CBT 分别代表同一坐标系{C}相对于{A}和{B}的描述。
第1章 机器人运动学
• 答:①左上角3X3矩阵表示新坐标系在旧坐 标系中的旋转方向。 • ②左上角3X3矩阵中的各列表示新坐标系的 各坐标轴的单位矢量在旧坐标系的各坐标 轴上的投影;各行表示旧坐标系的各坐标 轴的单位矢量在新坐标系的各坐标轴上的 投影;P表示新坐标系相对旧坐标系的平移 量,其各分量表示平移后新坐标系在旧坐 标系中的矢量。
• 例1.3 图1.7表示手部抓握物体Q,物体是 边长为2个单位的正立方体,写出表达该手 部位姿的矩阵表达式。
• 解 因为物体Q形心与手部坐标系OXYZ的坐标原点 O相重合,则手部位置的 4 1列阵为 • 手部坐标系X轴的方向可用单位矢量n来表示:
• 同理,手部坐标系Y轴与Z轴的方向可分别用单位矢 量o和a来表示:
• 1.1.2 动系的位姿表示 • 一、连杆的位姿表示 • 设有一个机器人的连杆,若给 定了连杆PQ上某点的位置和 该连杆在空间的姿态,则称该 连杆在空间是完全确定的。 • 如图1.4所示,O为连杆上任 一点,OXYZ为与连杆固接 的一个动坐标系,即为动系。 连杆PQ在固定坐标系OXYZ 中的位置可用一齐次坐标表示 为 • (1.5)
1.1.1 齐次坐标
• 二、齐次坐标表示 • 将一个n维空间的点用n + 1维坐标表示,则该 n + 1维坐标即为n维坐标的齐次坐标。一般情况 下w称为该齐次坐标中的比例因子,当取w = 1 时,其表示方法称为齐次坐标的规格化形式,即 • P = [PX PY PZ 1]T (1.2) • 当w不为1时,则相当于将该列阵中各元素同时乘 以一个非零的比例因子w,仍表示同一点P,即 • P = [a b c w]T(1.3) • 式中:a = wPX;b = wPY;c = wPZ。
第1章 机器人运动学
第1章 机器人运动学
第1章 机器学习基础
machinelearning机器学习是作为突破知识工程瓶颈之利器而出现的恰好在20世纪90年代中后期人类发现自己淹没在数据的汪洋中对自动数据分析技术机器学习的需求日益迫切汽车自动驾驶darpagrandchallenge机器学习已经无处不在入侵检测web搜索生物信息学决策助手darpa火星机器人jpl今天的机器学习已经是一个广袤的学科领域经常被谈到的深度学习deeplearning仅是机器学习中的一个小分支例如这是第32届国际机器学习大会的主题领域2006年美国cmu卡内基梅隆大学成立机器学习系大数据时代机器学习必不可少收集传输存储大数据的目的是为了利用大数据没有机器学习技术分析大数据利用无从谈起基本术语数据集
人工完成书页拼接十分困难
- 书页数量大,且分布在多处 - 部分损毁较严重,字迹模糊 - 需要大量掌握古文字的专业人才 近年来,古文献的数字化浪潮给自动文学修复提供了机会
例如:古文献修复 (文化)
以色列特拉维夫大学的学者将机器学习用于自动的书页拼接
已确定 相邻
已确定 不相邻
分类模型
判断 是否相邻
相邻
梵高(1853-1890) 的作品?
出自 [C. Johnson et al., IEEE-SP, 2008]
例如:画作鉴别 (艺术)
除专用技术手段外, 笔触分析 (brushstroke analysis) 是 画 作 鉴 定的重要工具;它旨在从视觉上 判断画作中是否具有艺术家的特 有“笔迹”。
第一阶段:推理期
1956-1960s: Logic Reasoning
出发点: “数学家真聪明!” 主要成就: 自动定理证明系统 (例如,
西蒙与纽厄尔的“Logic Theorist” 系统)
渐渐地,研究者们意识到,仅有逻辑 推理能力是不够的 …
人工完成书页拼接十分困难
- 书页数量大,且分布在多处 - 部分损毁较严重,字迹模糊 - 需要大量掌握古文字的专业人才 近年来,古文献的数字化浪潮给自动文学修复提供了机会
例如:古文献修复 (文化)
以色列特拉维夫大学的学者将机器学习用于自动的书页拼接
已确定 相邻
已确定 不相邻
分类模型
判断 是否相邻
相邻
梵高(1853-1890) 的作品?
出自 [C. Johnson et al., IEEE-SP, 2008]
例如:画作鉴别 (艺术)
除专用技术手段外, 笔触分析 (brushstroke analysis) 是 画 作 鉴 定的重要工具;它旨在从视觉上 判断画作中是否具有艺术家的特 有“笔迹”。
第一阶段:推理期
1956-1960s: Logic Reasoning
出发点: “数学家真聪明!” 主要成就: 自动定理证明系统 (例如,
西蒙与纽厄尔的“Logic Theorist” 系统)
渐渐地,研究者们意识到,仅有逻辑 推理能力是不够的 …
机器人学数学基础ppt课件
机器人技术数学基础
Mathematic Preparation for Robotics
• 2.1 位置和姿态的表示 • 2.2 坐标变换 • 2.3 齐次坐标变换 • 2.4 旋转矩阵
2.1 机器人位置和姿态的描述
• 机器人可以用一个开环关节链来建模
• 由数个驱动器驱动的转动或移动关节串联而成
• 一端固定在基座上,另一端是自由的,安装工具,用以 操纵物体
用矩阵表示为:
Px
Py
Pz
ix
jy
kz
i i i
ix jv jy jv kz jv
Pu
u
图2-4
ix jy kz
kw kw kw
P Pv Pw
(2-7)
ix
i
定义 旋转矩阵为:R jy i
kz i
ix jv jy jv kz jv
ix
kw
jy kw
kz
杆件参数
关节角
运动学正问题 杆件参数
末端执行器
关节角
运动学正问题
研究的对象
• 机器人从机构形式上分为两种,一种是关节式 串联机器人,另外一种是并联机器人。
PUMA560
Fanuc manipulator
Hexapod
这两种机器人有所不同: – 串联机器人:工作空间大,灵活,刚度差,负载小,误 差累积并放大。
P点在ΣO´uvw中是不变的仍然 成立,由于ΣO´uvw回转,则:
Pw P
v
o
Pv
y
Px Puvw ix ix (Pu iu Pv jv Pw kw )
(O')
Py Puvw jy jy (Pu iu Pv jv Pw kw ) x Pz Puvw jz jz (Pu iu Pv jv Pw kw )
Mathematic Preparation for Robotics
• 2.1 位置和姿态的表示 • 2.2 坐标变换 • 2.3 齐次坐标变换 • 2.4 旋转矩阵
2.1 机器人位置和姿态的描述
• 机器人可以用一个开环关节链来建模
• 由数个驱动器驱动的转动或移动关节串联而成
• 一端固定在基座上,另一端是自由的,安装工具,用以 操纵物体
用矩阵表示为:
Px
Py
Pz
ix
jy
kz
i i i
ix jv jy jv kz jv
Pu
u
图2-4
ix jy kz
kw kw kw
P Pv Pw
(2-7)
ix
i
定义 旋转矩阵为:R jy i
kz i
ix jv jy jv kz jv
ix
kw
jy kw
kz
杆件参数
关节角
运动学正问题 杆件参数
末端执行器
关节角
运动学正问题
研究的对象
• 机器人从机构形式上分为两种,一种是关节式 串联机器人,另外一种是并联机器人。
PUMA560
Fanuc manipulator
Hexapod
这两种机器人有所不同: – 串联机器人:工作空间大,灵活,刚度差,负载小,误 差累积并放大。
P点在ΣO´uvw中是不变的仍然 成立,由于ΣO´uvw回转,则:
Pw P
v
o
Pv
y
Px Puvw ix ix (Pu iu Pv jv Pw kw )
(O')
Py Puvw jy jy (Pu iu Pv jv Pw kw ) x Pz Puvw jz jz (Pu iu Pv jv Pw kw )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当相对于坐标系C进行变换时 以T右乘坐标系C,得到新坐标系的位置Q=CT:
0 1 0 30
0 0 1 10 1 0 0 0
0 0
0
1
说明:
“0”表示参考 系的编号
点A在坐标系之间的齐次变换
PA0
点A在坐标系Sj的齐次矩阵表示
x
i A
y
i A
z
i A
1
nx ny
nz 0
0 0 X A
0
0 YA
1
0
Z
A
0 1 1
简写为 A' Rot(Z, )A
式中:Rot(Z,)表示齐次坐标变换时绕Z轴的转动齐次
变换矩阵,又称旋转算子。旋转算子为:
c s 0 0
Rot(Z , ) s c 0 0
0 0 1 0
0
0 0 1
c 表示 cos s 表示 sin
同理,绕X轴转动的旋转算子和绕Y轴转动的旋转算子:
y0
z1
y2 O1
z2 O2
x0
x1
当S2是沿动系运动时用T2右乘 T10
第二种情况:沿基系S0运动
y1
z0
S2与S1完全重合 再绕z0旋转90°再沿x0移动10
y2
O0
y0
0 1 0 10
T2
1 0
0 0
0 1
0
0
0 y1 0
0
1
y2
z0
O0
y0
z1 z2 O1
O2
x2
x0
x1
y1
z0
O0
机器人手部的位置和姿态 机器人手部的位置和姿态用固连于手部的动系 {B}的位姿来表示。 手部的中心点为动系原点OB
关节轴为ZB轴,单位矢量a为接近矢量,指向朝外。 手指的连线为YB轴,单位矢量o为姿态矢量,指向可 任意选定。
XB轴与YB轴及ZB轴垂直,单位矢量n为法向矢量,指 向符合右手法则。
手部的位置矢量:动系原点(x0,y0,z0) 手部的方向矢量:n, o, a 手部位姿的(4×4)矩阵表达式:
0 1
0 0
20 0
T20
0 0 0
1
当S2是沿S0运动时用T2左乘 T10
练习:沿xi轴移动20形成S1,再绕zi轴转动90°形成系S2, 再沿z2移动10形成当前坐标系Sj,画出各坐标系并求Sj相对 于Si的位姿矩阵。
1 0 0 20
0 1 0 0
zi
解
T1
0 0
1 0
0 1
0
0
T2
1 0
要研究机器人,首先分析运 动学和动力学。
把坐标系固连在机器人的每 一个连杆关节上,用变换来 描述这些坐标系之间的相对 位置和方向,进行机器人的 位姿分析。
n
2 1
一、坐标系 采用参考坐标系和关节坐标系描述机器人位姿。 参考坐标系:位置和方向不随机器人各关节的运 动而变化,用来定义机器人相对于其他物体的运 动以及机器人运动路径等。
X = [1 0 0 0 ]T Y = [0 1 0 0]T
Z = [0 0 1 0]T
四、齐次变换
连杆的运动是由转动和平移组成的,引入齐次坐标变换矩阵描 述刚体运动。
1.平移的齐次变换 空间一点A (XA,YA,ZA),平移至A (XA,YA,ZA) ,A点和A 点的坐标关系为
或:
也可以简写为 A' Trans(X , Y, Z)A
第1章 机器人 学—数学基础
机器人本体结构
俯仰 肘转
肩转
滚转
腰、臂、肘产生 主运动,是机器 人的位置机构。 手腕具有多个自 由度,是机器人 的姿态机构,确 定空间方向。
腰转
末端执行器可以是各种夹持器,也可以是各种工具,如焊 枪、喷头等。操作时要求手部不仅能到达指定的位置,而 且要有正确的姿态。
一般将机器人简化成由连杆、 关节和末端执行器组成的空 间连杆开式链机构 。
1 0 0
0 0 1
10
0
0
换时,S2的位姿?
0 0 0
1
0
0
0
1
S1:先与S0重合,绕x0旋转90°再沿x0移动20
z0 z1
O0 O1 y1
x1 x0
z1 y0
x0
z0
y1
O0
y0 z1
O1
x1
x0
y1
z0
O0
y0
O1
x1
0 1 0 10
T2
1 0
0 0
0 1
0
0
0
0
0
1
第一种情况:沿动系S1变换
补充知识:旋转矩阵的两个正交性质
(1)R矩阵9个元素,3个是独立的,6个约束条件(正交条件)
n n o o a a 1,n o o a a n 0
n n nx2 n2y nz2 1 n o nxox nyoy nzoz 0
y2 y0
O2 x2
z1
O1
z2
x0
x1
z1
O1
x0
x1
O2 x2 z2
0 0 1 10
T20
1 0
0 1
0 0
20
0
0 0 0
1
y1
z0
O0
y2 y0
z1
O1
x0
x1
O2 x2 z2
0 1 0 30
T10T2
0 1
0 0
1 0
0 0
T20
0 0
0
0
0 0 1 10
T2 T10
1 0
S2与S1重合
绕z1旋转90°,沿x1移动10
y1
z0
y2
O0
y0
z1 z2 O1
O2
x2
x0
x1
y1
z0
x2
O0
y2
z1 z2 O1
O2
x0
x1
x2
y1
z0
y0
O0
y0
z1
y2 O1
z2 O2
0 1 0 30
T20
0 1
0 0
1 0
0
0
x0
x1
0 0
0
0
1 0 0 20
T10
0 0
0 1
1 0
现以iA为基础建立编号为A的坐标系,
3个轴分别为 iA、 jA、 kA :
cos i
Ai0
z0 jA
i
0 A
cos
i
A
j0
cos
i
Ak0
O0
cos
jAi0
j0A
cos
j
A
j0
cosk
Ai0
x0
k
0 AcoskΒιβλιοθήκη Aj0kA
cos
j
Ak0
cos
k
Ak0
例2 图示手部抓握物体Q,物体为边长2个单位的正立方体,写 出表达该手部位姿的矩阵式。
解 物体Q形心与手部坐标系的坐标原点O 相重合,
手部位置列阵为: P = [1 1 1 1]T
动系X 轴的单位方向矢量 n:
动系Y 轴的方向矢量 o: 动系Z 轴的方向矢量 a:
手部位姿矩阵为:
刚体的运动可分解为旋转和平移,旋转和平移的 描述可以用O系和O 系的齐次坐标变换矩阵来表 达,这是研究机器人运动姿态的基础。
jA
R0 A
cos
i
A
j0
cos jA j0
cos
k
A
j0
z0
cos
i
Ak0
cos jAk0
cos
k
Ak0
iA OA
pA
O0
kA
y0
x0
刚体的位姿可用 4×4矩阵来描述:
nx T ny
n0z
ox x oy y oz z
00
px
py pz 1
R|P
0|
1
例1 图示固连于刚体的坐标系{B}位于0B点,xb=10,yb=5,zb =o。Zb轴与画面垂直,坐标系{B}相对固定坐标系{A}有一个 300的偏转,试写出表示刚体位姿的坐标系{B}的(4×4)矩阵表 达式。
向量的方向
设向量iA是单位向量,与参考系轴x0的单位向量i0的 夹角为α;与轴y0的单位向量j0的夹角为β ;与轴z0 的单位向量k0的夹角为γ : 单位矢量在参考系O系上各坐标轴z投0 影方向余弦
cosα
i
0 A
c
os
cos
cos
O0 cos
α x0
iA y0
cos
坐标系方向的描述
三维空间固定坐标系OXYZ表述。
关节坐标系:用来描述机器 人每一个独立关节的运动。
二、刚体的位姿描述 若给定刚体上某一点的位置和该刚体在空间的姿 态,则这个刚体在空间完全定位。 设O 为刚体上任意一点,参考坐标OXYZ, O 在 O系中位置表示:
Ro = [xo yo zo]T
在刚体上建立动坐标系 O X Y Z ,动系坐标 轴的方向表示刚体的方 向。
齐次坐标(1 2 3 1)、(2 4 6 2)、(3 6 9 3) 均表示笛卡尔坐标下的空间点(1 2 3)
w = 1,为齐次坐标的规格化形式,即 P = [PX PY PZ 1]T
对于刚体位姿来说,采用齐次坐标和普通坐标没 有实质性的差别,却给矩阵运算提供了可行性和 方便性。 坐标轴的方向表示: i、j、k分别表示直角坐标系中X、Y、Z坐标轴的 单位矢量,用齐次坐标表示之,则有
