二次函数复习专项练习
中考数学复习《二次函数》专题训练-附带有参考答案
中考数学复习《二次函数》专题训练-附带有参考答案一、选择题1．下列函数中，是二次函数的是（）A．y=x2+1x B．y=12x(x-1) C．y=-2x-1 D．y=x(x2+1)．2．抛物线y=(x−2)2−3的顶点坐标是（）A．(2，−3)B．(−2，3)C．(2，3)D．(−2，−3)3．把抛物线y=5x2向左平移2个单位，再向上平移3个单位，得到的抛物线是（）A．y=5(x−2)2+3B．y=5(x+2)2−3C．y=5(x+2)2+3D．y=5(x−2)2−34．函数y＝ax2与y＝﹣ax+b的图象可能是（）A． B． C． D．5．函数y=kx2-6x+3的图象与x轴有交点，则k的取值范围是（）A．k<3 B．k<3且k≠0 C．k≤3且k≠0 D．k≤36．若A（−5，y1），B（1，y2），C（2，y3）为二次函数y=x2+2x+m的图象上的三点，则y1，y2，y3的大小关系是（）A．y1<y2<y3B．y2<y3<y1C．y2<y1<y3D．y3<y1<y27．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①b＞0；②当x＞0，y随着x 的增大而增大；③（a+c）2﹣b2＜0；④a+b≥m（am+b）（m为实数）．其中结论正确的个数为（）A．4个B．3个C．2个D．1个8．某服装店购进单价为15元的童装若干件，销售一段时间后发现：当销售价为25元时，平均每天能售出8件，而当销售价每降低2元时，平均每天能多售出4件，为使该服装店平均每天的销售利润最大，则每件的定价为（）A．21元B．22元C．23元D．24元二、填空题9．将二次函数y＝x2－2x化为y＝(x－h)2＋k的形式，结果为10．若抛物线y＝ax2＋bx＋c与x轴的两个交点坐标是（－1，0），（3，0），则此抛物线的对称轴是直线．11．将二次函数y＝x2﹣4x+a的图象向左平移1个单位，再向上平移1个单位，若得到的函数图象与直线y＝2有两个交点，则a的取值范围是.12．飞机着陆后滑行的距离y （单位：m）关于滑行时间t （单位：s）的函数解析式是y=60t-65t2，从飞机着陆至停下来共滑行米．13．已知如图：抛物线y=ax2+bx+c与直线y=kx+n相交于点A(−52，74)、B(0，3)两点，则关于x的不等式ax2+bx+c＜kx+n的解集是三、解答题14．如图，在平面直角坐标系中，一次函数y1=kx−7的图象与二次函数y2=2x2+bx+c的图象交于A(1，−5)、B(3，t)两点.（1）求y1与y2的函数关系式；（2）直接写出当y1<y2时，x的取值范围；（3）点C为一次函数y1图象上一点，点C的横坐标为n，若将点C向右平移2个单位，再向上平移4个单位后刚好落在二次函数y2的图象上，求n的值.15．某品牌服装公司新设计了一款服装，其成本价为60（元/件）.在大规模上市前，为了摸清款式受欢迎状况以及日销售量y（件）与销售价格x（元/件）之间的关系，进行了市场调查，部分信息如表：销售价格x（元/件）80 90 100 110日销售量y（件）240 220 200 180（1）若y与x之间满足一次函数关系，请直接写出函数的解析式（不用写自变量x的取值范围）；（2）若该公司想每天获利8000元，并尽可能让利给顾客，则应如何定价？（3）为了帮助贫困山区的小朋友，公司决定每卖出一件服装向希望小学捐款10元，该公司应该如何定价，才能使每天获利最大？（利润用w表示）16．如图，抛物线y=−x2+bx+c与x轴交于A，B两点（A在B的左侧），与y轴交于点N，过A点的直线：l：y=−x−1与y轴交于点C，与抛物线y=−x2+bx+c的另一个交点为D(5，−6)，已知P点为抛物线y=−x2+bx+c上一动．点（不与A、D重合）．（1）求抛物线的解析式；（2）当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值；（3）设M为直线l上的动点，以NC为一边且顶点为N，C，M，P的四边形是平行四边形，直接写出所有符合条件的M点坐标．17．如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点作水平线的垂线为y轴，建立平面直角坐标系，图中的抛物线C1：y=−18x2+32x+32近似表示滑雪场地上的一座小山坡，某滑雪爱好者小张从点O正上方A点滑出，滑出后沿一段抛物线C2：y=−14x2+bx+c 运动．（1）当小张滑到离A处的水平距离为8米时，其滑行高度为10米，求出b，c的值；（2）在(1)的条件下，当小张滑出后离的水平距离为多少米时，他滑行高度与小山坡的竖直距离为是5米？2（3）若小张滑行到坡顶正上方，且与坡顶距离不低于4米，求b的取值范围．18．如图，在平面直角坐标系中，抛物线y=ax2+bx−4与x轴交于A(4，0)、B(−3，0)两点，与y轴交于点C．（1）求这条抛物线所对应的函数表达式．（2）如图①，点D是x轴下方抛物线上的动点，且不与点C重合．设点D的横坐标为m，以O、A、C、D 为顶点的四边形面积为S，求S与m之间的函数关系式．（3）如图②，连结BC，点M为线段AB上一点，点N为线段BC上一点，且BM=CN=n，直接写出当n为何值时△BMN为等腰三角形．参考答案 1．B 2．A 3．C 4．B 5．D 6．B 7．B 8．B9．y =(x −1)2−1 10．x ＝1 11．a ＜5 12．75013．x <−52或x >014．（1）解：把点A(1，−5)代入y 1=kx −7得−5=k −7 ∴y 1=2x −7；把点B(3，t)代入y 1=2x −7中，得t =−1 ∴A(1，−5)把点A 、B 分别代入y 2=2x 2+bx +c 中，得{−2=2+b +c−1=18+3b +c 解得{b =−6c =−1∴y 2=2x 2−6x −1； （2）x <1或x >3（3）解：∵点C 为一次函数y 1图象上一点，∴C(n ，2n −7)将点C 向右平移2个单位，再向上平移4个单位后得到点C ′(n +2，2n −3) 把C ′代入y 2=2x 2−6x −1，得2n −3=2(n +2)2−6(n +2)−1 解得n =±1 所以n 的值为1或-1 15．（1）y=-2x+400（2）解：由题意，得：(x −60)(−2x +400)=8000解得x 1=100，x 2=160 ∵公司尽可能多让利给顾客 ∴应定价100元（3）解：由题意，得w =(x −60−10)(−2x +400)=−2x 2+540x −28000 =−2(x −135)2+8450∵−2<0∴当x =135时，w 有最大值，最大值为8450. 答：当一件衣服定为135元时，才能使每天获利最大. 16．（1）解：∵直线l ：y =−x −1过点A∴A(−1，0)又∵D(5，−6)将点A ，D 的坐标代入抛物线表达式可得：{−1−b +c =0−25+5b +c =−6 解得{b =3c =4．∴抛物线的解析式为：y =−x 2+3x +4． （2）解：如图设点P(x ，−x 2+3x +4) ∵PE ∥x 轴，PF ∥y 轴则E(x 2−3x −5，−x 2+3x +4)，F(x ，−x −1) ∵点P 在直线l 上方的抛物线上∴−1<x <5∴PE =|x −(x 2−3x −5)|=−x 2+4x +5，PF =|−x 2+3x +4−(−x −1)|=−x 2+4x +5 ∴PE +PF =2(−x 2+4x +5)=−2(x −2)2+18． ∴当x =2时，PE +PF 取得最大值，最大值为18．（3）符合条件的M 点有三个：M 1(4，−5)，M 2(2+√14，−3−√14)， M 3(2−√14，−3+√14)． 17．（1）解：由题意可知抛物线C 2：y=−14x 2+bx+c 过点(0， 4)和(8， 10) 将其代入得：{4=c10=−14×82+8b +c解得 ∴b=114，c=4（2）解：由(1)可得抛物线Cq 解析式为： y=−14x 2+114x+4设运动员运动的水平距离为m 米时，运动员与小山坡的竖直距离为52米，依题意得： −14m 2+114m +4−(−18m 2+32m +32)=52解得： m 1=10，m 2=0(舍)故运动员运动的水平距离为10米时，运动员与小山坡的竖直距离为为52米． （3）解：∵抛物线C 2经过点(0， 4) ∴c=4抛物线C 1： y=−18x 2+32x +32=−18(x −6)2+6 当x=6时，运动员到达坡项 即−14×62+6b+4≥4+6． ∴b ≥15618．（1）解：把A(4，0)、B(−3，0)代入y =ax 2+bx −4中 得{16a +4b −4=09a −3b −4=0解得{a =13b =−13∴这条抛物线所对应的函数表达式为y =13x 2−13x −4． （2）解：当x =0时y =−4∴C(0，−4)当−3<m <0时S =S △ODC +S △OAC =12×4×(−m)+12×4×4=−2m +8当0<m <4时S =S △ODC +S △OAD =12×4×m +12×4×(−13m 2+13m +4)=−23m 2+83m +8． （3）解：n =52，n =2511，n =3011．。
初中数学二次函数知识点专题复习练习 含答案
初中数学二次函数知识点专题复习练习一、选择题（共15题）1．已知抛物线y ＝a 2x －3x+1与x 轴有交点，则a 的取值范围是（ ） A ．B ．C ．D ．2．已知a<-1，点（a-1，1y ），（a ，2y ），（a+1，3y ）都在函数y=x²的图象上，则（ ） A ．1y ＜2y ＜3yB ．1y ＜3y ＜2yC ．3y ＜2y ＜1yD ．2y ＜1y ＜3y3．如图，四边形ABCD 中，AB=AD ，CE ⊥BD ，CE =12BD ．若△ABD 的周长为20cm ，则△BCD 的面积S （cm 2）与AB 的长x （cm ）之间的函数关系式可以是（ ）A ．21101004S x x =-+ B ．2240200S x x =-+ C ．220100S x x =-+D ．220100S x x =++4．下列二次函数的图象中经过原点的是（ ） A ．21y x =+B ．225y x x =+C ．2(2)y x =-D ．223y x x =+-5．在平面直角坐标系中，点A 是抛物线y=x 2在第一象限上的一点，连结OA ，过点O 作OB ⊥OA ，交抛物线于点B ，若四边形AOBC 为正方形，则顶点C 的坐标为（ ） A ．（0，1） B ．（﹣1，1） C ．（0，2） D ．（0，﹣2） 6．抛物线y=﹣x 2+x+2与y 轴的交点坐标是（ ） A ．（1，2） B ．（0，﹣1） C ．（0，1） D ．（0，2） 7．若二次函数y=x 2＋bx ＋5配方后为y=(x-2)2＋k ，则b ，k 的值分别为( ) A ．0，5B ．0，1C ．-4，5D ．-4，18．一个二次函数y=ax 2+bx+c 的图像如图所示，该二次函数二次项系数a 的值可能是（ ）A ．-2B ．3C ．12D ．2.39．函数2122y x x =-++有最值为（ ） A ．最大值32B ．最小值32 C ．最大值12-D ．最小值12-10．如图1，点E 为矩形ABCD 边AD 上一点，点P ，点Q 同时从点B 出发，点P 沿BE→ED→DC 运动到点C 停止，点Q 沿BC 运动到点C 停止，它们运动的速度都是1cm/s ，设P ，Q 出发t 秒时，△BPQ 的面积为ycm ，已知y 与t 的函数关系的图形如图2（曲线OM 为抛物线的一部分），则下列结论：①AD=BE=5cm ；②当0＜t≤5时，22y t 5=；③直线NH 的解析式为5y t 272=-+；④若△ABE 与△QBP 相似，则t=294秒．其中正确的结论个数为（ ）A ．4B ．3C ．2D ．111．已知二次函数y=ax 2+bx+c 的图象如图所示，它与x 轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b+2a=0；②abc ＞0；③a ﹣2b+4c ＜0；④8a+c ＞0．其中正确的有（ ）个．A ．1个B ．2个C ．3个D ．4个12．如图，在平面直角坐标系中，点A （430）是x 轴上一点，以OA 为对角线作菱形OBAC ，使得BOC ∠=60°，现将抛物线2y x 沿直线OC 平移到2()y a x m h =-+，则当抛物线与菱形的AB 边有公共点时，则m 的取值范围是（ ）A 333m ≤B ．103333m ≤C 10163333m ≤D 16333m ≤13．对于抛物线y ＝2（x ＋3）2＋1，下列说法错误的是（ ） A ．开口向上B ．对称轴是直线x ＝－3C ．当x ＞－3时，y 随x 的增大而减小D ．当x ＝3时，函数值有最小值是114．在二次函数y=ax 2+bx +c ，x 与y 的部分对应值如下表：则下列说法中正确的是（ ） x … ﹣2 0 2 3 … y …83…A ．图象经过原点；B ．图象开口向下；C ．图象经过点（﹣1，3）； D ．当x ＞0时，y 随x 的增大而增大； E.方程ax 2+bx +c =0有两个不相等的实数根．15．表中所列x 、y 的7对值是二次函数2y ax bx c =++图象上的点所对应的坐标，其中1234567x x x x x x x <<<<<<x ⋯ 1x 2x 3x 4x 5x 6x 7x⋯ y⋯6 m11 k 11 m6⋯根据表中提供约信息，以下4个判断中正确的是（ ） A ．0a < B ．611m << C ．当262x x x +=时，y 的值是k D ．24()b a c k - 二、非选择题16．如图，拱桥的形状是抛物线，其函数关系式为213y x =-，当水面离桥顶的高度为253米时，水面的宽度为__________米．17．将抛物线y ＝x 2+2x 向右平移1个单位后的解析式为_____．18．已知二次函数22y x x m =-++的图象如图所示，则关于x 的一元二次方程220x x m -++=的根为________；不等式220x x m -++>的解集是________；当x ________时，y 随x 的增大而减小．19．已知二次函数y ＝ax 2+bx +c （a 、b 、c 为常数，a ≠0）的图象如图所示，下面四个结论，①abc ＜0；②a +c ＜b ；③2a +b ＝1；④a +b ≥m （am +b ），其中全部正确的是______20．若二次函数的图象的对称轴方程是x =1，并且图象过A （0，-4）和B （4，0），求此二次函数的解析式． 21．某服装厂批发应季T 恤衫，其单价y (元)与批发数量x （件）(x 为正整数)之间的函数关系如图所示.（1）请你直接写出当100＜x ≤500且x 为整数时，y 与x 的函数关系式；（2）一个批发商一次购进200件T 恤衫，所花的钱数是多少元？(其他费用不计)；（3）若每件T 恤衫的成本价是45元，当100＜x ≤500件(x 为正整数)时，求服装厂所获利润w (元)与x (件)之间的函数关系式，并求一次批发多少件时所获利润最大,最大利润是多少？22．已知：如图，抛物线2y ax bx c =++与坐标轴分别交于点()0,6A ，()2,0C -，tan 1ABO ∠=，点P 是线段AB 上方抛物线上的一个动点． （1）求抛物线的解析式；（2）当点P运动到什么位置时，PAB△的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做//PE x轴交抛物线于点E，连结DE，请问是否存在点P使PDE△为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．23．如图，已知抛物线y＝x2+bx+c与x轴交于点A，B，AB＝2，与y轴交于点C，对称轴为直线x＝2．（1）求抛物线的函数表达式；（2）设D为抛物线的顶点，连接DA、DB，试判断△ABD的形状，并说明理由；（3）设P为对称轴上一动点，要使PC﹣PB的值最大，求出P点的坐标．参考答案1．D 【详解】试题分析：∵抛物线y=ax 2-3x+1与x 轴有交点， ∴a≠0，△≥0， ∴9-4a×1≥0， ∴a≤94， 故答案为a≤94且a≠0． 故选D. 2．C 【分析】根据函数y=x 2的图象的特点：函数y=x 2的图象的开口向上，对称轴是y 轴；在y 轴的左侧y 随x 的增大而减小；在y 轴的右侧y 随x 的增大而增大． 【详解】 解：∵1a <-， ∴110a a a -<<+<， 由函数2yx 的图象知：当0x <时y 随着x 的增大而减小，∴321y y y <<. 故选：C. 3．C 【分析】先求解,BD CE 的长度，再利用三角形的面积公式列二次函数关系式即可. 【详解】解： AB=AD ，△ABD 的周长为20cm ，设,AB x =202,BD x1,2CEBD 120210,2CEx x,CE BD2112021020100,22BDCSBD CE x x x x故选：C 4．B 【分析】本题只需要将x=0代入函数解析式，然后看所得出的函数值是否为零即可得出正确答案． 【详解】A 、将x=0代入可得y=1，故不经过原点；B 、将x=0代入可得y=0，故经过原点；C 、将x=0代入可得y=4，故不经过原点；D 、将x=0代入可得y=－3，故不经过原点；故选B ． 5．C 【分析】根据题意和正方形的性质可以得到点C 所在的位置和点C 的坐标，从而可以解答本题． 【详解】解：∵点A 是抛物线y=x 2在第一象限上的一点，连结OA ，过点O 作OB ⊥OA ，交抛物线于点B ，四边形AOBC 为正方形，∴点B 和点A 关于y 轴对称，点C 在y 轴上， 设点A 的坐标为（a ，a 2）， 则a=a 2（a ＞0）， 解得，a=1，∴点C 的坐标为（0，2）， 故选C ． 6．D 【详解】试题分析：把x=0代入解析式求出y 的值，根据y 轴上点的特征和二次函数图象上点的坐标特征解答即可． 解：当x=0时，y=2，故抛物线y=﹣x 2+x+2与y 轴的交点坐标是（0，2）． 故选D ． 7．D 【详解】∵y=（x-2）2+k=x 2-4x+4+k=x 2-4x+（4+k ），又∵y=x2+bx+5，∴x2-4x+（4+k）=x2+bx+5，∴b=-4，k=1．故选D8．A【分析】根据二次函数的性质即可得到结论．【详解】解：∵抛物线开口向下∴a＜0∴符合条件的为a=-2.故答案为：A.9．A【分析】把二次函数解析式整理成顶点式形式，然后根据二次函数的最值问题解答．【详解】∵y=-x2+2x+12=-（x-1）2+32，∴二次函数有最大值32．故选A．10．B【详解】根据图（2）可得，当点P到达点E时点Q到达点C，∵点P、Q的运动的速度都是1cm/秒，∴BC=BE=5cm．∴AD=BE=5，故结论①正确．如图1，过点P作PF⊥BC于点F，根据面积不变时△BPQ 的面积为10，可得AB=4， ∵AD ∥BC ，∴∠AEB=∠PBF ． ∴AB 4sin PBF sin AEB BE 5∠=∠==． ∴PF=PBsin ∠PBF=45t ． ∴当0＜t≤5时，y=12BQ•PF=12t•45t=22t 5．故结论②正确． 根据5～7秒面积不变，可得ED=2，当点P 运动到点C 时，面积变为0，此时点P 走过的路程为BE+ED+DC=11，故点H 的坐标为（11，0）．设直线NH 的解析式为y=kx+b ，将点H （11，0），点N （7，10）代入可得：11k b 0{7k b 10+=+=，解得：5k 2{55b 2=-=．∴直线NH 的解析式为：555y t 22=-+．故结论③错误．如图2，当△ABE 与△QBP 相似时，点P 在DC 上，∵tan ∠PBQ=tan ∠ABE=34，∴PQ 3BQ 4=，即11t 354-=． 解得：t=294．故结论④正确． 综上所述，①②④正确，共3个．故选B ． 11．D 【详解】试题解析：根据图象可得：抛物线开口向上，则a >0.抛物线与y 交于负半轴，则c <0， 对称轴：02bx a=->， ①∵它与x 轴的两个交点分别为(−1,0),(3,0)，∴对称轴是x =1， 12ba，∴-=∴b +2a =0，故①正确； ②∵开口向上， ∴a >0， 02bx a=->，∴b <0， ∵抛物线与y 轴交于负半轴， ∴c <0，∴abc >0，故②正确； ③∵a −b +c =0， ∴c =b −a ，∴a −2b +4c =a −2b +4(b −a )=2b −3a ， 又由①得b =−2a ， ∴a −2b +4c =−7a <0， 故③正确；④根据图示知，当x =4时，y >0， ∴16a +4b +c >0， 由①知，b =−2a ， ∴8a +c >0； 故④正确； 故选D. 12．D 【分析】连接BC 交OA 于M ，由四边形OBAC 是菱形，得到OA ⊥BC ，OM=AM=12∠BOA=12∠BOC=30°，求得BM=2，于是得到B （2），C （-2），求得直线OC的解析式为：，得到y=（x-m ）2，把A （0）B （2）代入y=（x-m ）2即可得到结论． 【详解】连接BC交OA于M，∵四边形OBAC是菱形，∴OA⊥BC，OM=AM=123∠BOA=12∠BOC=30°，∴BM=2，∴B（32），C（3-2），∴直线OC的解析式为：3，∵抛物线y=x2沿直线OC平移，∴3，∴y=a（x-m）2+h为y=（x-m）23，∵当抛物线与菱形的AB边有公共点时，把A（30）代入y=（x-m）23得0=（3）23，解得3163，∵3163，∴163，把B（32）代入y=（x-m）23得，2=（3）23，解得103，31033∴33163，故选D ．13．CD【分析】根据抛物线的性质由2a =得到图像开口向上，根据顶点式得到顶点坐标为(3,1)-，对称轴为直线3x =-，当3x >-时，y 随x 增大而增大．【详解】解：由抛物线y ＝2（x ＋3）2＋1得抛物线开口向上，故A 正确，不符合题意；由抛物线顶点式可知顶点坐标为(3,1)-，对称轴为直线3x =-，故B 正确，不符合题意； 由抛物线对称轴以及开口方向可知，当3x >-时，y 随x 增大而增大，故C 错误，符合题意； 当当x ＝－3时，函数值有最小值是1，故D 错误，符合题意；故答案为：CD ．14．ACE【分析】根据二次函数图象的性质，结合表中数据，逐一分析判断即可．【详解】解：A 、由表中数据可知，二次函数图象过(0,0)，选项正确；B 、函数图象过(0,0),(2,0)，则知对称轴为1x =，当1x <时，由表中数据知，y 随x 的增大而减小；当1x >时，y 随x 的增大而增大，所以开口向上，选项错误；C 、因为函数的对称轴为1x =，所以由函数对称性知，()()1,3,3,3-关于1x =对称，选项正确；D 、当1x >时，y 随x 的增大而增大，选项错误；E 、当y=0时，方程ax 2+bx +c =0有两个不相等的实数根120,2x x ==，选项正确故选：ACE15．ABD【分析】首先根据x 1＜x 2＜x 3＜x 4＜x 5＜x 6＜x 7，其对应的函数值是先增大后减小，可得抛物线开口向下，所以a ＜0；然后根据函数值是先增大后减小，可得6＜m ＜11＜k ；最后根据a ＜0，可得二次函数有最大值，而且二次函数的最小值244ac b a -，所以b 2≥4a （c -k ），据此判断即可．【详解】解：∵x 1＜x 2＜x 3＜x 4＜x 5＜x 6＜x 7，其对应的函数值是先增大后减小，∴抛物线开口向下，∴a ＜0，A 符合题意；∴6＜m ＜11＜k ，∴6＜m ＜11，B 符合题意； 根据图表中的数据知，只有当262x x x +=是抛物线的对称轴，抛物线的顶点坐标纵坐标不一定是k ，故C 不符合题意； ∵244ac b a -≥k ，a ＜0，∴4ac -b 2≤4ak ，∴b 2≥4a （c -k ），D 符合题意． 综上，可得判断正确的是：ABD ．故选ABD ．16．10．【分析】 令253y =-，解方程即可求出水面的宽度． 【详解】 解：根据题意，令253y =-， 2251=33x -- 解得：5x =±故水面的宽度为2×5=10米．答：水面的宽度为10米．故答案为：10．17．y ＝x 2﹣1．【分析】通过配方法先求出原抛物线的顶点坐标，继而得到平移后新抛物线的顶点坐标，然后利用顶点式即可求得新抛物线的解析式.【详解】∵y=x 2 +2x=(x+1)2-1 ，∴原抛物线的顶点为(-1，-1)，∵将抛物线y ＝x 2+2x 向右平移1个单位得到新的抛物线，∴新抛物线的顶点为(0，-1)，∴新抛物线的解析式为y=x 2-1，故答案为：y=x 2 -1．18．1x =-或3x = 13x -<< 1>【分析】根据二次函数y=-x 2+2x+m 的图象可以得到其对称轴和与x 轴一个交点，由此可以得到抛物线与x 轴的另一个交点坐标，然后就可得m 的值，那么解方程就能求得一元二次方程的解，可得到函数与x 轴的交点，那么x 轴上方的函数图象所对应的x 的取值即为不等式-x 2+2x+m ＞0的解集，对称轴的右侧，y 随x 的增大而减小．【详解】解：∵对称轴为x=1，一个根为3， ∴32x + =1， ∴x=-1，∴-x 2+2x+m=0的根为x 1=-1，x 2=3，∴不等式-x 2+2x+m ＞0的解集是-1＜x ＜3，当x ＞1时，y 随x 的而减小．19．①②④．【分析】根据抛物线开口确定a 符号，根据对称轴结合a 确定b 的符号，根据抛物线与y 轴交点确定c 的符号，即可判断①正确；把x =-1代入抛物线解析式，结合图象即可判断②正确，根据抛物线对称轴方程即可确定③错误，根据抛物线图象得到当x =1时，抛物线有最大值，即可判断④正确．【详解】解：∵抛物线开口向下，∴a ＜0，∵对称轴在y 轴右侧，∴a ，b 异号，b ＞0，∵抛物线与y 轴交点在y 轴正半轴，∴c ＞0，∴abc ＜0，故①正确；由图象得当x ＝-1时，y ＝a -b +c ＜0，∴a +c ＜b ，故②正确；∵图象对称轴为直线x ＝2b a-＝1， ∴﹣b ＝2a ，即2a +b ＝0，故③错误；由a +b ≥m （am +b ）得a +b +c ≥am 2+bm +c ，∵x ＝1时函数值y ＝a +b +c 为最大值，故④正确．故答案为：①②④．20．2142y x x =-- 【分析】先根据二次函数对称轴和B 点的坐标可以求出二次函数与x 轴的另一个交点坐标为（-2，0），由此可将二次函数解析式设为交点式，然后代入A 点坐标求解即可．【详解】解：∵二次函数的对称轴为直线1x =且与x 轴的一个交点为B （4，0），∴二次函数与x 轴的另一个交点坐标为（-2，0）， ∴设二次函数的解析式为()()24y a x x =+-，又∵二次函数经过A （0，-4），∴()()40204a -=+-， ∴12a =， ∴二次函数的解析式为()()21124=422y x x x x =+---． 21．（1） 当100＜x ≤500且x 为整数，18520y x =-+；（2）15000元；（3）w =214020x x -+，一次批发400件时所获利润最大,最大利润是8000元.22．（1）21262y x x =-++；（2）当点P 运动到153,2⎛⎫ ⎪⎝⎭时，PAB △的面积有最大值；（3）存在，()4,6P ．【分析】（1）由题意易得OA =OB =6，则有()6,0B ，然后可设二次函数解析式为()()26y a x x =+-，进而把点A 的坐标代入求解即可；（2）过点P 作PD ∥y 轴，交AB 于点D ，由题意易得直线AB 的解析式为6y x =-+，然后可设点21,262P a a a ⎛⎫-++ ⎪⎝⎭，则(),6D a a -+，然后可得PAB △的面积为()22113276332222S a a a ⎛⎫=⨯⨯-+=--+ ⎪⎝⎭，进而问题可求解； （3）由题意可得如图，设21,262P a a a ⎛⎫-++ ⎪⎝⎭，由（2）可得2132PD a a =-+，二次函数对称轴为直线2x =，进而可得点E 的横坐标，然后根据等腰直角三角形的性质可得PD =PE ，则问题可求解．【详解】解：（1）∵点()0,6A ，∴6OA =，∵tan 1ABO ∠=，∴6OB OA ==，∴()6,0B ，设二次函数解析式为()()26y a x x =+-，则把点A 的坐标代入得：126a -=，∴12a =-， ∴二次函数解析式为()()211262622y x x x x =-+-=-++； （2）过点P 作PD ∥y 轴，交AB 于点D ，如图所示：由（1）可设点21,262P a a a ⎛⎫-++ ⎪⎝⎭，设直线AB 的解析式为y kx b =+，把点A 、B 坐标代入得： 606k b b +=⎧⎨=⎩，解得：16k b =-⎧⎨=⎩， ∴直线AB 的解析式为6y x =-+，∴(),6D a a -+，∴根据铅垂法可得水平宽为点A 、B 的水平距离，即为6，铅垂高为2211266322PD a a a a a =-+++-=-+，则有： PAB △的面积为()22113276332222S a a a ⎛⎫=⨯⨯-+=--+ ⎪⎝⎭， ∴当a =3时，PAB △的面积为最大，∴点153,2P ⎛⎫ ⎪⎝⎭， ∴当点P 运动到153,2⎛⎫ ⎪⎝⎭时，PAB △的面积有最大值； （3）存在一点()4,6P 使PDE △为等腰直角三角形，理由如下：由题意可得如图所示：由（2）仍设点21,262P a a a ⎛⎫-++ ⎪⎝⎭，则2132PD a a =-+，由题意得二次函数的对称轴为直线2x =，∴根据二次函数的对称性可得点E 的横坐标为4E x a =-，∴24PE a =-，∵PE PD =，∴213242a a a -+=-， 解得：124,2a a ==-（不符合题意，舍去），∴点()4,6P ．23．（1）抛物线的函数表达式为y ＝x 2﹣4x +3；（2）△ADB 是等腰直角三角形；理由见解析；（3）P （2，﹣3）．【分析】（1）根据抛物线对称轴的定义易求A （1，0），B （3，0）．所以1、3是关于x 的一元二次方程x 2+bx +c ＝0的两根．由韦达定理易求b 、c 的值；（2）先求出顶点D 的坐标，再由勾股定理的逆定理证明△ABD 是直角三角形，再由对称得AD ＝BD ，进而得△ABD 是等腰直角三角形；（3）连接CA ，延长CA 与直线x ＝2交于点P ，连接BP ，此时P 点就是PC ﹣PB 的值最大的点，求出直线AC 的解析式，再求直线AC 与直线x ＝2的交点坐标便可．【详解】（1）如图，∵AB ＝2，对称轴为直线x ＝2．∴点A 的坐标是（1，0），点B 的坐标是（3，0）． ∵抛物线y ＝x 2+bx +c 与x 轴交于点A ，B ，∴1、3是关于x 的一元二次方程x 2+bx +c ＝0的两根．由韦达定理，1+3＝﹣b ，1×3＝c ，∴b ＝﹣4，c ＝3，∴抛物线的函数表达式为y ＝x 2﹣4x +3；（2）∵y ＝x 2﹣4x +3＝（x ﹣2）2﹣1，∴D （2，﹣1），∴AD 2+BD 2＝（2﹣1）2+（﹣1）2+（2﹣3）2+（﹣1）2＝4，∵AB 2＝22＝4，∴AD 2+BD 2＝AB 2，∴△ADB 是直角三角形，由对称性有AD ＝BD ，∴△ADB是等腰直角三角形；（3）连接CA，延长CA与直线x＝2交于点P，连接BP，如图2，∵A、B两点关于直线x＝2对称，∴PB＝P A，∴PC﹣PB＝PC﹣P A＝AC其值最大（∵另取一点P′，有P′C﹣P′B＝P′C﹣P′A＜AC），令x＝0，得y＝x2﹣4x+3＝3，∴C（0，3），∵A（1，0），∴易求直线AC的解析式为：y＝﹣3x+3，当x＝2时，y＝﹣3x+3＝﹣3，∴P（2，﹣3）．。
二次函数专项练习完整版
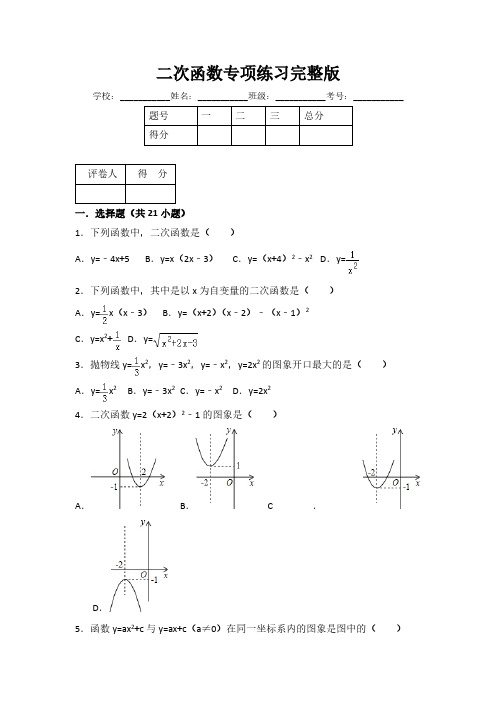
2．下列函数中，其中是以 x 为自变量的二次函数是（ A．y= x（x﹣3） B．y=（x+2） （x﹣2）﹣（x﹣1）2 C．y=x2+ D．y=
3．抛物线 y= x2，y=﹣3x2，y=﹣x2，y=2x2 的图象开口最大的是（ A．y= x2 B．y=﹣3x2 C．y=﹣x2 D．y=2x2 ）
A．先向左平移 2 个单位，再向上平移 1 个单位 B．先向左平移 2 个单位，再向下平移 1 个单位 C．先向右平移 2 个单位，再向上平移 1 个单位 D．先向右平移 2 个单位，再向下平移 1 个单位 18．抛物线 y=x2 向左平移 1 个单位，再向下平移 2 个单位，得到新的图象的二 次函数表达式是（ A．y=（x+1）2+2 ） B．y=（x﹣1）2﹣2 C．y=（x+1）2﹣2 D．y=（x﹣1）2+2
12．抛物线 y=﹣x2+2x+6 在直线 y=﹣2 上截得的线段长度为（ A．2 B．3 C．4 D．6
13．已知二次函数 y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②a﹣b+c＜0；③2a+b＜0；④abc＞0，其中所有正确结论的序号是（ ）
A．③④
B．②③
28．已知抛物线 y=ax2+bx+c（a＜0）过 A（﹣2，0） 、O（0，0） 、B（﹣3，y1） 、 C（3，y2）四点，则 y1 与 y2 的大小关系是 ．
29．如图，已知抛物线 y=ax2+bx+c 与 x 轴交于 A、B 两点，顶点 C 的纵坐标为﹣ 2，现将抛物线向右平移 2 个单位，得到抛物线 y=a1x2+b1x+c1，则下列结论正确 的是 ①b＞0 ②a﹣b+c＜0 ． （写出所有正确结论的序号）
二次函数专题复习
(5) y=2x2向左平移2个单位，再向下平移3个单位得到
函数解析式是 y=2(x+2)2-3。
（6）已知二次函数y=x2-4x-5 ， 求下列问题
△PAB，求P的坐标；
（4）第（3）题改为在直线y= -x+3上是否存在 点坐P标，；使若S不△PA存C=在，12说S明△P理AB？由若。存答在案，一求样出吗点？P的
P
y
（0，3） C
A
Q
o
y
（0，3） CP
B（3，0） A
x
oQ
（B 3，0） x
再见
得的图象解析式是 y=3x2
。
4、已知二次函数y=a（x-h）2+k的图象过原点， 最小值是-8，且形状与抛物线y=0.5x2-3x-5的形
状相同，其解析式为 y=0.5（x-16。）2-8
5、若x为任意实数，则二次函数y=x2+2x+3的函
数值y的取值范围是 y≥2 。
6、抛物线y=2x2-4x-1是由抛物线y=2x2-bx+c向
1.已知一个二次函数的图象经过点 （0，0），（1，﹣3），（2，﹣8）。
2.已知二次函数的图象的顶点坐标为 （－2，－3），且图象过点（－3，－2）。
3.已知二次函数的图象的对称轴是直线x=3, 并且经过点(6,0),和(2,12)
4.矩形的周长为60，长为x，面积为y，则y关于
x的函数关系式
。
如何判别a、b、c、b2-4ac，2a+b，a+b+c的符 号
二次函数复习基础练习题(含答案)(可编辑修改word版)
练习四 函数 y ax h2 的图象与性质
1、抛物线 y 1 x 32 ，顶点坐标是
,当 x
2
时,y 随 x 的增大而减小， 函数有最 值
2、试写出抛物线 y 3x 2 经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标.
2
（1）右移 2 个单位；（2）左移 个单位；（3）先左移 1 个单位，再右移 4 个单位.
10、已知二次函数 y ax 2 c(a 0), 当 x=1 时，y= -1；当 x=2 时，y=2，求该函数解析式.
11、富根老伯想利用一边长为 a 米的旧墙及可以围成 24 米长的旧木料，建造猪舍三间，如图，它们的平面图是一 排大小相等的长方形. （1） 如果设猪舍的宽 AB 为 x 米，则猪舍的总面积 S（米 2）与 x 有怎样的函数关
b 4、抛物线 y x 2 bx c 与 x 轴的正半轴交于点 A、B 两点，与 y 轴交于点 C，且线段 AB 的
9
长为 1，△ABC 的面积为 1，则 b 的值为______.
5、已知二次函数 y ax 2 bx c 的图象如图所示，则 a___0，b___0，c___0， b2 4ac ____0；
x (1 + x) ；③ y =
x2 (x2 + x)-
4；④ y =
1 x2
+
x
；
⑤ y = x (1- x) ，其中是二次函数的是
，其中a =
，b =
，c =
3、当 m
时，函数y = (m - 2) x2 + 3x - 5（m 为常数）是关于 x 的二次函数
4、当m = _ _ _ _ 时，函数y = (m2 + )m xm2- 2m- 1 是关于 x 的二次函数
二次函数综合复习附答案
二次函数综合复习学校:___________姓名：___________班级：___________考号：___________一、单选题 1．关于二次函数()215y x =-+，下列说法正确的是（ ） A ．函数图象的开口向下 B ．函数图象的顶点坐标是()1,5- C ．该函数有最大值，是大值是5D ．当1x >时，y 随x 的增大而增大2．如图，某公司准备在一个等腰直角三角形ABC 的绿地上建造一个矩形的休闲书吧PMBN ，其中点P 在AC 上，点NM 分别在BC，AB 上，记PM=x ，PN=y ，图中阴影部分的面积为S ，若NP 在一定范围内变化，则y 与x ，S 与x 满足的函数关系分别是（ ）A ．反比例函数关系，一次函数关系B ．二次函数关系，一次函数关系C ．一次函数关系，反比例函数关系D ．一次函数关系，二次函数关系3．二次函数21y ax bx =++的图象与一次函数2y ax b =+在同一平面直角坐标系中的图象可能是（ ）A ．B ．C ．D ．4．如图，已知抛物线22y ax bx =+-的对称轴是=1x -，直线l x ∥轴，且交抛物线于点()()1122,,,P x y Q x y ，下列结论错误．．的是（ ）A ．28b a >-B ．若实数1m ≠-，则2a b am bm -<+C ．320a ->D ．当2y >-时，120x x ⋅<5．如图，二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴交于A 、B 两点，与y 轴交于C 点，且对称轴为直线x ＝1，点B 坐标为（﹣1，0）．则下面的四个结论：①2a +b ＝0；①4a ﹣2b +c ＞0；①abc ＞0；①当y ＜0时，x ＜﹣1或x ＞3．其中正确的是（ ）A ．①①B ．①①C ．①①D ．①①6．记某商品销售单价为x 元，商家销售此种商品每月获得的销售利润为y 元，且y 是关于x 的二次函数．已知当商家将此种商品销售单价分别定为55元或75元时，他每月均可获得销售利润1800元；当商家将此种商品销售单价定为80元时，他每月可获得销售利润1550元，则y 与x 的函数关系式是（ ） A ．y ＝﹣（x ﹣60）2+1825 B ．y ＝﹣2（x ﹣60）2+1850 C ．y ＝﹣（x ﹣65）2+1900D ．y ＝﹣2（x ﹣65）2+20007．已知抛物线22()1y x =-+，下列结论错误的是（ ） A ．抛物线开口向上 B ．抛物线的对称轴为直线2x = C ．抛物线的顶点坐标为(2,1)D ．当2x <时，y 随x 的增大而增大8．已知抛物线y =ax 2 +bx +c 的对称轴为x =1，与x 轴正半轴的交点为A （3，0），其部分图象如图所示，有下列结论：①abc >0；①2c ﹣3b <0；①5a +b +2c =0；①若B （43，y 1）、C （13，y 2）、D （13-，y 3）是抛物线上的三点，则y 1<y 2<y 3．其中正确结论的个数有（ ）A ．1B ．2C ．3D ．4二、填空题 9．如图，已知P 是函数y 214x =-1图象上的动点，当点P 在x 轴上方时，作PH ①x 轴于点H ，连接PO ．小华用几何画板软件对PO ，PH 的数量关系进行了探讨，发现PO ﹣PH 是个定值，则这个定值为 _____．10．如图，二次函数2(0)y ax bx c a =++≠的图像过点(－1，0)，对称轴为直线x =2，下列结论：①4a +b =0；①9a +c <3b ；①8a +7b +2c >0；①若点A (－3，1y )、点B (21,2y -)、点C (37,2y )在该函数图像上，则132y y y <<：①若方程()()153a x x +-=-的两根为12,x x ，且12x x <，则1215.x x <-<<其中正确的结论有__________． (只填序号)11．已知二次函数223y x x =--+，当12a x 时，函数值y 的最小值为1，则a 的值为_______．12．抛物线y ＝ax 2+bx +c （a ≠0）的部分图象如图所示，其与x 轴的一个交点坐标为（﹣3，0），对称轴为x ＝﹣1，则当y ＜0时，x 的取值范围是_____．13．北仑梅山所产的草莓柔嫩多汁，芳香味美，深受消费者喜爱．有一草莓种植大户，每天草莓的采摘量为300千克，当草莓的零售价为22元/千克时，刚好可以全部售完．经调查发现，零售价每上涨1元，每天的销量就减少30千克，而剩余的草莓可由批发商以18元/千克的价格统一收购走，则当草莓零售价为___元时，该种植户一天的销售收入最大．14．如图，一次足球训练中，一球员从球门正前方将球射向球门，球射向球门的路线呈抛物线，当球飞行的水平距离为6米时，球达到最高点，此时球离地面3米，当足球下落到离地面53米时，足球飞行的水平距离为__________米．三、解答题 15．某超市经销一种商品，每件成本为50元．经市场调研，当该商品每件的销售价为60元时，每个月可销售300件，若每件的销售价每增加1元，则每个月的销售量将减少10件．设该商品每件的销售价为x 元，每个月的销售量为y 件． （1）求y 与x 的函数表达式；（2）当该商品每件的销售价为多少元时，每个月的销售利润最大？最大利润是多少？ 16．某商品的进价为每件40元，如果售价为每件50元，每个月可卖出210件；如果售价超过50元但不超过80元，每件商品的售价每上涨1元，则每个月少卖1件，如果售价超过80元后，若再涨价，则每涨1元每月少卖3件．设每件商品的售价x 元（x 为整数），每个月的销售量为y 件．（1）求y 与x 的函数关系式并直接写出自变量x 的取值范围； （2）设每月的销售利润为W ，请直接写出W 与x 的函数关系式．17．如图，三孔桥横截面的三个孔都呈抛物线形，左右两个抛物线形是全等的，正常水位时，大孔水面宽度为20m ，顶点距水面6m ，小孔顶点距水面4.5m ．当水位上涨刚好淹没小孔时，求大孔的水面宽度．18．如图，点(),3P a 在抛物线C ：()246y x =--上，且在C 的对称轴右侧．(1)写出C 的对称轴和y 的最大值，并求a 的值；(2)坐标平面上放置一透明胶片，并在胶片上描画出点P 及C 的一段，分别记为P '，C '．平移该胶片，使C '所在抛物线对应的函数恰为269y x x =-+-．求点P '移动的最短路程．19．某商场新进一批拼装玩具，进价为每个10元，在销售过程中发现．，日销售量y （个）与销售单价x （元）之间满足如图所示的一次函数关系．(1)求y 与x 的函数关系式（不要求写出自变量x 的取值范围）；(2)若该玩具某天的销售利润是600元，则当天玩具的销售单价是多少元？(3)设该玩具日销售利润为w 元，当玩具的销售单价定为多少元时，日销售利润最大？最大利润是多少元？20．丹东是我国的边境城市，拥有丰富的旅游资源．某景区研发一款纪念品，每件成本为30元，投放景区内进行销售，规定销售单价不低于成本且不高于54元，销售一段时间调研发现，每天的销售数量y （件）与销售单价x （元/件）满足一次函数关系，部分数据如下表所示：(1)直接写出y 与x 的函数关系式；(2)若每天销售所得利润为1200元，那么销售单价应定为多少元？ (3)当销售单价为多少元时，每天获利最大？最大利润是多少元？21．在平面直角坐标系xOy 中，抛物线()2420y ax ax a a =-+≠的顶点为P ，且与y 轴交于点A ，与直线y a =-交于点B ，C （点B 在点C 的左侧）.（1）求抛物线()2420y ax ax a a =-+≠的顶点P 的坐标（用含a 的代数式表示）；（2）横、纵坐标都是整数的点叫做整点，记抛物线与线段AC 围成的封闭区域（不含边界）为“W 区域”.①当2a =时，请直接写出“W 区域”内的整点个数；①当“W 区域”内恰有2个整点时，结合函数图象，直接写出a 的取值范围.22．为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量y 千克与每平方米种植的株数x （28x ≤≤，且x 为整数）构成一种函数关系．每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克． (1)求y 关于x 的函数表达式．(2)每平方米种植多少株时，能获得最大的产量？最大产量为多少千克？ 23．在平面直角坐标系中，设二次函数22y ax bx =++（a ，b 是常数，0a ≠）． (1)若1a =，当=1x -时，4y =．求y 的函数表达式．(2)写出一题a ，b 的值，使函数22y ax bx =++的图象与x 轴只有一个公共点，并求此函数的顶点坐标．(3)已知，二次函数22y ax bx =++的图象和直线4y ax b =+都经过点（2，m ），求证2212a b +≥．24．跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点K 为飞行距离计分的参照点，落地点超过K 点越远，飞行距离分越高．2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA 为66m ，基准点K 到起跳台的水平距离为75m ，高度为m h （h 为定值）．设运动员从起跳点A 起跳后的高度(m)y 与水平距离(m)x 之间的函数关系为2(0)y ax bx c a =++≠．(1)c的值为__________；(2)①若运动员落地点恰好到达K点，且此时19,5010a b=-=，求基准点K的高度h；①若150a=-时，运动员落地点要超过K点，则b的取值范围为__________；(3)若运动员飞行的水平距离为25m时，恰好达到最大高度76m，试判断他的落地点能否超过K点，并说明理由．参考答案：1．D【分析】由抛物线的表达式和函数的性质逐一求解即可． 【详解】解：对于y =（x -1）2+5， ①a =1>0，故抛物线开口向上，故A 错误； 顶点坐标为（1，5），故B 错误；该函数有最小值，最小值是5，故C 错误； 当1x >时，y 随x 的增大而增大，故D 正确， 故选：D ．【点睛】本题考查的是抛物线与x 轴的交点，主要考查函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法，及这些点代表的意义及函数特征． 2．D【分析】先求出AM =PM ，利用矩形的性质得出y =﹣x +m ，最后利用S =S △ABC －S 矩形PMBN 得出结论．【详解】设AB =m （m 为常数）．在△AMP 中，①A =45°，AM ①PM ， ①△AMP 为等腰直角三角形， ①AM =PM ，又①在矩形PMBN 中，PN =BM ，①x +y =PM +PN =AM +BM =AB =m ，即y =﹣x +m ， ①y 与x 成一次函数关系，①S =S △ABC －S 矩形PMBN =12m 2-xy =12m 2-x （﹣x +m ）=x 2-mx +212m ，①S 与x 成二次函数关系． 故选D ．【点睛】本题考查了一次函数的实际应用及二次函数的实际应用，解题的关键是掌握根据题意求出y 与x 之间的函数关系式． 3．A【分析】先分析二次函数21y ax bx =++的图像的开口方向即对称轴位置，而一次函数2y ax b =+的图像恒过定点(,0)2ba-，即可得出正确选项．【详解】二次函数21y ax bx =++的对称轴为2bx a=-，一次函数2y ax b =+的图像恒过定点(,0)2b a -，所以一次函数的图像与二次函数的对称轴的交点为(,0)2ba-，只有A 选项符合题意． 故选A ．【点睛】本题考查了二次函数的图像与性质、一次函数的图像与性质，解决本题的关键是能推出一次函数2y ax b =+的图像恒过定点(,0)2ba-，本题蕴含了数形结合的思想方法等． 4．C【分析】先根据抛物线对称轴求出2b a =，再由抛物线开口向上，得到0a >，则228480b a a a +=+>由此即可判断A ；根据抛物线开口向上在对称轴处取得最小值即可判断B ；根据当1x =时，20y a b =+-<，即可判断C ；根据2y >-时，直线l 与抛物线的两个交点分别在y 轴的两侧，即可判断D ．【详解】解：①抛物线22y ax bx =+-的对称轴是=1x -， ①12ba-=-， ①2b a =，①抛物线开口向上， ①0a >，①228480b a a a +=+>，①28b a >-，故A 说法正确，不符合题意； ①抛物线开口向下，抛物线对称轴为直线x =-1， ①当x =-1时，=2y a b --最小值，①当实数1m ≠-，则222a b am bm --<+-，①当实数1m ≠-时，2a b am bm -<+，故B 说法正确，不符合题意； ①当1x =时，20y a b =+-<，①a +2a -2＜0，即3a -2＜0，故C 说法错误，符合题意； ①2y >-，①直线l 与抛物线的两个交点分别在y 轴的两侧，①120x x ⋅<，故D 说法正确，不符合题意；故选C ．【点睛】本题主要考查了根据二次函数的图象去判断式子符号，二次函数的系数与图象之间的关系等等，熟知二次函数的相关知识是解题的关键．5．C【分析】根据对称轴为x ＝1可判断①；当x ＝﹣2时，4a ﹣2b +c ＜0即可判断①；根据开口方向，对称轴以及与y 轴交点即可判断①，求出A 点坐标，根据图象即可判断①．【详解】解：①对称轴为x ＝1，①x ＝﹣2b a＝1， ①b ＝﹣2a ，①2a +b ＝0，故选项①正确；①点B 坐标为（﹣1，0），①当x ＝﹣2时，4a ﹣2b +c ＜0，故选项①错误；①图象开口向下，①a ＜0，①b ＝﹣2a ＞0，①图象与y 轴交于正半轴上，①c ＞0，①abc ＜0，故选项①错误；①对称轴为x ＝1，点B 坐标为（﹣1，0），①A 点坐标为：（3，0），①当y ＜0时，x ＜﹣1或x ＞3．故选项①正确；故选：C ．【点睛】本题考查了二次函数的图象与系数的关系：二次函数y ＝ax 2+bx +c （a ≠0）的图象为抛物线，当a ＞0，抛物线开口向上；对称轴为直线x ＝﹣2b a；抛物线与y 轴的交点坐标为（0，c ）；当b 2﹣4ac ＞0，抛物线与x 轴有两个交点；当b 2﹣4ac ＝0，抛物线与x 轴有一个交点；当b 2﹣4ac ＜0，抛物线与x 轴没有交点．6．D【分析】设二次函数的解析式为：y ＝ax 2＋bx ＋c ，根据题意列方程组即可得到结论．【详解】解：设二次函数的解析式为：y ＝ax 2+bx+c ，①当x ＝55，y ＝1800，当x ＝75，y ＝1800，当x ＝80时，y ＝1550，①222555518007575180080801550a b c a b c a b c ⎧++=⎪++=⎨⎪++=⎩，解得a ＝−2，b ＝260，c ＝−6450，①y 与x 的函数关系式是y ＝﹣2x 2+260x ﹣6450＝﹣2（x ﹣65）2+2000，故选：D ．【点睛】本题考查了根据实际问题列二次函数关系式，正确的列方程组是解题的关键．7．D【分析】根据二次函数的开口方向、对称轴、顶点坐标以及增减性对各选项分析判断即可得解．【详解】解：抛物线22()1y x =-+中，a ＞0，抛物线开口向上，因此A 选项正确，不符合题意；由解析式得，对称轴为直线2x =，因此B 选项正确，不符合题意；由解析式得，当2x =时，y 取最小值，最小值为1，所以抛物线的顶点坐标为(2,1)，因此C 选项正确，不符合题意；因为抛物线开口向上，对称轴为直线2x =，因此当2x <时，y 随x 的增大而减小，因此D 选项错误，符合题意；故选D ．【点睛】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在()2y a x h k =-+中，对称轴为x h =，顶点坐标为(,)h k ． 8．B【分析】根据二次函数的图象与性质一一判断即可．【详解】解：由图象可知，开口向上，图象与y 轴负半轴有交点，则0a >，0c <， 对称轴为直线12b x a=-=，则20b a =-<， ①0abc >，故①正确；当3x =时，930y a b c =++=，①2b a =-，①30a c +=，即3a c =-①()()2323320c b a a -=⨯--⨯-=，故①错误；①对称轴为直线12b x a=-=， ①抛物线与x 轴负半轴的交点为（1-，0），①0a b c -+=，①930a b c ++=，两式相加，则10220a b c ++=，①50a b c ++=，故①错误； ①14133--=，12133-=，41133-=， ①421333>>， ①根据开口向上，离对称轴越近其对应的函数值越小，则有321y y y >>，故①正确； ①正确的结论有2个，故选：B【点睛】本题考查了二次函数的图象及性质；熟练掌握二次函数图象及性质，能够通过函数图象提取信息是解题的关键．9．2【分析】设p (x ，14x 2-1)，则OH =|x |，PH =|14x 2-1|，因点P 在x 轴上方，所以14x 2-1>0，由勾股定理求得OP =14x 2+1，即可求得OP -PH =2，得出答案． 【详解】解：设p (x ，14x 2-1)，则OH =|x |，PH =|14x 2-1|， 当点P 在x 轴上方时，①14x 2-1>0, ①PH =|14x 2-1|=14x 2-1， 在Rt △OHP 中，由勾股定理，得OP 2=OH 2+PH 2=x 2+(14x 2-1)2=(14x 2+1)2， ①OP =14x 2+1， ①OP -PH =（14x 2+1）-（14x 2-1）=2，故答案为：2．【点睛】本题考查二次函数图象上点的坐标特征，勾股定理，利用坐标求线段长度是解题的关键．10．①①①①【分析】根据二次函数的图象与系数的关系即可求出答案．【详解】解：①由对称轴可知：x ＝−2b a＝2， ①4a ＋b ＝0，故①正确；①由图可知：x ＝−3时，y ＜0，①9a −3b ＋c ＜0，即9a ＋c ＜3b ，故①正确；①令x ＝−1，y ＝0，①a −b ＋c ＝0，①b ＝−4a ，①c ＝−5a ，①8a ＋7b ＋2c＝8a −28a −10a＝−30a由开口可知：a ＜0，①8a ＋7b ＋2c ＝−30a ＞0，故①正确；①由抛物线的对称性可知：点C 关于直线x ＝2的对称点为（12，y 3），①−3＜−12＜12，①y 1＜y 2＜y 3故①错误；①由题意可知：（−1，0）关于直线x ＝2的对称点为（5，0），①二次函数y ＝ax 2＋bx ＋c ＝a （x ＋1）（x −5），令y ＝−3，①直线y ＝−3与抛物线y ＝a （x ＋1）（x −5）的交点的横坐标分别为x 1，x 2，①x 1＜−1＜5＜x 2故①正确；故答案为：①①①①．【点睛】本题考查二次函数的图象，解题的关键是正确理解二次函数的图象与系数之间的关系，本题属于中等题型．11．1-1【分析】先把函数解析式化为顶点式可得当1x <-时，y 随x 的增大而增大，当1x >-时，y 随x 的增大而减小，然后分两种情况讨论：若1a ≥-；若1a <-，即可求解．【详解】解：()222314y x x x =--+=-++，①当1x <-时，y 随x 的增大而增大，当1x >-时，y 随x 的增大而减小，若1a ≥-，当12a x时，y 随x 的增大而减小， 此时当12x =时，函数值y 最小，最小值为74，不合题意， 若1a <-，当x a =时，函数值y 最小，最小值为1，①2231a a --+=，解得：1a =-1-；综上所述，a 的值为1-故答案为：1-【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数的图象和性质是解题的关键．12．﹣3＜x ＜1【分析】根据抛物线与x 轴的一个交点坐标和对称轴，由抛物线的对称性可求抛物线与x 轴的另一个交点，再根据抛物线的增减性可求当y ＜0时，x 的取值范围．【详解】解：①抛物线y ＝ax 2+bx +c （a ≠0）与x 轴的一个交点为（﹣3，0），对称轴为x ＝﹣1，①抛物线与x 轴的另一个交点为（1，0），由图象可知，当y ＜0时，x 的取值范围是﹣3＜x ＜1．故答案为：﹣3＜x ＜1．【点睛】本题考查了二次函数的性质和数形结合能力，熟练掌握并灵活运用是解题的关键．13．25【分析】设草莓的零售价为x 元/千克，销售收入为y 元，由题意得y =-30x 2+1500x -11880，再根据二次函数的性质解答即可．【详解】解：设草莓的零售价为x 元/千克，销售收入为y 元，由题意得，y =x [300-30（x -22）]+18×30（x -22）=-30x 2+1500x -11880， 当150025260b x a =-=-=-时，y 最大， ①当草莓的零售价为25元/千克时，种植户一天的销售收入最大．故答案为：25．【点睛】本题考查二次函数的实际应用，熟练掌握二次函数的性质是解题关键． 14．10【分析】设抛物线的解析式为2(6)3y a x =-+，代入原点，确定解析式为2112y x x =-+，当y =53米时，求得x 的值即可． 【详解】设抛物线的解析式为2(6)3y a x =-+，代入原点，得：20(06)3a =-+，解得a =112-， ①抛物线的解析式为2112y x x =-+， 当y =53米时， 215123x x -+=， 解得x =10，x =2（舍去），足球飞行的水平距离为10米，故答案为：10．【点睛】本题考查了抛物线的解析式，已知函数值求自变量值，熟练掌握待定系数法是解题的关键．15．（1）y ＝-10x+900；（2）每件销售价为70元时，获得最大利润；最大利润为4000元【分析】（1）根据等量关系“利润＝（售价﹣进价）×销量”列出函数表达式即可．（2）根据（1）中列出函数关系式，配方后依据二次函数的性质求得利润最大值．【详解】解：（1）根据题意，y ＝300﹣10（x ﹣60）=-10x+900，①y 与x 的函数表达式为：y ＝-10x+900；（2）设利润为w ，由（1）知：w ＝（x ﹣50）（-10x+900）=﹣10x 2＋1400x ﹣45000， ①w ＝﹣10（x ﹣70）2＋4000，①每件销售价为70元时，获得最大利润；最大利润为4000元．【点睛】本题考查的是二次函数在实际生活中的应用．此题难度不大，解题的关键是理解题意，找到等量关系，求得二次函数解析式．16．（1）260(5080)4203(80140)x x y x x -<⎧=⎨-<⎩；（2）2230010400(5080)354016800(80140)x x x W x x x ⎧-+-<=⎨-+-<⎩【分析】（1）根据题意先分类讨论，当售价超过50元但不超过80元时，上涨的价格是()50x -元，就少卖()50x -件，用原来的210件去减()50x -得到销售量；当售价超过80元，超过80的部分是()80x -元，就少卖()380x -件，用原来的210件先减去售价从50涨到80之间少卖的30件再减去()380x -得到最终的销售量．（2）根据利润=（售价-成本）⨯销量，现在的单件利润是()40x -元，再去乘以（1）中两种情况下的销售量，得到销售利润关于售价的式子．【详解】（1）当5080x <时，210(50)y x =--，即260y x =-．当80140x <时，210(8050)3(80)y x =----，即4203y x =-，则260(5080),4203(80140).x x y x x -<⎧=⎨-<⎩ （2）由利润=（售价-成本）×销售量可以列出函数关系式为2230010400(5080),354016800(80140).x x x W x x x ⎧-+-<=⎨-+-<⎩【点睛】本题考查二次函数实际应用中的利润问题，关键在于根据题意列出销量与售价之间的一次函数关系式以及熟悉求利润的公式，需要注意本题要根据售价的不同范围进行分类讨论，结果要写成分段函数的形式，还要标上x 的取值范围．17．此时大孔的水面宽度为10m ．【分析】根据题意，建立如图所示的平面直角坐标系，可以得到A 、B 、M 的坐标，设出函数关系式，待定系数求解函数式．根据NC 的长度，得出函数值y ，代入解析式，即可得出E 、F 的坐标，进而得出答案．【详解】解：如图，建立如图所示的平面直角坐标系，由题意得，M 点坐标为（0，6），A 点坐标为（-10，0），B 点坐标为（10，0），设中间大抛物线的函数式为y =ax 2+6，①点B 在此抛物线上，①0=a ×102+6，解得a =-350， ①函数式为y =-350x 2+6． ①NC =4.5m ，①令y =4.5，代入解析式得-350x 2+6=4.5， x 1=5，x 2=-5， ①可得EF =5-（-5）=10．此时大孔的水面宽度为10m ．【点睛】本题是二次函数的实际应用，考查了待定系数法求二次函数的解析式，由函数值求自变量的值，解答时求出函数的解析式是关键．18．(1)对称轴为直线6x =，y 的最大值为4，7a =(2)5【分析】（1）由2()y a x h k =-+的性质得开口方向，对称轴和最值，把(),3P a 代入()246y x =--中即可得出a 的值；（2）由2269(3)y x x x =-+-=--，得出抛物线269y x x =-+-是由抛物线C ：()246y x =-+-向左平移3个单位，再向下平移4个单位得到，即可求出点P '移动的最短路程．（1）()2244)6(6y x x -=--=-+，①对称轴为直线6x =，①10-<，①抛物线开口向下，有最大值，即y 的最大值为4，把(),3P a 代入()246y x =--中得： 24(6)3a --=，解得：5a =或7a =，①点(),3P a 在C 的对称轴右侧，①7a =；（2）①2269(3)y x x x =-+-=--，①2(3)y x =--是由()246y x =-+-向左平移3个单位，再向下平移4个单位得到，5，①P '移动的最短路程为5．【点睛】本题考查二次函数2()y a x h k =-+的图像与性质，掌握二次函数2()y a x h k =-+的性质以及平移的方法是解题的关键．19．(1)2100y x =-+；(2)40元或20元；(3)当玩具的销售单价定为30元时，日销售利润最大；最大利润是800元；【分析】（1）直接由待定系数法，即可求出一次函数的解析式；（2）根据题意，设当天玩具的销售单价是x 元，然后列出一元二次方程，解方程即可求出答案；（3）根据题意，列出w 与x 的关系式，然后利用二次函数的性质，即可求出答案．（1）解：由图可知，设一次函数的解析式为y kx b =+，把点（25，50）和点（35，30）代入，得25503530k b k b +=⎧⎨+=⎩，解得2100k b =-⎧⎨=⎩， ①一次函数的解析式为2100y x =-+；（2）解：根据题意，设当天玩具的销售单价是x 元，则(10)(2100)600x x -⨯-+=，解得：140x =，220x =，①当天玩具的销售单价是40元或20元；（3）解：根据题意，则(10)(2100)w x x =-⨯-+，整理得：22(30)800w x =--+；①20-<，①当30x =时，w 有最大值，最大值为800；①当玩具的销售单价定为30元时，日销售利润最大；最大利润是800元．【点睛】本题考查了二次函数的性质，二次函数的最值，一次函数的应用，解一元二次方程，解题的关键是熟练掌握题意，正确的找出题目的关系，从而进行解题．20．(1)y ＝﹣2x +160(2)销售单价应定为50元(3)当销售单价为54元时，每天获利最大，最大利润1248元【分析】（1）设每天的销售数量y （件）与销售单价x （元/件）之间的关系式为y ＝kx +b ，用待定系数法可得y ＝﹣2x +160；（2）根据题意得（x ﹣30）•（﹣2x +160）＝1200，解方程并由销售单价不低于成本且不高于54元，可得销售单价应定为50元；（3）设每天获利w 元，w ＝（x ﹣30）•（﹣2x +160）＝﹣2x 2+220x ﹣4800＝﹣2（x ﹣55）2+1250，由二次函数性质可得当销售单价为54元时，每天获利最大，最大利润，1248元．【详解】（1）解：设每天的销售数量y （件）与销售单价x （元/件）之间的关系式为y ＝kx +b ，把（35，90），（40，80）代入得：35904080k b k b +=⎧⎨+=⎩， 解得2160k b =-⎧⎨=⎩， ①y ＝﹣2x +160；（2）根据题意得：（x ﹣30）•（﹣2x +160）＝1200，解得x 1＝50，x 2＝60，①规定销售单价不低于成本且不高于54元，①x ＝50，答：销售单价应定为50元；（3）设每天获利w 元，w ＝（x ﹣30）•（﹣2x +160）＝﹣2x 2+220x ﹣4800＝﹣2（x ﹣55）2+1250，①﹣2＜0，对称轴是直线x ＝55，而x ≤54，①x ＝54时，w 取最大值，最大值是﹣2×（54﹣55）2+1250＝1248（元），答：当销售单价为54元时，每天获利最大，最大利润，1248元．【点睛】本题考查一次函数，一元二次方程和二次函数的应用，解题的关键是读懂题意，列出函数关系式和一元二次方程．21．（1）顶点P 的坐标为()2,2a -；（2）① 6个；①112a <≤，112a -≤<-． 【分析】（1）由抛物线解析式直接可求；（2）①由已知可知A （0，2），C （ ，-2），画出函数图象，观察图象可得； ①分两种情况求：当a ＞0时，抛物线定点经过（2，-2）时，a=1，抛物线定点经过（2，-1）时，a=12 ，则12＜a≤1；当a ＜0时，抛物线定点经过（2，2）时，a=-1，抛物线定点经过（2，1）时，a=-12，则-1≤a<-12．【详解】解：（1）①y=ax 2-4ax+2a=a （x-2）2-2a ，①顶点为（2，-2a ）；（2）如图，①①a=2，①y=2x 2-8x+2，y=-2，①A（0，2），C （，-2），①有6个整数点；①当a ＞0时，抛物线定点经过（2，-2）时，a=1，抛物线定点经过（2，-1）时，，12a =； ① 112a <≤． 当a<0时，抛物线顶点经过点（2，2）时，1a =-；抛物线顶点经过点（2，1）时，12a =-； ① 112a -≤<-． ①综上所述：112a <≤，112a -≤<-． 【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质是解题的关键．22．(1)0.55y x =-+（28x ≤≤，且x 为整数）(2)每平方米种植5株时，能获得最大的产量，最大产量为12.5千克【分析】（1）由每平方米种植的株数每增加1株，单株产量减少0.5千克，即可得求得解析式；（2）设每平方米小番茄产量为W 千克，由产量=每平方米种植株数×单株产量即可列函数关系式，由二次函数性质可得答案．【详解】（1）解：①每平方米种植的株数每增加1株，单株产量减少0.5千克， ①40.5(2)0.55y x x =--=-+（28x ≤≤，且x 为整数）；（2）解：设每平方米小番茄产量为W 千克，22(0.55)0.550.5(5)12.5=-+=-+=--+w x x x x x ．①当5x =时，w 有最大值12.5千克．答：每平方米种植5株时，能获得最大的产量，最大产量为12.5千克．【点睛】本题考查二次函数的应用，解题的关键是读懂题意，列出函数关系式．23．(1)y ＝x 2−x ＋2(2)（−1，0）(3)见解析【分析】（1）把a ＝1代入二次函数的关系式，再把x ＝−1，y ＝4代入求出b 的值，进而确定二次函数的关系式；（2）令y ＝0，则ax 2＋bx ＋2＝0，当Δ＝0时，求得b 2＝8a ，据此写出一组a ，b 的值，化成顶点式即可求得顶点坐标；（3）根据题意得到4a ＋2b ＋2＝2a ＋4b ，整理得b ＝a ＋1，则a 2＋b 2＝2a 2＋2a ＋1＝2（a ＋12）2＋12，根据二次函数的性质即可得到a 2＋b 2≥12．（1）解：把a ＝1代入得，y ＝x 2＋bx ＋2，①当x ＝−1时，y ＝4，①4＝1−b ＋2，①b ＝−1，①二次函数的关系式为y ＝x 2−x ＋2；（2）解：令y ＝0，则ax 2＋bx ＋2＝0，当Δ＝0时，则b 2−8a ＝0，①b 2＝8a ，①若a ＝2，b ＝4时，函数y ＝ax 2＋bx ＋2的图象与x 轴只有一个公共点，①此时函数为y＝2x2＋4x＋2＝2（x＋1）2，①此函数的顶点坐标为（−1，0）；（3）证明：①二次函数y＝ax2＋bx＋2的图象和直线y＝ax＋4b都经过点（2，m），①4a＋2b＋2＝2a＋4b，①2a＋2＝2b，①b＝a＋1，①a2＋b2＝a2＋（a＋1）2＝2a2＋2a＋1＝2（a＋12）2＋12，①a2＋b2≥12．【点睛】本题考查二次函数图象与系数的关系，二次函数图象上点的坐标特征，二次函数的性质，待定系数法求二次函数的解析式，解题的关键：（1）熟知待定系数法；（2）求得b＝a＋1；（3）熟知二次函数的性质．24．(1)66(2)①基准点K的高度h为21m；①b＞9 10；(3)他的落地点能超过K点，理由见解析．【分析】（1）根据起跳台的高度OA为66m，即可得c＝66；（2）①由a＝﹣150，b＝910，知y＝﹣150x2+910x+66，根据基准点K到起跳台的水平距离为75m，即得基准点K的高度h为21m；①运动员落地点要超过K点，即是x＝75时，y＞21，故﹣150×752+75b+66＞21，即可解得答案；（3）运动员飞行的水平距离为25m时，恰好达到最大高度76m，即是抛物线的顶点为（25，76），设抛物线解析式为y＝a（x﹣25）2+76，可得抛物线解析式为y＝﹣2125（x﹣25）2+76，当x＝75时，y＝36，从而可知他的落地点能超过K点．【详解】（1）解：①起跳台的高度OA为66m，①A（0，66），把A（0，66）代入y＝ax2+bx+c得：c＝66，故答案为：66；（2）解：①①a＝﹣150，b＝910，①y＝﹣150x2+910x+66，①基准点K到起跳台的水平距离为75m，①y＝﹣150×752+910×75+66＝21，①基准点K的高度h为21m；①①a＝﹣150，①y＝﹣150x2+bx+66，①运动员落地点要超过K点，①当x＝75时，y＞21，即﹣150×752+75b+66＞21，解得b＞9 10，故答案为：b＞9 10；（3）解：他的落地点能超过K点，理由如下：①运动员飞行的水平距离为25m时，恰好达到最大高度76m，①抛物线的顶点为（25，76），设抛物线解析式为y＝a（x﹣25）2+76，把（0，66）代入得：66＝a（0﹣25）2+76，解得a＝﹣2 125，①抛物线解析式为y＝﹣2125（x﹣25）2+76，当x＝75时，y＝﹣2125×（75﹣25）2+76＝36，①36＞21，①他的落地点能超过K点．【点睛】本题考查二次函数的应用，解题的关键是读懂题意，能根据题意把实际问题转化为数学问题．。
九年级数学二次函数专项训练含答案-精选5篇
九年级数学二次函数专题精练含答案一、单选题1．关于二次函数22(4)6y x =-+的最大值或最小值，下列说法正确的是（ ） A ．有最大值4 B ．有最小值4 C ．有最大值6 D ．有最小值6 2．已知抛物线24y x x c =-++经过点(4,3)，那么下列各点中，该抛物线必经过的点是（ ）A ．(0,2)B ．(0,3)C ．(0,4)D ．(0,5) 3．在平面直角坐标系中，已知抛物线245y x x =-+，将该抛物线沿y 轴翻折所得的抛物线的表达式为（ ）A ．245y x x =--+B ．245y x x =++C ．245y x x =-+-D ．245y x x =--- 4．正方形的边长为4，若边长增加x ，那么面积增加y ，则y 关于x 的函数表达式为( ) A ．216y x =+ B ．2(4)y x =+ C ．28y x x =+ D ．2164y x =- 5．把抛物线22y x =向右平移2个单位，然后向下平移1个单位，则平移后得到的抛物线解析式是（ ）A ．22(2)1y x =-+-B ．22(2)1y x =--+C ．22(2)1y x =++D ．22(2)1y x =--6．如图，二次函数2y ax bx c =++的图象关于直线1x =对称，与x 轴交于1(,0)A x ，2(,0)B x 两点，若121x -<<-，则下列四个结论：①234x <<，①320a b +>，①24b a c ac >++，①a c b >>．正确结论的个数为（ ）A ．1个B ．2个C ．3个D ．4个7．对于抛物线23(1)2y x =-+-，下列说法正确的是（ ）A ．抛物线开口向上B ．当1x >-时，y 随x 增大而减小C ．函数最小值为﹣2D ．顶点坐标为（1，﹣2）8．关于二次函数()215y x =-+，下列说法正确的是（ ）A ．函数图象的开口向下B ．函数图象的顶点坐标是()1,5-C ．该函数有最大值，是大值是5D ．当1x >时，y 随x 的增大而增大 9．已知A (−3，−2) ，B (1，−2)，抛物线y =ax 2+bx +c (a >0)顶点在线段AB 上运动，形状保持不变，与x 轴交于C ，D 两点（C 在D 的右侧），下列结论：①c ≥−2 ；①当x >0时，一定有y 随x 的增大而增大；①若点D 横坐标的最小值为−5，点C 横坐标的最大值为3；①当四边形ABCD 为平行四边形时，a =12． 其中正确的是（ ）A ．①①B ．①①C ．①①D ．①①① 10．已知二次函数2243y mx m x =--（m 为常数，0m ≠），点(),p p P x y 是该函数图象上一点，当04p x ≤≤时，3p y ≤-，则m 的取值范围是（ ）A ．m 1≥或0m <B ．m 1≥C ．1m ≤-或0m >D ．1m ≤-11．已知函数()211y ax a x =-++，则下列说法不正确的个数是（ ）①若该函数图像与x 轴只有一个交点，则1a =①方程()2110ax a x -++=至少有一个整数根①若11x a<<，则()211y ax a x =-++的函数值都是负数 ①不存在实数a ，使得()2110ax a x -++≤对任意实数x 都成立A ．0B ．1C ．2D ．312．如图，在正方形ABCD 中，4AB =，点P 从点A 出发沿路径A B C →→向终点C 运动，连接DP ，作DP 的垂直平分线MN 与正方形ABCD 的边交于M ，N 两点，设点P 的运动路程为x ，PMN 的面积为y ，则下列图象能大致反映y 与x 函数关系的是（ ）A ．B ．C ．D ．二、填空题13．已知点（3，a ）在抛物线y =-2x 2+2x 上，则=a ______．14．如图是二次函数21y ax bx c =++ 和一次函数y 2＝kx +t 的图象，当y 1≥y 2时，x 的取值范围是_____．15．小亮同学在探究一元二次方程2ax bx c 0++=的近似解时，填好了下面的表格：根据以上信息请你确定方程2ax bx c 0++=的一个解的范围是________．16．已知二次函数223y x x =--+，当12a x时，函数值y 的最小值为1，则a 的值为_______．17．已知抛物线2122y x bx =+-与x 轴交于A ，B 两点，与y 轴交于C 点．（1）若(1,0)A -，则b =______．（2）若(1,0)M -，(1,0)N ，抛物线2122y x bx =+-与线段MN 没有交点，则b 的取值范围为______．三、解答题18．已知抛物线经过点()1,0A -，()5,0B ，()0,5C ，求该抛物线的函数关系式 19．如图，抛物线212y x bx c =++与直线132y x =+分别相交于A 、B 两点，其中点A 在y 轴上，且此抛物线与x 轴的一个交点为()3,0C -．（1）求抛物线的解析式（2）在抛物线对称轴l 上找一点M ，使MBC ∆的周长最小，请求出这个周长的最小值．20．如图，一次函数y A 、B ，二次函数2y bx c ++图象过A 、B 两点．（1）求二次函数解析式；（2）点B 关于抛物线对称轴的对称点为点C ，点P 是对称轴上一动点，在抛物线上是否存在点Q ，使得以B 、C 、P 、Q 为顶点的四边形是菱形？若存在，求出Q 点坐标；若不存在，请说明理由．21．如图，二次函数y ＝ax 2+bx +c 的图象与x 轴交于点A (﹣2，0)和点B (8，0)，与y 轴交于点C (0，﹣8)，连接AC ，D 是抛物线对称轴上一动点，连接AD ，CD ，得到①ACD ．（1）求该抛物线的函数解析式．（2）①ACD 周长能否取得最小值，如果能，请求出D 点的坐标；如果不能，请说明理由．（3）在（2）的条件下，在抛物线上是否存在点E ，使得①ACE 与①ACD 面积相等，如果存在，请求出点的坐标；如果不存在，请说明理由．参考答案1--10DBCCD BBDDA 11--12CA13．-1214．﹣1≤x ≤215．3.24x 3.25<<16．1-17． 32- 3322b -<< 18．解：①抛物线经过点()1,0A -，()5,0B ，()0,5C ，①设抛物线的表达式为()()15y a x x =+-，将点()0,5C 代入得：55a =-，解得：1a =-，①()()21545y x x x x =-+-=-++．①该抛物线的函数关系式为245y x x =-++．19．.解：（1）抛物线212y x bx c =++与直线132y x =+交于y 轴上一点A ， 令0,x = 则3,y = ∴ 点()0,3A把()0,3A ，()3,0C -代入212y x bx c =++得： 39302c b c =⎧⎪⎨-+=⎪⎩， 解得：523b c ⎧=⎪⎨⎪=⎩， ∴抛物线的解析式是215322y x x =++； （2）将直线132y x =+与二次函数215322y x x =++联立得方程组： 213215322y x y x x ⎧=+⎪⎪⎨⎪=++⎪⎩ 215133,222x x x ∴++=+ 240,x x ∴-=解得：0x =或4x =-，04,,31x x y y ==-⎧⎧∴⎨⎨==⎩⎩()0,3A ，()4,1B ∴-BC ∴==如图，要使MBC △的周长最小，则MB MC +最小，设二次函数215322y x x =++与x 轴的另一交点为D ，抛物线的对称轴为：552,1222x=-=-⨯()3,0C-∴点()2,0D-，连接,BD交对称轴于,MMD MC∴=，此时，MB MC MB MD BD+=+=最小，此时：BD=MBC∴20．解：（1）对于y x=x=0时，y=当y=0时，03x-=，妥得，x=3①A（3，0），B（0，把A（3，0），B（0，2y bx c++得：+=0b cc⎧⎪⎨=⎪⎩解得，bc⎧=⎪⎨⎪=⎩①抛物线的解析式为：2y x x=-（2）抛物线的对称轴为直线12bxa=-==故设P（1，p），Q（m，n）①当BC为菱形对角线时，如图，①B ，C 关于对称没对称，且对称轴与x 轴垂直，①①BC 与对称轴垂直，且BC //x 轴①在菱形BQCP 中，BC ①PQ①PQ ①x 轴①点P 在x =1上，①点Q 也在x =1上，当x =1时，211y①Q （1，）； ①当BC 为菱形一边时，若点Q 在点P 右侧时，如图，①BC //PQ ，且BC =PQ①BC //x 轴，①令y =2y 解得，120,2x x ==①(2,C①PQ=BC=22①PB=BC=2①迠P在x轴上，①P(1,0)①Q(3，0)；若点Q在点P的左侧，如图，同理可得，Q（-1，0）综上所述，Q点坐标为（1，）或(3，0)或（-1，0）21．解：（1）由题意可得：0=4206488a b ca b cc-+⎧⎪=++⎨⎪=-⎩，解得：1238abc⎧=⎪⎪=-⎨⎪=-⎪⎩，①抛物线的解析式为：y＝12x2﹣3x﹣8；（2）△ACD周长能取得最小值，①点A（﹣2，0），点B（8，0），①对称轴为直线x＝3，①①ACD周长＝AD+AC+CD，AC是定值，①当AD+CD取最小值时，△ACD周长能取得最小值，①点A，点B关于对称轴直线x＝3对称，①连接BC交对称轴直线x＝3于点D，此时AD+CD有最小值，设直线BC 解析式为：y ＝kx ﹣8，①0＝8k ﹣8，①k ＝1，①直线BC 解析式为：y ＝x ﹣8，当x ＝3，y ＝﹣5，①点D （3，﹣5）；（3）存在，①点A （﹣2，0），点C （0，﹣8），①直线AC 解析式为y ＝﹣4x ﹣8，如图，①①ACE 与①ACD 面积相等，①DE ①AC ，①设DE 解析式为：y ＝﹣4x +n ，①﹣5＝﹣4×3+n ，①n ＝7，①DE 解析式为：y ＝﹣4x +7， 联立方程组可得：2471382y x y x x =-+⎧⎪⎨=--⎪⎩，解得：12111x y ⎧=⎪⎨=-⎪⎩，22111x y ⎧=⎪⎨=⎪⎩， ①点E1，﹣1，）．九年级上册数学二次函数同步练习一、单选题1．下列函数中，是二次函数的是（ ） A ．y ＝（2x ﹣1）2 B ．y ＝（x +1）2﹣x 2 C ．y ＝ax 2D ．y ＝2x +32．若抛物线258(3)23m m y m x x -+=-+-是关于x 的二次函数，那么m 的值是（ ）A ．3B ．2-C ．2D ．2或33．若抛物线y =x 2-x -2经过点A （3，a ），则a 的值是（ ） A ．2B ．4C ．6D ．84．已知二次函数2135y x x =-+，则其二次项系数a ，一次项系数b ，常数项c 分别是（ ） A ．1,3,5a b c ==-= B ．1,3,5a b c ===C ．5,3,1a b c ===D ．5,3,1a b c ==-=5．如果函数2(2)25y a x x =-+-是二次函数，则a 的取值范围是（ ） A ．2a ≠ B ．a≥0C ．a=2D ．a>06．下列函数中①31y x ；①243y x x =-；①1y x=；①225=-+y x ，是二次函数的有（） A ．①①B ．①①C ．①①D ．①①7．若抛物线2y x bx c =-++经过点()2,3-，则247c b --的值是（ ） A ．6B ．7C ．8D ．208．函数y=ax2+bx+c(a ，b ，c 是常数)是二次函数的条件是( ) A ．a≠0，b≠0，c≠0 B ．a<0，b≠0，c≠0 C ．a>0，b≠0，c≠0 D ．a≠0二、填空题 9．若()2321m m y m x --=+是二次函数，则m 的值为______．10．若22ay x -=是二次函数，则=a ________．11．在二次函数21y x =-+中，二次项系数、一次项系数、常数项的和为_____． 12．下列函数一定是二次函数的是__________．①2y ax bx c =++；①3y x =-；①2431y x x =-+；①2(1)y m x bx c =-++；①y =(x -3)2-x 213．当常数m ≠______时，函数y =（m 2﹣2m ﹣8）x 2+（m +2）x +2是二次函数；当常数m =___时，这个函数是一次函数． 14．已知函数2135m y x -=-① 当m ＝ _________时，y 是关于x 的一次函数； ① 当m ＝_________时，y 是关于x 的二次函数 ．15．二次函数()22339y m x x m =+++-的图象经过原点，则m =__________．16．已知二次函数2y x bx 3=-++，当x 2=时，y 3=．则这个二次函数的表达式是________． 三、解答题17．下列函数中（x ，t 是自变量），哪些是二次函数？ 22322113,25,22,1522y x y x x y x s t t =-+=-+=+=++．18．已知函数y =（m 2-2）x 2+（m x +8． （1）若这个函数是一次函数，求m 的值； （2）若这个函数是二次函数，求m 的取值范围.19．若函数y=（a -1）x b+1+x 2+1是二次函数，试讨论a 、b 的取值范围.20．篱笆墙长30m ，靠墙围成一个矩形花坛，写出花坛面积y(m 2)与长x 之间的函数关系式，并指出自变量的取值范围.参考答案：1．A 2．C 3．B 4．D 5．A 6．B 7．B 8．D 9．4 10．2± 11．0 12．①13． 4，-2 4 14． 1 3215．316．2y x 2x 3=-++17．2132y x =-+和215s t t =++是二次函数18．（1）m （2）m ≠m ≠19．①a≠0；①b=0或-1，a 取全体实数①当a=1，b 为全体实数时，y=x 2+1是二次函数 20．y= 21152x x -+, x 的取值范围为0<x<30.九年级数学上册二次函数的图象与性质练习题（附答案）一．选择题1．如果在二次函数的表达式y ＝ax 2+bx +c 中，a ＞0，b ＜0，c ＜0，那么这个二次函数的图象可能是（ ）A．B．C．D．2．已知y＝（m+2）x|m|+2是关于x的二次函数，那么m的值为（）A．﹣2B．2C．±2D．03．已知A（，y1），B（2，y2），C（﹣，y3）是二次函数y＝3（x﹣1）2+k图象上三点，则y1、y2、y3的大小关系为（）A．y1＞y2＞y3B．y2＞y1＞y3C．y3＞y2＞y1D．y2＞y3＞y14．二次函数的部分图象如图所示，对称轴是直线x＝﹣1，则这个二次函数的表达式为（）A．y＝﹣x2+2x+3B．y＝x2+2x+3C．y＝﹣x2+2x﹣3D．y＝﹣x2﹣2x+3 5．在同一平面直角坐标系中，一次函数y＝ax+b和二次函数y＝ax2+bx+c的图象可能为（）A．B．C．D．6．关于抛物线y＝﹣x2+2x﹣3的判断，下列说法正确的是（）A．抛物线的开口方向向上B．抛物线的对称轴是直线x＝﹣1C．抛物线对称轴左侧部分是下降的D．抛物线顶点到x轴的距离是27．已知二次函数y＝x2﹣4x+5（0≤x≤3），则它的最大值是（）A．1B．2C．3D．58．如图为二次函数y＝ax2+bx+c的图象，给出下列说法：①ab＜0；②方程ax2+bx+c＝0的根为x1＝﹣1，x2＝3；③a+b+c＞0；④当x＜1时，y随x值的增大而增大；⑤当y＞0时，x＜﹣1或x＞3．其中，正确的说法有（）A．①②④B．①②⑤C．①③⑤D．②④⑤9．已知函数y＝2（x+1）2+1，则（）A．当x＜1 时，y随x的增大而增大B．当x＜1 时，y随x的增大而减小C．当x＜﹣1 时，y随x的增大而增大D．当x＜﹣1 时，y随x的增大而减小10．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论中不正确的有（）个．①abc＞0；②2a+b＝0；③9a+3b+c＜0；④4ac﹣b2＜0；⑤a+b≥m（am+b）（m为任意实数）．A．3B．2C．1D．0二．填空题11．已知四个二次函数的图象如图所示，那么a1，a2，a3，a4的大小关系是．（请用“＞”连接排序）12．抛物线y＝3x2+6x+11的顶点坐标为．13．二次函数y＝3（x﹣1）2+5的最小值为．14．已知二次函数y＝2x2+bx+4顶点在x轴上，则b＝．15．二次函数y＝x2﹣2x+1在2≤x≤5范围内的最小值为．16．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①2a+b＝0；②a+c＞b；③抛物线与x轴的另一个交点为（3，0）；④abc＞0．其中正确的结论是（填写序号）．三．解答题17．已知二次函数的顶点坐标为A（1，﹣4），且经过点B（3，0）．（1）求该二次函数的解析式；（2）判断点C（2，﹣3）是否在该函数图象上，并说明理由．18．如图，已知直线l过点A（4，0），B（0，4）两点，它与二次函数y＝ax2的图象在第一象限内交于点P，若S△AOP＝4，试求二次函数的表达式．19．如图，直线L1：y＝bx+c与抛物线L2：y＝ax2的两个交点坐标分别为A（m，4），B（1，1）．（1）求m的值；（2）过动点P（n，0）且垂直于x轴的直线与L1，L2的交点分别为C，D，当点C位于点D上方时，请直接写出n的取值范围．20．已知二次函数y＝a（x+a）（x+a﹣1）．（1）当a＝2时，求该二次函数图象的对称轴．（2）当a＜0时，判断该二次函数图象的顶点所在的象限，并说明理由．（3）当0＜x＜3时，y随着x增大而增大，求a的取值范围．21．已知二次函数y＝ax2（a≠0）与一次函数y＝kx﹣2的图象相交于A、B两点，如图所示，其中A（﹣1，﹣1），求△OAB的面积．22．抛物线y＝﹣x2+bx+c经过点A（3，0）和点B（0，3），且这个抛物线的对称轴为直线l，顶点为C．（1）求抛物线的解析式；（2）连接AB、AC、BC，求△ABC的面积．23．如图，在平面直角坐标系中，直线AB与抛物线y＝﹣x2+bx+c交于A（﹣1，0）和B（2，3）两点，抛物线与y轴交于点C．（1）求一次函数和二次函数的解析式；（2）求△ABC的面积．参考答案一．选择题1．解：∵a＞0，b＜0，c＜0，∴﹣＞0，∴抛物线的图象开口向上，对称轴在y轴的右边，交y轴于负半轴，故选：C．2．解：∵y＝（m+2）x|m|+2是y关于x的二次函数，∴|m|＝2且m+2≠0．解得m＝2．故选：B．3．解：∵二次函数y＝3（x﹣1）2+k图象的对称轴为直线x＝1，而A（，y1）到直线x＝1的距离最近，C（﹣，y3）到直线x＝1的距离最远，∴y3＞y2＞y1．故选：C．4．解：由图象知抛物线的对称轴为直线x＝﹣1，设抛物线解析式为y＝a（x+1）2+k，将（﹣3，0）、（0，3）代入，得：，解得：，则抛物线解析式为y＝﹣（x+1）2+4＝﹣x2﹣2x+3，故选：D．5．解：A、由抛物线可知，a＜0，x＝﹣＜0，得b＜0，由直线可知，a＜0，b＜0，故本选项正确；B、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误；C、由抛物线可知，a＞0，x＝﹣＞0，得b＜0，由直线可知，a＞0，b＞0，故本选项错误；D、由抛物线可知，a＞0，由直线可知，a＜0，故本选项错误．故选：A．6．解：∵y＝﹣x2+2x﹣3＝﹣（x﹣1）2﹣2，∴抛物线开口向下，对称轴为x＝1，顶点坐标为（1，﹣2），在对称轴左侧，y随x的增大而增大，∴A、B、C不正确；∵抛物线顶点到x轴的距离是|﹣2|＝2，∴D正确，故选：D．7．解：y＝x2﹣4x+5＝（x﹣2）2+1，由于0≤x≤3，所以当x＝2时，y有最小值1，当x＝0时，y有最大值5．故选：D．8．解：根据图象可知：①对称轴﹣＞0，故ab＜0，正确；②方程ax2+bx+c＝0的根为x1＝﹣1，x2＝3，正确；③x＝1时，y＝a+b+c＜0，错误；④当x＜1时，y随x值的增大而减小，错误；⑤当y＞0时，x＜﹣1或x＞3，正确．正确的有①②⑤．故选：B．9．解：∵y＝2（x+1）2+1，∴当x＞﹣1时，y随x的增大而增大，故选项A错误，当x＜﹣1时，y随x的增大而减小，故选项B错误、选项C错误、选项D正确；故选：D．10．解：∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x＝﹣＝1，∴b＝﹣2a＞0，∵抛物线与y轴的交点坐标在x轴上方，∴c＞0，∴abc＜0，所以①错误；∵b＝﹣2a，∴2a+b＝0，所以②正确；∵x＝3时，y＜0，∴9a+3b+c＜0，所以③正确．∵抛物线与x轴有2个交点，∴Δ＝b2﹣4ac＞0，即4ac﹣b2＜0，所以④正确；∵抛物线的对称轴为直线x＝1，∴函数的最大值为a+b+c，∴a+b+c≥am2+bm+c（m为任意实数），即a+b≥m（am+b），所以⑤正确．故选：C．二．填空题11．解：如图所示：①y＝a1x2的开口小于②y＝a2x2的开口，则a1＞a2＞0，③y＝a3x2的开口大于④y＝a4x2的开口，开口向下，则a4＜a3＜0，故a1＞a2＞a3＞a4．故答案为：a1＞a2＞a3＞a412．解：∵y＝3x2+6x+11＝3（x+1）2+8，∴抛物线y＝3x2+6x+11的顶点坐标为（﹣1，8），故答案为（﹣1，8）．13．解：由于二次函数y＝3（x﹣1）2+5中，a＝3＞0，所以当x＝1时，函数取得最小值为5，故答案为5．14．解：∵二次函数y＝2x2+bx+4顶点在x轴上，∴＝0，解得b＝，故答案为：±4．15．解：∵二次函数y＝x2﹣2x+1＝（x﹣1）2，∴当x＞1时，y随x的增大而增大，∴在2≤x≤5范围内，当x＝2时，y取得最小值，此时y＝（2﹣1）2＝1，故答案为：1．16．解：∵抛物线的对称轴为直线x＝﹣＝1，∴2a+b＝0，所以①正确；∵x＝﹣1时，y＜0，∴a﹣b+c＜0，即a+c＜b，所以②错误；∵抛物线与x轴的一个交点为（﹣2，0）而抛物线的对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（4，0），所以③错误；∵抛物线开口向上，∴a＞0，∴b＝﹣2a＜0，∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＞0，所以④正确．故答案为①④．三．解答题17．解：（1）设二次函数的解析式是y＝a（x﹣h）2+k，∵二次函数的顶点坐标为A（1，﹣4），∴y＝a（x﹣1）2﹣4，∵经过点B（3，0），∴代入得：0＝a（3﹣1）2﹣4，解得：a＝1，∴y＝（x﹣1）2﹣4，即二次函数的解析式为y＝x2﹣2x﹣3；（2）点C（2，﹣3）在该函数图象上，理由是：把C（2，﹣3）代入y＝x2﹣2x﹣3得：左边＝﹣3，右边＝4﹣4﹣3＝﹣3，即左边＝右边，所以点C在该函数的图象上．18．解：设直线l的解析式为y＝kx+b，把A（4，0），B（0，4）分别代入得，解得，∴直线l的关系式为y＝﹣x+4，设P（t，﹣t+4），∵S△AOP＝4，∴×4×（﹣t+4）＝4，解得t＝2，∴P（2，2），把P（2，2）代入y＝ax2得4a＝2，解得a＝，∴二次函数的表达式为y＝x2．19．解：（1）把B（1，1）代入y＝ax2得：a＝1，∴抛物线解析式为y＝x2．把A（m，4）代入y＝x2得：4＝m2，∴m＝±2．∵点A在二象限，∴m＝﹣2．（2）观察函数图象可知：当﹣2＜x＜1时，直线在抛物线的上方，∴n的取值范围为：﹣2＜n＜1．20．解：（1）当a＝2时，y＝2（x+2）（x+1），∴二次函数的对称轴为x＝．（2）由题知二次函数与x轴的交点坐标为（﹣a，0），（1﹣a，0）；∵a＜0，∴二次函数的开口方向向下；又﹣a＞0，1﹣a＞0，所以对称轴所在直线为x＝＝＞0，当x＝时，y＝﹣＞0，所以顶点坐标（，﹣）在第一象限．（3）由（2）知，二次函数的对称轴为直线x＝，∵当0＜x＜3时，y随着x增大而增大，∴当a＞0时，≤0，解得a≥；当a＜0，≥3，解得a≤﹣．∴a的取值范围为a≥或a≤﹣．21．解：∵一次函数y＝kx﹣2的图象相过点A（﹣1，﹣1），∴﹣1＝﹣k﹣2，解得k＝﹣1，∴一次函数表达式为y＝﹣x﹣2，∴令x＝0，得y＝﹣2，∴G（0，﹣2），∵y＝ax2过点A（﹣1，﹣1），∴﹣1＝a×1，解得a＝﹣1，∴二次函数表达式为y＝﹣x2，由一次函数与二次函数联立可得，解得，，∴S△OAB＝OG•|A的横坐标|+OG•点B的横坐标＝×2×1+×2×2＝1+2＝3．22．解：（1）∵抛物线经过A、B（0，3）∴由上两式解得∴抛物线的解析式为：；（2）由（1）抛物线对称轴为直线x＝把x＝代入，得y＝4则点C坐标为（，4）设线段AB所在直线为：y＝kx+b，则有，解得∴AB解析式为：∵线段AB所在直线经过点A、B（0，3）抛物线的对称轴l于直线AB交于点D∴设点D的坐标为D将点D代入，解得m＝2∴点D坐标为，∴CD＝CE﹣DE＝2过点B作BF⊥l于点F∴BF＝OE＝∵BF+AE＝OE+AE＝OA＝∴S△ABC＝S△BCD+S△ACD＝CD•BF+CD•AE∴S△ABC＝CD（BF+AE）＝×2×＝23．解：（1）∵抛物线y＝﹣x2+bx+c交于A（﹣1，0）和B（2，3）两点∴，解得：，∴抛物线解析式为y＝﹣x2+2x+3，设直线AB的解析式为y＝mx+n（m≠0），则，解得，∴直线AB的解析式为y＝x+1；（2）令x＝0，则y＝﹣x2+2x+3＝3，∴C（0，3），则OC＝3，BC＝2，BC∥x轴，∴S△ABC＝×BC×OC＝＝3．九年级数学上册二次函数单元综合测试卷一．选择题（共10小题）1．下列各式中，是y关于x的二次函数的是（）A．y＝4x B．y＝3x﹣5C．y＝D．y＝2x2+12．已知：a＞b＞c，且a+b+c＝0，则二次函数y＝ax2+bx+c的图象可能是下列图象中的（）A．B．C．D．3．二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（）A．（2，6）B．（4，6）C．（3，﹣5）D．（3，5）4．将二次函数y＝x2+2x﹣1转化为y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x+1）2C．y＝（x+1）2﹣1D．y＝（x+1）2﹣2 5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣66．顶点坐标为（3，1），形状与函数y＝的图象相同且开口方向相反的抛物线的解析式为（）A．y＝+1B．y＝+1C．y＝﹣+1D．y＝﹣+17．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1 8．抛物线y＝ax2+bx+c纵坐标y的对应值如下表：x…﹣2﹣1012…y…04664…则下列说法中正确的个数是（）①方程ax2+bx+c＝0，有两根为x1＝﹣2，x2＝3；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x＝1；④抛物线开口向上．A．1B．2C．3D．49．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，E，F分别为边BC，CD上的点（点E，F不与线段BC，CD的端点重合），BE＝CF，连接OE，OF，EF．关于以下三个结论，下列判断正确的是（）结论Ⅰ：∠BOF始终是90°；结论Ⅱ：△OEF面积的最小值是2；结论Ⅲ：四边形OECF的面积始终是8．A．结论Ⅰ和Ⅱ都对，结论Ⅲ错B．结论Ⅰ和Ⅱ都对，结论Ⅱ错C．结论Ⅱ和Ⅲ都对，结论Ⅰ错D．三个结论都对10．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（）A．37.5°B．40°C．42.5°D．45°二．填空题（共6小题）11．函数是二次函数，则m的值为．12．已知抛物线y＝x2﹣4x+c．与直线y＝m相交于A，B两点，若点A的横坐标；x A＝﹣1，则点B的横坐标．x B的值为．13．已知二次函数y＝ax2开口向上，且|2﹣a|＝3，则a＝．14．已知抛物线y＝x2﹣3x+1的图象上有一点A（m，n），则m﹣n的最大值是．15．如图，在平面直角坐标系中，抛物线y＝﹣x2+2x+c与x轴交于点A、B，与y轴交于点C，过点C作CD∥x轴，交抛物线于另一点D，若AB+CD＝3，则c的值为．16．如图，在矩形ABCD中，AB＝12，BC＝16，点E、F分别是边AB、BC上的动点，且EF＝10，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为．三．解答题（共7小题）17．看图回答．（1）当y＝0时，求x的值；（2）当y＞5时，求x的范围；（3）y随x的增大而增大时，求x的范围．18．已知二次函数y＝x2﹣6x+8．（1）将解析式化成顶点式；（2）写出它的开口方向、对称轴和顶点坐标；（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．19．如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系：h＝﹣5r2+20t，求小球飞行高度达到最高时的飞行时间．20．“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种，在云南省广泛种植．长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动，经过调查往年的统计数据发现，云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售，平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元，那么平均每天的销售量会增加10斤，为了尽快减少库存，该水果商决定降价销售．（1）若降价2元，则每天的销售利润是多少元（2）若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元，那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元？（其它成本忽略不计）（3）将商品的销售单价定为多少元时，商场每天销售该商品获得的利润w最大？最大利润是多少元？21．如图，抛物线与x轴交于A（﹣1，0）、B（4，0），与y轴交于C．（1）求抛物线的解析式；（2）如图1，已知线段DE与线段BC关于平面内某点成中心对称，其中DE的两端点刚好一个落在抛物线上，一个落在对称轴上，求落在对称轴上的点的坐标；（3）如图2，点M为第二象限抛物线上，作MN∥BC交抛物线于点N，直线NB、MC 交于点P，求P点的横坐标．22．在平面直角坐标系xOy中，对于点P（x，y）和Q（x，y'），给出如下定义：若y'＝，则称点Q为点P的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．（1）点（﹣5，﹣2）的“可控变点”坐标为；（2）若点P在函数y＝﹣x2+16的图象上，其“可控变点”Q的纵坐标y′是7，求“可控变点”Q的横坐标；（3）若点P在函数y＝﹣x2+16（﹣5≤x≤a）的图象上，其“可控变点”Q的纵坐标y′的取值范围是﹣16≤y′≤16，求实数a的取值范围．23．在平面直角坐标系中，抛物线y＝x2+bx+c经过A（﹣4，0），点M为抛物线的顶点，点B在y轴上，直线AB与抛物线在第一象限交于点C（2，6），如图①．（1）求抛物线解析式；（2）直线AB的函数解析式为，点M的坐标为．（3）在y轴上找一点Q，使得△AMQ的周长最小，具体作法如图②，作点A关于y轴的对称点A'，连接MA′交y轴于点Q，连接AM，AQ，此时△AMQ的周长最小，请求出点Q的坐标；（4）在坐标平面内是否存在点N，使以点A，O，C，N为顶点的四边形是平行四边形？若存在请直接写出点N的坐标；若不存在，请说明理由．参考答案一．选择题（共10小题）1．下列各式中，是y关于x的二次函数的是（）A．y＝4x B．y＝3x﹣5C．y＝D．y＝2x2+1解：A．根据二次函数的定义，y＝4x是一次函数，不是二次函数，故A不符合题意．B．根据二次函数的定义，y＝3x﹣5不是二次函数，是一次函数，故B不符合题意．C．根据二次函数的定义，y＝是反比例函数，不是二次函数，故C不符合题意．D．根据二次函数的定义，y＝2x2+1是二次函数，故D符合题意．故选：D．2．已知：a＞b＞c，且a+b+c＝0，则二次函数y＝ax2+bx+c的图象可能是下列图象中的（）A．B．C．D．解：A、由图知a＞0，﹣＝1，c＞0，即b＜0，∵已知a＞b＞c，故本选项错误；B、由图知a＜0，而已知a＞b＞c，且a+b+c＝0，必须a＞0，故本选项错误；C、图C中条件满足a＞b＞c，且a+b+c＝0，故本选项正确；D、∵a+b+c＝0，即当x＝1时a+b+c＝0，与图中与x轴的交点不符，故本选项错误．故选：C．3．二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（）A．（2，6）B．（4，6）C．（3，﹣5）D．（3，5）解：∵二次函数可化为y＝（x﹣3）2+5，∴二次函数y＝（x﹣2）（x﹣4）+6的顶点坐标是（3，5），故选：D．4．将二次函数y＝x2+2x﹣1转化为y＝a（x﹣h）2+k的形式，结果为（）A．y＝（x﹣1）2B．y＝（x+1）2C．y＝（x+1）2﹣1D．y＝（x+1）2﹣2解：y＝x2+2x﹣1＝（x2+2x+1）﹣2＝（x+1）2﹣2，即y＝（x+1）2﹣2．故选：D．5．已知0≤x≤，则函数y＝﹣2x2+8x﹣6的最大值是（）A．﹣10.5B．2C．﹣2.5D．﹣6解：y＝﹣2x2+8x﹣6＝﹣2（x﹣2）2+2，∴当x＜2时，y随着x增大而增大，∴当x＝时有最大值y＝﹣2（﹣2）2+2＝﹣2.5，故选：C．6．顶点坐标为（3，1），形状与函数y＝的图象相同且开口方向相反的抛物线的解析式为（）A．y＝+1B．y＝+1C．y＝﹣+1D．y＝﹣+1解：设所求的抛物线解析式为y＝a（x﹣3）2+1，∵所求抛物线与函数y＝的图象相同且开口方向相反，∴a＝﹣，∴所求的抛物线解析式为y＝﹣（x﹣3）2+1．故选：D．7．已知点A（﹣1，y1），B（1，y2），C（2，y3）都在二次函数y＝（x﹣1）2的图象上，则y1，y2，y3的大小关系正确的是（）A．y1＜y2＜y3B．y2＜y1＜y3C．y2＜y3＜y1D．y3＜y2＜y1解：当x＝﹣1时，y1＝（x﹣1）2＝（﹣1﹣1）2＝4；当x＝1时，y2＝（x﹣1）2＝（1﹣1）2＝0；当x＝2时，y3＝（x﹣1）2＝（2﹣1）2＝1，所以y2＜y3＜y1．故选：C．8．抛物线y＝ax2+bx+c纵坐标y的对应值如下表：x…﹣2﹣1012…y…04664…则下列说法中正确的个数是（）①方程ax2+bx+c＝0，有两根为x1＝﹣2，x2＝3；②抛物线与y轴的交点为（0，6）；③抛物线的对称轴是直线x＝1；④抛物线开口向上．A．1B．2C．3D．4解：根据表格数据可知：抛物线的对称轴是直线x＝＝，∴③错误；∵抛物线与x轴的一个交点为（﹣2，0），∴抛物线与x轴的另一个交点为（3，0），∴方程ax2+bx+c＝0有两根为x1＝﹣2，x2＝3；故①正确；从表格可知当x＝0时，y＝6，∴抛物线与y轴的交点为（0，6）；∴②正确；从表格可知：当x＜时，y随x的增大而增大，当x＞时，y随x的增大而减小，∴抛物线开口向下，故④错误．故选：B．9．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，E，F分别为边BC，CD上的点（点E，F不与线段BC，CD的端点重合），BE＝CF，连接OE，OF，EF．关于以下三个结论，下列判断正确的是（）结论Ⅰ：∠BOF始终是90°；结论Ⅱ：△OEF面积的最小值是2；结论Ⅲ：四边形OECF的面积始终是8．A．结论Ⅰ和Ⅱ都对，结论Ⅲ错B．结论Ⅰ和Ⅱ都对，结论Ⅱ错C．结论Ⅱ和Ⅲ都对，结论Ⅰ错D．三个结论都对解：∵四边形ABCD是正方形，∴OB＝OC，∠BOC＝90°，∴∠OBE＝∠OCF＝45°，∵BE＝CF，∴△BOE≌△COF，∴OE＝OF，∠BOE＝∠COF，∴∠BOE+∠COE＝∠COF+∠COE，即∠EOF＝∠BOC＝90°，且S△COE+S△COF＝S△COE+S△BOE，即S四边形OECF＝S△BOC＝S正方形ABCD＝×4×4＝4，由垂线段最短可得，当OE⊥BC时，OE＝BC＝×4＝2，△OEF面积取最小值为×2×2＝2，∴结论Ⅰ和Ⅱ都对，结论Ⅲ错，故选：A．10．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0＜x≤90）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（）A．37.5°B．40°C．42.5°D．45°解：把（25，0.725），（50，0.06），（60，0.09）代入y＝ax2+bx+c得：，解得，∴y＝0.0001x2﹣0.008x+0.21＝0.0001（x﹣40）2+0.05，∵0.0001＞0，∴x＝40时，y最小为0.05，∴燃气灶烧开一壶水最节省燃气的旋钮角度约为40°，故选：B．二．填空题（共6小题）11．函数是二次函数，则m的值为3．解：∵函数是二次函数，∴m2﹣7＝2且m+3≠0，解得：m＝3．则m的值为3．故答案为：3．12．已知抛物线y＝x2﹣4x+c．与直线y＝m相交于A，B两点，若点A的横坐标；x A＝﹣1，则点B的横坐标．x B的值为5．解：∵y＝x2﹣4x+c，∴抛物线开口向上，对称轴为直线x＝﹣＝2，∴点A，B关于直线x＝2对称，∵点A横坐标为﹣1，∴点B横坐标为5，故答案为：5．13．已知二次函数y＝ax2开口向上，且|2﹣a|＝3，则a＝5．解：∵|2﹣a|＝3，∴2﹣a＝±3，解得：a＝﹣1或5，又二次函数y＝ax2开口向上，则a＞0，故a＝5．故答案为：5．14．已知抛物线y＝x2﹣3x+1的图象上有一点A（m，n），则m﹣n的最大值是3．解：∵点A（m，n）在抛物线y＝x2﹣3x+1上，∴n＝m2﹣3m+1，∴m﹣n＝﹣m2+4m﹣1＝﹣（m﹣2）2+3，∴当m＝2时，m﹣n有最大值为3，故答案为：3．15．如图，在平面直角坐标系中，抛物线y＝﹣x2+2x+c与x轴交于点A、B，与y轴交于点C，过点C作CD∥x轴，交抛物线于另一点D，若AB+CD＝3，则c的值为﹣．解：设A（x1，0），B（x2，0），令y＝0，则y＝﹣x2+2x+c＝0，由根与系数的关系得：x1+x2＝2，x1•x2＝﹣c，则AB＝|x1﹣x2|＝＝＝2，令x＝0，则y＝c，∴C（0，c），∵CD∥x轴，∴点D纵坐标为c，当y＝c时，则﹣x2+2x+c＝c，解得：x＝2，或x＝0，∴D（2，c），∴CD＝2，∵AB+CD＝3，∴2+2＝3，解得：c＝﹣，故答案为：﹣．16．如图，在矩形ABCD中，AB＝12，BC＝16，点E、F分别是边AB、BC上的动点，且EF＝10，点G是EF的中点，AG、CG，则四边形AGCD面积的最小值为142．解：连接AC，过B作BH⊥AC于H，以B为圆心，BG为半径作圆，交BH于G'，如图：∵四边形ABCD是矩形，∴∠EBF＝90°，∵EF＝10，点G是EF的中点，∴BG＝EF＝10＝5，∴G在以B为圆心，5为半径的弧上，当G运动到G'时，S△ACG最小，此时四边形AGCD 面积的最小值，最小值即为四边形AG'CD的面积，∵AB＝12＝CD，BC＝16＝AD，∴AC＝20，S△ACD＝×12×16＝96，∴BH＝＝，∴G'H＝BH﹣5＝﹣5＝，∴S△ACG'＝AC•G'H＝×20×＝46，∴S四边形AG'CD＝S△ACD+S△ACG'＝46+96＝142，即四边形AGCD面积的最小值是142．故答案为：142．三．解答题（共7小题）17．看图回答．（1）当y＝0时，求x的值；（2）当y＞5时，求x的范围；（3）y随x的增大而增大时，求x的范围．解：（1）由图象可知，抛物线经过点（﹣1，0），对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（3，0），∴当y＝0时，x的值为﹣1和3；（2）∵抛物线经过点（﹣1，0），（3，0），（0，﹣3），∴设抛物线的解析式为y＝a（x+1）（x﹣3），代入（0，﹣3）得，﹣3＝﹣3a，解得a＝1，∴抛物线的解析式为y＝（x+1）（x﹣3），令y＝5得5＝（x+1）（x﹣3），解得x1＝4，x2＝﹣2，∴当y＞5时，求x的范围是x＞4或x＜﹣2；（3）∵y＝（x+1）（x﹣3）＝（x﹣1）2+4，∴抛物线开口向上，顶点为（1，4），对称轴为直线x＝1，∴y随x的增大而增大时，x的范围是x＞1．18．已知二次函数y＝x2﹣6x+8．（1）将解析式化成顶点式；（2）写出它的开口方向、对称轴和顶点坐标；（3）x取什么值时，y随x的增大而增大；x取什么值时，y随x增大而减小．解：（1）y＝x2﹣6x+8＝x2﹣6x+9﹣1＝（x﹣3）2﹣1；（2）开口向上，对称轴是直线x＝3，顶点坐标是（3，﹣1）；（3）x＞3时，y随x的增大而增大；x＜3时，y随x增大而减小．19．如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线．若不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系：h＝﹣5r2+20t，求小球飞行高度达到最高时的飞行时间．解：∵h＝﹣5t2+20t＝﹣5（t﹣2）2+20，且﹣5＜0，∴当t＝2时，h取最大值20，答：小球飞行高度达到最高时的飞行时间为2s．20．“阳光玫瑰葡萄”品种是近几年来广受各地消费者青睐的优质新品种，在云南省广泛种植．长沙市某品牌水果经销商计划在2023年五一期间进行商业促销活动，经过调查往年的统计数据发现，云南省批发“阳光玫瑰葡萄”的最低价格为每斤15元若按每斤30元的价格到市区销售，平均每天可售出60斤若每斤“阳光玫瑰葡萄”的售价每降低1元，那么平均每天的销售量会增加10斤，为了尽快减少库存，该水果商决定降价销售．（1）若降价2元，则每天的销售利润是多少元（2）若该经销商计划销售“阳光玫瑰葡萄”每天盈利1100元，那么每斤“阳光玫瑰葡萄”的售价应降至每斤多少元？（其它成本忽略不计）（3）将商品的销售单价定为多少元时，商场每天销售该商品获得的利润w最大？最大利润是多少元？解：（1）根据题意，降价2元则销售量为60+2×10＝80（斤），销售利润为：（30﹣15﹣2）×80＝1040（元），。
完整版)初三数学二次函数专题训练(含标准答案)-
完整版)初三数学二次函数专题训练(含标准答案)-二次函数专题训练（含答案）一、填空题1.把抛物线y=-1/2x向左平移2个单位得抛物线，接着再向下平移3个单位，得抛物线.2.函数y=-2x+x^2图象的对称轴是x=1，最大值是1.3.正方形边长为3，如果边长增加x面积就增加y=x^2+6x+9.4.二次函数y=-2x+8x-6，通过配方化为y=a(x-2)^2-2的形为.5.二次函数y=ax+c（c不为零），当x取x1，x2（x1≠x2）时，函数值相等，则x1与x2的关系是x1+x2=-2a/c.6.抛物线y=ax^2+bx+c当b=0时，对称轴是x=0，当a，b同号时，对称轴在y轴侧，当a，b异号时，对称轴在x=-b/2a 处.7.抛物线y=-2(x+1)^2-3开口向下，对称轴是x=-1，顶点坐标是(-1,-3).如果y随x的增大而减小，那么x的取值范围是x<-1.8.若a5/2a时，函数值随x的增大而减小.9.二次函数y=ax^2+bx+c（a≠0）当a>0时，图象的开口向上；当a<0时，图象的开口向下，顶点坐标是(-b/2a,c-b^2/4a).10.抛物线y=-2(x-2)^2+2，开口向下，顶点坐标是(2,2)，对称轴是x=2.11.二次函数y=-3(x-1)^2+2的图象的顶点坐标是（1，2）.12.已知y=(x+1)^2-2，当x≥1时，函数值随x的增大而减小.13.已知直线y=2x-1与抛物线y=5x+k交点的横坐标为2，则k=9，交点坐标为(2,13).14.用配方法将二次函数y=x^2+x-2化成y=a(x-(-1/2))^2-9/4的形式是y=(x+1/2)^2-9/4.15.如果二次函数y=x^2-6x+m的最小值是1，那么m的值是10.二、选择题：16.在抛物线y=2x^2-3x+1上的点是（D）（3，4）17.直线y=5x/2-2与抛物线y=x^2-x的交点个数是（C）2个18.关于抛物线y=ax^2+bx+c（a≠0），下面几点结论中，正确的有（A、B、C）①当a>0时，对称轴左边y随x的增大而减小，对称轴右边y随x的增大而增大，当a<0时，情况相反。
二次函数专题训练(含答案)
二次函数专题训练（含答案）一、 填空题1.把抛物线221x y -=向左平移2个单位得抛物线 ，接着再向下平移3个 单位，得抛物线 .2.函数x x y +-=22图象的对称轴是 ，最大值是 .3.正方形边长为3，如果边长增加x 面积就增加y ，那么y 与x 之间的函数关系是 .4.二次函数6822-+-=x x y ，通过配方化为k h x a y +-=2)(的形为 .5.二次函数c ax y +=2（c 不为零），当x 取x 1，x 2（x 1≠x 2）时，函数值相等，则 x 1与x 2的关系是 .6.抛物线c bx ax y ++=2当b=0时，对称轴是 ，当a ，b 同号时，对称轴在y 轴 侧，当a ，b 异号时，对称轴在y 轴 侧.7.抛物线3)1(22-+-=x y 开口 ，对称轴是 ，顶点坐标是 .如果y 随x 的增大而减小，那么x 的取值范围是 .8.若a <0，则函数522-+=ax x y 图象的顶点在第 象限；当x >4a -时，函数值随x 的增大而 .9.二次函数c bx ax y ++=2（a ≠0）当a >0时，图象的开口a <0时，图象的开口 ，顶点坐标是 .10.抛物线2)(21h x y --=，开口 ，顶点坐标是 ，对称轴是 . 11.二次函数)()(32+-=xy 的图象的顶点坐标是（1，-2）. 12.已知2)1(312-+=x y ，当x 时，函数值随x 的增大而减小. 13.已知直线12-=x y 与抛物线k x y +=25交点的横坐标为2，则k= ，交点坐标为 .14.用配方法将二次函数x x y 322+=化成k h x a y +-=2)(的形式是 . 15.如果二次函数m x x y +-=62的最小值是1，那么m 的值是 .二、选择题：16.在抛物线1322+-=x x y 上的点是（ ）A.（0，-1）B.⎪⎭⎫ ⎝⎛0,21C.（-1，5）D.（3，4）17.直线225-=x y 与抛物线x x y 212-=的交点个数是（ ） A.0个 B.1个 C.2个 D.互相重合的两个18.关于抛物线c bx ax y ++=2（a ≠0），下面几点结论中，正确的有（ ）① 当a >0时，对称轴左边y 随x 的增大而减小，对称轴右边y 随x 的增大而增大，当 a <0时，情况相反.② 抛物线的最高点或最低点都是指抛物线的顶点.③ 只要解析式的二次项系数的绝对值相同，两条抛物线的形状就相同.④ 一元二次方程02=++c bx ax （a ≠0）的根，就是抛物线c bx ax y ++=2与x 轴 交点的横坐标.A.①②③④B.①②③C. ①②D.①19.二次函数y=(x+1)(x-3)，则图象的对称轴是（ ）A.x=1B.x=-2C.x=3D.x=-320.如果一次函数b ax y +=的图象如图代13-3-12中A 所示，那么二次函+=2ax y bx -3的大致图象是（ ）图代13-2-1221.若抛物线c bx ax y ++=2的对称轴是,2-=x 则=b a （ ） A.2 B.21 C.4 D.41 22.若函数xa y =的图象经过点（1，-2），那么抛物线3)1(2++-+=a x a ax y 的性 质说得全对的是（ ）A. 开口向下，对称轴在y 轴右侧，图象与正半y 轴相交B. 开口向下，对称轴在y 轴左侧，图象与正半y 轴相交C. 开口向上，对称轴在y 轴左侧，图象与负半y 轴相交D. 开口向下，对称轴在y 轴右侧，图象与负半y 轴相交23.二次函数c bx x y ++=2中，如果b+c=0，则那时图象经过的点是（ ）A.(-1，-1)B.(1，1)C.(1，-1)D.（-1，1）24.函数2ax y =与xa y =（a <0）在同一直角坐标系中的大致图象是（ ）图代13-3-1325.如图代13-3-14，抛物线c bx x y ++=2与y 轴交于A 点，与x 轴正半轴交于B ， C 两点，且BC=3，S △ABC =6，则b 的值是（ ）A.b=5B.b=-5C.b=±5D.b=4图代13-3-1426.二次函数2ax y =（a <0），若要使函数值永远小于零，则自变量x 的取值范围是 （ ）A ．X 取任何实数 B.x <0 C.x >0 D.x <0或x >027.抛物线4)3(22+-=x y 向左平移1个单位，向下平移两个单位后的解析式为 （ ）A.6)4(22+-=x yB.2)4(22+-=x yC.2)2(22+-=x yD.2)3(32+-=x y28.二次函数229k ykx x y ++=（k >0）图象的顶点在（ ）A.y 轴的负半轴上B.y 轴的正半轴上C.x 轴的负半轴上D.x 轴的正半轴上29.四个函数：xy x y x y 1,1,-=+=-=（x >0），2x y -=（x >0），其中图象经过原 点的函数有（ ）A.1个B.2个C.3个D.4个30.不论x 为值何，函数c bx ax y ++=2（a ≠0）的值永远小于0的条件是（ ）A.a >0，Δ>0B.a >0,Δ<0C ．a <0,Δ>0 D.a <0,Δ<0三、解答题31.已知二次函数1222+-+=b ax x y 和1)3(22-+-+-=b x a x y 的图象都经过x 轴上两上不同的点M ，N ，求a ，b 的值.32.已知二次函数c bx ax y ++=2的图象经过点A （2，4），顶点的横坐标为21，它 的图象与x 轴交于两点B （x 1，0），C （x 2，0），与y 轴交于点D ，且132221=+x x ，试问：y 轴上是否存在点P ，使得△POB 与△DOC 相似（O 为坐标原点）？若存在，请求出过P ，B 两点直线的解析式，若不存在，请说明理由.33.如图代13-3-15，抛物线与直线y=k(x-4)都经过坐标轴的正半轴上A ，B 两点，该抛物线的对称轴x=-21与x 轴相交于点C ，且∠ABC=90°，求：（1）直线AB 的解析式；（2）抛物线的解析式.图代13-3-15图代13-3-16 34.中图代13-3-16，抛物线c x ax y +-=32交x 轴正方向于A ，B 两点，交y 轴正方向于C 点，过A ，B ，C 三点做⊙D ，若⊙D 与y 轴相切.（1）求a ，c 满足的关系；（2）设∠ACB=α，求tg α；（3）设抛物线顶点为P ，判断直线PA 与⊙O 的位置关系并证明.35.如图代13-3-17，这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图，横断面的地平线为x 轴，横断面的对称轴为y 轴，桥拱的DGD ＇部分为一段抛物线，顶点C 的高度为8米，AD 和A ＇D ＇是两侧高为5.5米的支柱，OA 和OA ＇为两个方向的汽车通行区，宽都为15米，线段CD 和C ＇D ＇为两段对称的上桥斜坡，其坡度为1∶4. 求（1）桥拱DGD ＇所在抛物线的解析式及CC ＇的长；（2）BE 和B ＇E ＇为支撑斜坡的立柱，其高都为4米，相应的AB 和A ＇B ＇为两个方 向的行人及非机动车通行区，试求AB 和A ＇B ＇的宽；（3）按规定，汽车通过该桥下时，载货最高处和桥拱之间的距离不得小于0.4米，车载大型设备的顶部与地面的距离均为7米，它能否从OA （或OA ＇）区域安全通过？请说明理由.图代13-3-1736.已知：抛物线2)4(2+++-=m x m x y 与x 轴交于两点)0,(),0,(b B a A （a <b ）.O 为坐标原点，分别以OA ，OB 为直径作⊙O 1和⊙O 2在y 轴的哪一侧？简要说明理由，并指出两圆的位置关系.37.如果抛物线1)1(22++-+-=m x m x y 与x 轴都交于A ，B 两点，且A 点在x 轴 的正半轴上，B 点在x 同的负半轴上，OA 的长是a ，OB 的长是b.（1） 求m 的取值范围；（2） 若a ∶b=3∶1，求m 的值，并写出此时抛物线的解析式；（3） 设（2）中的抛物线与y 轴交于点C ，抛物线的顶点是M ，问：抛物线上是否存 在 点P ，使△PAB 的面积等于△BCM 面积的8倍？若存在，求出P 点的坐标；若不存在，请 说明理由.38.已知：如图代13-3-18，EB 是⊙O 的直径，且EB=6，在BE 的延长线上取点P ，使EP=EB.A 是EP 上一点，过A 作⊙O 的切线AD ，切点为D ，过D 作DF ⊥AB 于F ，过B 作AD 的垂线BH ，交AD 的延长线于H ，连结ED 和FH.图代13-3-18（1） 若AE=2，求AD 的长.（2） 当点A 在EP 上移动（点A 不与点E 重合）时，①是否总有FHED AH AD =？试证 明 你的结论；②设ED=x ，BH=y ，求y 与x 的函数关系式，并写出自变量x 的取值范围.39.已知二次函数)294(2)254(222+--+--=m m x m m x y 的图象与x 轴的交点为A ，B （点A 在点B 右边），与y 轴的交点为C.（1） 若△ABC 为Rt △，求m 的值；（2） 在△ABC 中，若AC=BC ，求∠ACB 的正弦值；（3） 设△ABC 的面积为S ，求当m 为何值时，S 有最小值，并求这个最小值.40.如图代13-3-19，在直角坐标系中，以AB 为直径的⊙C 交x 轴于A ，交y 轴于B ， 满足OA ∶OB=4∶3，以OC 为直径作⊙D ，设⊙D 的半径为2.图代13-3-19（1） 求⊙C 的圆心坐标.（2） 过C 作⊙D 的切线EF 交x 轴于E ，交y 轴于F ，求直线EF 的解析式.（3） 抛物线c bx ax y ++=2（a ≠0）的对称轴过C 点，顶点在⊙C 上，与y 轴交点为B ，求抛物线的解析式.41.已知直线x y 21=和m x y +-=，二次函数q px x y ++=2图象的顶点为M. （1） 若M 恰在直线x y 21=与m x y +-=的交点处，试证明：无论m 取何实数值， 二次函数q px x y ++=2的图象与直线m x y +-=总有两个不同的交点.（2） 在（1）的条件下，若直线m x y +-=过点D （0，-3），求二次函数q px x y ++=2的表达式，并作出其大致图象.图代13-3-20（3） 在（2）的条件下，若二次函数q px x y ++=2的图象与y 轴交于点C ，与x 同 的左交点为A ，试在直线x y 21=上求异于M 点P ，使P 在△CMA 的外接圆上. 42.如图代13-3-20，已知抛物线b ax x y ++-=2与x 轴从左至右交于A ，B 两点，与y 轴交于点C ，且∠BAC=α，∠ABC=β，tg α-tg β=2,∠ACB=90°.（1） 求点C 的坐标；（2） 求抛物线的解析式；（3） 若抛物线的顶点为P ，求四边形ABPC 的面积.参 考 答 案动脑动手1. 设每件提高x 元（0≤x ≤10），即每件可获利润（2+x ）元，则每天可销售（100-10x ）件，设每天所获利润为y 元，依题意，得)10100)(2(x x y -+=.360)4(10200801022+--=++-=x x x∴当x=4时（0≤x ≤10）所获利润最大，即售出价为14元，每天所赚得最大利润360元.2.∵43432+⎪⎭⎫ ⎝⎛+-=x m mx y ， ∴当x=0时，y=4. 当0,043432≠=+⎪⎭⎫ ⎝⎛+-m x m mx 时m m m 34,321==. 即抛物线与y 轴的交点为（0，4），与x 轴的交点为A （3，0），⎪⎭⎫⎝⎛0,34m B . （1） 当AC=BC 时， 94,334-=-=m m . ∴ 4942+-=x y （2） 当AC=AB 时，5,4,3===AC OC AO .∴ 5343=-m. ∴ 32,6121-==m m . 当61=m 时，4611612+-=x x y ； 当32-=m 时，432322++-=x x y . （3） 当AB=BC 时，22344343⎪⎭⎫ ⎝⎛+=-m m ， ∴ 78-=m . ∴ 42144782++-=x x y . 可求抛物线解析式为：43232,461161,494222+--=+-=+-=x x y x x y x y 或42144782++-=x x y .3.（1）∵)62(4)]5([222+---=∆m m0)1(122222+=++=m m m图代13-3-21∴不论m 取何值，抛物线与x 轴必有两个交点.令y=0，得062)5(222=+++-m x m x0)3)(2(2=---m x x ，∴ 3,2221+==m x x .∴两交点中必有一个交点是A （2，0）.（2）由（1）得另一个交点B 的坐标是（m 2+3,0）.12322+=-+=m m d ，∵ m 2+10>0，∴d=m 2+1.（3）①当d=10时，得m 2=9.∴ A （2，0），B （12，0）.25)7(241422--=+-=x x x y .该抛物线的对称轴是直线x=7，顶点为（7，-25），∴AB 的中点E （7，0）. 过点P 作PM ⊥AB 于点M ，连结PE ， 则2222)7(,,521a MEb PM AB PE -====，∴ 2225)7(=+-b a . ① ∵点PD 在抛物线上，∴ 25)7(2--=a b . ②解①②联合方程组，得0,121=-=b b .当b=0时，点P 在x 轴上，△ABP 不存在，b=0，舍去.∴b=-1.注：求b 的值还有其他思路，请读者探觅，写出解答过程.②△ABP 为锐角三角形时，则-25≤b <-1；△ ABP 为钝角三角形时，则b >-1，且b ≠0.同步题库一、 填空题 1.3)2(21,)2(2122-+-=+-=x y x y ； 2.81,41=x ； 3.9)3(2-+=x y ； 4. 2)2(22+--=x y ； 5.互为相反数； 6.y 轴，左，右； 7.下，x=-1,(-1,-3)，x >-1；8.四，增大； 9.向上，向下，a b x a b ac a b 2,44,22-=⎪⎪⎭⎫ ⎝⎛--； 10.向下，（h,0），x=h ； 11.-1，-2； 12.x <-1； 13.-17，（2，3）； 14.91312-⎪⎭⎫ ⎝⎛+=x y ； 15.10. 二、选择题16.B 17.C 18.A 19.A 20.C 21.D 22.B 23.B 24.D 25.B 26.D 27.C 28.C 29.A 30.D三、解答题31.解法一：依题意，设M （x 1，0），N （x 2，0），且x 1≠x 2，则x 1，x 2为方程x 2+2ax-2b+1=0的两个实数根，∴ a x x 221-=+，1x ²122+-=b x .∵x 1，x 2又是方程01)3(22=-+-+-b x a x 的两个实数根，∴ x 1+x 2=a-3，x 1²x 2=1-b 2.∴ ⎩⎨⎧-=+--=-.112,322b b a a解得 ⎩⎨⎧==;0,1b a 或⎩⎨⎧==.2,1b a 当a=1,b=0时，二次函数的图象与x 轴只有一个交点，∴a=1，b=0舍去.当a=1；b=2时，二次函数322-+=x x y 和322+--=x x y 符合题意.∴ a=1，b=2.解法二：∵二次函数1222+-+=b ax x y 的图象对称轴为a x -=，二次函数1)3(22-+-+-=b x a x y 的图象的对称轴为23-=a x ， 又两个二次函数图象都经过x 轴上两个不同的点M ，N ，∴两个二次函数图象的对称轴为同一直线.∴ 23-=-a a .解得 1=a .∴两个二次函数分别为1222+-+=b x x y 和1222-+--=b x x y . 依题意，令y=0，得01222=+-+b x x ，01222=-+--b x x .①+②得022=-b b .解得 2,021==b b .∴ ⎩⎨⎧==;0,1b a 或⎩⎨⎧==.2,1b a当a=1，b=0时，二次函数的图象与x 轴只有一个交点，∴a=1，b=0舍去.当a=1，b=2时，二次函数为322-+=x x y 和322+--=x x y 符合题意. ∴ a=1，b=2.32.解：∵c bx ax y ++=2的图象与x 轴交于点B （x 1，0），C （x 2，0）， ∴ a cx x a bx x =⋅-=+2121,.又∵132221=+x x 即132)(21221=-+x x x x ，∴ 132)(2=⋅--a ca b .① 又由y 的图象过点A （2，4），顶点横坐标为21，则有4a+2b+c=4， ② 212=-a b.③ 解由①②③组成的方程组得a=-1,b=1,c=6.∴ y=-x 2+x+6.与x 轴交点坐标为（-2，0），（3，0）.与y 轴交点D 坐标为（0，6）.设y 轴上存在点P ，使得△POB ∽△DOC ，则有（1） 当B （-2，0），C （3，0），D （0，6）时，有6,3,2,====OD OC OB ODOPOC OB . ∴OP=4，即点P 坐标为（0，4）或（0，-4）.当P 点坐标为（0，4）时，可设过P ，B 两点直线的解析式为y=kx+4.有 0=-2k-4. 得 k=-2. ∴ y=-2x-4. 或3,6,2,====OC OD OB OCOPOD OB . ∴OP=1，这时P 点坐标为（0，1）或（0，-1）.当P 点坐标为（0，1）时，可设过P ，B 两点直线的解析式为y=kx+1.有 0=-2k+1.得 21=k . ∴ 121+-=x y .当P 点坐标为（0，-1）时，可设过P ，B 两点直线的解析式为y=kx-1，有 0=-2k-1， 得 21-=k . ∴ 121--=x y . （2）当B （3，0），C （-2，0），D （0，6）时，同理可得y=-3x+9，或 y=3x-9，或 131+-=x y ， 或 131-=x y .33.解：（1）在直线y=k(x-4)中， 令y=0，得x=4.∴A 点坐标为（4，0）.∴ ∠ABC=90°. ∵ △CBD ∽△BAO ， ∴OBOA OC OB =，即OB 2=OA ²OC. 又∵ CO=1，OA=4，∴ OB 2=1³4=4. ∴ OB=2（OB=-2舍去） ∴B 点坐标为（0，2）.将点B （0，2）的坐标代入y=k(x-4)中，得21-=k . ∴直线的解析式为：221+-=x y . （2）解法一：设抛物线的解析式为h x a y ++=2)1(，函数图象过A （4，0），B （0， 2），得⎩⎨⎧=+=+.2,025h a h a 解得 .1225,121=-=h a ∴抛物线的解析式为：1225)1(1212++-=x y .解法二：设抛物线的解析式为：c bx ax y ++=2，又设点A （4，0）关于x=-1的对 称是D.∵ CA=1+4=5， ∴ CD=5. ∴ OD=6. ∴D 点坐标为（-6，0）. 将点A （4，0），B （0，2），D （-6，0）代入抛物线方程，得⎪⎩⎪⎨⎧=+-==++.0636,2,0416c b a c c b a 解得 2,61,121=-=-=c b a . ∴抛物线的解析式为：2611212+--=x x y . 34.解：（1）A ，B 的横坐标是方程032=+-c x ax 的两根，设为x 1,x 2（x 2>x 1），C 的 纵坐标是C.又∵y 轴与⊙O 相切，∴ OA ²OB=OC 2.∴ x 1²x 2=c 2. 又由方程032=+-c x ax 知ac x x =⋅21， ∴acc =2，即ac=1. （2）连结PD ，交x 轴于E ，直线PD 必为抛物线的对称轴，连结AD 、BD ，图代13-3-22∴ AB AE 21=. α=∠=∠=∠ADE ADB ACB 21. ∵ a >0,x 2>x 1， ∴ a a ac x x AB 54912=-=-=. aAE 25=. 又 ED=OC=c ， ∴ 25==DE AE tg α. （3）设∠PAB=β， ∵P 点的坐标为⎪⎭⎫⎝⎛-a a 45,23，又∵a >0， ∴在Rt △PAE 中，aPE 45=. ∴ 25==AE PE tg β. ∴ tg β=tg α. ∴β=α.∴∠PAE=∠ADE.∵ ∠ADE+∠DAE=90° ∴PA 和⊙D 相切. 35.解：（1）设DGD ＇所在的抛物线的解析式为c ax y +=2，由题意得G （0，8），D （15，5.5）.∴ ⎩⎨⎧+==.255.5,8c a c 解得⎪⎩⎪⎨⎧=-=.8,901c a∴DGD ＇所在的抛物线的解析式为89012+-=x y . ∵41=AC AD 且AD=5.5, ∴ AC=5.5³4=22(米).∴ 2215(2)(22+⨯=+⨯=='AC OA OC c c ） =74（米）. 答：cc ＇的长为74米.（2）∵4,41==BE BC EB ， ∴ BC=16.∴ AB=AC-BC=22-16=6（米）. 答：AB 和A ＇B ＇的宽都是6米.（3）在89012+-=x y 中，当x=4时， 45377816901=+⨯-=y .∵ 4519)4.07(45377=+->0. ∴该大型货车可以从OA （OA ＇）区域安全通过.36.解:（1）∵⊙O 1与⊙O 2外切于原点O ，∴A ，B 两点分别位于原点两旁，即a <0，b >0. ∴方程02)4(2=+++-m x m x 的两个根a ，b 异号. ∴ab=m+2<0，∴m <-2.（2）当m <-2，且m ≠-4时，四边形PO 1O 2Q 是直角梯形. 根据题意，计算得22121b S Q O PO =四边形（或221a 或1）. m=-4时，四边形PO 1O 2Q 是矩形. 根据题意，计算得22121b S Q O PO =四边形（或221a 或1）. （3）∵ 4)2()2(4)4(22++=+-+=∆m m m >0 ∴方程02)4(2=+++-m x m x 有两个不相等的实数根. ∵ m >-2， ∴ ⎩⎨⎧+=+=+.02,04 m ab m b a∴ a >0，b >0.∴⊙O 1与⊙O 2都在y 轴右侧，并且两圆内切. 37.解：（1）设A ，B 两点的坐标分别是（x 1，0）、（x 2，0）， ∵A ，B 两点在原点的两侧，∴ x 1x 2<0，即-（m+1）<0， 解得 m >-1.∵ )1()1(4)]1(2[2+⨯-⨯--=∆m m7)21(484422+-=+-=m m m 当m >-1时，Δ>0， ∴m 的取值范围是m >-1.（2）∵a ∶b=3∶1，设a=3k ，b=k （k >0），则 x 1=3k ，x 2=-k ，∴ ⎩⎨⎧+-=-⋅-=-).1()(3),1(23m k k m k k解得 31,221==m m . ∵31=m 时，3421-=+x x （不合题意，舍去）， ∴ m=2 ∴抛物线的解析式是32++-=x x y .（3）易求抛物线322++-=x x y 与x 轴的两个交点坐标是A （3，0），B （-1，0） 与y 轴交点坐标是C （0，3），顶点坐标是M （1，4）.设直线BM 的解析式为q px y +=，则 ⎩⎨⎧+-⋅=+⋅=.)1(0,14q p q p解得 ⎩⎨⎧==.2,2q p∴直线BM 的解析式是y=2x+2.设直线BM 与y 轴交于N ，则N 点坐标是（0，2）， ∴ MNC BCN BCM S S S ∆∆∆+=.111211121=⨯⨯+⨯⨯=设P 点坐标是（x,y ），∵ BCM ABP S S ∆∆=8， ∴1821⨯=⨯⨯y AB .即8421=⨯⨯y . ∴ 4=y .∴4±=y . 当y=4时，P 点与M 点重合，即P （1，4），当y=-4时，-4=-x 2+2x+3，解得 221±=x . ∴满足条件的P 点存在.P 点坐标是（1，4），)4,221(),4,221(---+. 38.（1）解：∵AD 切⊙O 于D ，AE=2，EB=6，∴ AD 2=AE ²AB=2³（2+6）=16. ∴ AD=4.图代13-2-23（2）①无论点A 在EP 上怎么移动（点A 不与点E 重合），总有FHEDAH AD =. 证法一：连结DB ，交FH 于G ， ∵AH 是⊙O 的切线，∴ ∠HDB=∠DEB. 又∵BH ⊥AH ，BE 为直径，∴ ∠BDE=90°有 ∠DBE=90°-∠DEB =90°-∠HDB =∠DBH. 在△DFB 和△DHB 中，DF ⊥AB ，∠DFB=∠DHB=90°，DB=DB ，∠DBE=∠DBH ， ∴ △DFB ∽△DHB. ∴BH=BF ， ∴△BHF 是等腰三角形. ∴BG ⊥FH ，即BD ⊥FH. ∴ED ∥FH ，∴FHEDAH AD =.图代13-3-24证法二：连结DB ， ∵AH 是⊙O 的切线，∴ ∠HDB=∠DEF. 又∵DF ⊥AB ，BH ⊥DH ，∴ ∠EDF=∠DBH. 以BD 为直径作一个圆，则此圆必过F ，H 两点， ∴∠DBH=∠DFH ，∴∠EDF=∠DFH.∴ ED ∥FH. ∴FHEDAH AD =. ②∵ED=x ，BH=，BH=y ，BE=6，BF=BH ，∴EF=6y. 又∵DF 是Rt △BDE 斜边上的高，∴ △DFE ∽△BDE ，∴EBED ED EF =，即EB EF ED ⋅=2. ∴)6(62y x -=，即6612+-=x y .∵点A 不与点E 重合，∴ED=x >0.A 从E 向左移动，ED 逐渐增大，当A 和P 重合时，ED 最大，这时连结OD ，则OD ⊥PH. ∴ OD ∥BH.又 12,936==+=+=PB EO PE PO ，4,=⋅==POPBOD BH PB PO BH OD ， ∴ 246,4=-=-===BF EB EF BH BF ， 由ED 2=EF ²EB 得12622=⨯=x ，∵x >0，∴32=x .∴ 0<x ≤32.（或由BH=4=y ，代入6612+-=x y 中，得32=x ） 故所求函数关系式为6612+-=x y （0<x ≤32）.39.解：∵]294)[2(2942254222⎪⎭⎫ ⎝⎛+--+=⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--=m m x x m m x m m x y , ∴可得⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--2942,0,0,294),0,2(22m m C m m B A . （1）∵△ABC 为直角三角形，∴OB AO OC⋅=2，即⎪⎭⎫ ⎝⎛+-⨯=⎪⎭⎫ ⎝⎛+-22942294422m m m m ，化得0)2(2=-m .∴m=2.（2）∵AC=BC ，CO ⊥AB ，∴AO=BO ，即22942=+-m m . ∴429422=⎪⎭⎫⎝⎛+-=m m OC .∴25==BC AC . 过A 作AD ⊥BC ，垂足为D ，∴ AB ²OC=BC ²AD. ∴ 58=AD .∴ 545258sin ===∠AC AD ACB.图代13-3-25（3）CO AB S ABC ⋅=∆21.1)1()2(2942229421222-+=+=⎪⎭⎫ ⎝⎛+-⋅⎪⎭⎫ ⎝⎛++-=u u u m m m m ∵ 212942≥+-=m m u ， ∴当21=u ，即2=m 时，S 有最小值，最小值为45.40.解：（1）∵OA ⊥OB ，OA ∶OB=4∶3，⊙D 的半径为2， ∴⊙C 过原点，OC=4，AB=8. A 点坐标为⎪⎭⎫⎝⎛0,532，B 点坐标为⎪⎭⎫⎝⎛524,0.∴⊙C 的圆心C 的坐标为⎪⎭⎫⎝⎛512,516. （2）由EF 是⊙D 切线，∴OC ⊥EF.∵ CO=CA=CB ，∴ ∠COA=∠CAO ，∠COB=∠CBO. ∴ Rt △AOB ∽Rt △OCE ∽Rt △FCO.∴ OBOCAB OF OA OC AB OE ==,. ∴ 320,5==OF OE .E 点坐标为（5，0），F 点坐标为⎪⎭⎫ ⎝⎛320,0， ∴切线EF 解析式为32034+-=x y . （3）①当抛物线开口向下时，由题意，得抛物线顶点坐标为⎪⎭⎫⎝⎛+4512,516，可得 ⎪⎪⎩⎪⎪⎨⎧==-=⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧==-=-.524,1,325.52453244,51622c b a c a b ac a b ∴ 5243252++-=x x y . ②当抛物线开口向上时,顶点坐标为⎪⎭⎫⎝⎛-4512,516，得 ⎪⎪⎩⎪⎪⎨⎧=-==⇒⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=-.524,4,85.524,5844,51622c b a c a b ac a b∴ 5244852+--=x x y . 综合上述，抛物线解析式为5243252++-=x x y 或5244852+-=x x y . 41.（1）证明：由⎪⎩⎪⎨⎧+-==,,21m x y x y 有m x x +-=21， ∴ m y m x m x 31,32,23===.∴交点)31,32(m m M .此时二次函数为m m x y 31322+⎪⎭⎫ ⎝⎛-=m m mx x 31943422++-=. 由②③联立，消去y ，有0329413422=-+⎪⎭⎫⎝⎛--m m x m x .⎪⎭⎫ ⎝⎛--⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=∆m m m 3294413422.013891613891622>=+-+-=mm m m ∴无论m 为何实数值，二次函数q px x y ++=2的图象与直线m x y +-=总有两个不同的交点.图代13-3-26（2）解：∵直线y=-x+m 过点D （0，-3）， ∴ -3=0+m ，∴ m=-3.∴M （-2，-1）.∴二次函数为)1)(3(341)2(22++=+-=-+=x x x x x y .图象如图代13-3-26.（3）解：由勾股定理，可知△CMA 为Rt △，且∠CMA=Rt ∠，∴MC 为△CMA 外接圆直径.∵P 在x y 21=上，可设⎪⎭⎫ ⎝⎛n n P 21,，由MC 为△CMA 外接圆的直径，P 在这个圆上， ∴ ∠CPM=Rt ∠.过P 分别作PN ⊥y ，轴于N ，PQ ⊥x 轴于R ，过M 作MS ⊥y 轴于S ，MS 的延长线与PR 的 延长线交于点Q.由勾股定理，有222QP MQ MP +=，即222121)2(⎪⎭⎫ ⎝⎛+++=n n MP . 22222213n n NP NC CP +⎪⎭⎫ ⎝⎛-=+=. 202=CM. 而 222CM CP MP=+， ∴ 20213121)2(2222=+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+++n n n n ， 即 062252=-+n n ， ∴ 012452=-+n n ，0)2)(65(=+-n n .∴ 2,5621-==n n . 而n 2=-2即是M 点的横坐标，与题意不合，应舍去.∴ 56=n ， 此时 5321=n . ∴P 点坐标为⎪⎭⎫⎝⎛53,56.42.解：（1）根据题意，设点A （x 1，0）、点（x 2，0），且C （0，b ），x 1<0，x 2>0，b >0， ∵x 1，x 2是方程02=++-b ax x 的两根，∴ b x x a x x -=⋅=+2121,.在Rt △ABC 中，OC ⊥AB ，∴OC 2=OA ²OB.∵ OA=-x 1,OB=x 2，∴ b 2=-x 1²x 2=b.∵b >0,∴b=1，∴C （0，1）.（2）在Rt △AOC 的Rt △BOC 中， 211212121==+-=--=-=-ba x x x x x x OB OC OA OC tg tg βα. ∴ 2=a .∴抛物线解析式为122++-=x x y.图代13-3-27（3）∵122++-=x x y ，∴顶点P 的坐标为（1，2），当0122=++-x x 时，21±=x . ∴)0,21(),0,21(+-B A .延长PC 交x 轴于点D ，过C ，P 的直线为y=x+1，∴点D 坐标为（-1，0）.∴ D CA D PB ABPC S S S ∆∆-=四边形 ).(22321)22(212)22(212121平方单位+=⨯-⨯-⨯+⨯=⋅-⋅⋅=yc AD y DB p。
中考数学《二次函数》专项练习(附答案解析)
中考数学《二次函数》专项练习（附答案解析）一、综合题1．如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．（1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（）（填方案一，方案二，或方案三），则B点坐标是（），求出你所选方案中的抛物线的表达式；（2）因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．2．如图，抛物线 y =-x2+3x +4 与x轴负半轴相交于A点，正半轴相交于B点，与 y 轴相交于C 点．（1）已知点D（m，m+1）在第一象限的抛物线上，求点D关于直线 BC 对称的点的坐标；（2）在（1）的条件下，连接BD，点P为抛物线上一点，且∠DBP=45°，求点P的坐标．3．如图，在直角坐标系中有一直角三角形AOB，O为坐标原点，OA=1，tan∠BAO=3，将此三角形绕原点O逆时针旋转90°，得到△DOC，抛物线y=ax2+bx+c经过点A，B，C．（1）求抛物线的解析式；（2）若点P是第二象限内抛物线上的动点，其横坐标为t，①设抛物线对称轴l与x轴交于一点E，连接PE，交CD于F，求出当△CEF与△COD相似时，点P的坐标；②是否存在一点P，使△PCD的面积最大？若存在，求出△PCD的面积的最大值；若不存在，请说明理由．4．已知抛物线C1：y=ax2+4ax+4a+b（a≠0，b＞0）的顶点为M，经过原点O且与x轴另一交点为A．（1）求点A的坐标；（2）若△AMO为等腰直角三角形，求抛物线C1的解析式；（3）现将抛物线C1绕着点P（m，0）旋转180°后得到抛物线C2，若抛物线C2的顶点为N，当b=1，且顶点N在抛物线C1上时，求m的值．5．如图，抛物线G：y=−x2+2mx−m2+m+3的顶点为P(x P，y P)，抛物线G与直线l：x=3交于点Q．（1）x P=，y P=（分别用含m的式子表示）；y P与x P的函数关系式为；（2）求点Q的纵坐标y Q（用含m的式子表示），并求y Q的最大值；（3）随m的变化，抛物线G会在直角坐标系中移动，求顶点P在y轴与l之间移动（含y轴与l）的路径的长．6．如图，抛物线的顶点D的坐标为（﹣1，4），抛物线与x轴相交于A.B两点（A在B的左侧），与y轴交于点C（0，3）.（1）求抛物线的表达式；（2）如图1，已知点E（0，﹣3），在抛物线的对称轴上是否存在一点F，使得△CEF的周长最小，如果存在，求出点F的坐标；如果不存在，请说明理由；（3）如图2，连接AD，若点P是线段OC上的一动点，过点P作线段AD的垂线，在第二象限分别与抛物线、线段AD相交于点M、N，当MN最大时，求△POM的面积.7．已知：如图，抛物线y=ax2﹣2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A、B，点A的坐标为（4，0）．（1）求该抛物线的解析式；（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CQE的面积最大时，求点Q的坐标；（3）若平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（2，0）．问：是否存在这样的直线l，使得△ODF是等腰三角形？若存在，请求出点P的坐标；若不存在，请说明理由．8．如图，在平面直角坐标系xOy中，O为坐标原点，点A(4,0)，点B(0,4)，ΔABO的中线AC与y轴交于点C，且⊙M经过O，A，C三点．（1）求圆心M的坐标；（2）若直线AD与⊙M相切于点A，交y轴于点D，求直线AD的函数表达式；（3）在过点B且以圆心M为顶点的抛物线上有一动点P，过点P作PE∥y轴，交直线AD于点E．若以PE为半径的⊙P与直线AD相交于另一点F．当EF=4√5时，求点P的坐标．9．如图1所示，已知抛物线y=−x2+4x+5的顶点为D，与x轴交于A、B两点(A左B右)，与y轴交于C点，E为抛物线上一点，且C、E关于抛物线的对称轴对称，作直线AE.（1）求直线AE的解析式；（2）在图2中，若将直线AE沿x轴翻折后交抛物线于点F，则点F的坐标为（直接填空）；（3）点P为抛物线上一动点，过点P作直线PG与y轴平行，交直线AE于点G，设点P的横坐标为m，当S△PGE∶S△BGE=2∶3时，直接写出所有符合条件的m值，不必说明理由.10．综合与探究如图，直线y=−23x+4与x轴，y轴分别交于B，C两点，抛物线y=ax2+43x+c经过B，C两点，与x轴的另一个交点为A（点A在点B的左侧），抛物线的顶点为点D．抛物线的对称轴与x轴交于点E．（1）求抛物线的表达式及顶点D的坐标；（2）点M是线段BC上一动点，连接DM并延长交x轴交于点F，当FM：FD=1：4时，求点M的坐标；（3）点P是该抛物线上的一动点，设点P的横坐标为m，试判断是否存在这样的点P，使∠PAB+∠BCO=90°，若存在，请直接写出m的值；若不存在，请说明理由．11．如图，点A，B在函数y=14x2的图像上．已知A，B的横坐标分别为－2、4，直线AB与y轴交于点C，连接OA，OB．（1）求直线AB的函数表达式；（2）求ΔAOB的面积；（3）若函数y=14x2的图像上存在点P，使得ΔPAB的面积等于ΔAOB的面积的一半，则这样的点P共有个．12．如图，已知二次函数y=ax2﹣2ax+c（a＜0）的图象与x轴负半轴交于点A（﹣1，0），与y 轴正半轴交于点B，顶点为P，且OB=3OA，一次函数y=kx+b的图象经过A、B．（1）求一次函数解析式；（2）求顶点P的坐标；，求点M （3）平移直线AB使其过点P，如果点M在平移后的直线上，且tan∠OAM=32坐标；（4）设抛物线的对称轴交x轴于点E，连接AP交y轴于点D，若点Q、N分别为两线段PE、PD上的动点，连接QD、QN，请直接写出QD+QN的最小值．13．如图，抛物线y=ax2+bx+4经过点A(−1,0)，B(2,0)两点，与y轴交于点C，点D是拋物线在x轴上方，对称轴右侧上的一个动点，设点D的横坐标为m．连接AC，BC，DB，DC．（1）求抛物线的解析式；（2）当△BCD的面积与△AOC的面积和为7时，求m的值；2（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形．若存在，请直接写出点M的坐标；若不存在，请说明理由．(x+m)(x−3m)图象的顶点为M，图象交x轴于A、14．如图，y关于x的二次函数y=−√33mB两点，交y轴正半轴于D点.以AB为直径作圆，圆心为C.定点E的坐标为(−3，0)，连接ED.(m>0)（1）写出A、B、D三点的坐标；（2）当m为何值时M点在直线ED上？判定此时直线与圆的位置关系；（3）当m变化时，用m表示△AED的面积S，并在给出的直角坐标系中画出S关于m的函数图象的示意图.15．在图1中，抛物线y＝ax2+2ax﹣8（a≠0）与x轴交于点A、B（点A在B左侧），与y轴负半轴交于点C，OC＝4OB，连接AC，抛物线的对称轴交x轴于点E，交AC于点F．（1）AB的长为，a的值为；（2）图2中，直线ON分别交EF、抛物线于点M、N，OM＝√17，连接NC．①求直线ON的解析式；②证明：NC∥AB；③第四象限存在点P使△BFP与△AOC相似，且BF为△BFP的直角边，请直接写出点P坐标．16．如图，直线AB的解析式为y=−43x+4，抛物线y=−13x2+bx+c与y轴交于点A，与x轴交于点C(6，0)，点P是抛物线上一动点，设点P的横坐标为m.（1）求抛物线的解析式；（2）如图（1），当点P在第一象限内的抛物线上时，求△ABP面积的最大值，并求此时点P的坐标；（3）过点A作直线l//x轴，过点P作PH⊥l于点H，将△APH绕点A顺时针旋转，使点H的对应点恰好落在直线AB上，同时恰好落在坐标轴上，请直接写出点P的坐标.参考答案与解析1．【答案】（1）解：方案一：点B的坐标为（5，0），设抛物线的解析式为：y=a(x+5)(x−5)．由题意可以得到抛物线的顶点为（0，5），代入解析式可得：a=−15，∴抛物线的解析式为：y=−15(x+5)(x−5)方案2：点B的坐标为（10，0）．设抛物线的解析式为：y=ax(x−10)．由题意可以得到抛物线的顶点为（5，5），代入解析式可得：a=−15，∴抛物线的解析式为：y=−15x(x−10)；方案3：点B的坐标为（5，−5），由题意可以得到抛物线的顶点为（0，0）．设抛物线的解析式为：y=ax2，把点B的坐标（5，−5），代入解析式可得：a=−15，∴抛物线的解析式为：y=−15x2；（2）解：方案一：由题意：把x=3代入y=−15(x+5)(x−5)，解得：y=165=3.2，∴水面上涨的高度为3.2m方案二：由题意：把x=2代入y=−15x(x−10)解得：y=165=3.2，∴水面上涨的高度为3.2m．方案三：由题意：把x=3代入y=−15x2解得：y=−95= −1.8，∴水面上涨的高度为5−1.8= 3.2m．2．【答案】（1）解: 将点D( m，m+1 )代入y=−x2+3x+4中，得：m+1=−m2+3m+4，解得：m=−1或3，∵点D在第一象限，∴m=3，∴点D的坐标为(3，4)；令y=0，则−x2+3x+4=0，解得：x1=−1，x2=4，令x=0，则y=4，由题意得A(-1，0)，B(4，0)，C(0，4)，∴OC=OB=4，BC= 4√2，CD=3，∵点C、点D的纵坐标相等，∴CD∥AB，∠OCB=∠OBC=∠DCB=45°，∴点D关于直线BC的对称点E在y轴上．根据对称的性质知：CD=CE=3 ，∴OE=OC−CE=4−3=1，∴点D关于直线BC对称的点E的坐标为(0，1)；（2）解: 作PF⊥AB于F，DG⊥BC于G，由(1)知OB=OC=4，∠OBC=45°．∵∠DBP=45°，∴∠CBD=∠PBF．∵CD=3，∠DCB=45°，∴CG=DG= 3√22，∵BC= 4√2，∴BG= 4√2−3√22=5√22∴tan∠PBF=tan∠CBD=DGBG =35．设PF=3t，则BF=5t，OF=5t−4．∴P(−5t+4，3t)，∵P点在抛物线上，∴3t=−(−5t+4)2+3(−5t+4)+4解得：t=2225或t=0(舍去)．∴点P的坐标为( −25，6625)．3．【答案】（1）解：在Rt△AOB中，OA=1，tan∠BAO= OBOA=3，∴OB=3OA=3．∵△DOC是由△AOB绕点O逆时针旋转90°而得到的，∴△DOC≌△AOB，∴OC=OB=3，OD=OA=1，∴A、B、C的坐标分别为（1，0），（0，3）（﹣3，0）．代入解析式为{a+b+c=09a−3b+c=0c=3，解得： {a =−1b =−2c =3．∴抛物线的解析式为y=﹣x 2﹣2x+3（2）解：①∵抛物线的解析式为y=﹣x 2﹣2x+3，∴对称轴l=﹣ b2a =﹣1，∴E 点的坐标为（﹣1，0）．如图， 当∠CEF=90°时，△CEF ∽△COD ．此时点P 在对称轴上，即点P 为抛物线的顶点，P （﹣1，4）；当∠CFE=90°时，△CFE ∽△COD ，过点P 作PM ⊥x 轴于点M ，则△EFC ∽△EMP ． ∴EMMP =EFFC =DO OC=13 ，∴MP=3EM ．∵P 的横坐标为t ，∴P （t ，﹣t 2﹣2t+3）．∵P 在第二象限，∴PM=﹣t 2﹣2t+3，EM=﹣1﹣t ，∴﹣t 2﹣2t+3=﹣（t ﹣1）（t+3），解得：t 1=﹣2，t 2=﹣3（因为P 与C 重合，所以舍去），∴t=﹣2时，y=﹣（﹣2）2﹣2×（﹣2）+3=3．∴P （﹣2，3）．∴当△CEF 与△COD 相似时，P 点的坐标为：（﹣1，4）或（﹣2，3）； ②设直线CD 的解析式为y=kx+b ，由题意，得{−3k +b =0b =1 ，解得： {k =13b =1，∴直线CD 的解析式为：y= 13 x+1．设PM 与CD 的交点为N ，则点N 的坐标为（t ， 13 t+1），∴NM= 13 t+1．∴PN=PM ﹣NM=﹣t 2﹣2t+3﹣（ 13 t+1）=﹣t 2﹣ 73t +2． ∵S △PCD =S △PCN +S △PDN ，∴S △PCD = 12 PN •CM+ 12 PN •OM= 12 PN （CM+OM ）= 12 PN •OC= 12 ×3（﹣t 2﹣ 73t +2）=﹣ 32 （t+76）2+ 12124 ，∴当t=﹣ 76 时，S △PCD 的最大值为 12124 ． 4．【答案】（1）解：∵抛物线C 1：y=ax 2+4ax+4a+b （a ≠0，b ＞0）经过原点O ， ∴0=4a+b ，∴当ax 2+4ax+4a+b=0时，则ax 2+4ax=0， 解得：x=0或﹣4，∴抛物线与x 轴另一交点A 坐标是（﹣4，0）（2）解：∵抛物线C1：y=ax2+4ax+4a+b=a（x+2）2+b（a≠0，b＞0），（如图1）∴顶点M坐标为（﹣2，b），∵△AMO为等腰直角三角形，∴b=2，∵抛物线C1：y=ax2+4ax+4a+b=a（x+2）2+b过原点，∴a（0+2）2+2=0，解得：a=﹣12，∴抛物线C1：y=﹣12x2﹣2x（3）解：∵b=1，抛物线C1：y=ax2+4ax+4a+b=a（x+2）2+b过原点，（如图2）∴a=﹣14，∴y=﹣14（x+2）2+1=﹣14x2﹣x，设N（n，﹣1），又因为点P（m，0），∴n﹣m=m+2，∴n=2m+2即点N的坐标是（2m+2，﹣1），∵顶点N在抛物线C1上，∴﹣1=﹣14（2m+2+2）2+1，解得：m=﹣2+ √2或﹣2﹣√2 5．【答案】（1）m；m+3；y P=x P+3（2）解：∵抛物线 G ：y =−x 2+2mx −m 2+m +3 与直线 l ：x =3 交于点 Q ， ∴把 x =3 代入 y =−x 2+2mx −m 2+m +3 ， 得 y Q =−m 2+7m −6 ．∵y Q =−m 2+7m −6=−(m −72)2+254，∴当 m =72 时， y Q 的最大值为 254 ．（3）解：∵点 P 在 y 轴与 l 之间沿直线 l 1：y =x +3 运动， 如图，设直线 l 1：y =x +3 与 y 轴和直线 l 分别交于点 B 和点 P 1 ，线段 BP 1 的长即为点 P 路径长．把 x B =0 ， x P 1=3 代入 y =x +3 得点 B(0，3) ，点 P 1(3，6) ， 过点 P 1 作 P 1M ⊥y 轴，垂足为M ， 则 P 1M =3，BM =3 ， 在 Rt △BMP 1 中， BP 1=√BM 2+MP 12=√32+32=3√2 ，∴点 P 路径长为 3√2 ．6．【答案】（1）解：设抛物线的表达式为：y ＝a （x+1）2+4， 把x ＝0，y ＝3代入得：3＝a （0+1）2+4，解得：a ＝﹣1 ∴抛物线的表达式为y ＝﹣（x+1）2+4＝﹣x 2﹣2x+3（2）解：存在.如图1，作C 关于对称轴的对称点C ′，连接EC ′交对称轴于F ，此时CF+EF的值最小，则△CEF的周长最小.∵C（0，3），∴C′（﹣2，3），易得C′E的解析式为：y＝﹣3x﹣3，当x＝﹣1时，y＝﹣3×（﹣1）﹣3＝0，∴F（﹣1，0）（3）解：如图2，∵A（﹣3，0），D（﹣1，4），易得AD的解析式为：y＝2x+6，过点D作DH⊥x轴于H，过点M作MG⊥x轴交AD于G，AH＝﹣1﹣（﹣3）＝2，DH＝4，∴AD＝√AH2+DH2=√22+42=2√5，设M（m，﹣m2﹣2m+3），则G（m，2m+6），（﹣3≤m≤﹣1），∴MG＝（﹣m2﹣2m+3）﹣（2m+6）＝﹣m2﹣4m﹣3，由题易知△MNG∽△AHD，∴MGMN =ADAH即MN=AH×MGAD =22√5=−√55(m+2)2+√55∵√55<0∴当m ＝﹣2时，MN 有最大值；此时M （﹣2，3），又∵C （0，3），连接MC ∴MC ⊥y 轴∵∠CPM ＝∠HAD ，∠MCP ＝∠DHA ＝90°， ∴△MCP ∽△DHA ， ∴PCAH =MCDH 即 PC2=24 ∴PC ＝1∴OP ＝OC ﹣PG ＝3﹣1＝2， ∴S △POM ＝ 12×2×2 ＝2，7．【答案】（1）解：由题意，得 {0=16a −8a +c 4=c解得 {a =−12c =4∴所求抛物线的解析式为：y=﹣ 12 x 2+x+4（2）解：设点Q 的坐标为（m ，0），过点E 作EG ⊥x 轴于点G ．由﹣ 12 x 2+x+4=0， 得x 1=﹣2，x 2=4∴点B 的坐标为（﹣2，0） ∴AB=6，BQ=m+2 ∵QE ∥AC ∴△BQE ∽△BAC∴EG CO =BQBA 即 EG4=m+26 ∴EG =2m+43∴S △CQE =S △CBQ ﹣S △EBQ = 12 BQ •CO ﹣ 12 BQ •EG = 12 （m+2）（4﹣2m+43）= −13m 2+23m +83 =﹣ 13 （m ﹣1）2+3 又∵﹣2≤m ≤4∴当m=1时，S △CQE 有最大值3，此时Q （1，0） （3）解：存在．在△ODF 中． （ⅰ）若DO=DF ∵A （4，0），D （2，0） ∴AD=OD=DF=2又在Rt △AOC 中，OA=OC=4 ∴∠OAC=45度 ∴∠DFA=∠OAC=45度∴∠ADF=90度．此时，点F 的坐标为（2，2） 由﹣ 12 x 2+x+4=2， 得x 1=1+ √5 ，x 2=1﹣ √5此时，点P 的坐标为：P （1+ √5 ，2）或P （1﹣ √5 ，2）． （ⅱ）若FO=FD ，过点F 作FM ⊥x 轴于点M由等腰三角形的性质得：OM= 12OD=1∴AM=3∴在等腰直角△AMF中，MF=AM=3∴F（1，3）由﹣12x2+x+4=3，得x1=1+ √3，x2=1﹣√3此时，点P的坐标为：P（1+ √3，3）或P（1﹣√3，3）．（ⅲ）若OD=OF∵OA=OC=4，且∠AOC=90°∴AC= 4√2∴点O到AC的距离为2√2，而OF=OD=2 <2√2，与OF≥2 √2矛盾，所以AC上不存在点使得OF=OD=2，此时，不存在这样的直线l，使得△ODF是等腰三角形综上所述，存在这样的直线l，使得△ODF是等腰三角形所求点P的坐标为：P（1+ √5，2）或P（1﹣√5，2）或P（1+ √3，3）或P（1﹣√3，3）8．【答案】（1）解：∵C为OB的中点，点B(0,4)，∴点C(0,2)，又∵M为AC中点，点A(4,0)，0+4 2=2,2+02=1，∴点M(2,1)（2）解：∵⊙P与直线AD，则∠CAD=90°，设：∠CAO=α，则∠CAO=∠ODA=∠PEH=α，tan∠CAO=OCOA =12=tanα，则sinα=√5，cosα=√5，AC=√10，则CD=ACsin∠CDA =√10sinα=10，则点D(0,−8)，设直线AD的解析式为：y=mx+n，将点A、D的坐标分别代入得：{0=4m+n−8=n，解得：{m=2n=−8，所以直线AD的表达式为：y=2x−8（3）解：设抛物线的表达式为：y=a(x−2)2+1，将点B坐标代入得：4=a(0-2)2+1，解得：a=34，故抛物线的表达式为：y=34x2−3x+4，过点P作PH⊥EF，则EH=12EF=2√5，cos∠PEH=EHPE =2√5PE=cosα=√5，解得：PE=5，设点P(x,34x2−3x+4)，则点E(x,2x−8)，则PE=34x2−3x+4−2x+8=5，解得x=143或2(舍去2)，则点P(143,193) .9．【答案】（1）解：∵抛物线的解析式为y=−x2+4x+5，∴该抛物线的对称轴为：x=−42×(−1)=2，令y=−x2+4x+5中x=0，则y=5，∴点C的坐标为(0，5)，∵C、E关于抛物线的对称轴对称，∴点E的坐标为(2×2−0，5)，即(4，5)，令y =−x 2+4x +5中y =0，则−x 2+4x +5=0， 解得：x 1=−1，x 2=5，∴点A 的坐标为(−1，0)、点B 的坐标为(5，0)， 设直线AE 的解析式为y =kx +b ，将点A(−1，0)、E(4，5)代入y =kx +b 中， 得：{0=−k +b 5=4k +b ，解得：{k =1b =1，∴直线AE 的解析式为y =x +1； （2）（6，-7）（3）解：符合条件的m 值为0、3、3−√412和3+√412.10．【答案】（1）解：当x =0时，得y =4， ∴点C 的坐标为（0，4），当y =0时，得−23x +4=0，解得：x =6， ∴点B 的坐标为（6，0）， 将B ，C 两点坐标代入，得{36a +43×6+c =0，c =4. 解，得{a =−13，c =4.∴抛物线线的表达式为y =−13x 2+43x +4.∵y =−13x 2+43x +4=−13(x 2−4x +4−4)+4=−13(x −2)2+163.∴顶点D 坐标为(2，163)． （2）解：作MG ⊥x 轴于点G ，∵∠MFG =∠DFE ，∠MGF =∠DEF =90°， ∴ΔMGF ∽ΔDEF ．∴FM FD =MG DE．∴14=MG163．∴MG =43当y =43时，43=−23x +4 ∴x =4．∴点M 的坐标为(4，43)．（3）解：∵∠PAB +∠BCO =90°，∠CBO +∠BCO =90°， ∴∠PAB =∠CBO ，∵点B 的坐标为（6，0），点C 的坐标为（0，4）， ∴tan ∠CBO =46=23， ∴tan ∠PAB =23， 过点P 作PQ ⊥AB ， 当点P 在x 轴上方时，−13m 2+4m +12m +2=23解得m=4符合题意， 当点P 在x 轴下方时，13m 2−4m −12m +2=23解得m=8符合题意， ∴存在，m 的值为4或8．11．【答案】（1）解：∵A ，B 是抛物线 y =14x 2 上的两点，∴当 x =−2 时， y =14×(−2)2=1 ；当 x =4 时， y =14×42=4 ∴点A 的坐标为（-2，1），点B 的坐标为（4，4） 设直线AB 的解析式为 y =kx +b ， 把A ，B 点坐标代入得 {−2k +b =14k +b =4解得， {k =12b =2所以，直线AB 的解析式为： y =12x +2 ； （2）解：对于直线AB ： y =12x +2 当 x =0 时， y =2 ∴OC =2∴S ΔAOB =S ΔAOC +S ΔBOC = 12×2×2+12×2×4 =6 （3）412．【答案】（1）解：∵A （﹣1，0）， ∴OA=1 ∵OB=3OA ， ∴B （0，3）∴图象过A 、B 两点的一次函数的解析式为：y=3x+3（2）解：∵二次函数y=ax 2﹣2ax+c （a ＜0）的图象与x 轴负半轴交于点A （﹣1，0），与y 轴正半轴交于点B （0，3）， ∴c=3，a=﹣1，∴二次函数的解析式为：y=﹣x 2+2x+3 ∴抛物线y=﹣x 2+2x+3的顶点P （1，4） （3）解：设平移后的直线的解析式为：y=3x+m ∵直线y=3x+m 过P （1，4）， ∴m=1，∴平移后的直线为y=3x+1 ∵M 在直线y=3x+1，且 设M （x ，3x+1）①当点M 在x 轴上方时，有 3x+1x+1=32 ，∴x =13 ， ∴M 1(13,2)②当点M 在x 轴下方时，有 −3x+1x+1=32 ，∴x =−59 ， ∴M 2(−59 ， −23)（4）解：作点D 关于直线x=1的对称点D ′，过点D ′作D ′N ⊥PD 于点N ， 当﹣x 2+2x+3=0时，解得，x=﹣1或x=3， ∴A （﹣1，0）， P 点坐标为（1，4），则可得PD 解析式为：y=2x+2， 根据ND ′⊥PD ，设ND ′解析式为y=kx+b ， 则k=﹣ 12 ，将D ′（2，2）代入即可求出b 的值， 可得函数解析式为y=﹣ 12 x+3，将两函数解析式组成方程组得： {y =−12x +3y =2x +2 ，解得 {x =25y =145 ，故N （ 25 ， 145 ），由两点间的距离公式：d= √(2−25)2+(2−145)2 = 4√55， ∴所求最小值为4√5513．【答案】（1）解：把A （-1,0），B （2,0）代入抛物线解析式得： {a −b +4=04a +2b +4=0，解得： {a =−2b =2∴抛物线的解析式为： y =−2x 2+2x +4 （2）解：如图，连接OD ，由 y =−2x 2+2x +4 可得： 对称轴为 x =−22×(−2)=12 ，C （0,4）∵D(m,−2m 2+2m +4)(12<m <2) ，A （-1,0），B （2,0） ∴∴S △BCD =S △OCD +S △BCD −S △OBC=12×4m +12×2·(−2m 2+4m +2)−12×2×4=−2m 2+4m S △AOC =12×1×4=2又∵S △BCD +S △AOC =72 ∴−2m 2+4m +2=72 ，∴4m 2−8m +3=0解得： m 1=12 ， m 2=32 ，当 m 1=12 时，点在对称轴上，不合题意，舍去，所以取 m 2=32 ， 综上， m =32（3）解： M 1(0,0) ， M 2(4,0) ， M 3(√142,0) ， M 4(−√142,0)14．【答案】（1）解：令y =0，则−√33m (x +m)(x −3m)=0，解得x 1=−m ，x 2=3m ；令x =0，则y =−√33m (0+m)(0−3m)=√3m .故A(−m ，0)，B(3m ，0)，D(0，√3m).（2）解：设直线ED 的解析式为y =kx +b ，将E(−3，0)，D(0，√3m)代入得：{−3k +b =0b =√3m解得，k =√33m ，b =√3m .∴直线ED 的解析式为y =√33mx +√3m .将y =−√33m (x +m)(x −3m)化为顶点式：y =−√33m (x −m)2+4√33m . ∴顶点M 的坐标为(m ，4√33m).代入y =√33mx +√3m 得：m 2=m∵m >0，∴m =1.所以，当m =1时，M 点在直线DE 上. 连接CD ，C 为AB 中点，C 点坐标为C(m ，0). ∵OD =√3，OC =1， ∴CD =2，D 点在圆上又∵OE =3，DE 2=OD 2+OE 2=12， EC 2=16，CD 2=4， ∴CD 2+DE 2=EC 2.∴∠EDC =90°∴直线ED 与⊙C 相切.（3）解：当0<m <3时，S △AED =12AE ⋅OD =√32m(3−m)S =−√32m 2+3√32m . 当m >3时，S ΔAED =12AE ⋅OD =√32m(m −3).即S =√32m 2_3√32m . S 关于m 的函数图象的示意图如右：15．【答案】（1）6；1（2）解：①由抛物线的表达式知，抛物线的对称轴为x＝﹣1，故设点M的坐标为（﹣1，m），则OM＝12+m2＝（√17）2，解得m＝4（舍去）或﹣4，故点M的坐标为（﹣1，﹣4），由点O、M的坐标得，直线OM（即ON）的表达式为y＝4x②，故答案为y＝4x；②联立①②并解得{x=−2y=−8，故点N（﹣2，﹣8），∵点C、N的纵坐标相同，故NC∥x轴，即NC∥AB；③当∠BFP为直角时，由A（﹣4，0），C（0，-8）可求AC解析式为y＝-2x﹣8，把x=-1，代入y＝-2x﹣8得，y＝-6，点F的坐标为：（-1，-6），由点F、B的坐标得，直线BF的表达式为y＝2x﹣4，当x＝﹣2时，y＝2x﹣4＝﹣8，故点N在直线BF上，连接FN，过点F作FP⊥BF交NC的延长线于点K，由直线BF 的表达式知，tan ∠BNK ＝2，则tan ∠FKN ＝ 12 ， 故设直线PF 的表达式为y ＝﹣ 12 x+t ， 将点F 的坐标代入上式并解得t ＝﹣ 132 ，则直线PF 的表达式为y ＝﹣ 12 x ﹣ 132 ，故设点P 的坐标为（m ，﹣ 12 m ﹣ 132 ）， 在Rt △AOC 中，tan ∠ACO ＝ AOCO ＝ 12 ，则tan ∠OCA ＝2， ∵△BFP 与△AOC 相似， 故∠FBP ＝∠ACO 或∠OAC ，则tan ∠FBP ＝tan ∠ACO 或tan ∠OAC ，即tan ∠FBP ＝ 12 或2， 由点B 、F 的坐标得：BF ＝ √32+62=3√5 ， 则PF ＝BFtan ∠FBP ＝3√52或6 √5 ，由点P 、F 的坐标得：PF 2＝（m+1）2+（﹣ 12 m ﹣ 132 +6）2＝（ 3√52）2或（6 √5 ）2， 解得m ＝2或﹣4（舍去）或11或﹣13（舍去）， 故点P 的坐标为（11，﹣12）或（2，﹣ 152 ）； 当∠PBF 为直角时，过点B 作BP ⊥BF ，同理可求直线PF 的表达式为y ＝﹣ 12 x+1，故设点P 的坐标为（m ，﹣ 12 m ﹣1），同理可得，PB ＝BFtan ∠FBP ＝3√52或6 √5 ，由点P 、B 的坐标得：PB 2＝（m-2）2+（﹣ 12 m+1）2＝（3√52）2或（6 √5 ）2，解得m＝-1（舍去）或5或14或﹣10（舍去），点P的坐标为（5，﹣32）或（14，-6）；综上，点P的坐标为（11，﹣12）或（2，﹣152）或（5，﹣32）或（14，-6）；16．【答案】（1）解：当x=0时，y=−43x+4=4，则A(0，4)，把A(0，4)，C(6，0)代入y=−13x2+bx+c得{−12+6b+c=0c=4，解得{b=43c=4，∴抛物线解析式为y=−13x2+43x+4；（2）连接OP，设P(m，−13m2+43m+4)，当y=0时，−43x+4=0，解得x=3，则B(3，0)，S△ABP=S△AOP+S△POB−S△AOB=12⋅4⋅m+12⋅3⋅(−13m2+43m+4)−12⋅3⋅4=−12m2+4m，=−12(m−4)2+8，当m=4时，△ABP面积有最大值，最大值为8，此时P点坐标为(4，4)；（3）在Rt△OAB中，AB=√32+42=5，当点P′落在x轴上，如图2，∵△APH绕点A顺时针旋转，使点H的对应点恰好落在直线AB上，同时恰好落在x 轴上∴P′H′=PH=4−(−13m2+43m+4)=13m2−43m，AH′=AH=m，∠P′H′A=∠PHA=90∘，∵∠P′BH′=∠ABO，∴△BP ′H ′ ∽ △BAO ，∴P ′H ′ ： OA =BH ′ ：OB ，即 (13m 2−43m) ： 4=BH ′ ：3， ∴BH ′=14m 2−m ， ∵AH ′+BH ′=AB ，∴m +14m 2−m =5 ，解得 m 1=2√5 ， m 2=−2√5( 舍去 ) ，此时P 点坐标为 (2√5，−8+8√53) ； 当点 P ′ 落在y 轴上，如图3，同理可得 P ′H ′=PH =13m 2−43m ， AH ′=AH =m ， ∠P ′H ′A =∠PHA =90∘ ， ∵∠P ′AH ′=∠BAO ， ∴△AH ′P ′′ ∽ △AOB ，∴P ′H ′ ： OB =AH ′ ：AO ，即 (13m 2−43m) ： 3=m ：4， 整理得 4m 2−25m =0 ，解得 m 1=254， m 2=0( 舍去 ) ，此时P 点坐标为 (254，−4348) ； 综上所述，P 点坐标为 (2√5，−8+8√53) 或 (254，−4348) ；。
中考数学总复习《二次函数》专项测试卷-附参考答案
中考数学总复习《二次函数》专项测试卷-附参考答案学校:___________姓名：___________班级：___________考号：___________一、单选题(共12题；共24分)1．二次函数y＝﹣x2+2x﹣4，当﹣1＜x＜2时，y的取值范围是（）A．﹣7＜y＜﹣4B．﹣7＜y≤﹣3C．﹣7≤y＜﹣3D．﹣4＜y≤﹣3 2．已知二次函数y=3(x−2)2+ℎ，当自变量x分别取-2，2，5时，对应的值分别为y1，y2和y 3则y1，y2和y3的大小关系正确的是()A．y3<y2<y1B．y1<y2<y3C．y2<y3<y1D．y3<y1<y23．小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数ℎ=3.5t−4.9t2（的单位：秒，h的单位：米）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（）A．0.71B．0.70C．0.63D．0.364．对于二次函数y=−14(x+2)2−1，下列说法正确的是（）A．当x>−2时，y随x的增大而增大B．当x=−2时，y有最大值−1C．图象的顶点坐标为(2，−1)D．图象与x轴有两个交点5．抛物线y=2x2−12x+22的顶点是（）A．(3,−4)B．(−3,4)C．(3,4)D．(2,4)6．如图，二次函数y＝ax2＋bx＋c（a≠0）的图像的顶点在第一象限，且过点（0，1）和（－1，0）下列结论：①ab＜0，②b2-4ac＞0，③a-b+c＜0，④c=1，⑤当x＞－1时，y＞0.其中正确结论的个数是（）A．2个B．3个C．4个D．5个7．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y1），（3，y2）是抛物线上两点，则y1＜y2，其中说法正确的是（）A．①②B．②③C．①②④D．②③④8．关于二次函数y=-（x -2）2＋3，以下说法正确的是（）A．当x＞-2时，y随x增大而减小B．当x＞-2时，y随x增大而增大C．当x＞2时，y随x增大而减小D．当x＞2时，y随x增大而增大9．如图，双曲线y= k x经过抛物线y=ax2+bx（a≠0）的顶点（﹣1，m）（m＞0），则下列结论中，正确的是（）A．a+b=k B．2a+b=0C．b＜k＜0D．k＜a＜010．如图，抛物线y=ax2+bx+c交x轴于(−1，0)，(3，0)两点，则下列判断中，不正确的是（）A．图象的对称轴是直线x=1B．当x>2时，y随x的增大而减小C ．当−1<x <1时D ．一元二次方程ax 2+bx +c =0的两个根是−1和311．已知点(x 1，y 1)，(x 2，y 2)(x 1<x 2)在y =−x 2+2x +m 的图象上，下列说法错误的是（ ）A ．当m >0时，二次函数y =−x 2+2x +m 与x 轴总有两个交点B ．若x 2=2，且y 1>y 2，则0<x 1<2C ．若x 1+x 2>2，则y 1>y 2D ．当−1≤x ≤2时，y 的取值范围为m −3≤y ≤m12．从底面竖直向上抛出一小球，小球的高度h （单位：m ）与小球运动时间t （单位：s ）之间的关系式是：h ＝30t ﹣5t 2这个函数图象如图所示，则小球从第3s 到第5s 的运动路径长为（ ）A ．15mB ．20mC ．25mD ．30m二、填空题(共6题；共6分)13．在二次函数 y =−x 2+bx +c 中，函数y 与自变量x 的部分对应值如下表：则m 、n 的大小关系为 m n ．（填“＜”，“＝”或“＞”）14．已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是 ．（只需写一个）15．二次函数 y =ax 2+bx +c 的图象与 x 轴相交于 (−1, 0) 和 (5, 0) 两点，则该抛物线的对称轴是 .16．函数y= {x 2+2x −3(x <0)x 2−4x −3(x ≥0) 的图象与直线y=﹣x+n 只有两个不同的公共点，则n 的取值为 ．17．已知二次函数y ＝﹣x 2+2mx+1，当﹣2≤x≤1时最大值为4，则m 的值为 ． 18．若函数y=（m ﹣2）x m 2−2+3是二次函数，则m=三、综合题(共6题；共70分)19．已知抛物线 y =a(x −4)2+2 经过点 (2,−2) ．（1）求a 的值；（2）若点A(m,y1),B(n,y2)(m<n<4)都在该抛物线上，试比较y1与y2的大小．20．宁波地区最近雾霾天气频繁，使得空气净化器得以畅销，某商场代理销售某种空气净化器，其进价是500元/台，经过市场销售后发现，在一个月内，当售价是1000元/台时，可售出50台，且售价每降低20元，就可多售出5台．若供货商规定这种空气净化器售价不能低于600元/台，代理销售商每月要完成不低于60台的销售任务．（1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；（2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？21．某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元.销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件.同时，在销售过程中，每月还要支付其他费用450元.设销售单价为x元，平均月销售量为y件.（1）求出y与x的函数关系式，并写出自变量x的取值范围.（2）当销售单价为多少元时，销售这种童装每月可获利1800元？（3）当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？22．如图，是一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m 的景观灯，把拱桥的截面图放在平面直角坐标系中。
二次函数专题训练题
二次函数专题训练题二次函数专题训练(一)1、已知抛物线 $y=ax^2+6ax+c$ 与x轴的一个交点为A （-2,0）①求抛物线与x轴的另一个交点B的坐标。
②点C是抛物线与y轴的交点，D是抛物线上一点，且以AB为一底的梯形ABCD的面积为32，求此抛物线的解析式。
③ E是第二象限内到x轴、y轴距离之比为3：1的点。
若E在②中的抛物线上，且a＞0,E和A在对称轴同侧。
问在抛物线的对称轴上是否存在P点，使△APE周长最小。
若存在，求出P点的坐标，若不存在，请说明理由。
解析：①因为点A在x轴的负半轴上，所以点B在x轴的正半轴上，设点B的坐标为（t,0），则由题意可得：begin{cases}a(-2)^2+6a(-2)+c=0 \\at^2+6at+c=0 \\end{cases}解得 $t=-\frac{c}{a}-4$所以点B的坐标为 $(-\frac{c}{a}-4,0)$②设抛物线的解析式为$y=ax^2+6ax+c$，则由题意可得：begin{cases}a(-2)^2+6a(-2)+c=0 \\at^2+6at+c=0 \\end{cases}解得 $a=2$，$c=-8$，所以抛物线的解析式为$y=2x^2+12x-8$③设抛物线的对称轴为直线 $x=k$，则点A的坐标为 $(-k,0)$，点E的坐标为 $(m,3m)$，其中 $m$ 为任意实数。
由题意可得：begin{cases}k=-\frac{b}{2a}=-3 \\a(m+2)^2+6a(m+2)-8=3m \\end{cases}解得 $m=-\frac{1}{2}$，所以点E的坐标为 $(-1,-\frac{3}{2})$。
由对称性可知，点P的坐标为 $(1,-\frac{3}{2})$，所以在抛物线的对称轴上存在点P，使△APE 周长最小。
2、已知二次函数 $y=x^2－2(m－1)x－1－m$ 的图像与x 轴交于两点A（$x_1$,0）和B（$x_2$,0），$x_1＜＜x_2$，与y轴交于点C，且满足 $\frac{AC}{OC}=\frac{1}{12}$。
中考数学专项复习《二次函数》练习题(附答案)
中考数学专项复习《二次函数》练习题(附答案)一、单选题1．周长是4m的矩形，它的面积S(m2)与一边长x(m)的函数图象大致是() A．B．C．D．2．边长为1的正方形OABC的顶点A在x轴正半轴上，点C在y轴正半轴上，将正方形OABC绕顶点O顺时针旋转75°，如图所示，点B恰好落在函数y=ax2（a< 0）的图象上，则a的值为（）A．−√2B．-1C．−3√24D．−√233．图中是有相同最小值的两条抛物线，则下列关系中正确的是（）A．k＜n B．h=m C．k+n=0D．h＜0，m＞04．在平面直角坐标系中二次函数y1=﹣x2+4x 和一次函数y2=2x 的图象如图所示，那么不等式﹣x2+4x＞2x 的解集是（）A．x＜0B．0＜x＜4C．0＜x＜2D．2＜x＜45．对于二次函数y=（x﹣1）2+2的图象，下列说法正确的是（）A．开口向下B．顶点坐标是（1，2）C．对称轴是x=﹣1D．有最大值是26．已知抛物线y=x2+2x上三点A（﹣5，y1），B（2.5，y2），C（12，y3），则y1，y2，y3满足的关系式为（）A．y1＜y2＜y3B．y3＜y2＜y1C．y2＜y1＜y3D．y3＜y1＜y2A．16B．15C．14D．13 8．一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是（）A．B．C．D．9．已知二次函数y=ax2+bx+c+2的图象如图所示，顶点为（﹣1，0），下列结论：①abc＜0；②b2﹣4ac=0；③a＞0；④4a﹣2b+c＞0．其中正确结论的个数是（）A．1B．2C．3D．4 10．将抛物线y=x2向右平移1个单位长度，再向下平移3个单位长度，所得到的抛物线为（）A．y=(x+1)2+3B．y=(x+1)2−3C．y=(x−1)2+3D．y=(x−1)2−311．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2；⑤2a﹣b＜c．其中正确的结论有（）A．1个B．2个C．3个D．4个12．已知抛物线y=x2﹣2bx+4的顶点在x轴上，则b的值一定是（）A．1B．2C．﹣2D．2或﹣2二、填空题13．如图，甲，乙两个转盘分别被三等分、四等分，各转动一次，停止转动后，将指针指向的数字分别记为a，b，使抛物线y=ax2−2x+b与x轴有公共点的概率为．14．将抛物线y=﹣x2+1向右平移2个单位长度，再向上平移3个单位长度所得的抛物线解析式为．15．若抛物线y=2(x−3)2−8与x轴的两个交点分别为点A和点B，则线段AB的长为．16．已知抛物线y=x2﹣x﹣1与x轴的一个交点的横坐标为m，则代数式m2﹣m+2016的值为．17．将抛物线y=x2向右平移2个单位，再向上平移3个单位，所得抛物线的表达式为．18．一个二次函数的图象顶点坐标为（2，1），形状与抛物线y=﹣2x2相同，试写出这个函数解析式三、综合题19．如图，某小区有一块靠墙（墙的长度不限）的矩形空地ABCD，为美化环境，用总长为100m的篱笆围成四块矩形花圃（靠墙一侧不用篱笆，篱笆的厚度不计）.（1）若四块矩形花圃的面积相等，求证：AE＝3BE；（2）在（1）的条件下，设BC的长度为xm，矩形区域ABCD的面积为ym2，求y 与x之间的函数关系式，并写出自变量x的取值范围.20．已知二次函数的图象以A(−1,4)为顶点，且过点B(2,−5)（1）求该函数的关系式；（2）求该函数图象与坐标轴的交点坐标；21．已知拋物线y=x2+bx+c经过点(−1，8)和(2，−7)．（1）试确定b，c的值．（2）直接写出x满足什么条件时y随x的增大而减小．22．已知抛物线y＝ax2＋bx＋5（a为常数，a≠0）交x轴于点A（－1，0）和点B（5，0），交y轴于点C．（1）求点C的坐标和抛物线的解析式；（2）若点P是抛物线上一点，且PB＝PC，求点P的坐标；（3）点Q是抛物线的对称轴l上一点，当QA＋QC最小时求点Q的坐标．23．在平面直角坐标系xOy中抛物线y＝x2﹣2mx+m2﹣1与y轴交于点C．（1）试用含m的代数式表示抛物线的顶点坐标；（2）将抛物线y＝x2﹣2mx+m2﹣1沿直线y＝﹣1翻折，得到的新抛物线与y轴交于点D，若m＞0，CD＝8，求m的值．（3）已知A（﹣k+4，1），B（1，k﹣2），在（2）的条件下，当线段AB与抛物线y＝x2﹣2mx+m2﹣1只有一个公共点时请求出k的取值范围．24．如图，平面直角坐标系中以点C（2，√3）为圆心，以2为半径的圆与x轴交于A，B两点．（1）求A，B两点的坐标；（2）若二次函数y=x2+bx+c的图象经过点A，B，试确定此二次函数的解析式．参考答案1．【答案】D2．【答案】D3．【答案】D4．【答案】C5．【答案】B6．【答案】C7．【答案】B8．【答案】C9．【答案】B10．【答案】D11．【答案】C12．【答案】D13．【答案】11214．【答案】y=﹣（x﹣2）2+415．【答案】416．【答案】201717．【答案】y=(x−2)2+318．【答案】y=﹣2（x﹣2）2+1或y=2（x﹣2）2+119．【答案】（1）证明：∵矩形MEFN与矩形EBCF面积相等∴ME＝BE，MG=GN.∵四块矩形花圃的面积相等，即S矩形AMND＝2S矩形MEFN∴AM＝2ME∴AE＝3BE；（2）解：∵篱笆总长为100m∴2AB+GH+3BC＝100即2AB+12AB+3BC=100∴AB=40−65BC.设BC的长度为xm，矩形区域ABCD的面积为ym2则y=BC⋅AB=x(40−65x)=−65x2+40x∵AB =40−65BC∴B E ＝10﹣ 310x ＞0解得x ＜ 1003∴y =65x 2+40x （0＜x ＜ 1003 ）. 20．【答案】（1）解：由顶点A （−1，4），可设二次函数关系式为y ＝a （x ＋1）2＋4（a≠0）．∵二次函数的图象过点B （2，−5） ∴点B （2，−5）满足二次函数关系式 ∴−5＝a （2＋1）2＋4 解得a ＝−1．∴二次函数的关系式是y ＝−（x ＋1）2＋4； （2）解：令x ＝0，则y ＝−（0＋1）2＋4＝3 ∴图象与y 轴的交点坐标为（0，3）； 令y ＝0，则0＝−（x ＋1）2＋4 解得x 1＝−3，x 2＝1故图象与x 轴的交点坐标是（−3，0）、（1，0）．答：图象与y 轴的交点坐标为（0，3），与x 轴的交点坐标是（−3，0）、（1，0）．21．【答案】（1）解：∵抛物线y =x 2+bx +c 经过点(−1，8)和(2，−7)∴{1−b +c =84+2b +c =−7解得{b =−6c =1；（2）解：由（1）可知，抛物线y =x 2−6x −1开口向上，对称轴为直线x =−−62×1=3 故在对称轴左侧，即当x <3时y 随x 的增大而减小．22．【答案】（1）解：对于y =ax 2+bx +5，当x =0时y =5∴C(0，5)∵抛物线y =ax 2+bx +5(a 为常数，a ≠0)交x 轴于点A(−1，0)和点B(5，0)∴{a −b +5=025a +5b +5=0解得{a =−1b =4∴抛物线的解析式为y =−x 2+4x +5；（2）解：∵B(5，0) C(0，5)∴OB =OC连接BC ，设BC 的中点为D∴D(52，52)∴直线OD 的解析式为y =x∵PB =PC∴点P 在直线OD 上 设P(m ，m)∵点P 是抛物线上一点∴m =−m 2+4m +5解得m =3±√292∴点P 的坐标为(3+√292，3+√292)或(3−√292，3−√292)；（3）解：由（1）知，抛物线的对称轴为直线x =2 ∵点A 与点B 关于l 对称，点Q 在直线l 上 ∴QA =QB QA +QC =QB +QC∴当B ，C ，Q 三点共线时QB +QC 最小，即QA +QC 最小 设直线BC 的解析式为y =kx +b∴{b =55k +b =5解得{k =−1b =5∴直线BC 的解析式为y =−x +5 把x =2代入y =−x +5得，y =3∴Q(2，3)∴当QA +QC 最小时求点Q 的坐标(2，3)．23．【答案】（1）解：∵y ＝x 2﹣2mx+m 2﹣1＝（x ﹣m ）2﹣1∴抛物线的顶点坐标为（m ，﹣1）（2）解：由对称性可知，点C 到直线y ＝﹣1的距离为4 ∴OC ＝3 ∴m 2﹣1＝3 ∵m ＞0 ∴m ＝2（3）解：∵m ＝2，∴抛物线为y ＝x 2﹣4x+3，当抛物线经过点A （﹣k+4，1）时k ＝2+ √2 或k ＝2﹣ √2 ；当抛物线经过点B （1，k ﹣2）时k ＝2；∵线段AB 与抛物线y ＝x 2﹣2mx+m 2﹣1只有一个公共点，则x 2-4x+3=x+k-3∴即x 2-5x+6-k=0的△=0∴25-4（6-k ）=0k=-0.25∵线段AB 与抛物线y ＝x 2﹣2mx+m 2﹣1只有一个公共点∴2﹣ √2 ＜k ＜2或k≥2+ √2 或k=-0.25．24．【答案】（1）解：过点C 作CM△x 轴于点M ，则MA=MB ，连结AC ，如图∵点C 的坐标为（2， √3 ） ∴OM=2 CM= √3 在Rt△ACM 中CA=2 ∴AM= √AC 2−CM 2 =1∴OA=OM ﹣AM=1 OB=OM+BM=3 ∴A 点坐标为（1，0），B 点坐标为（3，0）；（2）解：将A （1，0），B （3，0）代入y=x 2+bx+c 得 {1+b +c =09+3b +c =0解得 {b =−4c =3．所以二次函数的解析式为y=x 2﹣4x+3．。
中考数学专项复习《二次函数的三种形式》练习题带答案
中考数学专项复习《二次函数的三种形式》练习题带答案一、单选题1．二次函数y=x 2﹣2x+4化为y=a （x ﹣h ）2+k 的形式，下列正确的是（ ）A ．y=（x ﹣1）2+2B ．y=（x ﹣1）2+3C ．y=（x ﹣2）2+2D ．y=（x ﹣2）2+42．抛物线y=x 2﹣2x ﹣3的对称轴和顶点坐标分别是（ ）．A ．x=1，（1，﹣4）B ．x=1（1，4）C ．x=﹣1，（﹣1，4）D ．x=﹣1，（﹣1，﹣4）3．把y=4x 2﹣4x+2配方成y=a （x ﹣h ）2+k 的形式是（ ）A ．y=（2x ﹣1）2+1B ．y=（2x ﹣1）2+2C ．y=（x ﹣ 12）2+1D ．y=4（x ﹣ 12）2+24．若把抛物线y ＝x 2－2x ＋1先向右平移2个单位，再向下平移3个单位，所得到的抛物线的函数关系式为y ＝ax 2＋bx ＋c ，则b 、c 的值为（ ） A ．b ＝2，c ＝－2 B ．b ＝－8，c ＝14 C ．b ＝－6，c ＝6D ．b ＝－8，c ＝185．直角坐标平面上将二次函数y=x 2-2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ） A ．（0，0）B ．（1，-1）C ．（0，-1）D ．（-1，-1）6．将二次函数y=x 2+4x ﹣8化为y=（x+m ）2+n 的形式正确的是（ ）A ．y=（x+2）2+8B ．y=（x+2）2﹣8C ．y=（x+2）2+12D ．y=（x+2）2﹣127．若b<0，则二次函数y=x 2-bx-1的图象的顶点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．通过配方法将二次函数y=ax 2+bx+c （a≠0）化成y=a （x ﹣h ）2+k 的形式，此二次函数可变形为（ ）A ．y=a （x+ b 2a ）2+ 4ac−b 24aB ．y=a （x ﹣ b 2a ）2+ 4ac−b 24aC ．y=a （x+ b 2a ）2+ b 2−4ac 4aD ．y=a （x ﹣ b 2a ）2+ b 2−4ac 4a9．将二次函数y=x 2﹣2x+3化为y=（x ﹣h ）2+k 的形式，结果为（ ）A ．y=（x+1）2+4B ．y=（x+1）2+2C ．y=（x ﹣1）2+4D ．y=（x ﹣1）2+210．抛物线y=﹣ 15 x 2+ 25x ﹣1，经过配方化成y=a （x ﹣h ）2+k 的形式是（ ）A ．y =15(x +1)2−45B ．y =15(x −1)2+45C ．y =15(x −1)2−45D ．y =15(x +1)2+4511．如图，在 ΔABC 中 ∠B =90° ，tan ∠C =34,AB=6cm.动点P 从点A 开始沿边AB 向点B 以1cm/s 的速度移动，动点Q 从点B 开始沿边BC 向点C 以2cm/s 的速度移动.若P,Q 两点分别从A,B 两点同时出发，在运动过程中 ΔPBQ 的最大面积是( )A ．18cm 2B ．12cm 2C ．9cm 2D ．3cm 212．如图，在平面直角坐标系中抛物线所表示的函数解析式为y=﹣2（x ﹣h ）2+k ，则下列结论正确的是( )A ．h ＞0，k ＞0B ．h ＜0，k ＞0C ．h ＜0，k ＜0D ．h ＞0，k ＜0二、填空题13．二次函数 y =−x 2+2x +3 的图象与 x 轴交于 A 、 B 两点， P 为它的顶点，则S △PAB = ．14．把二次函数的表达式y=x 2﹣6x+5化为y=a （x ﹣h ）2+k 的形式，那么h+k= 15．将二次函数y=x 2﹣2x+4化成y=（x ﹣h ）2+k 的形式，则y= ． 16．若二次函数y=x 2+bx+5配方后为y=（x ﹣2）2+k ，则b+k= ．17．若将二次函数y=x 2﹣2x+3配方为y=（x ﹣h ）2+k 的形式，则y= ． 18．已知抛物线的表达式是y =2(x +2)2−1，那么它的顶点坐标是 ；三、综合题19．如图，抛物线的顶点M 在x 轴上，抛物线与y 轴交于点N ，且OM=ON=4，矩形ABCD 的顶点A 、B 在抛物线上，C 、D 在x 轴上．（1）求抛物线的解析式；（2）设点A的横坐标为t（t＞4），矩形ABCD的周长为l，求l与t之间函数关系式．20．已知二次函数y= 2x2 -4x-6.（1）用配方法将y= 2x2 -4x-6化成y=a (x-h) 2 +k的形式；并写出对称轴和顶点坐标。
考点12 二次函数(精练)(解析版)
考点12.二次函数（精练）限时检测1：最新各地模拟试题（50分钟）A ．B ．C ．D ．【答案】D【分析】根据反比例函数的图象得出b ＜0，逐一分析四个选项，根据二次函数图象的开口以及对称轴与y 轴的关系，抛物线与y 轴的交点，即可得出a 、b 、c 的正负，由此即可得出一次函数图象经过的象限，再与函数图象进行对比即可得出结论．【详解】解：∵反比例函数的图象在二、四象限，∴b ＜0，A 、∵二次函数图象开口向上，对称轴在y 轴右侧，交y 轴的负半轴，∴a ＞0，b ＜0，c ＜0，∴一次函数图象应该过第一、二、四象限，A 错误；B 、∵二次函数图象开口向下，对称轴在y 轴右侧，∴a ＜0，b ＞0，∴与b ＜0矛盾，B 错误；C 、∵二次函数图象开口向下，对称轴在y 轴右侧，∴a ＜0，b ＞0，∴与b ＜0矛盾，C 错误；D 、∵二次函数图象开口向上，对称轴在y 轴右侧，交y 轴的负半轴，∴a ＜0，b ＜0，c ＜0，∴一次函数图象应该过第一、二、四象限，D 正确．故选：D ．【点睛】本题主要考查了一次函数、反比例函数、二次函数的图象与性质，根据函数图象与系数的关系进行判断是解题的关键，同时考查了数形结合的思想．4．（2023·山东·中考模拟）小嘉说：将二次函数2y x =的图象平移或翻折后经过点(2,0)有4种方法：①向右平移2个单位长度②向右平移1个单位长度，再向下平移1个单位长度③向下平移4个单位长度④沿x 轴翻折，再向上平移4个单位长度你认为小嘉说的方法中正确的个数有()A ．1个B ．2个C ．3个D ．4个【答案】D 【分析】根据二次函数图象的平移可依此进行求解问题．【详解】解：①将二次函数2y x =向右平移2个单位长度得到：()22y x =-，把点(2,0)代入得：()2220y =-=，所以该平移方式符合题意；②将二次函数2y x =向右平移1个单位长度，再向下平移1个单位长度得到：()211y x =--，把点(2,0)代入得：()22110y =--=，所以该平移方式符合题意；③将二次函数2y x =向下平移4个单位长度得到：24y x =-，把点(2,0)代入得：2240y =-=，所以该平移方式符合题意；④将二次函数2y x =沿x 轴翻折，再向上平移4个单位长度得到：24y x =-+，把点(2,0)代入得：2240y =-+=，所以该平移方式符合题意；综上所述：正确的个数为4个；故选D ．【点睛】本题主要考查二次函数图象的平移，熟练掌握二次函数图象的平移是解题的关键．则点Q为满足图象上的点到轴距离的最大值为4的点，此时有【答案】2496572y x x =-+【分析】本题主要考查二次函数的实际应用，根据题意列出函数整理并求出【详解】解：根据题意，得【答案】34【分析】根据梯形面积求出CD 得到答案；【详解】四边形ABDC 是梯形，下底由()163152CD +⨯=，得4CD =∵214CD x x =-=，∴()212x x +又顶点纵坐标2344ac b a-=-②，【点睛】本题考查二次函数性质与几何图形应用，解题的关键是熟练掌握二次函数与一元二次方程之间的关系及二次函数的性质．13．（2023·四川成都·统考二模）在平面直角坐标系中，点上，若12y y =，则m =【答案】1213m <【分析】若12y y =，先求二次函数的对称轴，再利用二次函数的对称性对称两点的横坐标之和的一半等于【答案】①⑤/⑤①【分析】根据抛物线的对称轴是轴的交点位置得出,,a b c 为()2,0-，即可判断③39【答案】104 3x<<【分析】过A作AC⊥x轴于问题即可得到解答．由题意可得C x=103，所以当【点睛】本题考查函数图象应用，正确求解函数图象交点坐标及函数图象与坐标轴的交点坐标是解题关键．19．（2024·江苏无锡·校考模拟预测）②如图2，直线BM 过AC 中点，直线BM 解析式为1522y x =-+，AC 中点坐标为15,22a ⎛⎫⎪⎝⎭，待入直线求得910a =；③如图3，直线CM 过AB 中点，AB 中点坐标为()3,0，∴直线MB 与y 轴平行，必不成立；2）、当分成三角形和梯形时，过点M 的直线必与ABC 一边平行，所以必有“”A 所以相似比为1:2．④如图4，直线EM ∥AB ，∴CEN COA ∽∴12CE CN CO CA ==，∴51152a a -=，解得225a +=；⑤如图5，直线ME ∥AC ，MN CO ∥，则EMN ACO ∽∴12BE AB =，又4AB =，∴∵53222BN =-=<，∴不成立；⑥如图6，直线ME ∥BC ，同理可得12AE AB =，∴22AE =，222NE =-，tan tan MEN CBO ∠∠=，∴155222a =-，解得a =综上所述，910a =或225+或212+．【点睛】本题考查了二次函数的综合问题，解直角三角形，相似三角形的性质与判定，熟练掌握以上知识，并分类讨论是解题的关键．20．（2023·浙江杭州·校考二模）在平面直角坐标系中，当2x =-和4x =时，二次函数是常数，a ≠0）的函数值相等．(1)若该函数的最大值为1，求函数的表达式，并写出函数图象的顶点坐标．若该函数的图象与x 轴有且只有一个交点，求a ，b 的值．(3)记（2）中的抛物线为y 1移2个单位得到抛物线2y ，当2x m ≤≤－时，抛物线2y 的最大值与最小值之差为8，求限时检测2：最新各地中考真题（60分钟）1．（2023年江苏省南通市中考数学真题）若实数x ，y ，m 满足6x y m ++=，34x y m -+=，则代数式21xy -+5．（2023年甘肃省兰州市中考数学真题）已知二次函数()2323y x =---，下列说法正确的是（）A ．对称轴为2x =-B ．顶点坐标为()2,3C ．函数的最大值是－3D ．函数的最小值是－3【答案】C【分析】根据二次函数的图象及性质进行判断即可．【详解】二次函数()2323y x =---的对称轴为2x =，顶点坐标为()2,3-∵30-<∴二次函数图象开口向下，函数有最大值，为=3y -∴A 、B 、D 选项错误，C 选项正确故选：C【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数图象和性质是解题的关键．6．（2022·浙江温州·中考真题）已知点(,2),(,2),(,7)A a B b C c 都在抛物线2(1)2y x =--上，点A 在点B 左侧，下列选项正确的是（）A ．若0c <，则a c b <<B ．若0c <，则a b c<<C ．若0c >，则a c b<<D ．若0c >，则a b c<<【答案】D【分析】画出二次函数的图象，利用数形结合的思想即可求解．【详解】解：当0c >时，画出图象如图所示，根据二次函数的对称性和增减性可得a b c <<，故选项C 错误，选项D 正确；当0c <时，画出图象如图所示，根据二次函数的对称性和增减性可得c a b <＜，故选项A 、B 都错误；故选：D【点睛】本题考查二次函数的图象和性质，借助图象，利用数形结合的思想解题的解决问题的关键．7．（2023年湖北省中考数学真题）拋物线2(0)y ax bx c a =++<与x 轴相交于点()()3010A B -，，，．下列结论：①0abc <；②240b ac ->；③320b c +=；④若点()()122P m y Q m y -，，，在抛物线上，且12y y <，则9．（2022·湖南岳阳·中考真题）已知二次函数2243y mx m x =--（m 为常数，0m ≠），点(),p p P x y 是该函数图象上一点，当04p x ≤≤时，3p y ≤-，则m 的取值范围是（）A ．m 1≥或0m <B ．m 1≥C ．1m ≤-或0m >D ．1m ≤-【答案】A【分析】先求出抛物线的对称轴及抛物线与y 轴的交点坐标，再分两种情况：0m >或0m <，根据二次函数的性质求得m 的不同取值范围便可．【详解】解：∵二次函数2243y mx m x =--，∴对称轴为2x m =，抛物线与y 轴的交点为()0,3-，∵点(),p p P x y 是该函数图象上一点，当04p x ≤≤时，3p y ≤-，∴①当0m >时，对称轴20x m =>，此时，当4x =时，3y ≤-，即2244433m m ⋅-⋅-≤-，解得m 1≥；②当0m <时，对称轴20x m =<，当04x ≤≤时，y 随x 增大而减小，则当04p x ≤≤时，3p y ≤-恒成立；综上，m 的取值范围是：m 1≥或0m <．故选：A ．【点睛】本题考查了二次函数的性质，关键是分情况讨论．①124x x ⋅=-；②2124y y k +=+④若点(0,1)N -，则AN BN ⊥A ．1B ．2【答案】C【点睛】本题考查二次函数的知识，解题的关键是掌握二次函数的图象和性质，直角三角形的性质，两点间的距离公式．13．（2023年湖北省十堰市中考数学真题）已知点物线241y x x =+-上，若12y y =联立231941y x y x x =+⎧⎨=+-⎩解得：54x y =-⎧⎨=⎩或431x y =⎧⎨=⎩∴()5,4P -，由()224125y x x x =+-=+-，则()2,5Q --，对称轴为直线2x =-，设123m y y y ===，则点,,A B C 在y m =上，∵123y y y ==且123x x x <<，∴A 点在P 点的左侧，即15x <-，232x x <-<，当5m =-时，23x x =对于319y x =+，当5y =-，8x =-，此时18x =-，∴18x >-，∴185x -<<-∵对称轴为直线2x =-，则()23224x x +=⨯-=-，∴123x x x ++的取值范围是123129x x x -<++<-，故选：A ．【点睛】本题考查了二次函数的性质，一次函数的性质，数形结合熟练掌握是解题的关键．14.（2023年广东广州中考数学真题）已知点()11,A x y ，()22,B x y 在抛物线23y x =-上，且120x x <<，则1y 2y ．（填“<”或“>”或“=”）【答案】<【分析】先求出抛物线的对称轴，然后根据二次函数的性质解决问题．【详解】解：23y x =-的对称轴为y 轴，∵10a =>，∴开口向上，当0x >时，y 随x 的增大而增大，∵120x x <<，∴12y y <．故答案为：<．【点睛】本题主要考查了二次函数的增减性，解题的关键是根据抛物表达式得出函数的开口方向和对称轴，从而分析函数的增减性．【答案】4【分析】与抛物线2y ax bx c =++与x 轴相交于点由CD x ∥轴，可得C ，D 关于直线x 【详解】解：∵抛物线2y ax bx =++∴抛物线的对称轴为直线132x +==【答案】①③【分析】依据题意，根据所给图象可以得出从而由根与系数的关系，逐个判断可以得解．【详解】解：由图象可得，a >由题意，令2ax bx c kx ++=，∴又二次函数2y ax bx c =++的图象与正比例函数点B 的横坐标为2，2(ax b k ∴+-18．（2020·黑龙江大庆市·中考真题）已知关于x 的一元二次方程220x x a --=，有下列结论：①当1a >-时，方程有两个不相等的实根；②当0a >时，方程不可能有两个异号的实根；③当1a >-时，方程的两个实根不可能都小于1；④当3a >时，方程的两个实根一个大于3，另一个小于3．以上4个结论中，正确的个数为_________．【答案】①③④【分析】由根的判别式，根与系数的关系进行判断，即可得到答案．【详解】解：根据题意，∵一元二次方程220x x a --=，∴2(2)41()44a a ∆=--⨯⨯-=+；∴当440a +>，即1a >-时，方程有两个不相等的实根；故①正确；当12440•0a x x a +>⎧⎨=->⎩，解得：10a -<<，方程有两个同号的实数根，则当0a >时，方程可能有两个异号的实根；故②错误；抛物线的对称轴为：212x -=-=，则当1a >-时，方程的两个实根不可能都小于1；故③正确；由3a >，则223a x x =->，解得：3x >或1x <-；故④正确；∴正确的结论有①③④；故答案为：①③④．【点睛】本题考查了二次函数的性质，一元二次方程根的判别式，根与系数的关系，解题的关键是掌握所学的知识进行解题．由图可知：当<<0y 5时，2<<1x --或34x <<；（2）∵2223324b b y x bx x ⎛⎫=+-=+-- ⎪⎝⎭，∴当2b x =-时，y 有最小值为234b --；∵对于一切实数x ，若函数值y t >总成立，∴234bt <--；（3）∵2223324b b y x bx x ⎛⎫=+-=+-- ⎪⎝⎭，∴抛物线的开口向上，对称轴为2b x =-，又当m y n <<时（其中m n 、为实数，m n <），自变量x 的取值范围是12x <<，20．（2022·贵州遵义·中考真题）新定义：我们把抛物线2y ax bx c =++（其中0ab ≠）与抛物线2y bx ax c =++称为“关联抛物线”．例如：抛物线2231y x x =++的“关联抛物线”为：2321y x x =++．已知抛物线()21:4430C y ax ax a a =++-≠的“关联抛物线”为2C ．(1)写出2C 的解析式（用含a 的式子表示）及顶点坐标；(2)若0a >，过x 轴上一点P ，作x 轴的垂线分别交抛物线1C ，2C 于点M ，N ．①当6MN a =时，求点P 的坐标；②当42a x a -≤≤-时，2C 的最大值与最小值的差为2a ，求a 的值．【答案】(1)()24430y ax ax a a =++-≠，顶点为()23--，(2)①()1,0P -或()2,0；②2a =或a =【分析】（1）根据定义将一次项系数与二次项系数互换即可求得解析式，化为顶点式即可求得顶点坐标；（2）①设(),0P p ，则()2,443M p ap ap a ++-，()2,443N p ap ap a ++-，根据题意建立方程解方程即可求解；②根据题意，分三种情形讨论，根据点距离对称轴的远近确定最值，然后建立方程，解方程求解即可．(1)解： 抛物线()21:4430C y ax ax a a =++-≠的“关联抛物线”为2C ，根据题意可得，2C 的解析式()24430y ax ax a a =++-≠()2244323y ax ax a a x =++-=+- 顶点为()23--，(2)解：①设(),0P p ，则()2,443M p ap ap a ++-，()2,443N p ap ap a ++-()22443443MN ap ap a ap ap a ∴=++--++-233ap ap=- 6MN a =2336ap ap a ∴-=0a ≠ ∴22p p -=±当22p p -=时，解得11p =-，22p =当22p p -=-时，方程无解()1,0P ∴-或()2,0② 2C 的解析式()24430y ax ax a a =++-≠()2244323y ax ax a a x =++-=+-顶点为()23--，，对称轴为2x =-0a > ，22a ∴->-当()()()2422a a --->---时，即1a <时，函数的最大值为()2423a a -+-，最小值为3- 2C 的最大值与最小值的差为2a ()222a a a∴-=0a ≠ 2a ∴-=1222a a ==（1a <，舍去）2a ∴=当()()()2422a a ---<---时，且42a -<-即12a <<时，函数的最大值为()2223a a -+-，最小值为3- 2C 的最大值与最小值的差为2a 32a a∴=0a ≠a ∴=解得12a a ==12a <<，舍去）a ∴=当42a ->-时，即2a >时，抛物线开向上，对称轴右侧y 随x 的增大而增大，函数的最大值为()2223a a -+-33a =-，最小值为()()2242323a a a a -+-=-- 2C 的最大值与最小值的差为2a ∴()233232a a a a ---+=即()23220a a a a ---=0a ≠ 即()22220a a ---=解得32a =（2a >舍去）综上所述，2a =或a =【点睛】本题考查了二次函数的性质，求顶点式，二次函数的最值问题，分类讨论是解题的关键．。
中考数学考点专项复习——二次函数
中考数学考点专项复习——二次函数一、选择题：1．下列y 关于x 的函数中，属于二次函数的是（ ） A ．y ＝x ﹣1B ．y ＝1xC ．y ＝（x ﹣1）2﹣x 2D ．y ＝﹣2x 2＋12. 把抛物线y=2x 2向左平移2个单位，再向上平移1个单位，所得到的抛物线的解析式为（ ）A ．y=2（x+2）2+1B ．y=2（x+2）2﹣1C ．y=2（x ﹣2）2﹣1D ．y=2（x ﹣2）2+13．已知二次函数与轴两个交点坐标分别为，，若，则的值是（ ）A ．2B ．-1C ．1D ．-1或24．若函数2221()mm y m m x --=+是二次函数，则m 的值是（ ）A ．2B ．-1或3C ．-1D ．35．下列函数中，当x ＞0时，y 随x 的增大而减小的是（ ）A ．y=x+1B ．y=x 2﹣1C ．D ．y=﹣（x ﹣1）2+16．用配方法将2611y x x =-+化成()2y a x h k =-+的形式为（ ）.A ．()232y x =++B ．()232y x =--C ．()262y x =--D ．()232y x =-+ 7.一枚炮弹射出x 秒后的高度为y 米，且y 与x 之间的关系为y=ax 2+bx+c （a ≠0），若此炮弹在第3.2秒与第5.8秒时的高度相等，则在下列时间中炮弹所在高度最高的是（ ）A ．第3.3sB ．第4.3sC ．第5.2sD ．第4.6s8．已知：抛物线21y x x =--与x 轴的一个交点为（m ，0），则代数式22019m m -+的值是（ ）．A ．2017B ．2018C ．2019D ．20209．已知二次函数y=（x ﹣h ）2+1（h 为常数），在自变量x 的值满足1≤x ≤3的情况下，与其对应的函数y 的最小值为5，则h 的值是（ ） A ．﹣1B ．﹣1或5C ．5D ．﹣510．把二次函数2134y x x --=+用配方法化成()2y a x h k =-+的形式时，应为（ ） A ．()21224y x =--+ B ．()21244y x =--+ C ．()21244y x =-++D ．211322y x ⎛⎫=--+ ⎪⎝⎭11．在半径为4cm 的圆中，挖去了一个半径为x cm 的圆面，剩下一个圆环的面积为y cm 2，则y 与x 的函数关系式为（ ）A ．216y x ππ=-+B ．24y x π=-C ．2(2)y x π=-D ．2(4)y x =-+12．加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率y 与加工时间x （单位：min ）满足函数表达式y ＝﹣0.2x 2+1.5x ﹣2，则最佳加工时间为（ ） A ．3minB ．3.75minC ．5minD ．7.5min13．如图，Rt △OAB 的顶点A (－2，4)在抛物线y ＝ax 2上，将Rt △OAB 绕点O 顺时针旋转90°，得到△OCD ，边CD 与该抛物线交于点P ，则点P 的坐标为( )A ．(2，2)B ．(2，2)C ．(2，2)D ．(2，2) 14．如图，已知二次函数212433y x x =-的图象与正比例函数223y x =的图象交于点A （3，2），与x 轴交于点B （2，0），若120y y <<，则x 的取值范围是（ ）A ．0＜x ＜2B ．0＜x ＜3C ．2＜x ＜3D ．x ＜0或x ＞315．如图，在抛物线上有，两点，其横坐标分别为1，2；在轴上有一动点，当最小时，则点的坐标是（ ）A ．（0.0）B ．（0，）C ．（0，2）D ．（0，）二、填空题16．二次函数22my mx -=有最低点，则m=__________17．已知抛物线y ＝x 2，把该抛物线向上或向下平移，如果平移后的抛物线经过点A （2，2），那么平移后的抛物线的表达式是 ．18.已知抛物线c x ax y ++=2与x 轴交点的横坐标为1-，则c a +=_________.19．当﹣1≤x ≤3时，二次函数y ＝x 2﹣4x +5有最大值m ，则m ＝_____．20．已知点A （4，y 1），B （，y 2），C （﹣2，y 3）都在二次函数y ＝（x ﹣2）2+k 的图象上，则y 1、y 2、y 3的大小关系是 ．（请用“＞”连接）21.将二次函数322+-=x x y 配方成k h x y +-=2)(的形式，则y =_________________.22．已知反比例函数y ＝的图象经过点P （2，2），函数y ＝ax +b 的图象与直线y ＝﹣x 平行，并且经过反比例函数图象上一点Q （1，m ）．则函数y ＝ax 2+bx +有最 值，这个值是 ．23．一个小球被抛出后，如果距离地面高度（米）和运行时间（秒）的函数解析式为，那么小球达到最高点时距离地面高度是______米．24．如图是抛物线型拱桥，当拱顶离水面2m 时，水面宽4m ，水面下降2m ，水面宽度增加______m.25．如图所示四个二次函数的图象中，分别对应的是①y ＝ax 2；②y ＝bx 2；③y ＝cx 2；④y ＝dx 2．则a 、b 、c 、d 的大小关系为_____．26．人民币一年定期的年利率为x ，一年到期后，银行将本金和利息自动按一年定期储蓄转存．如果存款额是a 元，则两年后的本息和y （元）的表达式为________（不考虑利息税）． 27．如图，抛物线2y ax c =+与直线y mx n =+交于A(-1,P)，B(3,q)两点，则不等式2ax mx c n ++>的解集是_____．28．如图，己知抛物线y ＝ax 2+bx +c 与直线y ＝kx +m 交于A （﹣3，﹣1），B （0，3）两点．则关于x 的不等式ax 2+bx +c ＞kx +m 的解集是．29．点A （﹣1，﹣2）在抛物线y ＝﹣12（x ﹣1）2上，点A 、B 关于该抛物线的对称轴对称，则B 点坐标为_____．30. 如图,在平面直角坐标系中,菱形OABC 的顶点A 在x 轴正半轴上,顶点C 的坐标为(4,3),D 是抛物线y=-x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为________.三、解答题31．已知抛物线2()y a x m =+的对称轴是直线x =2，该抛物线与y 轴的交点坐标是(0，8)，求这个二次函数的解析式．32．已知二次函数（k 为常数）．（1）当该函数的图像与y 轴的交点在x 轴上方时，求k 的取值范围． （2）求证：无论k 为何值，该函数的图像与x 轴总有公共点；33.如图，一个二次函数的图象经过点A 、C 、B 三点，点A 的坐标为（﹣1，0），点B 的坐标为（3，0），点C 在y 轴的正半轴上，且AB=OC （1）求点C 的坐标；（2）求这个二次函数的解析式，并求出该函数的最大值．34．已知二次函数y＝﹣3x2﹣6x+5．（1）求这个函数图象的顶点坐标、对称轴以及函数的最大值；（2）若另一条抛物线y＝x2﹣x﹣k与上述抛物线只有一个公共点，求k的值．35.如图，已知二次函数y＝ax2+bx+c的图象的顶点坐标为（4，﹣2），且经过点B（0，6）．（1）求该二次函数的解析式；（2）求出二次函数图象与x轴的交点A和C的坐标．36．如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．（1）求二次函数与一次函数的解析式；（2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．37．在平面直角坐标系中，设二次函数()()1 1x a x y a =+--，其中0a ≠.（1）若函数1y 的图象经过点()1 2-，，求函数1y 的表达式； （2）若一次函数2y ax b =+的图象与1y 的图象经过x 轴上同一点，探究实数a b ，满足的关系式；（3）已知点()0 P x m ，和()1 Q n ，在函数1y 的图象上，若m n ＜，求0x 的取值范围.38.已知二次函数y ＝x 2﹣2x ．（1）请在表内的空格中填入适当的数；（2）请在所给的平面直角坐标系中画出y ＝x 2﹣2x 的图象；（3）当x 在什么范围内时，y 随x 的增大而减小；（4）观察y ＝x 2﹣2x 的图象，当x 在什么范围内时，y ＞0．39．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．40．如图，在平面直角坐标系中，直线与轴，轴相交于，两点．点的坐标是，连接，．（1）求过，，三点的抛物线的解析式，并判断的形状；（2）抛物线上是否存在着一点，使的面积为25？若存在，求出的坐标，若不存在，请说明理由；（3）在抛物线上，是否存在着一点，使为以为斜边的直角三角形？若存在，请直接写出的坐标；若不存在，请说明理由．41．某扶贫工作队为一贫困户提供了5万元的无息脱贫贷款．该贫困户利用这笔贷款，注册了一家网店，销售一种成本价为20元/件的农产品．已知销售价高于成本价，且不高于32元/件，网店每月需支付电费等其它费用1千元市场调查发现，该农产品每月销售量为y(百件)与销售价x(元/件)之间的函数关系如图所示（1）求该网店每月利润W(百元)与销售价x(元/件)之间的函数关系式，并注明自变量x的取值范围：（2）该贫困户从网店开业起，最快在第几个月可用销售利润还清42. 如图所示，已知抛物线经过点A（﹣2，0）、B（4，0）、C（0，﹣8），抛物线y=ax2+bx+c （a≠0）与直线y=x﹣4交于B、D两点．（1）求抛物线的解析式并直接写出D点的坐标；（2）点P为抛物线上的一个动点，且在直线BD下方，试求出△BDP面积的最大值及此时点P的坐标；（3）点Q是线段BD上异于B、D的动点，过点Q作QF⊥x轴于点F，交抛物线于点G，当△QDG为直角三角形时，求点Q的坐标．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
二次函数专项练习
一、二次函数图像及其性质有关
1、经过原点的抛物线是（ ）
A y=2x 2
+x B 2
21)y x =+（
C y=2x 2
-1 D y=2x 2
+1 2、已知反比例函数x
k y =的图象如图所示，则二次函数2
22k x kx y +-=的图象大致为（ ）
4．在反比例函数y=x k
中，当x ＞0时，y 随x 的增大而增大，则二次函数y=kx 2＋2kx 的图象大致是（ ）
5．二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（ ）
6二次函数y=ax 2
＋bx ＋c 与一次函数y=ax ＋c 在同一坐标系中的图象大致是图中的（ ）
7在同一坐标系中，函数y=ax 2
＋bx 与y=x
b
的图象大致是图中的（ ）
y
O x y
O x y O x
y O
x
y O
x
A B C D
8图中各图是在同一直角坐标系内，二次函数y=ax 2
＋（a ＋c ）x ＋c 与一次函数y=ax ＋c 的大致图象，有且只有一个是正确的，正确的是（ ）
9．如图，若a ＜0，b ＞0，c ＜0，则抛物线y=ax 2
＋bx ＋c 的大致图象为（ ）
10．函数y=ax 2
＋bx ＋c 和y=ax ＋b 在同一坐标系中，如图所示，则正确的是（ ）
二、与移动有关
1、抛物线y=
2
1x 2
向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是 A 、y=
2
1
(x －3)2－2 B 、y=
21(x －3)2+2 C 、y=21(x+3)2－2 D 、y=2
1
(x+3)2+2 2．将抛物线y=2x 2
向左平移1个单位，再向上平移3个单位得到的抛物线，其表达式为（ ） A ．y=2（x ＋1）2＋3 B ．y=2（x －1）2
－3 C ．y=2（x ＋1）2－3 D ．y=2（x －1）2
＋3
3．将抛物线y=3x 2
－2向左平移2个单位，再向下平移3个单位，则所得抛物线为（ ）
A ．y=3（x ＋2）2＋1
B ．y=3（x －2）2
－1 C ．y=3（x ＋2）2－5
D ．y=3（x －2）2
－2
4．抛物线y=2x 2
向左平移1个单位，再向下平移3个单位，得到的抛物线表达式 为
．
第1题
x
y
O
三、图像中与a ，b ，c 有关的题目
1二次函数y=ax 2
＋bx 2
＋c 的图象如图所示，则a 0，b 0，c 0（填“＞”或“＜”＝．）
2．一位篮球运动员跳起投篮，球沿抛物线y=ax 2＋bx ＋c 运行，图象如图所示，有下列结论：①a ＜－
807②－80
7
＜a ＜0③a ＋b ＋c ＜0④0＜b ＜－4a ，其中正确的是（ ）
A ．①②
B ．②④
C ．①④
D ．③④
3．已知二次函数y=ax 2＋bx ＋c 的图象与x 轴交于（x 1，0）、（x 2，0）两点，且0＜x 1＜1，1＜x 2＜2，与y 轴交于点（0，－2），下列结论：①2a ＋b ＞1；②3a ＋b ＞0；③a ＋b ＜2；④a ＜－1，其中正确结论的个数为（ ） A ．1 B ．2 C ．3 D ．4
4．关于二次函数y=ax 2
＋bx ＋c 的图象有下列命题：
①当c=0时，函数的图象经过原点；②当c ＞0且函数图象开口向下时，方程ax 2
＋bx ＋c=0
必有两个不等实根；③当a ＜0，函数的图象最高点的纵坐标是a
b a
c 442
；④当b=0时，函
数的图象关于y 轴对称．其中正确命题的个数有（ ）
A ．1个
B ．2个
C ．3个
D ．4个
5．二次函数y= ax 2
＋bx ＋c （a ≠0）的图象如图所示，下列结论：
①c ＜0；②b ＞0；③4a ＋2b ＋c ＞0；④（a ＋c ）2＜b 2
．其中正确的有（ ）
A ．1个
B ．2个
C ．3个
D ．4个
6．如图，坐标系中抛物线是函数y=ax 2
＋bx ＋c 的图象，则下列式子能成立的是（ ）
A ．abc ＞0
B ．a ＋b ＋c ＜0
C ．b ＜a ＋c
D ．2c ＜3b 7．二次函数y=－x 2
＋bx ＋c 的图象的最高点是（－1，－3），则b 、c 的值是（ ）
A ．b=2，c=4
B ．b=2，c=－4
C ．b=－2，c=4
D ．b=－2，c=－4 8．二次函数y=x 2
＋mx ＋n ，若m ＋n=0，则它的图象必经过点（ ）
A ．（－1，1）
B ．（1，－1）
C ．（－1，－1）
D ．（1，1）
9．已知抛物线y=ax 2
＋x ＋c 与x 轴交点的横坐标为－1，则a ＋c ＝
四、与X 轴的交点有关
1.抛物线y = a(x+1)2 -2与x 轴交于点（-3，0），则该抛物线与x 轴另一交点的坐标是（ ）
A 、（
2
1
，0） B 、（1，0） C 、（2，0） D 、（3，0） 2、若函数y =3x 2
与直线y =kx +3的交点为（2，b ），则k ＝＿＿，b ＝＿＿.
3.若抛物线c bx ax y ++=2
过两点A (2,6) ,B (-6,6) , 则抛物线的对称轴为 4．抛物线y=3x 2＋bx ＋c 的顶点坐标为（
3
2
，0），则b ＝ ，c ＝ 5．以P （－2，－6）为顶点的二次函数是（ ）
A ．y=5（x ＋2）2＋6
B ．y=5（x －2）2＋6
C ．y=5（x ＋2）2－6
D ．y=5（x －2）2－6
五、求函数表达式
1、已知二次函数y =ax 2
+bx +c 的图象与x 轴交于A (1，0)，B (3，0)两点，与y 轴交于点 C (0，3)，则二次函数的解析式是 ．
20、试写出一个开口方向向上，对称轴为直线2x =，且与y 轴的交点坐标为（0，3）的抛物线的表达式；
2、已知抛物线与x 轴交于点M （-1，0）、N （2，0），且经过点（1，2），求这个函数的表达式；
3、已知抛物线的顶点为（1，-1），且过点（2，1），求这个函数的表达式；
4、已知一个二次函数的图象经过点（1，-1），（0，1），（-1，13），求这个二次函数的解析式；
5．已知二次函数y=x 2
＋bx ＋c 的图象过（1，0），（2，5）两点，求这个二次函数的表达式。
6．已知二次函数y=ax 2＋bx ＋c 的图象开口向上，且经过（0，－1）和（3，5）两点，图象的顶点到x 轴的距离等于3，求这个函数的表达式
5.在体育测试时,初三的一名高个子男生推铅球,已知铅球所经过的路线是某二次函数图象的一部分(如图),若这个男生出手处A 点的坐标为(0,2),铅球路线的最高处B 点的坐标为B(6,5).
x
(1)求这个二次函数的表达式;
(2)该男生把铅球推出去多远?(精确到0.01米).
6.如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0) , 且x1+x2=4,
1 21 3
x
x
.(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.。