原子物理学 第四章
合集下载
原子物理学第4章.

~ 第二辅线系: sn
~ 第一辅线系: dn
R R ,n =3,4,5… 2 2 (2 D p ) (n D s )
R R ,n =3,4,5… 2 2 (2 D p ) (n D d )
柏格曼系:
~ fn
R R , n =4,5,6… (3 D d ) 2 (n D f ) 2 Na原子的?
s
=0 6 5 6 5 4 4
p =1 6 5 4
d =2 6 5 4
柏 格 曼 系
f
=3 H 6 5 4
3 3
3
3
图3.3 Na原子能级图
四、原子实的极化和轨道的贯穿
1、原子实模型
碱金属原子= 原子实(有效核电荷数Z*=1)+1个价电子 原子的化学性质及光谱决定于价电子。
Rhc Rhc Enl hcTnl *2 2 n (n D )
能级特点:
1、能量由(n, l)两个量子数决定,主量子数n 相同、角 量子数 l 不同的能级的高低差别很明显; 2、特别是n 较小时,如 n =2, 3,不同l 的能级差别大:
对于相同的n不同l 的能级, l 越小则能级位置越低, 与 氢原子相应能级的差别越大;
3、n相同时,能级的间隔随 l 的增大而减小,
l相同时,能级的间隔随 n 的增大而减小;
4、n很大时,能级与氢的很接近,少数光谱线的波数几 乎与氢的相同。
2、锂原子的能级跃迁
主线系:从l=1的p态→n=2, l=0的2s态, n=2,3,4… 锐线(二辅)系:从l=0的s态→n=2, l=1的2p态, n=3,4,5… 漫线 (一辅)系:从l=2的d态→n=2, l=1的2p态, n=3,4,5… 基线(柏格曼)系:从l=3的f态→n=3, l=2的3d态, n=4,5,6…
原子物理学课件--第四章

l = l1 + l2 , l1 + l2 −1,⋯,| l1 −l2 |
l1 = 0, l2 = 1;
l = 1;
s1 = s2 = 1/ 2
1 → j = 2,1, 0; → P0 , P , P2 1 s= 1 0 → j =1 → P 1
3 3 3
4.2.5.由电子组态到原子态 4.2.5.由电子组态到原子态(2) 由电子组态到原子
4.2.1.电子组态(1) 4.2.1.电子组态(1) 电子组态
• 电子组态:原子中各个电子所处的状态 电子组态: • 电子状态用nl 两个量子数描述 电子状态用 •例
–氢原子基态的电子组态: 1s 氢原子基态的电子组态: 1s 氢原子基态的电子组态 –氦原子基态的电子组态: 1s1s=(1s)2 氦原子基态的电子组态 氦原子基态的电子组态: 1s1s=(1s)
两种耦合得到的J值相同 两种耦合得到的 值相同 耦合得到的 两种耦合得到的原子态数相同 两种耦合得到的原子态数相同 耦合
4.2.5.由电子组态到原子态 4.2.5.由电子组态到原子态(3) 由电子组态到原子
• 例三 L-S 耦合 组态 例三: 耦合pd
l1 = 1, l2 = 2;
s1 = s2 = 1/ 2
3 3 3
3 l = 2; 1
1 s= ; 0
4.2.5.由电子组态到原子态(4) 4.2.5.由电子组态到原子态 由电子组态到原子
• 例四 L-S 耦合 组态 例四: 耦合ss 1 3 S0 , S1 • 例五 L-S 耦合 组态 例五: 耦合pp 1 S0 , 3S1 ; 1P , 3 P2,1,0 ; 1D2 , 3 D3,2,1 1 • 为什么电子组态一定,有两套能级? 为什么电子组态一定,有两套能级?
原子物理学,褚圣麟第四章
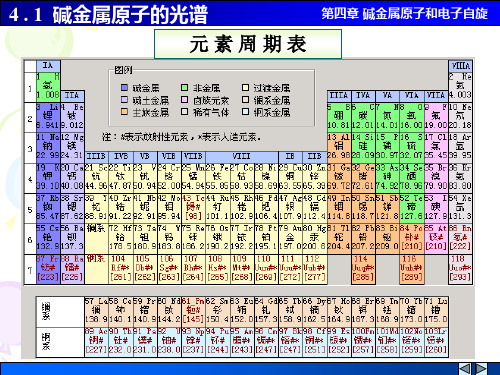
2 2 2 2
, n 2 ,3 ,
(锐线系) s
第一辅线系
~ n
, n 3,4 ,
(漫线系)
柏格曼线系
d n
~
, n 3,4 ,
(基线系)
f
~ n
, n 4 ,5 ,
4.1 碱金属原子的光谱
第四章 碱金属原子和电子自旋
钠原子光谱线系
主线系
p n
~ n
第四章 碱金属原子和电子自旋
碱金属原子三个光谱线系的精细结构示意图
主线系 np 2s 第二辅线系 ns 2p
线 系 限
第 四 条
第 三 条
第 二 条
第 一 条
第一辅线系 nd 2p
1)竖线表示光谱精细结构;2)高低代表谱线 强度;3)间隔表示谱线成分波数。
4 . 3 碱金属原子光谱的精细结构 第二辅线系(各S态
主线系
p n ~
第四章 碱金属原子和电子自旋
R (3 S )
2
R (n p )
2
, n 3,4 ,
共振线为主线系的第一条线 (原子从 3P
p ~ n
3S 跃迁)
1 589 . 3 10
6 1
9
589 . 3 nm
1 . 697 10 m m
6 1
第四章 碱金属原子和电子自旋
价电子:原子实外的那个价电子称作价电子。它 决定元素的化学性质,在较大的轨道上运动。
问:碱金属原子的能级为什么比氢原子的能级低?
2. 与氢原子的区别 原子实的极化
e
, n 2 ,3 ,
(锐线系) s
第一辅线系
~ n
, n 3,4 ,
(漫线系)
柏格曼线系
d n
~
, n 3,4 ,
(基线系)
f
~ n
, n 4 ,5 ,
4.1 碱金属原子的光谱
第四章 碱金属原子和电子自旋
钠原子光谱线系
主线系
p n
~ n
第四章 碱金属原子和电子自旋
碱金属原子三个光谱线系的精细结构示意图
主线系 np 2s 第二辅线系 ns 2p
线 系 限
第 四 条
第 三 条
第 二 条
第 一 条
第一辅线系 nd 2p
1)竖线表示光谱精细结构;2)高低代表谱线 强度;3)间隔表示谱线成分波数。
4 . 3 碱金属原子光谱的精细结构 第二辅线系(各S态
主线系
p n ~
第四章 碱金属原子和电子自旋
R (3 S )
2
R (n p )
2
, n 3,4 ,
共振线为主线系的第一条线 (原子从 3P
p ~ n
3S 跃迁)
1 589 . 3 10
6 1
9
589 . 3 nm
1 . 697 10 m m
6 1
第四章 碱金属原子和电子自旋
价电子:原子实外的那个价电子称作价电子。它 决定元素的化学性质,在较大的轨道上运动。
问:碱金属原子的能级为什么比氢原子的能级低?
2. 与氢原子的区别 原子实的极化
e
原子物理第四章

d 的标量形式为 dt
d sin ( sin ) dt
另一方面,设 在dt时间内旋进角度 d 则把式
d sin d
代入上式得
d dt
2. 轨道磁矩的量子表达式 根据量子力学的计算,角动量 L 是量子化的, 这包括它的大小和空间取向都是量子化的。
dL B dt
将 L 代入得
d B dt
令
B
有
d dt
这就是拉莫尔进动的角速度公式,它表明在均匀外磁 场 B 中,高速旋转的磁矩并不向 方向靠拢,而是 B 以一定的角速度 绕 B 作进动, 方向与 B 一致。
当n ,l ,m 都给定后,就给出了一个确定的状态;
所以我们经常说: (n ,l ,ml )描述了一个确定的态。 对于氢原子,能量只与n 有关,n 给定后,有n 个l , 每一个l 有2l+1 个ml ,所以氢原子的一个能级 En 对应 于 n2 个不同的状态,我们称这种现象为简并,相应的 状态数称为能级 En 的简并度。
e e L cos( L, J ) S cos( S , J ) 2m m 2 2 2 余弦定理: L J S 2JS cos(S , J ) 2 2 2 S J L 2JL cos(L, J )
j
e 1 e 1 ( J 2 L2 S 2 ) ( J 2 S 2 L2 ) 2m 2 J m 2J e J 2 L2 S 2 J (1 ) 2 2m 2J
均匀磁场中: 非均匀磁场中:
F 0 M B
《原子物理学》(褚圣麟)第四章 碱金属原子和电子自旋

波数 (cm-1 )
40000
30000
20000
10000
2500
3000
4000 5000 6000 7000 10000 20000
图 锂的光谱线系
波长(埃)
每个线系的每一条光谱线的波数都可以表式为两个光 谱项之差:
~n
~
R n2
• 等式右边的第一项是固定项,它决定线系限及末态。第二
项是动项,它决定初态。
多个角动量相加,由二二相加得到。
四、碱金属原子态符号n2ຫໍສະໝຸດ 2s+1L
j
j=+1/2 j=-1/2
0,1, 2, 3, 4, 5, S,P, D, F, G
n j 价电子的状态符号 原子态符号
1
碱
10
2
1s
金
1
属
02
2s
原2
1
子
12
2p
态 的 符
3
2
2p
号
01
2
3s
2S1
2
2S1
2
2 P1
2
2 P3
厘米-1
s =0
5 4
3
p =1
5 4
3
d =2
5 4
3
f =3
5 4柏
格 曼 系
H 567 4 3
2 2
2
四组谱线 三个终端 两个量子数 一个跃迁条件
图 3.2 锂原子能级图
特点:
(1)能量由(n, )两个量子数决定,主量 子数相同,角量子数不同的能级不相同。
(2)n相同时能级的间隔随角量子数的增大 而减小, 相同时,能级的间隔随主量子数随 n的增大而减小。
原子物理学4
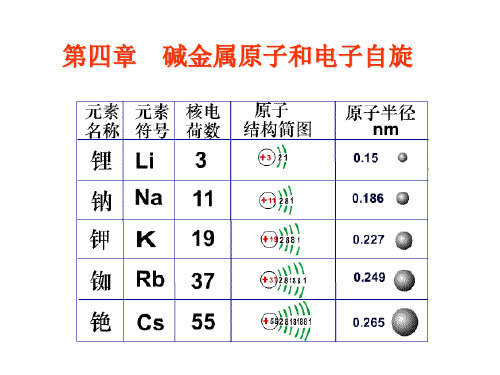
Ps s ( s 1) 3 B 3 2
s
电子的自旋轨道耦合
电子围着原子核做圆周运动, 原子的总磁矩和总角动量都来 源于电子的轨道运动和电子的 自旋。 j l s 总磁矩:
总角动量: P j Pl Ps
价电子
e
Ze
由量子力学可知,Pj也是量子化的, 相应的 总角动量量子数用 j 表示,且有
§4.4 电子自旋同轨道运动的相互作用
电子的自旋
Uhlenbeck and Goudsmit 在1925年提出: 实验依据: (1)史特恩-盖拉赫实验出现偶数分裂的事实 (2)碱金属原子光谱的精细结构
P 电子具有某种方式的自旋; s s ( s 1), s 1 2
相对于外磁场方向,自旋角动量Ps在空间只能取朝上和 P 1 朝下两种取向: s B Psz ms , ms z 自旋磁矩和自旋角动量的关系是:
碱金属原子态的符号:
电子态符号:l 0 ,1, 2 , 3 ,
s, p , d , f ,
比如: n=3时,3s, 3p, 3d
原子态符号:由价电子的诸量子数来描述
L 0 ,1, 2 , 3 , S , P , D , F ,
s 1 2 L l: j ls: ,2 s 1 2 :
2
j
*
j ( j 1) l ( l 1) s ( s 1)
c
j
l
*2
l
*
2
s
*
讨论: (1) n和l相同,s不变,只有j不同,不同的j值具有不同 的能量
l 0 时, j l s l 1 / 2 l 0 时, j l s l 1 / 2,或
s
电子的自旋轨道耦合
电子围着原子核做圆周运动, 原子的总磁矩和总角动量都来 源于电子的轨道运动和电子的 自旋。 j l s 总磁矩:
总角动量: P j Pl Ps
价电子
e
Ze
由量子力学可知,Pj也是量子化的, 相应的 总角动量量子数用 j 表示,且有
§4.4 电子自旋同轨道运动的相互作用
电子的自旋
Uhlenbeck and Goudsmit 在1925年提出: 实验依据: (1)史特恩-盖拉赫实验出现偶数分裂的事实 (2)碱金属原子光谱的精细结构
P 电子具有某种方式的自旋; s s ( s 1), s 1 2
相对于外磁场方向,自旋角动量Ps在空间只能取朝上和 P 1 朝下两种取向: s B Psz ms , ms z 自旋磁矩和自旋角动量的关系是:
碱金属原子态的符号:
电子态符号:l 0 ,1, 2 , 3 ,
s, p , d , f ,
比如: n=3时,3s, 3p, 3d
原子态符号:由价电子的诸量子数来描述
L 0 ,1, 2 , 3 , S , P , D , F ,
s 1 2 L l: j ls: ,2 s 1 2 :
2
j
*
j ( j 1) l ( l 1) s ( s 1)
c
j
l
*2
l
*
2
s
*
讨论: (1) n和l相同,s不变,只有j不同,不同的j值具有不同 的能量
l 0 时, j l s l 1 / 2 l 0 时, j l s l 1 / 2,或
原子物理学第4章

价电子的轨道:n ≥ 2
Li: Z=3=212+1 Na:Z=11=2(12+22)+1 K: Z=19=2(12+22+22)+1 Rb:Z=37=2(12+22+32+22)+1 Cs:Z=55=2(12+22+32+32+22)+1 Fr:Z=87=2(12+22+32+42+32+22)+1
3、Na原子的能级与能级跃迁
主线系:从l=1的p态→n=3, l=0的3s态, n=3,4… 锐线(二辅)系:从l=0的s态→n=3, l=1的3p态, n=4,5… 漫线 (一辅)系:从l=2的d态→n=3, l=1的3p态, n=4,5… 基线(柏格曼)系:从l=3的f态→n=3, l=2的3d态, n=4,5,6…
Rhc En 2 (n D l )
-e
●
r Rnl
●
2
2
21
20
n=2
r r1
图4-5、轨道的贯穿
0
4
r Rnl
2
2
32
31
30
n=3
r r1
0 9
l 越小,电子波 函数靠近核的概率 越大,贯穿的几率 越大,能量越低
小结:碱金属原子光谱
1、实验规律:
所有的碱金属原子的光谱,具有相仿的结构,实验观 察的谱线一般分为四个线系。
~D相同而n不同的光谱 和
R R 2、碱金属原子的光谱项: Tnl 2 n (n D l ) 2
• 量子数亏损:D l
nn
原子物理第四章

back next 目录 结束
3)与 s 对应的磁矩,由 r L 式知, 轨道磁矩 l 与轨道角动量 L 之间的对应 关系是
e l L 2m
(3)
back
next
目录
结束
与此相类比, s 与相应的
s 之间也应有
(4)
相应的对应关系,这个对应关系是
e s S m
S s(s 1)
(1)
next 目录 结束
其中S 称为自旋量子数
back
2)
有2l +1个空间取向,则 s 也应该有 2s+1个空间取向
L
S z ms h
ms s, s 1,…-s (2)
实验表明,对于电子来说
1 s 2
1 1 ms , 2 2
即
s
有两个空间取向。
hv E Em En
1 1 Rhc (4) ' 2 2 (n l ) (m l )
back next 目录 结束
所以碱金属光谱的波数为
~
1 1 v R ' 2 2 (n l ) (m l )
nL mL
'
back
(5)
next
目录
结束
第三节、碱金属原子光谱的精细结构
• 一、光谱的精细结构 • 1、概念 • 2、光谱的精细结构的特点 • 二、光谱的精细结构和能量的联系 • 三、结论
第四节:电子的自旋同轨道运动的相互作用
史特恩-盖拉赫实验中出现偶数分裂的事实 启示人们,电子的轨道运动似乎不是全部的 运动。换句话说,
3)与 s 对应的磁矩,由 r L 式知, 轨道磁矩 l 与轨道角动量 L 之间的对应 关系是
e l L 2m
(3)
back
next
目录
结束
与此相类比, s 与相应的
s 之间也应有
(4)
相应的对应关系,这个对应关系是
e s S m
S s(s 1)
(1)
next 目录 结束
其中S 称为自旋量子数
back
2)
有2l +1个空间取向,则 s 也应该有 2s+1个空间取向
L
S z ms h
ms s, s 1,…-s (2)
实验表明,对于电子来说
1 s 2
1 1 ms , 2 2
即
s
有两个空间取向。
hv E Em En
1 1 Rhc (4) ' 2 2 (n l ) (m l )
back next 目录 结束
所以碱金属光谱的波数为
~
1 1 v R ' 2 2 (n l ) (m l )
nL mL
'
back
(5)
next
目录
结束
第三节、碱金属原子光谱的精细结构
• 一、光谱的精细结构 • 1、概念 • 2、光谱的精细结构的特点 • 二、光谱的精细结构和能量的联系 • 三、结论
第四节:电子的自旋同轨道运动的相互作用
史特恩-盖拉赫实验中出现偶数分裂的事实 启示人们,电子的轨道运动似乎不是全部的 运动。换句话说,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1921年史特恩(Stern)和盖拉赫(Gerlach)从实 验中首次直接观察到了原子在外磁场中的取向量子化。
The Nobel Prize in Physics 1943
在电炉O内使银蒸发。银原子
通过狭缝S1和S2后,形成细束, 经过一个不均匀的磁场区域,
在磁场的垂直方向行进。最后撞
在相片P上,银原子经过的区域是
v
2 re
可以估计出电子的赤道速度
5
v me re
v
代入电子的经典半径公式
re
e2
4 0 me c 2
就有
v c 5 1 违反狭义相对论!
正确的理解:电子确实具有 大小的自旋角动量,电 子自旋是一种量子效应,把自旋看成电子的经典转动是不 恰当的,它是电子的一种内禀属性,没有经典对应。
电子自旋是一个新的自由度,与其空间运动完全无关!
第四章 原子的精细结构: 电子的自旋
主要内容:
1、电子轨道运动的磁矩 2、史特恩-盖拉赫实验 3、电子自旋的假设 4、碱金属双线 5、塞曼效应
重 点:
1、一个假设:电子自旋 2、三个实验:碱金属双线、塞曼效应、史-盖实验 3、四个量子数:n、l、 ml 、ms 4、氢原子光谱的五步进展
如果用分辨率足够高的摄谱仪观察,可以发现原子光谱 中每条谱线并不是简单的一条线,而是由多条谱线组成。
二、朗德g因子
单电子原子的总磁矩
原子内部封闭壳层的总轨道角动量和总自旋角动量 均为零,对原子磁矩没有贡献,只须考虑外层价电子。
电子作轨道运动时伴随有轨道磁矩 l
l
gl
e 2m
L
gl 1
电子具有自旋磁矩 s
s
gs
e 2m
S
gs 2
原子的总角动量为J=L+S,总磁矩为 l s,由 于 gl gs ,因此 不与J反平行。孤立原子的总角动量J 是守恒量,而轨道角动量L,自旋角动量S和总磁矩 不是
原子在纵向是作匀速直线运动,其速度 根据热平衡关系得到
mv2 3kT 则原子在磁场中运行的时间为 t D
v
而原子在横向受到磁场力的作用,将作加速运动,距离为
z1
1 2
Fz m
t2
则在屏上偏离的距离为
z2
z
Bz z
dD 3kT
其中,D为P离磁场区中心的距离。
在相片上出现了两条黑斑,表示有两个z2,即原子
如果设自旋量子数为s,按照关于轨道角动量取向的 考虑,自旋角动量的取向也应该有2s+1个。实验观察 到的能级是双层的,所以自旋取向只有两个,2s+1=2, 因此,s=1/2。
它在z方向的分量只有两个
sz
1 2
即自旋量子数在z方向的分量只能取 1 2
Sz ms
ms
1 2
洛仑兹的质疑
I
2 5
me re2
例如,氢原子的 H线并不是单线,而是由七条谱线组成;
常见的钠原子黄光是由 1 588.996nm 和2 589.593nm两条很 靠近的谱线组成的,其波长差约为0.6nm。
Na
0.6nm
谱线的这种细微结构称为光谱的精细结构。
§4.1、原子中电子轨道运动的磁矩
有关电磁学知识
1、电偶极矩 p ql
对原子的描述仍然不完整。
§4.3、电子自旋的假设
一、乌伦贝克和古兹米特提出电子自旋假设
要使2l+1为偶数,只有角动量为半整数,而轨道角动 量是不可能给出半整数的。
而且为了试图说明碱金属原子能级的双层结构以及后面 要提到的反常塞曼效应,在1925年,两位年轻的荷兰研究 生乌楞贝克(Uhlenbenck)和古德史密特(Goudsmit) 提出了关于电子自旋的大胆假设并解决了上述问题。
2J
J L
又
L2 S2 J 2 2SJ cossj
S
因此
S cos sj J 2 L2 S 2 s
2J
l
代入总磁矩表达式
j
1
J2
L2 2J 2
S2
e 2m
J
g
e 2m
J
g
1
J
2
L2 2J 2
S
2
—— 朗德g因子
于是
j j 1 l l 1 s s 1
g 1
dt
dt
即 d
dt
因此, 称为磁矩绕磁场方向进动的角速度。
由于原子在磁场中附加了拉莫尔进动,会使其能量 发生变化。进动角动量叠加到L在磁场方向的分量上, 将使系统能量增加(L和B方向一致或具有同向的分量) (图a),或使系统能量减少(L和B方向相反或具有反 向的分量)(图b) 。
二、量子表示式
守恒量,它们绕J进动,不断改变方向。 在 - J方向的分
量 是 j守恒量,因此一般将 定j 义为总磁矩。
要计算 j ,只需把 l 和 s 在J延长
线上的分量相加就可以了
J L
j l coslj s cossj
S
由余弦定理可得
s
S2 L2 J 2 2LJ coslj
l
由此可得
L cos lj J 轨道运动之外,还 存在着一种内禀运动,称为自旋。与轨道运动相联系,存 在轨道角动量L。与自旋运动相联系也存在一种角动量, 称为自旋角动量S,它是保持不变的,是电子的属性之一, 所以也称为电子的固有矩。
S的值与自旋量子数s有关,即
S s s 1
价电子绕原子实运动时,在固定于电子上的一个坐 标系中,就是相对于电子来说,带正电的原子实是绕 电子运动的。电子会感受到一个磁场的存在。这个磁 场的方向就是原子实绕电子的角动量方向,因而也就 是电子轨道运动角动量的方向。电子既然感受到了这 个磁场,它的自旋取向就要量子化。
根据j的取值,相邻的j均相差1,由于s=1/2,
所以对某一确定的 l ,j l 1 2, l 1 2 。
即当 l 0时,j只有两个取值 j l 1 2;当 l 0
时,j只有一个值1/2。
例1、求p电子的L,S和J的大小,并画出矢量图。
解:p电子对应的量子数为 l 1, s 1 2
所以 j 1 1 3 , 1 2 22
q
F qE
F 0
l
E
F
q
M l F l (qE) p E
2、磁矩
环形电流的磁矩 iSn0
z
i 方向与 方向满足右手螺旋关系。
i
均匀磁场中: F 0
M B
3、力和力矩
力是引起动量变化的原因:F
d
(m )
dt
力矩是引起角动量变化的原因: M
r
F
r
d (m )
原子的磁矩= 电子轨道运动的磁矩+电子自旋运动磁矩+核磁矩。
史特恩-盖拉赫实验在历史上有重要意义
• 证明了空间量子化的事实
• 证明电子自旋假设的正确,而且s=1/2
• 证明电子自旋磁矩数值的正确,s,z B,gs 2
他们同时也提出了一个重要的实验方法,其装置可以 做成粒子磁能态选择器。例如,在磁铁后面适当位置上安 放狭缝,可以选择处于某一能态的粒子通过,这类技术后 来被广泛应用。
dL
dt dt
一、经典表示式
电子轨道运动的闭合电流为: i e T
“-”表示电流方向与电子运动方向相反
面积: dS 1 r rd 1 r2dt
2
2
一个周期扫过的面积:
S dS T 1 r2dt 1
T mr2dt 1
T
L
Ldt T
02
2m 0
2m 0
2m
因此 iS e L L
抽成真空的。当时在显像后的相片上看到两条黑斑,表示银 原子在经过不均匀磁场区域时已分成两束。
不均匀的磁场是由不对称的磁极产生的。
实验的主要目的是要观察 在磁场中取向情况。用不均
匀的磁场是要把不同的 z值的原子分出来。磁场对原子的
力是垂直于它的前进方向的,这样,原子的路径会偏转。
N S
无磁场
有磁场
2me
—— 旋磁比
磁力矩为 B
力矩将引起角动量的变化
则 d B
dt
dL B
dt
或者
d B — 拉莫尔进动
dt
在外磁场B中,一个高速旋转的磁矩并不向B方向靠
拢,而是以一定的角速度 绕B作进动, 的方向与B一
致。
考虑磁矩 的进动
磁矩元
d sin d
则
d sin d sin
量子力学中角动量L是取量子化的
L l l 1
l — 轨道角量子数
因此磁矩为
l L
l l 1
l l 1 e
2me
在z方向的投影为
l,z Lz ml
e 2me ml
即
l l l 1B l 0,1, 2,
l,z ml B
ml 0, 1, , l
其中
B
e 2me
—— 玻尔磁子
束分为两条。在上式中,除了 z 外,其他都是常数, 因此,说明有两个 z。
z cos
也就是说有两个 值,即原子在磁场中有两个空 间取向。这就有力地证明了原子在空间的取向是 量子化的。
如果测得相片上两黑斑的距离,再把式中其他数值代
入,就可以计算出 z ,取 值分别为 0 和 180 ,就得
到 ,这样求得的 值正是一个玻尔磁子的理论值。
,g 4 3
(3)
4D1/ 2:
s
3 2
,
l
2, j
1 2
,
g
0
四、史特恩 - 盖拉赫实验的解释
考虑电子的自旋后,原子的总磁矩是由轨道磁矩 和自旋磁矩两部分合成的,于是
The Nobel Prize in Physics 1943
在电炉O内使银蒸发。银原子
通过狭缝S1和S2后,形成细束, 经过一个不均匀的磁场区域,
在磁场的垂直方向行进。最后撞
在相片P上,银原子经过的区域是
v
2 re
可以估计出电子的赤道速度
5
v me re
v
代入电子的经典半径公式
re
e2
4 0 me c 2
就有
v c 5 1 违反狭义相对论!
正确的理解:电子确实具有 大小的自旋角动量,电 子自旋是一种量子效应,把自旋看成电子的经典转动是不 恰当的,它是电子的一种内禀属性,没有经典对应。
电子自旋是一个新的自由度,与其空间运动完全无关!
第四章 原子的精细结构: 电子的自旋
主要内容:
1、电子轨道运动的磁矩 2、史特恩-盖拉赫实验 3、电子自旋的假设 4、碱金属双线 5、塞曼效应
重 点:
1、一个假设:电子自旋 2、三个实验:碱金属双线、塞曼效应、史-盖实验 3、四个量子数:n、l、 ml 、ms 4、氢原子光谱的五步进展
如果用分辨率足够高的摄谱仪观察,可以发现原子光谱 中每条谱线并不是简单的一条线,而是由多条谱线组成。
二、朗德g因子
单电子原子的总磁矩
原子内部封闭壳层的总轨道角动量和总自旋角动量 均为零,对原子磁矩没有贡献,只须考虑外层价电子。
电子作轨道运动时伴随有轨道磁矩 l
l
gl
e 2m
L
gl 1
电子具有自旋磁矩 s
s
gs
e 2m
S
gs 2
原子的总角动量为J=L+S,总磁矩为 l s,由 于 gl gs ,因此 不与J反平行。孤立原子的总角动量J 是守恒量,而轨道角动量L,自旋角动量S和总磁矩 不是
原子在纵向是作匀速直线运动,其速度 根据热平衡关系得到
mv2 3kT 则原子在磁场中运行的时间为 t D
v
而原子在横向受到磁场力的作用,将作加速运动,距离为
z1
1 2
Fz m
t2
则在屏上偏离的距离为
z2
z
Bz z
dD 3kT
其中,D为P离磁场区中心的距离。
在相片上出现了两条黑斑,表示有两个z2,即原子
如果设自旋量子数为s,按照关于轨道角动量取向的 考虑,自旋角动量的取向也应该有2s+1个。实验观察 到的能级是双层的,所以自旋取向只有两个,2s+1=2, 因此,s=1/2。
它在z方向的分量只有两个
sz
1 2
即自旋量子数在z方向的分量只能取 1 2
Sz ms
ms
1 2
洛仑兹的质疑
I
2 5
me re2
例如,氢原子的 H线并不是单线,而是由七条谱线组成;
常见的钠原子黄光是由 1 588.996nm 和2 589.593nm两条很 靠近的谱线组成的,其波长差约为0.6nm。
Na
0.6nm
谱线的这种细微结构称为光谱的精细结构。
§4.1、原子中电子轨道运动的磁矩
有关电磁学知识
1、电偶极矩 p ql
对原子的描述仍然不完整。
§4.3、电子自旋的假设
一、乌伦贝克和古兹米特提出电子自旋假设
要使2l+1为偶数,只有角动量为半整数,而轨道角动 量是不可能给出半整数的。
而且为了试图说明碱金属原子能级的双层结构以及后面 要提到的反常塞曼效应,在1925年,两位年轻的荷兰研究 生乌楞贝克(Uhlenbenck)和古德史密特(Goudsmit) 提出了关于电子自旋的大胆假设并解决了上述问题。
2J
J L
又
L2 S2 J 2 2SJ cossj
S
因此
S cos sj J 2 L2 S 2 s
2J
l
代入总磁矩表达式
j
1
J2
L2 2J 2
S2
e 2m
J
g
e 2m
J
g
1
J
2
L2 2J 2
S
2
—— 朗德g因子
于是
j j 1 l l 1 s s 1
g 1
dt
dt
即 d
dt
因此, 称为磁矩绕磁场方向进动的角速度。
由于原子在磁场中附加了拉莫尔进动,会使其能量 发生变化。进动角动量叠加到L在磁场方向的分量上, 将使系统能量增加(L和B方向一致或具有同向的分量) (图a),或使系统能量减少(L和B方向相反或具有反 向的分量)(图b) 。
二、量子表示式
守恒量,它们绕J进动,不断改变方向。 在 - J方向的分
量 是 j守恒量,因此一般将 定j 义为总磁矩。
要计算 j ,只需把 l 和 s 在J延长
线上的分量相加就可以了
J L
j l coslj s cossj
S
由余弦定理可得
s
S2 L2 J 2 2LJ coslj
l
由此可得
L cos lj J 轨道运动之外,还 存在着一种内禀运动,称为自旋。与轨道运动相联系,存 在轨道角动量L。与自旋运动相联系也存在一种角动量, 称为自旋角动量S,它是保持不变的,是电子的属性之一, 所以也称为电子的固有矩。
S的值与自旋量子数s有关,即
S s s 1
价电子绕原子实运动时,在固定于电子上的一个坐 标系中,就是相对于电子来说,带正电的原子实是绕 电子运动的。电子会感受到一个磁场的存在。这个磁 场的方向就是原子实绕电子的角动量方向,因而也就 是电子轨道运动角动量的方向。电子既然感受到了这 个磁场,它的自旋取向就要量子化。
根据j的取值,相邻的j均相差1,由于s=1/2,
所以对某一确定的 l ,j l 1 2, l 1 2 。
即当 l 0时,j只有两个取值 j l 1 2;当 l 0
时,j只有一个值1/2。
例1、求p电子的L,S和J的大小,并画出矢量图。
解:p电子对应的量子数为 l 1, s 1 2
所以 j 1 1 3 , 1 2 22
q
F qE
F 0
l
E
F
q
M l F l (qE) p E
2、磁矩
环形电流的磁矩 iSn0
z
i 方向与 方向满足右手螺旋关系。
i
均匀磁场中: F 0
M B
3、力和力矩
力是引起动量变化的原因:F
d
(m )
dt
力矩是引起角动量变化的原因: M
r
F
r
d (m )
原子的磁矩= 电子轨道运动的磁矩+电子自旋运动磁矩+核磁矩。
史特恩-盖拉赫实验在历史上有重要意义
• 证明了空间量子化的事实
• 证明电子自旋假设的正确,而且s=1/2
• 证明电子自旋磁矩数值的正确,s,z B,gs 2
他们同时也提出了一个重要的实验方法,其装置可以 做成粒子磁能态选择器。例如,在磁铁后面适当位置上安 放狭缝,可以选择处于某一能态的粒子通过,这类技术后 来被广泛应用。
dL
dt dt
一、经典表示式
电子轨道运动的闭合电流为: i e T
“-”表示电流方向与电子运动方向相反
面积: dS 1 r rd 1 r2dt
2
2
一个周期扫过的面积:
S dS T 1 r2dt 1
T mr2dt 1
T
L
Ldt T
02
2m 0
2m 0
2m
因此 iS e L L
抽成真空的。当时在显像后的相片上看到两条黑斑,表示银 原子在经过不均匀磁场区域时已分成两束。
不均匀的磁场是由不对称的磁极产生的。
实验的主要目的是要观察 在磁场中取向情况。用不均
匀的磁场是要把不同的 z值的原子分出来。磁场对原子的
力是垂直于它的前进方向的,这样,原子的路径会偏转。
N S
无磁场
有磁场
2me
—— 旋磁比
磁力矩为 B
力矩将引起角动量的变化
则 d B
dt
dL B
dt
或者
d B — 拉莫尔进动
dt
在外磁场B中,一个高速旋转的磁矩并不向B方向靠
拢,而是以一定的角速度 绕B作进动, 的方向与B一
致。
考虑磁矩 的进动
磁矩元
d sin d
则
d sin d sin
量子力学中角动量L是取量子化的
L l l 1
l — 轨道角量子数
因此磁矩为
l L
l l 1
l l 1 e
2me
在z方向的投影为
l,z Lz ml
e 2me ml
即
l l l 1B l 0,1, 2,
l,z ml B
ml 0, 1, , l
其中
B
e 2me
—— 玻尔磁子
束分为两条。在上式中,除了 z 外,其他都是常数, 因此,说明有两个 z。
z cos
也就是说有两个 值,即原子在磁场中有两个空 间取向。这就有力地证明了原子在空间的取向是 量子化的。
如果测得相片上两黑斑的距离,再把式中其他数值代
入,就可以计算出 z ,取 值分别为 0 和 180 ,就得
到 ,这样求得的 值正是一个玻尔磁子的理论值。
,g 4 3
(3)
4D1/ 2:
s
3 2
,
l
2, j
1 2
,
g
0
四、史特恩 - 盖拉赫实验的解释
考虑电子的自旋后,原子的总磁矩是由轨道磁矩 和自旋磁矩两部分合成的,于是
