计量经济学第2章第5节
《计量经济学》课程标准

《计量经济学》课程标准1. 课程的性质与设计思路1.1课程的性质《计量经济学》是教育部规定经济类专业核心课程之一, 是经济类专业的专业必修课。
在经济类的各个专业的教学中占有非常重要的地位。
《计量经济学》课程的主要特点是理论与实际应用并重, 既要认真学习基本理论知识, 又要注重经济计量方法在实践中的应用。
在教学中可以抛开复杂的数学计算以及繁琐的推导和证明, 但要将深入浅出的理论分析贯彻始终。
其目的是, 通过学习、掌握计量经济学的基本原理和常用方法, 研究经济中的有关问题, 训练学生运用计量方法、经济计量模型进行创造的思维方法。
并在此基础上, 培养学生利用经济计量学的方法, 学习和实践现代经济学的基本理论以及用定量的方法分析、解决实际经济生活中有关经济学问题的能力。
课程在内容与应用上与概率论与数理统计、统计学、时间序列分析、经济学等课程有关联。
所以, 学习本课程, 必须要先学习《微积分》、《线性代数》、《概率论和数理统计》、《西方经济学》等课程, 同时, 学习者要关注在经济计量学领域的一些最新发展。
只有这样, 才能在更好地理解和掌握课程内容与方法的基础上使经济计量模型的应用更具实践性。
1.2设计思路《计量经济学》建立在经济、统计学和数理统计的基础上, 是经济学中的一门重要的独立学科。
计量经济学结合数量方法来对经济活动进行认识分析, 并辅助于计算机专门软件, 具有较强的应用性和可操作性。
本课程主要介绍了计量经济学的一般概念及工作步骤、模型估计的基本方法、模型检验与修正方法, 典型计量经济模型专题讨论、联立方程组模型的基本知识(包括模型的识别、估计、检验及应用)、计量经济模型的应用案例。
学生在学习本课程之前, 应先学习了《微积分》、《线性代数》、《经济学》(包含微观经济学和宏观经济学)、《概率论与数理统计》和《经济统计学》等课程。
教师在讲授本课程时, 首先应特别注重对经济理论的认识和经济现象的分析, 强调已学的《经济学》基础;其次突出计量经济建模基本思想的讲授, 侧重在计量经济学研究对象的理解和《经济学》、《经济统计学》与《数学》相结合的知识背景上;再次应避免在理论部分的繁杂的纯数学证明, 但对于表述基本原理和模型应用分析中的数学推导是必要的, 故应强调《微积分》、《线性代数》与《概率论与数理统计》的基础知识;最后应加强对计量经济学概念的总结和应用实例的分析, 包括计量经济专门分析软件(Eviews)的应用操作。
第二章 双变量回归分析(计量经济学,南开大学)
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
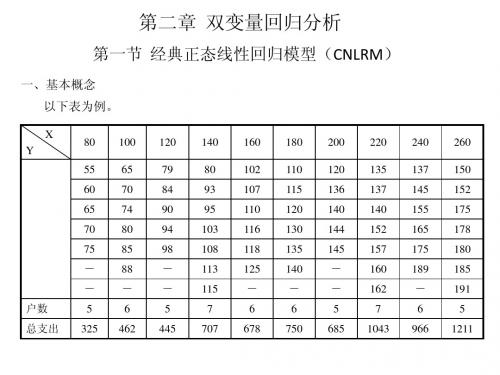
6、样本回归函数(SRF) 由于在大多数情况下,我们只知道变量值得一个样本,要用样本信息的基础 上估计PRF。(表) 样本1
X(收入) Y(支出) 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ: 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差:VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量(Estimator):一个估计量又称统计量(statistic),是指一个规则、公式 或方法,以用来根据已知的样本所提供的信息去估计总体参数。在应用中,由估 计量算出的数值称为估计(值)(estimate)。 样本回归函数SRF的随机形式为:
计量经济学教案

吉首大学
计量经济学课程教案
周次第1周课次第2次课时 2 时间任课教师
周次第2周课次第3次课时 2 时间任课教师
周次第3周课次第4次课时 2 时间任课教师
周次第3周课次第5次课时 2 时间任课教师
周次第4周课次第6次课时 2 时间任课教师
周次第5周课次第7次课时 2 时间任课教师
周次第5周课次第8次课时 2 时间任课教师
周次第6周课次第9次课时 2 时间任课教师
周次第7周课次第10次课时 2 时间任课教师
周次第7周课次第11次课时 2 时间任课教师
周次第8周课次第12次课时 2 时间任课教师
周次第9周课次第13次课时 2 时间任课教师
周次第10周课次第14次课时 2 时间任课教师
周次第11周课次第15次课时 2 时间任课教师
周次第11周课次第16次课时 2 时间任课教师
周次第12周课次第17次课时 2 时间任课教师。
计量经济学第二章 一元线性回归模型(1)(肖)

10
2.在经济学中,经济学家要研究个人
消费支出与个人可支配收入的依赖关系。
这种分析有助于估计边际消费倾向,就是
可支配收入每增加一元引起消费支出的平
均变化。
11
3.在企业中,我们很想知道人们对企
业产品的需求与广告费开支的关系。这种
研究有助于估计出相对于广告费支出的需
求弹性,即广告费支出每变化百分之一的
(2.3)
想想:结合表2.1的资料 ,怎样理解式(2.3)
变量Y 的原因, 给定变量X 的值也不能具
体确定变量Y的值, 而只能确定变量Y 的
统计特征,通常称变量X 与Y 之间的这种
关系为统计关系。
16
例如,企业总产出Y 与企业的资本投入
K 、劳动力投入L 之间的关系就是统计关 系。虽然资本K 和劳动力L 是影响产出Y 的两大核心要素,但是给定K 、L 的值并 不能确定产出Y 的值。因为,总产出Y 除 了受资本投入K、劳动力投入L 的影响外
在进入正式的回归理论之前,先斟酌一下变量y与变 量x可以互换的不同名称、术语。 Y 因变量 X 自变量
被解释变量 响应变量
被预测变量
解释变量 控制变量
预测变量
回归子
归回元
22
第二节
一、引例
一元线性回归模型
假定我们要研究一个局部区域的居 民消费问题,该区域共有80户家庭组成 ,将这80户家庭视为一个统计总体。
32
函数f (Xi)采取什么函数形式,是一个
需要解决的重要问题。在实际经济系统
中,我们不会得到总体的全部数据,因
而就无法据已知数据确定总体回归函数 的函数形式。同时,对总体回归函数的 形式只能据经济理论与经验去推断。
计量经济学第二章

第二章主要介绍了计量经济学 的基本概念、原理和方法,包 括经济变量、经济模型、数据 收集与处理、参数估计与假设 检验等。
第二章主要介绍了计量经济学 的基本概念、原理和方法,包 括经济变量、经济模型、数据 收集与处理、参数估计与假设 检验等。
第二章主要介绍了计量经济学 的基本概念、原理和方法,包 括经济变量、经济模型、数据 收集与处理、参数估计与假设 检验等。
异方差性概念及产生原因
异方差性概念
异方差性是指误差项的方差随自变量的变化 而变化,即不满足同方差性的假设。
产生原因
异方差性的产生原因可能包括模型设定偏误、 遗漏重要变量、数据测量误差、异常值影响 等。
异方差性检验方法
图形检验法
通过绘制残差图或残差与解释变量的散点图,观察是否存在异方差性。
等级相关系数法
最小二乘法原理及应用
最小二乘法原理
最小二乘法是一种数学优化技术,它通过最小化预测值与实际观测值之间的残差平方和来估计线性回归模型的参 数。这种方法可以使得模型的预测结果更加接近实际观测值。
最小二乘法应用
在实际应用中,最小二乘法被广泛应用于各个领域,如经济学、金融学、社会学等。它可以用于预测未来趋势、 评估政策效果、分析市场需求等。
03
多元线性回归模型
多元线性回归模型构建
02
01
03
模型设定
确定因变量和自变量,建立多元线性回归方程。
数据收集
收集样本数据,包括因变量和自变量的观测值。
参数估计
采用最小二乘法等方法,估计模型参数。
偏回归系数解释与检验
偏回归系数解释
偏回归系数表示在其他自变量不变的情 况下,某一自变量对因变量的影响程度 。
05
计量经济学讲义

第一章绪论第一节什么是计量经济学计量经济学含义.计量经济学是一个迅速发展的经济学分支,其目标是给出经济关系的经济内容。
.计量经济学可以定义为实际经济现象的定量分析,这种分析根据的是适当推断方法联系在一起的理论和观测的即时发展。
计量经济学运用数理统计知识分析经济数据,对构建于数理经济学基础上的数学模型提供经验支持,并得出数量结果。
.计量经济学是将经济理论、数学方法和统计推断等工具应用于经济现象分析的社会科学。
第二节计量经济学方法计量经济学方法的内容计量经济学研究包括两个基本要素:经济理论和事实。
将经济理论与现实情况结合起来,用统计技术估计经济关系。
最可用的形式就是模型。
计量经济分析步骤.陈述理论。
例如有关价格变动与需求量之间的关系的经济理论:在其他条件不变的情况下,一商品的价格上升(下降),则对该商品的需求量减少(增加)。
建立计量经济模型⑴需求函数的数学模型例如线性函数模型。
如果需求量与价格之间的关系式线性的,则数学上需求函数可以表示为Q P αβ=+()αβ和称为该函数的参数。
等号左边的变量称为因变量或被解释变量,等号右边的变量称为自变量或解释变量。
⑵计量经济模型式()假定需求量与价格之间的关系是一种确定关系,而现实的经济变量之间,极少有这种关系,更常见的是一种不确定性关系(见散点图),线性模型应该为Q P αβε=++()ε是随机扰动项。
收集数据估计计量经济模型中的参数之前,必须得到适当的数据。
在经验分析中常用的数据有两种:时间序列数据(纵向数据)和横截面数据(横向数据)。
有时会同时出现前面的纵向数据和横向数据,称之为混合数据。
面板数据是混合数据的一种特殊类型。
估计参数如利用收集的数据估计出式()中的参数,得回归模型76.05 3.88Q P =-()假设检验对回归模型以及模型中的系数进行检验。
预测和政策分析例如在回归模型()中,想预测价格时的需求量值时,则有76.05 3.8876.05 3.88 4.558.59Q P =-=-⨯=第二章线性回归分析第一节线性回归概述2.1.1回归模型简介如果(随机)变量y 与12,,,p x x x L存在相关关系12(,,,)p y f x x x ε=+L (2.1.1)其中y 是可观测的随机变量,12,,,p x x x L 为一般变量,ε是不可观测的随机变量;y 称为因变量(被解释变量),12,,,p x x x L 称为自变量(解释变量),ε称为随机误差。
第四讲(计量经济学第二章)PPT课件

12
六、参数估计量的概率分布及随机扰 动项方差的估计
13
经典假设下,普通最小二乘估计的分布
^
0 0 wii
ˆ1 1 ki i
^
0~N(0,2
w2) i
^
1~N(1,2
k2) i
14
古典假设下,随机扰动项方差的估计
^
2
1
n2
ei2
^2
(n2)2 ~2(n2) (证明略)
6
2、一元线性回归模型普通最小二乘估 计量的性质
高斯—马尔可夫定理(Gauss-Markov theorem)
在古典回归模型的基本假定下,最小 二乘估计量是具有最小方差的线性 无偏估计量,具有一致性。
7
无偏性:即
^
^
E00,E11
证: ˆ1 1 ki i
E ( ˆ 1 ) E ( 1 k ii ) 1 k i E ( i ) 1
1
x12i x22i(x1ix2i)2
[( x2 2i)x1iyi][( x1ix2i)x2iyi]
[ ]y x1 2i x2 2i(x1ix2i)2
( x2 2i)x1i( x1ix2i)x2i x12i x2 2i(x1ix2i)2 i
^
( x22i)x1i( x1ix2i)x2i
参数β0的区间估计所需要的统计量:
~t(n2) ^
T 00
0
S^
0
设置信水平 1
p{T|0|t}1
2
^
^
得置信区间: ( 0t2S^0, 0t2S^0)
17
二元线性回归模型
二元线性回归模型 Y i01 X 1 i2 X 2 i u i
计量经济学ppt课件 自相关

原因4-蛛网现象
许多农产品的供给呈现为 蛛网现象,供给对价格的 反应要滞后一段时间,因 为供给需要经过一定的时
间才能实现。如果时期 t
的价格 Pt 低于上一期的 价格 Pt-1 ,农民就会减少 时期 t 1的生产量。如
此则形成蛛网现象,此时 的供给模型为:
蛛网现象是微观经济学中的 一个概念。它表示某种商品 的供给量受前一期价格影响 而表现出来的某种规律性, 即呈蛛网状收敛或发散于供 需的均衡点。
18
第二节 自相关的后果
➢OLS估计虽然是线性无偏的,但不再是有 效的估计。 ➢OLS估计的标准误差估计不再准确(通常 是低估) ➢参数显著性 t 检验失效(通常是高估) ➢模型预测精度下降
19
第三节 自相关的检验
本节基本内容:
图示检验法 DW检验法 序列相关的LM检验
20
一、图示检验法
需要人为设定滞后期长度,一般从s=1开始, 多试几次,比如直到s=10左右。如果检验结 果均不显著,则可以认为不存在自相关性。
3399
第四节 自相关的补救
本节基本内容:
●相关系数已知时:广义差分法 ●计算相关系数:科克伦-奥克特迭代法 ●其他方法简介
40
一、广义差分法
对于自相关的结构已知的情形可采用广义差分法解决。
而建立模型时,模型设定为: Yt = 1 + 2 X 2t + ut
则 X3t 对 Yt 的影响便归入随机误差项 ut 中,由于 在不同观测点上是相关的,这就造成了 ut 在不同 观测点是相关的,呈现出系统模式,此时 ut 是自
相关的。
13
模型形式设定偏误也会导致自相关现象。如将成本 曲线设定为线性成本曲线,则必定会导致自相关。 由设定偏误产生的自相关是一种虚假自相关,可通 过改变模型设定予以消除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a a -+之中,以及如何求得a。在变量的显著性检验中已经知道: t s i i i
=
-
βββ~t n k (--1
这就是说,如果给定置信水平(1-α,从t分布表中查得自由度为(n k --1的临界值t α2
,
那么t值处在(,-t t αα的概率是(1-α。表示为:
e 0服从正态分布,即
e 0~N (,((012
01
0σμ+''-X X X X取e 0的方差的估计量为
((σσμe 0
2201
01=+''-X X X X (σσμe 0
101
0=+''-X X X X
构造统计量
t y
y e =- 000
σ
~t n k (--1
利用该统计量,类似于参数估计量置信区间的分析过程,得到在给定(1-α的置信水平下
(((((0000000100010010
=+-=+-''=+-''+=-''=---X X X X X X X Y X X X X X X X X X X B B
B B B N N μμμμ
V a re E e E ((
((((
002
00122
0101==-''=+''--μσμX X X X X X X X N
P t t t (-<<=-ααα2
2
1
即
P t s t i i i
(
-<
-<=-ααββαβ2
2
1
P t s t s i i i i
i
( βββαααββ
-⨯<<+⨯=-2
2
1于是得到:在(1-α的置信水平下βi的置信区间是
( , ββααββ
i i t s t s i
i
-⨯+⨯2
2
(2.5.1在例2.3.1中,如果给定α=001.,查表得:
在前面的课程中,我们已经知道,线性回归模型的参数估计量β是随机变量y iபைடு நூலகம்
的函数,即
(B
=''-X X X Y 1所以它也是随机变量。在多次重复抽样中,每次的样本观测值不可能完全相同,所以得到
的点估计值也不可能相同。现在我们用参数估计量的一个点估计值近似代表参数值,那么,二者的接近程度如何?以多大的概率达到该接近程度?这就要构造参数的一个区间,以点估计值为中心的一个区间(称为置信区间,该区间以一定的概率(称为置信水平包含
§2.5多元线性回归模型的置信区间
多元线性回归模型的置信区间问题包括参数估计量的置信区间和被解释变量预测值的置信区间两个方面,在数理统计学中属于区间估计问题。所谓区间估计是研究用未知参数的点估计值(从一组样本观测值算得的作为近似值的精确程度和误差范围,是一个必须回答的重要问题。
一、参数估计量的置信区间
在实际应用中,我们当然也希望置信水平越高越好,置信区间越小越好。如何才能缩小置信区间?从(2.5.2式中不难看出:①增大样本容量n。在同样的置信水平下,n越大,从t分布表中查得自由度为(n k --1的临界值t α越小;同时,增大样本容量,在一般情况下
可使σ
μ='--e e
n k 1
减小,因为式中分母的增大是肯定的,分子并不一定增大。②更主要
(0. 0937,0.3033
显然,参数β2的置信区间最小。
在实际应用中,我们当然希望置信水平越高越好,置信区间越小越好。如何才能缩小置信区间?从(2.5.1式中不难看出:①增大样本容量n。在同样的置信水平下,n越大,从t分布表中查得自由度为(n k --1的临界值t α2
越小;同时,增大样本容量,在一般情况下
y 0的置信区间是
( (y
t y y t 001
00001011-⨯+''<<+⨯+''--αασσμμX X X X X X X X
(2.5.2
这就是说,当给定解释变量值X 0后,只能得到被解释变量y 0以(1-α的置信水平处于该区间的结论。
经常听到这样的说法,“如果给定解释变量值,根据模型就可以得到被解释变量的预测值为…值”,这种说法是不科学的,也是计量经济学模型无法达到的。如果一定要给出一个具体的预测值,那么它的置信水平则为0;如果一定要回答以100%的置信水平处在什么区间中,那么这个区间是∞。
可使s c n k i ii β='--e e
1
减小,因为式中分母的增大是肯定的,分子并不一定增大。②更主
要的是提高模型的拟合优度,以减小残差平方和'e e。设想一种极端情况,如果模型完全拟
合样本观测值,残差平方和为0,则置信区间也为0。③提高样本观测值的分散度。在一般情况下,样本观测值越分散,c ii越小。置信水平与置信区间是矛盾的。置信水平越高,在其它情况不变时,临界值t α2
越大,置信区间
越大。如果要求缩小置信区间,在其它情况不变时,就必须降低对置信水平的要求。
越大,置信区间越大。如果要求缩小置信区间,在其它情况不
变时,就必须降低对置信水平的要求。
二、预测值的置信区间
计量经济学模型的一个重要应用是经济预测。对于模型
Y
X =B如果给定样本以外的解释变量的观测值X 0=(,,,,110200x x x k ,可以得到被解释变量的
预测值
y
00=X B但是,严格地说,这只是被解释变量的预测值的估计值,而不是预测值。原因在于两方面:
的是提高模型的拟合优度,以减小残差平方和'e e。设想一种极端情况,如果模型完全拟合样本观测值,残差平方和为0,则置信区间也为0。③提高样本观测值的分散度。在一般情况下,样本观测值越分散,作为('-X X 1的分母的'X X的值越大,致使区间缩小。置信水平与置信区间是矛盾的。置信水平越高,在其它情况不变时,临界值t α2
t n k t α11330120005((.
.--==从回归计算中得到:
.. .. .. ββββββ0
1
2
5405279081
04809001490198500348
1
2
======s s s
根据(2.5.1计算得到β0、β1、β2的置信区间分别为
(302. 33,778.71 (0.4360,0.5258
一是模型中的参数估计量是不确定的,正如上面所说的;二是随机项的影响。所以,我们得到的仅能是预测值的一个估计值,预测值仅以某一个置信水平处于以该估计值为中心的一个区间中。于是,又是一个区间估计问题。
下面进行置信区间的推导。如果已经知道实际的预测值y 0,那么预测误差为:
e y y
000=-容易证明
E e E E E E (( ((
