流体力学讲义——上海交通大学
上海交通大学流体力学

: (
我们取一个四面体流体微元(如图)建立它的运动方程(以 x 方向为例)
。
四面体微元体积
1
=
6
它在坐标平面上的三个三角形的面积构成斜切面矢量面积 = 在 x,y,z 方向上的投影
= = ( , , ) = ( , , ) = (
2
∬ 2 sin
=0 =0
+ 2 + 2 + 2
积分计算后可以得到
1
̅̅̅
= ( + + )
3
.
在一个相对平衡的流场中流体单元没有变形速度,根据流体的力学定义,它内部的任何切面
上切因力为零,应力张量矩阵为
同性的,它在一个空间点上的值与切面方向无关。实验测量证实了这个结论,这个法向应力
的大小就是热力学压强 p。由于它的作用方向与一个流体微元表面的的外法向方向相反,我
们有
= = = −
这个结论不仅对相对或绝对平衡的流体有效,因为在理想流体粘性切引力为零,它当然在运
动的理想流体中也是有效的。
张量为压强项,偏引力张量为粘性应力项。笛卡尔坐标系中:
(
− 0
)=( 0 −
0
0
0
0 )+(
−
)
或者用下标的形式
= − +
这个关系的张量表达式为: = − + , 为单位张量,笛卡尔坐标系中表达为对角线元素
为 1,其余为 0 的矩阵。下标表达式中 称为克罗内克符号,在 i=j 时为 1, ≠ 时为 0。
大学物理:第五章 流体力学 (Fluid Mechanics)

Aneurysm(动脉瘤)
若处动脉的半径增大N倍 血液流速就缩小N2倍 病灶处的压强大幅度上降 由于该处血管壁薄,使血 管容易破裂。
上海交通大学 物理系
Atherosclerosis(动脉粥样硬化)
动脉病变从内膜开始。一 般先有脂质和复合糖类积 聚、出血及血栓形成,纤 维组织增生及钙质沉着, 并有动脉中层的逐渐蜕变 和钙化,病变常累及弹性 及大中等肌性动脉,
?
? hB=0.5m
P0
?
0
1 2
v
2 c
ghc
Pc
1 2
v
2 A
ghA
PA
vc 2ghA 6 m / s
B,C点
1 2
v
2 c
ghc
Pc
1 2
v
2 B
ghB
PB
SBvB SCvC
PB P0 0.85g
PB P0 ghD
hD 0.85m
上海交通大学 物理系
一柱形容器,高1m、截面积为5x10-2 m2,储满水 ,在容器底部有一面积为2x10-4 m2 的水龙头,问 使容器中的水流尽需多少时间?
度变小,压强变大
压力
上海交通大学 物理系
马格纳斯效应
上海交通大学 物理系
机翼受到的举力
Q:用机翼上、下的流速变化,讨论其受到的升力,是否合理
上海交通大学 物理系
上海交通大学 物理系
压强的范围
太阳中心 地球中心 实验室能维持的最大压强 最深的海沟 尖鞋跟对地板 汽车轮胎 海平面的大气压 正常的血压 最好的实验室真空
四、液流连续原理(Principle of continuity of flow)
最新上海交通大学流体力学第三章只是分享精品课件

(2) 轴功率。 解: (1)由于b << d 可将轴承间隙内的周向流动简化为
无限大平行平板间的流动。
轴承固定, 而轴以线速度U=ωd /2运动, 带动润滑油作纯剪切流动, 即简单库埃特
u 1 dpy2
2dx
C1yC2
边界条件:
y = 0,u = 0,C2= 0
y
=
b,u
=
0,C1
1
2
dp dx
b
1.速度(sùdù)
分布
u 1 dp(y2 by)
2 dx
最大速度
(sùdù)
um
b2 8
dp dx
第三页,共49页。
C3.3.1 平板(píngbǎn)泊肃叶流动(4-4)
2. 切应力(yìnglì) 分布
流
2. 平均速度
V Q
R2
GR2
8
12umax
速度分布
u
2V
1
r2 R2
3. 沿程损失
hf pgGgl8glR 2V
第十四页,共49页。
C3.4.2 泊肃叶定律(dìnglǜ)(2-2)
4. 泊肃叶定律(dìnglǜ) 的意义
Q GR4 8
(1) 泊肃叶定律(dìnglǜ)解析式由哈根巴赫和纽曼(1859)分别用N-S 方程推出。哈根(1839)和泊肃叶(1840)分别用实验测得 Q 与 G、R4成正比关系;
T
0
udt
u=u+ u
基本方程
雷诺方程 包含雷诺应力
第十七页,共49页。
上海交大船舶流体力学课件5

Shanghai Jiao Tong UniversityShanghai Jiao Tong UniversityShanghai Jiao Tong University 加速度:当地加速度(局部加速度)变位加速度(迁移加速度)'(, y ,,)(,,,)lim t ()x x y z z t t x y z t t u v w t x y zt +∆+∆+∆+∆-=∆→∆∂∂∂∂=+⋅+⋅+⋅∂∂∂∂∂=+⋅∇∂V V a V V V V V V V2.1.3Euler Shanghai Jiao Tong University2.1.3Euler方法和Lagrange方法的区别Shanghai Jiao Tong University注意:Euler方法中的空间点(x, y, z)与Lagrange方法中质点位置x, y, z有区别,Euler方法中的空间点(x, y, z)是t 的独立变量即与t无关,而Lagrange方法中质点位置x, y, z是t 的函数。
2.1.3Euler Shanghai Jiao Tong University2.2迹线和流线Shanghai Jiao Tong University上一节主要从数学上描述流体运动。
在本节,将讲述流体运动的几何表示。
Shanghai Jiao Tong University 2.2.1迹线定义:流体质点在连续时间内描绘出来的曲线,就是迹线(pathline)。
由于迹线是流体质点运动过程的路径,在Lagrange 法中,就是流体质点的位置函数:(,,,)(,,,)(,,,)x x a b c t y y a b c t z z a b c t =⎧⎪=⎨⎪=⎩2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong UniversityShanghai Jiao Tong University一般情况给出的是u v wShanghai Jiao Tong University定义为参变量,积分时作常数处理。
上海交通大学流体力学

∑
=
关于流体中的表面力我们会在下一节课中进一步讨论。
今天我们对流体中的长程力,也就是体积力或质量力进行进一步的探讨,
体积力与质量力;重力;体积力的势
长程力直接作用在每一个物体单元(无论是流体还是固体)以及它所占据的空间体积元上,
我们称之为质量力或体积力。我们定义单位质量上的作用力为 f,那么单位体积上的作用力
若质量力有势,许多计算可以简化。例如我们在质量力场中将一个质量为 m 的物体单元沿
一条路线 s 从 移至 ,那么质量力对这个物体所做的功为
2
2
2
∫ ∙ = ∫ ∙ = − ∫ ∙ = −[( ) − ( )]
1
1
1
即质量力做的功与路径无关,只与起点和终点的质量力势有关。
达式是 3x3 的矩阵,由理论力学知识可以得知,这个矩阵必须是对称的。
: (
)
一个微元面是两个物体分隔面的一部分,它的外法向方向从受力体垂直于微元面指向施力
体。一个面积大小为,外法向方向为 n 的微元面所受到的表面力为 为
= ∙ = ∙
= 被称为微元面的矢量面积。这个微元面上单位面积表面力 为
=
= ∙ → = ∑
=
这里下标指微元面的朝向, 并不一定与平行。单位面积表面力也称为应力。
我们观察一个占据空间体积τ的流体单元:其表面为 A。A 由无数微元面 = 构成。那
短程力的主要形式作用在物体与物体间的接触面上(也包括物体内部的切面)
,被称为表面
力,我们这里用 表示;单位面积上的表面力被称为应力。一般情况下,应力(物体内部切
上海交通大学流体力学第二章

v2 2
gz
p
常数
(全流场)
C2.2 一般概念(2-2)
3. 斯托克斯定理 (封闭曲线、涡束)
开尔文定理 (无粘、正压、有势力)
蜒l v dr A ndA
d
0 (沿封闭流体线) dt
[例C2.2.2] 有自由面的势涡:无旋流伯努利方程
已知: 涡量处处为零的涡旋运动称为势涡(参见C2.4.3),速度分布为 v=v0=C/r,C为常数,r为径向坐标。
2. 求解驻点位置(θcr)
2Usincr2 aຫໍສະໝຸດ 0crsin
1
4 aU
|Γ|<4πaU 有两个驻点
|Γ|=4πaU 有一个驻点
|Γ|>4πaU 无驻点(自由驻点)
3. 表面压强系数
Cp
1 4sin2
2 sin aU
4
2
2a2U 2
4. 压强合力
Fx=0,
Fy=ρUΓ 升力公式
C2.6 绕机翼的平面势流
C2.2 一般概念
C2.1 引言(工程背景) C2.2 一般概念
1. 欧拉运动方程 (无粘)
v t
v
v
f
p
兰姆—葛罗米柯方程 (无粘)
2. 欧拉积分(无粘、无旋 正压、重力 、定常)
v
t
v2 2
v v
f
p
v2 gz
2
dp 常数
(全流场)
伯努利积分(无粘、无旋 不可压、重力、定常)
x2
y
1 2C
2
1 4C 2
[例C2.4.4] 兰金半体绕流:均流+点源(2-1)
已知: 位于原点的强度为Q(Q>0)的点源与沿x方向速度为U的均流叠
上海交通大学流体力学第二章

物理背景 点源点汇无限接近(δ→0)形成的流场。 (偶极矩M = Qδ= 常数,源→汇)
当偶极子位于原点 M cos
vr 2 r2 M sin
v 2 r2
M
2
cos
r
M
2
x x2 y2
M
2
sin
r
M
2
y x2 y2
等势线Φ=C 流线 Ψ=C
x
1 2C
2
y2
1 4C 2
Ursin
Q 2
(a)
(2)速度分布式为
Urcos
Q 2
lnr
(b)
vr
r
Ucos
Q 2 r
(c)
v
1 r
Usin
(d)
(3)流线方程为
Ursin
Q 2
C
(e)
C 取不同值代表不同流线。其中通过駐点的流线的一部分为该流场绕流 物体的轮廓线,即物面流线。
[例C2.4.4] 兰金半体绕流:均流+点源(2-2)
C2.2 一般概念
C2.1 引言(工程背景) C2.2 一般概念
1. 欧拉运动方程 (无粘)
v t
v
v
f
p
兰姆—葛罗米柯方程 (无粘)
2. 欧拉积分(无粘、无旋 正压、重力 、定常)
v
t
v2 2
v v
f
p
v2 gz
2
dp 常数
(全流场)
伯努利积分(无粘、无旋 不可压、重力、定常)
(4)物面流线的左半支是负x轴的一部分(θ=π),驻点A(-b,0)由
下式决定
vr,
( Ucos
上海交通大学流体力学第三章
F
p x
dx
r2
2
rdx
0
dp 2
dx r
p仅与x 有关, τ与x 无关. 只有均为常数才相等. 令比压降为 G p dp 常数 l dx
1 dp r G r
2 dx 2 上式称为斯托克斯公式,说明切应力沿径向线性分布。
C3.4.1 用动量方程求解速度分布(2-2)
4. 平均速度
V
Q b
b2
12
dp dx
2 3
um
C3.3.2 平板库埃特流(2-1)
C3.3.2 平板库埃特流动
在平板泊肃叶流上再增加上板以U 运动条件,方程不变。
1. 速度分布
u
1
2
dp dx
y2
C1y
C2
y 0,u 0, C2 0
U b dp
yb,
u U
,
C1
b
2
dx
u U y 1 dp ( y2 by)
b 2 dx
平板剪切流
泊肃叶流
上式表示流场为平板剪切流与泊肃叶流叠加的结果。
无量纲形式为
u U
y b
B 1
y b
y b
,
B b2 dp
2U dx
C3.3.2 平板库埃特流(2-2)
平板库埃特流流场取决于U 和 dp(或B)的大小和方向。设U> 0 dx
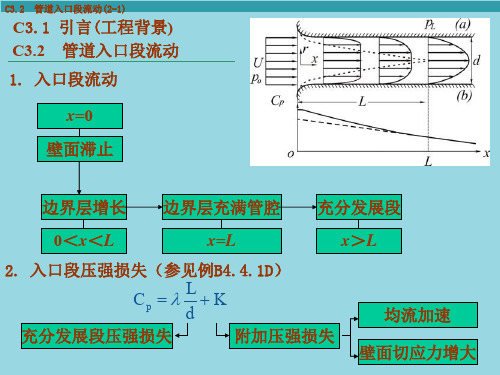
C3.2 管道入口段流动(2-1)
C3.1 引言(工程背景) C3.2 管道入口段流动 1. 入口段流动
x=0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/3/22
18
2.4.3 粘性流体总流的伯努利方程
理想流体总流的伯努利方程
z1p 121cgf21z2p222cgf22
理想流体运动:总机械能守恒; 粘性流体运动:流层间的摩擦阻力会消耗机械能,因此,
总机械能将沿流程减小。
z1p 12 1cgf21z2p 222c gf22hw
单位质量流体从断面 1-1到2-2消耗的机械
水力半径:液流断面面积A与湿周的比值 RA/U
de
4R
4A U
反映了液流断面形状、尺寸对过流能力 的影响,水力半径愈大,过流能力愈强
湿周 ,表示液流的有效断面与固体相接触的周界
2020/3/22
31
湿周
r
U2(hb)
de
2020/3/22
2hb hb
U(d1d2)
de d2 d1
U d
de
4S1S2
能—流体能量损失。
粘性流体的伯努利方程
2020/3/22
19
沿程损失—摩擦阻力引起的能 量损失与流程长度成正比 h f
局部损失—流体流经局部障碍 (如:管接头、弯头、闸阀、 管径突变)时,由于边界形状 急剧变化流体微团发生碰撞、
产生旋涡等引起能量损失 h j
沿程损失系数
hf
l d
c
2 f
2g
管长 管内流体的平均速度
11
2.3.2 迹线、流线
迹线—— 流体质点在空间运动的轨迹线。
流线——各点的速度矢量与之相切的有向曲线。 ●定常流动中,流线不随时间变化; ●除在速度为零或无穷大的那些点,流线不能相交。
2.3.3 流管、流束、总流
• 流管—某一瞬时,通过曲线C上 各点的所有流线构成一管状曲面。
• 流束—管内所有流线的总和。
g
hf
64 l Red
cf2 2g
l
d
cf2 2g
r0 d 2
Recfd
达西公式
64 Re
圆管层流的沿程损失系数与雷诺 数成反比,与管壁粗糙度无关。
2020/3/22
26
2.5.3 管内紊流
紧靠管壁处有一极薄的流体(厚度一般为十分之几毫米) 因受管壁限制,脉动现象很弱。粘性起主要作用,流速梯度 很大,这一极薄流体层称为粘性底层。在粘性底层之外,有 很薄的过渡层,过渡层之外是紊流核心区(紊流区),紊流 核心区脉动较为充分,速度分布趋于均匀化。圆管中紊流的 速度分布与流体性质及管壁情况有关。
比固体更易变形与压缩 流体只能承受压力,几乎不能承受拉力
2.1.2连续介质假设
1mm3水中有3.34×1020个分子,平均经过10-11s,分子就会 从一个平衡位置 转向另一平衡位置,而在一般工程问题中描 述流体运动的空间尺度精确到0.01mm就满足精度要求。
连续介质假设
流体力学研究流体的宏观特性,忽略流体的分子构成,把 它看作一种连续性的介质,认为其中没有任何间隙。
应用总流伯努利方程时应注意: (1) 流体是理想、不可压缩;流动是定常;质量力仅是重力; (2) 所取的两个有效断面一定要处于缓变流区域,但在这两个 有效断面之间可以有急变流; (3) 在所取的两个有效断面之间不能有能量输入或输出;
(4) 在缓变流的同一有效断面上 z p 是常数,因此可以在
断面上的任意点取值,一般取断面形心处的值较方便。
圆管内平均速度
cf, max
p
4l
r02
cf qA V 8plr0212cf,max 圆管层流的最大速度等
于平均速度的两倍。 ●阻力损失
水平等径圆管内仅有沿程损失,且沿程损失就等于压力损失。
h f p
2020/3/22
hf
8l r02
cf
25
hf
8l r02
cf
圆管层流沿程损失
与平均速度成正比
位置水头 压力水头 速度水头 三种水头之和称为总水头 (静压力) (动压力)
伯努利方程的几何意义
在流场中或沿流线, 任意点的位置水头、压 力水头与速度水头之和 是常数。
2020/3/22
16
2.4.2 总流的伯努利方程
工程实际(管道、渠道)中要解决的是总流流动的问题。由于 在总流的有效断面上,各运动参数一般是变化的,因此要将沿流 线的伯努利方程进行的修正。
把整个管子或渠道中的流体看作总的流束,这种由无限多微元 流束所组成的总的流束称为总流。
缓变流——流线几乎平行的直线的流动情况。
实验已证明缓变流沿有效断面 z p 常数
2020/3/22
17
z1p 112 cf2 g1 z2p 222 cf2 g 2 总流的伯努利方程
工业管道通常的工作状态下=1.051.12,一般可近似取1
气体
2020/3/22
h 1 1 2 c f 2 1 g z 1 h 2 1 2 c f 2 2 g z2 h 1 2 c f 2 g z
h11 2cf21h21 2cf22h1 2cf2
13
2-4 流体的伯努利方程
2.4.1 理想流体的伯努利方程
h u pv u p
h 1 1 2 c f 2 1 g z 1 h 2 1 2 c f 2 2 g z2 h 1 2 c f ห้องสมุดไป่ตู้ g z u 1 p 1 v 1 1 2 c f 2 1 g z 1 u 2 p 2 v 2 1 2 c f 2 2 g z 2 u p v 1 2 c f 2 g z
2.6.1 圆管沿程阻力损失和莫迪图
圆管沿程阻力损失高度表达式,hf
l d
c
2 f
2g
适用于层流与紊流
层流:λ= 64/Re;
紊流:主要依靠实验。
圆管中的水流分成五个区域:
层流区
层流向紊流转变的临界区
紊流光滑区
0.4
或
4000 Re 80 d
紊流过渡区
0.4 6
或 80d Re1000d
先按理想流体处理,然后再考虑粘性影响加以修正,以解决
工20程20/3实/22 际问题。
5
2-2 流体静力学的基本方程
流体静力学研究流体在静止状态下的力学规律。
2.2.1 静止流体中的应力特征
●流体不能承受拉力; ●静止时不存在切向应力,静止流体中的应力垂直于作用面,
这种法向应力称为压力(或压强) ●静止流体中的任意一给定点上,静压力 不论来自何方向,其值均相等。
2020/3/22
7
2.2.3 流体静力学基本方程
1. 流体静力学基本方程
假设:质量力仅为重力;
流体均质不可压缩( =常数)
dpgdz
dz dp 0
单位质量流体的位势能; 是相对于基准面的高度, 又称位置高度或位置水头
位势能与压力势能之和称为总势能; 位置水头与压力水头之和称为静水头
单位质量流体的 压力势能。
2020/3/22
23
判别准则 无量纲数Re数
定型尺寸
Re cfd cfd
动力粘度
运动粘度
圆管内流动 Re<2 320 层流
Re>2 320 紊流
104Re2320过度流 Re 104 旺盛紊流
2020/3/22
24
2.5.2 黏性流体圆管中的层流
●速度分布 半径为r0的水平直圆管,流体作定常流动, 层流的速度分布为 抛物线规律变化。
与一段液柱高度相当,
z p C
又称之为压力高度或 压力水头。
z1
p1
z2
p2
2020/3/22
流体静力学基本方程
9
2. 流体静力学基本方程物理意义:
z1p 1 z2p 2 zpC
当均质不可压缩流体在重力场中处于静止时,在流体中的 任意点上,单位重量流体的总势能是常数。也可叙述为:任 意点的静水头均相等。
3. 帕斯卡原理
流体静力学基本方程用于液面上一点
与液体内淹深为h的任意一点
z p zh p0
p p0 h
静止液体中,任意一点的压力等于液面
压力加上高度为h的液柱所产生的压力。
液面上的压力变化,液体内其余点的压力
也会随之变化同样的数值。
2020/3/22 --压力传递的帕斯卡原理。
10
2020/3/22
d
d
32
2.6.3 局部阻力损失
管路中流体在通过各种管件,如阀门、三通、弯管时,使 流体运动中产生旋涡和剧烈的碰撞摩擦形成的局部能量损失。
产生原因: ●旋涡流动的能量损失 ●流体质点的碰撞 ●速度重新分布带来的能量损失 ●流向改变造成的能量损失
由连续介质假设出发,流体运动中的压力、流动速度等都
可2视020为/3/22连续变量。
2
2.1.4 流体的粘性
●流体粘性的表现: ★流体与固体壁面相接触,
会粘附于固壁表面。
★相邻两层流体作相对运动时也会产生摩擦阻力。
●动力粘性系数和运动粘性系数 流体内摩擦力的大小与速度U成正比,与
接触面积A成正比,与两板间距离h成反比:
F AU h
动力粘性系数简称粘性系数或粘度,N·s/m2或Pa·s
2020/3/22
4
运动粘性系数 :—— 与流体密度 之比值
单位:m2/s。有时也用cm2/s,称为斯。
动力粘性系数 的大小与流体的种类、温度以及压
力有关。但压力的影响很小,一般只考虑温度的影响。
▲液体的粘性系数随温度升高而降低;
2cf2g1 z2p2
cf22 2g
单位质量流 体的位势能
单位质量流 单位质量流体的动能 体的压力势能
伯努利方程的物理意义
在流场中或沿流线,单位质量流体具有的位势能、压力 势能及动能之和是一个常数,或,总机械能是常数。
