2019全国MBA联考综合能力真题及答案
2019年全国硕士研究生入学统一考试管理类联考综合能力(199)真题

2019年全国硕士研究生入学统一考试管理类联考综合能力(199)真题一、问题求解:第1—15小题,每小题3分,共45分。
下列每题给出的A 、B 、C 、D 、E 五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1、某车间计划10天完成一项任务,工作了3天后因故停工2天,若要按原计划完成任务,则工作效率需要提高( )A.20%B.30%C.40%D.50%E.60% 2、设函数2()2af x x x=+(a >0)在(0,+∞)内的最小值为0()12f x =,则x 0=( )。
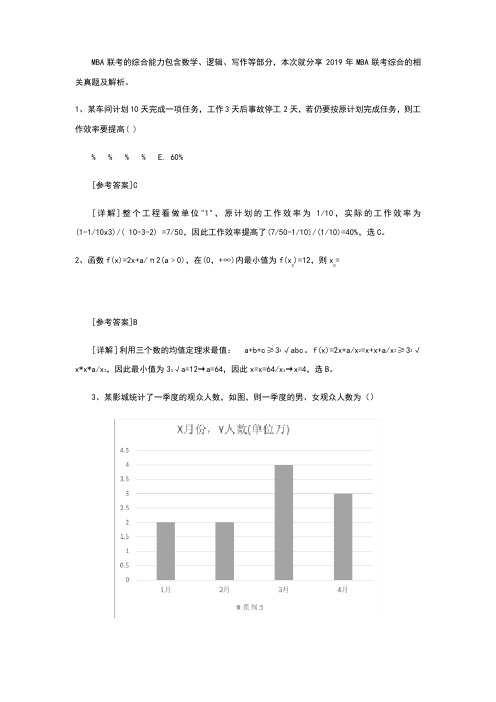
A.5B.4C.3D.2E.13、某影城统计了一季度的观众人数,如图,则一季度的男、女观众人数之比为( )。
A.3:4B.5:6C.12:13D.13:12E.4:34、设实数a ,b 满足ab =6,6a b a b ++-=,则22a b += A.10 B.11 C.12 D.13 E.145、设圆C 与圆22(5)2x y -+=关于直线y =2x 对称,则圆C 的方程为( )。
1女性观众人数A.22(3)(4)2x y -+-=B. 22(4)(3)2x y ++-=C.22(3)(4)2x y -++=D.22(3)(4)2x y +++=E.22(3)(4)2x y ++-=6、在分别记了数字1、2、3、4、5、6的6张卡片中,甲随机抽取1张后,乙从余下的卡片中再随机抽取2张,乙的卡片数字之和大于甲的卡片数字的概率为( )。
A.1160 B.1360 C.4360D.4760E.4960 7、将一批树苗种在一个正方形花园的边上,四角都种,如果每隔3米种一颗,那么剩余10颗树苗,如果每隔2米种一颗那么恰好种满正方形的3边,则这批树苗有( )。
A.54颗B.60颗C.70颗D.82颗E.94颗 8、10名同学的语文和数学的成绩如表:语文和数学成绩的均值分别为E 1和E 2,标准差分别为σ1和σ2,则( )。
MBA复试管理学真题题库及答案

2019 年全国硕士研究生入学统一考试管理类专业学位联考综合能力一、问题求解:第1~15 题,每小题3 分,共45 分。
下列每题给出的A、B、C、D、E 五个选项中,只有一项是符合试题要求的。
1. 某车间计划10 天完成一项任务,工作3 天后因故停工2 天。
若要按原计划完成任务,则需要工作效率提高()。
A. 20%B. 30%C. 40%D. 50%E. 60%2.A. 5B. 4C. 3D.2E.13. 某影城统计了一季度的观众人数,如图,则一季度男女观众人数之比为()A. 3:4B. 5:6C. 12:13D. 13:12E.4:34. 设实数a,b满足ab = 6,a+ b + a - b = 6,则a2 + b2 = ()A. 10B. 11C. 12D. 13E.145. 设圆C 与圆(x-5)2+y2=2关于y=2x对称,则圆C 的方程为()A. (x-3)2+(y-4)2=2 C. (x-3)2+(y+4)2=2B. (x+4)2+(y-3)2=2 D. (x+3)2+(y+4)2=212E. ( x + 3)2 + ( y - 4)2= 26. 将一批树苗种在一个正方形花园边上,四角都种,如果每隔 3 米种一棵,那么剩下 10 棵树苗;如果每隔 2 米种一棵,那么恰好种满正方形的 3 条边,则这批树苗有()棵。
A. 54B. 60C. 70D. 82E. 947. 有分别标记 1,2,3,4,5,6 的 6 张卡片,甲抽取 1 张,乙从余下的卡片中再抽取 2 张, 乙的卡片数字之和大于甲的卡片数字的概率为()A. 11 60B. 13 60C. 43 60D. 4760E. 49 608. 10 名同学的语文和数学成绩如下:语文和数学的均值分别是 E 1和E 2 ,标准差分别为σ1和σ 2 ,则( )A. E 1 > E 2 ,σ1 > σ2B. E 1 > E 2 ,σ1 < σ2C. E 1 > E 2 ,σ1 = σ2D. E 1 < E 2 ,σ1 > σ2E. E 1 < E 2 ,σ1 < σ29. 如图,正方体位于半径为 3 的球内,且一面位于球的大圆上,则正方体表面积最大为 ( )A. 12B. 18C. 24D. 30E. 3610. 在三角形 ABC 中, AB = 4, AC = 6, BC = 8, D 为BC 中点,则AD =( )C. 3D.311. 某单位要铺设草坪,若甲乙两公司合作需要 6 天完成,工时费共 2.4 万元。
2019年MBA联考综合能力真题及答案解析

第14题
某中学的5个学科各推荐2名教师作为支教候选人,若从中选派来自不同学科的2人参加支教工作,则不同的选派方案有______
A.20种
B.24种
C.30种
D.40种
E.45种
上一题下一题
(15/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中,只有一个选项符合试题要求.
第15题
设数列{an}满足a1=0,an+1-2an=1,则a100=______
A.299-1
B.299
C.299+1
D.2100-1
E.2100+1
上一题下一题
(16~25/共10题)二、条件充分性判断
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论.A、B、C、D、E五个选项为判断结果,请选择一项符合试题要求的判断.
A.条件(1)充分,但条件(2)不充分。B.条件(2)充分,但条件(1)不充分。C.条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。D.条件(1)充分,条件(2)也充分。E.条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
第16题
甲、乙、丙三人各自拥有不超过10本图书,甲再购入2本图书后,他们拥有图书的数量能构成等比数列。则能确定甲拥有图书的数量。
C.(x-3)2+(y+4)2=2
D.(x+3)2+(y+4)2=2
E.(x+3)2+(y-4)2=2
上一题下一题
(6/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中,只有一个选项符合试题要求.
2019年1月MBA综合真题及答案word精品文档14页

2019年全国硕士研究生入学统一考试管理类专业学位联考综合能力试题说明:由于2019年试题为一题多卷,因此现场试卷中的选择题部分,不同考生有不同顺序。
请在核对答案时注意题目和选项的具体内容。
一、问题求解(第1~15小题,每小题3分,共45分,下列每题给出的A 、B 、C 、D 、E 五个选项中,只有一个是符合试题要求的,请在答题卡上将所选项的字母涂黑)。
1.某工厂生产一批零件,计划10天完成任务,实际提前两天完成,则每天的产量比计划平均提高了( )。
A.15%B.20%C.25%D.30%E.35%2.甲乙两人同时从A 地出发,沿400米跑道同向匀速行走,25分钟后乙比甲少走了一圈。
若乙行走一圈需要8分钟,则甲的速度是( )米/分钟A.62B.65C.66D.67E.693.甲班共有30名学生,在一次满分为100分的考试中,全班平均成绩为90分,则成绩低于60分的学生至多有( )个。
A.8B.7C.6D.5E.44.某工程由甲公司承包需60天完成,由甲、乙两公司共同承包需28天完成,由乙、丙两公司共同承包需35天完成,则由丙公司承包并完成该工程需要的天数是( )A.85B.90C.95D.100E.105 5.已知)10)(9(1)3)(2(1)2)(1(1)(+++⋅⋅⋅++++++=x x x x x x x f ,则=)8(f ( ) A.91 B.101 C.161 D.171 E.181 6.甲乙两商店同时购进了某品牌电视机,当甲商店售出了15台时乙商店售出了10台,此时两店的库存比为8:7,库存差为5,则甲乙两店总进货量为( )A.75B.80C.85D.100E.1257.如图,在直角三角形ABC 中,4=AC ,3=BC ,BC DE //,已知梯形BCDE 的面积为3,则=DE ( ) A.3 B.13+ C.434- D.223 E.12+8.点)4,0(关于关于直线012=++y x 的对称点为( )A.)0,2(B.)0,3(-C.)1,6(-D.)2,4(E.)2,4(- 9.在52)53(++x x 的展开式中,2x 的系数为( )A.5B.10C.45D.90E.9510.有一批水果要装箱,一名熟练工单独装箱需要10天,每天报酬为200元;一名普通工单独装箱需要15天,每天报酬为120元。
2019年管理类MBA综合考试数学真题及详细答案解析(pdf版)

2019年管理类MBA 综合考试数学真题及详细答案解析一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A 、B 、C 、D 、E五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1. 某车间计划10天完成一项任务,工作了3天后因故停工2天,若要按原计划完成任务,则工作效率需要提高( ).A .20% B. 30% C. 40% D. 50% E. 60%解析:(C )解法1:将整个任务的工作量看作单位“1”,则原计划的工作效率为110.工作3天后因故停工2天,余下的工作量为17131010-⨯=,需要5天完成,则工作效率为7751050÷=,工作效率提高了71501040%10-=.解法2:工作3天后因故停工2天,若要按原计划完成任务,就要在剩余的5天内完成原计划7天的工作量,则工作效率需要提高11757100%1100%40%157⎛⎫- ⎪⎛⎫⨯=-⨯= ⎪ ⎪⎝⎭ ⎪⎝⎭。
2. 设函数2()2(0)af x x a x=+>在(0,)+∞内的最小值为0()12f x =,则0x =( ).A. 5B. 4C. 3D. 2E. 1解析:(B )利用三个数的均值定理求最值:a b c ++≥,且“=”只在a b c ==时取到。
322()231264a a f x x x x x x a a x x =+=++≥==⇒=, 此时有2644x x x x==⇒= 注:本解法中2x 一定要拆成两个相等的数相加,即x x +,如果拆成其它形式(如0.5 1.5x x +),则不等式取等号的条件就不满足了。
3. 某影城统计了一季度的观众人数,如图,则一季度的男性观众人数与女性观众之比为( ) A. 3:4 B. 5:6 C. 12:13 D. 13:12 E. 4:3 解析:(C )由图可得一季度男女观众人数分别为:男:54312++=万人; 女:63413++=万人因此一季度男女人数比为:12:134. 设实数,a b 满足6,6ab a b a b =++-=,则22a b +=( ). A. 10 B. 11 C. 12 D. 13 E. 14解析:(D )解法1:想办法去掉绝对值,由60ab =>知,a b 同号,若同正,不妨设0a b >>,此时263a b a b a b a b a a ++-=++-==⇒=,进而62b a==,代入得2213a b +=;若同负,不妨设0a b <<,此时263a b a b a b a b a a ++-=---+=-=⇒=-,进而62b a==-,代入得2213a b +=。
2019年MBA联考综合真题及答案
语文成绩: 90、92、94、88、86、85、87、89、91、93
数学成绩: 94、88、96、93、90、85、84、80、82、98
语文和数学成绩的均値分别为 E1 和 E2,柝准差分别为&1 和&2,则
>E2, &1>&2 >E2, &1<&2
>E2, &1=&2
<E2, &1>&2 <E2, &1<&28
E. 14 [参考答案]D [解析] : ab=6,特值法 a=2,b=3 満足条件,a2+b2=4+9=13,选 D。 5、设圆 C 与圆(x-5)2+y2=2,关于 y=2x 时称,则圆 C 方程为( ) A. (x-3)2+(y-4)2=2 B.(x+4)2+(y-3)2=2 B. (x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2 E. (x+3)2+(y-4)2= 2 [参考答案]E 6、将一批树苗种在应该正方形花园边上,四角都种,如果每隔 3 米种一棵,那么剩下 10 课树苗,如果每隔 2 米种一棵那么种满正方形的 3 条边,则这批树苗有( ) 棵 A、54B、60 C、70D、82 E、94 [参考答案]D [详解]设正方形的边长为 x,由已知可得方程 4x/3+10=3x/2+1,求解得 x=54 故树苗有(54x4)/3+10=82,选 D。
2、函数 f(x)=2x+a/π2(a﹥0),在(0,+∞)内最小值为 f(x )=12,则 x =
MBA联考综合能力真题2019年附答案解析

MBA联考综合能力真题2019年2. 设函数在(0,+∞)内的最小值为f(x0)=12,则x0=______ •B[解析] 本题考查均值不等式。
由于x>0,a>0,则f(x)的表达式各项均大于0,考虑运用均值不等式分析其最小值。
则a=64,当且仅当,即x=4时取等号。
故本题选B。
•方法二(计算法):两圆圆心关于直线y=2x 对称,即两点连线的中点在y=2x 上,两点连线与y=2x垂直。
设圆C 的圆心为(a ,b),则满足方程组解得即圆C 的圆心为(-3,4),半径与已知圆半径相等,所以圆C 的方程为(x+3)2+(y-4)=2。
故本题选E 。
6. 将一批树苗种在一个正方形花园的边上,四角都种。
如果每隔3米种一棵,那么剩余10棵树苗;如果每隔2米种一棵,那么恰好种满整个正方形的3条边,则这批树苗有______D[解析] 本题考查植树问题。
设正方形边长为x,四个角都种树且每隔3米种一棵树,四边种满,则所种树总数为;四个角都种树且每隔2米种一棵树,种满三边,则所种树总数为。
根据题意有,得x=54。
这批树苗共有棵。
故本题选D。
注:在封闭路线上植树,植树总棵数=距离÷间距。
在非封闭路线上植树,若两端都植树,植树总棵数=距离÷间距+1。
7. 在分别标记了数字1,2,3,4,5,6的6张卡片中,甲随机抽取1张后,乙从余下的卡片中再随机抽取2张,乙的卡片数字之和大于甲的卡片数字的概率为______A.B.C.D.E.D[解析] 本题考查古典概型。
甲先抽取到每一个数字的概率均为。
乙从剩下的卡片中抽取两张,不同的情况总数均为,其中有一些情况不满足大于甲所抽取的卡片数字。
如下表:所求事件概率为。
故本题选D。
B[解析] 本题考查均值与方差。
语文成绩从小到大排序,86,87,88,89,90,91,92,93,94,95,为连续自然数,均值;数学成绩从小到大排序,80,82,84,85,88,90,93,94,96,98,前后对应位置两个数之和都相等,均值。
2019年全国硕士研究生入学统一考试管理类联考综合能力(199)真题

全国硕士研究生入学统一考试管理类联考综合能力(199)真题一、问题求解:第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1.某品牌的电冰箱连续两次降价10%后的售价是降价前的()。
(A)80%(B)81%(C)82%(D)83%(E)85%2.张老师到一所中学进行招生咨询,上午接受了45名同学的咨询,其中的9人下午又咨询了张老师,占他下午咨询学生的10%,一天张老师咨询的学生人数为()。
(A)81(B)90(C)115(D)126(E)1351(A4. x(A5.(A6.(A7.备,则购买的甲、乙办公设备的件数分别为( )。
(A )3,5 (B )5,3 (C )4,4 (D )2,6 (E )6,28.老师问班上50名同学周末复习的情况,结果有20人复习过数学,30人复习过语文,6人复习过英语,且同时复习了数学和语文的有10人,语文和英语的有2人,英语和数学的有3人,若同时复习过这三门课的人数为0,则没复习过这三门课程的学生人数为( )。
(A )7 (B )8 (C )9 (D )10 (E )119.如图1,在扇形AOB 中,π∠⊥AOB=,OA=1,ACOB,4则阴影部分的面积为( )。
(A )1π-84 (B )1π-88 (C )1π-42 (D )1π-44 (E )1π-48 1和100之间,能被9整除的正数的平均值是( )。
27(B )36(C )45(D )54(E )63已知ABC ∆和A B C '''∆满足:'''''∠∠πAB:AB=AC:AC=23,A+A=,ABC 与A B C '''∆的面积之比为( )。
(A )2:3 (B )3:5 (C )2:3 (D ):25(E )4:9 12.甲从1,2,3中抽取一数,记为a ,乙从1,2,3,4中抽取一数,记为b,规定当a>b或a+1<b时甲获胜,则甲获胜的概率为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、某车间计划10天完成一项任务,工作3天后事故停工2天,若仍要按原计划完成任务,则工作效率要提高( )% % % % E. 60%[参考答案]C[详解]整个工程看做单位"1",原计划的工作效率为1/10,实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50,因此工作效率提高了(7/50-1/10)/(1/10)=40%,选C。
2、函数f(x)=2x+a/π²(a﹥0),在(0,+∞)内最小值为f(x0)=12,则x0=[参考答案]B[详解]利用三个数的均值定理求最值:a+b+c≥33√abc。
f(x)=2x+a/x2=x+x+a/x2≥33√x*x*a/x2,因此最小值为33√a=12→a=64,因此x=x=64/x2→x=4,选B。
(3、某影城统计了一季度的观众人数,如图,则一季度的男、女观众人数为():4 :6 :13 :12 :3[参考答案]C[详解]如图可得:一季度男女观众人数分別为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= l3w故一季度男女人数比的: 12:13,选C。
4、;2+b2=( )5、没实数a,b満足ab=6,|a+b| +|a-b|=6,则aE. 14[参考答案]D[解析] : ab=6,特值法a=2,b=3満足条件,a2+b2=4+9=13,选D。
6、设圆C与圆(x-5)2+y2=2,关于y=2x时称,则圆C方程为( )A.(x-3)2+(y-4)2=2B.(x+4)2+(y-3)2=2B.(x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2E.(x+3)2+(y-4)2= 2…[参考答案]E7、将一批树苗种在应该正方形花园边上,四角都种,如果每隔3米种一棵,那么剩下10课树苗,如果每隔2米种一棵那么种满正方形的3条边,则这批树苗有( ) 棵A、54B、60C、70D、82E、94[参考答案]D[详解]设正方形的边长为x,由已知可得方程4x/3+10=3x/2+1,求解得x=54故树苗有(54x4)/3+10=82,选D。
7、在分别标记1、2、3、4、5、6的6张卡片里,甲抽取1张,乙从余下的卡片中再抽取2张,乙的卡片的数字之和大于甲的卡片数字的概率为( )A. 11/60 60 60 60 60$[参考答案]D[解析]样本空间Ω=C16xC25;事件A:反面考虑,穷举法甲抽6,乙有(5,1);(4,2);(4,1);(3,1);(3,2);(1,2)共6种甲抽5,乙有(4,1);(3,1);(3,2);(1,2)共4种 ;甲抽4,乙有(3,1);(1,2)共2种,甲抽3,乙有(1,2)共1种综上事件A=6+4+2+1=13种,1-P(A)=1-13/(C16+C25)=47/60,选D。
】8、10名同学的語文和数学成绩如下:语文成绩: 90、92、94、88、86、85、87、89、91、93数学成绩: 94、88、96、93、90、85、84、80、82、98语文和数学成绩的均値分別为E1和E2,柝准差分別为&1和&2,则>E2, &1>&2 >E2, &1<&2 >E2, &1=&2<E2, &1>&2 <E2, &1<&28[参考答案]B[详解]简化两組数据,以90为基数,如下:'语文: 0,2,4,-2,4,5,-3,-1,1,3,平均值: 5/10=,故E1=数学: 4,-2,6,3,0,-5,-6,-10,-8,8, 平均值: -1,故E2=89因此: E1> E2,观察两组数据的稳定性可知:语文较数学稳定,因此&1>&2,选B。
9、如图,正方体于半径为3m球内,且一面位于球的大圆上,则正方体的表面积最大为()[参考答案] E[解析] :欲使正方体的表面积最大,正方体与球的位置关系如下图:—面ABCD在过球心的大圆上,点A、B、C、D、在球面上球心O与球面上一点C连接即为半径: OC=3在△OCC中利用勾股定理,设正方体边长为a,则a2+(√2/2*a)2=32→a=√6,故正方体表面积S=6a2=36,选E。
10、在三角形ABC中,AB=4,AC=6,BC=8,D为BC中点,则AD=()A.√11B.√10 √2 E.√7[参考答案]B[详解]设5个学科的人分别为Aa,Bb,Cc,Dd,Ee,现从10人中选2人,2人来自不同学科,反面考虑: Ω=C210,反面即为来自同一学科C15=5,故共有C210-5=40种,选D。
11、某单位要铺设草坪,若甲乙两公司合作需6天完成,工时费共万元,若甲公司单独做,4天后由乙公司接着做天完成,工时费共计万元。
若由甲公司单独完成该项目,则工时费共计()万元参考答案]E…[详解]设甲乙的工作效率分别是x,y;甲乙每天的工时费分别是a,b;由已知可得方程组如下6x+6y=1和4x+9y=1,故得出x=1/10;6a+6b=和4a+4b=,故得出a=。
故甲单独做的工时费为=,选E。
12、如下图,六边形ABCDEF是平面与棱长为2的正方体所截得到的,若A、B、D. B分别为相应棱的中点,则六边形ABCDEF的面积为()√2 B.√3 √3 √3 √3[参考答案]D[详解]六边形ABCDEF从正方体中拿出如下图: O为球心:】由勾股定理可得:DE= AB=√2,OD=√2,同理: OE=0A=OB=√2,因此ABCDEF为正六边形,由6个等边三角形组成,即S ABCDEF=6xS△OAB=6*√3/4(√2)2=3√3,选D。
13、货车行驶72km用时1小时,速度V与行驶时间t的关系如图所示,则V0= ()[参考答案]C[详解]如图,梯形的面积即为货车行驶的路程,梯形的高即为V,因此S=[ +1]xV0/2=72,解得V0=90,选C。
14、某中学的5个学科各推荐2名教师作为支教候选人,若从中选派来自不同学科的2人参加支教工作,则不同的选派方式有()([参考答案] D[详解]过A作BC的高AH,设BH=x ,则CH=8-x.在Rt△ABH中,AH=√(42-x2),在Rt△AHC中,AH=√[62-(8-x)2] ,AH=AH,得√(42-x2) =√[62-(8-x)2]。
解得x=11/4,则DH=BD- BH=4-11/4=4/5。
在Rt△AHD中,由勾股定理得: AH2+ DH2= AD2 ,其中DH2=25/16,AH2=AB2- BH2=42- (11/4)2= [(16-11)*(16+11)]/16=135/16,带入解得AD=√10,选B。
15.设数列满足{an}满足a1=0,a n+1-2a n=1, 则a100=()+1 E. 2100+1([参考答案] A[详解]构造等比数列:a n+1-2a n=1,有a n+1=2a n+1,令a n+1+t=2(2a n+t)→a n+1=2a n+t,所以t=1,所以a n+1+1=2(a n+1),所以a n+1是以a 1+1=1为首项,公比为2的等比数列,所以a n=2n-1-1,a n=299-1,选A。
16.甲乙丙三人各自拥有不超过10本图书,甲丙购入2本图书后,他们拥有的图书数量构成等比数列,则能确定甲拥有图书的数量(1)已知乙拥有的图书数量(2)已知己拥有的图书数量[参考答案] A17.有甲、乙两袋奖券,获奖率分別为p和q。
某人从两袋中各随机抽取1张奖券,则此人获奖的概率不小于3/4(1)已知p+q=1(2)¥(3)已知pq=1/4[参考答案] D18、直线y=kx与圆x2+y2-4x+3=0有两个交点(1)√3/3<k<0(2)0<k<√2/2[参考答案]A19、能确定小明年龄(1)小明年龄是完全平方数(2)#(3)20年后小明年龄是完全平方数[参考答案]C[详解]单独两个条件显然不充分,完全平方数,列举如下:0,1,4,9,16,25,36,49,64,81,100,121,..... 观察可发现相邻两个完全平方数之差成等差数列,首项为1,公比为2,因此相差为20的两个完全平方数必出现在100之前,只有16和36,因此小明是16岁,充分。
20、关于x的方程x +ax+b=0有实根。
(1) a+b=0(2) a-b=0[参考答案]D[详解]一元二次方程根的判别式△=a2-4b,:条件(1)a+b=0→a=- b→△=b2-4b = b(b-4)无法确定正负性,不充分;条件(2)a-b=0→a=b→△=b2-4b= b(b-4)同上,不充分:条件(1)+条件(2) 可得出a+b=0和a-b=0→a=b=0,故方程为x2-=0有根,充分,选C。
21.如图,已知正方形ABCD面积,O为BC上一点,P为AO的中点,Q为DO上一点,则能确定△PQD面积(1) O为BC的三等分点 (2) Q为DO的三等分点[参考答案] B[详解]如图MOD的面积恒定,与点O的具体位置无关,…S△AOD=1/2AD*h=1/2AD*DC,故△POD的面积也恒定,点P为AO的中点,所以S△POD=S△AOD。
因此,两个条件都充分,选D。
22、设n为正整数,则能硝定n除以5的余数(1)已知n除以2的余数(2)已知n除以3的余数[参考答案]E[详解]举反例条件(1)如余数为0,即n为2, 4, 6,8, 10......显然推不出题干,不充分:条件(2)如余数为0,即n为3, 6,912,15......显然不充分条件(1) + (2),举反例:如余数为0,即n为6的倍数,如6,12,18......也不充分,选E。
23、某校理学员五个系列每年录取人数如下表今年与去年相比,物理系平均分没变,则理学员录取平均分升高了(1)数学系录取平均分提高了3分,生物系录取平均分降低了2分(2)化学系录取平均分提高了1分,地理学系录取平均分降低了4分[参考答案] C—[详解]显然两个条件都不充分,条件(1)+条件(2),数学系比去年多了60x3分物理系不变,化学系多了90x1分,生物系少了60x2分,地学系少了30x4分。
故,60x3+90x1- 60x2-30x4= 30分,平均分升高,充分,选C。
24、设三角区域D由直銭x+8y-56=0 ,x-6y+42=0与kx-y+8- 6k=0(k <0)围成,则对任意的(x,y),有㏒(x2+y2)≤2(1) k∈(-∞,-1](2)k∈(-1,1/8][参考答案] A25、设数列{an}的前n项和为S n,则{an}等差。
