江苏省宿迁市高中数学第二章圆锥曲线与方程第9课时双曲线的几何性质1导学案(无答案)苏教版选修2-1
江苏省宿迁中学高中数学选修2-1导学案:第2章 圆锥曲

第7课时 双曲线的标准方程(1)【学习目标】1.掌握双曲线的定义,标准方程. 2.根据已知条件求双曲线的标准方程. 【问题情境】1.类比椭圆标准方程的建立过程推导出双曲线的标准方程.2.把椭圆定义中的“距离的差的绝对值”改为“距离的差”,那么点的轨迹会怎样? 【合作探究】 双曲线的标准方程F 1 ,F 2 F 1 ,F 2 想一想:如何判断方程)0,0(12222>>=-b a b y a x 和)0,0(12222>>=-b a bx a y 所表示的双曲线焦点的位置?【展示点拨】例1.已知双曲线两个焦点的坐标为)0,5()0,5(21F F ,-,双曲线上一点P 到21F F ,的距离之差的绝对值等于8,求双曲线标准方程变式1:若|PF 1|-|PF 2|=8呢? 变式2:若||PF 1|-|PF 2||=10呢? 变式3:若||PF 1|-|PF 2||=6呢?例2.求满足下列条件的双曲线的标准方程(1)a =3,b = 4,焦点在x 轴上; (2)a =25,经过点)5,2(-A ,焦点在y 轴上.例3.如果方程1222=--my m x 表示双曲线,求m 的取值范围.例4.已知A ,B 两地相距800m ,一炮弹在某处爆炸,在A 处听到炮弹爆炸声的时间比在B 处迟2s ,设声速为340/m s .(1)爆炸点在什么曲线上?(2)求这条曲线的方程.【学以致用】1.双曲线192522=-x y 的焦点坐标为 .2.若k ∈R ,则方程x 2k +3+y 2k +2=1表示焦点在x 轴上的双曲线,则k 的取值范围是________.3.已知双曲线的两个焦点分别为1100(,)F -,2100(,)F ,双曲线上一点P 到1F ,2F 的距离的差的绝对值等于12,求双曲线的标准方程. 4. 求适合下列条件的双曲线的标准方程:(1)5=c ,3=b ,焦点在y 轴上;(2)焦点为)6,0(-,)6,0(,3=a .5.已知双曲线过点()3,2-,且与椭圆224936x y +=有相同的焦点,求双曲线的方程.第7课时 双曲线的标准方程(1)【基础训练】1.双曲线192522=-x y 的焦点坐标为 . 2. 方程15922=---k y k x 表示焦点在x 轴上的双曲线,则k 的取值范围是________.3.已知P 是双曲线19422=-y x 上一点,F 1.F 2分别是双曲线的左.右焦点,若PF 1=3,则PF 2等于 .49=,得 .5.设错误!未找到引用源。
高中数学第二章圆锥曲线与方程2.2.2双曲线的几何性质预习导学案
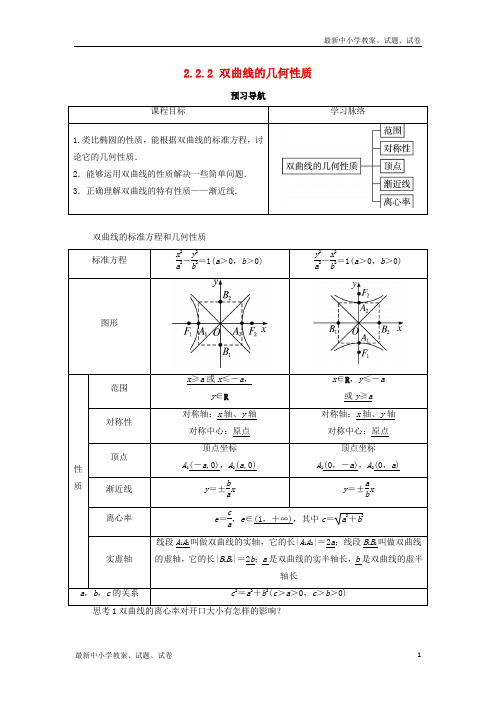
x∈R,y≤-a
或y≥a
对称性
对称轴:x轴、y轴
对称中心:原点
对称轴:x轴、y轴
对称中心:原点
顶点
顶点坐标
A1(-a,0),A2(a,0)
顶点坐标
A1(0,-a),A2(0,a)
渐近线
y=± x
y=± x
离心率
e= ,e∈(1,+∞),其中c=
实虚轴
线段A1A2叫做双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫做双曲线的虚轴பைடு நூலகம்它的长|B1B2|=2b;a是双曲线的实半轴长,b是双曲线的虚半轴长
名师点拨双曲线与椭圆的六个不同点:
双曲线
椭圆
图形
两支曲线
封闭的曲线
顶点
两个顶点
四个顶点
轴
实、虚轴
长、短轴
渐近线
有渐近线
无渐近线
离心率
e>1
0<e<1
a,b,c关系
a2+b2=c2
a2-b2=c2
a,b,c的关系
c2=a2+b2(c>a>0,c>b>0)
思考1双曲线的离心率对开口大小有怎样的影响?
提示:双曲线的离心率e= 反映了双曲线开口的大小,e越大,双曲线的开口就越大.
思考2双曲线的焦点始终在什么轴所在的直线上?
提示:实轴.
思考3一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点?
提示:1个.
2.2.2双曲线的几何性质
预习导航
课程目标
学习脉络
1.类比椭圆的性质,能根据双曲线的标准方程,讨论它的几何性质.
2.能够运用双曲线的性质解决一些简单问题.
3.正确理解双曲线的特有性质——渐近线.
江苏省宿迁市高中数学 第2章 圆锥曲线与方程 第10课时

第10课时 双曲线的几何性质(2)【学习目标】能用双曲线的简单几何性质解决一些简单问题. 【问题情境】1.回顾双曲线的范围.对称轴.顶点.离心率.渐近线;2.已知双曲线的方程为221914x y -=,写出顶点和焦点坐标. 实半轴长.虚半轴长.离心率.渐近线方程. 【合作探究】试比较椭圆与双曲线的几何性质的异同【展示点拨】例1.设双曲线22221x y a b-=的半焦距为c ,直线l 过( , 0) (0 , )a b 、两点,且原点到直线l ,求双曲线的离心率.例2.求与双曲线221169x y -=共渐近线,且经过()3A -点的双曲线的标准方程.例3.焦点在坐标轴上的双曲线,它的两条渐近线方程为02=±y x ,焦点在渐近线的距离为8,求此双曲线方程.例4.若21,F F 是双曲线116922=-y x 的左右焦点,点P 在双曲线上,且3221=⋅PF PF ,求21PF F ∠的大小.【学以致用】1.双曲线1253622=-y x 的渐近线方程是 .2.已知双曲线)0,0(12222>>=-b a by a x 的一条渐近线方程为x y 34=,则双曲线的离心率为 .3.若双曲线的渐近线方程为x y 3±=,它的一个焦点是(10,0),则双曲线的方程是 .4.与椭圆1492422=+y x 共焦点,而与双曲线1643622=-y x 共渐近线的双曲线的方程为 .5.求满足下列条件的双曲线的标准方程.(1)离心率e =()5,3M -;(2)两条渐近线的方程是23y x =±,经过点9,12M ⎛⎫- ⎪⎝⎭. (3)双曲线的一个焦点是)0,3(1-F ,过右焦点2F 作垂直于x 轴的直线交双曲线于点,P 且1230PF F ∠=︒.第10课时 双曲线的几何性质(2)【基础训练】1.双曲线2x 2-y 2=8的实轴长是 .2.当817k <<时,双曲线221178x y k k+=--的焦距为__________________. 3.设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为__________________.4.已知双曲线的中心在坐标原点,一个焦点为(10,0)F ,两条渐近线的方程为43y x =±,则该双曲线的标准方程为______ __.5.圆1)(22=+-y a x 与双曲线122=-y x 的渐近线相切,则a 的值为 .6.双曲线C 1:)0,0(12222>>=-b m b y m x 与椭圆)0(12222>>=+b a by a x 有相同的焦点,双曲线C 1的离心率为1e ,椭圆C 2的离心率为2e ,则222111e e += . 【思考应用】7.根据下列条件,求双曲线的标准方程(1)已知双曲线的渐近线方程为x y 21±=,焦距为10; (2)已知双曲线的渐近线方程为x y 32±=,且过点M (1,29-);(3)与椭圆1244922=+y x 有公共焦点,且离心率45=e .8.求满足下列条件的双曲线的离心率: (1)双曲线的渐近线方程为32y x =±;(2)过焦点且垂直于实轴的弦与另一焦点的连线所成角为90o .9.双曲线)0,1(12222>>=-b a by a x 的焦距为2c, 直线l 过点)且点(,和(,01),0)0,(b a 到直线l 的距离与点)0,1(-到直线l 的距离之和,54c s ≥求双曲线的离心率e 的取值范围.10.一炮弹在某处爆炸,在F 1(-5000,0)处听到爆炸声的时间比在F 2(5000,0)处晚s 17300,已知坐标轴的单位长度为1m ,声速为340m/s ,爆炸点应在什么样的曲线上?并求爆炸点所在的曲线方程.【拓展提升】11.双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为15m,高为55m,试选择适当的坐标系,求出此双曲线的方程.12.连结双曲线22221x y a b-=和22221x y a b -=-的四个顶点的四边形的面积为1S ,连结四个焦点的四边形的面积为2S ,求12S S 的最大值.。
江苏省宿迁市高中数学第2章圆锥曲线与方程第8课时双曲线的标准方程2导学案(无答案)苏教版选修1_1

第8课时 双曲线的标准方程(2)【学习目标】1.掌握双曲线的定义,标准方程; 2.根据已知条件求双曲线的标准方程. 【问题情境】焦点在x 轴上的双曲线标准方程为 ; 焦点在y 轴上的双曲线标准方程为.【合作探究】试比较双曲线与椭圆的异同:【展示点拨】例1.若双曲线k y x =-222的焦距为6,求实数k 的值.例2.若双曲线112422=-y x 上的一点P 到它的右焦点的距离为8,求点P 到它的左焦点的距离.例3.已知双曲线与双曲线141622=-y x 有相同焦点,且经过点)2,23(,求双曲线的方程.例4.已知方程422=+y kx ,其中k 为实数,对于不同的范围的k 值分别指出方程所表示的曲线类型.【学以致用】1.方程22115x y k k =-++表示双曲线的充要条件是k ∈____. 2.已知双曲线2288kx ky -= 的一个焦点为(0,3),则k = .3.以椭圆221169144x y +=的焦点为顶点,顶点为焦点的双曲线的标准方程是 . 4.已知双曲线1366422=-y x 的焦点为1F ,2F ,点P 在双曲线上,且02190=∠PF F ,求21PF F ∆的面积.5.在△MNG 中,已知NG =4,当动点M 满足条件M N G sin 21sin sin =-时,求动点M 的轨迹方程.第8课时 双曲线的标准方程(2)【基础训练】1.椭圆2x 2-3y 2=1焦点坐标为 .2.已知方程2211x y k k-=-表示双曲线,则k 的取值范围是 .3.焦距为(3,5)M -的双曲线的标准方程为 .4.设双曲线191622=-y x 上的点P 到点)0,5(的距离为15,则P 点到)0,5(-的距离是 .5.已知焦点为12(4,0),(4,0)F F -,且经过点M 的双曲线的标准方程是 .6.若椭圆14222=+my x 与双曲线1222=-y m x 有相同焦点,则实数m 的值为 . 【思考应用】7.若表示何种变化时,方程则当1,,222222=-+-∈>λλλλb y a x R b a 曲线?它们是否有相同的焦点?8.求焦点的坐标轴上,且经过)523,2(1-P 和)4,734(2P 两点的双曲线的标准方程.9.求以椭圆22185x y +=的焦点为顶点,而以椭圆的顶点为焦点的双曲线的方程;10.已知221,13x y k k -=---○1方程表示双曲线;○2表示焦点在x 轴上的双曲线;③表示焦点在y 轴上的双曲线【拓展提升】11.已在双曲线与椭圆1362722=+y x 有相同的焦点且与椭圆的一个交点的纵坐标为4,求双曲线的方程.12.在周长为48的390,tan =4oRt MPN MPN PMN ∆∠=∠中,,求以M,N 为焦点,且过点P 的双曲线方程.。
江苏省宿迁市高中数学 第2章 圆锥曲线与方程 第7课时

第7课时 双曲线的标准方程(1)【学习目标】1.掌握双曲线的定义,标准方程. 2.根据已知条件求双曲线的标准方程. 【问题情境】1.类比椭圆标准方程的建立过程推导出双曲线的标准方程.2.把椭圆定义中的“距离的差的绝对值”改为“距离的差”,那么点的轨迹会怎样? 【合作探究】 双曲线的标准方程F 1 ,F 2 F 1 ,F 2 想一想:如何判断方程)0,0(12222>>=-b a b y a x 和)0,0(12222>>=-b a bx a y 所表示的双曲线焦点的位置?【展示点拨】例1.已知双曲线两个焦点的坐标为)0,5()0,5(21F F ,-,双曲线上一点P 到21F F ,的距离之差的绝对值等于8,求双曲线标准方程变式1:若|PF 1|-|PF 2|=8呢? 变式2:若||PF 1|-|PF 2||=10呢? 变式3:若||PF 1|-|PF 2||=6呢?例2.求满足下列条件的双曲线的标准方程(1)a =3,b = 4,焦点在x 轴上; (2)a =25,经过点)5,2(-A ,焦点在y 轴上.例3.如果方程1222=--my m x 表示双曲线,求m 的取值范围.例4.已知A ,B 两地相距800m ,一炮弹在某处爆炸,在A 处听到炮弹爆炸声的时间比在B 处迟2s ,设声速为340/m s .(1)爆炸点在什么曲线上?(2)求这条曲线的方程.【学以致用】1.双曲线192522=-x y 的焦点坐标为 .2.若k ∈R ,则方程x 2k +3+y 2k +2=1表示焦点在x 轴上的双曲线,则k 的取值范围是________.3.已知双曲线的两个焦点分别为1100(,)F -,2100(,)F ,双曲线上一点P 到1F ,2F 的距离的差的绝对值等于12,求双曲线的标准方程. 4. 求适合下列条件的双曲线的标准方程:(1)5=c ,3=b ,焦点在y 轴上;(2)焦点为)6,0(-,)6,0(,3=a .5.已知双曲线过点()3,2-,且与椭圆224936x y +=有相同的焦点,求双曲线的方程.第7课时 双曲线的标准方程(1)【基础训练】1.双曲线192522=-x y 的焦点坐标为 .2. 方程15922=---k y k x 表示焦点在x 轴上的双曲线,则k 的取值范围是________.3.已知P 是双曲线19422=-y x 上一点,F 1.F 2分别是双曲线的左.右焦点,若PF 1=3,则PF 2等于 .49=,得 .5.设m 为常数,若点(0,5)F 是双曲线2219y x m -=的一个焦点,则m = . 6.设12,F F 分别是双曲线221169x y -=的左右焦点,AB 是双曲线过点1F 的弦,且AB =6,则三角形2ABF 的周长是 .【思考应用】7.根据下列条件,求双曲线的标准方程:⑴焦点的坐标是()6,0-.()6,0,并且经过点()5,2A -;⑵经过点(3,P -和()7Q --,焦点在y 轴上.8.求与椭圆14922=+y x 有相同焦点,并且经过点)3,2(-的双曲线的标准方程.9.已知双曲线224640x y -+=上一点M 到它的一个焦点的距离等于1,求M 到另一个焦点的距离.10.已知圆C 1:1)3(22=++y x 和圆C 2:9)3(22=+-y x ,动圆M 同时与圆C 1及圆C 2相外切,求动圆圆心M 的曲线方程.【拓展提升】11.在△ABC 中,B (-6,0),C (6,0),直线AB ,AC 的斜率乘积为94,求顶点A 的轨迹.12.某中心接到其正东.正西.正北方向三个观察点的报告:正西.正北两个观察点同时听到了一声巨响,正东观察点听到该巨响的时间比其他两个观察点晚4s .已知各观察点到该中心的距离都是1020m .试确定该巨响发生的位置(假定当时声音传播的速度为340m/s ;相关点均在同一平面内).。
「精品」高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质学案苏教版选修1_1
2.3.2 双曲线的几何性质学习目标 1.了解双曲线的几何性质,如范围、对称性、顶点、渐近线和离心率等.2.能用双曲线的简单性质解决一些简单问题.3.能区别椭圆与双曲线的性质.知识点一 双曲线的几何性质思考 类比椭圆的几何性质,结合图象,你能得到双曲线x 2a 2-y 2b2=1(a >0,b >0)的哪些几何性质?梳理知识点二 双曲线的离心率思考1 如何求双曲线的渐近线方程?思考2 在椭圆中,椭圆的离心率可以刻画椭圆的扁平程度,在双曲线中,双曲线的“张口”大小是图象的一个重要特征,怎样描述双曲线的“张口”大小呢?梳理 双曲线的焦距与实轴长的比c a,叫做双曲线的________,其取值范围是________.e 越大,双曲线的张口________.知识点三 双曲线的相关概念1.双曲线的对称中心叫做双曲线的________.2.实轴和虚轴等长的双曲线叫做________双曲线,它的渐近线方程是________.类型一 已知双曲线的标准方程研究几何性质例1 求双曲线x 2-3y 2+12=0的实轴长、虚轴长、焦点坐标、顶点坐标、渐近线方程、离心率.反思与感悟 已知双曲线方程求其几何性质时,若不是标准方程的要先化成标准方程,确定方程中a ,b 的对应值,利用c 2=a 2+b 2得到c ,然后确定双曲线的焦点位置,从而写出双曲线的几何性质.跟踪训练1 求双曲线9y 2-4x 2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.类型二 由双曲线的几何性质确定标准方程 例2 求适合下列条件的双曲线的标准方程: (1)虚轴长为12,离心率为54;(2)顶点间距离为6,渐近线方程为y =±32x ;(3)求与双曲线x 2-2y 2=2有公共渐近线,且过点M (2,-2)的双曲线方程.反思与感悟 (1)求双曲线的标准方程的步骤:①确定或分类讨论双曲线的焦点所在的坐标轴;②设双曲线的标准方程;③根据已知条件或几何性质列方程,求待定系数;④求出a ,b ,写出方程.(2)①与双曲线x 2a 2-y 2b 2=1共焦点的双曲线方程可设为x 2a 2-λ-y 2b 2+λ=1(λ≠0,-b 2<λ<a 2).②与双曲线x 2a 2-y 2b 2=1具有相同渐近线的双曲线方程可设为x 2a 2-y 2b2=λ(λ≠0).③渐近线方程为ax ±by =0的双曲线方程可设为a 2x 2-b 2y 2=λ(λ≠0). 跟踪训练2 求适合下列条件的双曲线的标准方程: (1)一个焦点为(0,13),且离心率为135;(2)双曲线过点(3,92),离心率e =103; (3)渐近线方程为y =±12x ,且经过点A (2,-3).类型三 求双曲线的离心率例3 分别求适合下列条件的双曲线的离心率: (1)双曲线的渐近线方程为y =±32x ;(2)双曲线x 2a 2-y 2b2=1(0<a <b )的半焦距为c ,直线l 过(a,0),(0,b )两点,且原点到直线l 的距离为34c .反思与感悟 求双曲线的离心率,通常先由题设条件得到a ,b ,c 的关系式,再根据c 2=a 2+b 2,直接求a ,c 的值.而在解题时常把c a 或ba 视为整体,把关系式转化为关于c a 或b a的方程,解方程求之,从而得到离心率的值.在本题的(2)中,要注意条件0<a <b 对离心率的限制,以保证题目结果的准确性.跟踪训练3 已知F 1,F 2是双曲线x 2a 2-y 2b2=1(a >0,b >0)的两个焦点,PQ 是经过F 1且垂直于x 轴的双曲线的弦,如果∠PF 2Q =90°,求双曲线的离心率.类型四 直线与双曲线的位置关系例4 斜率为2的直线l 被双曲线x 23-y 22=1截得的弦长为6,求l 的方程.引申探究若某直线l 与本例中的双曲线相交,求以点P (3,1)为中点的直线l 的方程.反思与感悟 (1)求弦长的两种方法①距离公式法:当弦的两端点坐标易求时,可直接求出交点坐标,再利用两点间距离公式求弦长. ②弦长公式法:当弦的两端点坐标不易求时,可利用弦长公式求解,即若直线l :y =kx +b (k ≠0)与双曲线C :x 2a 2-y 2b2=1(a >0,b >0)交于A (x 1,y 1),B (x 2,y 2)两点,则AB =1+k 2|x 1-x 2|=1+1k 2|y 1-y 2|.特别提醒:若直线方程涉及斜率,要注意讨论斜率不存在的情况. (2)中点弦问题与弦中点有关的问题主要用点差法,根与系数的关系解决.另外,要注意灵活转化,如垂直、相等等问题也可以转化成中点、弦长等问题解决.跟踪训练4 设双曲线C :x 2a2-y 2=1(a >0)与直线l :x +y =1相交于两个不同的点A ,B .(1)求双曲线C 的离心率e 的取值范围;(2)设直线l 与y 轴的交点为P ,且PA →=512PB →,求a 的值.1.双曲线的一个顶点坐标为(-1,0),一条渐近线方程为y =-2x ,则双曲线方程为____________.2.设双曲线x 2a +y 29=1的渐近线方程为3x ±2y =0,则a =________.3.如果双曲线x 2a 2-y 2b 2=1的两条渐近线互相垂直,则双曲线的离心率为________.4.若双曲线x 24-y 2m =1的渐近线方程为y =±32x ,则双曲线的焦点坐标是________.5.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为________.1.渐近线是双曲线特有的性质,两方程联系密切,把双曲线的标准方程x 2a 2-y 2b2=1(a >0,b >0)右边的常数“1”换为“0”,就是渐近线方程.反之由渐近线方程ax ±by =0变为a 2x 2-b 2y 2=λ,再结合其他条件求得λ就可得双曲线方程.2.准确画出几何图形是解决解析几何问题的第一突破口.对圆锥曲线来说,渐近线是双曲线特有的性质.利用双曲线的渐近线来画双曲线特别方便,而且较为精确,只要作出双曲线的两个顶点和两条渐近线,就能画出它的近似图形.提醒:完成作业 第2章 §2.3 2.3.2答案精析问题导学 知识点一思考 范围、对称性、顶点、离心率、渐近线. 梳理 x ≥a 或x ≤-a y ≥a 或y ≤-a 坐标轴 原点 坐标轴 原点A 1(-a ,0),A 2(a,0) A 1(0,-a ),A 2(0,a )知识点二思考1 将方程x 2a 2-y 2b 2=1(a >0,b >0)右边的“1”换成“0”,即由x 2a 2-y 2b 2=0,得x a ±yb =0,如图,作直线x a ±y b =0,当双曲线x 2a 2-y 2b2=1的各支向外延伸时,与两直线逐渐接近,但始终不会相交,把这两条直线叫做双曲线的渐近线.思考 2 双曲线x 2a 2-y 2b 2=1的各支向外延伸逐渐接近渐近线,所以双曲线的“张口”大小取决于b a 的值,设e =c a ,则b a =c 2-a 2a=e 2-1.当e 的值逐渐增大时,b a的值增大,双曲线的“张口”逐渐增大. 梳理 离心率 (1,+∞) 越大 知识点三 1.中心 2.等轴 y =±x 题型探究例1 解 将方程x 2-3y 2+12=0化为标准方程为y 24-x 212=1,∴a 2=4,b 2=12, ∴a =2,b =23,∴c =a 2+b 2=16=4.∴双曲线的实轴长为2a =4,虚轴长为2b =43;焦点坐标为F 1(0,-4),F 2(0,4);顶点坐标为A 1(0,-2),A 2(0,2);渐近线方程为y =±33x ;离心率e =2.跟踪训练1 解 将9y 2-4x 2=-36变形为x 29-y 24=1,即x 232-y 222=1.∴a =3,b =2,c =13, 因此顶点坐标为(-3,0),(3,0); 焦点坐标为(-13,0),(13,0); 实轴长是2a =6,虚轴长是2b =4; 离心率e =c a =133; 渐近线方程为y =±b a x =±23x .例2 解 (1)设双曲线的标准方程为x 2a 2-y 2b 2=1或y 2a 2-x 2b 2=1(a >0,b >0).由题意知2b =12,c a =54,且c 2=a 2+b 2, ∴b =6,c =10,a =8.∴双曲线的标准方程为x 264-y 236=1或y 264-x 236=1.(2)设以y =±32x 为渐近线的双曲线方程为x 24-y29=λ(λ≠0).当λ>0时,a 2=4λ, ∴2a =24λ=6⇒λ=94;当λ<0时,a 2=-9λ, ∴2a =2-9λ=6⇒λ=-1.∴双曲线的标准方程为x 29-y 2814=1或y 29-x 24=1.(3)设与双曲线x 22-y 2=1有公共渐近线的双曲线方程为x 22-y 2=λ(λ≠0).将点(2,-2)代入双曲线方程,得λ=222-(-2)2=-2.∴双曲线的标准方程为y 22-x 24=1.跟踪训练2 解 (1)依题意可知,双曲线的焦点在y 轴上,且c =13,又c a =135,∴a =5,b =c 2-a 2=12, 故所求双曲线的标准方程为y 225-x 2144=1.(2)由e 2=109,得c 2a 2=109,设a 2=9k (k >0),则c 2=10k ,b 2=c 2-a 2=k .∴设所求双曲线方程为x 29k -y 2k =1①或y 29k -x 2k=1②.将(3,92)代入①,得k =-161,与k >0矛盾,无解; 将(3,92)代入②,得k =9. 故所求双曲线的标准方程为y 281-x 29=1.(3)方法一 ∵双曲线的渐近线方程为y =±12x ,若焦点在x 轴上,设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),则b a =12.① ∵A (2,-3)在双曲线上, ∴4a 2-9b2=1.②联立①②,无解.若焦点在y 轴上,设所求双曲线的标准方程为y 2a 2-x 2b 2=1(a >0,b >0),则a b =12.③ ∵A (2,-3)在双曲线上, ∴9a 2-4b2=1.④联立③④,解得a 2=8,b 2=32.故所求双曲线的标准方程为y 28-x 232=1.方法二 由双曲线的渐近线方程为y =±12x ,可设双曲线方程为x 222-y 2=λ(λ≠0).∵A (2,-3)在双曲线上, ∴2222-(-3)2=λ,即λ=-8. 故所求双曲线的标准方程为y 28-x 232=1.例3 解 (1)若焦点在x 轴上,则b a =32, ∴e =b 2a 2+1=132; 若焦点在y 轴上,则a b =32,即b a =23, ∴e =b 2a 2+1=133. 综上可知,双曲线的离心率为132或133. (2)依题意得直线l :bx +ay -ab =0. 由原点到l 的距离为34c , 得ab a 2+b 2=34c , 即ab =34c 2,∴16a 2b 2=3(a 2+b 2)2, 即3b 4-10a 2b 2+3a 4=0,∴3⎝ ⎛⎭⎪⎫b 2a 22-10×b 2a 2+3=0.解得b 2a 2=13或b 2a 2=3.又∵0<a <b ,∴b 2a2=3.∴e =1+b 2a2=2.跟踪训练3 解 设F 1(c,0),将x =c 代入双曲线的方程,得 c 2a 2-y 2b 2=1,解得y =±b 2a. ∴PF 1=b 2a. 由双曲线对称性,PF 2=QF 2且∠PF 2Q =90°,知F 1F 2=12PQ =PF 1, ∴b 2a=2c ,则b 2=2ac , ∴c 2-2ac -a 2=0,∴⎝ ⎛⎭⎪⎫c a 2-2×c a-1=0,即e 2-2e -1=0,∴e =1+2或e =1-2(舍去). ∴所求双曲线的离心率为1+ 2.例4 解 设直线l 的方程为y =2x +m . 由⎩⎪⎨⎪⎧ y =2x +m ,x 23-y 22=1, 得10x 2+12mx +3(m 2+2)=0.(*)设直线l 与双曲线交于A (x 1,y 1),B (x 2,y 2)两点, 由根与系数的关系,得x 1+x 2=-65m ,x 1x 2=310(m 2+2). 又y 1=2x 1+m ,y 2=2x 2+m ,∴y 1-y 2=2(x 1-x 2).∴AB 2=(x 1-x 2)2+(y 1-y 2)2=5(x 1-x 2)2=5[3625m 2-4×310(m 2+2)]. ∵AB =6,∴365m 2-6(m 2+2)=6, 解得m =±15.由(*)式得Δ=24m 2-240,把m =±15代入上式得Δ>0.∴m 的值为±15,∴所求l 的方程为y =2x ±15. 引申探究解 设相交的两点为A (x 1,y 1),B (x 2,y 2). 则⎩⎪⎨⎪⎧x 213-y 212=1, ①x 223-y 222=1, ② ①-②,可得 x 1+x 2x 1-x 23-y 1+y 2y 1-y 22=0.③ ∵P 为AB 的中点,且P 的坐标为(3,1), ∴⎩⎪⎨⎪⎧x 1+x 22=3,y 1+y 22=1,即⎩⎪⎨⎪⎧ x 1+x 2=6,y 1+y 2=2. 将其代入③式,得2(x 1-x 2)-(y 1-y 2)=0, 即k =y 1-y 2x 1-x 2=2, 故直线l 的方程为y -1=2(x -3),即y =2x -5. 经检验知y =2x -5符合题意. 跟踪训练4 解 (1)将y =-x +1代入双曲线x 2a 2-y 2=1中, 得(1-a 2)x 2+2a 2x -2a 2=0,①所以⎩⎪⎨⎪⎧1-a 2≠0,4a 4+8a 21-a 2>0, 解得0<a <2且a ≠1,又双曲线的离心率e =1+a 2a = 1a 2+1,所以e >62且e ≠ 2. (2)设A (x 1,y 1),B (x 2,y 2). 因为P 为直线与y 轴的交点, 所以P (0,1). 因为PA →=512PB →,所以(x 1,y 1-1)=512(x 2,y 2-1). 由此得x 1=512x 2. 由于x 1,x 2是方程①的两根, 且1-a 2≠0,所以1712x 2=-2a 21-a 2,512x 22=-2a 21-a 2. 消去x 2得-2a 21-a 2=28960. 由a >0,解得a =1713.当堂训练1.x 2-y 24=1 2.-4 3. 2 4.(±7,0) 5.y =±22x。
(新)高中数学第二章圆锥曲线与方程2_2_2双曲线的几何性质一1教案新人教A版选修1-1

1、双曲线的性质:
椭圆
双曲线
不同点
标准方程
图象
范围
对称性
顶点
渐近线
1、课本 练习第1,2题
〖备选习题〗:
A组
1、求与双曲线 有共同渐近线,且过点 的双曲线的方程。
B组
1.双曲线 的离心率为 ,双曲线 的离心率为 ,则 的最小值是( )
A. B.2 C. D.4
2.求证:双曲线 ( )与双曲线 有共同的渐近线。
说明:①由c>a>0可得e>1;
②双曲线的离心率越大,它的开口越阔.
探究二:
课本51页例3
双曲线型自然通风塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面(见课本),它的最小半径为 ,上口半径为 ,下口半径为 ,高 ,选择适当的坐标系,求出此双曲线的方程(精确到 )
探究三:
例3.求与双曲线 有共同渐近线,且过点 的双曲线的方程。
令 ,没有实根,因此双曲线和y轴没有交点。
1)注意:双曲线的顶点只有两个,这是与椭圆不同的(椭圆有四个顶点),
双曲线的顶点分别是实轴的两个端点。
2)实轴:线段 叫做双曲线的实轴,它的长等于 叫做双曲线的实半轴长。
虚轴:线段 叫做双曲线的虚轴,它的长等于 叫做双曲线的虚半轴长。
在作图时,我们常常把虚轴的两个端点画上(为要确定渐进线),但要注意他们并非是双曲线的顶点。
2、渐近线:注意到开课之初所画的矩形,矩形确定了两条对角线,这两条直线即称为双曲线的渐近线。从图上看,双曲线 的各支向外延伸时,与这两条直线逐渐接近。
在初中学习反比例函数 时提到x轴y轴都是它的渐近线。高中三角函数 ,渐近线是 。
所谓渐近,既是无限接近但永不相交。
高中数学-圆锥曲线双曲线简单几何性质(一)教案新课标人教B版选修2

双曲线简单几何性质(一)合作学习导纲
1、下列方程中,以x±2y=0为渐近线的双曲线方程是:
A 、141622=-y x
B 、116
42
2=-y x
C 、1222=-y x
D 、12
2
2=-y x
2、求中心在原点,一个焦点为(3,0),一条渐近线方程2x-3y=0的双曲线方程。
作业:
必做题:教课书113页习题8.4(1、3、4题)
选做题:1、双曲线18
42
2=-y x 的两渐近线所夹锐角的正切值。
2、已知双曲线
1162
22=-b y x 的实轴的一个端点为A 1,虚轴的一个端点为 B 1,且 A 1 B 1=5,求双曲线方程。
课外研讨题:若直线1-=kx y 与双曲线422=-y x 有:①一个公共点;②两个公共点;③无公共点;④在右支上有两个公共点;⑤在右支上有一个公共点,求k 的取值范围。
人教版高中数学第二册(上)
8.4双曲线简单几何性质(一)
教案
抚顺县高级中学数学教师:吴春义
2006年12月1日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第9课时双曲线的几何性质(1)
【学习目标】1•了解双曲线的简单几何性质,如范围•对称性•顶点•渐近线和离心率等.
2 •能用双曲线的简单几何性质解决一些简单问题.
【问题情境】
1•椭圆有哪些几何性质,是如何探讨的?
2•双曲线的两种标准方程是什么?
【合作探究】
双曲线的几何性质
【展示点拨】
2 2
X y
例1 •求双曲线1的实轴长和虚轴长•焦点的坐标•离心率.渐近线方程.
例2.已知双曲线的中心在原点,焦点在y 轴上,焦距为16,离心率为-,求双曲线的方程.
3
变式:“焦点在y 轴上”变为“焦点在坐标轴上”
2
J 1有相同焦点且经过点(0,1)的双曲线的标准方程.
8
M,N 两点,以MN 为直径的圆恰好过双曲线的右顶点,求该双曲线的离心率.
【学以致用】
1 •说出下列双曲线的顶点,焦点,焦距,实轴长,虚轴长,离心率和渐近线方程:
2 2 2 2
/八 x y , y x .
(1) 1 ; (2) 1 .
9 16 4 5
例3•求与椭圆
例4 •过双曲线
X 2 a 2
2 ■y 2
1(a 0,b 0)的左焦点且垂直于
b 2
x 轴的直线与双曲线相交于
2.求适合下列条件的双曲线的标准方程:
(1) 实轴的长是10,虚轴长是8,焦点在x 轴上; (2) 焦距是10,虚轴长是8,焦点在y 轴上.
5
,且与椭圆 —1
- 1有公共焦点,求此双曲线的标准方程.
3 40 15
5.已知F 1 , F 2是双曲线的两个焦点, 以线段F 1F 2为边作正 MF 1F 2,若边MR 的中点在此 双曲线上,求此双曲线的离心率.
第9课时双曲线的几何性质(1)
【基础训练】
2 2
1•双曲线—
y 1的焦点坐标为
49 25
2 2
2•双曲线—
1的两条渐近线的方程
16 9
3•等轴双曲线的中心在原点, 它的一个焦点为 F(0,2J2)则双曲线的标准方程是 _____________ 4•双曲线的两条渐近线线互相垂直,那么它的离心率是
3•已知双曲线的两条渐近线的方程是 y
方程.
4
-x ,焦点为(5,0), (5,0),求此双曲线的标准 3
4.双曲线的离心率为
2
5•双曲线x 2 -
1的两条渐近线所成的锐角是
3
2 2
6•已知双曲线— 厶 1的离心率e (1,2),实数k 的取值范围是
4 k
【思考应用】
7•求满足下列条件的双曲线的标准方程. (1 )两焦点的距离为14,两顶点间的距离为 12; (2) —焦点坐标为(0, -4 ), 一条渐近线为3y 2x 0 •
2 2
&过双曲线 笃1(a
0,b 0)的焦点且垂直于实轴的弦与另一焦点的连线所成角为
a 2
b 2
90o ,求此双曲线的离心率.
5 2 2
5,且与椭圆40 15 1有公共焦点,求此双曲线的标准方程.
支上,且PF=4PR ,则此双曲线的离心率 e 的最大值.
9.已知双曲线的离心率为
2 v
10.已知双曲线—
a
b 2
1(a 0,b 0)的左•右焦点分别为
F 1, F 2,点P 在双曲线的右
【拓展提升】
11.焦点在坐标轴上的双曲线,它的两条渐近线方程为 • 3x y
为3,求此双曲线的方程.
F | PF 2的面积.
12.已知双曲线
2
x
25
2
y
=1,焦点为 15
F 1, F 2, P 为双曲线上一
点,
,且 F 1PF 2
1200,求
0 ,焦点到渐近线的距离。
