八年级数学下学期插班生招生考试题201305
八年级下学期数学入学测试卷及答案

八年级下学期数学入学测试卷(考试时间:90分钟,试卷满分120分)一、选择题(本大题10小题,每小题3分,共30分)1.以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A..B..C..D..2.下列每组数据中,能作为三角形三边边长的是( ) A.3、4、8 B.8、7、15C.5、5、11D.13、12、203.分式32-x y 有意义的条件是( )A.x 0B.y 0C.x 3D.x -34.如图,1=2,AB=AD ,则ABC ≌ADC ,采用的判定方法是( )A.SSSB.SASC.ASAD.AAS5.下列分解因式正确的是( ) A.﹣a+a 3=﹣a(1+a 2)B.2a ﹣4b+2=2(a ﹣2b)C.a 2﹣4=(a ﹣2)2 D.a 2﹣2a+1=(a ﹣1)26.等腰三角形的一个角为,则顶角为( )A.040B.0100C.040或0100D.0707.下列运算中,正确的是( ) A.4m ﹣m =3 B.(﹣m 3n)3=﹣m 6n 3C.m 6m 3=m 2D.(m ﹣3)(m+2)=m 2﹣m ﹣68.如图,ABC 中,A=,ABC 的两条角平分线交于点P ,BPD 的度数是( ) A.B.C.D.9.如图,Rt ABC 中,C=,AD 平分BAC ,交BC 于点D ,AB=10,S ABD =15,则CD 的长为( ) A.3 B.4 C.5 D.610.一件工作,甲单独做a 小时完成,乙单独做b 小时完成,则甲、乙两人合作完成需要( )小时。
A.b a11+B.ab 1C.ba +1D.ba ab +二、填空题(每题4分,共28分) 11.约分的结果是________.12.已知3x =5,3y =2,则3x+y 的值是_______.13. 已知m+n=-6,mn=4,则m 2-mn+n 2的值为_______. 14. 一个n 边形的内角和等于0720,则n =_______. 15. 如图,ABC ≌ADE ,若C =,D =,DAC =,则BAD =_______.16.如图,在ABC 中,ACB =,CD 是AB 边上的高,A =,AB =20,则BD =_______.(15题图) ( 16题图) (17题图)17.如图,已知ABC 中,AC =AB=5,BC =3,DE 垂直平分AB ,点D 为垂足,交AC 于点 E .那么EBC 的周长为_______.三、解答题(一)(本大题3小题,每小题6分,共18分)18.计算:()()()()33442x y x y x y xy xy +---÷19.如图,AB=AC ,AD=AE ,∠BAC=∠DAE .求证:BE=CD .20.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=35°,∠C=65°.求∠DAE 的度数.四、解答题(二)(本大题3小题,每小题8分,共24分)21.ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上22.今年新冠肺炎疫情在全球肆虐,为降低病亡率,某工厂平均每天比原计划多生产10台呼吸机,现在生产120台呼吸机的时间与原计划生产90台呼吸机所需时间相同.求该工厂原来平均每天生产多少台呼吸机?23.已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:(1)AD平分∠BAC.(2)DF=DE五、解答题(三)(本大题2小题,每小题10分,共20分)24.请认真观察图形,解答下列问题:(1)根据图中条件,试用两种不同方法表示阴影部分的面积.方法1:;方法2:.(2)从中你能发现什么结论?请用乘法公式表示该结论:.(3)运用你所得到的结论,解决问题:已知6,25)2==+xyyx(求22x y+的值.25.如图,△ABC和△ADE都是等腰三角形,BC、DE分别是这两个等腰三角形的底边,且∠BAC=∠DAE.(1)求证:BD=CE;(2)连接DC.如果CD=CE,试说明直线AD垂直平分线段BC.(1)作出ABC关于x轴对称的111A B C△,并写出点1A,1B,1C 的坐标;(2)在y轴上找点D,使得AD BD+最小。
八年级下学期插班生数学卷(含答案)

八年级插班生数学卷一.单项选择题(共20小题)1.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是()A.,,B.1,,C.6,7,8 D.2,3,42.的算术平方根是()A.2 B.±2 C.D.±3.在二次根式,,,,,中,最简二次根式的个数是()A.1 B.2 C.3 D.44.如图,△ABC的顶点A、B、C在边长为1的正方形网格的格点上,BD⊥AC于点D.则BD的长为()A.B. C. D.5.如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,得到△A′B′C,将△A′B′C向下平移5个单位,得△A″B″C″,那么点A的对应点A″的坐标是()A.(﹣3,﹣2)B.(3,﹣8)C.(﹣2,﹣1)D.(1,﹣1)6.已知函数y=,当x=2时,函数值y为()A.5 B.6 C.7 D.87.王芳同学到文具店购买中性笔和笔记本,中性笔每支0.8元,笔记本每本1.2元,王芳同学花了10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于0.8元)()A.6 B.7 C.8 D.98.已知是方程组的解,则a+b的值是()A.﹣1 B.2 C.3 D.49.为了了解某校学生对篮球、足球、羽毛球、乒乓球、网球等五类的喜爱,小李采用了抽样调查,在绘制扇形图时,由于时间仓促,还有足球、网球等信息还没有绘制完成,如图所示,根据图中的信息,这批被抽样调查的学生最喜欢足球的人数不可能是()A.100人B.200人C.260人D.400人10.数据10,10,x,8的众数与平均数相同,那么这组数的中位数是()A.10 B.8 C.12 D.411.如图三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是()A.∠γ=∠α+∠βB.2∠γ=∠α+∠β C.3∠γ=2∠α+∠βD.3∠γ=2(∠α+∠β)12.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于()A.130°B.138°C.140°D.142°13.下列命题的逆命题一定成立的是()①对顶角相等;②同位角相等,两直线平行;③若a=b,则|a|=|b|;④若x=3,则x2﹣3x=0.A.①②③ B.①④C.②④D.②14.如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=5,AD=2,则图中长为的线段有()A.4条B.3条C.2条D.1条15.若k<<k+1(k是整数),则k=()A.6 B.7 C.8 D.916.2015年4月25日尼泊尔发生了里氏8.1级强烈地震,地震波及我区某县.我军某部奉命前往灾区,途中遇到塌方路段,经过一段时间的清障,该部加速前进,最后到达救灾地点.则该部行进路程y与行进时间x的函数关系的大致图象是()A.B.C.D.17.甲、乙两人参加植树活动,两人共植树20棵,已知甲植树数是乙的1.5倍、如果设甲植树x棵,乙植树y棵,那么可以列方程组()A.B.C.D.18.2015年7月份,某市一周空气质量报告中某项污染指数的数据是:31,35,31,33,30,33,31.則下列关于这列数据表述正确的是()A.众数是30 B.中位教是31 C.平均数是33 D.极差是3519.如图,在矩形ABCD中,由8个面积均为1的小正方形组成的L型模板如图放置,则矩形ABCD的周长为()A.B. C. D.20.如果是二次根式,那么x,y应满足的条件是()A.x≥1,y≥0 B.(x﹣1)•y≥0 C.≥0 D.x≥1,y>0二.填空题(共10小题)21.的算术平方根是.22.已知=5,则=.23.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为55cm,此时木桶中水的深度是cm.24.小林每天下午5点放学时,爸爸总是从家开车按时到达学校接他回家,有一天学校提前一个小时放学,小林自己步行回家,在途中遇到开车来接他的爸爸,结果比平时早20分钟到家,则小林步行分钟遇到来接他的爸爸.25.如图,在正方形ABCD中,点E,F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于.26.如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.27.一次函数y=kx+b(k≠0)的图象经过A(1,0)和B(0,2)两点,则它的图象不经过第象限.28.如图,定点A(﹣2,0),动点B在直线y=x上运动,当线段AB最短时,点B的坐标为.29.如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=.30.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB 上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度.参考答案一.选择题(共20小题)1.B 2.C 3.C 4.C 5.A 6.A 7.B 8.B 9.D 10.A 11.B 12.B 13.D 14.B 15.D 16.D 17.C 18.B 19.B20.C二.填空题(共10小题)21.22.-4或-1 23.20 24.50 25. 26.10 27.三28.(-1,-1)29.70°30.85。
初中插班入学考试试卷数学

1. 下列各数中,有理数是()A. √2B. πC. 2/3D. 3√32. 已知x² - 5x + 6 = 0,则x的值为()A. 2或3B. 1或4C. 1或6D. 2或43. 若a、b是实数,且a² + b² = 1,则|a + b|的最大值为()A. 1B. √2C. 2D. √34. 下列方程中,无解的是()A. x² + 2x + 1 = 0B. x² - 2x + 1 = 0C. x² + 2x - 1 = 0D. x² - 2x -1 = 05. 已知函数f(x) = 2x - 3,若f(2) = f(x),则x的值为()A. 1B. 2C. 3D. 46. 在等腰三角形ABC中,底边BC的长度为6,腰AC的长度为8,则顶角A的度数为()A. 30°B. 45°C. 60°D. 90°7. 下列命题中,正确的是()A. 若a > b,则a² > b²B. 若a > b,则a³ > b³C. 若a > b,则a² < b²D. 若a > b,则a³ < b³8. 下列各数中,正数是()A. -√2B. π/2C. -√3D. -π9. 若x² - 4x + 4 = 0,则x的值为()A. 1B. 2C. 3D. 410. 已知函数f(x) = x² - 2x + 1,若f(2) = f(x),则x的值为()A. 1B. 2C. 3D. 411. 若a、b是实数,且a² + b² = 1,则|a - b|的最小值为______。
12. 已知x² - 5x + 6 = 0,则x的值为______。
13. 在等腰三角形ABC中,底边BC的长度为6,腰AC的长度为8,则底角B的度数为______。
初二插班生水平测试卷(答)

初二插班生水平测试卷(答卷)命题人:余 刚 审核人:陈 刚(本试卷共24题,满分120分,答题时间为100分钟。
)姓名__________得分_________一、精心选一选(每小题3分,共30分)二、细心填一填(每小题4分,共24分)11._________;12._________;13._________;14._________________________; 15._________;16._________;三、耐心答一答(本题共66分)17.(本题满分6分)已知:2323+=-=,b a ,分别求下列代数式的值:(1)22ab b a -(2)22b ab a ++18. (本题满分6分)如图,在△ABC 中,点D 是AB 的中点,CE ⊥AB 于点E ,∠BCE =60°,∠ACE =45°若DE =10,求CE 的长.(结果保留根号)19. (1)第二小组(160~169次)有 人.(2)在这次测试中,跳绳次数的中位数落在 小组内.(3)若一分钟跳绳次数达到180次的成绩为优秀,那么该校八年级学生中约有多少人达到优秀?20. (本题满分8分)如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC 上用其他材料造了宽为1米的两个小门。
(1)设花圃的宽AB 为x 米,请你用含x 的代数式表示BC 的长; (2)求x 的取值范围;(3)若此时花圃的面积刚好为452m ,求此时花圃的宽.21. (本题满分8分)如图,已知四边形ABC D 是梯形,D C ∥AB ,四边形AC ED 是平行四边形,延长D C 交BE 于点G ,延长E C 交AB 于点H . (1)求证:C E H C =;(2)若3C G =,求BH 的长。
22.(本题满分8分)阅读下面的例题: 解方程022=--x x解:(1)当x ≥0时,原方程化为x 2– x –2=0,解得:x 1=2,x 2= - 1(不合题意,舍去)(2)当x <0时,原方程化为x 2 + x –2=0,解得:x 1=1,(不合题意,舍去)x 2= -2∴原方程的根是x 1=2, x 2= - 2(3)请参照例题解方程0112=---x x23. (本题满分10分)在△ABC 中,AB=AC ,点D 是直线BC 上一点(不与B 、C 重合),以AD 为一边在AD 的右侧作△ADE ,使AD=AE ,∠DAE=∠BAC,连接CE. (1)如图1,当点D 在线段BC 上,求证ACE ABD ∆≅∆. (2)设∠BAC=α,∠BCE=β.①如图2,当点D 在线段BC 上移动,则α,β之间有怎么样的数量关系?请说明理由;②当点D 在线段CB 的延长线上时,则α,β之间有怎么样的数量关系,请画出图形并直接写出你的结论.ABDE图1ACDE图2BC24. (本题满分12分)如图,梯形ABCD中,AD∥BC,AB=CD=3cm,∠C=60°,BD⊥CD。
八年级考试试题
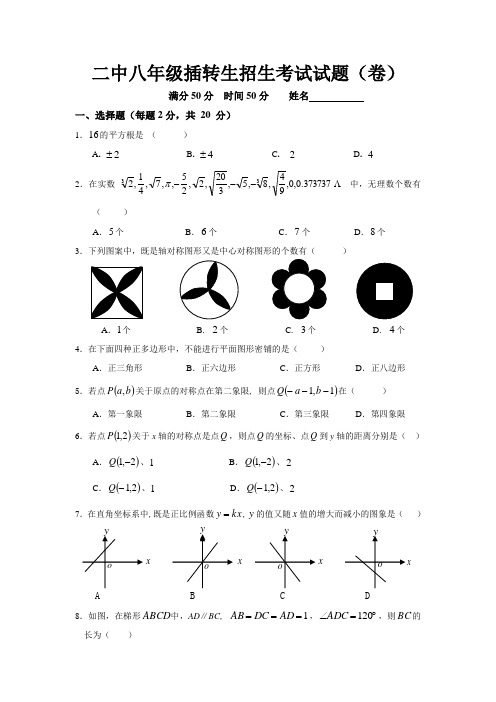
二中八年级插转生招生考试试题(卷)满分50分 时间50分 姓名一、选择题(每题2分,共 20 分)1.16的平方根是 ( )A . 2±B . 4±C . 2D . 4 2.在实数373737.0,0,94,8,5,320,2,25,,7,41,233---π 中,无理数个数有( )A .5个B .6个C .7个D .8个 3.下列图案中,既是轴对称图形又是中心对称图形的个数有( )A .1个B . 2个C . 3个D . 4个 4.在下面四种正多边形中,不能进行平面图形密铺的是( )A .正三角形B .正六边形C .正方形D .正八边形 5.若点()b a P ,关于原点的对称点在第二象限, 则点()1,1---b a Q 在( )A .第一象限B .第二象限C .第三象限D .第四象限 6.若点()2,1P 关于x 轴的对称点是点Q ,则点Q 的坐标、点Q 到y 轴的距离分别是( )A .()2,1-Q 、1B .()2,1-Q 、2C .()2,1-Q 、1D .()2,1-Q 、27.在直角坐标系中,既是正比例函数kx y =,y 的值又随x 值的增大而减小的图象是( )A B C D8.如图,在梯形ABCD 中,AD ∥BC ,1===AD DC AB ,︒=∠120ADC ,则BC 的长为( )x xxxxCFEA .1B .2C .3D .29.二元一次方程组⎩⎨⎧=+=-13273y x y x 的解是关于y x , 的二元一次方程9-=kx y 的一个解,则k 的值为( )A .2-B .1-C .3D .410.如图,□ABCD 的周长为18cm ,对角线AC 、BD 相 交于点O ,OG ⊥AC 交AB 于G ,则△CGB 的周长是( A .18cmB .9cmC .5.4cmD .以上都不对 二、填空题( 每题2分,共 8分 )11.直角三角形的两直角边边长分别为9和12,则它的斜边长为 . 12.某班第一小组101人25分、4人26分、1人27分、3人28分、1人30这组数据的平均数为 ,众数为 ,中位数为 .13.如图,经过平移后,小船上的点A ()5,7移到了点B ()3,1,则点C 在小船平移后对应点的坐标为 .14.如图,将矩形ABCD 折叠,使点D 落在边BC 上点F 处,折痕为AE ,已知8=AB cm ,10=BC cm ,则EF 的长为 .xD三、解答题15.(3分)化简:12581845+-+16.(6分)已知一次函数bkxy+=的图象经过点()2,3--A和点()6,1B.(1)求一次函数的解析式;(2)求这个一次函数图象与坐标轴所围成三角形的面积.17.(6分)如图,在□ABCD中,点H是对角线AC的中点,直线EF过点H分别交AB、CD于点E、点F.求证:FHEH=;18.(7分)某天,一名蔬菜经营户用60元钱从蔬菜批发市场批发了西红柿和豆角共40千克到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:(1)求该蔬菜经营户当天批发了西红柿和豆角各多少千克?(2)如果当天卖完这些西红柿和豆角,该蔬菜经营户能赚多少钱?。
八年级下学期数学入学考试试卷及答案

八年级下学期数学入学考试试卷一.选择题(共10小题,每题3分)1.在以下节能、回收、绿色食品、节水四个标志中,是轴对称图形的是()A.B.C.D.2.下列长度的三条线段能组成三角形的是()A.1,2,3 B.2,2,4 C.2,3,4 D.2,4,83.下列图形中具有稳定性的是()A.正方形B.长方形C.等腰三角形D.平行四边形4.点M(3,1)关于y轴的对称点的坐标为()A.(﹣3,1)B.(3,﹣1)C.(﹣3.﹣1)D.(1,3)5.已知x2﹣8x+a可以写成一个完全平方式,则a可为()A.4 B.8 C.16 D.﹣166.化简+的结果为()A.1 B.﹣1 C.D.7.下列运算正确的是()A.x2+x2=2x4B.a2.a3=a5C.(﹣2a2)4=16x6D.a6÷a2=a38.下列各式从左到右的变形中,属于因式分解的是()A.﹣12x3y=﹣3x3•4y B.m(mn﹣1)=m2n﹣mC.y2﹣4y﹣1=y(y﹣4)﹣1 D.ax+ay=a(x﹣y)9.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是()A.∠COP=∠DOP B.PC=PD C.OC=OD D.∠COP=∠OPD10.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是()A.1对B.2对C.3对D.4对二.填空题(共7小题,每题4分)11.若分式的值为0,则x的值为12.分解因式:mx2﹣4m=.13.水由氢原子和氧原子组成,其中氢原子的直径约为0.0000000001米,用科学记数法表示为米.14. 已知,则的值为________.15.如图,在△ABC中,∠BAC=90°.AD⊥BC于点D,若∠C=30°,BD=1,则线段CD 的长为.16.如图,在底边BC为2,腰AB为2的等腰三角形ABC中,DE垂直平分AB于点D,交BC于点E,则△ACE的周长.17. 在△ABC中,,AB=4,,则AC=______.三.解答题(共8小题,共62分)18.(6分)化简:(m+2)(m﹣2)﹣×3m.19.(6分)解方程:20.(6分)如图,在△ABC中,AB=AC,∠A=36°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求与作法);(2)在(1)的条件下,求∠BDC的度数.21.(6分)先化简(1﹣)•,再在1,2,3中选取一个适当的数代入求值.22.(8分)如图,在正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别是(﹣4,6),(﹣1,4).(1)请在图中的网格平面内建立平面直角坐标系(直接在图中画出);(2)请画出△ABC关于x轴对称的△A1B1C1;(3)写出点A1、C1的坐标.23.(10分)如图,AC=BC,AE⊥CD于点A,BD⊥CE于点B.(1)求证:CD=CE;(2)若点A为CD的中点,求∠C的度数.24.(8分)某商店在2016年至2018年期间销售一种礼盒.2016年,该商店用2200元购进了这种礼盒并且全部售完:2018年,这种礼盒每盒的进价是2016年的一半,且该商店用2100元购进的礼盒数比2016年的礼盒数多100盒.那么,2016年这种礼盒每盒的进价是多少元?25.(12分)将一副三角板按如图所示的方式摆放,A D是等腰直角三角板ABC斜边BC上的高,另一块三角板DMN的直角顶点与点D重合,DM、DN分别交AB、AC于点E、F.(1)请判别△DEF的形状.并证明你的结论;(2)若BC=4,求四边形AEDF的面积.八年级数学下学期入学考试答案参考答案与试题解析一.选择题(共10小题)1.在以下节能、回收、绿色食品、节水四个标志中,是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、不是轴对称图形,故此选项错误;B、不是轴对称图形,故此选项错误;C、是轴对称图形,故此选项正确;D、不是轴对称图形,故此选项错误;故选:C.2.下列长度的三条线段能组成三角形的是()A.1,2,3 B.2,2,4 C.2,3,4 D.2,4,8【分析】根据三角形的三边关系进行分析判断.【解答】解:根据三角形任意两边的和大于第三边,得A中,1+2=3,不能组成三角形;B中,2+2<4,不能组成三角形;C中,3+2>4,能够组成三角形;D中,2+4<8,不能组成三角形.故选:C.3.下列图形中具有稳定性的是()A.正方形B.长方形C.等腰三角形D.平行四边形【分析】根据三角形具有稳定性解答.【解答】解:正方形,长方形,等腰三角形,平行四边形中只有等腰三角形具有稳定性.故选:C.4.点M(3,1)关于y轴的对称点的坐标为()A.(﹣3,1)B.(3,﹣1)C.(﹣3.﹣1)D.(1,3)【分析】根据关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变可得答案.【解答】解:点M(3,1)关于y轴的对称点的坐标为(﹣3,1),故选:A.5.已知x2﹣8x+a可以写成一个完全平方式,则a可为()A.4 B.8 C.16 D.﹣16【分析】根据完全平方式的结构是:a2+2ab+b2和a2﹣2ab+b2两种,据此即可求解.【解答】解:∵x2﹣8x+a可以写成一个完全平方式,∴则a可为:16.故选:C.6.化简+的结果为()A.1 B.﹣1 C.D.【分析】原式变形后利用同分母分式的减法法则计算即可得到结果.【解答】解:原式=﹣==1.故选:A.7.下列运算正确的是()A.x2+x2=2x4B.a2.a3=a5C.(﹣2a2)4=16x6D.a6÷a2=a3【分析】直接利用积的乘方运算以及同底数幂的乘除运算法则分别化简得出答案.【解答】解:A、x2+x2=2x2,故此选项错误;B、a2•a3=a5,正确;C、(﹣2a2)4=16x8,故此选项错误;D、a6÷a2=a4,故此选项错误;故选:B.8.下列各式从左到右的变形中,属于因式分解的是()A.﹣12x3y=﹣3x3•4y B.m(mn﹣1)=m2n﹣mC.y2﹣4y﹣1=y(y﹣4)﹣1 D.ax+ay=a(x﹣y)【分析】根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.【解答】解:A、左边不是多项式,不是因式分解,故本选项不符合题意;B、是整式的乘法运算,故本选项不符合题意;C、没把一个多项式转化成几个整式积的形式,故本选项不符合题意;D、把一个多项式转化成几个整式积的形式,故本选项符合题意;故选:D.9.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是()A.∠COP=∠DOP B.PC=PD C.OC=OD D.∠COP=∠OPD 【分析】先根据角平分线的性质得出PC=PD,∠POC=∠POD,再利用HL证明△OCP≌△ODP,根据全等三角形的性质得出OC=OD即可判断.【解答】解:∵OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,∴PC=PD,∠POC=∠POD,故A,B正确;在Rt△OCP与Rt△ODP中,,∴Rt△OCP≌Rt△ODP(HL),∴OC=OD,故C正确.不能得出∠COP=∠OPD,故D错误.故选:D.10.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是()A.1对B.2对C.3对D.4对【分析】根据线段垂直平分线上的点到线段两端点的距离相等可得OA=OC,然后判断出△AOE和△COE全等,再根据等腰三角形三线合一的性质可得AD⊥BC,从而得到△ABC 关于直线AD轴对称,再根据全等三角形的定义写出全等三角形即可得解.【解答】解:∵EF是AC的垂直平分线,∴OA=OC,又∵OE=OE,∴Rt△AOE≌Rt△COE,∵AB=AC,D是BC的中点,∴AD⊥BC,∴△ABC关于直线AD轴对称,∴△AOC≌△AOB,△BOD≌△COD,△ABD≌△ACD,综上所述,全等三角形共有4对.故选:D.二.填空题(共7小题)11.若分式的值为0,则x的值为﹣2【分析】根据分子为零且分母不为零分式的值为零,可得答案.【解答】解:由题意,得x+2=0且x≠0,解得x=﹣2,故答案为:﹣2.12.分解因式:mx2﹣4m=m(x+2)(x﹣2).【分析】首先提取公因式m,进而利用平方差公式分解因式即可.【解答】解:mx2﹣4m=m(x2﹣4)=m(x+2)(x﹣2).故答案为:m(x+2)(x﹣2).13.水由氢原子和氧原子组成,其中氢原子的直径约为0.0000000001米,用科学记数法表示为1×10﹣10米.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 000 0001=1×10﹣10,故答案为:1×10﹣10.14.答案是:45.15.如图,在△ABC中,∠BAC=90°.AD⊥BC于点D,若∠C=30°,BD=1,则线段CD 的长为 3 .【分析】求出∠BAD=∠BAC﹣∠DAC=30°,求出AB=2,求出BC=4,则CD可求出.【解答】解:∵AD⊥BC于点D,∠C=30°,∴∠DAC=60°,∵∠BAC=90°,∴∠BAD=∠BAC﹣∠DAC=30°,∴在Rt△ABD中,AB=2BD=2,∴Rt△ABC中,∠C=30°,∴BC=2AB=4,∴CD=BC﹣BD=4﹣1=3.故答案为:3.16.如图,在底边BC为2,腰AB为2的等腰三角形ABC中,DE垂直平分AB于点D,交BC于点E,则△ACE的周长2+2.【分析】根据DE垂直平分AB,可得BE=AE,进而AE+CE=BE+CE=BC=2,即可求得△ACE的周长.【解答】解:∵DE垂直平分AB,∴BE=AE,∴AE+CE=BE+CE=BC=2,∴△ACE的周长为:AC+AE+CE=AC+BC=2+2.故答案为:2+2.17.答案为2.三.解答题(共8小题)18.化简:(m+2)(m﹣2)﹣×3m.【分析】利用平方差公式计算:(m+2)(m﹣2),再计算后面的乘法,最后合并同类项即可.【解答】解:原式=m2﹣4﹣m2=﹣4.19.X=-420.如图,在△ABC中,AB=AC,∠A=36°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求与作法);(2)在(1)的条件下,求∠BDC的度数.【分析】(1)直接利用角平分线的作法得出BD;(2)利用等腰三角形的性质以及角平分线的性质分析得出答案.【解答】解:(1)如图所示:BD即为所求;(2)∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠ABC=36°,∴∠BDC=∠A+∠ABD=72°.21.先化简(1﹣)•,再在1,2,3中选取一个适当的数代入求值.【分析】先算括号内的减法,再算乘法,最后代入求出即可.【解答】解:原式=•=•=,∵x﹣1≠0,x﹣3≠0,∴x≠1且x≠3,∴x只能选取2,把x=2代入得:原式==﹣2.22.【分析】(1)根据A、C两点坐标根据平面直角坐标系即可;(2)画出A、B、C关于x轴对称的A1、B1、C1即可;(3)根据所作图形求解可得.【解答】解:(1)如图所示;(2)如图所示,△A1B1C1即为所求.(3)点A1的坐标为(﹣4,﹣6)、C1的坐标为(﹣1,﹣4)..【点评】本题考查作图﹣轴对称变换,解题的关键是熟练掌握轴对称变换的定义和性质及其平面直角坐标系的概念.23.如图,AC=BC,AE⊥CD于点A,BD⊥CE于点B.(1)求证:CD=CE;(2)若点A为CD的中点,求∠C的度数.【分析】(1)证明△CAE≌△CBD(ASA),可得出结论;(2)根据题意得出△CDE为等边三角形,进而得出∠C的度数.【解答】解:(1)∵AE⊥CD于点A,BD⊥CE于点B,∴∠CAE=∠CBD=90°,在△CAE和△CBD中,,∴△CAE≌△CBD(ASA).∴CD=CE;(2)连接DE,∵由(1)可得CE=CD,∵点A为CD的中点,AE⊥CD,∴CE=DE,∴CE=DE=CD,∴△CDE为等边三角形.∴∠C=60°.24.【分析】设2016年这种礼盒每盒的进价是x元,则2018年这种礼盒每盒的进价是x 元,根据数量=总价÷单价结合2018年该商店用2100元购进的礼盒数比2016年的礼盒数多100盒,即可得出关于x的分式方程,解之经检验后即可得出结论.【解答】解:设2016年这种礼盒每盒的进价是x元,则2018年这种礼盒每盒的进价是x 元,根据题意得:﹣=100,解得:x=20,经检验,x=20是原方程的解,且符合题意.答:2016年这种礼盒每盒的进价是20元.25.将一副三角板按如图所示的方式摆放,AD是等腰直角三角板ABC斜边BC上的高,另一块三角板DMN的直角顶点与点D重合,DM、DN分别交AB、AC于点E、F.(1)请判别△DEF的形状.并证明你的结论;(2)若BC=4,求四边形AEDF的面积.【分析】(1)可得∠CAD=∠B=45°,根据同角的余角相等求出∠CDF=∠ADE,然后利用“角边角”证明△ADE和△CDF全等,则结论得证;(2)根据全等三角形的面积相等可得S△ADE=S△CDF,从而求出S四边形AEDF=S△ABD=,可求出答案.【解答】(1)解:△DEF是等腰直角三角形.证明如下:AD⊥BC,∠BAD=45°,∴∠EAD=∠C,∵∠MDN是直角,∴∠ADF+∠ADE=90°,∵∠CDF+∠ADF=∠ADC=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF(ASA),∴DE=DF,又∵∠MDN=90°,∴∠EDF=90°,∴△DEF是等腰直角三角形;(2)∵△ADE≌△CDF,∴S△ADE=S△CDF,∴S四边形AEDF=S△ABD====2.。
八年级数学下学期插班考试试题试题
54D3E21C B A第十HY 学2021-2021学年八年级下学期插班考试数学试题〔无答案〕新人教版一、选择题〔3分×10=30分〕1. 在直角坐标系中,点P 〔6-2x ,x -5〕在第二象限,•那么x 的取值范围是〔 〕.A 、3<x<5B 、x> 5C 、x<3D 、-3<x<52. 点A 〔3,-5〕向上平移4个单位,再向左平移3个单位到点B ,那么点B 的坐标为( )3. A 、(1,-8) B 、(1, -2) C 、(-7,-1 ) D 、( 0,-1)4. 如右图,以下不能断定AB ∥CD 的条件是( ).A 、︒=∠+∠180BCDB B 、21∠=∠;C 、43∠=∠;D 、 5∠=∠B . 5. 假设x=2是不等式2x <a 的解,那么常数a 满足〔 〕 A 、a=4 B 、a>4 C 、a<4 D 、a ≥4 6. 能用以下两种正多边形镶嵌一个平面的是( )A .正三角形和正五边形B .正五边形和正十边形C .正六边形和正八边形D .正方形和正八边形7. 假设点P 是第二象限内的点,且点P 到x 轴的间隔 是4,到y 轴的间隔 是3,那么点P 的坐标是 〔 〕A 、〔-4,3〕B 、〔4,-3〕C 、〔-3,4〕D 、〔3,-4〕8. 与方程组⎩⎨⎧x+2y -3=02x+y=0有完全一样的解的方程是〔 〕。
A 、x+2y=3B 、2x+y=0C 、(x+2y -3)( 2x+y)=0D 、|x+2y -3|+(2x+y)2=09. 假设方程组⎩⎨⎧=-=+1293y x y ax 无解,那么a 为〔 〕A 、6B 、-6C 、19D 、30 10. 以下命题中真命题的个数是〔 〕①过一点有一条直线与直线垂直;②过一点有一条直线与直线平行;③每一条直线都有一条直线与它平行;④每一条直线都有一条垂线;⑤两条直线不平行就相交。
插班考试八年级数学测2试卷docx
八年级数学测试满分 50分 总时量 60分钟一、选择题:(每小题3分,共18分)1、在函数65--=x x y 中,自变量x 的取值范围是( ) A 、x >5 B 、x ≥5且x ≠6 C 、x ≥5 D 、x >5且x ≠62、下列命题中正确的是( )A 、矩形的对角线互相垂直;B 、菱形的对角线相等;C 、平行四边形是轴对称图形;D 、等腰梯形的对角线相等。
3、下列运算中不正确的是( )A 、a a a 2333=+B 、a a a 532=⨯C 、()a a 923=- D 、a a a 2223=÷ 4、如果分式2312+--x x x 的值为0,那么x 的值等于( )A 、-1B 、1C 、-1或1D 、1或25、反比例函数)0(>=x xk y 在第一象限内的图形如图,P 为该函数图象上任意一点,PQ ⊥x 轴于Q,设△POQ 的面积为S ,则S 与k 之间的关系是( ) A 、2k S = B 、4k S = C 、k S = D 、k S > 6、下列图形,既是轴对称图形又是中心对称图形的是( )A 、等腰梯形;B 、等边三角形C 、平行四边形D 、菱形二、填空题:(每小题3分,共18分)7、9的平方根是 ;8、等腰梯形一个角是135°,上底为4cm,高为3cm,则面积为 ;9、点A (2a-6,a-7)在第四象限内,则a 的取值范围是 ;10、化简111112-÷⎪⎪⎭⎫ ⎝⎛-+a a = ; 11、0.00000607用科学记数法表示是 ;12、方程311312-+=--x x x 的解是 ; 三、解答题:(每小题7分,共14分)13、先化简,再求值:423252+-÷⎪⎭⎫ ⎝⎛+--x x x x ,其中32-=x14、如图,点B 、F 、C 、E 在同一直线上,点A 、D 在直线BE 的两侧,AB ∥DE ,AC ∥DF ,BF=CE 。
2013年初中招生数学试卷及答案
2013年初中招生数学试卷一、填空(每空3分,共33分)1、用2、3、4、5、6、0组成最大的六位数是( )把它“四舍五入”到万位约是( )2、一只挂钟时针长5厘米,分针长8厘米,从12时到18时,分针尖端走了( )厘米,时针扫过的面积是( )3、有一个开关能控制两盏灯,按第一次第一盏灯亮,第二次第二盏灯亮,按第三次两盏灯亮,再按一次两灯全灭,当按到第98次时第( )盏灯亮,再按( )次两灯全灭。
4、甲数比乙数多25%,乙数比甲数少( )%,如果乙数是20,那么甲数是( )5、用8个1立方厘米的小正方体拼成一个大正方体,拿去一个小正方体后,表面积是( )平方厘米。
6、如果6x 是假分数,7x是真分数时,那么x =( )7、在2.06里面有( )个百分之一。
二、选择(每题3分,共30分)1、一个5分硬币大约厚度是1( )?A 、毫米B 、厘米C 、分米2、因为2:4=21, 12.5:41=21, 所以2:4和12.5:41可以组成比例,这是根据什么判断的?( )A 、比例的意义B 、比的基本性质C 、比例的基本性质3、打印一份文稿,小云用了8分钟,小静用了10分钟,小云与小静的工作效率比是( )A 、8:10B 、5:4C 、101:814、在120=2×2×2×3×5中,5是120的( )A 、质因数B 、公因数C 、倍数5、笼中共有30只鸡和兔,共100只脚,鸡有( )只。
A 、20B 、15C 、106、下列说法正确的是谁?( )A 、一条射线长50米B 、假分数的倒数一定是真分数C 、北京承办奥运会的这一年二月有29天7、按照时间的长短比较下列时间,最长的是谁( )?A 、152日 B 、200分钟 C 、3.25时8、甲数是乙数的3倍,那么甲、乙两数的最小公倍数是谁?( )A 、3B 、甲数C 、乙数9、都不能化成有限小数的是哪一组?( )A 、72和153B 、161和254C 、125和9310、想一想,你向后转,共旋转多少度?( )A 、90°B 、180°C 、360°三、1、简算(每题4分)① 56×125 ② 16.39-(6.39+107)-7.32、计算:① 2-136÷269-32 ② 41:x =21:61四、应用题1、某商店同时卖出两件商品,各卖60元,但其中一件赚了20%,另一件亏本20%,这个商店卖出两件商品是赚了还是亏本?(5分)2、一个圆形水池,水池内壁和底面都要涂上水泥,水池底面直径是6米,深1.5米,需要涂水泥多少平方米?如果向池中注入1.2米深的水,水的体积是多少? (6分)3、用一批纸装订练习本,若每本装订90页,可装订40本;若要装订50本,每本多少页?(用比例解)(5分)4、从北京到沈阳的铁路长738千米,一列火车从沈阳开往北京,每小时行41千米,这列火车行驶10小时后距沈阳有多少千米?(5分)答案一、⑴、654320 65万 ⑵、301.44厘米 39.25平方厘米⑶、二 两 ⑷、20 25 ⑸、24 ⑹、6 ⑺、206 二、1、A 2、A 3、B 4、A 5、C6、C7、B8、B9、C 10、B三、1、1① 56×125=7×8×125=7×1000=7000 ② 16.39-(6.39+107)-7.3=16.39-6.39-0.7-7.3 =10-8=2 2、① 2-136÷269-32=0 ② 41:x =21:61 解:x =121四、1、60÷(1+20%)=50(元)60÷(1-20%)=75(元) 50+75=125(元) 60×2=120元 125元>120元 答:亏了。
八年级插班生试卷
八年级插班生入学考试试卷( )1. After dinner he often ________ in the park.A. take a walkB. takes a walkC. taking a walk( )2.What does she soap operas? She can’t stand them.A. thinksB. think of C like( )3. He _______ his friends last weekend.A. visitsB. visitedC. visit( )4. Listen! Some of the girls about Harry Potter.A . are talking B. will talk C. talked( )5. ---_____? ---It’s cloudy.A. How’s the weather like in ShanghaiB. How’s the weather in ShanghaiC. What is the weather in Shanghai( )6. _______ arrive late for school.A. Don’tB. NotC. Doesn’t( )7. She has to ______ up early every morning.A. getsB. getC. got( )8. I can’t watch TV ______ school nights.A. inB. atC. on( )9. _________ , is there a pay phone in the neighborhood?A. I’m sorryB. SorryC. Excuse meD. Excuse( )10. ---Thank you very much. ---________.A. You're welcomeB. That's rightC. You're rightD. Don't thank me Ⅱ、完形填空(10小题,共10分)Dear Annie,Thank you for your letter.I'm glad you like your school.I go to school from Monday to Friday.We have four 11 in the morning and two in the afternoon.We have 12 to do after class.13 Monday and Thursday afternoon we 14 sports.On Tuesday afternoon 15 of us have 16 singing class.And on Thursday afternoon some have a 17 class.On Friday afternoon we practice(练习) 18 English.My Chinese friends would like 19 with me in English.They think I am like an English teacher.Isn't it great?On Saturdays and Sundays I don't go to school.Very often I go to the parks and have a good time 20 my family there( )11.A.classes B.lesson C.class ( )12.A.anything B.any things C many things( )13.A.To B.In C.On ( )14.A.has B.have C.having ( )15.A.any B.one C.some ( )16.A.a B.an C.the ( )17.A.draw Bdraws C.drawing ( )18.A.speak B.speaks C.spe aking( )19.A.talk B.talks C.to talk ( )20.A.for B.with C.atШ、. 阅读理解(15分) (A)Dear Dr Know,I’m not happy. I have too many rules in my house. I have to get up at six o’clock every morning. I can’t meet my friends after school because I have to do myhomework. I can’t watch TV on school nights. And I have to be in bed by ten o’clock. On weekends, I have to clean my room and wash my clothes. Then I have to help my mom make dinner. Later I have to go to the children’s palace to learn the piano. I never have any fun. What can I do?Zhao Pei 根据短文内容,判断下列各句正(T)、误(F)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学下学期插班生招生考试题
一、选择题(每小题3 分,共30分)
1.下列运算正确的是( ) (A )4
22
2x
x x
=+ (B )3
26
x
x x
=÷ (C )
326x x x =-(D )5
32x
x x =∙
2、下列艺术汉字中,不是轴对称的是( ) (A )奇 (B )中 (C )王 (D )喜
3、在△ABC 和△A 1B 1C 1中,下面给出
了四组条件,其中不一定能判定△ABC ≌△A 1B 1C 1是( ) (A )AB=A 1B 1, BC=B 1C 1, CA=C 1A 1(B )∠C=∠C=90, AB=A 1B 1, BC=B 1C 1 (C )AB=A 1B 1, , CA=C 1A 1,∠B=∠B 1(D )AB=A 1B 1, , CA=C 1A 1,∠A==∠A 1 4、有公共顶点的角可能是( )
A.同位角
B.内错角
C.对顶角
D.同旁内角 5、2.如图是某地一的长方形大理石广场示意图,如果小琴要
从A 角走到C 角,至少走( )米 A. 90 B. 100 C. 120 D. 140 6、使两个直角三角形全等的条件是
A .斜边相等
B .两直角边对应相等
C .一锐角对应相等
D .两锐角对应相等
7、分析下列说法中正确的有( )种 ①长方体、正方体都是棱柱 ; ②球体的三种视图均为同样大小的图形;③三棱柱的侧面是三角形; ④直六棱柱有六个侧面、侧面为长方形; ⑤圆锥的三视图中:主视图、左视图是三角形,俯视图是圆. A.2 B.3 C.4 D.5
A
B D
C 80米
60米
(第5题)图)
姓名____________________
考号________________
得分_______________
----------------------------------------------------密---------------------------------封--------------------------------线------------------------------------------------
8、下列命题错误的是( )
A .等腰三角形两腰上的中线相等
B .等腰三角形两腰上的高相等
C .等腰三角形的中线与高重合
D .等腰三角形顶角平分线上任一点到底边两端点的距离相等
9、有10个数据的平均数为6,另有20个数据的平均数为3,那么所有这30个数据的平均数是( ) A. 3.5 B.4 C. 4.5 D.5 10、八年级(1)班50名学生的年龄统计 结果如右表所示:则此班学生年龄的众数、 中位数分别为( )
A .14,14
B .15,14
C .14,15
D .15,16 二、填空题(每小题3分,共30分)
11.一个直角三角形的两直角边分别是3和 4 ,则斜边上的高为 。
12.计算=2
3)2(y x 。
13. 等腰三角形的顶角是120º,底边上的高是1cm ,则腰长为______cm 。
14.观察下列几组数:①3,4,5 ② 1,2,3 ③5,12,13 ④8,15,15、 ⑤9,12,15;
其中能作为直角三角形三边长的是: (填序号). 16、在函数3y x =+中,自变量x 的取值范围是 . 17、计算10(23)(21)----的结果是_________. 18、 分解因式:
,
A
E
F
G
D
C
B
(第9题图)
年龄 13 14 15 16 人数
4
22 23
1
19、已知是完全平方式,则m=________
20、在△ABC和△DEF中,AB=ED,AC=EF,∠A=∠E,则△ABC≌△______ 。
三、解答与证明题(每小题8分,共40分)
21、先化简后求值,当,时,求
的值.
22、解方程:
23.如图,点C 、E 、B 、F 在一条直线上,AB ⊥CF 于B,DE ⊥CF 于E,AC=DF, AB=DE 。
求证:CE=BF 。
24.已知一次函数y=kx+b 的图象经过点(1,1),且k 、b 满足k-b=-5.试确定该函数的解析式。
25.晶晶同学想知道学校旗杆的高,他发现从旗杆顶上挂下来的绳子垂直到地面还多1米,当他把绳子拉开离旗杆底部5米后,绳子下端刚好接触地面;请你帮晶晶同学算一算学校旗杆高度.
B
C
F
A
E
D
答案
1.D
2.A
3.C
4.C
5.B
6.B
7.C
8.D
9.B 10.B
11. 2.4 12. 13. 2 14.①③⑤ 15. 16.x大于等于-3
17.0 18。
(2X+3)(2X-3) 19、6或-6 20、△EDF 21、 22、X=-23、证明△ACB与△DFE可得BC=EF,有BC-BE=EF-BE 所以CE=BF
24、Y=-2X+3 25、设旗杆高X米则有,所以X=12。
