题型-河南近几年中考数学第23题(全部整合)
河南省近5年中考数学试卷结构(按知识点分)
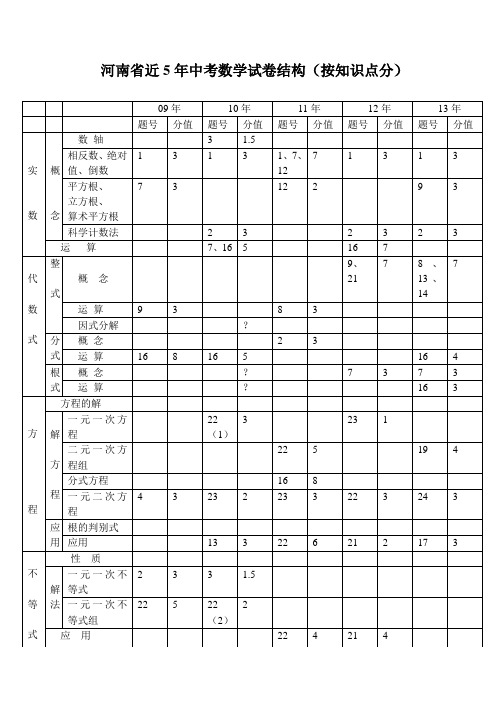
河南省近5年中考数学试卷结构（按知识点分）
近几年河南中考数学试卷题型结构
近几年河南中考数学试卷难度结构
近5年河南中考数学试卷结构（按年级分）
近5年河南中考数学压轴题拆分
基本活动经验和基本数学思想方法）。
试题内容略有变化,较好地考查了主干内容。
近几年的试题的形式朴实无华，少有创新。
难度稍有提高，考试成绩与学生平时的学习态度、学习习惯和心态调整有更大的相关性。
目前我们学生存在的问题：1、阅读习惯差、审题能力差；2、计算能力弱，影响思维与结果；3、数学语言知识少，书写不规范；4、基础知识不全面；5、不会使用数学思想、方法，缺乏思维策略。
变形、拓展能力欠缺。
同学们：要想取得好成绩,就要扎扎实实地学好基础知识,“低起点、多归纳、快反馈”，做好“保本”工作，学习数学≠做题，对典型问题的解决必须有学生自己的深入理解、分析与感悟，不能急于赶功课,然后不得已再“烫剩饭”。
要练好基本技能,保证能够快速、准确地解答常规问题。
数学：懂了≠会了≠对了≠快了≠得分了。
题型：河南近几年中学考试数学第23题(新颖)
近几年中考数学第23题23.（11分）（2016）如图1，直线y=-43x+n交x轴于点A，交y轴于点C（0，4）抛物线y=23x2+bx+c经过点A,交y轴于点B（0,-2）.点P为抛物线上的一个动点，过点P作x轴的垂线PD，过点B作BD⊥PD于点D,连接PB.（1）求抛物线的解析式.（2）当△BDP为等腰直角三角形时，求线段PD的长.（3）如图2，将△BDP绕点B逆时针旋转，得到△BD/P/，且∠PBP/=∠OAC，当点P的对应点P/落在坐标轴上时，请直接写出P点的坐标.解：（1）由y=-43x+n过点C（0，4），得n=4，则y=-43x+4当y=0时，得-43x+4=0，解得：x=3，∴点A坐标是（3,0）…………………………………………………1分∵y=23x2+bx+c经过点A（3,0）, B（0,-2）图1备用图∴22033b+c32c⎧=⨯+⎪⎨⎪-=⎩，解得：4b3c2⎧=-⎪⎨⎪=-⎩∴抛物线的解析式是23x2-43x-2……………………………………………3分（2）∵点P的横坐标为m，∴P（m，23m2-43m-2），D（m，-2）…………4分若△BDP为等腰直角三角形时，则PD=BD;①当点P在直线BD上方时，PD=23m2-43m-2+2=23m2-43m，（ⅰ）若P在y轴左侧，则m＜0，BD=-m；∴23m2-43m=-m，解得：m=12或m=0（舍去）…………………………………5分（ⅱ）若P在y轴右侧，则m＞0，BD=m；∴23m2-43m=m，解得：m=72或m=0（舍去）…………………………………6分②当点P在直线BD下方时，PD=-2-(23m2-43m-2) =-23m2+43m，则m＞0，BD=m；∴-23m2+43m=m，解得：m=12或m=0（舍去）……………………………7分综上：m=72或m=12。
即当△BDP为等腰直角三角形时， PD的长为72或12。
2020年河南中考数学23题解析
2020年河南中考数学23题解析在紧张而有序的中考备考中，数学考试中的第23题往往是一个备受关注的部分。
它不仅考察了学生对数学知识的掌握程度，更对学生的思维能力和解题技巧提出了较高的要求。
下面，我们将对2020年河南中考数学中的23题进行深入解析，希望能帮助学生们更好地理解题目，找到解题的关键。
首先，我们来看一下2020年河南中考数学23题的背景。
这道题主要考察了二次函数与一元二次方程的综合应用，涉及到了图象的交点、根的判别式以及增减性等知识点。
题目设计既全面又具有挑战性，对于学生的数学综合能力提出了较高的要求。
接下来，我们逐一分析题目中的各个考点。
首先，题目给出了一个二次函数的图象，需要学生根据图象判断何时有两个交点，何时只有一个交点，甚至没有交点。
这要求学生能够准确理解二次函数图象的性质，并能够根据图象进行判断。
其次，题目还涉及到一元二次方程的根的判别式，需要学生能够灵活运用这一知识点来解决问题。
最后，题目还考察了增减性的问题，需要学生能够根据函数图象的走势，判断函数的增减性。
这些考点的综合应用，对学生的数学思维提出了较高的要求。
在解题过程中，学生们可能会遇到一些困难。
此时，我们需要引导学生们找到问题的关键，理清解题思路。
首先，我们需要根据二次函数图象的性质，判断何时有两个交点，并找到相应的判别式范围。
其次，我们需要根据根的判别式，找到相应的方程解的情况。
最后，我们需要根据函数的增减性，找到函数的最大值或最小值。
通过这样的分析，学生们可以逐渐找到解题的突破口。
为了更好地应对中考数学中的23题，学生们可以从以下几个方面进行提升。
首先，加强基础知识的学习和掌握，尤其是二次函数、一元二次方程等重点知识。
其次，加强解题方法的训练和思维能力的培养，学会从多个角度思考问题，灵活运用所学知识解决问题。
最后，加强数学阅读能力的培养，学会读懂图表中的信息，理解图形的性质和特点。
总的来说，2020年河南中考数学23题是一道具有挑战性的题目，考察了学生对数学知识的掌握程度和思维能力的锻炼。
2021河南中招数学23题
23.(10分)下面是某数学兴趣小组探究用不同方法作一个角 的平分线的讨论片段，请仔细阅读，并完成相应的任务。
小明：如图1，（1）分别在射线OA ，OB 上截取OC=OD ，OE=OF （C, E 不重合）；（2）分别作线段CE ，DF 的垂直平分线l[1,]l[2],交点为P ，垂足分别为G ，H ；（3）作射线OP ，射线OP 即为∠AOB 的角平分线.简述理由如下：由作图知，∠PGO=∠PHO=90°, OG=0H,OP=OP,所以Rt △PGO ≅Rt △PHO,则射线OP 是∠AOB 的平分线。
小军：我认为小明的作图方法很有创意，但是太麻烦了，可以改进如下，如图2，（1）分别在OA,OB 上截取OC=OD ，OE=OF （点C,E 不重合）（2）连接DE ，CF ，交点为P ；（3）作射线OP ，射线OP 即为∠AOB 的平分线，…… 任务：（1）小明得出Rt △PGO ≅Rt △PHO 的依据是______(填序号) ①SSS ②SAS ③AAS ④ASA ⑤HL （2）小军作图得到的射线OP 是∠AOB 的角平分线吗？请判 断并说明理由（3）如图3，已知∠AOB=60°,点E ，F 分别在射线OA ，OB 上，且OE=OF=√3+1.点C ，D 分别为射线OA ，OB 上的动点.且OC=OD ，连接DE ，CF ，交点为P. 当∠CPE=30°时，直接写出OC 的长。
图2OB图1解：（1）⑤（2）射线OP 是∠AOB 的平分线，理由如下： 解法一：连接EF 在△EOD 与△FOC 中 OD=OC ∠EOD=∠FOC OE=OF∴△EOD ≅△FOC(SAS) ∴∠OED=∠OFC ∵OE=OF ∴∠OEF=∠OFE ∴∠PEF=∠PFE ∴PE=PF ∵OE=OF图3BO图4BO∴OP 垂直平分EF ∴∠EOP=∠FOP∴OP 是∠AOB 的角平分线。
河南中考数学10年压轴题集锦
河南中考数学压轴题汇集(2010)23．（11分）在平面直角坐标系中，已知抛物线经过A(4,0)，B(0,4)，C(2,0)三点．（1）求抛物线的解析式；y（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y x上的动点，判断有A O xC几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．MB（2011）23. （11 分）如图，在平面直角坐标系中，直线33y x与4212抛物线y x bx c交于A、B 两点，点 A 在x轴上，点 B 的横坐标4为－8.（1）求该抛物线的解析式；（2）点P 是直线A B 上．方．的抛物线上一动点（不与点A、B 重合），过点P 作x轴的垂线，垂足为C，交直线A B 于点D，作PE⊥AB 于点 E.①设△PDE 的周长为l，点P 的横坐标为x，求l 关于x 的函数关系式，并求出l 的最大值；②连接PA，以PA为边作图示一侧的正方形APFG .随着点P 的运动，正方形的大小、位置也随之改变.当顶点 F 或G 恰好落在y轴上时，直接写出对应的点P 的坐标.1，在平面直角坐标系中，直线y x 1 与抛物线（2012）23.(11 分)如图2y2 bxy ax 3交于A、B 两点，点A 在x轴上，点B 的纵点（不与上一动为3。
点P 是直线A B 下方的抛物线坐标交直线A B 于点C，点P 作x轴的垂线点A、B 重合），过C B作PD⊥AB 于点C，作PD⊥AB 于点D。
D （1）求a、b及sin∠ACP 的值；O x 为m. A点P 的横坐标（2）设P段，并求出线①用含m 的代数式表示线段PD 的长PD长的最大值；接PB，线段PC 把△PDB 分成两个三角形，是②连两个三角形的面积之比为9:10？，使这否存在合适的m值第23 题明理由。
2015河南数学中考第23题提炼题(1)(2)
2015年全国中考数学压轴题研究2015年河南中考数学第23题提炼题（1） 〖抛物线焦点·两点之间线段最短·垂线段最短〗如图，边长为8的正方形OABC 的两边在坐标轴上，以C 为顶点的抛物线经过点A ，P 是抛物线上点A ，C 间的一个动点（含端点），过点P 作PF ⊥BC 于点F ，点D ，E 的坐标分别是（0，6），（－4，0），连接PD ，PE ，DE ．（1）求抛物线的解析式； （2）求证PD 与PF 的差为定值；（3）若△PDE 的周长取得最小值，求点P 的坐标．解：（1）由顶点（0，8）设82+=ax y ． 由A （－8，0）得81-=a ．∴8812+-=x y ．（2）设点P 的坐标为（m ，8812+-m ），则PF ＝281m ． 依勾股定理，得2PD ＝22)281(+m ，PD ＝2812+m ． ∴PD －PF ＝2．即PD 与PF 的差为定值．（3）由（1）得PD ＝PF ＋2， DE 为定值，∴当PF ＋PE 取得最小值时，PD ＋PE ＋DE 取得最小值， 这时，点P 在线段EF 上，且EF ⊥BC ， 则点E 的横坐标为－4．把x ＝－4代入8812+-=x y ，得y ＝6，∴P （－4，6）． 〖类似考题------------2011·宜宾·24〗第23题图第23题备用图2015年河南中考数学第23题提炼题（2） 〖三角形面积·二次函数的整数值〗如图，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，我们容易求得抛物线的解析式为8812+-=x y ．P 是抛物线上点A ，C 间的一个动点（含端点），点D ，E 的坐标分别是（0，6），（－4，0），连接PD ，PE ，DE ．（1）设点P 的横坐标为m ， △PDE 的面积为S ，求S 关于m 的函数解析式；（2）若将“使△PDE 的面积为整数”的点P 记作“好点”，请直接写出所有“好点”的个数．解：（1）如答图①，连接OP ，POD S ∆＝－3m ， POE S ∆＝16412+-m ，DOE S ∆＝12，∴S ＝POD S ∆＋POE S ∆－DOE S ∆＝43412+--m m＝13)6(412++-m ．注意到m 的取值范围是－8≤m ≤0， 画出S 关于m 的图象如答图②．从图中可以得到，顶点的纵坐标是整数，对称轴的右侧有9个点的纵坐标是整数，对称轴的左侧有1个点的纵坐标是整数，抛物线上一共有11个点的纵坐标为整数．∴“好点”一共有11个．（类似考题------------2011·珠海·22）附录 2015年河南中考数学第23题如图，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上点A ，C 间的一个动点（含端点）过点P 作PF ⊥BC 于点F ，点D ，E 的坐标分别是（0，6），（－4，0），连接PD ，PE ，DE ．（1）直接写出抛物线的解析式；（2）小明探究点P 的位置发现：当点P 与点A 或点C 重合时，PD 与PF 的差为定值．进而猜想：对于任意一点P ，PD 与PF 的差为定值．请你判断该猜想是否正确，并说明理由．（3）小明进一步探究得出结论：若将“使△PDE 的面积为整数”的点P 记作“好点”，则存在多个“好点”， 且使△PDE 的周长最小的点P 也是一个“好点”．请直接写出所有“好点”第23题图第23题答图①的个数，并求出△PDE 的周长最小时“好点”的坐标．解：（1）由顶点（0，8）设82+=ax y ． 由A （－8，0）得81-=a ．∴8812+-=x y ．（2）设点P 的坐标为（m ， 8812+-m ），则PF ＝281m ， 依勾股定理，得2PD ＝22)281(+m ，PD ＝2812+m ． ∴PD －PF ＝2．∴猜想正确．（2） 解：（1）如答图①，连接OP ，POD S ∆＝－3m ， POE S ∆＝16412+-m ，DOE S ∆＝12，∴S ＝POD S ∆＋POE S ∆－DOE S ∆＝43412+--m m＝13)6(412++-m ．注意到m 的取值范围是－8≤m ≤0， 画出S 关于m 的图象如答图②．从图中可以得到，顶点的纵坐标是整数，对称轴的右侧有9个点的纵坐标是整数，对称轴的左侧有1个点的纵坐标是整数，抛物线上一共有11个点的纵坐标为整数．∴“好点”一共有11个． （3）由（1）得PD ＝PF ＋2，∴当PF ＋PE 取得最小值时，PD ＋PE ＋DE 取得最小值，这时，点P 在线段EF 上，且EF ⊥BC ，这时，点E 的横坐标为－4．把x ＝－4代入8812+-=x y ，得y ＝6，∴P （－4，6）．此时，PDE S ∆＝12．第23题图第23题备用图第23题答图①。
中考数学第23-24题(解答中档题：圆、二次函数的实际应用)考前预测
押中考数学第23-24题（解答中档题：圆、二次函数的实际应用）专题诠释：圆和二次函数的实际应用在了历年的中考中均有所考察，分值一般在20-24之间，分值较高且有一定的难度。
圆常常会结合勾股定理、全等、相似或锐角三角函数一起考察；二次函数的实际应用考察最多的是利润问题。
能根据题意进行合理的转化是做题的关键！知识点一：圆〖押题冲关〗1．（2023·四川成都·统考二模）如图，在Rt△ABC中，∠BAC=90°，BO平分∠ABC，交AC于点O．以点O为圆心，OA为半径作⊙O，交BO于点D，连接AD．(1)求证：BC为⊙O的切线；(2)若OA=3，OC=27，求AB的长；7(3)在（2）的条件下，求tan∠BAD的值．2．（2023·四川达州·统考一模）如图，△ABC为⊙O的内接三角形，P为BC延长线上一点，∠PAC=∠B，AD为⊙O的直径，过C作CG⊥AD交AD于E，交AB于F，交⊙O于G．(1)判断直线PA与⊙O的位置关系，并说明理由；(2)求证：AG2=AB⋅AF．3．（2023·浙江台州·统考一模）如图，△ABC内接于半圆O，已知AB是半圆O的直径．AB=10，AD平分∠BAC，分别交半圆O和BC于点D，E，过点D作DH⊥AB，垂足为点H，交BC于点F．(1)求证：EF=DF；⌢的长．(2)连接OD交BC于点G，若EG=FG，求BC4．（2023·安徽滁州·统考二模）如图，△ABC中，∠C=90°，BD平分∠ABC交AC于点D，BD的垂直平分线交AB于点O，以O为圆心，OB长为半径作⊙O．(1)求证：AC与⊙O相切于点D．(2)若BC=3，AC=4，求⊙O的半径．5．（2023·广东东莞·校考二模）如图，四边形ABCD内接于⊙O，AB为直径，BC=CD，过点C作CE⊥AB于点E，CH⊥AD交AD的延长线于点H，连接BD交CE于点G．(1)求证：CH是⊙O的切线：(2)若点D为AH的中点，求证：AD=BE；，CG=10，求BD的长．(3)若cos∠DBA=456．（2023·四川成都·统考二模）如图，D是以AB为直径的⊙O上一点，过点D的切线交AB的延长线于点E，过点B作BF⊥DE，垂足为点F，延长BF交AD的延长线于点C．(1)求证：AB=BC；(2)若⊙O的直径为5，sinA=3，求线段BF和BE的长．57．（2023·陕西西安·统考二模）如图，⊙O中两条互相垂直的弦AB，CD交于点E．(1)OM⊥CD，OM=6，⊙O的半径为10，求弦CD的长；(2)过点A作AN⊥BD交CD于点F，求证：CE=EF．8．（2023·北京房山·统考一模）如图，△ABC中，AB=AC，以BC为直径作⊙O，与边AC交于点D，过点D的⊙O的切线交BC的延长线于点E．(1)求证：∠BAC=2∠DBC；(2)若cos∠BAC=3，DE=4，求BE的长．59．（2023·安徽合肥·校考一模）如图，在Rt△ABC中，∠ACB=90°，以AC为弦作⊙O，交BC的延长线于点D，且DC=BC，∠CAB=∠BDE．(1)求证：DE为⊙O的切线；(2)若⊙O的半径为2，AB=BE，求劣弧AC的长．10．（2023·安徽阜阳·统考二模）如图，以△ABC的边AB为直径作半圆O交AC于点D，且OD∥BC，半圆O交BC于点E．(1)求证：∠C=∠CED．，AD=4，求半圆O的半径r．(2)若CE=83知识点二：二次函数的实际应用〖押题冲关〗(1)求此桥拱截面所在抛物线的表达式；4．（2023·四川成都·统考二模）2022年卡塔尔世界杯期间，某网点直接从工厂购进A，B两款拉伊卜吉祥物手办，A款的购进单价比B款贵20元，用400元购进A款手办的数量比用400元购进B款手办的数量少一件．A，B两款手办的销售单价分别是120元和95元．（注：利润=销售价-购进价）(1)求A，B两款手办的购进单价分别是多少元？(2)世界杯结束后，为了尽快减少库存，加快资金周转，网店决定对A款拉伊卜吉祥物手办进行调价销售，如果按照原价销售，平均每天可销售5件，经调查发现，每降价2元就可以多销售1件，试问将销售价定为每件多少元时，才能使A款手办平均每天的销售利润最大？5．（2023·安徽蚌埠·校考二模）如图，蚌埠花博园要建造一圆形喷水池，在水池中央垂直于水面安装一个柱子OA，O恰在水面中心，OA高3米，如图1，由柱子顶端处的喷头向外喷水，水流在各方面沿形状相同的抛物线落下．(1)如果要求设计成水流在离OA距离为1米处达到最高点，且与水面的距离是4米，那么水池的内部半径至少要多少米，才能使喷出的水不致落到池外；（利用图2所示的坐标系进行计算）(2)若水流喷出的抛物线形状与（1）相同，水池内部的半径为5米，要使水流不落到池外，此时水流达到的最高点与水面的距离应是多少米？6．（2023·河南三门峡·统考一模）如图，在某中学的一场篮球赛中，李明在距离篮圈中心5.5m （水平距离）处跳起投篮，球出手时离地面2.2m，当篮球运行的水平距离为3m时达到离地面的最大高度4m．已知篮球在空中的运行路线为一条抛物线，篮圈中心距地面3.05m．(1)建立如图所示的平面直角坐标系，求篮球运动路线所在抛物线的函数解析式；(2)场边看球的小丽认为，李明投出的此球不能命中篮圈中心．请通过计算说明小丽判断的正确性；(3)在球出手后，未达到最高点时，被防守队员拦截下来称为盖帽．但球到达最高点后，处于下落过程时，防守队员再出手拦截，属于犯规．在（1）的条件下，防守方球员张亮前来盖帽，已知张亮的最大摸球高度为3.2m，则他应该在李明前面多少米范围内跳起拦截才能盖帽成功？7．（2023·辽宁葫芦岛·统考一模）超市需购进某种商品，每件的进价为10元，该商品的销售单价不低于进价，且不高于20元，在销售过程中发现，该商品的日销售量y（件）与销售单价x（元）之间存在如图所示的一次函数关系：(1)求y与x之间的函数关系式，并直接写出自变量x的取值范围；(2)当该商品的销售单价为多少元时，销售这种商品的日销售利润最大？最大利润是多少？8．（2023·陕西西安·统考二模）2023兔年春节期间，全国各地举办焰火晚会，庆祝农历新年的到来．九年级学生王毅也在父母的陪同下前往指定区域燃放一种手持烟花，这种烟花每隔2s发射一枚花弹，每枚花弹的飞行路径视为同一条抛物线，飞行相同时间后发生爆炸，王毅燃放的手持烟花发射出的第一枚花弹的飞行高度h（单位：m）随飞行时间t（单位：s）变化的规律如下表：。
河南23题二次函数培优课件
（1）求抛物线的解析式； （2）如图②，当点F恰好在抛物线上时，求线段OD的长； （3）在（2）的条件下： ①连接DF，求tan∠FDE的值； ②试探究在直线l上，是否存在点G，使∠EDG = 45°，若存在，请 直接写出点G 的坐标；若不存在，请说明理由.
类型二
面积问题
2
1.（2015攀枝花）如图，已知抛物线 y = + x bx + c与x轴 交于A（-1,0）,B（3,0）两点，与 y轴交于点C，抛物线的对 称轴与抛物线交于点 P,与直线 BC相交于点M，连接PB. （1）求该抛物线的解析式； （2）在（1）中位于第一象限内的抛物线上是否存在点D， 使得△BCD的面积最大？若存在，求出点D的坐标及△BCD 面积的最大值；若不存在，请说明理由； （3）在（1）中的抛物线上 是否存在点Q，使得△QMB 与△PMB的面积相等？若存 在，求出点Q的坐标；若不 存在，请说明理由.
数关系问题. 解题技巧一般是过特殊点作x轴或y轴的垂线，将所
求面积进行分割，从而将面积问题转化为线段问题，建立未知 量和已知变量之间的联系，通过二次函数的增减性得到相应的
最值.
【方法指导】 特殊图形的判定问题，常与点的存在 性问题相结合，解决此类问题的关键是要熟练掌握特殊 图形的判定方法及性质，如：对边平行且相等的四边形 是平行四边形，等边三角形的三边相等. 解决此类问题 最常用的方法是假设法，一般先假设存在满足题意的点， 根据特殊图形的性质画出草图，确定点的位置，然后根 据题中已知条件和特殊图形的性质及判定方法建立动点 与已知点的关系，最后列方程求解. 在画草图时，要做 到不重不漏地画出所有可能的情况，以免在求解过程中 遗漏答案， 对所求出的结果要进行检验，看是否符合题 意，如果不符合题意，应舍去.
【河南中考面对面】中考数学总复习 题型6 第23题函数动态变化问题课件
性质求解.
解：∵设点P的横坐标为t， 17 5 2 ∴点M坐标为（t，- t + t+1）， 4 4 设直线AB的解析式为y=kx+b， 将A(0,1),B(3, 5 )代入， 2 b＝ 1 得 5 3 k +b ＝ ， 1 2 k＝ 解得 2 b＝ 1， 1 ∴直线AB的解析式为y＝ x+1， 2 ∵点P在直线AB上，点P的横坐标为t，
∴AD2＝［5-（-3）］2＝64， 5 121 2 2 2 2 BD ＝4 ＝16，AE ＝［ -(-3)］ = , 2 4 EM2=m2, 25 BF2=(5- 5 )2= ,MF2=(4-m)2, 4 2 ∴在Rt△ABD中，AB2=AD2+BD2=80, 121 在Rt△AEM中，AM2=AE2+EM2=m2+ , 25 4 2 2 2 在Rt△BFM中，BM =BF +MF = +(4-m)2. 4 要使△ABM是以AB为直角边的直角三角形，
∴线段PQ等于抛物线与直线的纵坐标之差，
1 3 1 2 x +56x+4)-( x+ ) 2 2 6 5 1 2 1 =- x + x+ 2 6 3 1 8 2 =- (x-1) + . 6 3 由此可见，当点P的横坐标为1（-3≤x≤5）时， 8 线段PQ有最大值 ． 3
即y=(-
（3）【思路分析】借助两点之间的线段长
【方法指导】三角形周长与四边形判定结
合的函数动态问题可从以下几个方面思考：
2023年河南省中考数学真题
2023年河南省普通高中招生考试时间：100分钟 满分：120分一、选择题(每小题3分，共30分)下列各小题均有四个选项，其中只有一个是正确的． 1. 下列各数中最小的数是( ) A. －1 B. 0 C. 1 D. 32. 北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一，具有极高的历史价值、文化价值．如图所示，关于它的三视图，下列说法正确的是( ) A. 主视图与左视图相同 B. 主视图与俯视图相同 C. 左视图与俯视图相同 D. 三种视图都相同第2题图3. 2022年河南省出版的4.59亿册图书，为贯彻落实党的二十大关于深化全民阅读活动的重要精神，建设学习型社会提供了丰富的图书资源．数据“4.59亿”用科学记数法表示为( ) A. 4.59×107 B. 45.9×108 C. 4.59 ×108 D. 0.459×1094. 如图，直线AB ，CD 相交于点O ，若∠1＝80°，∠2＝30°，则∠AOE 的度数为( ) A. 30° B. 50° C. 60° D. 80°第4题图5. 化简a －1a ＋1a 的结果是( )A. 0B. 1C. aD. a －26. 如图，点A ，B ，C 在⊙O 上，若∠C ＝55°，则∠AOB 的度数为( )第6题图A. 95°B. 100°C. 105°D. 110°7. 关于x 的一元二次方程x 2＋mx －8＝0的根的情况是( ) A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 只有一个实数根 D. 没有实数根8. 为落实教育部办公厅、中共中央宣传部办公厅关于《第41批向全国中小学生推荐优秀影片片目》的通知精神，某校七、八年级分别从如图所示的三部影片中随机选择一部组织本年级学生观看，则这两个年级选择的影片相同的概率为( ) A. 12 B. 13 C. 16 D. 19第8题图9. 二次函数y ＝ax 2＋bx 的图象如图所示，则一次函数y ＝x ＋b 的图象一定不经过( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限第9题图10. 如图①，点P 从等边三角形ABC 的顶点A 出发，沿直线运动到三角形内部一点，再从该点沿直线运动到顶点B.设点P 运动的路程为x ，PBPC ＝y ，图②是点P 运动时y 随x 变化的关系图象，则等边三角形ABC的边长为( )第10题图A. 6B. 3C. 43D. 23二、填空题(每小题3分，共15分)11. 某校计划给每个年级配发n 套劳动工具，则3个年级共需配发________套劳动工具．12. 方程组⎩⎪⎨⎪⎧3x ＋y ＝5，x ＋3y ＝7 的解为________．13. 某林木良种繁育试验基地为全面掌握“无絮杨”品种苗的生长规律，定期对培育的1 000棵该品种苗进行抽测．如图是某次随机抽测该品种苗的高度x (cm)的统计图，则此时该基地高度不低于300 cm 的“无絮杨”品种苗约有________棵．第13题图14. 如图，P A 与⊙O 相切于点A ，PO 交⊙O 于点B ，点C 在P A 上，且CB ＝CA .若OA ＝5，P A ＝12，则CA 的长为________．第14题图15. 矩形ABCD 中，M 为对角线BD 的中点，点N 在边AD 上，且AN ＝AB ＝1.当以点D ，M ，N 为顶点的三角形是直角三角形时，AD 的长为________． 三、解答题(本大题共8个小题，共75分) 16. (10分)(1)计算：|－3|－9 ＋5－1；(2)化简：(x－2y)2－x(x－4y).17. (新考法真实问题情境) (9分)蓬勃发展的快递业，为全国各地的新鲜水果及时走进千家万户提供了极大便利．不同的快递公司在配送、服务、收费和投递范围等方面各具优势．樱桃种植户小丽经过初步了解，打算从甲、乙两家快递公司中选择一家合作，为此，小丽收集了10家樱桃种植户对两家公司的相关评价，并整理、描述、分析如下：a. 配送速度得分(满分10分)：甲：66777899910乙：67788889910b．服务质量得分统计图(满分10分)：c．配送速度和服务质量得分统计表：根据以上信息，回答下列问题：(1)表格中的m＝________；s2甲________s2乙(填“>”“＝”或“<”)；(2)综合上表中的统计量，你认为小丽应选择哪家公司？请说明理由；(3)为了从甲、乙两家公司中选出更合适的公司，你认为还应收集什么信息(列出一条即可)?18. (9分)如图，△ABC 中，点D 在边AC 上，且AD ＝A B.(1)请用无刻度的直尺和圆规作出∠A 的平分线(保留作图痕迹，不写作法)； (2)若(1)中所作的角平分线与边BC 交于点E ，连接DE .求证：DE ＝BE .第18题图19. (9分)小军借助反比例函数图象设计“鱼形”图案，如图，在平面直角坐标系中，以反比例函数y ＝kx 图象上的点A (3 ，1)和点B 为顶点，分别作菱形AOCD 和菱形OBEF ，点D ，E 在x 轴上，以点O 为圆心，OA 长为半径作A C ，连接BF . (1)求k 的值；(2)求扇形AOC 的半径及圆心角的度数； (3)请直接写出图中阴影部分面积之和．第19题图20. (9分)综合实践活动中，某小组用木板自制了一个测高仪测量树高，测高仪ABCD为正方形，AB＝30 cm，顶点A处挂了一个铅锤M.如图是测量树高的示意图，测高仪上的点D，A与树顶E在一条直线上，铅垂线AM交BC于点H.经测量，点A距地面1.8 m，到树EG的距离AF＝11 m，BH＝20 cm.求树EG的高度(结果精确到0.1 m).第20题图21. (9分)某健身器材专卖店推出两种优惠活动，并规定购物时只能选择其中一种．活动一：所购商品按原价打八折；活动二：所购商品按原价每满．．300元减80元．(如：所购商品原价为300元，可减80元，需付款220元；所购商品原价为770元，可减160元，需付款610元)(1)购买一件原价为450元的健身器材时，选择哪种活动更合算？请说明理由；(2)购买一件原价在500元以下的健身器材时，若选择活动一和选择活动二的付款金额相等，求一件这种健身器材的原价；(3)购买一件原价在900元以下的健身器材时，原价在什么范围内，选择活动二比选择活动一更合算？设一件这种健身器材的原价为a元，请直接写出a的取值范围．22. (10分)小林同学不仅是一名羽毛球运动爱好者，还喜欢运用数学知识对羽毛球比赛进行技术分析，下面是他对击球线路的分析．如图，在平面直角坐标系中，点A，C在x轴上，球网AB与y轴的水平距离OA＝3 m，CA＝2 m，击球点P在y轴上．若选择扣球，羽毛球的飞行高度y(m)与水平距离x(m)近似满足一次函数关系y＝－0.4x＋2.8；若选择吊球，羽毛球的飞行高度y(m)与水平距离x(m)近似满足二次函数关系y＝a(x－1)2＋3.2.(1)求点P的坐标和a的值；(2)小林分析发现，上面两种击球方式均能使球过网．要使球的落地点到C点的距离更近，请通过计算判断应选择哪种击球方式．第22题图23. (新考法综合与实践) (10分)李老师善于通过合适的主题整合教学内容，帮助同学们用整体的、联系的、发展的眼光看问题，形成科学的思维习惯．下面是李老师在“图形的变化”主题下设计的问题，请你解答．(1)观察发现如图①，在平面直角坐标系中，过点M(4，0)的直线l∥y轴，作△ABC关于y轴对称的图形△A1B1C1，再分别作△A1B1C1关于x轴和直线l对称的图形△A2B2C2和△A3B3C3，则△A2B2C2可以看作是△ABC绕点O 顺时针旋转得到的，旋转角的度数为________；△A3B3C3可以看作是△ABC向右平移得到的，平移距离为________个单位长度．(2)探究迁移如图②，▱ABCD中，∠BAD＝α(0°<α<90°)，P为直线AB下方一点，作点P关于直线AB的对称点P1，再分别作点P1关于直线AD和直线CD的对称点P2和P3，连接AP，AP2，请仅就图②的情形解决以下问题：①若∠P AP2＝β，请判断β与α的数量关系，并说明理由；②若AD＝m，求P，P3两点间的距离．(3)拓展应用在(2)的条件下，若α＝60°，AD＝23，∠P AB＝15°，连接P2P3.当P2P3与▱ABCD的边平行时，请直接写出AP的长．2023年河南省普通高中招生考试解析快速对答案详解详析一、选择题 1. A 2. A3. C 【解析】∵1亿＝108，∴4.59亿＝4.59×108.4. B 【解析】∵直线AB ，CD 相交于点O ，∴∠AOD ＝∠1＝80°，∴∠AOE ＝∠AOD －∠2＝80°－30°＝50°.5. B 【解析】原式＝a －1＋1a ＝a a＝1.6. D 【解析】根据圆周角定理可得∠AOB ＝2∠C ＝110°.7. A 【解析】∵b 2－4ac ＝m 2－4×(－8)＝m 2＋32＞0，∴方程有两个不相等的实数根． 8. B 【解析】设三部影片分别用甲、乙、丙表示，画树状图如解图：第8题解图由树状图可知，共有9种等可能结果，其中两个年级选择的影片相同的结果有3种，故P (两个年级选择的影片相同)＝39 ＝13.9. D 【解析】由图象可得抛物线开口向下，∴a ＜0.∵对称轴在y 轴的右侧，∴－b2a ＞0，∴b ＞0.∵k ＝1＞0，∴一次函数y ＝x ＋b 的图象经过第一、二、三象限，不经过第四象限．10. A 【解析】如解图，设等边三角形内一点为点D ，由图象可知：当0≤x ≤2 3 时，y ＝PBPC＝1，即PB＝PC ，∴点P 在BC 的垂直平分线上，∴∠DAB ＝∠DAC ＝30°，且当点P 运动到点D 时，P A ＝2 3 ；根据函数图象与x 轴交于(4 3 ，0)，∴BD ＝4 3 －2 3 ＝2 3 ，∴BD ＝AD ，∴∠DAB ＝∠DBA ＝30°.过点D 作DE ⊥AB ，垂足为E ，在Rt △AED 中，AE ＝AD ·cos 30°＝3，∴AB ＝2AE ＝6.第10题解图(命题立意)本题考查函数图象的分析，对传统类似题目进行创新设计，试题用图象刻画出运动中变量之间的函数关系，赋予了图形所具有的学科内涵，体现了“稳中求新，引领教改动向” . (方法指导) 解决函数图象的分析问题的方法： (1)要明确横纵坐标的意义；(2)关注起点、拐点、终点在图象中对应的值；(3)借助特殊点的值与几何图形变量之间的关系利用图形的性质进行求解． 二、填空题11. 3n 【解析】配发的总数＝每个年级配发数×年级数＝3n .12. ⎩⎪⎨⎪⎧x ＝1y ＝2 【解析】令⎩⎪⎨⎪⎧3x ＋y ＝5①x ＋3y ＝7② ，①×3－②得8x ＝8，解得x ＝1，将x ＝1代入①，得3＋y ＝5，解得y ＝2，∴方程组的解为⎩⎪⎨⎪⎧x ＝1y ＝2 .13. 280 【解析】由题意得，1 000×(18%＋10%)＝280(棵). 14.103【解析】如解图，连接OC ，∵P A 与⊙O 相切于点A ，∴∠P AO ＝90°，∴OP ＝AO 2＋AP 2 ＝52＋122 ＝13，∴BP ＝OP －OB ＝OP －OA ＝13－5＝8.∵AO ＝BO ，OC ＝OC ，AC ＝BC ，∴△AOC ≌△BOC ，∴∠OBC ＝∠P AO ＝90°，∴∠PBC ＝90°.设AC ＝BC ＝x ，则PC ＝12－x ，在Rt △PBC 中，由勾股定理得82＋x 2＝(12－x )2，解得x ＝103 ，即AC ＝103.第14题解图(一题多解)如解图，连接OC ，∵P A 与⊙O 相切于点A ，∴∠P AO ＝90°，∴OP ＝AO 2＋AP 2 ＝52＋122 ＝13，∴BP＝OP －OB ＝OP －OA ＝13－5＝8.∵AO ＝BO ，OC ＝OC ，AC ＝BC ，∴△AOC ≌△BOC ，∴∠OBC ＝∠P AO＝90°，∴∠PBC ＝∠P AO ＝90°.∵∠P ＝∠P ，∴△P AO ∽△PBC ，∴P A PB ＝AO BC ，∴128 ＝5BC ，∴BC ＝103，∴AC ＝103. (一题多解)如解图，连接OC ，∵P A 与⊙O 相切于点A ，∴∠P AO ＝90°，∴OP ＝AO 2＋AP 2 ＝52＋122 ＝13.∵AO＝BO ，OC ＝OC ，AC ＝BC ，∴△AOC ≌△BOC ，∴∠OBC ＝∠P AO ＝90°，∴∠PBC ＝∠P AO ＝90°.∵∠P＝∠P ，∴sin P ＝BC PC ＝AO PO ，∴BC 12－BC ＝513，∴BC ＝103 ，∴AC ＝103 . (命题立意)本题考查了切线的性质、相似三角形的性质及勾股定理等内容，发展学生的几何直观、推理能力等核心素养．15. 2或 2 ＋1 【解析】分两种情况，①当∠DNM ＝90°时，如解图①，则MN ∥AB ，∴AN BM ＝AD BD.∵M 是BD 的中点，∴BD ＝2BM ，∴AD ＝2AN ＝2；②当∠DMN ＝90°时，如解图②，连接BN ，∵M 是BD 的中点，∠DMN ＝90°，∴BN ＝DN ＝AB 2＋AN 2 ＝12＋12 ＝ 2 ，∴AD ＝ 2 ＋1.综上所述，AD 的长为2或 2 ＋1.第15题解图(命题立意) 本题以矩形结合直角三角形的存在性为背景，题目无图形呈现，要求学生先根据题意画出图形，再进行推理和计算，对学生的空间观念和几何直观进行了更深入的考查，这是河南中考数学的一种大胆变化(以前该题从没有无图情况)，很好的体现了素养立意．(方法指导)解决图形形状不确定性的问题方法：(1)分类：依据图形的形状不确定进行分类，如以D ，M ，N 为顶点的三角形是直角三角形，三个点分别为直角顶点进行分类；(2)画图：根据分类，分析图形特征，由图形特征画出图形；(3)计算：根据图形特征，利用勾股定理、三角函数、相似进行计算．三、解答题16. 解：(1)原式＝3－3＋15(3分) ＝15；(5分) (2)原式＝x 2－4xy ＋4y 2－x 2＋4xy (8分)＝4y 2.(10分)17. 解：(1)7.5；＜；(4分)(解法提示)根据甲配送速度的得分得中位数m ＝7＋82＝7.5，由图可知甲服务质量得分波动比乙服务质量波动的小，故s 2甲 ＜s 2乙 .(2)我认为小丽应该选择甲公司，理由如下：因为甲公司的服务质量得分的方差小于乙公司，所以甲公司的服务质量比较稳定；(答案不唯一，合理即可)(7分)(3)还应该收集两个公司的收费标准．(答案不唯一，合理即可)(9分)18. (1)解：如解图所示，射线AP 即为所求；(4分)第18题解图(作法提示)分别以点B ，D 为圆心，以大于12BD 的长为半径画弧，两弧交于点P ，作射线AP ，射线AP 即为所求(方法不唯一).(2)证明：如解图，∵AE 平分∠BAD ，∴∠BAE ＝∠DAE ，(6分)在△BAE 和△DAE 中，⎩⎪⎨⎪⎧AB ＝AD ∠BAE ＝∠DAE AE ＝AE， ∴△BAE ≌DAE (SAS)，∴DE ＝BE .(9分)(新考法解读)本题把传统的几何证明与尺规作图相结合，考查了用尺规作图作出角平分线，在作图的基础上进行证明，两问之间的联系更加紧密，且在相关知识联系中凸显出角平分线的数学本质，这种考法在近几年河南中考中当属首次．19. 解：(1)∵反比例函数y ＝k x图象经过点A ( 3 ，1)， ∴k ＝ 3 ×1＝ 3 ；(3分)(2)如解图，连接AC ，交x 轴于点M ，(4分)第19题解图∵四边形AOCD 是菱形，∴AC ⊥OD ，M 是AC 的中点，由A ( 3 ，1)得：AM ＝1，OM ＝ 3 ，AC ＝2AM ＝2，在Rt △OMA 中，OA ＝AM 2＋OM 2 ＝1＋3 ＝2，(5分)∴OA ＝OC ＝AC ，∴△AOC 是等边三角形，∴∠AOC ＝60°，综上所述，扇形AOC 的半径为2，圆心角为60°；(7分) (3)3 3 －23π.(9分) (解法提示)由(2)可得∠AOC ＝60°，OA ＝2.∵四边形OBEF 为菱形，点E 在x 轴上，∴S △OBF ＝S △OBE .∵点B 在反比例函数y ＝3x 的图象上，∴S △OBE ＝ 3 ，∴S 阴影＝S △OBE ＋S 菱形AOCD －S 扇形AOC ＝ 3 ＋2 3 －60π·22360＝3 3 －2π3. 20. 解：由题意得∠AFE ＝∠ABH ＝90°，∠BAE ＝∠F AH ＝90°，点A 到地面的距离即FG 的长，∴∠EAF ＝90°－∠BAF ＝∠HAB ，∴△AFE ∽△ABH ，(4分) ∴EF HB ＝AF AB ， ∴EF 0.2 ＝110.3，解得EF ≈7.33 m ，(7分)∴EG＝EF＋1.8＝9.13≈9.1 m.答：树EG的高度约为9.1 m．(9分)(新考法解读) 本题通过“自制测高仪”计算高度，创新了此类测量问题，解决途径不再局限于利用三角函数求解，而是借助比例式进行求解，其中比例式的获得可以通过相似，亦可通过三角函数得到，降低了繁琐的计算，求解更灵活，是命题的尝试和创新．21. 解：(1)选择活动一时，需花费450×0.8＝360元，选择活动二时，需花费450－80＝370元，∵360<370，∴选择活动一更合算；(3分)(2)设一件这种健身器材的原价是x元，(4分)根据题意得0.8x＝x－80，解得x＝400，答：一件这种健身器材的原价是400元；(7分)(3)300≤a<400或600≤a<800.(9分)(解法提示)①当0＜a＜300时，活动一的付款金额比活动二的付款金额小，不合题意；②当300≤a＜600时，活动一的费用为0.8a元，活动二的费用为(a－80)元，0.8a－(a－80)＞0，解得a＜400，故当300≤a＜400时，活动一的付款金额比活动二的付款金额大，选择活动二更合算；③当600≤a＜900时，活动一的费用为0.8a元，活动二的费用为(a－160)元，0.8a－(a－160)＞0，解得a＜800，故当600≤a＜800时，活动一的付款金额比活动二的付款金额大，选择活动二更合算．综上所述，当a的取值范围为300≤a＜400或600≤a＜800时，选择活动二比活动一更合算．22. 解：(1)在y＝－0.4x＋2.8中，x＝0时，y＝2.8，∴点P的坐标为(0，2.8).(2分)把点P的坐标代入抛物线解析式得a＋3.2＝2.8，解得a＝－0.4，∴点P的坐标为(0，2.8)，a的值为－0.4；(4分)(2)令y＝－0.4x＋2.8＝0，解得x＝7，令y＝－0.4(x－1)2＋3.2＝0，解得x1＝1－2 2 (舍去)，x2＝1＋2 2 .(6分)由题意得点C的坐标为(5，0)，选择吊球时，落点到C的距离为5－(1＋2 2 )＝4－2 2 ，选择扣球时，落点到C的距离为7－5＝2，(8分)∵4－2 2 －2＝2－2 2 <0，∴4－2 2 <2，因此，应该选择吊球．(10分)(新考法解读)本题运用数学知识对羽毛球比赛进行技术分析，将实际问题抽象成函数模型后，利用函数的知识解决问题，关注细节的考查，体现了数学与生活之间联系，数学源于生活、服务生活，也有体现学科内及学科间知识联系，及数学学习的价值取向，培养了学生的模型观念和应用意识，与数学课程标准中的“会用数学的思维思考现实世界”理念一致．23. 解：(1)180°；8；(2分)(解法提示)通过观察发现可以看出△A 2B 2C 2可以看作是△ABC 绕点O 顺时针旋转180°得到的；△A 3B 3C 3可以看作是△ABC 向右平移8个单位长度得到的．(2)①β＝2α，理由如下：如解图①，连接AP 1，第23题解图①∵P 和P 1关于直线AB 对称，∴∠P 1AB ＝∠P AB ＝12∠P AP 1. ∵P 2和P 1关于直线AD 对称，∴∠P 1AD ＝∠P 2AD ＝12∠P 1AP 2，(4分) ∴∠BAD ＝∠P 1AD ＋∠P 1AB ＝12 ∠P 1AP 2＋12 ∠P AP 1＝12 (∠P 1AP 2＋∠P AP 1)＝12∠P AP 2， ∴∠P AP 2＝2∠BAD ，即β＝2α；(5分)②如解图②，连接PP 3，分别交CD ，AB 于点M ，N ，过点D 作DH ⊥AB 于点H ，第23题解图②易证P，P1，P3在同一条直线上，四边形DMNH为矩形，∴NM＝DH＝AD·sin ∠BAD＝m sin α.(6分)∵P和P1关于直线AB对称，P3和P1关于直线CD对称，∴PP1＝2NP1，P1P3＝2P1M，(7分)故PP3＝PP1＋P1P3＝2NP1＋2P1M＝2(NP1＋P1M)＝2NM＝2m sin α，答：P，P3两点间的距离为2m sin α；(8分)(3)2 6 或3 2 － 6 .(10分)(解法提示)如解图③，连接PP3，P1P2，分别与CD，AD交于E，F，连接EF，则E，F分别是P1P3，P1P2的中点，∴EF∥P2P3，∴要使P2P3∥AD，则点E与点D重合，如解图④；要使P2P3∥CD，则点F与点D重合，如解图⑤；①当P2P3∥AD时，如解图④，则∠P3＝∠ADP1＝90°－60°＝30°，由对称可得∠BAP1＝∠P AB＝15°，∠P AP1＝2∠P AB＝30°，∠AP1P＝75°，由(2)可知∠P AP2＝2∠BAD＝120°，∴∠P2AP1＝90°，∴△P2AP1是等腰直角三角形，∴∠AP1P2＝45°，∴∠DP1P2＝60°，∴∠P1P2P3＝∠DFP1＝90°，设AP＝AP1＝x，则P1P2＝ 2x，∴AF＝P1F＝22x，∴DF＝ 3 P1F＝62x，∴22x＋62x＝2 3 ，解得x＝3 2 － 6 ；②当P2P3∥CD时，如解图⑤，设AP＝AP1＝x，则P1P2＝ 2 x，∴AD＝12P1P2＝22x，∴22x＝2 3 ，解得x＝2 6 .综上所述，AP的长为3 2 － 6 或2 6 .第23题解图(新考法解读)本题以“观察发现”→“探究迁移”→“拓展应用”为主线，选取“图形的变化”为主题，对图形的平移、轴对称和旋转等知识进行了整合，还通过创设适切的数学情境，让学生经历从观察发现到拓展应用的过程，有条理地思考问题，并用“整体的、联系的、发展的眼光”来思考和解决问题，形成结构化的知识体系，培养了学生的推理能力和创新意识．。
2013年河南省中考数学22、23题
22.（10分）如图1，将两个完全相同的三角形纸片ABC 和DEC 重合
放置，其中∠C =90°，∠B =∠E =30°. （1）操作发现
如图2，固定△ABC ，使△DEC 绕点C 旋转，当点D 恰好
落在AB 边上时，填空：
①线段DE 与AC 的位置关系是_________；
②设△BDC 的面积为S 1，△AEC 的面积为S 2，则S 1与S 2的数量关系是_________________.
（2）猜想论证
当△DEC 绕点C 旋转到图3所示的位置时，小明猜想（1）中S 1与S 2的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC
中BC 、CE
A (D )
B (E )
C
图1
图2 图3
（3）拓展探究
已知∠ABC=60°，点D是其角平分线上一点，BD=CD=4，DE//AB 交BC于点E（如图4）.
若在射线BA上存在点F，使S△DCF=S△
请直接写出
．．．．相应的BF的长.
图4
23.（11分）如图，抛物线y =-x 2+bx +c 与直线22
1
+=x y 交于C 、D 两点，其中点C 在y 轴上，点D 的坐标为)2
7 3(，. 点P 是y 轴右侧的抛物线上一动点，过点P 作PE ⊥x 轴于点E ，交CD 于点F . （1）求抛物线的解析式；
（2）若点P 的横坐标为m ，当m 为何值时，以O 、C 、P 、F 为顶
点的四边形是平行四边形？请说明理由.
（3）若存在点P ，使∠PCF =45°，请直接写出．．．．
相应的点P 的坐标.
备用图。
河南省中考数学第23题压轴题(2010-2020)
河南省中考数学第23题压轴题（2010-2020）2020年中考23题将正方形ABCD 的边AB 绕点A 逆时针旋转至'AB ,记旋转角为α.连接',BB 过点D 作DE 垂直于直线'BB ,垂足为点E ,连接',.DB CE()1如图1,当60α︒=时,'DEB ∆的形状为 ,连接BD ,可求出'BB CE的值为()2当0360α︒︒<<且90α︒≠时，①()1中的两个结论是否仍然成立?如果成立，请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点',,,B E C D 为顶点的四边形是平行四边形时,请直接写出'BEB E的值.2019年中考23题如图，抛物线212y ax x c =++交x 轴于A ，B 两点，交y 轴于点C ．直线122y x =--经过点A ，C ． （1）求抛物线的解析式．()()()()22141241202162,00,42,00,42212-+=∴⎪⎩⎪⎨⎧-==∴⎩⎨⎧-==--↓→----→--=x x y c a c c a C A C A x y 抛物线（2）点P 是抛物线上一动点，过点P 作x 轴的垂线，交直线AC 于点M ，设点P 的横坐标为m ．①当△PCM 是直角三角形时，求点P 的坐标；21P AC C C P y C P PC M y PM 的垂线交抛物线于点作处的作图方法是：过点点轴的平行线交抛物线于作处的作图方法是：过点处都可能是直角处不可能是直角轴，∥直角三角形的存在性：∴()()()10,62222141222212,22214122,0221222P x y x x y x y x y P x x C CP CP AC ∴⎪⎩⎪⎨⎧-=-+=-=--=--∴-+=--②作点B 关于点C 的对称点B′，则平面内存在直线l ，使点M ，B ，B′到该直线的距离都相等．当点P 在y 轴右侧的抛物线上，且与点B 不重合时，请直接写出直线l ：y =kx +b 的解析式．（k ，b 可用含m 的式子表示）的中位线所在的直线这一问就是求△M BB 12018年中考23题如图，抛物线y =ax 2+6x +c 交x 轴于A ，B 两点，交y 轴于点C ．直线y =x -5经过点B ，C ．（1）求抛物线的解析式． ()()()()565,00,55,00,552-+-=→--→-=x x y C B C B x y 抛物线 （2）过点A 的直线交直线BC 于点M ．①（两定两动）当AM ⊥BC 时，过抛物线上一动点P （不与点B ，C 重合），作直线AM 的平行线交直线BC 于点Q ，若以点A ，M ，P ，Q 为顶点的四边形是平行四边形，求点P 的横坐标；32118,P P AP PBC AP A BC P A BC AM AMPQ PQAM 个单位，就得到直线向下平移将交抛物线于点∥作过点直线的距离相等到∥∴⊥=∴ ()⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛+,2415,2415,4321P P P②连接AC ，当直线AM 与直线BC 的夹角等于∠ACB 的2倍时，请直接写出点M 的坐标．()()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-====-+=+===67,623,617,6136223,6213621323222522212122221212M M CM CM m m m AM DM AD BC BD AD2017年中考23题如图，直线23y x c =-+与x 轴交于点A (3，0)，与y 轴交于点B ，抛物线243y x bx c =-++经过点A ，B ．（1）求点B 的坐标和抛物线的解析式；()()()2310342,00,32,02322++-=→→+-=→x x y B A B x y A 抛物线（2）M (m ，0)为x 轴上一动点，过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P ，N ．①点M 在线段OA 上运动，若以B ，P ，N 为顶点的三角形与△APM 相似，求点M 的坐标；⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛∴⊥2,25,,811,,2211N N AB B B N N x B N N B P AB BP y x PN 的垂线交抛物线于点作处直角：过点点轴的平行线交抛物线于作处直角：过点处有直角处不能有直角上，在直线轴轴，即平行于M,N,P 三点的横坐标一样②点M 在x 轴上自由运动，若三个点M ，P ，N 中恰有一点是其它两点所连线段的中点（三点重合除外），则称M ，P ，N 三点为“共谐点”．请直接写出使得M ，P ，N 三点成为“共谐点”的m 的值．()()()()023223103432310342232:2232223103410,231034,232,2222=+-+++-⎪⎭⎫⎝⎛++-=+-⎪⎭⎫ ⎝⎛+-=++-⎪⎭⎫⎝⎛++-⎪⎭⎫⎝⎛+-m m m M m m m N m m m P m M m m m N m m P 是中点：是中点是中点：2016年中考23题如图1，直线43y x n =-+交x 轴于点A ，交y 轴于点C (0，4)．抛物线223y x bx c=++经过点A ，交y 轴于点B (0，-2)．点P 为抛物线上一个动点，过点P 作x 轴的垂线PD ，过点B 作BD ⊥PD 于点D ，连接PB ，设点P 的横坐标为m ．（1）求抛物线的解析式；234322--=x x y （2）当△BDP 为等腰直角三角形时，求线段PD 的长；()()1271,27343234323432,2,2,023432,2222或或==∴=∴-=-=-∴=-==--⎪⎭⎫⎝⎛--PD BD m m m m m m m PDBD m m PD m BD m D B m m m P（2）如图2，将△BDP 绕点B 逆时针旋转，得到△BD ′P ′，且旋转角∠PBP ′=∠OAC ，当点P 的对应点P ′落在坐标轴上时，请直接写出点P 的坐标．()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 52543432532211==+⎪⎭⎫ ⎝⎛-==+m m m m OB I D HD ()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 8255334325422==⎪⎭⎫ ⎝⎛-=m m m m BIH P()()mm PD m BD m D B m m m P 3432,2,2,023432,22-=-=--⎪⎭⎫⎝⎛-- ()525434325325453223333-==--⎪⎭⎫ ⎝⎛-=-=-m m m m ID D P HI HD图2DD'P'CO y ABxP2015年中考23题如图，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上点A ，C 间的一个动点（含端点），过点P 作PF ⊥BC 于点F ．点D ，E 的坐标分别为（0，6），（-4，0），连接PD ，PE ，DE ．（1）请直接写出抛物线的解析式．8812+-=x y（2）小明探究点P 的位置发现：当点P 与点A 或点C 重合时，PD 与PF的差为定值．进而猜想：对于任意一点P ，PD 与PF 的差为定值．请你判断该猜想是否正确，并说明理由．()猜想正确22812812816881,881,0,818,881,2222222222222=-∴+=∴⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-+=+=-+-==⎪⎭⎫ ⎝⎛+-=⎪⎭⎫⎝⎛+-PF PD m PD m m m DH PH PD m DH m PH m H m PF m F m m P（3）小明进一步探究得出结论：若将“使△PDE 的面积为整数”的点P 记作“好点”，则存在多个“好点”，且使△PDE 的周长最小的点P 也是一个“好点”．请直接写出所有“好点”的个数，并求出△PDE 的周长最小时“好点”的坐标．()081364143412142238122381623,881,62322222≤≤-++-=+--=⨯⨯⎪⎭⎫⎝⎛+--=+--=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-+=m m m m m m S m m PM m m M m m P x y PED DE △个点中周长最小的点在这时，有两个点但是面积是个面积整数共有，到面积从11121013,12,11,910,8,7,6,5,41342014年中考23题如图，抛物线2y x bx c =-++与x 轴交于A (-1，0)，B (5，0)两点，直线334y x =-+与y 轴交于点C ，与x 轴交于点D ．点P 是x 轴上方的抛物线上一动点，过点P作PF ⊥x 轴于点F ，交直线CD 于点E ．设点P 的横坐标为m ．（1）求抛物线的解析式；542++-=x x y （2）若PE =5EF ，求m 的值；()()2691,2343524193432419510,,343,54,222+=∴+-=++-+-=++-=-⎪⎭⎫⎝⎛+-++-m m m m m EF m m PE m m F m m E m m m P ()()269134352419204213205234434352419222+=∴⎪⎭⎫⎝⎛+--=++-==--=+-⎪⎭⎫ ⎝⎛+-=++-m m m m m m m m m m m m（3）若点E'是点E 关于直线PC 的对称点，是否存在点P ，使点E'落在y 轴上？若存在，请直接写出相应的点P 的坐标；若不存在，请说明理由．P 点在y 轴和直线CD 的角平分线上()4,21433524194335343,,3,0241922-=∴=++-∴=⎪⎭⎫⎝⎛+-++-==m m m m mCE m m E C m m PE CE PE()()()()5,113,3112,1135432323215,414324411舍掉，超过了知：互相垂直根据邻补角的角平分线）知由（+--∴⎩⎨⎧++-=+-=+-=+=P P x x y x y x y x y P CP CP CP2013年中考23题如图，抛物线y =-x 2+bx +c 与直线221+=x y 交于C ，D 两点，其中点C 在y 轴上，点D 的坐标为)273(，．点P 是y 轴右侧的抛物线上一动点，过点P 作PE ⊥x轴于点E ，交CD 于点F ．（1）求抛物线的解析式．()25.32,02++-=x x y C（2）（两定两动）若点P 的横坐标为m ，当m 为何值时，以O ，C ，P ，F 为顶点的四边形是平行四边形？请说明理由．()()2173,2,1232325.0,25.3,222-=∴=+-∴=+-=+++-m m m CO PF OC m m PF m m F m m m P ∥（3）若存在点P ，使∠PCF =45°，请直接写出．．．．相应的点P 的坐标．由此可知P应该有两个点212532525221111=∴=+-∴=∴==∴==∴m m m m m F P m CF FG CG G P FG G P FG P CFH ∵∽△△()⎪⎭⎫ ⎝⎛∴=∴⎪⎪⎩⎪⎪⎨⎧++-=+-=+-=+=⎪⎭⎫⎝⎛1813,6236232272312312327,211221221P x x x y x y x y x y P CP CP CP 得到互相垂直由于邻补角的角平分线得到知由2012年中考23题如图，在平面直角坐标系中，直线112y x =+与抛物线23y ax bx =+-交于A ，B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上一动点（不与点A ，B 重合），过点P 做x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a ，b 及sin ACP ∠的值；()()()()3212121,213,40,23,40,21212--=-==→--→+=x x y b a B A B A x y 抛物线55252sin sin 51,2)1,0==∠=∠=∴==AEO ACP AE EO AO E E y AB 为（，则点轴交于点与设直线（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；PC PD PC PD AE AO EAO DPC AE EO AO 55255252cos cos 51,2=∴====∠=∠=∴== 5594121552,12121421552421121,,32121,222=⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛-⨯-=⎪⎭⎫⎝⎛++-=∴++-=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛--为最大时，当PD m m m PD m m PC m m C m m m P②（铅锤法求面积）连接PB ，线段PC 把△PDB 分成两个三角形，是否存在合适的m 的值，使这两个三角形的面积之比为9:10？若存在，直接写出m 的值；若不存在，说明理由．以PC 为底，面积之比，也就是底之比，⎪⎭⎫⎝⎛++-==⎪⎭⎫ ⎝⎛++-∴∠==∠-===4215251421552sin sin 491010922m m DF m m DF EAO PD DF DPC mBG BG DF BG DF 或 932,2591052109525244215242152491010922==+=+∴+=-⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛++-=-===m m m m m m m BG DF m m DF mBG BG DF BG DF 或或2011年中考23题如图，在平面直角坐标系中，直线3342y x =-与抛物线214y x bx c =-++交于A ，B 两点，点A 在x 轴上，点B 的横坐标为-8．（1）求该抛物线的解析式．2543412+--=x x y（2）点P 是直线AB 上方的抛物线上一动点（不与点A ，B 重合），过点P 作x 轴的垂线，垂足为C ，交直线AB 于点D ，作PE ⊥AB 于点E ． ①设△PDE 的周长为l ，点P 的横坐标为x ，求l 关于x 的函数关系式，并求出l 的最大值；⎪⎭⎫ ⎝⎛+--==+--=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+--42341512512423412343,254341,222x x PD l x x PD x x D x x x P 15341223-最大为最大时，当l l x -=⎪⎭⎫ ⎝⎛--= ②连接PA ，以PA 为边作图示一侧的正方形APFG ．随着点P 的运动，正方形的大小、位置也随之改变．当顶点F 或G 恰好落在y 轴上时，直接写出对应的点P 的坐标．双垂直全等的横纵坐标一样即P PMPC =22的纵坐标是即P OA PC ==⎪⎪⎭⎫⎝⎛+-+-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+-2897,2897,2,2173,2,2173P2010年中考23题在平面直角坐标系中，已知抛物线经过A （-4,0）B （0，-4）C （2,0）（1）求抛物线的解析式4212-+=x x y（2）（面积的铅锤法）若点M 为第三象限内抛物线上一个动点，点M 的横坐标为m ，△AMB 的面积为S ，求S 关于m 的函数关系式，并求出S 的最大值()()42124-42142212214,4421,2222时面积最大，最大为当△-=--=--=⨯⨯⎪⎭⎫⎝⎛--=+=----=⎪⎭⎫ ⎝⎛-+m mm m m S mm MD m m D x y m m m M ABM B A（3）（两定两动，考虑OB 是边和对角线）若点P 是抛物线上的动点，点Q 是直线y=-x 上的动点，判断有几个位置能使以点P,Q,B,O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标()4,522,52244221,421,422---+-==-+=-⎪⎭⎫ ⎝⎛-+==m m m PQ m m Q m m m P PQ OB PQ OB 时∥当()()()4442104,0,0,0,421,22=∴⎪⎩⎪⎨⎧-=--+=+∴--⎪⎭⎫ ⎝⎛-+n n m m n m B O n n Q m m m P OB 是对角线时当。
河南省中考数学23题汇总
2008-2013 年河南省中考数学第23 题汇总4（2008 年）23．（12 分）如图，直线y= x 4和x 轴、y 轴的交点分别为B，C。
3 点A 的坐标是（－2,0 ）（1）试说明△ABC是等腰三角形；（2）动点M从点A 出发沿x 轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒 1 个单位长度，当其中一个动点到达终点时，它们都停止运动，设点运动t 秒时，△MON的面积为s。
①求s 与t 的函数关系式；②当点M在线段OB上运动时，是否存在s=4 的情形？若存在，求出对应的t 值；若不存在，说明理由；③在运动过程中，当△MON为直角三角形时，求t 的值。
(2009 年)23. （11 分）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）. 抛物线y=ax2+bx 过A、C两点.(1) 直接写出点 A 的坐标，并求出抛物线的解析式；(2) 动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动．速度均为每秒 1 个单位长度，运动时间为t 秒. 过点P作PE⊥AB交AC于点E①过点E作EF⊥AD于点F，交抛物线于点G.当t 为何值时，线段EG最长?②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?请直接写出相应的t 值.教育资料（2010 年）23．（11 分）在平面直角坐标系中，已知抛物线经过A( 4,0) ，B(0, 4) ，C(2,0) 三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．yA O xCMB（2011 年）23. （11 分）如图，在平面直角坐标系中，直线 3 3y x 与抛物线4 212y x bx c 交于A、B两点，点A在x 轴上，点B的横坐标为－8.4（1）求该抛物线的解析式；（2）点P是直线AB上．方．的抛物线上一动点（不与点A、B重合），过点P作x 轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.①设△PDE的周长为l ，点P的横坐标为x，求l 关于x 的函数关系式，并求出l 的最大值；②连接PA，以PA为边作图示一侧的正方形APFG. 随着点P的运动，正方形的大小、位置也随之改变. 当顶点 F 或G恰好落在y 轴上时，直接写出对应的点P的坐标.教育资料教育资料（2013 年）23．（11 分）如图，抛物线 2y x bx c 与直线1y x 2交于C、D两点，2其中点C在y 轴上，点D的坐标为（3，72），点P 是y 轴右侧的抛物线上的一动点，过点P作PE⊥x 轴于点E，交CD于点F。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
河南近几年中考数学第23题23.（11分）（2016河南）如图1，直线y=-43x+n交x轴于点A，交y轴于点C（0，4）抛物线y=23x2+bx+c经过点A,交y轴于点B（0,-2）.点P为抛物线上的一个动点，过点P作x轴的垂线PD，过点B作BD⊥PD于点D,连接PB.（1）求抛物线的解析式.（2）当△BDP为等腰直角三角形时，求线段PD的长.（3）如图2，将△BDP绕点B逆时针旋转，得到△BD/P/，且∠PBP/=∠OAC，当点P的对应点P/落在坐标轴上时，请直接写出P点的坐标.解：（1）由y=-43x+n过点C（0，4），得n=4，则y=-43x+4当y=0时，得-43x+4=0，解得：x=3，∴点A坐标是（3,0）…………………………………………………1分∵y=23x2+bx+c经过点A（3,0）, B（0,-2）图1备用图∴22033b+c32c⎧=⨯+⎪⎨⎪-=⎩，解得：4b3c2⎧=-⎪⎨⎪=-⎩∴抛物线的解析式是23x2-43x-2……………………………………………3分（2）∵点P的横坐标为m，∴P（m，23m2-43m-2），D（m，-2）…………4分若△BDP为等腰直角三角形时，则PD=BD;①当点P在直线BD上方时，PD=23m2-43m-2+2=23m2-43m，（ⅰ）若P在y轴左侧，则m＜0，BD=-m；∴2 3m2-43m=-m，解得：m=12或m=0（舍去）…………………………………5分（ⅱ）若P在y轴右侧，则m＞0，BD=m；∴2 3m2-43m=m，解得：m=72或m=0（舍去）…………………………………6分②当点P在直线BD下方时，PD=-2-(23m2-43m-2) =-23m2+43m，则m＞0，BD=m；∴-23m2+43m=m，解得：m=12或m=0（舍去）……………………………7分综上：m=72或m=12。
即当△BDP为等腰直角三角形时，PD的长为72或12。
(3) P43）或P43-）或P（258，1132）【提示】∵∠PBP/=∠OAC,OA=3,OC=4；∴AC=5，∴sin∠PBP/=45，cos∠PBP/=35，①当点P/落在x轴上时，过点D/作D/N⊥x轴于N，交BD于点M，∠DBD/=∠ND/P/=∠PBP/,如图1，ND/-MD/=2,图2即35×(23m 2-43m)-（-45m ）=2 如图2，ND /-MD /=2， 即35×(23m 2-43m)-（-45m ）=2 解得：P43） 或P）②当点P /落在y 轴上时，如图3，过点D /作D /M ⊥x 轴交BD 于点M ， 过点P /作P /N ⊥y 轴，交MD /的延长线于点N ， ∠DBD /=∠ND /P /=∠PBP /, ∵PN=BM,即 45×(23m 2-43m)= 35m ∴P （258，1132）23.（11分）（2015河南）如图，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上点A,C 间的一个动点（含端点）过点P 作PF ⊥BC 于点F ，点D,E 的坐标分别是（0，6），（-4，0），连接PD,PE,DE.(1)直接写出抛物线的解析式.（2）小明探究点P 的位置发现：当点P 与点A 或点C 重合时，PD 与PF 的差为定值.进而猜想：对于任意一点P ，PD 与PF 的差为定值.请你判断该猜想是否正确，并说明理由.（3）小明进一步探究得出结论：若将“使△PDE 的面积为整数”的点P 记作“好点”，且存在多个“好点”， 且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE 的周长最小时“好点”的坐标.图3理由：设P （x ，2- x +88） 则PF=8-(21- x +88)=21x 8…………………………………………………4分过P 作PM ⊥y 轴于点M ，则PD 2=PM 2+DM 2=(-x)2+2216--x +88⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦=4211x +x +4642=221x +28⎛⎫⎪⎝⎭∴PD=21x 8+2, …………………………………………6分 ∴PD-PF=21x 8+2-21x 8=2,∴猜想正确. …………………………………………7分 (3)“好点”共有11个。
……………………………………9分 当点P 运动时，∴PE 与PD ∵PD-PF=2,∴∴当P 、E 、F此时点P 、E 的横坐标是-4， 将x=-4代入y=21-x +88，得y=6. ∴P （-4，6），此时△且△PDE 的面积是12∴△PDE （-4，6）提示：直线ED 设P （x ，21- x +88），则PN=21- x +88-（32x+6）=2- x x+282-△ PDE 的面积S=12×4×（213- x x+282-）=21-x -3x+44=()21-x+6+134，由-8≤x ≤0，知4≤S ≤13，所以S 的整数值有10个，由图像可知，当S=12时，对应的“好点”有2个， 所以“好点”共有11个。
23.(11分）（2014河南）如图，抛物线y=－x 2+bx+c 与x 轴交于A(-1,0),B(5,0）两点，直线y=－34x+3与y 轴交于点C ，，与x 轴交于点D.点P 是x 轴上方的抛物线上一动点，过点P 作PF ⊥x 轴于点F ，交直线CD 于点E.设点P 的横坐标为m 。
（1）求抛物线的解析式； （2）若PE =5EF,求m 的值；（3）若点E /是点E 关于直线PC 的对称点、是否存在点P ，使点E /落在y 轴上？若存在，请直接写出相应的点P 的坐标；若不存在，请说明理由。
23.（2014河南）(1)∵抛物线y=－x 2+bx+c 与x 轴交于A (-1,0) , B(5,0)两点，∴220=1b+c 0=55b+c⎧---⎨-+⎩（） ∴b=4c=5⎧⎨⎩ ∴抛物线的解析式为y=-x 2+4x+5．………………………………………………3分 （2）点P 横坐标为m ，则P(m,－m 2＋4m ＋5）,E(m,－34m+3)，F(m,0), ∵点P 在x 轴上方，要使PE=5EF,点P 应在y 轴右侧，∴ 0＜m ＜5. PE=-m 2＋4m ＋5－(-34m ＋3)= -m 2＋194m ＋2……………………………4分 分两种情况讨论：①当点E 在点F 上方时，EF=－34m ＋3. ∵PE=5EF ，∴-m 2＋194m ＋2=5(-34m ＋3)即2m 2－17m ＋26=0，解得m 1=2，m 2=132（舍去）………………………………6分②当点E 在点F 下方时，EF=34m －3.∵PE=5EF ，∴-m 2＋194m ＋2=5(34m －3)，即m 2－m －17=0，解得m 3，m 4（舍去）， ∴m 的值为2或12………………………………………………………………8分 (3),点P 的坐标为P 1(-12，114),P 2(4，5), P 3-3).……………………11分 【提示】∵E 和E /关于直线PC 对称，∴∠E /CP=∠ECP; 又∵PE ∥y 轴，∴∠EPC=∠E /CP=∠PCE, ∴PE=EC, 又∵CE ＝CE /，∴．四边形PECE /为菱形． 过点E 作EM ⊥y 轴于点M,∴△CME ∽△COD ，∴CE=5m 4. ∵PE=CE,∴-m 2＋194m ＋2=54m 或-m 2＋194m ＋2=-54m ， 解得m 1=-12，m 2=4， m 3，m 4（舍去）可求得点P 的坐标为P 1(-12，114),P 2(4，5), P 3(3-11，211-3)。
23.（11分）（2013河南）如图，抛物线y =-x 2+bx +c 与直线221+=x y 交于C 、D 两点，其中点C 在y 轴上，点D 的坐标为)27 3(，. 点P 是y 轴右侧的抛物线上一动点，过点P 作PE ⊥x 轴于点E ，交CD 于点F . （1）求抛物线的解析式；（2）若点P 的横坐标为m ，当m 为何值时，以O 、C 、P 、F 为顶点的四边形是平行四边形？请说明理由.（3）若存在点P ，使∠PCF =45°，请直接写出．．．．相应的点P 的坐标.PEOFCDBAxy OCDBA 备用图yxOP BDCA xy23（11分）（2012河南）如图，在平面直角坐标系中，直线112y x =+与抛物线23y ax bx =+-交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上一动点（不与点A 、B 重合），过点P 做x AB 于点C ，作PD ⊥AB 于点D ．（1）求a ，b 及sin ACP ∠的值； （2）设点P 的横坐标为m ，①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连接PB ，线段PC 把△PDB 分成两个三角形，是否存在合适的m 的值，使这两个三角形的面积之比为9:10？若存在，直接写出m 的值；若不存在，说明理由．23．（2012河南）解：（1）由110,2,(2,0)2x x A +==--得∴． ∵y =ax 2+bx -3经过A 、B 两点，设直线AB 与y 轴交于点E ，则E （0,1）． ∵PC ∥y 轴，∴∠ACP =∠AEO ．∴sin ∠ACP =sin ∠AEO=..................................................45OA AE ． （分）（2）①由（1）知，抛物线的解析式为211322y x x =--． 113,4,(4,3)2x x B +==由得∴．22(2)230,11,....................................................3224433a b a b a b ⎧-⋅--=⎪==-⎨⋅+-=⎪⎩∴ ∴． （分）．在Rt △PCD 中，sin PD PC ACP =⋅∠②存在满足条件的m 值．53229m =或．………（11分） 【提示】如图，分别过点D 、B 作DF ⊥PC ，BG ⊥PC ，垂足分别为F 、G ．在Rt △PDF 中，DF==又BG =4-m ,x2111(,3),(,1)222P m m m C m m --+∴．2211111(3)4...........................................62222PC m m m m m =+---=-++． （分）221(4)2(1)5m m m =-++⨯=--+0,1.................................................855m PD -=∵∴当时，有最大值 （分）21(28)2545295,510221032,599PCD PBCPCD PBC PCD PBC m m S DF m S BG m S m m S S m m S ∆∆∆∆∆∆---+===-+===+===∴．当时解得；当时解得．23.（11分）（2011河南）如图，在平面直角坐标系中，直线3342y x =-与抛物线214y x bx c =-++交于A 、B 两点，点A 在x 轴上，点B 的横坐标为－8.（1）求该抛物线的解析式；（2）点P 是直线AB 上方．．的抛物线上一动点（不与点A 、B 重合），过点P 作x 轴的垂线，垂足为C ，交直线AB 于点D ，作PE ⊥AB 于点E .①设△PDE 的周长为l ，点P 的横坐标为x ，求l 关于x 的函数关系式，并求出l 的最大值；②连接PA ，以PA 为边作图示一侧的正方形APFG .随着点P 的运动，正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时，直接写出对应的点P 的坐标.23.（2011河南）（1）对于3342y x =-，当y =0，x =2.当x =-8时，y =-152. ∴A 点坐标为（2，0），B 点坐标为15(8,).2--………………………1分 由抛物线214y x bx c =-++经过A 、B 两点，得 012,15168.2b c b c =-++⎧⎪⎨-=--+⎪⎩解得235135..42442b c y x x =-=∴=--+，…………………………………………3分 （2）①设直线3342y x =-与y 轴交于点M 当x =0时，y =32-. ∴OM =32.∵点A 的坐标为（2，0），∴OA =2.∴AM 5.2=……………………4分 ∵OM ：OA ：AM =3∶4：5.由题意得，∠PDE =∠OMA ，∠AOM =∠PED =90°，∴△AOM ～△PED .∴DE ：PE ：PD =3∶4：5.…………………………………………………………………5分∵点P 是直线AB 上方的抛物线上一动点，∴PD =y P -y D 213533()()44242x x x =--+-- =213444x x --+.………………………………………………………………………6分 ∴21213(4)542l x x =--+ 231848.555x x =--+…………………………………………………………………7分 23(3)15.315.5l x x l ∴=-++∴=-=最大时，……………………………………8分②满足题意的点P 有三个，分别是1233(2),(2),22P P --3P ……………………………………………………………11分 【解法提示】当点G 落在y 轴上时，由△ACP ≌△GOA 得PC =AO =2，即21352442x x --+=，解得x =以1233(2),(,2).22P P -+--当点F 落在y 轴上时，同法可得3P ，4P （舍去）. 23．（11分）（2010河南）在平面直角坐标系中，已知抛物线经过A )0,4(-，B )4,0(-，C )0,2(三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是直线x y -=上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．M C BA O xy。