工程流体力学 禹华谦 习题答案 第7章
工程流体力学水力学--禹华谦-章习题解答

, ,
在液面上为大气压,
2-12.如图所示盛水U形管,静止时,两支管水面距离管口均为h,当U形管绕OZ轴以等角速度ω旋转时,求保持液体不溢出管口的最大角速度ωmax.
[解]由液体质量守恒知,管液体上升高度与管液体下降高度应相等,且两者液面同在一等压面上,满足等压面方程:
液体不溢出,要求 ,
[证明]形心坐标
则压力中心的坐标为
当 ,闸门自动打开,即
第三章流体动力学基础
3—1.检验 不可压缩流体运动是否存在?
[解](1)不可压缩流体连续方程
(2)方程左面项
; ;
(2)方程左面=方程右面,符合不可压缩流体连续方程,故运动存在。
3—2.某速度场可表示为 ,试求:(1)加速度;(2)流线;(3)t= 0时通过x=-1,y=1点的流线;(4)该速度场是否满足不可压缩流体的连续方程?
80℃时,水的密度
则增加的体积为
1—2.当空气温度从0℃增加至20℃时,运动粘度 增加15%,重度 减少10%,问此时动力粘度 增加多少(百分数)?
[解]
此时动力粘度 增加了3.5%
1-3.有一矩形断面的宽渠道,其水流速度分布为 ,式中 、 分别为水的密度和动力粘度, 为水深。试求 时渠底(y=0)处的切应力。
[解]左侧水作用于闸门的压力:
右侧水作用于闸门的压力:
2—8.一扇形闸门如图所示,宽度b=1.0m,圆心角 =45°,闸门挡水深h=3m,试求水对闸门的作用力及方向
[解]水平分力:
压力体体积:
铅垂分力:
合力:
方向:
2-9.如图所示容器,上层为空气,中层为 的石油,下层为 的甘油,试求:当测压管中的甘油表面高程为9。14m时压力表的读数。
流体力学6,7,8章课后题答案

第六章 6-1解:层流状态下雷诺数Re 2000< 60.1Re 6.710vdv υ-⨯==⨯ ⇒60.120006.710v -⨯<⨯⇒62000 6.710/0.10.134(/)v m s -<⨯⨯= 即max 0.134/v m s =223max max max 0.13.140.1340.00105/ 1.05/44d Q Av v ms L sπ===⨯⨯≈=6-2解:层流状态下雷诺数Re 2000<3Re 20000.910120000.0450.1()vd d m d ρυ-=<⨯⨯⨯⇒<⇒<6-3解:3221.66100.21(/)0.13.1444Q v m s d π-⨯==≈⨯临界状态时Re 2000=52533Re Re0.210.1 1.0510(/)20001.05100.88109.2410()vd vd m s Pa s υυυμυρ---=⇒=⨯⇒==⨯⇒==⨯⨯⨯=⨯⋅ 6-4解:当输送的介质为水时:32210101270131444.(/)..Q v m s d π-⨯===⨯ 612701838632000151910..Re .vd υ-⨯===>⨯水 3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力粗糙。
当输送的介质为石油时:质量流量与水相等3310101010(/)Q kg s -=⨯⨯=31000118850.(/)Q m s == 2200118150********..(/)..Q v m s d π===⨯ 415030113184200011410..Re .vd υ-⨯===>⨯水3015100001501...d -∆⨯== 根据雷诺数和相对粗糙度查莫迪图可知流态为水力光滑。
6-5解:判断流态需先求出雷诺数()2900036009000088023144./..Re Q v m s Avd υ÷===⨯=冬季:421101./m s υ-⨯=40088021608820001110..Re ..vd υ-⨯===<⨯ ⇒ 流态为层流。
《工程流体力学》习题1~7章参考答案

解:本题利用流体静压强的计算公式 p = ρ gh 和等压面的性质(同种液体) 油 液 所 在 的 水 平 面 为 等 压 面 , 等 压 面 上 的 相 对 压 强 ρ 1000 ρ油 gh = ρ水 g ( 3 − 2 ) ⇒ h = 水 = ≈ 1.22m ; 加 入 木 块 后 相 当 于 左 侧 容 器 加 入 了 体 积 为 ρ油 820
参考答案 4
图 3-10 习题 3-2 附图
解:根据已知条件,船底长度 12m,舱体宽度(垂直于纸面)上下均为 6m,水面上船的长度为 12+2×2.4=16.8m,于是,船排开水的体积为 1 V = (16.8 + 12 ) × 2.4 × 6 = 207.36m3 2 根据阿基米德定律,船上货物的总质量等于船排开的水的质量 m = ρ 海水V = 1000 × 207.36 = 207360kg 习题 3-4 一个充满水的密闭容器以等角速度 ω 绕一水平轴旋转,同时需要考虑重力的影响。 试证明其等压面是圆柱面,且等压面的中心轴线比容器的转动轴线高 g ω 2 。 解:根据图示的坐标(z 轴水平)可知,单位质量流体的质量力分量为 g x = 0, g y = − g , g z = 0 流体绕 z 轴以匀角速度 ω 旋转时,半径 r 处流体团的加速度 a 位于 x-y 的平面内,大小为 rω , 方向指向转动中心。 于是按达朗贝尔原理, 单位质量流体受到的惯性力(离心力)则为 −a , 2 大小为 rω ,方向沿径向朝外,其 x, y, z 方向的分量为 − ax = rω 2 cos θ = xω 2
高
等
学
校
教
材
过程装备与控制工程专业核心课程教材
工程流体力学
习题参考答案
主讲:陈庆光
《工程流体力学(水力学)》第二版 禹华谦 课后习题答案 西南交通大学出版社

《工程流体力学(水力学)》第二版禹华谦课后习题答案西南交通大学出版社欢迎光临阳光大学生网, 提供最全面的大学生课后习题答案和复习试题免费下载,////0>.阳光大学生网我们希望呵护您的眼睛,关注您的成长,给您一片绿色的环境,欢迎加入我们,一起分享大学里的学习和生活感悟,免费提供:大学生课后答案 ,大学考试题及答案 ,大学生励志书籍。
《水力学》李炜徐孝平主编 2000 年 6 月武汉水利电力大学出版社共 12 章全部习题的解答第一章1-1 解:3 3 3ρ 1.03g cm 1030kg m , 比重s 1.03, γ 10.094kN m1-2 解:2γ9789N /m3ρ 998.88kg m ,g 9.8?3 2μ gμ9.8 ×1.002 ×10 N ?S /m?6 2ν 1.003 ×10 m /sργ 9789?4γ11.82 × 0.15 ×10?5 2以上为水,以下为空气μρνν 1.089 ×10 N ?S /m g 9.81-3 解:d ν9 7dp ?K ?2.19 ×10 × ?1% 2.19 ×10 Pav1-4 解:3 3γ G v 0.678 /10 678kgf /m①用工程单位制:2 4ργ g 678 / 9.8 69.18kgfs /mγγ ×9.8N kgf 6644.4N m②用国单位制: (SI 制) :3ργ g 678kg m1-5 解:du u 1.531流速梯度 3.75 ×10 3sdy δ 0.4 ×10u3 2切应力τμ 0.1 ×3.75 ×10 3.75 ×10 Paδ2活塞所受的摩擦阻力 F τ A τπdl 3.75 ×10 ×3.14 ×0.14 ×0.16 26.38N1-6 解:作用在侧壁上粘性切力产生的力矩du r 0.2M A μr 2 πr h μω+1 2 ×3.14 × 0.2 × 0.4 × μ×101 + 68.3 μdy δ 0.003M 4.905∴μ 0.072Pa ?S68.3 68.31-7 解:2设u Ay +By +c; ①根据实际流体的无滑移现象,当 y0 时 u0∴C 0 (第三个常数项为零); ②∵y0.04m 时,u1m/sdu2则有 1A ×0.04 +B ×0.04; ③E 点的流体切应力为零,有 2Ay +B 0 , dy10.0016A + 0.04B 1 A ?625?则由联立方程求得解得:0.08A +B 0 B 50?du du-3?6τμυρ 1.0 ×10 ×1000 × 2 Ay+B )1 ×10 (-1250y+50 )dy dy-2当y0 处,τ 5 ×10 Pa-2当y0.02 处,τ 2.5 ×10 Pa当 y0.04 处,τ0 Pa由此可见均匀流横断面上切应力是呈直线分布的。
流体力学课后答案第七章doc资料

1. 已知平面流场的速度分布为xy x u x +=2,y xy u y 522+=。
求在点(1,-1)处流体微团的线变形速度,角变形速度和旋转角速度。
解:(1)线变形速度:y x xu xx +=∂∂=2θ 54+=∂∂=xy yu y y θ角变形速度:()x y y u x u x y z +=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=222121ε 旋转角速度:()x y x u x u x y z -=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=222121ω 将点(1,-1)代入可得流体微团的1=x θ,1=y θ;23/z =ε;21/z =ω2.已知有旋流动的速度场为z y u x 32+=,x z u y 32+=,y x u z 32+=。
试求旋转角速度,角变形速度和涡线方程。
解:旋转角速度:2121=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=z u y u y z x ω 2121=⎪⎭⎫⎝⎛∂∂-∂∂=x u z u z x y ω2121=⎪⎪⎭⎫⎝⎛∂∂-∂∂=y u x u xyz ω 角变形速度:2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=z u y u y z x ε 2521=⎪⎭⎫⎝⎛∂∂+∂∂=x u z u z x y ε2521=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=y u x u x y z ε 由zyxdzdydxωωω==积分得涡线的方程为:1c x y +=,2c x z +=3.已知有旋流动的速度场为22z y c u x +=,0=y u ,0=z u ,式中c 为常数,试求流场的涡量及涡线方程。
解:流场的涡量为:0=∂∂-∂∂=zu y u yz x Ω22zy cz xu z u zx y +=∂∂-∂∂=Ω22zy cyy u xu x y z +-=∂∂-∂∂=Ω 旋转角速度分别为:0=x ω222zy cz y +=ω222zy cy z +-=ω则涡线的方程为:c dzdyzy+=⎰⎰ωω即c y dzz dy +-=⎰⎰可得涡线的方程为:c z y =+224.求沿封闭曲线222b yx =+,0=z 的速度环量。
流体力学答案第七章习题及答案2 2.doc

习题及答案7 —9薄壁孔口出流,直径d=2mm,水箱水位恒定H=2m,试求: (1)孔口流量。
;⑵此孔口外接圆柱形管嘴的流量Q;(3) 管嘴收缩断面的真空。
解:(1 ) @=心顷~ j2gx2=1.22 n?/s(2) Q n = ^,A^H = 0.82^2gx2 =1.61 m3/s(3) 4 = 0.75//=0.75x2 = 1.5 mPg7 —10水箱用隔板分为A、B两室,隔板上开一孔口,其直径d 户4cm,在B室底部装有圆柱形外管嘴,其直径d2=3cm0 已知H=3m, h3=0. 5m,试求:(1) »、h2; (2)流出水箱的流量Q。
解:(1) & ="专7^ =「冬山(丑—4)=00.62 x 郴•。
町皿 = 0.82x得hi=1.07m h2=H- hFl.43m(2) Q=/Z^7^=0.62X"°:4)j2gxl.O7 =3.57 Vs7-12游泳池长25m,宽10m,水深1.5m,池底设有直径10cm 的放水孔直通排水地沟,试求放尽池水所需的时间。
V =25x10x1.5 = 375m31Qmax = M X/2^O = O^x-7rd2d2gH o =2.64xl0-2m3 解: 42Vt =——= 7.89/iQmax7-14虹吸管将A池中的水输入B池,已知长度/F3m, Z2=5m, 直径d=75mm,两池水面高差H=2m,最大超高h=1.8m,沿程阻力系数入二0.02,局部阻力系数:进口J = 0.5,转弯支=0. 2,出口J = 1。
试求流量及管道最大超高断面的真空度。
80.075 、2 2— = 3.83—2g2g 19.6x23.20 m/s3.83 (0.075)2 Q = D * = 3.20X —~ -------------- =14.13 41/s列上游水池和最大超高处的伯诺里方程 〃噫+。
3噫g +如 (I> 决如十讦+检斗l ・5H 1+-^- + 0 = H 2+0 + 0 + /Z Z Pg(d\卜勺+£+£+与+易 1 2x98000 仁 l+ --------------- =5+16.4— 9800 2g解:( 10 0.025x —— 2g I 0.025 i} i}^0.5+4+3x03+1 —=16.4—2g 2g(i +i 宙《解:列上下游水池的伯诺里方程丑+0 + 0 = ° + 0 + 0 + "『罗斋= 3.E7-16水从密闭容器A,沿直径d=25mm,长Z=10m 的管道流 入容器B,已知容器A 水面的相对压强pF2at,水面高HFlm, Hi =1 m, H2=5m,沿程阻力系数入=0.025,局部阻力系数:阀 门C a=4. 0,弯头£b=0.3,试求流量。
流体力学第七章习题答案
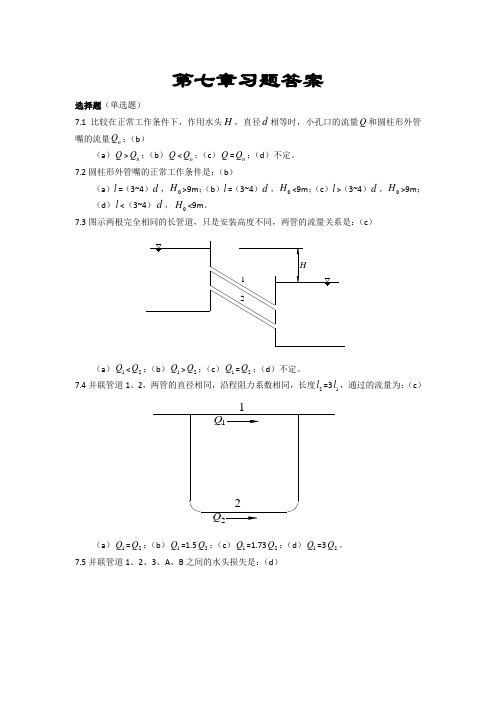
第七章习题答案选择题(单选题)7.1比较在正常工作条件下,作用水头H ,直径d 相等时,小孔口的流量Q 和圆柱形外管嘴的流量n Q :(b )(a )Q >n Q ;(b )Q <n Q ;(c )Q =n Q ;(d )不定。
7.2圆柱形外管嘴的正常工作条件是:(b )(a )l =(3~4)d ,0H >9m ;(b )l =(3~4)d ,0H <9m ;(c )l >(3~4)d ,0H >9m ;(d )l <(3~4)d ,0H <9m 。
7.3图示两根完全相同的长管道,只是安装高度不同,两管的流量关系是:(c )(a )1Q <2Q ;(b )1Q >2Q ;(c )1Q =2Q ;(d )不定。
7.4并联管道1、2,两管的直径相同,沿程阻力系数相同,长度2l =31l ,通过的流量为:(c )2(a )1Q =2Q ;(b )1Q =1.52Q ;(c )1Q =1.732Q ;(d )1Q =32Q 。
7.5并联管道1、2、3、A 、B 之间的水头损失是:(d )1(a )fAB h =1f h +2f h +3f h ;(b )fAB h =1f h +2f h ;(c )fAB h =2f h +3f h ;(d )fAB h =1f h =2f h =3f h 。
7.6长管并联管道各并联管段的:(c )(a )水头损失相等;(b )水里坡度相等;(c )总能量损失相等;(d )通过的流量相等。
7.7并联管道阀门为K 全开时各段流量为1Q 、2Q 、3Q ,现关小阀门K ,其他条件不变,流量的变化为:(c )(a )1Q 、2Q 、3Q 都减小;(b )1Q 减小,2Q 不变,3Q 减小;(c )1Q 减小,2Q 增加,3Q 减小;(d )1Q 不变,2Q 增加,3Q 减小。
7.8 有一薄壁圆形孔口,直径d 为10mm ,水头H 为2m。
[工程流体力学(水力学)]__禹华谦1-10章习题解答
![[工程流体力学(水力学)]__禹华谦1-10章习题解答](https://img.taocdn.com/s3/m/70a8d70dbb68a98271fefa59.png)
第一章 绪论1-1.20℃的水2.5m 3,当温度升至80℃时,其体积增加多少? [解] 温度变化前后质量守恒,即2211V V ρρ= 又20℃时,水的密度31/23.998m kg =ρ 80℃时,水的密度32/83.971m kg =ρ 321125679.2m V V ==∴ρρ 则增加的体积为3120679.0m V V V =-=∆1-2.当空气温度从0℃增加至20℃时,运动粘度ν增加15%,重度γ减少10%,问此时动力粘度μ增加多少(百分数)? [解] 原原ρννρμ)1.01()15.01(-+==原原原μρν035.1035.1==035.0035.1=-=-原原原原原μμμμμμ此时动力粘度μ增加了3.5%1-3.有一矩形断面的宽渠道,其水流速度分布为μρ/)5.0(002.02y hy g u -=,式中ρ、μ分别为水的密度和动力粘度,h 为水深。
试求m h 5.0=时渠底(y =0)处的切应力。
[解] μρ/)(002.0y h g dydu-=)(002.0y h g dydu-==∴ρμτ 当h =0.5m ,y =0时)05.0(807.91000002.0-⨯⨯=τPa 807.9=1-4.一底面积为45×50cm 2,高为1cm 的木块,质量为5kg ,沿涂有润滑油的斜面向下作等速运动,木块运动速度u=1m/s ,油层厚1cm ,斜坡角22.620 (见图示),求油的粘度。
[解] 木块重量沿斜坡分力F 与切力T 平衡时,等速下滑yu AT mg dd sin μθ== 001.0145.04.062.22sin 8.95sin ⨯⨯⨯⨯==δθμu A mg s Pa 1047.0⋅=μ1-5.已知液体中流速沿y 方向分布如图示三种情况,试根据牛顿内摩擦定律yud d μτ=,定性绘出切应力沿y 方向的分布图。
[解]第二章 流体静力学2-1.一密闭盛水容器如图所示,U 形测压计液面高于容器内液面h=1.5m ,求容器液面的相对压强。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.1 水以来流速度v 0=0.2m/s 顺流绕过一块平板。
已知水的运动粘度s /m 10145.126-⨯=ν,试求距平板前缘5m 处的边界层厚度。
【解】计算x=5m 处的雷诺数50x 107.8/x v Re ⨯=ν=该处的边界层属湍流m 12.0)107.8(537.0Re x 37.051551x=⨯==δ7.2 流体以速度v 0=0.8m/s 绕一块长 L=2m 的平板流动,如果流体分别是水(s /m 10261-=ν)和油(s /m 108252-⨯=ν),试求平板末端的边界层厚度。
【解】先判断边界层属层流还是湍流水:610L 106.1/L v Re ⨯=ν= 油:520L 102/L v Re ⨯=ν=油边界层属层流m 077.08.02108477.5v L 477.5502=⨯⨯=ν=δ-水边界层属湍流m 042.0)106.1(237.0Re L 37.051651L=⨯==δ7.3 空气以速度v 0=30m/s 吹向一块平板,空气的运动粘度s /m 101526-⨯=ν,边界层的转捩临界雷诺数6xcr 10Re =,试求距离平板前缘x=0.4m 及x=1.2m 的边界层厚度。
空气密度3m /kg 2.1=ρ。
【解】(1)x=0.4m ,xcr 60x Re 108.0/x v Re <⨯=ν=,为层流边界层m 0024.0304.01015477.5v x 477.560=⨯⨯=ν=δ- (2)x=1.2m ,xcr 60x Re 104.2/x v Re >⨯=ν=,为湍流边界层m 023.0)104.2(2.137.0Re x 37.051651x=⨯==δ7.4 边长为1m 的正方形平板放在速度v 0=1m/s 的水流中,求边界层的最大厚度及双面摩擦阻力,分别按全板都是层流或者都是湍流两种情况进行计算,水的运动粘度s /m 1026-=ν。
【解】b=1m, L=1m, 60L 10/L v Re =ν=层流: m 005.01110477.5v L 477.560=⨯=ν=δ- 3Lf 1046.1Re 46.1C -⨯==N 46.1bL 2C v 21F f 20D =ρ=湍流: m 023.0)101(137.0Re L 37.051651L =⨯==δ 32.0L f 105.4)(Re 072.0C -⨯==N 5.4bL 2C v 21F f 20D =ρ=7.5 水渠底面是一块长L=30m ,宽b=3m 的平板,水流速度v 0=6m/s ,水的运动粘度s /m 1026-=ν,试求:(1)平板前面x=3m 一段板面的摩擦阻力;(2)长L=30m 的板面的摩擦阻力【解】设边界层转捩临界雷诺数5xcr 105Re ⨯=,因为5cr 0105/x v ⨯=ν,所以 m 083.0x cr =(1) x=3m ,平板边界层为混合边界层60x 1018/x v Re ⨯=ν=0025.01805)002.00053.0(0026.0Re Re )Re 46.1Re 074.0(Re 074.0C xxcr xcr 5xcr5xfm =--=--=N 406bL v 21C F 20fmD =ρ= (2) L=30m ,平板边界层为混合边界层60L 10180/L v Re ⨯=ν=00159.018005)002.00053.0(0016.0Re Re )Re 46.1Re 074.0(Re 074.0C Lxcr xcr 5xcr5Lfm =--=--=N 2577bL v 21C F 20fm D =ρ=7.6 一块面积为m 8m 2⨯的矩形平板放在速度s /m 3v 0=的水流中,水的运动粘度s /m 1026-=ν,平板放置的方法有两种:以长边顺着流速方向,摩擦阻力为F 1;以短边顺着流速方向,摩擦阻力为F 2。
试求比值F 1/F 2。
【解】设定转捩雷诺数5xcr105Re ⨯=,那么 m 17.0310105v Re x 650xcr cr =⨯⨯=ν⨯=-长边顺着流速方向时,b 1=2m ,L 1=8m ,L 1>x cr ,整个平板边界层为混合边界层,那么摩擦阻力为11201fm 1L b 2v C F ρ=短边顺着流速方向时,b 2=8m ,L 2=2m ,L 2>x cr ,整个平板边界层也为混合边界层,那么摩擦阻力为22202fm 2L b 2v C F ρ= 这里 51L xcrxcr 5xcr 51L 1fm 1040.2Re Re )Re 46.1Re 074.0(Re 074.0C -⨯=--=52L xcrxcr5xcr52L 2fm 1098.2Re Re )Re 46.1Re 074.0(Re 074.0C -⨯=--=所以804.0C C F F 2fm 1fm 21==7.7 平底船的底面可视为宽b=10m ,长L=50m 的平板,船速v 0=4m/s ,水的运动粘度6210m /s -ν=,如果平板边界层转捩临界雷诺数5xcr Re 510=⨯,试求克服边界层阻力所需的功率。
【解】60L 10200/L v Re ⨯=ν=,平板边界层为混合边界层0016.020005)002.00054.0(0016.0Re Re )Re 46.1Re 074.0(Re 074.0C Lxcr xcr 5xcr5Lfm =--=--=N 6400bL v 21C F 20fm D =ρ=KW 6.25v F P 0D ==7.8有45kN 的重物从飞机上投下,要求落地速度不超过10m/s ,重物挂在一张阻力系数C 2D =的降落伞下面,不计伞重,设空气密度为3m /kg 2.1=ρ,求降落伞应有的直径。
【解】物体重量G=45kN ,降落时,空气阻力为F 4d C v 212D 2D πρ=不计浮力,则阻力F D 应大于重力G ,即G 4d C v 212D 2≥πρ d m 85.21≥7.9汽车以80km/h 的时速行驶,其迎风面积为A=2m 2,阻力系数为C D =0.4,空气的密度为3m /kg 25.1=ρ,试求汽车克服空气阻力所消耗的功率。
【解】v=80km/h=22.2m/sN 42.246AC v 21F D 2D =ρ=P=vF =D 5.470KW7.10 列车上的无线电天线总长3m ,由三节组成,每节长均为1m ,它们的直径从根部到顶部分别为cm 50.1d 1=,cm 0.1d 2=,cm 50.0d 3=。
列车速度v=60km/h ,空气密度3m /kg 293.1=ρ,圆柱体的阻力系数2.1C D =,计算空气阻力对天线根部产生的力矩。
【解】由阻力计算公式D 2D AC v 21F ρ=,得到各段的阻力分别为 N 23.3F 1=,N 15.2F 2=,N 08.1F 3=对天线根部产生的力矩为m N 54.7F 25F 23F 21M 321⋅=++=7-11炉膛的烟气以速度V 0=0.5m/s 向上腾升,气体的密度为3m /kg 25.0=ρ,动力粘性系数25m /s N 105⋅⨯=μ-,粉尘的密度3m /kg 1200=ρ',试估算此烟气能带走多大直径的粉尘?【解】当粉尘受到的气流作用力和浮力大于重力时,粉尘将被气流带走。
气流作用于粉尘的力就是阻力F D :F A C V 21D 2D ρ=A 为迎风面积,粉尘可近似地作圆球,迎风面积就是圆面积。
Re=V 0d/1<ν,则C Re /24D = F Vd 3d Vd 24V 2122D μπ=π⨯⎪⎪⎭⎫ ⎝⎛ρμ⨯ρ=粉尘重量为 G=g d 613ρ'π 粉尘的浮力为 F g d 613B ρπ=因此 F+F G B >Vd 3g )(d 613μπ<ρ-ρ'π d g)(V182ρ-ρ'μ≤代入数字,得d ,m 109556.14-⨯≤ Re=149.0/d V 0<=μρ7.12 使小钢球在油中自由沉降以测定油的粘度。
已知油的密度3m /kg 900=ρ,小钢球的直径mm 3d =,密度3'm /kg 7788=ρ,若测得钢球最终的沉降速度v=12cm/s ,求油的功力粘度。
【解】钢球所受阻力的计算公式为A C v 21F D 2D ρ=C Re /24D = F vd 3d vd 24v 2122D μπ=π⨯⎪⎪⎭⎫ ⎝⎛ρμ⨯ρ=钢球重量为 G=g d 613ρ'π 钢球的浮力为 F g d 613B ρπ=因此 F+F G B =vd 3g )(d 613μπ=ρ-ρ'π d g)(v182ρ-ρ'μ=代入数据,得到 s Pa 28.0⋅=μ。
