直墙拱结构的设计计算步骤及实例-原稿
直墙拱形衬砌结构计算说明书(浙理地下建筑结构课程设计)

直墙拱形衬砌结构设计计算说明书设计资料: 1. 围岩特征某隧道埋深85 m ,围岩为Ⅲ级围岩,RQD=85%,R c =57.4MPa ,容重γ0=25 kN/m 3,侧向和基底弹性抗力系数均为51.410K =⨯kPa/m 。
2. 衬砌材料采用整体式直墙拱混凝土衬砌,混凝土标号为C20,弹性模量E=26GPa ,容重γ=25 kN/m 3,混凝土轴心抗压强度设计值f c =10MPa ,弯曲抗压强度设计值f cm =11MPa ,抗拉强度设计值f t =1.1MPa 。
钢筋采用25MnSi 钢,强度设计值f y =340MPa ,弹性模量E=200GPa 。
3. 结构尺寸顶拱是变厚度的单心圆拱,拱的净矢高f 0=3.7m ,净跨l 0=11.3m 。
开挖宽度11.5m ,开挖高度7.7m 。
初步拟定拱顶厚度0400d =mm ,拱脚厚度n 516d =mm ,边墙的厚度为c 716d =mm ,墙底厚度增加d 200d =mm 。
目录(一)结构几何尺寸计算 (1)(二)计算拱圈的单位变位 (2)(四)计算拱圈的弹性抗力位移 (5)(五)计算墙顶(拱脚)位移 (5)(六)计算墙顶竖向力、水平力和力矩 (7)(七)计算多余未知力 (7)(八)计算拱圈截面力 (9)(九)计算边墙截面力 (10)(十)验算拱圈和侧墙的截面强度 (13)(十一)计算配筋量 (14)参考文献 (16)(一)结构几何尺寸计算(1)拱圈圆几何尺寸(2)拱圈轴线圆的几何尺寸 拱脚截面和拱顶截面厚度之差轴线圆与圆的圆心距:轴线圆半径0.4131=(3)拱圈外圆几何尺寸(4)侧墙的几何尺寸侧墙的计算长度(从拱脚中心算起)直墙拱形结构尺寸图如图1所示。
图 1 直墙拱结构尺寸图(二)计算拱圈的单位变位拱圈结构单位变位的计算公式:(三)计算拱圈的荷载变位1.计算荷载(1)围岩压力围岩竖直均布压力计算:围岩水平均布压力:(2)超挖回填引起的荷载按拱部平均超挖0.1m ,(3)衬砌拱圈自重引起的荷载综合以后各项,作用在结构上的荷载有垂直均布荷载和水平均布荷载:2.计算载变位(1拱圈结构荷载变位的计算公式:(2拱圈结构荷载变位的计算公式:将以上两种荷载引起的位移相叠加,则得:(四)计算拱圈的弹性抗力位移拱圈结构弹性抗力位移的计算公式:(五)计算墙顶(拱脚)位移则侧墙属于短梁。
拱结构及其案例分析
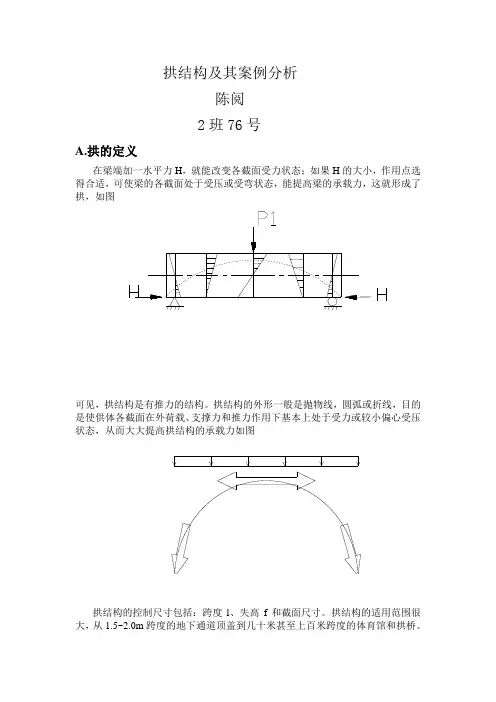
拱结构及其案例分析陈阅2班76号A.拱的定义在梁端加一水平力H,就能改变各截面受力状态;如果H的大小,作用点选得合适,可使梁的各截面处于受压或受弯状态,能提高梁的承载力,这就形成了拱,如图可见,拱结构是有推力的结构。
拱结构的外形一般是抛物线,圆弧或折线,目的是使供体各截面在外荷载、支撑力和推力作用下基本上处于受力或较小偏心受压状态,从而大大提高拱结构的承载力如图拱结构的控制尺寸包括:跨度l、失高f和截面尺寸。
拱结构的适用范围很大,从1.5~2.0m跨度的地下通道顶盖到几十米甚至上百米跨度的体育馆和拱桥。
例如清华大学综合体育中心、东凯尔勃莱德游泳馆等都采用拱结构。
拱结构的支撑形式一般有四种,如下图所示,由图a到图d分别为为:a.拉杆拱,b.落地拱,c.由框架支撑的拱,d.由水平屋盖支撑的拱。
B.拱的受力分析a.如下图所示是拱在集中荷载作用下的受力图简支拱的弯矩M与简支水平梁对应截面的弯矩M0相等。
拱的剪力Q和轴力N 等于简支水平梁对应截面上剪力Q0的两个投影。
即M= M0Q= Q0cosφN=- Q0sinφ式中,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。
b.如下图所示是拱在均布荷载作用设拱的轴线为抛物线,其方程为y=4fx(l-x)/l2求出相应的简支水平梁的弯矩和剪力M0=0.5qx(l-x) Q0=q(0.5l-x)因此,拱的内力为M=0.5qx(l-x)Q= q(0.5l-x)cosφN=- q(0.5l-x)sinφ其M图,Q图,N图分别如下图φ计算Q和N时,先要由轴线方程的一阶导数求出tgφ=dy/dx=4f (l-2x)/l2,再由此式求得截面的倾角φ。
C.三绞拱受力分析拱结构中一种比较合理的方式是三绞拱,如图所示内力计算M= M0-Hy,Q= Q0cosφ-HsinφN= -Q0sinφ-Hcosφ其中H=M0C/f ,M0和Q0分别是简支水平梁的弯矩和剪力,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。
结构力学—拱结构(建筑力学)

拱结构应用——大跨度体育馆
拱结构应用——农业大棚
拱结构应用——农业大棚
筒拱
砌体结构的赵州桥如果改用水平砌体的梁,是否可行?
水平的梁为纯弯曲变形,在弯矩产生的拉应力作用下砌 体会断裂,因此赵州桥无法用砌体建造水平梁
古代拱结构的应用——砌体屋顶
欧洲教堂的石砌拱形屋顶同样利用了拱结构时石材受压 而不是受拉
拱结构应用——大跨度桥梁
拱结构应用——砌体桥梁
拱结构应用——大跨度体育馆
拱截面有弯矩、剪力、轴力三个内力,
实际是弯曲变形与轴压变形的组合变形
轴向压缩产生的压应力可以抵消或者减小弯矩产生的 拉应力,使得整个横截面处于压缩状态或者仅有很 小的拉应力
拱抵抗水平力的方式
拱的矢高对水平推力的影响
拱矢高越大,拱结构的水平推力越小
拱结构特点:
1) 由于推力的存在,三铰拱截面弯矩比简支梁弯矩小。
1、拱结构
悬索 拱
拱的受力机制
竖向支座反力在 截面上产生的弯矩
外力P
外力P在截面上 产生的弯矩MP
水平支座反力H在截面上 产生的弯矩MH
水平支座反力H
竖向支座反力
拱与梁最大的差别是拱的支座反力有水平力,任意截面的弯 矩由竖向支座反力产生的弯矩、外荷载产生的弯矩、水平 支座反力产生的弯矩,水平支座反力产生的弯矩可以抵消 前两者产生的弯矩使得拱结构没有弯矩或者使得前两者产 生的弯矩减小
5) 三铰拱受向内的推力,因此需给基础施加向外的推力。 所以三铰拱的基础要比基础大,或加拉杆,以减小对 墙的推力。
古代拱结构的应用——砌体桥梁
赵州桥
砌体结构由砖石等块材用砂是抗拉能力差,拱结构为弯曲变形和轴 压变形的组合变形,轴向压应力会抵消弯曲产生的拉应力 或者减小拉应力,使得砌体处于完全受压状态或者有拉应 力也很小,因此拱结构可以建造大跨度桥梁
直墙拱结构的设计计算步骤及实例-原稿

中国矿业大学力学与建筑工程学院2014~2015学年度第二学期《地下建筑结构》课程设计学号********班级12级土木8班姓名肖浩汉力学与建筑工程学院教学管理办公室中国矿业大学力学与建筑工程学院《地下建筑结构》课程设计任务书《地下建筑结构》课程设计是教学计划要求中的一个重要教学环节,是在通过学习地下建筑结构相关知识、相关理论的基础上,结合地下工程专业方向的具体特点而进行的一次教学实践活动。
通过课程设计,结合相关的设计要求,掌握地下建筑结构设计中的部分设计内容,使学生所学到的基础理论和专业技术知识系统、巩固、延伸和拓展,培养学生自身独立思考和解决工程实际问题的能力,学会使用各种相关的工具书及查找资料。
完成地下建筑结构设计书一份,内容包括设计计算书、内力图和设计截面图。
一、设计题目某整体式直墙拱形衬砌的计算。
二、设计资料某隧道埋深85m,围岩为Ⅲ级围岩,RQD=85%,R c=57.4MPa,容重γ0=25 kN/m3,弹性抗力系数51.410K=⨯kPa。
采用整体式直墙拱混凝土衬砌,混凝土标号为C30。
顶拱是变厚度的单心圆拱,拱的净矢高f0=3.7m,净跨l0=11.3m。
墙净高按 3.5米算。
初步拟定拱顶厚度0250d x=+mm,拱脚厚度n 300d y=+mm,边墙的厚度为c n 200d d=+mm,墙底厚度增加d 200d=mm。
试进行衬砌内力计算与截面校核。
若截面校核不通过,请重新设计衬砌厚度并进行计算与校核。
变量x和y根据个人学号确定,具体方法为:设学号后三位为abc,则max(,)y ab bc=,min(,)x ab bc=。
例如:abc=123,则23y=,12x=。
三、课程设计要求本课程设计目的在于培养学生独立阅读资料、掌握技术信息、分析问题和解决问题的能力。
每个同学必须认真设计、独立完成,主要内容包括:1、结合设计资料,编写设计计算书;2、根据计算结果绘制直墙拱的内力图和设计截面图。
拱形计算公式

拱形计算公式摘要:1.拱形计算公式的概述2.拱形计算公式的分类3.拱形计算公式的计算方法4.拱形计算公式的应用实例5.拱形计算公式的发展前景正文:1.拱形计算公式的概述拱形计算公式,是一种用于计算拱形结构各个部分的长度、角度和面积的数学公式。
拱形结构在建筑、桥梁和隧道等领域中有着广泛的应用,其独特的结构特性使得拱形计算公式成为了工程技术人员必须掌握的重要工具。
2.拱形计算公式的分类根据拱形结构的不同特性,拱形计算公式可以分为以下几类:(1)圆拱计算公式:主要用于计算圆拱结构的各个部分,如圆拱的半径、高度和面积等。
(2)椭圆拱计算公式:主要用于计算椭圆拱结构的各个部分,如椭圆拱的半长轴、半短轴、高度和面积等。
(3)抛物线拱计算公式:主要用于计算抛物线拱结构的各个部分,如抛物线拱的焦点坐标、顶点坐标、高度和面积等。
3.拱形计算公式的计算方法拱形计算公式的计算方法主要包括以下几个步骤:(1)确定拱形结构的类型,如圆拱、椭圆拱或抛物线拱等。
(2)根据拱形结构的类型,确定需要计算的参数,如半径、高度、角度等。
(3)利用基本的几何知识和数学公式,计算出所需参数的值。
4.拱形计算公式的应用实例拱形计算公式在实际工程中有着广泛的应用,例如:(1)在建筑设计中,利用拱形计算公式可以计算出拱形屋顶的各个部分,从而确保屋顶结构的稳定性和美观性。
(2)在桥梁设计中,利用拱形计算公式可以计算出拱桥的各个部分,从而确保拱桥结构的稳定性和承载能力。
(3)在隧道设计中,利用拱形计算公式可以计算出隧道拱顶的各个部分,从而确保隧道结构的稳定性和安全性。
5.拱形计算公式的发展前景随着科技的发展和工程技术的进步,拱形计算公式也在不断地发展和完善。
未来,拱形计算公式将在以下几个方面进行拓展和深化:(1)开发新的拱形计算公式,以适应不断涌现的新型拱形结构。
(2)利用计算机技术和数值分析方法,提高拱形计算公式的计算精度和效率。
拱结构及其案例分析

拱结构及其案例分析陈阅2班76号A.拱的定义在梁端加一水平力H,就能改变各截面受力状态;如果H的大小,作用点选得合适,可使梁的各截面处于受压或受弯状态,能提高梁的承载力,这就形成了拱,如图可见,拱结构是有推力的结构。
拱结构的外形一般是抛物线,圆弧或折线,目的是使供体各截面在外荷载、支撑力和推力作用下基本上处于受力或较小偏心受压状态,从而大大提高拱结构的承载力如图拱结构的控制尺寸包括:跨度l、失高f和截面尺寸。
拱结构的适用范围很大,从1.5~2.0m跨度的地下通道顶盖到几十米甚至上百米跨度的体育馆和拱桥。
例如清华大学综合体育中心、东凯尔勃莱德游泳馆等都采用拱结构。
拱结构的支撑形式一般有四种,如下图所示,由图a到图d分别为为:a.拉杆拱,b.落地拱,c.由框架支撑的拱,d.由水平屋盖支撑的拱。
B.拱的受力分析a.如下图所示是拱在集中荷载作用下的受力图简支拱的弯矩M与简支水平梁对应截面的弯矩M0相等。
拱的剪力Q和轴力N 等于简支水平梁对应截面上剪力Q0的两个投影。
即M= M0Q= Q0cosφN=- Q0sinφ式中,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。
b.如下图所示是拱在均布荷载作用设拱的轴线为抛物线,其方程为y=4fx(l-x)/l2求出相应的简支水平梁的弯矩和剪力M0=0.5qx(l-x) Q0=q(0.5l-x)因此,拱的内力为M=0.5qx(l-x)Q= q(0.5l-x)cosφN=- q(0.5l-x)sinφ其M图,Q图,N图分别如下图φ计算Q和N时,先要由轴线方程的一阶导数求出tgφ=dy/dx=4f (l-2x)/l2,再由此式求得截面的倾角φ。
C.三绞拱受力分析拱结构中一种比较合理的方式是三绞拱,如图所示内力计算M= M0-Hy,Q= Q0cosφ-HsinφN= -Q0sinφ-Hcosφ其中H=M0C/f ,M0和Q0分别是简支水平梁的弯矩和剪力,φ是拱各点切线的倾角,自水平轴至杆轴切线为逆时针方向时φ为正号。
(完整word版)拱式结构计算
二次衬砌内力计算书二次衬砌内力计算书一基本资料:围岩级别”级,丫=20kN/m3,弹性抗力系数K=0.4 X 106kN/m3 ,二次衬砌类型C20混凝土45cm, 丫=23KN/m,弹性模量丘=2.7 X 10 kPa,设计时速100km/m,结构断面如图1所示。
10S041图1衬砌结构断面(尺寸单位:cm)二荷载确定:1. 竖向围岩压力:q=0.45 X 2s-1丫3式中:s――围岩类别,此处s=4;丫--- 围岩容重,此处丫=20kN/m3;3 ――跨度影响系数, 3 =1+i(l斤5)3 =1+0.1 X (13.044575-5)=1.8044575mq=0.45 X 24-1X 20 X 1.8044575=129.92094kPa考虑到初期支护承担大部分荷载,二次衬砌作为安全储备,故对围岩压力进行折减,对本隧道按42%进行折减,取为54.5668kPa2. 水平围岩压力:e=0.35 X q=0.25 X 54.5668=13.6417 kPa三衬砌几何要素1. 衬砌几何尺寸内轮廓半径m= 5.7074m,r 2= 8.2m ,内径r1 , r 2所画圆曲线终点截面与竖直轴的夹角$ 1=90o,© 2=98.421132 o,拱顶截面厚度d o=O.4m,墙底截面厚度d n=0.8m此处墙底截面为自内轮廓半径为「2的圆心向内轮廓墙底做连线并延长至与外轮廓相交, 其交点到内轮廓墙底间的连线。
内轮廓线与外轮廓线相应圆心的垂直距离为:代入数值计算得:m=0.35490916m外轮廓线半径:R i=m+r i +d o=6.4623O916mR?=m+「2+d o=8.9549O916m拱轴线与内轮廓线相应的垂直距离为m =0.1759934m拱轴线半径:r i / =m +r 计0.5d o=6.O833934m「2/ =m/ +「2+0.5d o= 8.5759934m拱轴线各段圆弧中心角0 i =90o, 0 2=7.259732 o2. 半拱轴线长度S及分段周长△ S分段轴线长度:S1 』S= =90/180 X 3.14159265 X 6.0833934=9.555772m1B0- 1阻:=7.259732/180 X 3.14159265 X 8.5759934=1.08663176mISO-:半拱轴线长度:S= S1+ S2 = 9.555772+1.08663176=10.64240376m 将半拱轴线等分为8段,每段长为:S△ S = =10.64240376/8=1.33030047me3. 各分块接缝中心几何要素:(1)与竖直轴夹角a iM 1BO{.a 1=^0 1= X --------- =12.52929038「a 2=^0 1+ a 1=12.529290381 +12.529290381 =25.05858076 oa 3=^0 1+ a 2=12.52929038 I +25.05858076 0=37.58787114 oa 4=^0 1+a 3=12.52929038「+37.58787114 ; =50.11716152 0 a 5=^0 1+a 4=12.5292903^+50.11716152 0=62.6464519 0a 6=^0 1+a 5=12.52929038「+62.6464519「=75.17574228 0△ S=7 △ S-S1=7*1.33030047-9.555772=-0.24366871ma 7=0 i +一 X —=88.3720616249 oa 8= a 7 + -X=97.259732 o另一方面 a 8=900+7.259732 0=97.259732 o 角度闭合差0(2) 接缝中心点坐标计算x i =r i sin 1=6.0833934 X sin 12.52929038 =1.31972334mX 2=r isin2=6.0833934 X sin25.05858076 o=2.57658888m X 3=r 1 sin3=6.0833934 X sin37.58787114 o=3.71073268m X 4=r 1 sin4=6.0833934 X sin50.11716152 o=4.66813602mX 5=m / sin a 5=6.0833934 X sin62.6464519 o=5.4031982m X 6=\ / sin a 6=6.0833934 X sin75.17574228o=5.880908576ma 2= (8.5759934-6.0833934 )X sin90 o=2.4926X 7=「2, sin a 7 - a 2=8.5759934 X sin88.3720616249 o-a 2 =6.07963197m X 8=「2, sin a 8 - a 2=8.5759934 X sin97.259732-a 2 =6.01434395m y 1=r 1 / (1-cosa 1)= 6.0833934X( 1-cos12.52929038 '=0.154007my 2=r 1 / (1-cos a 2)= 6.0833934 X (1-cos25.05858076 o)= 0.606834m y s =r 1 x(1-cos a 3):=6.0833934 X (1-cos37.58787114 o)=1.331456my 4=r 1 ' '(1-cos a 4)= :6.0833934 X (1-cos50.11716152 o)=2.284608m y 5=r 1 / (1-cos a 5): =6.0833934 X (1-cos62.6464519 o)=3.409395my 6=\ ‘ '(1-cos a 6)= :6.0833934 X (1-cos75.17574228 o)=4.638674ma 1=(r 2 / -r 1 / )cos 0 1= (8.5759934-6.0833934 ) X cos90 o=0 y 7=「1,- r2 / cos a 7=5.15985-10.473 X cos94.0804 o=5.90507m y s =r 1 / - r2 / cos a8=5.15985-10.473 X cos100.995 o=7.1573m 当然也可以直接从图 2中量出X i ,y i ,以后计算中只取四位有效数字。
拱结构分析
拱结构及案例分析一拱结构的分析拱结构式是建筑工程中常用的结构之一,是一种主要承受轴向压力并由两端推力维持平衡的曲线或折线构件。
拱结构由拱圈及其支座组成。
支座可做成能承受垂直力、水平推力以及弯矩的支墩;也可用墙、柱或基础承受垂直力而用拉杆承受水平推力。
拱圈主要承受轴向压力,与同跨度的梁相比,弯矩和剪力较小,从而能节省材料、提高刚度、跨越较大空间。
拱的类型,按材料分:土拱、砖石拱、木拱、混凝土拱、钢筋混凝土拱、刚拱等;按拱轴线型分:圆弧拱、抛物线拱、悬链线拱等;按所含铰的数目分:三铰拱、双铰拱、无铰拱等;按拱圈截面形式分:实体拱、箱形拱、桁架拱等。
如下图为拱的分类图:拱结构的受力分析:如上图,当拱承受均布荷载时,主要靠的压力和推力支撑,由Th+chMx=可知,支撑弯矩靠力臂的改变,而力臂的增加靠形态的改变。
因此拱的外形一般是抛物线、圆弧线或折线,目的是使拱体各截面在外荷载、支撑反力和推力作用下基本处在受压或较小偏心受压状态,从而大大提高拱结构的承载力。
当拱自身重力产生的弯矩Mx为0 时,此时称为合理拱轴线(也叫压力线),即截面产生的弯矩为0。
当选择拱轴线时,偏于合理拱轴线以上的为负弯矩,偏于合理拱轴线以下的为正弯矩,与合理拱轴线相交的点的弯矩为0 。
拱结构在设计中最重要的是水平推力的处理。
在实际工程中常用的有以下几种做法:由拉杆承受水平力——优点是结构自身平衡,使基础受力简单;可用作上部结构构件,代替大跨度屋架;由基础承受——施工设计时要注意承受水平推力的基础的做法;由侧面结构物承受——要求此结构必须有足够的抗侧力刚度;由侧面水平构件承受——一般有设置在拱脚处的水平屋盖构件承受,水平推力先由此构件作为刚性水平方向的梁承受,在传递给两端的拉杆或竖向抗侧力结构;此外还应注意当拱承受过大内力时的失稳现象;防止失稳的办法是在拱身两侧加足够的侧向支撑点。
二拱结构的案例分析阿罗丝渡槽如右图,渡槽设设计为一个124ft(37.8m)长,支撑在间隔62ft(18.9m)的支架上,两端伸臂各长31ft(9.45m)的单元。
直墙拱计算书
精心整理中国矿业大学力学与建筑工程学院《地下建筑结构》课程设计任务书《地下建筑结构》课程设计是教学计划要求中的一个重要教学环节,是在通过学习地下建筑结构相关知识、相关理论的基础上,结合地下工程专业方向的具体特点而进行的一次教学实践活动。
系数K =0250d =d 200d =mm 核。
),min(,)x ab bc =。
例如:abc=123,则23y =,12x =。
三、课程设计要求本课程设计目的在于培养学生独立阅读资料、掌握技术信息、分析问题和解决问题的能力。
每个同学必须认真设计、独立完成,主要内容包括: 1、结合设计资料,编写设计计算书;2、根据计算结果绘制直墙拱的内力图和设计截面图。
衬砌结构示意图中国矿业大学力学与建筑工程学院《地下建筑结构》课程设计计算书1几何尺寸计算2计算主动荷载2.1围岩压力洞室采用光面爆破开挖,平均超挖值拱部取0.10m,边墙取0.12m,则毛洞跨度为:根据围岩垂直压力的综合经验公式计算,以及对围岩分级表的查询,取N0=1.5m,则围岩垂直均布压力为围岩水平均布压力取0.1q,为:12.22.333.13.1.1根据参考资料的附表,可得系数为3.1.2边墙换算高度为且,可见,衬砌边墙属弹性地基短梁。
墙顶的单位变位按公式计算,有:3.1.3基本结构的单位变位按公式计算,有3.2基本结构载变位3.2.1主动荷载的载变位①基本结构拱脚刚性固定时拱圈的载变位,系数的确定,通过查阅参考资料的附表得:由水平均布荷载e引起墙顶的变位,按公式计算,为基本结构墙顶的载变位为③主动荷载作用下基本结构载变位3.33.4弹性抗力3.4.1基本结构拱脚刚性固定时拱圈弹性抗力的载变位3.4.2墙顶的载变位:这时墙顶的载变位,仅由拱圈弹性抗力传来的力矩、竖向力及水平力所引起,其中系数n1-n3通过查阅参考资料的附表得:则由公式得,取3.4.3拱圈弹性抗力时,基本结构变位:按公式计算,得3.5弹性抗力作用下多余未知力计算由多余未知力计算公式,得弹性抗力作用下多余未知力为3.6计算弹性抗力拱脚弹性抗力计算公式为3.73.8为拱圈弹性抗力使基本结构拱圈抗力区内任一截面产生的轴力及弯矩,仅才存在表1拱圈内力计算结果表3.10.1拱圈的强度校核:选取拱顶截面可得偏心距:精心整理判断为大偏心受压。
6直墙拱形衬砌
§6.4 影响衬砌结构内力的因素分析
§6.4 影响衬砌结构内力的因素分析
§6.4 影响衬砌结构内力的因素分析
§6.5 衬砌轮廓的修正
§6.5 衬砌轮廓的修正
§6.5 衬砌轮廓的修正
§6.5 衬砌轮廓的修正
§6.5 衬砌轮廓的修正
§6.5 衬砌轮廓的修正
§6.6 装配式直墙拱形衬砌的构造与计算
拟定及构造
贴壁整体式直培拱形衬砌,根据地质条件、 使用要求、洞室大小、施工条件、材料供应等 情况,可做成现浇整体式混凝土或钢筋混凝土 结构,装配整体式钢筋混凝土结构及砌体(料 石或混凝土预制块)结构。目前,一般采用现 浇整体式结构,它具有较好的整体性及防水性 能。由于这种衬砌适用范围较广,除应符合第 三章的一般设计技术要求外,其固有的构造特 点难以统一。因此,设计时要重视经验及工程 类比,下面介绍一些要求。
§6—1 整体式宜墙拱形衬砌的尺寸 拟定及构造
其构造要求如下:
§6—1 整体式宜墙拱形衬砌的尺寸 拟定及构造
§6—1 整体式宜墙拱形衬砌的尺寸 拟定及构造
§6—1 整体式宜墙拱形衬砌的尺寸 拟定及构造
§6—1 整体式宜墙拱形衬砌的尺寸 拟定及构造
§6—2 整体式直墙拱形衬砌的计算
衬砌的设计,应保证其强度及稳定,使材 料消耗和造价尽可能合理,达到安全与经济 的统一。计算仅是衬砌设计的一个方面,要 搞好设计,必须将计算与工程类比及设计、 施工、使用的经验结合起来。计算属于理论 分析的范畴,其结果是否符合实际工作情况, 要通过使用来检验从这一点讲,目前的计算 理论还远末达到完善的程度,有待进一步总 结研究,充实完善。
§6—2 整体式直墙拱形衬砌的计算
§6—2 整体式直墙拱形衬砌的计算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中国矿业大学力学与建筑工程学院2014~2015学年度第二学期《地下建筑结构》课程设计学号********班级12级土木8班姓名肖浩汉力学与建筑工程学院教学管理办公室中国矿业大学力学与建筑工程学院《地下建筑结构》课程设计任务书《地下建筑结构》课程设计是教学计划要求中的一个重要教学环节,是在通过学习地下建筑结构相关知识、相关理论的基础上,结合地下工程专业方向的具体特点而进行的一次教学实践活动。
通过课程设计,结合相关的设计要求,掌握地下建筑结构设计中的部分设计内容,使学生所学到的基础理论和专业技术知识系统、巩固、延伸和拓展,培养学生自身独立思考和解决工程实际问题的能力,学会使用各种相关的工具书及查找资料。
完成地下建筑结构设计书一份,内容包括设计计算书、内力图和设计截面图。
一、设计题目某整体式直墙拱形衬砌的计算。
二、设计资料某隧道埋深85m,围岩为Ⅲ级围岩,RQD=85%,R c=57.4MPa,容重γ0=25 kN/m3,弹性抗力系数51.410K=⨯kPa。
采用整体式直墙拱混凝土衬砌,混凝土标号为C30。
顶拱是变厚度的单心圆拱,拱的净矢高f0=3.7m,净跨l0=11.3m。
墙净高按 3.5米算。
初步拟定拱顶厚度0250d x=+mm,拱脚厚度n 300d y=+mm,边墙的厚度为c n 200d d=+mm,墙底厚度增加d 200d=mm。
试进行衬砌内力计算与截面校核。
若截面校核不通过,请重新设计衬砌厚度并进行计算与校核。
变量x和y根据个人学号确定,具体方法为:设学号后三位为abc,则max(,)y ab bc=,min(,)x ab bc=。
例如:abc=123,则23y=,12x=。
三、课程设计要求本课程设计目的在于培养学生独立阅读资料、掌握技术信息、分析问题和解决问题的能力。
每个同学必须认真设计、独立完成,主要内容包括:1、结合设计资料,编写设计计算书;2、根据计算结果绘制直墙拱的内力图和设计截面图。
衬砌结构示意图整体式直墙拱形衬砌的计算某隧道埋深85m ,围岩为Ⅲ级围岩,RQD=85%,R c =57.4MPa ,容重γ0=25 kN/m 3,弹性抗力系数51.410K =⨯kPa 。
采用整体式直墙拱混凝土衬砌,混凝土标号为C30。
顶拱是变厚度的单心圆拱,拱的净矢高f 0=3.7m ,净跨l 0=11.3m 。
墙净高按3.5米算。
初步拟定拱顶厚度do=0.254m ,拱脚厚度dn=0.307m ,边墙的厚度为dc=0.507m ,墙底厚度增加d 200d =mm 。
试进行衬砌内力计算与截面校核。
若截面校核不通过,请重新设计衬砌厚度并进行计算与校核。
(一)结构几何尺寸计算 (1)拱圈内圆几何尺寸内圆净跨:l 0=11.3m ,内圆矢高f 0=3.7m内圆半径计算:20202002)(R l f R =⎪⎭⎫ ⎝⎛+-,从而有:2200004 6.1648l f R m f +== (2)拱圈轴线圆的几何尺寸拱脚截面与拱顶截面厚度之差:00.3070.2540.053n d d m ∆=-=-=轴线圆与内圆的圆心距:22220000(0.5) 6.164(6.1640.50.053)0.0442(0.5)2(3.70.50.053)R R m m f --∆--⨯===-∆-⨯轴线圆半径:00 6.3352d R R m m =++= 0/2sin 0.914018/2n l R d ϕ==-066.066653ϕ=cos 0.405471ϕ= sin 0.280604h n d d m ϕ== cos 0.124480v n d d m ϕ==计算跨度:011.30.28060411.580604m h l l d =+=+=计算矢高:00 3.76476022vd d f f m =+-= (3)拱圈外圆几何尺寸外圆跨度:10211.861208h l l d m =+= 外圆矢高:100 3.829520v f f d d m =+-=外圆半径:2211114 6.5069898l f R m f +==外圆与轴线圆的圆心距:1100.2159892d m R R m =--= (4)校核公式 外圆与轴线的圆心距:010.259989m m m m =+=cos 6.503994 6.1638690.1054180.234707j d m ϕ==--=(5)侧墙的几何尺寸拱脚中心到侧墙中心线的垂直距离:()/20.013198h n h e d d m =-=侧墙的计算长度(从拱脚中心算起):0/2 3.640302y v h h d m =+=结构总高:1/27.469822k y v h h d f m =++= (二)计算拱顶单位变位采用分块总和法计算变位,将半拱轴线长分10等分,计算过程列于表1,故拱顶单位变位:097166.06665116.335 3.14159268.116406103103180103310j s R E E ϕ-∆==⨯⨯⨯⨯=⨯⨯⨯10941108.1164061013967.52893 1.133661103i i in s E I δ--=∆==⨯⨯=⨯∑ 1094122108.1164061012194.951810.989792103i i i i n s y E I δδ--=∆===⨯⨯=⨯∑ 10102242200(cos ) 1.916782103i i i i i i i in n s y E I F δϕ-==∆=+=⨯∑∑校核计算:22-3[(1)cos ]38.905349103ss s n ny E I Fδϕ∆=++=⨯∑∑4-41112222(11336610.989792 1.916782)10 5.03002710δδδ-++=++⨯=⨯判别:()0103-29ss 221211≈⨯=++-δδδδ 说明单位变位计算结果正确。
表1 变截面圆拱拱顶单位变位计算(见附图) (三)计算拱顶载变位1计算荷载(1)岩石坚固系数10i f =,隧道半跨度:11/213.76470.68823520i i l a h m f f ====(考虑到有一定的间隙) 隧道埋深H=85m>(2-2.5)h 1,属于深埋 因此围岩竖直压力:1h 25000 2.96530274132.55q Pa γ==⨯=地(采用均布荷载模式)1125(3.829520 2.965302)21.60545q f h kpa γγ∆=-=⨯-=地(2)自重计算h 0250.254 6.35q d kPa γ==⨯=自n h 0d 0.307()25000(0.254)12.578604cos 0.405471q d kPa γϕ∆=-=⨯-=自 因此:q 80.482550Pa q q k =+=地自12.578604Pa q q k ∆=∆=自在实际设计中,外载还应包括超挖回填引起的拱顶荷载,一般取30cm 回填高度,可忽略不计。
2计算载变位先分别计算在均布荷载和三角形荷载作用下的载变位,然后叠加,计算过程列于表2。
表2 变截面圆拱拱顶载变位计算(见附图) 在均布荷载q 作用下的载变位:10''100.0427753i ppi i in s M E I =∆∆==-∑1010'''200(cos )-0.07833563i i ppi i pi i i i i i n n s M y N E I F ϕ==∆∆=+=∑∑ 在三角荷载q ∆作用下的载变位:10''''100.0371993i ppi i in s M E I =∆∆==-∑ 1010''''''200(cos )-0.0785883i i ppi i pi i i i i in n s M y N E I F ϕ==∆∆=+=∑∑ 拱顶总载变位:'''1110.079974p p p ∆=∆+∆=-'''2220.156924p p p ∆=∆+∆=-校核计算:'''[(1)cos ]0.1417453sp p p s n n M y N E I Fϕ∆∆=++=-∑∑ '''120p p sp∆+∆-∆≈,可见计算正确。
''''''[(1)cos ]0.1157873sp p p s n n M y N E I Fϕ∆∆=++=-∑∑''''''120p p sp ∆+∆-∆= , 满足要求!(四)在荷载作用下多余未知力的计算1判别侧墙类型0.572501α=== 侧墙特征长度:0.572501 3.640302 2.084076y h α=⨯=<2.75,故侧墙属于短梁 2计算墙顶单位变位。
根据查表得:98.7150ψ=108.5578ψ=118.2161ψ=128.2151ψ=138.4604ψ=1410.8071ψ=1511.9556ψ=33690.482431bKA B K α==36111219104 3.57371410A KA ϕϕαβϕϕ-⎡⎤+==⨯⎢⎥+⎣⎦261311129102 3.52594310A u K A ϕϕαβϕϕ-⎡⎤+===⨯⎢⎥+⎣⎦61013291027.15988310A u KA ϕϕαϕϕ-⎡⎤+==⨯⎢⎥+⎣⎦ 38139102 4.510e A KA αϕβϕϕ-⎡⎤==-⨯⎢⎥+⎣⎦28023910 3.28212610e A u K A αϕϕϕ-⎡⎤==⨯⎢⎥+⎣⎦543910[] 1.78520910e A e K Aψψαβψψ-+=-=-⨯+ 414159101[] 1.203179610e A u e K Aψψψψ-+=-=-⨯+ 3由外载引起的墙顶弯矩与水平力11()()16.840219 5.6261431426.112446hp h h l lM ql e l q e q q =-+-∆+=--∆=0=hp H4计算多余未知力4111112 1.20513510a δβ-=+=⨯41221122122 1.3293910a a f δββ-==++=⨯ 242222221242 4.0860510a u f f δββ-=+++=⨯510112 6.018213100.080202p hp hp a M H q ββ-=∆++=-⨯-42021212()0.158125 2.8594710p hp hp hp hp a f M H M u H u qββ-=∆++++=--⨯22101220121211220.425180372.191716337.972a a a a X q a a a -==-+=- 11201210221211220.838144265.89543333.51396a a a a X q a a a -==+=- (五)弹性抗力作用下多余未知力的计算1计算1=j σ时引起的墙顶截面内力及变位通过积分可得到:2222[cos sin cos )]0.9601133(12cos )jR M σϕϕϕϕϕ=---=--222[cos sin cos )]0.1515213(12cos )j RN σϕϕϕϕϕ=--=-2[4cos sin cos )]10.5348563(12cos )j RQ σϕϕϕϕϕ=++=-因此墙顶内力(要考虑偏心距):(sin cos ) 1.018317j j j h h M M N Q e σσσσϕϕ-=-+=- cos sin 9.567611j j h H N Q σσσϕϕ-=-=-sin cos 4.410071h j j V N Q σσσ=+=墙顶变位:512 3.737410h h M H σσσβββ---=+=-⨯5127.2093510h h u M u H u σσσ---=+=-⨯2计算1=j σ时的拱顶载变位采用分块总和法计算,将弹性抗力所分布拱轴线长对应圆心角045ϕϕ=-四等分00066.0666545 5.2666634ϕ-∆==2234312300[cos sin cos )]40.133810(12cos )3[(1cos )]i i i i i i j i n R E d m σϕϕϕϕϕϕϕ-=--∆∆=-=-⨯-+-∑2244223002224200-3[cos sin cos )](1cos )4(12cos )3[(1cos )]cos [cos sin cos )]3(12cos )3(1cos )0.369810i i i i i i i j i i i i i i i i j i n R E d m n R E d m σϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕϕ==---∆∆=-+-+---∆-+-=-⨯∑∑3计算1=j σ时的多余未知力4111112 1.20513510a δβ-=+=⨯41221122122 1.3293910a a f δββ-==++=⨯ 242222221242 4.0860510a u f f δββ-=+++=⨯411 1.7117410σσσαβ-=∆+=-⨯422 5.82597610f u σσσσαβ-=∆++=-⨯221122121211220.237804a a a a X a a a σσσ-==-- 11212122121122 1.50319a a a a X a a a σσσ-==- 4计算弹性抗力根据01u K h =σ及01sin sin j h u K σσϕϕ==55521122222111010471.0109416.1109402.1)()()(------⨯-⨯∆+⨯=++++++++=j j hp hp j j j q q u u H u M fu X X u X X u X X u σσσσσσσσσ从而可求得 j 11.8144σ=5.在弹性抗力作用下多余未知力计算11 2.80951158j X X σσσ==-2217.75929j X X σσσ==(六)计算弹性抗力及外载共同作用下的多余未知力 111335.1625j X X X σσ'=+= 222353.273248j X X X σσ'=+= (七)计算拱圈内力1.拱圈任一截面的内力σM M y X X M p ++'+'=212cos p N X N N σϕ'=++ 各截面的内力计算见表3(八)计算边墙内力因对称,故仅计算左边墙。
