第八章 材料的变形和断裂
材料科学基础答案 王章忠

简答题第一章材料结构的基本知识1、说明结构转变的热力学条件与动力学条件的意义。
答:结构转变的热力学条件决定转变是否可行,是结构转变的推动力,是转变的必要条件;动力学条件决定转变速度的大小,反映转变过程中阻力的大小。
2、说明稳态结构与亚稳态结构之间的关系。
答:稳态结构与亚稳态结构之间的关系:两种状态都是物质存在的状态,材料得到的结构是稳态或亚稳态,取决于转交过程的推动力和阻力(即热力学条件和动力学条件),阻力小时得到稳态结构,阻力很大时则得到亚稳态结构。
稳态结构能量最低,热力学上最稳定,亚稳态结构能量高,热力学上不稳定,但向稳定结构转变速度慢,能保持相对稳定甚至长期存在。
但在一定条件下,亚稳态结构向稳态结构转变。
3、说明离子键、共价键、分子键和金属键的特点。
答:离子键、共价键、分子键和金属键都是指固体中原子(离子或分子)间结合方式或作用力。
离子键是由电离能很小、易失去电子的金属原子与电子亲合能大的非金属原于相互作用时,产生电子得失而形成的离子固体的结合方式。
共价键是由相邻原子共有其价电子来获得稳态电子结构的结合方式。
分子键是由分子(或原子)中电荷的极化现象所产生的弱引力结合的结合方式。
当大量金属原子的价电子脱离所属原子而形成自由电子时,由金属的正离子与自由电子间的静电引力使金属原子结合起来的方式为金属键。
第二章材料的晶体结构1、在一个立方晶胞中确定6个表面面心位置的坐标。
6个面心构成一个正八面体,指出这个八面体各个表面的晶面指数、各个棱边和对角线的晶向指数。
解八面体中的晶面和晶向指数如图所示。
图中A、B、C、D、E、F为立方晶胞中6个表面的面心,由它们构成的正八面体其表面和棱边两两互相平行。
ABF面平行CDE面,其晶面指数为;ABE面平行CDF面,其晶面指数为;ADF面平行BCE面,其晶面指数为;ADE面平行BCF面,其晶面指数为(111)。
棱边,,,,,,其晶向指数分别为[110],,[011],,[101]。
第8章 金属高温下的变形与断裂

8
9
典型的蠕变曲线
金属蠕变过程用蠕变曲线来描述。 金属蠕变过程用蠕变曲线来描述。典型的蠕变曲线如图。 (1)Oa线段:是试样在t 温度下承受恒定拉应力σ时所产 线段: 线段 生的起始伸长率δq。 若应力超过金属在该温度下的屈服强度,则δq包括弹性伸长 弹性伸长 塑性伸长率两部分。 率和塑性伸长率 塑性伸长率 此应变还不算蠕变 应变还不算蠕变,而是由外载荷引起的一般变形过程。 应变还不算蠕变
20
(二)扩散蠕变
(二)扩散蠕变 扩散蠕变: 扩散蠕变:是在较高温度(约比温度(T/Tm)远超过0.5)下的 ( 一种蠕变变形机理。 它是在高温下大量原子和空位定向移动造成的 高温下大量原子和空位定向移动造成的。 高温下大量原子和空位定向移动造成的 在不受外力情况下,原子和空位的移动无方向性,因而宏观 上不显示塑性变形。 但当受拉应力σ作用时,在多晶体内产生不均匀的应力场 产生不均匀的应力场。 产生不均匀的应力场
17
刃位错攀移克服障碍的几种模型: 刃位错攀移克服障碍的几种模型: 可见,塞积在某种障碍前的位错通过热激活可以在新的滑移 面上运动(a),或与异号位错相遇而对消(b),或形成亚 晶界(c),或被晶界所吸收(d)。
18
当塞积群中某一个位错被激活而发生攀移时,位错源便可能 再次开动而放出一个位错,从而形成动态回复过程 动态回复过程。 动态回复过程 这一过程不断进行,蠕变得以不断发展。
7
本章介绍内容: 本章介绍内容: 阐述金属材料在高温长时载荷作用下的蠕变现象 蠕变现象。 蠕变现象 讨论蠕变变形和断裂的机理 蠕变变形和断裂的机理。 蠕变变形和断裂的机理 介绍高温力学性能指标及影响因素。 为正确选用高温金属材料和合理制定其热处理工艺提供基础 知识。
第8章材料的变形与断裂

第8章材料的变形与断裂材料的变形与断裂是材料科学中的重要研究内容,对于了解材料的性能和使用寿命具有重要意义。
材料的变形是指在外力作用下,材料的形状、尺寸或结构发生改变的过程。
而断裂则是指在外力作用下,材料由于受到极限载荷或破坏源的影响,导致形成裂纹最终导致材料的破裂。
材料的变形可以分为弹性变形和塑性变形两种情况。
在小应力作用下,材料会发生弹性变形,即在去除外力后能够恢复其原状。
而在大应力作用下,材料会发生塑性变形,即即使去除外力,材料也无法完全恢复其原状。
材料的弹性模量是一个衡量材料抗弹性变形能力的重要参数,不同材料具有不同的弹性模量,常见材料如金属具有较大的弹性模量,而聚合物则具有较小的弹性模量。
材料的塑性变形是材料工程中非常重要的一个特性,塑性变形不仅与材料的力学性能有关,还与材料的微观结构和晶格缺陷等因素有关。
材料在塑性变形过程中会产生塑性应变和塑性应力,塑性应变是材料发生塑性变形时所引起的应变,而塑性应力则是材料发生塑性变形时所引起的应力。
常见的材料塑性变形包括屈服、流动、硬化等过程。
材料的断裂是指在外力作用下,材料发生了破裂。
材料的断裂主要分为两种形式:韧性断裂和脆性断裂。
韧性断裂是指材料在外力作用下具有一定韧性,在发生破裂前能够发生大量的塑性变形。
而脆性断裂则是指材料在外力作用下没有发生明显的塑性变形,很快发生破裂。
韧性断裂常见于许多金属材料,而脆性断裂则常见于一些玻璃、陶瓷等材料。
材料的断裂形式可以通过断口分析来确定。
不同的断口形式对应着不同的材料断裂机制。
常见的断裂形式有拉断、韧窝断裂、脆窝断裂等。
拉断是指材料发生拉伸断裂,断口两侧平整光滑,常见于高强度的金属材料。
而韧窝断裂则是指材料发生韧性断裂,断口两侧有明显的韧窝。
脆窝断裂则是指材料发生脆性断裂,断口两侧有明显的断裂窝。
通过对断口形态的观察可以判断材料的断裂机制和断裂韧性。
材料的变形和断裂不仅仅涉及到力学性能的研究,还和材料的制备工艺、微观结构、晶体缺陷、应力和温度等因素有关。
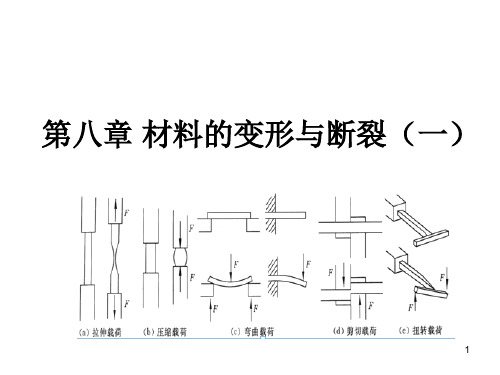
大学材料科学基础第八章材料的变形与断裂(1)

六方晶系则需画图判定。
滑移系数量与金属的塑性 滑移系代表了晶体滑移时可能采取的空间取向,晶 体中滑移系数量越多,滑移时可能采取的空间取向就 越多,滑移就越容易进行,金属的塑性便越好。 面 心 立 方 金 属 : Cu,Al,Au,Ag,,Ni,γ-Fe, 奥氏体钢,体心立方金属α-Fe,铁素体,Mo,Nb的 塑性很好,而密排六方金属Mg,Zr,Be,Zn的塑性 则较差。当然滑移系数量并不是决定金属塑性高低唯 一的因素,合金的成分、强度的高低、加工硬化的能 力等也会影响到金属的塑性。试验表明,奥氏体钢的 塑性要优于铁素体钢。
金属拉伸曲线分析。 1 弹性变形阶段:ζ-ε呈直线关系。
(弹)塑性变形阶段: ζ-ε不遵循虎克定律
2 均匀塑性变形阶段:屈服阶段:ε增加,ζ基本保 持不变, ζ-ε呈非线性关系。 3 颈缩阶段(局部变形阶段):变形集中在局部区 域。 4 断裂阶段:从颈缩到断裂。
拉伸试验可以得到以下强度指标和塑性指标:
拉伸条件下滑移系上分切应力的计算。
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning ™ is a trademark used herein under license.
θ-滑移面法线与拉伸轴的夹角
4 力轴作用在任意方向
二、孪晶(孪生)变形
孪生也是金属塑性变形的一种形式,一般情况下, 金属晶体优先以滑移的方式进行塑性变形,但是当滑 移难以进行时,塑性变形就会以生成孪晶的方式进行, 称为孪生。例如滑移系较少的密排六方晶格金属,当 处于硬取向时,滑移系难以开动,就常以孪生方式进 行变形。滑移系较多的fcc、bcc结构的金属一般不发 生孪生变形,但在极低的温度下变形或是形变速度极 快时,也会以孪生的方式进行塑性变形。 定义:晶体在难以进行滑移时而发生的另一种塑 性变形方式,其特点是变形以晶体整体切变的形式 进行而不是沿滑移系发生相对位移。
高分子物理第八章

银纹现象为聚合物所特有,常出现在非晶态聚合物PS、 PMMA、PC、PSF,在晶态聚合物PP等也有发现
33
Microstructure of crazing
微纤 Microfibril
也称为银纹质
微纤与外力方向平行,银纹 长度方向与外力垂直。
高度取向的高分子链组成
34
银纹方向和分子链方向
聚合物横向收缩不足补偿塑 性伸长,致使银纹体内产生大量
Cross-section area
形变时,V不变
A0 l0 A0 A l (1 )
true (1 )
22
Considère 作图法:
在真应力-应变曲线上确 定与工程应力-应变屈服 点Y所对应的B点 Y点
d e 0 d
true (1 )
d true true true d 1
球晶大,一般断裂伸长率和韧性降低
15
(c) 结晶度The Degree of Crystallization
结晶度增加,屈服应力、强度、模量、硬度等提 高;断裂伸长率、冲击性能等下降
16
8.1.1.3 Different types of stress-strain curve
17
聚合物力学类型
42
试样发生脆性或者韧性断裂与材料组成有关 ,除此之外,同一材料是发生脆性或韧性断 裂还与温度T 和拉伸速度 有关。
低温的脆性断裂在高温可以变成韧性
应变速率: 速度增加,韧性可以变成脆性断裂
43
Comparing of brittle and ductile fractures (分析判断)
脆性断裂
8.1.1.1 非晶态聚合物的应力-应变曲线
华南师范大学材料科学与工程教程第八章 材料的变形与断裂(二)
20
C =S cos cos
施密特定律首先在六方晶系如Zn、Mg中得到证实。
右图中显示了纯度 99.999 %(质量 分数)的单晶锌在拉伸时的屈服点随晶 体位向变化的实验结果。 面心立方金属也符合施密特定律 但对体心立方金属,则不服从施密特定
位错宽度如何确定?阻力大小?
10
• 位错宽度的界定:位错中心A处,离两端平衡位置为b/2,一直往 两侧延伸到原子列偏离原平衡位置的位移为b/4时,位错两侧的宽度以W 表示,即为位错宽度。
•派-纳力(τP-N) 理想晶体中位错在点阵周期场中运动时所 需克服的阻力。
τP-N的大小主要取决于位错宽度W,W越小,τP-N就 越大,材料就难变形,相应的屈服强度也越大;
• cos cos 值大者,称为软取向,此时材料的屈服点
较ห้องสมุดไป่ตู้;
• 反之, cos cos 值小者,称为硬取向,材料屈服点
也较高
• 取向因子最大值在 + =90o的情况下, cos cos =1/2; • 当滑移面垂直于拉力轴或平行于拉力轴时,在滑移面 上的分切应力为零,因此不能滑移。
7
三、滑移与孪晶变形
1、滑移观察 1)光学显微镜观察
试样表面内有许多平行的或几组交叉的细线,是相
对滑移的晶体层与试样表面的交线
——滑移带
2)电子显微镜观察
滑移带是由是由更多的一组平行线构成
——滑移线
试样内的滑移带不是均匀分布的,滑移线构成的滑移台阶高约100nm, 如果滑移 b=0.25,则从滑移台阶的高度可粗略估计约有 400个位错移出了 8 晶体表面。
( 作 用 能 ) 平衡距离
第八章材料的变形与断裂
质原子切变模量较大,对位错有斥力,反之切变模量较小时则有 吸力。
第八章材料的变形与断裂
间隙式的溶质原子 对于间隙式的溶质原子,当其溶于体心立方中,会造成
不对称畸变。这时,溶质原子不仅和刃型位错,也和螺型位 错有强烈的交互作用,因而产生了很强的固溶强化效果。
第八章材料的变形与断裂
2)双交滑移机制 高层错能的面心立方和体心立方,变形时的 位错增殖主要是靠双交滑移。 见书上P342
第八章材料的变形与断裂
合金的变形与强化
固溶强化: 合金在形成单相固溶体后,变形时的临界切应力都高于
纯金属。
置换式的溶质原子,考虑溶质原子与溶剂原子尺寸的差别。 尺寸相差越大,溶解度越小,强化效果越大。 原子尺寸差别(或称错配)所引起的晶格畸变,会产生一
第八章材料的变形与断裂
三. 位错的增殖
1)F-R源(弗兰克-瑞德源) 塑性变形的过程中,尽管位错移出晶体产生滑移
台阶,但位错的数量(位错密度)却在不断的增加,这 是因为在外应力作用下发生塑性变形时位错会发生增 殖。
例如
第八章材料的变形与断裂
位错的增殖
利用Fnak-Read源说明增殖的过程。若滑移面上 有一段位错,CD两点钉住不可滑移,在外力作用下位 错应向右移动,这段位错将弯曲、扩张,相遇为异号 位错相消,产生一位错环,内部CD段还存在。反复可 生成一系列的位错环,扩展到晶体外的产生滑移台阶 可为柏氏矢量的整数倍。
3 消除:去应力退火。
第八章材料的变形与断裂
金属的断裂
一. 理论断裂强度 利用原子间结合力的模型可以求出金属的理论断裂强度。
第八章材料的变形与断裂
变形与断裂总结
第一章:单向静拉伸试验:是应用最广泛的力学性能试验方法之一。
1)可揭示材料在静载下的力学行为(三种失效形式):即:过量弹性变形、塑性变形、断裂。
2)可标定出材料最基本力学性能指标:如:屈服强度、抗拉强度、伸长率、断面收缩率等。
拉伸力-伸长曲线拉伸曲线:拉伸力F -绝对伸长△L 的关系曲线。
在拉伸力的作用下,退火低碳钢的变形过程四个阶段:1)弹性变形:O ~e2)不均匀屈服塑性变形:A ~C3)均匀塑性变形:C ~B4)不均匀集中塑性变形:B ~k5)最后发生断裂。
k ~第二章:弹性变形:当外力去除后,能恢复到原形状或尺寸的变形。
特点:可逆性、单值线性、同相位、变形量小本质:都是构成材料的原子(离子)或分子从平衡位置产生可逆位移的反映。
弹性模量E :是表征材料对弹性变形的抗力,工程称材料的刚度.E 值越大,在相同应力下产生的弹性变形就越小。
弹性模量是结构材料的重要力学性能指标之一。
影响因素:1、键合方式 2、原子结构 3、晶体结构 4、化学成分 5.微观组织 6.温度 弹性模量 E 与切变模量 G 关系:(其中: ν-泊松比。
)比例极限σp :是材料弹性变形按正比关系变化的最大应力,即拉伸应力一应变曲线上开始偏离直线时的应力值。
弹性极限:材料由弹性变形过渡到弹-塑性变形时的应力,当应力超过弹性极限σe 后,便开始产生塑性变形。
(比例极限σp 和弹性极限σe 与屈服强度的概念基本相同,都表示材料对微量塑性变形的抗力,影响因素也基本相同。
)弹性比功ae :(弹性比能、应变比能)表示材料在弹性变形过程中吸收弹性变形功的能力。
一般用材料开始塑性变形前单位体积吸收的最大弹性变形功表示。
物理意义:吸收弹性变形功的能力。
几何意义:应力σ -应变ε曲线上弹性阶段下的面积。
欲提高材料的弹性比功:提高σe ,或降低 E2E G ν=(1+)弹簧钢:含碳较高并添加Si 、Mn 等合金元素强化基体,经淬火+中温回火获得回火托氏体组织及冷变形强化,以提高其弹性极限,使弹性比功ae 和弹性提高。
材料力学笔记(第八章)
材料力学(土)笔记第八章 组合变形及连接部分的计算1.概 述工程实际中,构件在荷载作用下往往发生两种或两种以上的基本变形若几种变形所对应的应力(变形)属于同一数量级,则构件的变形成为组合变形对于组合变形下的构件,在线弹性、小变形条件下,可按构件的原始形状和尺寸进行计算 可先将荷载简化为符合基本变形外力作用条件的外力系分别计算构件在每一种基本变形下的内力、应力或变形利用叠加原理,综合考虑各基本变形的组合情况以确定构件的危险截面、危险点的位置及危险点的应力状态,并据此进行强度计算 若构件的组合变形超过了线弹性范围,或虽在线弹性范围内但变形较大则不能按其初始形状或尺寸进行计算,不能用叠加原理工程实际中,经常需要将构件相互连接铆钉、螺栓、键等起连接作用的部件,统称为连接件连接件(或构件连接处)的变形往往比较复杂,而其本身尺寸都比较小在工程设计中,通常按照连接的破坏可能性采用既能反映受力的基本特征,又能简化计算的假设,计算其名义应力然后根据直接试验的结果,确定其相应的许用应力,来进行强度计算这种简化计算的方法,称为工程实用计算法2.两相互垂直平面内的弯曲对于横截面具有对称轴的梁当横向外力或外力偶作用在梁的纵向对称面内时,梁发生对称弯曲 这是,梁变形后的轴线是一条位于外力所在平面内的平面曲线碰到双对称截面梁在水平和垂直两纵向对称平面内同时承受横向外力的作用情况这时梁分别在水平纵对称面(Oxz 平面)和铅垂纵对称面(Oxy 平面)内发生对称弯曲 在梁的任意横截面m-m 上,由1F 和2F 引起的弯矩值依次为1y M F x = 和 2()z M F x a =-梁的任一横截面m-m 上任一点(,)C y z 处与弯矩y M 和z M 相应的正应力分别为'yyM z I σ= 和 ''z z M y I σ=- 由叠加原理,在1F 和2F 同时作用下,截面m-m 上C 点处的正应力为 '''y z y z M M z y I I σσσ=+=-式中y I 和z I 分别为横截面对于两对称轴y 和z 的惯性矩y M 和z M 分别是截面上位于水平和铅垂对称平面内的弯矩且其力矩矢量分别与y 轴和z 轴的正向相一致在具体计算中,也可先不考虑弯矩和坐标的正负号,以其绝对值代入然后根据梁在荷载分别作用下的变形情况,判断由其引起该点处正应力的正负号为确定横截面上最大正应力点的位置,需求截面上中性轴的位置由于中性轴上各点处的正应力均为零,令0y 、0z 代表中性轴上任一点的坐标则由上式可得中性轴方程000yz yzM M z y I I -=由上式可见,中性轴是一条通过横截面形心的直线其与y 轴的夹角为θ,且tan tan y y z I I z M y M I I θϕ==⨯= 对于圆形、正方形等y z ,有由于梁各横截面上的合成弯矩M 所在平面的方位一般不相同所以,虽然每一截面的挠度都发生在该截面的合成弯矩所在平面内梁的挠曲线一般仍是一条空间曲线梁的挠曲线方程仍应分别按两垂直平面内的弯曲来计算,不能直接用合成弯矩计算 确定中性轴位置后,作平行于中性轴的两条直线,分别与横截面周边相切于两点该两点即分别为横截面上拉应力和压应力为最大的点对于工程中常用的矩形、工字型等截面梁其横截面都有都有两个互相垂直的对称轴,且截面的周边具有棱角故横截面上的最大正应力必发生在截面的棱角处于是,可根据梁的变形情况,直接确定截面上最大拉、压应力点的位置,无需定出中性轴 在确定了梁的危险截面和危险点的位置,并算出危险点处的最大正应力之后由于危险点处于单轴应力状态,可按正应力强度条件计算横截面上的切应力,对于一般实体截面梁,其数值较小,可不必考虑3.拉伸(压缩)与弯曲3.1 横向力与轴向力共同作用等直杆受横向力和轴向力共同作用时,杆将发生弯曲与拉伸(压缩)组合变形对于弯曲刚度EI 较大的杆,由于横向力引起的挠度与横截面的尺寸相比很小因此,由轴向力在相应挠度上引起的弯矩可略去不计可分别计算由横向力和轴向力引起的杆横截面上的正应力按叠加原理求其代数和,即得在组合变形下,杆横截面上的正应力max ,max N t t b F M A Wσσσ=+=+ 当材料的许用拉应力和许用压应力不相等时杆内的最大拉应力和最大压应力必须分别满足杆件的拉、压强度条件对于弯曲刚度EI 较小的杆件,在压缩和弯曲组合变形下轴向压力引起的附加弯矩较大,且其转向与横向力引起的弯矩相同因此不能按杆的原始形状来计算,叠加原理也不再适用3.2 偏心拉伸(压缩)作用在直杆上的外力,当其作用线与杆的轴线平行但不重合时,将引起偏心拉伸或偏心压缩 横截面具有两对称轴的等直杆承受矩截面形心为e (称为偏心距)的偏心拉力F 为例 先将作用在杆端截面上A 点处的拉力F 向截面形心1O 点简化得到轴向拉力F 和力偶矩Fe ,将力偶矩分解为ey M 和ez Msin ey F M Fe Fz α==cos ez F M Fe Fy α==式中,坐标轴y 、z 为截面的两个对称轴F y 、F z 为偏心拉力F 作用点(A 点)的坐标于是的得到一个包含轴向拉力和两个在纵对称面内的力偶的静力等效力系此力系将分别使杆发生轴向拉伸和在两相互垂直的纵对称面内的纯弯曲当杆的弯曲刚度较大时,同样可按叠加原理求解在上述力系作用下任一横截面n-n 上的任一点(,)C y z 处相应于轴力N F F =和两个弯矩的正应力,由叠加原理,的C 点处的正应力F F y zFz z Fy y F A I I σ⨯⨯=++ 利用惯性矩与惯性半径间的关系 2y yI A i =⨯,2z z I A i =⨯ 式子可改写为22(1)FF y zz z y y F A i i σ=++ 上式是一个平面方程,表明正应力在横截面上按线性规律变化应力平面与横截面相交的直线(沿该直线0σ=)就是中性轴令0y 、0z 代表中性轴上任一点的坐标,代入即得中性轴方程002210F F y z z y z y i i ++= 在偏心拉伸(压缩)情况下,中性轴是一条不通过截面形心的直线为定出中性轴的位置,可利用其在y 、z 两轴上的截距y a 和z a在上式中,令00z =,相应的0y 即为截距y a ,而令00y =,相应的0z 即为截距z a 由此求得2z y F i a y =-,2y z Fi a z =- A 在第一象限内,F y 、F z 都为正值,则y a 、z a 均为负值即中性轴与外力作用点分别处于截面形心的相对两侧对于周边无棱角的截面,可作两条与中性轴平行的直线与横截面的周边相切两切点即为横街面上最大拉应力和最大压应力所在的危险点将危险点的坐标代入公式即可求得最大拉应力和最大压应力对于周边具有棱角的截面,其危险点必定在截面的棱角处,并可根据杆件的变形来确定 最大拉应力,max t σ和最大压应力,max c σ,其值为,max ,max t F F c yz Fz Fy F A W W σσ⎫⎪=±±⎬⎪⎭ 式子对箱型、工字形等具有棱角的截面都适用当外力的偏心距(F y 、F z )较小时,中性轴可能不与横截面相交即横截面就可能不出现与轴力异号的应力由于危险点仍处于单轴应力状态,可按正应力的强度条件进行计算3.3 截面核心如前所述,当偏心轴向力F 的偏心距较小时,杆横截面上就可能不出现异号应力 因此当偏心压力F 的偏心距较小时,杆的横截面上可能不出现拉应力外力作用点离形心越近,中性轴距形心就越远当外力作用点位于截面形心附近的一个区域内时,就可以保证中性轴不与横截面相交,这个区域就称为截面核心当外力作用在截面核心的边界上时相对应的中性轴正好与截面的周边相切,利用这一关系就可确定截面核心的边界为确定任意形状截面的截面核心边界,可将与截面周边相切的任一直线视作中性轴 在y 和z 形心主惯性轴上的截距分别为1y a 和1z a可确定与该中性轴对应的外力作用点1按上述方法求得与其对应的截面核心边界上的点2、3、…的坐标连接这些点所得到的一条封闭曲线,即为所求截面核心的边界该边界曲线所包围的带阴影线的区域,即为截面核心圆截面对于圆心O 时极对称的,因此,截面核心的边界对于圆心也是极对称的为一圆心为O 的圆作一条与圆截面周边相切于A 点的直线,将其视为中性轴取OA 为y 轴,于是,该中性轴在y 和z 形心主惯性轴上的截距为1/2y a d =, 1z a =∞圆截面的222/16y z i i d ==,将其代入公式即得与其对应的截面核心边界上点1的坐标2211/16/28z y y i d d a d ρ=-=-=-,2110y z z i a ρ=-= 从而可知,截面核心边界是一个以O 为圆心,/8d 为半径的圆对于边长为b h ⨯的矩形截面,两对称轴y 和z 为截面的形心主惯性轴将与AB 向切的直线①视作中性轴,其在y 和z 轴上的截距分别为,矩形截面2212yb i =,2212z h i = 将上式代入,即得中性轴①对应的截面核心边界点上点1的坐标为2211/12/26z y y i h h a h ρ=-=-=-, 2110y z z i a ρ=-= 同理,分别将与矩形边界相切的直线②、③、④视作中性轴可得对应的截面核心边界上点2、3、4的坐标从而得到了截面核心边界上的4个点当中性轴从截面的一个侧边绕截面的顶点旋转到其相邻边时 将得到一系列通过边界点B 但斜率不同的中性轴而B 点的坐标(,)B B y z 是一系列中性轴共有的 将其代入中性轴方程,经改写后得2222110F F B B B B F F y z y z z y z y z y z y i i i i ++=++= 上式中,B y 、B z 为常数 因此该式就可看作时表示外力作用点坐标(,)F F y z 间关系的直线方程即当中性轴绕B 点旋转时,相应的外力作用点移动的轨迹是一条连接点1、2的直线将1、2、3、4四点中相邻的两点连以直线,即得矩形截面的截面核心边界截面核心为位于截面中央的菱形对于具有棱角的截面,均可按照上述方法确定其截面核心对于周边有凹进部分的截面(例如槽型或T 字型截面等)在确定截面核心边界时,应该注意不能取与凹进部分的周边相切的直线作为中性轴,因为这种直线显然约横截面相交4.扭转与弯曲一般的传动轴通常发生扭转与弯曲组合变形讨论杆件发生扭转与弯曲组合变形时的强度计算直径为d 的等直圆杆AB ,A 端固定,B 端具有与AB 成直角的刚臂,并受铅垂力F 作用,将F 简化为一作用于杆端截面形心的横向力F 和一作用于杆端的力偶矩e M Fa = 杆AB 将发生弯曲与扭转组合变形分别作杆的弯矩图和扭矩图,可见杆的危险截面为固定端截面,内力分量分别为M Fl =, e T M Fa ==由弯曲和扭转的应力变化规律可知危险截面上的最大弯曲正应力σ发生在铅垂直径的上、下两端点对于许用拉应力,压应力相等的塑性材料来说,该两点的危险程度相同 研究任一点,围绕该点分别用横截面、径向纵截面和切向纵截面截取单元体 该点应力状态如图所示,可见该点处于平面应力状态,其三个主应力为132σσσ⎫=⎬⎭ 20σ= 对于塑性材料制成的杆件,选用第三或第四强度理论来建立强度条件用第三、第四强度理论,将上述各应力代入向相应的应力表达式求得相当应力后,即可根据材料的许用应力[]σ来建立强度条件,对杆进行强度计算 其中弯曲正应力/M W σ=,扭转切应力/p T W τ=,对于圆截面杆2p W W =截面周边各点处弯曲正应力的数值和正负号都将随着轴的转动而交替变化这种应力称为交变应力,交变应力下工作的构件另有相应的计算准则5.连接件的实用计算法5.1 剪切的实用计算设两块钢板用螺栓连接后承受拉力F螺栓在两侧面上分别收到大小相等、反向相反、作用线相距很近的两组分布力系的作用 螺栓在这样的作用下,将沿两侧外力之间,并与外力作用线平行的截面m-m 发生相对错动称为剪切面应用截面法,可得剪切面上的内力,即剪力s F在剪切实用计算中,假设剪切面上各点处的切应力相等 于是剪切面上的名义切应力为S sF A τ=式中s A 为剪切面面积,s F 为剪切面上的剪力 通过试验得到剪切破坏时材料的极限切应力u τ,除以安全因数,得许用应力[]τ 剪切强度表示为[]S sF A ττ=≤ 名义切应力并不反映剪切面上切应力的精确理论值只是剪切平面上的平均切应力但对于低碳钢等塑性材料材料制成的连接件,变形较大而临近破坏时剪切面上的切应力将逐渐趋于均匀而且满足剪切强度条件式,不至于发生剪切破坏,从而满足工程需要对于大多数的连接件来说,剪切变形及剪切强度时主要的5.2 挤压的实用计算螺栓连接中,在螺栓与钢板相互接触的侧面上,将发生彼此间的局部承压现象,称为挤压 在接触面上的压力,称为挤压力,并记为bs F挤压力可根据被连接件所受的外力,由静力平衡条件求得当挤压力过大时,可能引起螺栓压扁或钢板在孔缘压皱,从而导致连接松动失效在挤压实用计算中,假设名义挤压应力的计算式为bs bs bsF A σ= 式中,bs F 为接触面上的挤压力;bs A 为计算挤压面面积当接触面为圆柱面时,计算挤压面面积bs A 取为实际接触面在直径平面上的投影面积 理论表明,这类圆柱状连接件与钢板孔壁间接触面上的理论挤压应力沿圆柱的变化情况如图 计算所得的名义挤压应力与接触面中点处的最大理论挤压应力值相近当连接件与被连接构件的接触面为平面时,计算挤压面面积即为实际接触面的面积 通过试验,按名义挤压应力公式得到的材料的极限挤压应力,除以安全因数确定许用挤压应力[]bs σ,则挤压强度条件可表达为[]bs bs bs bsF A σσ=≤ 注意,挤压应力是在连接件和被连接件之间相互作用的当两者材料不同时,应校核其中许用挤压应力较低的材料的挤压强度6.铆钉连接的计算铆钉连接在建筑结构中被广泛采用铆接的方式主要有搭接、单盖板对接和双盖板对接三种搭接和单盖板对接中的铆钉具有一个剪切面(称为单剪)双盖板对接中的铆钉具有两个剪切面(称为双剪)6.1 铆钉组承受横向荷载在搭接和单盖板对接中,由铆钉的受力可见铆钉(或钢板)显然将发生弯曲在铆钉组连接中,在弹性变形阶段两端铆钉的受力与中间铆钉的受力并不完全相同 为简化计算,并考虑到连接在破坏前将发生塑性变形,在铆钉计算中假设①不论铆接的方式如如何,均不考虑弯曲的影响②若外力的作用线通过铆钉组横截面的形心,且同一组内各铆钉的材料与直径均相同,则每个铆钉的受力相等 按照上述假设,即可得每个铆钉的受力1F 为1F F n= 式中,n 为铆钉组中的铆钉数求得每个铆钉的受力1F 后,即可分别校核其剪切强度和挤压强度被连接件由于铆钉孔的削弱,其拉伸强度应以最弱截面(轴力较大,截面积较小)为依据 不考虑集中应力的影响对于销钉或螺栓连接,其分析计算方法与铆钉连接相同6.2 铆钉组承受扭转荷载承受扭转荷载的铆钉组,由于被连接件(钢板)的转动趋势每一铆钉的受力将不再相同令铆钉组横截面形心为O 点 假设钢板的变形不计,可视为刚体于是,每一铆钉的平均切应变与该铆钉截面中心至O 点的距离成正比,其方向垂直于该点与O 点的连线由合力矩定理,每一铆钉上的力对O 点力矩的代数和等于钢板所受的扭转力偶矩e M ,即 e i i M Fe Fa ==∑式中,i F 为铆钉i 所受的力;i a 为该铆钉截面中心至铆钉组截面形心的距离对于承受偏心横向荷载的铆钉组可将偏心荷载F 向铆钉组截面形心O 简化得到一个通过O 点的荷载F 和一个绕O 点旋转的扭转力偶矩e M Fe =若同一铆钉组中每一铆钉的材料和直径均相同则可分别计算由力F 引起的力'i F 和由转矩e M 引起的力''i F铆钉i 的受力为'i F 和''i F 的矢量和求得铆钉i 的受力i F 后,可分别校核受力最大的铆钉的剪切强度和挤压强度。
第八章材料蠕变
34
(3)晶界滑动蠕变机理 晶界在外力作用下,会发生相对滑动变形,但在常温下晶界变形极不明显,可以忽略不计。 在高温蠕变条件下,由于晶界强度降低,晶界的相对滑动引起的变形量很大,有时甚至占总蠕变 变形量的一半,从而产生明显的蠕变变形。
35
晶界滑动示意图
晶格畸变区
晶粒1
晶粒1
39
断裂方式:晶间断裂是蠕变断裂的普遍形式,高温低应力下情况更是如此。 等强温度: 晶界和晶内强度相等的温度。 因为温度升高,多晶体晶内 及晶界强度都随之降低,但后者 降低速率更快,造成高温下晶界 的相对强度较低的缘故。随应变速度下降,等强温度降低,从而使晶界断裂倾向增大。
晶粒2
晶粒2
36
晶界变形-----晶界滑动和迁移
● ●●
37
❖ 晶界的变形是由晶界的滑动和迁移交替进行的过程。 ❖ 晶界的滑动对变形产生直接的影响,晶界的迁移虽不提供变形量,但它能消除由于晶界滑动而在晶界
附近产生的晶格畸变区,为晶界的进一步滑动创造条件。 ❖ 因此,可以认为晶界滑动是硬化过程,而晶界迁移是软化过程。
第八章材料蠕变
温度对材料的力学性能影响很大,而且不同材料的力学性能随温度变化的规律不同。 金属材料:随着 温度 T 的升高---❖ 强度极限逐渐降低。 ❖ 断裂方式由穿晶断裂逐渐向沿晶断裂过渡。 ❖ 常温下可用来强化材料的手段,如加工硬化、固溶强化及沉淀强化等,强化效果逐渐削弱甚至消失。 陶瓷材料: ❖ 常温下脆性断裂;而在高温,借助于外力和热激活作用,变形的一些障碍得以克服,材料内部质点发
TL 20℃
20℃ 160℃ 341℃ 1091℃
5
8.1.1 蠕变现象
8.1 蠕变现象和蠕变曲线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
名词解释
(1)加工硬化(变形强化):当金属外加应力超过屈服强度后,随着变形程度的增加,变形的抗力也增加,要继续变形,必须增加外力,这种现象就叫加工硬化。
(2)颈缩:当应力达到抗拉强度时,试样不在均匀伸长,而是试样局部地方截面开始变细。
(3)位错宽度:
(4)孪晶变形:晶体在切应力作用下沿着一定的晶面和晶向,在一个区域内发生连续顺序的切变,变形导致这部分的晶体取向改变了。
(5)多滑移:在多个滑移系上同时或交替进行的滑移。
(6)交滑移:晶体在两个或者多个滑移面上沿同一滑移方向进行的滑移。
(7)发生多系滑移时,在两个相交滑移面上运动的位错必然会互相交截,原来一直线位错经过交截后就会出现弯折部分,如果弯折部分仍在滑移面上,就叫扭折,若弯折部分不再滑移面上,就叫割阶。
(8)派纳力:在理想晶体中位错在点阵周期场中运动时所需克服的阻力
(9)纤维组织:金属经过冷变形后,等轴状晶粒沿受力方向拉长,其中的夹杂物或者第二相也随之拉长。
(10)形变织构:金属在形变时,晶体的滑移面会移动,使滑移层逐渐转向与拉力轴平行。
原来的各个晶粒是任意取向的,现在由于晶粒的转动使各个晶粒的取向趋于一致,这就形成了晶体的择优取向。
(11)回复:在加热温度较低时,由于金属中的点缺陷及位错近距离迁移而引起的晶体某些变化。
(12)再结晶:冷变形金属由拉长的变形晶粒生成无畸变的新的等轴晶粒的过程。
(13)二次再结晶:
(14)热变形:金属在再结晶温度以上的加工变形。
(15)蠕变:材料在高温下的变形不仅与应力有关,而且和应力作用的时间有关。
(16)应变时效:低碳钢经过少量预变形后,如果去载后立即再行加载则不会出现明显的屈服平台;若在室温下放置一较长的时间或在低温下经过短时加热后在进行拉伸试验,则屈服点又复出现,且屈服应力提高。
(17)第二相强化:当第二相以细小弥散的微粒均匀分布于基体相中时,将会产生显著的强化作用。
(18)固溶强化:合金在形成单向固溶体后,变形时的临界切应力都高于纯金属,这叫做固溶强化。
(19)再结晶后晶粒的大小由变形度和退火温度决定。
(20)回复和再结晶的驱动力是弹性畸变能,晶粒长大的驱动力是自身界面能。
填空
(1)位错宽度越窄,界面能越小,弹性畸变能越高,位错运动需克服的能垒越大,位错越难运动,派纳力越大。
(2)位错宽度主要取决于结合键的本性和晶体结构。
(3)位错只有沿着原子排列最紧密的面及原子密排方向上运动,派纳力才最小。
面心立方金属和沿几何面(0001)滑移的密排六方金属,派纳力最小。
(4)最容易发生交滑移的是体心立方结构。
(5)任意两种类型位错相互交割时,只要形成割阶,一定为刃型割阶,割阶的大小和方向取决于穿过位错的柏氏矢量。
(6)固溶强化,两者原子的尺寸差别越大,溶解度越小,强化效果越大。
(7)低碳钢的屈服现象是由于柯氏气团和位错增殖两个因素共同作用的结果。
(8)第二相强化,当第二相尺寸较小且与基体保持共格时,能被位错切过;当第二相尺寸较大且与基体失去共格时,位错绕过第二相。
(9)变形强化和其他强化方式相比,能最有效提高强度,但塑性和韧性降低的也最多。
(10)金属冷变形,残余拉应力会降低表面疲劳强度;残余压应力会提高表面疲劳强度。
(11)冷变形金属加热时经历回复、再结晶、晶粒长大三个阶段。
(12)多晶体的变形有两个特点:变形的传递,变形的协调。
(13)位错的增殖方式有:弗兰克—瑞德源、双交滑移机制。
(14)再结晶在局部高能量区域内,以多边化形成的亚晶为基础形核。
简答
1.简述变形的传递过程?
当一个晶粒位错在某一滑移系上动作后,在位错遇到晶界时便塞积起来,位错在塞积产生了大的应力集中;当应力集中能使位错塞积产生的应力集中得以松弛,这就是滑移的传播过程。
2.用霍尔佩奇公式解释晶粒越细,材料强度越大和粗晶粒容易萌生裂纹?
一个粗晶粒一个细晶粒,在同样的外加切应力作用下,在晶界附近塞积的位错数为粗晶粒多细晶粒少,这样,粗晶粒产生的应力集中就更大,更容易使相邻晶粒的位错源开动,因而粗晶粒的屈服强度较低。
但是如果应力集中不能被松弛,则在近邻晶粒某一特定方向产生很大的拉应力,形成裂纹,导致粗晶粒容易萌生裂纹,断裂时显示的塑性也较低。
3.请对比回复与再结晶的回复动力学?
回复:(1)没有孕育期。
(2)在一定的温度下,初期的回复速度很大,随后逐渐变慢,并趋于0。
(3)每一温度下的回复程度有一极限值,退火温度越高,极限值越高,而且所需时间也越短。
再结晶:(1)在一个固定温度下,转变曲线形如S,发生再结晶需要孕育期,退火温度越高,孕育期越短。
(2)开始时,转变速率很低,随着转变量的增加,转变速率逐渐加快,在转变量为50%速率最快,然后变慢。
(3)在固定温度下,随着时间的延长,再结晶能完全进行。
4.试说明不同温度下的回复机制
低温回复:主要发生点缺陷的迁移,导致点缺陷明显下降,电阻率相应下降。
中温回复:发生了位错的运动和重新分布。
通过位错滑移,同一滑移面上的异号位错相互吸引而抵消,使得位错密度略有降低。
高温回复:刃型位错获得足够的能量发生攀移。
导致滑移面上不规则位错重新分布,刃型位错垂直排列成墙,显著降低弹性应变能,并且形成了亚晶。
5.影响再结晶的因素
(1)在给定温度下发生再结晶需要一个最小变形量,即临界变形度,低于此变形度,不能发生再结晶。
(2)变形度越小,开始再结晶的温度就越高,即临界变形度随退火温度的升高而减小。
(3)再结晶后晶粒大小主要决定于变形程度。
变形量越大,再结晶后的晶粒越细。
(4)微量杂质元素可明显升高再结晶温度或者推迟再结晶过程的进行。
(5)第二相的影响。
当第二相尺寸较大,间距较宽时,促进再结晶;Mn当第二相尺寸较小且又较密集时,会阻碍再结晶的进行。
Nb、V、Al (6)原始晶粒越细,或者退火时间增长,都会降低再结晶温度。
6. 有一70MPa 应力作用在fcc 晶体的[001]方向上,求作用在(111)和(111)滑移系上的分切应力。
滑移系:
滑移系:
(7) 有一bcc 晶体的[111]滑移系的临界分切力为60MPa ,试问在[001]和
[010]方向必须施加多少的应力才会产生滑移?
方向:
故在此方向上无论施加多大应力都不能产生
滑移。
方向:
[]110[]
101
()]110[111)(577.283270cos cos MPa =⋅==φλστ()[]101 1110
30
70cos cos =⨯=
=φλστ)011([]001∞=⨯==
03160cos cos φλτσc []010)(97.146213160cos cos MPa c =⨯==
φλτσ。
