10基本初等函数知识点总结

合集下载

初等基本函数知识点总结

初等基本函数知识点总结函数是数学中最基本的概念之一，它在数学的各个分支中都有着重要的应用。

初等基本函数是指在初等数学范围内常见的基本函数，包括常数函数、一次函数、二次函数、指数函数、对数函数、幂函数、三角函数等。

本文将对这些初等基本函数的概念、性质等进行总结和介绍。

一、常数函数常数函数的定义是f(x) = c （c为常数）。

这里的c就是常数函数的函数值，它是一个常数，和x的取值无关。

在坐标系中，常数函数的图象是一条水平的直线，它的斜率为0。

常数函数的性质有：1. 常数函数的图象是一条水平的直线。

2. 常数函数的定义域是全体实数集R，值域为{c}。

3. 常数函数的导数为0，即f'(x) = 0。

4. 常数函数是一个一一对应的函数。

5. 常数函数是奇函数，偶函数，周期函数，增函数，减函数等的特殊情况。

二、一次函数一次函数的定义是f(x) = kx + b （k和b为常数，k≠0）。

在坐标系中，一次函数的图象是一条通过点P(k，b)的直线，它的斜率为k，截距为b。

一次函数的性质有：1. 一次函数的图象是一条直线，斜率k决定了直线的倾斜程度，截距b决定了直线与y轴的交点位置。

2. 一次函数的定义域是全体实数集R，值域是一切实数集R。

3. 一次函数的导数为k，即f'(x) = k。

4. 当k>0时，一次函数是增函数；当k<0时，一次函数是减函数；当k=0时，一次函数是常数函数。

5. 一次函数是一个奇函数，因为f(-x) = -kx + b = -f(x)。

三、二次函数二次函数的定义是f(x) = ax^2 + bx + c （a、b和c为常数，a≠0）。

二次函数的图象是一个开口向上或者向下的抛物线，它的开口方向由a的正负决定。

当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

二次函数的性质有：1. 二次函数的图象是一个抛物线，它关于y轴对称，对称轴方程为x = -b/2a。

10基本初等函数知识点总结

基本初等函数知识点总结一、指数函数的概念（1）、指数函数的定义一般地，函数xy a =（0a >，且1a ≠）叫做指数函数，其中x 是自变量，函数的定义域是R 。

（2）、因为指数的概念已经扩充到有理数和无理数，所以在底数0a >且1a ≠的前提下，x R ∈。

（3）、指数函数x y a =（0a >且1a ≠）解析式的结构特征 1、底数：大于0且不等于1的常数。

2、指数：自变量x 。

3、系数：1。

二、指数函数的图象与性质一般地，指数函数xy a =（0a >，且1a ≠）的图象与性质如下表：三、幂的大小比较方法比较幂的大小常用方法有：（1）、比差（商）法；（2）、函数单调性法；（3）、中间值法：要比较A 与B 的大小，先找一个中间值C ，再比较A 与C 、B 与C 的大小，由不等式的传递性得到A 与B 之间的大小。

四、底数对指数函数图象的影响（1）、对函数值变化快慢的影响1、当底数1a >时，指数函数xy a =是R 上的增函数，且当0x >时，底数a 的值越大，函数图象越“陡”，说明其函数值增长得越快。

2、当底数01a <<时，指数函数xy a =是R 上的减函数，且当0x <时，底数a 的值越小，函数图象越“陡”，说明其函数值减小得越快。

（2）、对函数图象变化的影响指数函数x y a =与x y b =的图象的特点：1、1a b >>时，当0x <时，总有01x x a b <<<；当0x =时，总有1x x a b ==；当0x >时，总有1x x a b >>。

2、01a b <<<时，当0x <时，总有1x x a b >>；当0x =时，总有1x x a b ==；当0x >时，总有01x x a b <<<。

基本初等函数知识总结

1
1
0
x
y loga x
y log2 x
y log3 x y log1 x x
3
y log1 x
2
性质
底数互为倒数的两个指数
一函数的图象关于y轴对称。
底数互为倒数的两个对数函数的图象关于x轴对称。
性
质在 y轴的右边看图象,图象二越高底数越大.即底大图高
在 x=1的右边看图象,图象越高底数越小.即底小图高
幂函数
函数y=xα叫做幂函数, 其中x是自变量, α是常数.
对于幂函数，我们只
讨论 1, 2, 3, 1 , 1
2
时的情形
y y x3
y x2
1 -1
O1
-1
yx
1
y x2
y1 x
x
幂函数的性质
函数性质
定义域值域
奇偶性
单调性
公共点
y=x y=x2
R
R
R [0,+∞) 奇偶
增
[0,+∞)增
n am
同时: 0的正分数指数幂等于0； 0的负分数指数幂
没有意义
2.有理数指数幂的运算性质
a a a r s
r s(a 0,r, s Q) 同底数幂相乘,底数不变指数相加
r
a a r -s (a 0,r, s Q) 同底数幂相除, 底数不变指数相减 as
(a ) a r s
rs (a 0,r, s Q) 幂的乘方底数不变,指数相乘
o
x
①x∈ (0,+∞) ； ② y∈ R;
③过定点(1, 0)
性 ④当x＞ 1时,y＞ 0, 质 0＜ x＜ 1时, y＜ 0

基本初等函数知识点归纳

基本初等函数知识点归纳1.常值函数：常值函数是指在定义域上的值始终相同的函数。

常见的常值函数有恒等于0的零函数和恒等于1的单位函数。

常值函数的图像是一条与x轴平行的直线。

2.幂函数：幂函数是指形如y=x^n的函数，其中n是一个实数。

当n 为正偶数时，函数的图像在原点右侧递增；当n为正奇数时，图像在全定义域递增；当n为负数时，图像在全定义域递减。

特殊地，当n为0时，函数为常值函数13.指数函数：指数函数是形如y=a^x的函数，其中a为正实数且a≠1、指数函数的图像可以是递增或递减的曲线，具体取决于底数a的大小关系。

当a>1时，函数递增；当0<a<1时，函数递减。

指数函数特点是它们的图像都经过点(0,1)。

4. 对数函数：对数函数是指形如y = log_a(x)的函数，其中a为正实数且a ≠ 1、对数函数是指数函数的反函数，因此它们的图像是关于y = x对称的。

对数函数的图像在定义域上递增，对数函数的唯一一个特殊点是(1,0)。

5. 三角函数：三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。

这些函数在三角学中起着重要的作用，并且它们的图像都是周期性的。

正弦函数和余弦函数的图像是一条在[-1,1]之间往复的波浪线，而正切函数和余切函数的图像是一条通过原点的无数个波浪线。

6. 反三角函数：反三角函数是三角函数的反函数。

反三角函数包括反正弦函数asin(x)、反余弦函数acos(x)、反正切函数atan(x)等。

它们的定义域和值域与所对应的三角函数的范围正好相反。

反三角函数的图像和所对应的三角函数的图像关于y = x对称。

以上是基本初等函数的主要内容，它们是数学中最常见的函数，不仅在实际问题中有着广泛的应用，而且还在高中数学的教学中起到了重要的作用。

通过对这些函数的学习与理解，可以更好地掌握数学知识，提高数学解题的能力。

专题10 基本初等函数(知识梳理)(新高考地区专用)(解析版)

专题10 基本初等函数（知识梳理）一、指数与指数函数(一)指数式的化简与求值1、化简原则：①化根式为分数指数幂；②化负指数幂为正指数幂； ③化小数为分数； ④注意运算的先后顺序。

提醒：有理数指数幂的运算性质中，其底数都大于零，否则不能用性质来运算。

2、结果要求：①题目以根式形式给出，则结果用根式表示；②题目以分数指数幂形式给出，则结果用分数指数幂形式表示；③结果不能同时含有根式和分数指数幂，也不能既有分母又有负分数指数幂。

例1-1．已知41<a ，则化简42)14(-a 的结果是( )。

A 、a 41-- B 、14--a C 、14-a D 、a 41- 【答案】D【解析】a a a 41)41()14(4242-=-=-，故选D 。

变式1-1．化简3a a ⋅-的结果是( )。

A 、65a - B 、65a -- C 、65a - D 、52a -【答案】B【解析】∵0≤a ，则656565312131213)()()()()(a a a a a a a a a --=--=--=-⋅--=⋅-=⋅-，故选B 。

变式1-2．已知31=+-x x ，求下列各式的值：(1)2121-+xx ；(2)22-+x x ；(3)2323-+xx 。

【解析】(1)∵52)(2)()(1221212122122121=++=+⋅+=+----x x xxx x xx ，∴52121±=+-x x ，又由31=+-x x 得0>x ，∴52121=+-xx ；(2)72)(2122=-+=+--x x x x ； (3)]1))[((])())[(()()(12121221212122121213213212323-++=+⋅-+=+=+-------x x xx xxx x xx xx xx52)13(5=-=。

(二)指数函数的图像和性质1、定义：一般地，函数x a x f =)((0>a 且1≠a )叫做指数函数，其中x 是自变量。

基本初等函数定义及性质知识点归纳

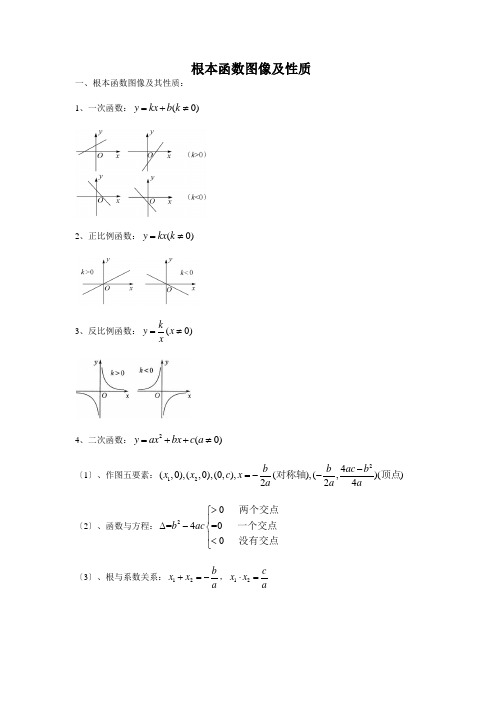
根本函数图像及性质一、根本函数图像及其性质： 1、一次函数：(0)y kx b k =+≠2、正比例函数：(0)y kx k =≠3、反比例函数：(0)ky x x=≠4、二次函数：2(0)y ax bx c a =++≠〔1〕、作图五要素：2124(,0),(,0),(0,),(),(,)()224b b ac b x x c x a a a -=--对称轴顶点〔2〕、函数与方程：2=4=00b ac >⎧⎪∆-⎨⎪<⎩两个交点一个交点没有交点〔3〕、根与系数关系：12b x x a +=-，12c x x a⋅=5、指数函数：(0,1)x y a a a =>≠且〔1〕、图像与性质：〔i 〕1()(0,1)x xy a y a a a==>≠与且关于y 轴对称。

〔ii 〕1a >时，a 越大，图像越陡。

(2)、应用：〔i 〕比拟大小：〔ii 〕解不等式： 1、回忆：〔1〕()mmmab a b =⋅ 〔2〕()mm m a a b b=2、根本公式：〔1〕m n m na a a+⋅= 〔2〕m m n n a a a-= 〔3〕()m n m na a ⨯=3、特殊:〔1〕01(0)a a =≠ 〔2〕11(0)aa a-=≠ 〔3〕1;0)na n a R n a =∈≥为奇数，为偶数，（4;0;0||a n aa aa a n ≥⎧⎧==⎨⎨-<⎩⎩为奇其中，为偶例题1：〔1〕22232[()()]3x x y xy y x x y x y ---÷；32235()()(5)x xy xy ÷（2）112032170.027()(2)1)79----+-；20.520371037(2)0.1(2)392748π--++-+（3例题2：〔1〕化简：212212)9124()144(+-+++a a a a（2）方程016217162=+⨯-xx 的解是。

基本初等函数知识点总结

基本初等函数知识点总结基本初等函数是数学中常见的一类函数，包括多项式函数、指数函数、对数函数、三角函数和反三角函数等。

它们在数学和实际问题中具有广泛的应用，因此掌握基本初等函数的性质和特点对于学习和理解数学非常重要。

下面将对基本初等函数的知识点进行总结。

一、多项式函数多项式函数是由常数乘以各个整数幂的变量构成的函数。

它的一般形式为：$$f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0$$其中，$a_n, a_{n-1},\dots,a_1,a_0$为常数，$n$为正整数，$a_n \neq 0$。

多项式函数的特点包括：定义域为实数集，值域为实数集，可导且导函数为次数比原来次数低一的多项式函数。

二、指数函数指数函数的一般形式为：$$f(x) = a^x$$其中，$a$为正实数且不等于1。

指数函数的特点包括：定义域为实数集，值域为正实数集，可导且导函数为$a^x\ln a$。

三、对数函数对数函数的一般形式为：$$f(x) = \log_a x$$其中，$a$为正实数且不等于1，$x$为正实数。

对数函数的特点包括：定义域为正实数集，值域为实数集，可导且导函数为$\frac{1}{x\ln a}$。

四、三角函数三角函数包括正弦函数、余弦函数、正切函数等。

它们的一般形式为：$$\sin x, \cos x, \tan x$$其中，$x$为实数。

三角函数的特点包括：定义域为实数集，值域为闭区间[-1, 1]，具有周期性，可导且导函数是相关三角函数的倍数。

五、反三角函数反三角函数包括反正弦函数、反余弦函数、反正切函数等。

它们的一般形式为：$$\arcsin x, \arccos x, \arctan x$$其中，$x$在相应的定义域内。

反三角函数的特点包括：定义域为闭区间[-1, 1]，值域为实数集，可导且导函数是相关函数的倒数。

基本初等函数的性质还包括：1. 奇偶性对于函数$f(x)$，如果对于定义域内的任意$x$，有$f(-x)=-f(x)$，则称函数为奇函数；如果对于定义域内的任意$x$，有$f(-x)=f(x)$，则称函数为偶函数。

基本初等函数知识总结

基本初等函数1.根式的运算性质：①当n 为任意正整数时，(n a )n =a②当n 为奇数时，nna =a ；当n 为偶数时，nna =|a|=⎩⎨⎧<-≥)0()0(a a a a2.分数指数幂的运算性质：)()(),()(),(Q n b a ab Q n m a a Q n m a a a n n n mn n m n m n m ∈⋅=∈=∈=⋅+ 3.指数式与对数式的互化：log b a a N N b =⇔=4.重要公式： 01log =a ，1log =a a 对数恒等式N aNa =log5.对数的运算法则：如果0,1,0,0a a N M >≠>>有log ()log log a a a MN M N =+；log log log aa a MM N N=-；log log n a a M n M = 6.对数换底公式：aNN m m a log log log =( a > 0 ,a ≠ 1 ，m > 0 ,m ≠ 1,N>0)7.指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a的图象与性质x=1x=1y=1y=1在(0,+∞)内是减函数在(0,+∞)内是增函数在(- ∞,+∞)内是减函数在(- ∞,+∞)内是增函数0<x<1时,y<0;x>1时，y>0.0<x<1时,y>0;x>1时，y<0.x<0时,0<y<1;x>0时，y>1.x<0时，y>1;x>0时，0<y<1.(1,0)，即x=1时，y=0.(0,1)，即x =0时，y=1.(0,+∞)(0,+∞)(- ∞,+∞)(- ∞,+∞) 单调性y 值区域过定点值域定义域图象a>10<a<1a>10<a<1a y=log a xy=a x函数11O O OO1axy1a xy1axy1a xy8.同底的指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a 互为反函数，其图象关于直线x y =对称9.幂函数y x α=的概念、图像和性质：结合函数y=x,y=x 2 ,y=x 3,y=12,y x y x--==,y=12x 的图像，了解它们的变化情况.①α＞0时，图像都过（0,0）、（1,1）点，在区间（0，+∞）上是增函数；注意α＞1与0<α＜1的图像与性质的区别.②α＜0时，图像都过（1,1）点，在区间（0，+∞）上是减函数；在第一象限内，图像向上无限接近y 轴，向右无限接近x 轴.③当x>1时，指数大的图像在上方.幂函数复习一、幂函数定义：形如)(R x y ∈=αα的函数称为幂函数，其中x 是自变量，α是常数。

基本初等函数知识点

基本初等函数知识点1.函数的定义：函数是一种特殊的关系，它将一个或多个输入数值映射到唯一的输出数值。

函数通常用f(x)来表示，其中x是输入变量，f(x)是输出变量。

函数可以用图形、符号或表格来表示。

2.定义域和值域：函数的定义域是所有可输入的数值的集合，而函数的值域是所有可能的输出数值的集合。

定义域可写作D(f)，值域可写作R(f)。

3.线性函数：线性函数是一种具有常数斜率的函数。

它的形式为f(x) = mx + b，其中m是斜率，b是截距。

线性函数的图形是一条直线。

4.幂函数：幂函数是一种形如f(x) = ax^b的函数，其中a和b是常数。

幂函数的图形通常是一条平滑的曲线。

当b为正偶数时，曲线在x轴的正半轴都是上升的；当b为负偶数时，曲线在x轴的正半轴是下降的。

5.指数函数：指数函数是以常数e为底的函数，它的形式为f(x)=a^x，其中a是指数底数。

指数函数的图形为一条逐渐增长（或逐渐减小）的曲线。

6.对数函数：对数函数是指以常数a为底的对数函数，它的形式为f(x) =log_a(x)，其中a为底数，x为函数的输入值。

对数函数是指数函数的反函数，即f(x) = a^x的反函数。

7.三角函数：三角函数是有关三角形角度与边长之间的关系的函数。

常见的三角函数包括正弦函数、余弦函数和正切函数。

三角函数的图形是周期性的曲线，周期为2π。

8.反函数：反函数是指满足f(f^(-1)(x))=x和f^(-1)(f(x))=x的函数对。

反函数可以通过交换函数的输入和输出得到。

9.复合函数：复合函数是指将一个函数的输出作为另一个函数的输入的函数关系。

复合函数可以表示为f(g(x))，其中g(x)是一个函数，f(x)是另一个函数。

10.奇偶函数：奇函数是满足f(-x)=-f(x)的函数，而偶函数是满足f(-x)=f(x)的函数。

奇函数的图形关于原点对称，偶函数的图形关于y轴对称。

这些是基本初等函数的一些常见知识点，掌握了这些知识点可以帮助你理解函数的基本概念、性质和图像，为进一步学习更高级的数学知识打下坚实的基础。

基本初等函数知识总结

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数（y=C）（1）定义域: D（f）＝（-∞，+∞）（2）值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0，C)在y轴上截距为C的直线(4 )图像：(5)周期性：常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T，f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义：形如y=x^a(a为常数）的函数，即以底数为自变量，幂为因变量，指数为常量的函数称为幂函数.(2)性质：在(0，+∞)内总有意义①当α＞0时函数图像过点(0，0)和(1，1)，在(0，+∞)内单调增加且无界②当α＜0时函数图像过点(1，1)，在(0，+∞)内单调减少且无界(3)图像：3.指数函数y=a^x(a>0且a≠1)(1)定义域：x∈R(2)值域：(0，+∞)(3)性质：①单调性：1.当0＜a＜1时，在(-∞，+∞)内单调减少 2.当a ＞1时，在(-∞，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(4)图像：①由指数函数y=a^x与直线x=1相交于点（1，a)可知：在y轴右侧，图像从下到上相应的底数由小变大。

②由指数函数y=a^x与直线x=-1相交于点（-1，1/a）可知：在y轴左侧，图像从下到上相应的底数由大变小。

③指数函数的底数与图像间的关系可概括的记忆为：在y轴右边“底大图高”；在y轴左边“底大图低” 如图：(5)运算法则：①②③④4.对数函数y=logax（a>0 且a≠1）(1)定义：如果a^x=N（a>0，且a ≠1），那么数x叫做以a为底N的对数，记作x=logaN，读作以a为底N的对数，其中a叫做对数的底数，N叫做真数一般地，函数y=logax（a>0，且a ≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数(2)定义域：(0，+∞)，即x>0(3)值域：R(4)性质：①单调性：1.当0＜a＜1时，在(0，+∞)内单调减少 2.当a ＞1时，在(0，+∞)内单调增加②奇偶性：非奇非偶函数③周期性：非周期函数④有界性：无界函数(5)图像：【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式：5.三角函数⑴正弦函数y=sin x(1)定义：对边与斜边的比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ(K∈Z)时，Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：奇函数③对称性：对称中心是(Kπ,0)，K ∈Z；对称轴是直线x=Kπ+π/2，K ∈Z④单调性：在[2Kπ-π/2,2Kπ+π/2]，K∈Z上单调递增；在[2Kπ+π/2,2Kπ+3π/2]，K∈Z上单调递减⑤有界性：有界函数(6)图像：(2)余弦函数y=cos x(1)定义：邻边与斜边之比(2)定义域：R(3)值域：【-1，1】(4)最值：1.当X=2Kπ +π /2(K∈Z)时，Y取最大值1 2.当X=2Kπ +π (K∈Z)时，Y取最小值－1(5)性质：①周期性：最小正周期都是2πT=2π②奇偶性：偶函数③对称性：对称中心是(Kπ+π/2,0)，K∈Z；对称轴是直线x=Kπ，K∈Z④单调性：在[2Kπ,2Kπ+π]，K∈Z上单调递减；在[2Kπ+π,2Kπ+2π]，K∈Z上单调递增⑤有界性：有界函数(6)图像：(3)正切函数y=tan x(1)定义：对边与邻边之比(2)定义域：{x∣x≠Kπ+π/2,K∈Z}(3)值域：R(4)最值：无最大值和最小值(5)性质：①周期性：最小正周期都是πT=π②奇偶性：奇函数③对称性：对称中心是(Kπ/2,0)，K∈Z④单调性：在[Kπ-π/2,Kπ+π/2]，K∈Z上单调递增⑤有界性：无界函数(6)图像：(4)余切函数y=cot x(1)定义：在直角三角形中，某锐角的相邻直角边和相对直角边的比，叫做该锐角的余切。

基本初等函数知识点总结

基本初等函数知识点总结1.常数函数：常数函数是指函数的值在定义域内都保持不变的函数。

表示为f(x)=c，其中c是常数。

常数函数的图像是一条平行于x轴的直线。

常数函数的性质是恒等性，即f(x)=f(x')，对于任意x和x'都成立。

2.平方函数：平方函数是指函数的值与自变量的平方成正比的函数。

表示为f(x)=x²。

平方函数的图像是一条开口向上的抛物线。

平方函数的性质是奇偶性，即f(-x)=f(x)，对于任意实数x都成立。

3.立方函数：立方函数是指函数的值与自变量的立方成正比的函数。

表示为f(x)=x³。

立方函数的图像是一条通过原点且存在于所有象限的曲线。

立方函数的性质是单调性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)或f(x₁)>f(x₂)成立。

4.绝对值函数：绝对值函数是指函数的值与自变量的绝对值成正比的函数。

表示为f(x)=，x。

绝对值函数的图像是一条以原点为顶点且对称于y轴的V字形曲线。

绝对值函数的性质是非负性，即对于任意实数x，有f(x)≥0成立。

5.指数函数：指数函数是指函数的值与自变量的指数幂成正比的函数。

表示为f(x)=aˣ，其中a是一个正实数且a≠1、指数函数的图像是一条通过点(0,1)且与x轴和y轴都无交点的曲线。

指数函数的性质是增长性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)成立。

6. 对数函数：对数函数是指函数的值与自变量的对数成正比的函数。

表示为f(x)=logₐ(x)，其中a是一个正实数且a≠1、对数函数的图像是一条通过点(1, 0)且与x轴和y轴都无交点的曲线。

对数函数的性质是单调性，即在定义域内，当x₁<x₂时，有f(x₁)<f(x₂)成立。

7. 三角函数：三角函数包括正弦函数、余弦函数、正切函数等。

正弦函数表示为f(x)=sin(x)，余弦函数表示为f(x)=cos(x)，正切函数表示为f(x)=tan(x)。

(完整版)基本初等函数知识点及函数的基本性质

对数函数
定义
函数y logax(a 0且a
1）叫做对数函数
a1
0a1
x1
x1
yx 1
y
y logax
yy logax
图象
(1,0)
O
(1,0)
x
Ox
定义域
(0,,0)，即当x
1时，y 0．
奇偶性
非奇非偶
② 对数函数对底数的限制：（a 0，且a1）．三、对数函数的图像和性质：
指数函数及其性质
、指数与指数幂的运算
一）根式的概念
1、如果xna,a R,x R,n1，且n N，那么x叫做a的n次方根．当n是奇数时，a
函数名称
指数函数
定义
函数y ax（a 0且a1）叫做指数函数
图象
a1
0a1
y 1yy ax
(0,1)
Ox
y axy
y 1(0,1)
Ox
定义域
R
值域
(0,+∞)
过定点
在第一象限内，a越小图象越高，越靠近y轴；
图象影响
在第二象限内，a越大图象越低，越靠近x轴．
在第二象限内，a越小图象越低，越靠近x轴．
注意：利用函数的单调性，结合图象还可以看出：
1）
在[a，
b]上，
f (x)
ax(a 0且a
1)值域是[f (a),f(b)]或[f(b),f(a)]
2）
若x
0，则
对数函数及其性质
、对数与对数的运算
一）对数
1．对数的概念：一般地，如果ax
N (a
0,a
1），那么数x叫做以．a为．底．N的对数，记作：
x

基本初等函数知识点

4.对数的运算性质如果，那么①ห้องสมุดไป่ตู้法：
②减法：
③数乘：
④
⑤
⑥换底公式：
知识点四：对数函数及其性质
2
1.对数函数定义一般地，函数 2.对数函数性质：函数名称定义函数对数函数且叫做对数函数叫做对数函数，其中是自变量，函数的定义域 .
图象
定义域值域过定点奇偶性单调性在上是增函数图象过定点，即当非奇非偶在上是减函数时， .
4
4.函数值域： ①y
3 2x
②y
x3 5 x
5、函数图像变换知识 ①平移变换：形如：y=f(x+a)：把函数 y=f(x)的图象沿ｘ轴方向向左或向右平移｜a｜个单位，就得到 y=f(x+a)的图象。形如：y=f(x)+a：把函数 y=f(x)的图象沿ｙ轴方向向上或向下平移｜a｜个单位，就得到 y=f(x)+a 的图象 ②.对称变换 y=f(x)→ y=f(－x),关于ｙ轴对称 y=f(x)→ y=－f(x) ,关于ｘ轴对称 ③.翻折变换 y=f(x)→y=f|x|, (左折变换) 把ｙ轴右边的图象保留，然后将ｙ轴右边部分关于ｙ轴对称 y=f(x)→y=|f(x)|（上折变换）把ｘ轴上方的图象保留，ｘ轴下方的图象关于ｘ轴对称在第一象限内，底数越大，图像（逆时针方向）越靠近 y 轴。 6 函数的表示方法 ①列表法：通过列出自变量与对应的函数值的表来表达函数关系的方法叫列表法 ②图像法：如果图形 F 是函数 y f ( x) 的图像，则图像上的任意点的坐标满足函数的关系式，反之满足函数关系的点都在图像上.这种由图形表示函数的方法叫做图像法. ③如果在函数 y f ( x) ( x A) 中， f ( x) 是用代数式来表达的，这种方法叫做解析法 7．分段函数在函数的定义域内，对于自变量 x 的不同取值区间，有着不同的对应法则，这样的函数通常叫做分段函数。 8 函数单调性及证明方法: ①增函数：一般地 , 设函数 f(x) 的定义域为 D, 如果对于定义域 D 内的某个区间上的任意两个自变量的值 x1,x2 , 当 x1<x2 时 , 都有 f(x1)< f(x2), 那么就说 f(x) 在这个区间上是增函数。此区间就叫做函数 f(x) 的单调增区间。 ②减函数：一般地 , 设函数 f(x) 的定义域为 D, 如果对于定义域 D 内的某个区间上的任意两个自变量的值 x1,x2 , 当 x1<x2 时 , 都有 f(x1)> f(x2), 那么就说 f(x) 在这个区间上是减函数。此区间叫做函数 f(x) 的单调减区间。 ③证明方法第一步：设 x1、x2 是给定区间内的两个任意的值，且 x1<x2；第二步：作差 f(x2)-f(x1)，并对“差式”变形，主要采用的方法是“因式分解”或“配方法”；第三步：判断差式 f(x2)-f(x1)的正负号，从而证得其增减性 9.函数的奇偶性 ⑴奇函数 ①设函数 y=f（x）的定义域为 D，如果对 D 内的任意一个 x，都有-x∈D，且 f(-x)=-f(x)，则这个函数叫做奇函数。 ②奇函数图象关于原点（0，0）中心对称。

基本初等函数知识点总结

基本初等函数知识点总结1.多项式函数多项式函数是由常数和幂函数通过加减乘除运算得到的函数，它的一般形式是f(x)=anx^n+an-1x^(n-1)+...+a1x+a0，其中an,...,a0是常数，n是非负整数。

多项式函数的最高次数决定了函数的增长速度，函数的图像通常是一个平滑的曲线。

2.指数函数指数函数的形式是f(x)=a^x，其中a是一个正实数且不等于1、指数函数的图像呈现出递增或递减的趋势，具有不断增长的特点。

指数函数的特点是：当a>1时，函数递增；当0<a<1时，函数递减；当a=1时，函数恒为1；当x=0时，函数的值为13.对数函数对数函数的形式是f(x)=log_a(x)，其中a是一个正实数且不等于1，x是一个正实数。

对数函数与指数函数是互逆的关系，即对数函数是指数函数的逆函数。

对数函数的特点是：当a>1时，函数递增；当0<a<1时，函数递减；当a=1时，函数恒为0；当x=1时，函数的值为0。

4.三角函数三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)等。

它们的图像是周期性的，周期为2π。

三角函数是以圆上的点的坐标来定义的，它们与三角关系密切相关，具有很多重要的应用，如波动、振动、旋转等。

5.反三角函数反三角函数是三角函数的逆函数，如反正弦函数arcsin(x)，反余弦函数arccos(x)，反正切函数arctan(x)等。

它们的定义域是[-1,1]，值域是[-π/2,π/2]。

反三角函数可以用来解三角方程和求解三角函数的值，也在三角函数应用中起到重要作用。

6.指数对数函数指数对数函数是指数函数和对数函数的组合，如指数函数的反函数指数对数函数f(x)=log_a(x)，对数函数的反函数指数对数函数f(x)=a^x。

指数对数函数具有特定的增长速度和性质，广泛应用于科学、金融、工程等领域。

总结起来，基本初等函数是初等函数的基础知识，包括多项式函数、指数函数、对数函数和三角函数等。

基本初等函数知识点

基本初等函数知识点一、引言在数学中，初等函数是由基本初等函数经过有限次的四则运算（加、减、乘、除）以及复合运算得到的函数。

基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数以及反三角函数。

本文将详细介绍这些基本初等函数的定义、性质和图像。

二、常数函数定义：常数函数 $ f(x) = c $，其中 $ c $ 是一个实数常数。

性质：常数函数的图像是一条平行于 $ x $ 轴的直线，其所有点的函数值都等于常数 $ c $。

图像：见附录图1。

三、幂函数定义：幂函数 $ f(x) = x^n $，其中 $ n $ 是实数。

性质：幂函数的性质取决于指数 $ n $ 的值。

当 $ n $ 为正整数时，函数图像是 $ n $ 次幂的曲线；当 $ n $ 为负整数时，函数图像是倒数的幂函数曲线。

图像：见附录图2。

四、指数函数定义：指数函数 $ f(x) = a^x $，其中 $ a > 0 $ 且 $ a\neq 1 $。

性质：指数函数的底数 $ a $ 决定了函数图像的形状。

当 $ a > 1 $ 时，函数是增长的；当 $ 0 < a < 1 $ 时，函数是衰减的。

图像：见附录图3。

五、对数函数定义：对数函数 $ f(x) = \log_a(x) $，其中 $ a > 0 $ 且$ a \neq 1 $。

性质：对数函数是指数函数的逆函数。

当 $ a > 1 $ 时，函数是单调增加的；当 $ 0 < a < 1 $ 时，函数是单调减少的。

图像：见附录图4。

六、三角函数1. 正弦函数 $ \sin(x) $2. 余弦函数 $ \cos(x) $3. 正切函数 $ \tan(x) $定义：这些函数与单位圆上的点的坐标有关。

性质：三角函数具有周期性，它们的周期为 $ 2\pi $。

(完整版)基本初等函数知识点及函数的基本性质

指数函数及其性质一、指数与指数幂的运算（一）根式的概念1、如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a的n次方根用符号n 是偶数时，正数a 的正的n的n次方根用符号0的n 次方根是0；负数a 没有n 次方根．2n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．3、根式的性质：na =；当n 为奇数时，a =；当n 为偶数时，(0)|| (0)a a a a a ≥⎧==⎨-<⎩．（二）分数指数幂的概念1、正数的正分数指数幂的意义是：0,,,m na a m n N +>∈且1)n >．0的正分数指数幂等于0． 2、正数的负分数指数幂的意义是： 1()0,,,mm nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数． 3、a 0=1 (a ≠0) a -p = 1/a p (a ≠0；p ∈N *) 4、指数幂的运算性质(0,,)r s r s a a a a r s R +⋅=>∈ ()(0,,)r s rs a a a r s R =>∈ ()(0,0,)r r r ab a b a b r R =>>∈5、0的正分数指数幂等于0,0的负分数指数幂无意义。

二、指数函数的概念一般地，函数)1a ,0a (a y x≠>=且叫做指数函数，其中x 是自变量，函数的定义域为R ．注意：○1 指数函数的定义是一个形式定义； ○2 注意指数函数的底数的取值范围不能是负数、零和1．（1）在[a ，b]上，)1a 0a (a )x (f x≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [ （2）若0x ≠，则1)x (f ≠；)x (f 取遍所有正数当且仅当R x ∈ （3）对于指数函数)1a 0a (a )x (f x≠>=且，总有a )1(f =（4）当1a >时，若21x x <，则)x (f )x (f 21< 四、底数的平移对于任何一个有意义的指数函数：在指数上加上一个数，图像会向左平移；减去一个数，图像会向右平移。

基本初等函数知识点

基本初等函数知识点一、函数的概念：函数是自变量与因变量之间的一种对应关系。

其中，自变量是函数的输入，因变量是函数的输出。

函数可以用来描述不同变量之间的关系或者用来描述一些变量随着另一个变量的变化而发生的变化。

二、函数的表示法：函数可以用不同的表示法来表示。

最常见的表示法有解析式表示法、图像表示法和表格表示法。

例如，一元一次函数y=ax+b就是一个常见的初等函数。

三、函数的性质：1.定义域和值域：函数的定义域是自变量的取值范围，值域是函数的因变量的可能取值范围。

2.奇偶性：对于函数f(x)，如果对于任意x，有f(-x)=f(x)成立，则函数具有偶性；如果对于任意x，有f(-x)=-f(x)成立，则函数具有奇性。

3.单调性：如果对于任意x1>x2，有f(x1)>f(x2)成立，则函数为递增函数；如果对于任意x1>x2，有f(x1)<f(x2)成立，则函数为递减函数。

4.周期性：如果对于任意x，有f(x+T)=f(x)成立，则函数具有周期T。

四、常见初等函数的性质和图像：1.常数函数：f(x)=c（c为常数），图像为平行于x轴的一条直线。

2. 一次函数：f(x) = ax + b（a和b为常数），图像为一条直线，斜率a决定了直线的倾斜程度，b为与y轴交点的纵坐标。

3.幂函数：f(x)=x^n（n为常数），图像的形状与n的奇偶性以及正负有关，例如，当n为正奇数时，图像的右上和左下部分都在x轴上方。

4.指数函数：f(x)=a^x（a为常数且大于0且不等于1），图像呈现出一种快速增长的趋势。

5. 对数函数：f(x) = loga(x)（a为常数且大于0且不等于1），图像为一条光滑的上升曲线，a决定了函数增长的速度。

五、初等函数的运算：1.四则运算：对于两个初等函数f(x)和g(x)，可以进行加减乘除运算，得到新的初等函数。

2.复合运算：对于两个初等函数f(x)和g(x)，可以将g(x)的值代入f(x)进行运算，得到新的初等函数。

基本初等函数考点归纳(强烈推荐)

知识归纳：1、指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a 互为反函数，它们的图象关于直线x y =对称，其图象性质见下表：（1）定义：)1,,,0(1,>∈>==*-n N n m a aaa anm nm n m nm（2）运算性质：),,0,0()(,)(,Q t s b a b a ab a a a a a s s s st t s t s ts∈>>===⋅+3、对数定义及运算性质（1）定义：若)1,0(≠>=a a N a b，则数b 叫做以a 为底N 的对数，记作b N a =log（2）常用对数、自然对数对数)1,0(log ≠>a a N a 当底数10=a 时，叫常用对数，记作N lg ；当底数e a =时，叫自然对数，记作N ln（3）对数恒等式：)0,1,0(log >≠>=N a a N aNa （4）换底公式：)0,1,,0,(log log log >≠>=N b a b a aNN b b a （5）对数运算法则N M MN a a a log log )(log += )1,0,0,0(≠>>>a a N MN M NM b a a log log log -= )1,0,0,0(≠>>>a a N MN n N a n a log log = )1,0,0(≠>>a a NN n N a n a log 1log = )1,0,0(≠>>a a Nb n mb a m a n log log = )1,0,0,0(≠>>≠a a b nab b a log 1log = )1,0,1,0(≠>≠>a a b b考点1指数函数与对数函数的定义域、值域例1.设2()lg 2x f x x +=-，则2()()2x f f x+的定义域为 A ．(4,0)(0,4)- B ．(4,1)(1,4)-- C ．(2,1)(1,2)-- D ．(4,2)(2,4)--考点2指数函数与对数函数的图像例2．函数xe y -=的图象（） A ．与x e y =的图象关于y 轴对称 B ．与xe y =的图象关于坐标原点对称C ．与x ey -=的图象关于y 轴对称D ．与xey -=的图象关于坐标原点对称例3．为了得到函数xy )31(3⨯=的图象，可以把函数xy )31(=的图象（） A ．向左平移3个单位长度 B ．向右平移3个单位长度C ．向左平移1个单位长度D ．向右平移1个单位长度考点3由指数函数与对数函数的图像确定参数的值或范围例4.若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1，0)和(0，1)，则（） A ．a =2,b=2 B ．a = 2 ,b=2 C ．a =2,b=1 D ．a = 2 ,b= 2例5.若直线y=2a 与函数y=|a x-1|(a >0,且a ≠1)的图象有两个公共点，则a 的取值范围是考点4指数函数与对数函数的互为反函数关系例6.记函数y=1+3-x的反函数为()y g x =，则g(10)=（）A ． 2B ． 2-C ． 3D ． 1-考点5指数方程与对数方程例7.解方程 11214=-+xx .例8.(2006年上海文科卷第8题) 方程x x 323log 1)10(log +=-的解是 .考点6指数函数与对数函数的单调性例9.设()2log log ,2log ,3log 3232===R Q P ,则( )A.P Q R <<B.Q R P <<C.P R Q <<D.Q P R <<例10.求函数()()24log 23f x x x =+-的单调区间考点7求参数的取值范围例11、若()log 3a y ax =-在[]0,1上是x 的减函数，则a 的取值范围是（） A 、()0,1 B 、()1,3 C 、()0,3 D 、[)3,+∞点评：由常规的具体函数判断单调性或求已知函数的单调区间，变换为由函数的单调性反过来确定函数中的底数a 的范围，同时要求对对数函数的概念和性质有深刻的理解。

10基本初等函数知识点总结

初等基本函数知识点总结

10基本初等函数知识点总结

基本初等函数知识总结

基本初等函数知识点归纳

专题10 基本初等函数(知识梳理)(新高考地区专用)(解析版)

基本初等函数定义及性质知识点归纳

基本初等函数知识点总结

基本初等函数知识总结

基本初等函数知识点

基本初等函数知识总结

基本初等函数知识点总结

(完整版)基本初等函数知识点及函数的基本性质

基本初等函数知识点

基本初等函数知识点总结

基本初等函数知识点

(完整版)基本初等函数知识点及函数的基本性质

基本初等函数知识点

基本初等函数考点归纳(强烈推荐)

最新整理基本初等函数的图象及函数常用知识点总结汇总