二体问题与折合质量
二体问题资料课件

03
二体问题的解析解法
微分方程的求解
建立二体问题微分方程
根据牛顿第二定律和万有引力定律,建立二体 问题的微分方程。
求解微分方程
通过解析方法或数值方法求解微分方程,得到 物体的运动轨迹和速度。
验证解的正确性
通过将解代入原微分方程进行验证,确保解的正确性。
椭圆轨道和双曲轨道
椭圆轨道
当两个物体之间的距离足 够远时,它们的运动轨迹 近似为椭圆。
二体问题资料课件
目录
• 二体问题简介 • 二体问题的数学模型 • 二体问题的解析解法 • 二体问题的近似解法 • 二体问题的实际应用 • 二体问题的发展前景
01
二体问题简介
二体问题的定义
二体问题是指两个质点在万有引力作用下的运动 01 规律问题。
它描述了两个物体在相互吸引的力(如地球和月 02 亮)作用下,如何运动的问题。
运动方程的建立
总结词
根据牛顿第二定律和万有引力定律建立的描述天体运动的方程
详细描述
在二体问题中,根据牛顿第二定律和万有引力定律,可以建立描述两个天体之间相对位置和相对运动的运动方程 。这些方程通常是非线性的微分方程,用于求解天体的轨道和运动规律。通过对方程进行数值积分,可以得到天 体的精确运动轨迹。
详细描述
牛顿第二定律指出,物体受到的合外力等于其质量与加速度的乘积,即F=ma。它揭示了力、质 量和加速度之间的联系,是描述物体运动状态变化规律的定律。在二体问题中,牛顿第二定律 用于分析两个天体之间的相互作用力和运动状态变化。
万有引力定律
总结词
描述任意两个质点之间引力作用的定律
详细描述
万有引力定律指出,任意两个质点之间都存在引力作用,其大小与两质点质量的 乘积成正比,与它们之间距离的二次方成反比,即F=G*m1*m2/r^2。在二体问 题中,万有引力定律用于计算两个天体之间的引力,是天体运动分析的基础。
第三章 两体问题

第三章 两体问题教学目的和基本要求:正确理解两体问题的物理意义,掌握将两体问题化为单粒子问题的方法;能够运用有效势分析并熟练掌握单粒子在中心势场中的运动规律,了解中心势场中粒子运动轨道的稳定性、弹性碰撞、散射截面等物理规律和概念。
教学重点:在理解两体问题意义的基础上,熟练掌握单粒子在中心势场中的运动规律。
教学难点:在中心势场中单粒子的运动规律的分析讨论。
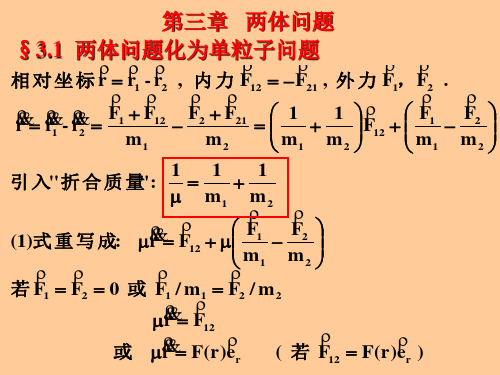
§3.1 两体问题化为单粒子问题一:两体问题:1.定义:两个相互作用着的粒子所组成的力学体系的力学问题为两体问题,可分为三类。
2.分类:两体问题可分为三类。
(1)束缚态问题:两体之间保持有限的距离。
入电子绕原子核运动,行星绕太阳运动。
(2)散射或碰撞问题:两粒子从无穷远处逐渐接近,经过短暂的相互作用后各自改变运动状态后相互分离至无穷远处。
(3)俘获或衰变问题:作用前后粒子数从2变为1或从1变为2。
二:两体问题的处理方法1.一般过程:两体问题中粒子的运动可分为随质心的运动和两粒子相对于质心的运动。
每个粒子的绝对运动可看成是两种运动的合成。
2.将两体问题分解为质心的运动和单粒子的运动:○1分解过程:首先约定用)z ,y ,x (r表示两粒子间相对位置矢量,用)z ,y ,x (r 0000 表示粒子在惯性系中位置,如图3.1所示。
r ,r ,r 0201中的位矢和相对位矢。
则有:20222011r m 21r m 21T +=(1.1),V )r (V V c 0)e ( +=(1.4),)r (V c 0)e ( 是两粒子处在外场中的势能,仅与c 0r )r (V )i (是两粒子相互作用的势能,仅与0201r r r -= (1.3)有关。
因两粒子的自由度为6,可取c 0r 、r为广义坐标,则有:r m m m r r 212c 001 ++=,r m m m r r 211c 002+-= (1.5)。
将两式代入动能T 的表达式后再代入拉格朗日函数L=T-V ,化简后可得:21)i (2r c 0)e (2C 021L L )r (V r m 21)r (V r )m m (21L +=-+-+= (1.6) 其中2121rm m m m m +=,称为折合质量;)()(210)(20211c e C r V r m m L -+=, (1.7) )(21)(22r V r m L i r -= (1.8)○2结论:从21L L L +=可看出,两体问题中两粒子的运动可分解为反映质心运动的)r ,r (L c0C 01 及反映两粒子间相对运动的)r ,r (L 2 两个相互独立的部分。
第二章有心运动和两体问题

U ( r ) 0 r
2U (r ) 0 2 r
为稳定平衡
圆轨道稳定条件:
2 n
F ' (ro ) 3 F (ro ) ro
19
若: F (r ) k r 则 n 3
§2-4与平方反比的斥力作用——α 粒子的散射
1 Qq F e 2 r 4 o r
α粒子散射实验
E1 0 相当于双曲线 E2 0 相当于椭圆
E0 EC
相当于抛物线 相当于圆运动
47
2
§2-2 平方反比引力下的质点运动
(一)轨道
1 F 2 r
k2 F 2 er r
若万有引力:
2
F 与 er 反向
若静电场力:
k GMm
q1q2 k 4
2
m h2 / k 2 r 2 2 1 Am h / k cos( o )
A 和θo 为积分常数,由初始条件定:t = 0 θ=θo
或用极坐标表示: 若有约束,维数要减 少。如:有心力 相当于两个约束方程 相轨迹为二维曲面 用极坐标来表示:
(r, , pr , p ) 四维空间
m 2 2 E ( x y ) V ( x, y ) 2 2 L mr m( x y y x )
pr2 L2 V (r ) E 2 2m 2mr
2 k 2 1 2 ( ) ∵ 能量越大,椭圆越扁,半长轴越长 v m r a ∴ v越大,椭圆越扁.
第三种情况
E=0 e=1 轨道为抛物线 v=vII
第二宇宙速度:vII ——使航天器能脱离地球引力场所需的最小发射速度
2 k 1 2 mvII 0 Re 2
用折合质量法解答2022年高考全国乙卷第25题

用折合质量法解答2022年高考全国乙卷第25题2022年高考已落下帷幕,对高考试题的分析是一线教师研究命题规律、把握考向的重要手段。
笔者用折合质量法分析了2022年高考全国乙卷理综物理压轴题,提出复习课不是重复再现,而是深度再学习过程,以供借鉴。
1 引言(2022·全国乙卷·25)如图1,一质量为m的物块A与轻质弹簧连接,静止在光滑水平面上;物块B向A运动,t=0 时与弹簧接触,到t=2t0时与弹簧分离,第一次碰撞结束,A、B的v-t图像如图2所示。
已知从t=0到t=t0时间内,物块A运动的距离为0.36v0t0。
A、B分离后,A滑上粗糙斜面,然后滑下,与一直在水平面上运动的B再次碰撞,之后A再次滑上斜面,达到的最高点与前一次相同。
斜面倾角为θ(sinθ=0.6),与水平面光滑连接。
碰撞过程中弹簧始终处于弹性限度内。
求:图1图2(1)第一次碰撞过程中,弹簧弹性势能的最大值;(2)第一次碰撞过程中,弹簧压缩量的最大值;(3)物块A与斜面间的动摩擦因数。
2022年高考全国乙卷理综物理压轴题第25题,实质是二体问题。
对于这种问题,如果在地面参考系与A(或B)参考系间切换,则科学思维更流畅、方程更简捷、计算更简化、解答更明了,会使问题变得十分简单;但在以A(或B)为参考系时,需要将另一物体B(或A)的质量进行折合,两质点质量分别为m1、m2,则其折合质量μ=。
下面笔者运用折合质量法进行解答。
2 解答过程2.1 质点系的动能——柯尼希定理Ek=为S系中质心的动能,得出S系中质点系的动能可视为质心动能与S′系中质点系的动能之和,即著名的柯尼希定理。
第3问与第1问都是能量关系问题,解决了第1问,接着思考第3问。
第一次碰撞后,物块A以2v0速度沿斜面上滑,假设上滑最大路程为s,由动能定理得设物块A下滑离开斜面时速度大小为v,同理物块A以速度v向左运动,与以速度0.8v0向右运动的B相互作用,作用结束,B速度变为vB,因A到达的最高点和前一次相同,则A仍以2v0速度沿斜面上滑。
1二体问题和折合质量

4.ξ氢原子上节所讲的中心力,在空间中是一有一个固定的力心。
但在实际物理系统中,质心才是相对固定的,而相互作用着的一个个粒子,都处在不停的运动中,以系统中只包含两个粒子的二体问题为例,一方面,两个粒子间的相互作用依赖于它们的相对位置,另一方面,两个粒子又分处于其质心的两侧不停的运动,所以,在空间中并不存在一个真正的固定力心,但可以象理论力学中做过的一样,对二体问题分解为质心坐标和相对坐标一样来处理。
1二体问题和折合质量设在二体系统中,两个粒子的质量分别为.12μμ和,其坐标分别为12r r →→和它们间的作用,只依赖于其距离12r r r →→=-于是,系统满足的定态方程为:()222212121211,,.....22U r r r E r r ψψμμ→→→→⎡⎤⎛⎫⎛⎫-∇-∇+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ ① 引入质心坐标和相对坐标11221212,,()c r r r r r r M Mμμμμ→→→→→→+==-=+可证以下微分公式:2222111112222222222222221212,,(),2,,2,1111c c c c c c c r MMMMMMM μμμμμμμμμ∇=∇+∇∇=∇∇=∇+∇∇+∇∇=∇-∇∇=∇+∇∇+∇∇+∇=∇+∇ 结果得:、、、②式中1212μμμμμ=+为折合质量将②代回.①得: ()2222',,.....22c c c U r r r E r r ψψμμ→→→→⎡⎤⎛⎫⎛⎫-∇-∇+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ ③方程③中c r r →→和两个变量可以分离。
设总态函数为,c c r r r r ψφϕ→→→→⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭得到分别描述质心运动和相对运动的两个方程:22'22.....2......2c c c c r r E r U r r E r φφμϕϕμ→→→→→⎛⎫⎛⎫-∇= ⎪ ⎪⎝⎭⎝⎭⎡⎤⎛⎫⎛⎫⎛⎫-∇+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ ④⑤式中,c E 和r E 分别代表系统质心运动和相对运动的能量,两者之和等于总能量c r E E E =+方程④描述的是,在系统不受外界影响时,质心所做的自由运动。
理论力学 两体问题

双星系统的研究有助于理解恒星的形成和演化过程,以及宇宙中的星系形成。
行星与卫星系统是一个行星和一个或多个卫星组成的系统,卫星绕着行星旋转,受到行星的万有引力作用。
行星与卫星的运动规律也是由万有引力定律和运动定律来描述,通过求解微分方程可以得出它们的轨道和运动规律。
理论力学 两体问题
目录
两体问题的基本概念 两体问题的动力学模型 两体问题的运动学模型 两体问题的经典问题 两体问题的数值模拟方法 两体问题的应用领域
01
CHAPTER
两体问题的基本概念
两体问题是指两个质点在万有引力或库仑力等作用下的运动问题。
两个质点在相互之间的力作用下,同时受到其他力的作用,这些力满足牛顿第三定律。
卫星轨道设计
卫星轨道设计是航天工程中的重要环节,而两体问题提供了卫星绕地球或其他天体运动的基本规律,为轨道设计提供了理论基础。
月球和火星探测
月球和火星探测任务中,两体问题用于研究探测器的轨道运动、着陆和巡视等任务。
航天工程
1
2
3
地球自转和极移是地球物理学研究的重要内容,两体问题提供了地球自转和极移的理论基础。
行星与卫星系统的研究有助于了解地球的气候变化、地质构造、天体演化等自然现象。
01
02
03
行星与卫星系统
哈雷彗星的轨道问题主要是研究其轨道的稳定性、变化规律以及与其他天体的相互作用。
哈雷彗星轨道问题的研究有助于了解太阳系的演化历史和天体的动力学行为。
哈雷彗星是太阳系中的一颗周期性彗星,其轨道非常长,大约需要76年才能绕行一周。
哈雷彗星轨道问题
理论力学 两体问题
§3.4 有心力场中粒子运动轨道的稳定性 d 2u 2 2 比耐公式 : u ( 2 + u ) = mF(r ) / L dθ d 2ε 2 d 2u o m dF 其中: + Aε = 0. 其中:A = 3 + + 2 2 2 2 dθ u o dθ u o L du 线性增加; 若A=0,ε 随 θ ( 从而随 t ) 线性增加; , 若A<0,ε 随 t 线性增加. , 线性增加. 若A> 0,ε 作简谐振动,轨道稳定. , 作简谐振动,轨道稳定. 轨道稳定条件: 轨道稳定条件: 2 2m 3 dU m 4 d U A = 1+ 2 r + 2r >0 2 L dr L dr
2
d 2u o d 2 ε m 2 2 (u o + 2u o ε + ε ) + 2 + u o + ε = 2 F(u o + ε ) 2 dθ dθ L dF F ( u o + ε ) = F (u o ) + uo ε + du d 2ε 2 d 2u o m dF 其中: + Aε = 0. 其中: A = 3 + + 2 2 uo 2 2 dθ u o dθ u o L du
例:如质点受有心力作 用而作双纽线 r = a cos 2θ
2 2
3ma 4 h 7 的运动时, 试证明之. , 试证明之. 的运动时,则 F = 7 r 1 1 证明: 证明: u = = r a cos 2θ du 1 3/ 2 = sin 2θ(cos 2θ ) dθ a d 2u 1 = [ 2(cos 2θ ) 1 / 2 + 3 sin 2 2θ(cos 2θ ) 5 / 2 ] 2 dθ a
例析二体问题的折合质量解法

规律ꎬ即是电阻的变化趋势与电压㊁电流和功率的变化趋势ꎬ满足 与变化电阻存在串联关系电路中的用电器ꎬ其电压㊁电流及功率与变化的阻值变化趋势相反 ㊁ 与变化电阻存在并联关系电路中的用电器ꎬ其电压㊁电流及功率与变化的阻值变化趋势相同 的规律ꎬ浓缩起来即是串反并同.例3已知如图3所示电路图ꎬ当滑动变阻器由方向a向b移动时ꎬ下面说法中正确的是(㊀㊀).图3A.电压表读数变大ꎬ电流表读数变小B.电压表读数变小ꎬ电流表读数变大C.两表读数均变大D.两表读数均变小解析㊀由题意可知ꎬ当滑动变阻器由方向a向b移动时ꎬR3的阻值增大.根据串反并同原理ꎬ与电阻R3串联的电流表读数变小.此时ꎬ进一步将外电路等效为一个可变电阻ꎬ由于电阻R3的阻值增大ꎬ则外电阻也增大ꎬ电压表与外电阻并联ꎬ则电压表读数也变大.综上选项A即是正确选项.值得注意的是ꎬ在使用串反并同法时ꎬ必须强调其适用条件ꎬ保证答案正确性.简言之ꎬ该法的适用条件分为两种:1)电源并非理想型ꎬ即存在电源内阻ꎻ2)电路中的电阻呈现单一变化规律.在实际求解过程中ꎬ紧抓串反并同的适用条件ꎬ谨记串反并同法的内核ꎬ实现高效求解.总之ꎬ动态电路问题是一类综合性问题ꎬ涉及多个电学知识及规律.本文中提出的三类动态电路求解方法必定不能有效包含全部的动态电路求解方法ꎬ还需要广大一线物理教师在实际教学过程中ꎬ继续总结ꎬ有效分类ꎬ完善此类问题的求解技巧.㊀㊀参考文献:[1]刘天赞.高中物理电路动态分析问题的应对[J].中国高新区ꎬ2018(1):95.[2]王丽媛.简析高中物理电路动态分析问题的策略[J].新智慧ꎬ2018(26):60.[3]王开荣.电路动态分析问题的命题变化[J].物理教师ꎬ1997:21-22.[责任编辑:李㊀璟]例析二体问题的折合质量解法谢汝成(吉林省辽源市第五中学㊀136200)摘㊀要:处理孤立二体系统时引入折合质量的概念ꎬ可以有效地降低问题的思维难度ꎬ有利于学生的理解.关键词:二体问题ꎻ参考系ꎻ折合质量中图分类号:G632㊀㊀㊀㊀㊀㊀文献标识码:A㊀㊀㊀㊀㊀㊀文章编号:1008-0333(2020)16-0074-02收稿日期:2020-03-05作者简介:谢汝成(1986.1-)ꎬ男ꎬ本科ꎬ中学一级教师ꎬ从事高中物理教学研究.基金项目:吉林省教育科学 十三五 规划课题«乡村振兴背景下的乡村教师专业发展研究»子课题«提高物理课堂教学效果策略的研究»ꎬ课题批准号GHKT-20190034.㊀㊀孤立的二体系统问题在高考试题和自主招生试题中比较常见ꎬ在解决该类问题时ꎬ通过引入折合质量的概念ꎬ可将复杂的二体问题变为单体问题.本文利用三道题目的分析求解ꎬ凸显出该种方法在解决此类问题的巧妙之处.㊀㊀一㊁折合质量推导如图1所示ꎬ宇宙中两颗相距较近的天体均为 双星 ꎬ它们以二者连线上的某一点为圆心做匀速圆周运动ꎬ而不至因为万有引力的作用而吸引到一起.设两者的质量分别为m1和m2ꎬ两者相距L.图1双星m1和m2ω1=ω2=ω①m1ω21r1=m2ω22r2②r1+r2=L③由①②③可得r1=m2m1+m2L分析m1的匀速圆周运动Gm1m2L2=m1ω2r1=m1ω2m2m1+m2L=m1m2m1+m2ω2L㊀④令μ=m1m2m1+m2ꎬ④式变为Gm1m2L2=μω2Lꎬ由此可以看出ꎬ在m2这一非惯性系中ꎬ将m1的质量换成折合质量后ꎬ47m1受到m2的万有引力充当它绕m2做匀速圆周运动的向心力ꎬ物体仍遵循相应的动力学方程.此时将两体问题转化为单体问题ꎬ有效的简化分析过程ꎬ提高解题效率.㊀㊀二㊁应用例1㊀如图2所示ꎬ一质量为mB长方形木板B放在光滑的水平地面上ꎬ在其右端放一质量为mA的小木块Aꎬ图2现以地面为参照系ꎬ给A和B以方向相反的初速度V1和V2ꎬ使A开始向左运动ꎬB开始向右运动ꎬ但最后A刚好没有滑离B板.若已知A㊁B之间的动摩擦因数为μ.求满足条件的木板至少为多长?解析㊀以B为参考系ꎬ则滑块A的折合质量为μ=mAmBmA+mB①A相对B的初速度VAB=V1+V2ꎬ当A相对B静止时在B上相对滑动位移最大.-μmAgL=0-12μV2AB②由①和②可以求得:L=mBV1+V2()μmA+mB()注:本题的常规解法为相对运动或等效完全非弹性碰撞模型ꎬ但计算过程较上面的解法略复杂.图3例2㊀如图3所示ꎬ一人手持质量为m的小球ꎬ乘坐在热气球下的吊篮里ꎬ气球㊁吊篮和人的总质量为Mꎬ气球以速度v0匀速上升ꎬ经过时间t0后接到小球.若人手在抛接小球时相对吊篮的位置不变ꎬ求抛球过程中人做的功.解析㊀以M为参考系m的折合质量为μ=MmM+m①m相对M以速度vᶄ竖直上抛mg=MmM+ma㊀㊀②㊀㊀vᶄ=12at③由①②③可得vᶄ=M+m()2Mgt④以地面为参考系ꎬ设抛出重物后M的速度变为v2ꎬm对地的抛出速度为(vᶄ+v0)浮力和重力平衡ꎬ系统动量守恒:m(vᶄ+v0)+Mv2=M+m()v0人做的功等于系统动能增量:W=12m(vᶄ+v0)2+12Mv22-12M+m()v20=m8MM+m()g2t2例3㊀(2015中科大自主招生)两个带点小球所带电量相等ꎬ符号相反.质量分别为m和2mꎬ初始时刻ꎬ它们间距离为dꎬ小球2m静止.小球m沿着与两者连线垂直的方向以速度v运动.随后ꎬ它们多次处于相距3d的位置上ꎬ求小球所带的电荷量.知识准备:取无穷远为电势能零点ꎬ则在q2的电场中ꎬq1在距q2为r1位置所具有的电势能Ep1=kq1q2r1ꎬq1在距q2为r2位置所具有的电势能Ep2=kq1q2r2(其中q1和q2带有正负号).解析㊀(1)以2m为参考系ꎬm绕2m转动ꎬ轨迹为椭圆ꎬ2m处于椭圆的焦点.m的初始位置距离2m最近为dꎬ距2m最远点r满足:rȡ3d㊀①m的折合质量为μ=23m㊀②设m运动到椭圆轨道最远点的速度为vᶄ由角动量守恒有:mvd=mvᶄr㊀③对椭圆长轴两端点列能量守恒:12μv2+-kq2dæèçöø÷=12μvᶄ2+-kq2ræèçöø÷㊀④由①②③④可解:qɤ4mdv29k(2)两球多次处于相距3dꎬ故m不能到达无穷远.12μν2+-kq2dæèçöø÷<0㊀⑤由②和⑤可得q>mdv23k折合质量的引入ꎬ为两体碰撞㊁类碰撞ꎬ双星系统ꎬ特殊简谐运动等问题的分析求解提供了一个明显便捷的计算方法ꎬ适用范围广ꎬ但在应用的过程中应重点关注的是:折合质量的概念仅适用于孤立的两体系统ꎬ即不受外力的系统.若系统受外力ꎬ本解法将不再使用.㊀㊀参考文献:[1]程稼夫.中学奥林匹克竞赛物理教程 力学篇[M].安徽:中国科学技术大学出版社ꎬ2014.[2]陆天明.荣誉物理 力学篇[M].南京:东南大学出版社ꎬ2016.[3]郑金.折合质量的妙用[J].物理教学ꎬ2016ꎬ38(05):66-68+65.[责任编辑:李㊀璟]57。
