九年级《三角函数》知识点、经典例题
初中三角函数知识点总结及中考真题讲解
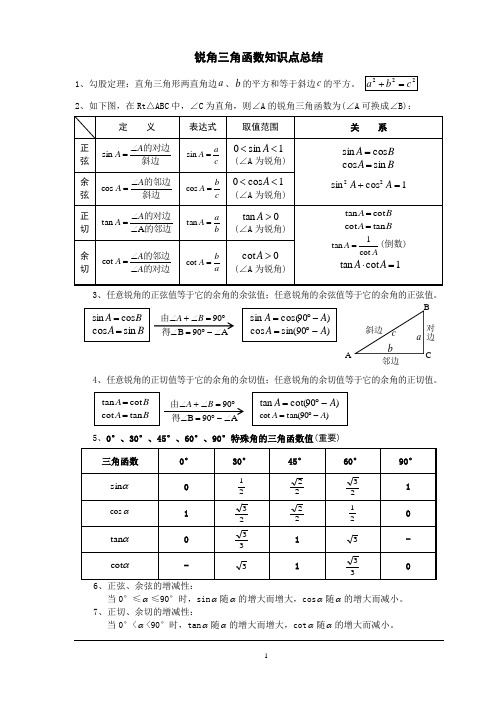
锐角三角函数知识点总结1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。
A90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 C A90B 90∠-︒=∠︒=∠+∠得由B A8、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。
依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。
(注意：尽量避免使用中间数据和除法)9、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
坡度一般写成1:m 的形式，如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。
(完整版)新北师大初三三角函数知识点总结及中考真题汇总有答案
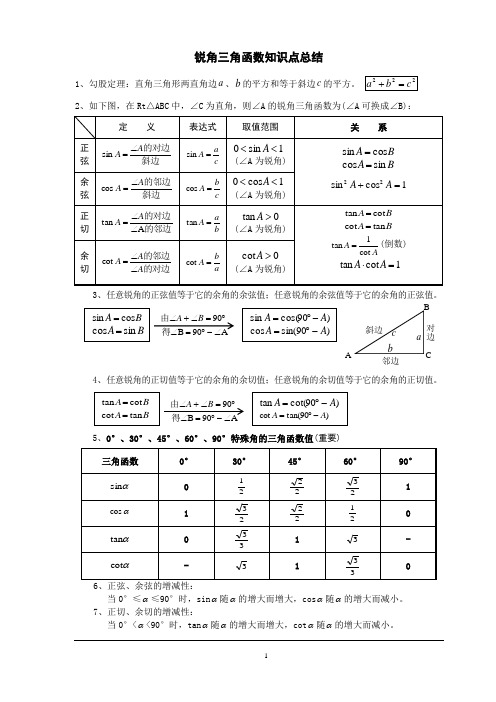
锐角三角函数知识点总结1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。
A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 C A90B 90∠-︒=∠︒=∠+∠得由B A8、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。
依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。
(注意：尽量避免使用中间数据和除法)9、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
坡度一般写成1:m 的形式，如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。
初三下学期锐角三角函数知识点总结及经典例题
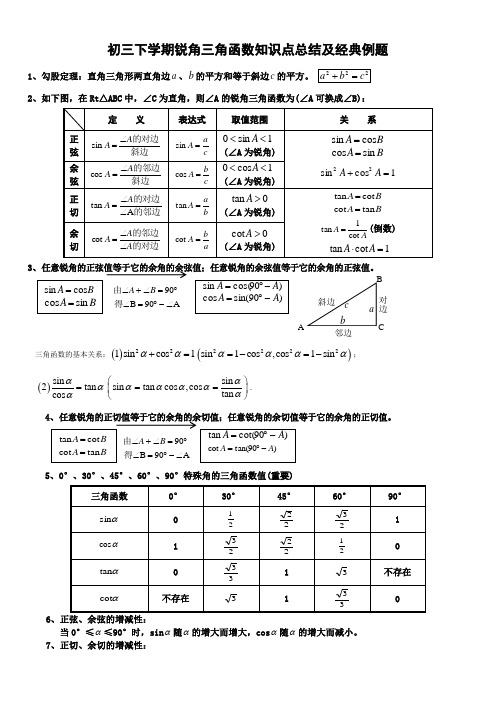
初三下学期锐角三角函数知识点总结及经典例题1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
三角函数的基本关系：()221sin cos 1αα+=()2222sin 1cos ,cos 1sin αααα=-=-；()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭．5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边当0°<α<90°时，tanα随α的增大而增大，cotα随α的增大而减小。
8、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。
用字母i表示，即hil=。
坡度一般写成1:m的形式，如1:5i=等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tanhilα==。
3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA、OB、OC、OD的方向角分别是：45°、135°、225°。
4、指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角。
如图4,OA、OB、OC、OD的方向角分别是：北偏东30°（东北方向），南偏东45°（东南方向），南偏西60°（西南方向），北偏西60°（西北方向）。
九年级数学三角函数全章知识点整理
初中三角函数整理复习一．三角函数定义。
siaA=斜边的对边A ∠,cosA=斜边的邻边A ∠,tanA=的邻边的对边A A ∠∠二、特殊角的三角函数： sia 30°、cos45° 、 tan60° 归纳结果练习： 求下列各式的值（1）sia 30°+cos30°（2）2sia 45°-21cos30°(3)04530cos sia +ta60°-tan30°三．解直角三角形主要依据(1)勾股定理：a 2+b 2=c 2(2)锐角之间的关系：∠A+∠B=90°(3)边角之间的关系：tanA=的邻边的对边A A ∠∠例题评析：例1、在△ABC 中，∠C 为直角，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ， 且b=2 ，a=6，解这个三角形．例2、在△ABC 中，∠C 为直角，∠A 、∠B 、∠C 所对的边分别为a 、b 、c ，且b= 20B ∠=350，解这个三角形（精确到0.1）． 斜边的邻边A A ∠=cos 斜边的对边A A ∠=sin例 3、在Rt △ABC 中，a=104.0，b=20.49，解这个三角形．例4、在△ABC 中，∠C 为直角，AC=6，BAC ∠的平分线AD=43，解此直角三角形。
四．仰角、俯角当我们进行测量时，在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，在水平线下方的角叫做俯角． 例1如图(6-16)，某飞机于空中A 处探测到目标C ，此时飞行高度AC=1200米，从飞机上看地平面控制点B 的俯角α=16°31′，求飞机A 到控制点B 距离(精确到1米)解：在Rt △ABC 中sinB=AB AC∴AB=B AC sin =2843.01200=4221(米)答：飞机A 到控制点B 的距离约为4221米．巩固练习：1．热气球的探测器显示，从热气球看一栋高楼顶部的仰角为，看这栋楼底部的俯角为600，热气球与高楼的水平距离为120m，这栋高楼有多高（结果精确到0.1`m）2．如图6-17，某海岛上的观察所A发现海上某船只B并测得其俯角α=80°14′．已知观察所A的标高(当水位为0m时的高度)为43.74m，当时水位为+2.63m，求观察所A到船只B的水平距离BC(精确到1m)3 如图6-19，已知A、B两点间的距离是160米，从A点看B点的仰角是11°，AC长为1.5米，求BD的高及水平距离CD．例2．如图，一艘海轮位于灯塔P的北偏东650方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南东340方向上的B处。
三角函数知识点及典型例题
三角函数知识点及典型例题三角函数知识点及典型例题§1.1.1、任意角1、正角、负角、零角、象限角的概念.2、与角α终边相同的角的集合：{}|360,S k k Z ββα==+?∈.§1.1.2、弧度制1、把长度等于半径长的弧所对的圆心角叫做1弧度的角.2、 rl =α.3、弧长公式： R4、扇形面积公式： S=21 lr=21αr 2.§1.2.1、任意角的三角函数1、设α是一个任意角，它的终边与单位圆交于点()y x P ,，那么：xyx y ===αααtan ,cos ,sin . 2、设点()00,y x A 为角α终边上任意一点，那么：（设2020y x r +=）_______sin r y =α，________cos rx=α，_____tan x y =α.3、αsin ，αcos ，αtan 在四个象限的符号一正二正弦三切四余和三角函数线的画法. 4、诱导公式一：()()()_tan _2tan _cos _2cos _sin _2sin απααπααπα=+=+=+kk k （Z k ∈）5、特殊角0°，30°，45°，60°，90°，180°，270°的三角函数值. §1.2.2、同角三角函数的基本关系式1、平方关系：22sin cos 1αα+=.2、商数关系：sin tan cos ααα=. §1.3、三角函数的诱导公式1、诱导公式二：()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ=+-=+-=+2、诱导公式三：()()()._tan _tan _____,cos _cos _,sin _sin αααααα-=-=--=-3、诱导公式四：()()()._tan _tan _,cos _cos _,sin _sin ααπααπααπ-=--=-=-4、诱导公式五：._sin _2cos _,cos _2sin ααπααπ=??-=-5、诱导公式六：._sin _2cos _,cos _2sin ααπααπ-=??+=+ §1.4.1、正弦、余弦函数的图象1、记住正弦、余弦函数图象：2、能够对照图象讲出正弦、余弦函数的相关性质：定义域、值域、最大最小值、对称轴、对称中心、奇偶性、单调性、周期性. 3、会用五点法作图.§1.4.2、正弦、余弦函数的性质1、周期函数定义：对于函数()x f ，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有()()x f T x f =+，那么函数()x f 就叫做周期函数，非零常数T 叫做这个函数的周期.§1.4.3、正切函数的图象与性质 1、记住正切函数的图象：2、能够对照图象讲出正切函数的相关性质：定义域、值域、对称中心、奇偶性、单调性、周期性. §1.5、函数()?ω+=x A y sin 的图象1、能够讲出函数x y sin =的图象和函数()b x A y ++=?ωsin 的图象之间的平移伸缩变换关系.2、对于函数：()()0,0sin >>++=ω?ωA b x A y 有：振幅A ，周期ωπ2=T ，初相?，相位?ω+x ，频率πω21==f .第三章、三角恒等变换两角和与差的正弦、余弦、正切公式cos()cos cos sin sin αβαβαβ-=+cos()cos cos sin sin αβαβαβ+=-sin()αβ+=sin cos cos sin αβαβ+sin()sin cos cos sin αβαβαβ-=-tan()αβ-tan tan 1tan tan αβαβ-=+ . tan()αβ+tan tan 1tan tan αβαβ+=-二倍角的正弦、余弦、正切公式1、_cos sin 2_2sin ααα=，变形：cos α=ααsin 22sin .2、22cos2cossin ααα=-22cos 1α=-212sin α=-变形1：21cos 2cos 2αα+=，变形2：21cos 2sin 2αα-=. 3、22tan tan 21tan ααα=- 1、注意正切化弦、平方降次. 解三角形 1、正弦定理R CcB b A a 2sin sin sin === 2、余弦定理a A bc c b cos 222-+=变形 cosA=bca cb 2222-+b B ac c a cos 2222-+=变形 cosB=acb c a 2222-+c C ab b a cos 2222-+=变形cosC=abc b a 2222-+3、三角形面积公式： S =21absinC=21bcsinA=21acsinB 课本题(必修4)1.（P 11 习题13）若扇形的周长为定值l ，则该扇形的圆心角为多大时，扇形的面积最大？22.（P 23 练习4）已知sin （4π-x ）=-51，且0<x<="">623.（ P 24 习题9(2)）设tan α=-21，计算αααα22cos 2cos sin sin 1--。
初三下学期锐角三角函数知识点总结及经典例题
初三下学期锐角三角函数知识点总结及经典例题1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
三角函数的基本关系：()221sin cos 1αα+=()2222sin 1cos ,cos 1sin αααα=-=-；()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭．5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。
8、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
坡度一般写成1:m 的形式，如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。
三角函数知识点及题型归纳
三角函数知识点及题型归纳三角函数是数学中的一个重要分支，在几何、物理、工程等领域都有广泛的应用。
下面我们来详细归纳一下三角函数的知识点和常见题型。
一、三角函数的基本概念1、角的概念角可以分为正角、负角和零角。
按旋转方向，逆时针旋转形成的角为正角，顺时针旋转形成的角为负角，没有旋转的角为零角。
2、弧度制把长度等于半径长的弧所对的圆心角叫做 1 弧度的角。
用弧度作为单位来度量角的制度叫做弧度制。
弧度与角度的换算公式为：180°＝π 弧度。
3、任意角的三角函数设角α的终边上任意一点 P 的坐标为(x, y)，它与原点的距离为 r(r ＝√（x²＋ y²) ＞ 0)，则角α的正弦、余弦、正切分别为：sinα ＝ y/r，cosα ＝ x/r，tanα ＝ y/x（x ≠ 0）。
4、三角函数线有正弦线、余弦线、正切线，它们分别是角α的终边与单位圆交点的纵坐标、横坐标、纵坐标与横坐标的比值。
二、同角三角函数的基本关系1、平方关系：sin²α ＋cos²α ＝ 12、商数关系：tanα ＝sinα/cosα三、诱导公式诱导公式可以将任意角的三角函数转化为锐角的三角函数。
例如：sin(π ＋α) ＝sinα，cos(π α) ＝cosα 等。
四、三角函数的图象和性质1、正弦函数 y ＝ sin x图象：是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ ＋π/2（k∈Z），对称中心为(kπ, 0)（k∈Z）。
性质：在π/2 ＋2kπ, π/2 ＋2kπ（k∈Z）上单调递增，在π/2 ＋2kπ, 3π/2 ＋2kπ（k∈Z）上单调递减。
2、余弦函数 y ＝ cos x图象：也是一条波浪形曲线，周期为2π，对称轴为 x ＝kπ（k∈Z），对称中心为(π/2 ＋kπ, 0)（k∈Z）。
性质：在π ＋2kπ, 2kπ（k∈Z）上单调递增，在2kπ, π ＋2kπ（k∈Z）上单调递减。
初三《三角函数》经典习题汇编(易错题、难题)
初三《三角函数》经典习题汇编(易错题、
难题)
初三《三角函数》经典题汇编（易错题、难题）
概述
本文档以初三数学学科的《三角函数》为主题，整理了一些经
典的题，主要包括易错题和难题。
这些题旨在帮助学生加深对三角
函数的理解和应用能力。
题目列表
1. 题目：已知直角三角形的一条直角边为5，斜边为13，求另
一条直角边的长度。
难度：易错题
答案：12
2. 题目：已知角A的正弦值为1/2，求角A的度数。
难度：易错题
答案：30°
3. 题目：已知角B的余弦值为3/5，求角B的度数。
难度：易错题
答案：53.13°
4. 题目：已知角C的正切值为2，求角C的度数。
难度：难题
答案：63.43°
5. 题目：已知直角三角形的一条直角边为8，角A的正弦值为3/4，求斜边的长度。
难度：难题
答案：10
6. 题目：已知角A的弧度为π/6，求角A的正弦值。
难度：难题
答案：1/2
7. 题目：已知角B的弧度为5π/6，求角B的正切值。
难度：难题
答案：√3
结论
通过解答这些经典习题，学生可以巩固对三角函数的基本概念和相关计算方法的掌握。
这些题目既包括易错题，帮助学生强化知识记忆，又包括难题，提高学生的解题能力。
建议学生针对这些题目进行练习，加深对三角函数的理解和应用能力，从而在考试中取得好成绩。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
九年级《三角函数》知识点、例题、中考真题1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6 当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。
8、解直角三角形的定义：已知边和角（两个，其中必有一边）→所有未知的边和角。
A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边ACA90B 90∠-︒=∠︒=∠+∠得由B A依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。
(注意：尽量避免使用中间数据和除法)9、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
坡度一般写成1:m 的形式，如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
10、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。
11、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。
12、解斜三角形所根据的定理 (在△ABC 中)① 正弦定理：SinCcSinB b SinA a ===2R. (R 是△ABC 外接圆半径). ② 余弦定理： c 2=a 2+b 2－2abCosC ； b 2=c 2+a 2－2ca CosB ； a 2=c 2+b 2－2cbCosA. ③ 互补的两个角的三角函数的关系：Sin(180ο－A)= sinA ， Cos(180ο－A)= － cosA ， tan(180ο－A)=－cotA ， cotA(180ο－A)=－tanA. ④ S △ABC ＝21absinC=21bcsinA=21casinB.三角函数中考试题分类例题解说一、三角函数的定义:i h l=hlα图1例1：（滨州市） 如图1，梯子（长度不变）跟地面所成的锐角为A ，关于A ∠的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）A ．sin A 的值越大，梯子越陡B ．cos A 的值越大，梯子越陡C ．tan A 的值越小，梯子越陡D ．陡缓程度与A ∠的函数值无关分析：由锐角的正切、正弦和余弦的定义可知：锐角的正切、正弦值越大，梯子越陡，余弦值越小，梯子越陡。
因此选A 。
二、利用特殊角的三角函数值计算例4：（辽宁省十二市） 计算：242(2cos 45sin 60)4︒-︒+ 解：23262(2)224=⨯-+原式66222=-+ 2=点评：熟记特殊角的三角函数值是解决此类问题的关键。
三、求线段的长度例5：（云南省） 已知：如图3，在△ABC 中，∠B = 45°，∠C = 60°，AB = 6。
求BC 的长（结果保留根号）．分析：解决此类问题需要根据题意构造直角三角形，在直角三角形中加以研究。
如图4，过点A 作AD ⊥BC 于点D 。
在Rt △ABD 中，∠B =45°，则AD = BD 。
不妨设AD = x ，又AB = 6，所以有x 2＋ x 2= 62，解得x =32，即AD = BD =32。
在Rt △ACD 中，由∠ACD = 60°得∠CAD = 30°而tan30°=CD AD ，即32CD3=3，解得CD =6。
因此BC = BD + DC =32+6。
下面也是2007年关于锐角三角函数的中考题，请自己完成。
1、（江西省） 如图5，在Rt ABC △中，90C ∠=°，a b c ，，分别是A B C ∠∠∠，，的对边，若2b a =，则tan A = ．2、（大连市）在△ABC 中，∠C ＝90°，AB ＝10cm ，sinA ＝54，则BC 的长为___cm 。
3、（丽水市） 如图6，一架梯子斜靠在墙上，若梯子到墙的距离AC =3米，3cos 4BAC ∠=，则梯子AB 的长度为 米。
4、（天津市） οο45cos 45sin +的值等于（ ）A.2B.213+ C.3D. 15、（连云港市）计算：02122sin 45--+o6、（岳阳市）计算：10)21()13(---＋|2-3|＋sin 245°图3图4ACBcb图5图6ABC7、（眉山市） 计算： 2sin450＋cos300·tan600—2)3(8、（中山市） 如图7，Rt △ABC 的斜边AB ＝5，cosA ＝53。
(1)用尺规作图作线段AC 的垂直平分线l(保留作图痕迹，不要求写作法、证明)；(2)若直线l 与AB 、AC 分别相交于D 、E 两点，求DE 的长。
答案：1、12。
2、8。
3、4。
4、A 。
5、2。
6、 12。
7、- 12。
8、2。
图7AC B一、选择题1.（2009·漳州中考）三角形在方格纸中的位置如图所示，则tanα的值是（）A ．35B．43C．34D．452.（2008·威海中考）在△ABC中，∠C＝90°，tan A＝13，则sin B＝（）A．1010B．23C．34D．310103.（2009·湖州中考）如图，在Rt ABC△中，ACB∠=Rt∠，1BC=，2AB=，则下列结论正确的是（）A．3sin2A=B．1tan2A=C．3cos2B=D．tan3B=3 题4题5题4.（2008·温州中考）如图，在Rt ABC△中，CD是斜边AB上的中线，已知2CD=，3AC=，则sin B的值是（）A．23B．32C．34D．435（2007·泰安中考）如图，在ABC△中，90ACB∠=o，CD AB⊥于D，若23AC=，32AB=，则tan BCD∠的值为（）（A）2（B）22（C）6（D）3二、填空题6.（2009·梧州中考）在△ABC中，∠C＝90°，BC＝6 cm，53sin=A，则AB的长是cm．7.（2009·孝感中考）如图，角α的顶点为O，它的一边在x轴的正半轴上，另一边OA上有一点P（3，4），则sinα=．7题8题ACBD8.（2009·庆阳中考）如图，菱形ABCD 的边长为10cm ，DE ⊥AB ，3sin 5A =，则这个菱形的面积= cm 2． 三、解答题9.（2008·宁夏中考）如图，在△ABC 中，∠C =90°，sin A =54，AB =15，求△ABC 的周长和tan A 的值．10.（2007·芜湖中考）如图，在△ABC 中，AD 是BC 上的高，tan cos B DAC =∠，(1) 求证：AC=BD ； (2)若12sin 13C =，BC =12，求AD 的长． 一、选择题2.（2009·长春中考）．菱形OABC 在平面直角坐标系中的位置如图所示，452AOC OC ∠==°，，则点B 的坐标为（ ）A ．2，B ．2)，C ．211)，D ．(121)，3.(2009·定西中考)某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（ ）A ．8米B ．83C ．833米 D ．433米 4.（2008·宿迁中考）已知α为锐角，且23)10sin(=︒-α，则α等于（ ） Ａ．︒50 Ｂ．︒60 Ｃ．︒70 Ｄ．︒805.（2008·毕节中考） A （cos60°，－tan30°）关于原点对称的点A 1的坐标是（ ）A ．1323⎛- ⎝⎭，B ．3323⎛⎫- ⎪ ⎪⎝⎭，C ．1323⎛-- ⎝⎭， D ．1322⎛⎫- ⎪ ⎪⎝⎭，6.（2007·襄樊中考）计算：2cos 45tan 60cos30+o o og 等于（ ）（A ）1 （B ）2 （C ）2 （D ）3 二、填空题7. （2009·荆门中考）104cos30sin 60(2)(20092008)-︒︒+---=______．8.（2009·百色中考）如图，在一次数学课外活动中，测得电线杆底部B 与钢缆固定点C 的距离为4米，钢缆与地面的夹角为60º，则这条钢缆在电线杆上的固定点A 到地面的距离AB 是 米．（结果保留根号）．10.（2007·济宁中考）计算sin 60tan 45cos30︒-︒︒的值是 。
三、解答题11.（2009·黄石中考）计算：3－1+(2π－1)0－33tan30°－tan45° 12.（2009·崇左中考）计算：0200912sin 603tan 30(1)3⎛⎫-++- ⎪⎝⎭°°．要点三、解直角三角形在实际问题中的运用 一、选择题1.（2009·白银中考）某人想沿着梯子爬上高4米的房顶，梯子的倾斜角（梯子与地面的夹角）不能大于60°，否则就有危险，那么梯子的长至少为（ ） A ．8米 B ．83 C 83 D 43米 2.（2009·衢州中考）为测量如图所示上山坡道的倾斜度，小明测得图中所示的数据(单位：米)，则该坡道倾斜角α的正切值是（ ） A ．14B ．4C 17D 173.（2009·益阳中考）如图，先锋村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB 为（ ） A. αcos 5 B.αcos 5C. αsin 5D. αsin 51题2题3题4.（2009·兰州中考）如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4m．如果在坡度为0.75的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（）A．5m B．6m C．7m D．8m4题5题5.(2009·潍坊中考)如图，小明要测量河内小岛B到河边公路l的距离，在A点测得30BAD∠=°，在C点测得60BCD∠=°，又测得50AC=米，则小岛B到公路l的距离为（）米．A．25 B．253C．10033D．25253+二、填空题6.（2009·沈阳中考）如图，市政府准备修建一座高AB＝6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为35，则坡面AC的长度为m．7. （2009·南宁中考）如图，一艘海轮位于灯塔P的东北方向，距离灯塔402海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则海轮行驶的路程AB为_____________海里（结果保留根号）．6题7题8题9题8.(2008·庆阳中考)如图，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，3cos4BAC∠=，则梯子长AB = 米.9.（2007·湖州中考）小明发现在教学楼走廊上有一拖把以15°的倾斜角斜靠在栏杆上，严重影响了同学们的行走安全。