北京科技大学控制实验报告
北京科技大学过程控制实验报告

实验报告课程名称:过程控制系统实验项目名称:被控对象特性测试实验日期与时间: 2022.07 指导教师:班级:姓名:学号:成绩:一、实验目的要求1.了解控制对象特性的基本形式。
2.掌握实验测试对象特性的方法,并求取对象特性参数二、实验内容本节实验内容主要完成测试对象特性,包含以下两部分内容:1.被控对象特性的实验测定本实验采用飞升曲线法(阶跃向应曲线法)测取对象的动特性。
飞升曲线是指输入为阶跃信号时的输出量变化的曲线。
实验时,系统处于开环状态,被控对象在某一状态下稳定一段时间后,输入一阶跃信号,使被控对象达到另一个稳定状态,得到被控对象的飞升曲线。
在实验时应注意以下的一些问题:1)测试前系统应处于正常工作状态,也就是说系统应该是平衡的。
采取一切措施防止其他干扰的发生,否则将影响实验结果。
2)在测试工作中要特别注意工作点与阶跃幅度的选取。
作为测试对象特性的工作点,应该选择正常工作状态,也就是在额定负荷及正常的其他干扰下,因为整个控制过程将在此工作点附近进行。
阶跃作用的取值范围为其额定值的 5-10%。
如果取值太小,由于测量误差及其它干扰的影响,会使实验结果不够准确。
如果取值过大,则非线性影响将扭曲实验结果。
不能获得应有的反应曲线,同时还将使生产长期处于不正常的工作状态,特别是有进入危险区域的可能性,这是生产所不能允许的。
3)实验时,必须特别注意的是,应准确地记录加入阶跃作用的计时起点,注意被调量离开起始点时的情况,以便计算对象滞后的大小,这对以后整定控制器参数具有重要的意义。
4)每次实验应在相同的条件下进行两次以上,如果能够重合才算合格。
为了校验线性,宜作正负两种阶跃进行比较。
也可作不同阶跃量的实验。
2.飞升曲线数据处理在飞升曲线测得以后,可以用多种方法来计算出所测对象的微分方程式,数据处理方法有面积法、图解法、近似法等。
面积法较复杂,计算工作量较大。
近似法误差较大,图解法较方便,误差比近似法小。
控制工程实验报告

控制工程实验报告1. 引言控制工程是一门研究如何通过设计和操作系统来达到预期目标的学科。
实验是控制工程学习过程中重要的一部分,通过实验可以加深对控制理论的理解,提高实际操作能力。
本实验报告旨在总结和分析在进行控制工程实验时所遇到的问题和解决方法。
2. 实验背景本次实验旨在研究单输入单输出(SISO)的控制系统。
通过建模、设计和实施控制器,我们将探讨如何使系统达到期望的性能指标。
在实验过程中,我们使用了控制工程中常用的方法和工具,如PID控制器、校正方法和稳定性分析等。
3. 实验目标本实验的主要目标是设计一个PID控制器来控制一个特定的系统,使其满足给定的性能要求。
具体目标如下: - 理解PID控制器的原理和工作方式; - 利用实验数据建立系统的数学模型; - 利用系统模型设计优化的PID控制器; - 分析和评估实验结果,判断控制系统的稳定性和性能。
4. 实验过程实验分为以下几个步骤: ### 4.1 建立系统模型首先,我们需要对所控制的系统进行建模。
使用传感器收集系统的输入和输出数据,并通过系统辨识方法分析这些数据,得到系统的数学模型。
常用的辨识方法包括最小二乘法和频域分析法。
4.2 设计PID控制器基于系统模型的分析,我们可以设计PID控制器。
通过调整PID控制器的参数,如比例增益、积分时间常数和微分时间常数,我们可以优化控制系统的性能。
4.3 实施控制器将设计好的PID控制器实施到实际系统中。
在实验中,我们需要将传感器和控制器与被控对象连接,并配置合适的控制策略。
4.4 性能评估通过收集系统的输入和输出数据,并利用系统模型进行仿真和分析,我们可以评估控制系统的性能。
常见的评估指标包括超调量、上升时间和稳态误差等。
5. 实验结果与分析根据实验数据和分析结果,我们得到了以下结论: - PID控制器可以有效地控制被控对象,使其稳定在期望值附近; - 通过适当调整PID控制器的参数,我们可以优化控制系统的性能; - 预测模型与实际系统存在一定差异,可能需要进一步改进和校正。
北京科技大学计算机控制系统实验报告

北京科技大学计算机控制系统实验报告计算机控制技术课程实验报告书姓名:班级:学号:专业:学院:指导老师:孙昌国完成日期:2017年4月5日星期三实验一输入与输出通道1、实验目的(1)学习A/D 转换器原理及接口方法,并掌握ADC0809 芯片的使用;(2)学习D/A 转换器原理及接口方法,并掌握TLC7528 芯片的使用。
2、实验内容(1)编写实验程序,将-5V ~ +5V 的电压作为ADC0809 的模拟量输入,将转换所得的8 位数字量保存于变量中。
(2)编写实验程序,实现D/A 转换产生周期性三角波,并用示波器观察波形。
3、实验设备PC 机一台、TD-ACC+实验系统一套、i386EX 系统板一块4、实验原理与步骤4.1 A/D 转换实验原理根据实验内容的第一项要求,可以设计出如图1.1 所示的实验线路图。
单次阶跃模数转换单元控制计算机图1.1 A/D 转换实验线路图图1.1中,AD0809 的启动信号“STR”是由控制计算机定时输出方波来实现的。
“OUT1” 表示386EX 内部1#定时器的输出端,定时器输出的方波周期等于定时器时常。
主程序流程如图1.2所示。
图1.2 主程序流程图4.2A/D转换实验步骤1)按图1.1接线,连接好后,仔细检查,无错误后开启设备电源。
2)装载完程序后,自行设置程序起点,将光标放在起点处,再通过调试菜单项中设置起点或者直接点击设置起点图标,即可将程序起点设在光标处。
3)加入变量监视,打开“设置”菜单项中的“变量监视”窗口或者直接点击“变量监视”图标,将程序中定义的全局变量“AD0~AD9”加入到变量监视中。
4)在主程序JMP AGAIN 语句处设置断点。
5)打开虚拟仪器菜单项中的万用表选项或者直接点击万用表图标,选择“电压档”用示波器单元中的“CH1”表笔测量图1.1中的模拟输入电压“Y”端,点击虚拟仪器中的“运行”按钮,调节图1.1 中的单次阶跃中的电位器,确定好模拟输入电压值。
北科机控实习报告

一、实习背景为了使我对机械控制专业有更深入的了解,提高我的实际操作能力,北京科技大学机械控制专业组织了一次为期两周的实习活动。
此次实习于2022年7月15日至7月29日在某知名企业进行,我作为一名机械控制专业的学生,有幸参加了此次实习。
二、实习目的1. 了解机械控制专业的实际应用,提高自己的专业素养。
2. 培养自己的动手能力和团队合作精神。
3. 提高自己的沟通能力和问题解决能力。
4. 为今后的就业和职业发展打下坚实基础。
三、实习内容1. 实习单位简介此次实习的单位是一家专注于机械控制领域的企业,主要产品包括工业自动化设备、机器人等。
公司拥有先进的生产设备和技术,具备较强的研发实力。
2. 实习岗位及工作内容在实习期间,我担任了机械控制工程师助理的职务。
主要工作内容包括:(1)协助工程师进行机械控制系统的设计、调试和维护。
(2)学习机械控制系统的原理和结构,了解各种控制算法和传感器的工作原理。
(3)协助工程师进行现场设备调试,解决生产过程中出现的问题。
(4)参与团队讨论,提出自己的意见和建议。
3. 实习过程(1)第一阶段:熟悉工作环境和岗位职责在实习的第一周,我主要熟悉了公司的工作环境、同事和岗位职责。
通过和工程师的交流,我对机械控制专业在实际生产中的应用有了初步的了解。
(2)第二阶段:学习机械控制原理和结构在第二周,我开始学习机械控制系统的原理和结构。
通过查阅资料、请教工程师和实际操作,我对各种控制算法和传感器有了更深入的了解。
(3)第三阶段:参与现场设备调试在实习的第三周,我开始参与现场设备的调试工作。
在工程师的指导下,我学会了如何根据设备的技术参数进行调试,并解决了生产过程中出现的一些问题。
四、实习体会与收获1. 提高了自己的专业素养通过此次实习,我对机械控制专业有了更深入的了解,提高了自己的专业素养。
在实习过程中,我学会了如何将理论知识应用到实际工作中,为今后的学习和工作打下了坚实基础。
2. 增强了动手能力和团队合作精神在实习过程中,我积极参与现场设备的调试工作,提高了自己的动手能力。
北京科技大学控制实验报告1

北京科技大学控制实验报告1实验一典型系统的时域响应和稳定性分析一、实验目的1.研究二阶系统的特征参量 (ζ、ωn) 对过渡过程的影响。
2.研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3.熟悉Routh判据,用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台,TD-ACC+教学实验系统一套。
三、实验原理及内容1.典型的二阶系统稳定性分析(1) 结构框图:如图1-1所示。
R(S)+_E(S)1T0 SK1T S+11C(S)图1-1(2) 对应的模拟电路图:如图1-2所示。
1uF20K200K2uFRr(t) 20K_500K__输入20K-C(t)输出10K10K_C (t)输出测量端图1-2(3) 理论分析系统开环传递函数为:G(s)= K1/[(T0S)(T1S+1)] 开环增益: K=K1/T0(4) 实验内容先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中由图1-2,可以确定图1-1中的参数。
T0??, T1??,K1?? ?K??T0 = 1s, T1 = 0.2s, K1 = 200/R, K=200/R系统闭环传递函数为:W(s)?? W(s) = K/(S2+5S+K) 其中自然振荡角频率:?n??√(K/T1)=10√(10/R) ;阻尼比:???。
√(10R)/40 2.典型的三阶系统稳定性分析 (1) 结构框图:如图1-3所示。
R(S)+_E(S)1T0 SK1T 1 S+1K2T 2 S+1C(S)图1-3(2) 模拟电路图:如图1-4所示。
100K1uF500K20K2uF1uFRr(t) 20K_500K_100K__输入10K20K10K_C(t)输出测量端图1-4(3) 理论分析系统的开环传函为:G(s)H(s)?? G(s)H(s) = (500/R)/[s(0.1s+1)(0.5s+1)]系统的特征方程为:1?G(s)H(s)?0。
实验二北京科技大学自控实验(3)
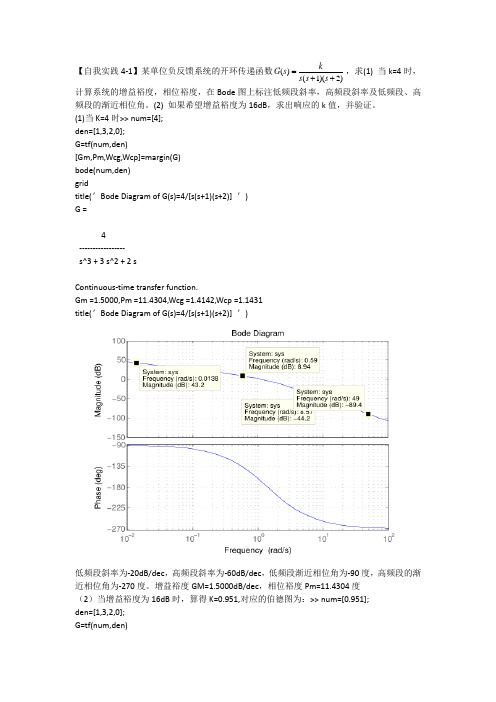
【自我实践4-1】某单位负反馈系统的开环传递函数()(1)(2)kG s s s s =++,求(1) 当k=4时,计算系统的增益裕度,相位裕度,在Bode 图上标注低频段斜率,高频段斜率及低频段、高频段的渐近相位角。
(2) 如果希望增益裕度为16dB ,求出响应的k 值,并验证。
(1)当K=4时>> num=[4]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G =4----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =1.5000,Pm =11.4304,Wcg =1.4142,Wcp =1.1431 title(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′)低频段斜率为-20dB/dec ,高频段斜率为-60dB/dec ,低频段渐近相位角为-90度,高频段的渐近相位角为-270度。
增益裕度GM=1.5000dB/dec ,相位裕度Pm=11.4304度 (2)当增益裕度为16dB 时,算得K=0.951,对应的伯德图为:>> num=[0.951]; den=[1,3,2,0]; G=tf(num,den)[Gm,Pm,Wcg,Wcp]=margin(G) bode(num,den) gridtitle(′Bode Diagram of G(s)=4/[s(s+1)(s+2)] ′) G = 0.951 ----------------- s^3 + 3 s^2 + 2 sContinuous -time transfer function.Gm =6.3091,Pm =54.7839,Wcg =1.4142,Wcp =0.4276 title(′Bode Diagram ′)【自我实践4-2】系统开环传递函数()(0.51)(0.11)kG s s s s =++,试分析系统的稳定性。
控制原理实验报告

一、实验目的1. 理解控制原理的基本概念和基本方法;2. 掌握控制系统的分析和设计方法;3. 培养实验操作能力和数据处理能力。
二、实验原理控制原理是研究如何使系统按照既定的规律进行运动和变化的一门学科。
控制系统的基本组成包括控制器、被控对象和反馈环节。
本实验主要研究线性控制系统的稳定性、稳态误差和动态性能。
三、实验仪器与设备1. 控制系统实验箱;2. 示波器;3. 计算机及控制软件。
四、实验内容及步骤1. 系统稳定性分析(1)搭建实验系统:将控制系统实验箱中的被控对象和控制器按照实验要求连接,确保电路连接正确。
(2)进行实验:打开控制系统实验箱,启动计算机及控制软件,设置实验参数,进行系统稳定性分析。
(3)数据处理:观察示波器显示的波形,记录实验数据,分析系统稳定性。
2. 系统稳态误差分析(1)搭建实验系统:与稳定性分析实验相同。
(2)进行实验:设置实验参数,进行系统稳态误差分析。
(3)数据处理:观察示波器显示的波形,记录实验数据,分析系统稳态误差。
3. 系统动态性能分析(1)搭建实验系统:与稳定性分析实验相同。
(2)进行实验:设置实验参数,进行系统动态性能分析。
(3)数据处理:观察示波器显示的波形,记录实验数据,分析系统动态性能。
五、实验结果与分析1. 系统稳定性分析根据实验数据,绘制系统开环传递函数的波特图,分析系统稳定性。
通过比较实验数据与理论分析结果,验证控制系统的稳定性。
2. 系统稳态误差分析根据实验数据,计算系统稳态误差,分析系统稳态性能。
通过比较实验数据与理论分析结果,验证控制系统的稳态性能。
3. 系统动态性能分析根据实验数据,绘制系统阶跃响应曲线,分析系统动态性能。
通过比较实验数据与理论分析结果,验证控制系统的动态性能。
六、实验总结1. 通过本次实验,掌握了控制原理的基本概念和基本方法;2. 熟悉了控制系统实验箱的操作和实验步骤;3. 提高了实验操作能力和数据处理能力;4. 发现了理论分析与实际操作之间的差异,为今后的学习和工作积累了经验。
控制系统实训实验报告

一、实验目的1. 了解控制系统的基本组成和原理。
2. 掌握控制系统调试和性能测试方法。
3. 培养动手能力和团队协作精神。
4. 熟悉相关实验设备和软件的使用。
二、实验原理控制系统是指通过某种方式对某个系统进行控制,使其按照预定的要求进行运行。
控制系统主要由控制器、被控对象和反馈环节组成。
控制器根据被控对象的输出信号,通过调节输入信号,实现对被控对象的控制。
本实验主要研究PID控制系统的原理和应用。
三、实验仪器与设备1. 实验箱:用于搭建控制系统实验电路。
2. 数据采集卡:用于采集实验数据。
3. 计算机:用于运行实验软件和数据处理。
4. 实验软件:用于控制系统仿真和调试。
四、实验内容1. 控制系统搭建:根据实验要求,搭建PID控制系统实验电路,包括控制器、被控对象和反馈环节。
2. 控制系统调试:对搭建好的控制系统进行调试,包括控制器参数的整定、系统稳定性和响应速度的调整等。
3. 控制系统性能测试:对调试好的控制系统进行性能测试,包括系统稳定性、响应速度、超调量等指标。
4. 控制系统仿真:利用实验软件对控制系统进行仿真,分析系统在不同参数下的性能。
五、实验步骤1. 控制系统搭建:按照实验要求,连接控制器、被控对象和反馈环节,搭建PID控制系统实验电路。
2. 控制系统调试:根据实验要求,调整控制器参数,使系统达到预定的性能指标。
3. 控制系统性能测试:对调试好的控制系统进行性能测试,记录测试数据。
4. 控制系统仿真:利用实验软件对控制系统进行仿真,分析系统在不同参数下的性能。
六、实验结果与分析1. 控制系统搭建:成功搭建了PID控制系统实验电路。
2. 控制系统调试:通过调整控制器参数,使系统达到预定的性能指标。
3. 控制系统性能测试:系统稳定性、响应速度、超调量等指标均达到预期效果。
4. 控制系统仿真:仿真结果表明,系统在不同参数下具有良好的性能。
七、实验总结1. 通过本次实验,了解了控制系统的基本组成和原理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 利用MATLAB 进行时域分析一、实验目的(1) 学会使用MATLAB 编程绘制控制系统的单位阶跃响应曲线;(2) 研究二阶控制系统中,?、?n 对系统动态特性和时域指标的影响; (3) 掌握准确读取动态特性指标的方法;(4) 分析二阶系统闭环极点和闭环零点对系统动态性能的影响;(5) 研究三阶系统单位阶跃响应及其动态性能指标与其闭环极点的关系; (6) 研究闭环极点和闭环零点对高阶系统动态性能的影响; (7) 了解高阶系统中主导极点与偶极子的作用;(8) 了解系统阶跃响应、脉冲响应和斜坡响应输出曲线之间的联系与差别。
二、实验原理及内容 1. 求系统的特征根若已知系统的特征多项式D (s),利用roots ( ) 函数可以求其特征根。
若已知系统的传递函数,利用eig ( ) 函数可以直接求出系统的特征根。
2、求系统的闭环根、ζ和ωn函数damp ( ) 可以计算出系统的闭环根、ζ和?n 。
3、零极点分布图可利用pzmap()函数绘制连续系统的零、极点图,从而分析系统的稳定性,调用格式为: pzmap(num,den)【范例3-1】给定传递函数:2724364523)(2345234+++++++++=s s s s s s s s s s G 利用下列命令可自动打开一个图形窗口,显示该系统的零、极点分布图,如错误!未找到引用源。
所示。
>> num=[3,2,5,4,6]; den=[1,3,4,2,7,2];pzmap(num,den)title(1Pole-Zero Map1) % 图形标题。
图3- 1 MATLAB 函数零、极点分布图4、求系统的单位阶跃响应step ( ) 函数可以计算连续系统单位阶跃响应(impulse( ) 函数可以计算连续系统单位脉冲响应):step (sys) 或step ( sys , t ) 或step (num , den)函数在当前图形窗口中直接绘制出系统的单位阶跃响应曲线,对象sys 可以由tf ( ),zpk ( ) 函数中任何一个建立的系统模型。
第二种格式中t 可以指定一个仿真终止时间,也可以设置为一个时间矢量(如t =0 : dt : Tfinal ,即dt 是步长,Tfinal 是终止时刻)。
如果需要将输出结果返回到MATLAB 工作空间中,则采用以下调用格式: c=step(sys)此时,屏上不会显示响应曲线,必须利用plot()命令查看响应曲线。
plot 可以根据两个或多个给定的向量绘制二维图形。
【范例3-2】已知传递函数为:25425)(2++=s s s G利用以下MATLAB 命令可得阶跃响应曲线如错误!未找到引用源。
所示。
>> num=[0,0,25]; den=[1,4,25];step(num,den)grid % 绘制网格线。
title(1Unit-Step Response of G(s)=25/(s^2+4s+25) 1) % 图像标题图3- 2 MATLAB 绘制的响应曲线还可以用下面的语句来得出阶跃响应曲线 >> G=tf([0,0,25],[1,4,25]);t=0::5; % 从0到5每隔取一个值。
c=step(G,t); % 动态响应的幅值赋给变量cplot(t,c) % 绘二维图形,横坐标取t ,纵坐标取c 。
Css=dcgain(G) % 求取稳态值。
系统显示的图形类似于上一个例子,在命令窗口中显示了如下结果 Css= 15、求阶跃响应的性能指标MATLAB 提供了强大的绘图计算功能,可以用多种方法求取系统的动态响应指标。
首先介绍一种最简单的方法――游动鼠标法。
对于例2,在程序运行完毕后,在曲线中空白区域,单击鼠标右键,在快捷菜单中选择”characteristics ”,包含:Peak response (峰值); settling time (调节时间);Rise time(上升时间);steady state(稳态值);在相应位置出现相应点,用鼠标单击后,相应性能值就显示出来。
用鼠标左键点击时域响应曲线任意一点,系统会自动跳出一个小方框,小方框显示了这一点的横坐标(时间)和纵坐标(幅值)。
这种方法简单易用,但同时应注意它不适用于用plot()命令画出的图形。
【自我实践1】若已知单位负反馈前向通道的传递函数为:2100()5G s s s=+,试作出其单位阶跃响应曲线,准确读出其动态性能指标,并记录数据。
另一种比较常用的方法就是用编程方式求取时域响应的各项性能指标。
与游动鼠标法相比,编程方法稍微复杂,但可以获取一些较为复杂的性能指标。
若将阶跃响应函数step( )获得系统输出量返回到变量y 中,可以调用如下格式 [y,t]=step(G)该函数还同时返回了自动生成的时间变量t ,对返回变量y 和t 进行计算,可以得到时域性能指标。
① 峰值时间(timetopeak)可由以下命令获得:[Y,k]=max(y); timetopeak=t(k)②最大(百分比)超调量(percentovershoot)可由以下命令得到:C=dcgain(G);[Y,k]=max(y);percentovershoot=100*(Y-C)/Cdcgain( )函数用于求取系统的终值。
③上升时间(risetime)可利用MATLAB中控制语句编制M文件来获得。
要求出上升时间,可以用while语句编写以下程序得到:C=dcgain(G);n=1;while y(n)<Cn=n+1;endrisetime=t(n)在阶跃输入条件下,y 的值由零逐渐增大,当以上循环满足y=C时,退出循环,此时对应的时刻,即为上升时间。
对于输出无超调的系统响应,上升时间定义为输出从稳态值的10%上升到90%所需时间,则计算程序如下:C=dcgain(G);n=1;while y(n)<*Cn=n+1;endm=1;while y(n)<*Cm=m+1;endrisetime=t(m)-t(n)④调节时间(setllingtime)可由while语句编程得到:C=dcgain(G);i=length(t);while(y(i)>*C)&(y(i)<*C)i=i-1;endsetllingtime=t(i)用向量长度函数length( )可求得t序列的长度,将其设定为变量i的上限值。
自我检测1:>> G1=tf([0,0,100],[1,5,0]);G2=1;G=feedback(G1,G2)Transfer function:100---------------s^2 + 5 s + 100>> num=[0,0,100];>> den=[1,5,100];>> step(num,den)>> grid>> title('Unit-Step Response') >>上升时间:;峰值时间:;调节时间:;超调:42% 稳态值:1【范例3-3】已知二阶系统传递函数为:)31)(31(3)(i s i s s G ++-+=利用下面的程序可得到阶跃响应如错误!未找到引用源。
及性能指标数据。
>> G=zpk([ ],[-1+3*i,-1-3*i ],3); % 计算最大峰值时间和超调量。
C=dcgain(G) [y,t]=step(G);plot(t,y) grid[Y,k]=max(y); timetopeak=t(k)percentovershoot=100*(Y-C)/C % 计算上升时间。
n=1;while y(n)<C n=n+1; endrisetime=t(n)% 计算调节时间。
i=length(t);while(y(i)>*C)&(y(i)<*C)i=i-1;endsetllingtime=t(i)运行后的响应图如错误!未找到引用源。
,命令窗口中显示的结果为C = timetopeak =percentovershoot = risetime =setllingtime =图3-3 二阶系统阶跃响应用游动鼠标法求取此二阶系统的各项性能指标与本例是一致的。
6、分析ωn不变时,改变阻尼比?,观察闭环极点的变化及其阶跃响应的变化。
【自我实践2】二阶系统,ωn=10,当?=0,,,,1,时,求对应系统的闭环极点、自然振荡频率及阶跃响应曲线;并分析?对系统性能的影响。
参考程序:阶跃响应曲线:00.20.40.60.81 1.2 1.4 1.6 1.820.20.40.60.811.21.41.61.82ξ=0ξ=0.25ξ=0.5ξ=0.75ξ=1ξ=1.25阻尼比不同时的阶跃响应曲线Time (sec)A m p l i t u d e自我实践2: >> num=100;i=0; for sigma = 0::den = [1 2*sigma*10 100]; damp(den)sys = tf(num,den);i=i+1;step(sys,2)hold onendEigenvalue Damping Freq. (rad/s)+000 + +001i +000 +001+000 - +001i +000 +001Eigenvalue Damping Freq. (rad/s)+000 + +000i +001+000 - +000i +001Eigenvalue Damping Freq. (rad/s)+000 + +000i +001+000 - +000i +001Eigenvalue Damping Freq. (rad/s)+000 + +000i +001+000 - +000i +001Eigenvalue Damping Freq. (rad/s)+001 +000 +001+001 +000 +001Eigenvalue Damping Freq. (rad/s)+001 +000 +001+000 +000 +000>> gridhold offtitle('阻尼比不同时的阶跃响应曲线')lab1='zunibi = 0';text,,lab1),lab2='zunibi = ';text,,lab2),>> lab3='zunibi = ';text,,lab3),lab4='zunibi = ';text(0,3,,lab4),lab5='zunibi = 1';text(0,35,,lab5),lab6='zunibi = ';text(0,35,,lab6)>>ωn不变时,改变阻尼比?,当ξ>1时,系统为过阻尼系统,系统的阶跃响应为非震荡过程,瞬态特性为单调变化曲线,无超调和震荡;当0<ξ<1时,系统为欠阻尼系统,系统的阶跃响应为非震荡过程,ξ越小,超调量越大,震荡次数越多,调节时间越长。
