高中化学 晶体结构的分析与计算
高中化学知识点复习 晶体计算类型归纳

面(实际为椅式结构),碳原子为 sp3 杂化
(3)每个碳原子被 12 个六元环共用,每个共价键被 6 个六元环共用,一个六元
1
环实际拥有 个碳原子
2
(4)C 原子数与 C—C 键数之比为 1∶2,12g 金刚石中有 2 mol 共价键
(5)密度=8×12 g·mol-1 NA×a3
(a 为晶胞边长,NA 为阿伏加德罗常数)
NA×a3
离子晶体的配位数
离子晶体中与某离子距离最近的异性离子的数目叫该离子的配位数
(1)正、负离子半径比:AB 型离子晶体中,阴、阳离子的配位数相等,但正、
影响离子晶体配位数的因素
负离子半径比越大,离子的配位数越大。如:ZnS、NaCl、CsCl (2)正、负离子的电荷比。如:CaF2 晶体中,Ca2+和 F-的配位数不同
晶体
晶体结构
结构分析
干冰
(1)面心立方最密堆积:立方体的每个顶点有一个 CO2 分子,每个面上也有一
个 CO2 分子,每个晶胞中有 4 个 CO2 分子
(2)每个 CO2 分子周围等距且紧邻的 CO2 分子有 12 个
(3)密度=4×44 g·mol-1 NA×a3
(a 为晶胞边长,NA 为阿伏加德罗常数)
Cu Ag Au 12 4
2 a=4r
2
Mg Zn Ti 12
6或2
——
(2)金属晶胞中原子空间利用率计算: 空间利用率 V球
球数 4 r3
3
V晶胞
a3
①简单立方堆积:如图所示,原子的半径为 r,立方体的棱长为 2r,则 V 球=43πr3,V 晶胞=(2r)3=8r3,空间利
(4)在 NaCl 晶体中,每个 Na+周围与它最接近且距离相等的 Na+共有 12 个,
晶体结构计算范文

晶体结构计算范文一、晶体结构计算的原理和方法晶体结构是由一个个原子或离子组成的有序排列,这种有序排列在结晶体中呈现出周期性的空间分布。
晶体结构计算的主要目标是确定晶体中原子的准确位置和其之间的相互作用,以及晶格参数等信息。
晶体结构计算的方法主要有实验方法、理论计算方法和模拟方法等。
实验方法包括X射线衍射、电子衍射、中子衍射等,通过分析衍射的图样可以确定晶体的结构。
理论计算方法主要是基于量子力学原理,包括密度泛函理论、分子力学等,通过计算得到晶体的能量、晶格参数和原子位置等信息。
模拟方法主要有分子动力学模拟、蒙特卡洛模拟等,模拟系统的原子运动和相互作用,从而得到晶体的结构和性质。
二、晶体结构计算的应用晶体结构计算在材料科学、物理化学等领域具有广泛的应用。
首先,晶体结构计算可以用于研究材料的物理和化学性质。
通过计算分析可以预测材料的电子能带结构、光学性质、磁性等,为材料的设计和应用提供理论基础。
其次,晶体结构计算可以用于材料的合成和工艺优化。
通过计算和模拟可以预测材料的晶体生长行为,优化合成工艺,提高材料的质量和性能。
此外,晶体结构计算还可以用于研究材料的相变过程、相图和微观性质变化等,对材料的相变机制和性质变化规律进行深入研究。
三、晶体结构计算的实际案例展示为了更好地展示晶体结构计算的应用,我们以典型的半导体材料硅Sio2为例进行分析。
硅是一种广泛应用于电子器件中的材料,其结构具有平面型和空间型两种。
通过晶体结构计算可以得到硅的结构参数、晶体中原子的位置等信息。
首先,通过X射线衍射实验可以得到硅的晶胞结构和晶格参数。
然后,利用密度泛函理论和分子动力学模拟等方法进行计算分析,得到硅晶体中原子的位置以及相互作用等信息。
通过计算和模拟可以发现硅晶体中的晶格缺陷、晶界和表面等问题,并对其进行优化和修复,得到具有优异性能的硅晶体材料。
在实际应用中,硅晶体的结构计算可以用于电子器件的设计和性能优化。
通过模拟和计算可以预测材料的电子能带结构,优化器件的导电性能和光学特性,提高器件的效率和可靠性。
高中化学新教材同步选择性必修第二册第3章微专题6:晶体结构的分析与计算
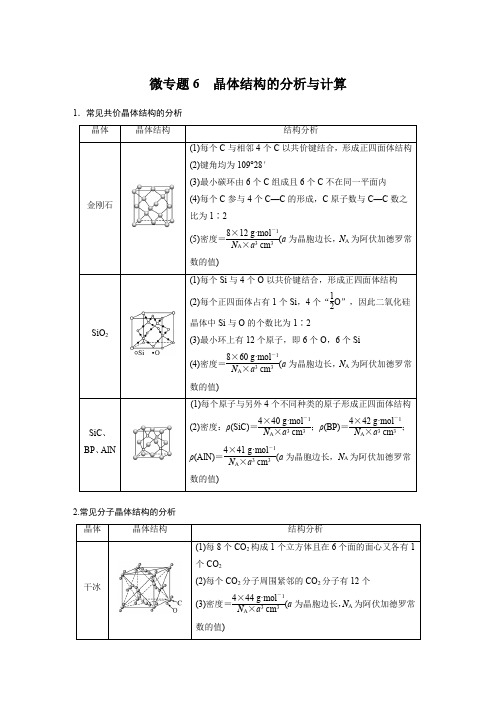
微专题6晶体结构的分析与计算1.常见共价晶体结构的分析晶体晶体结构结构分析金刚石(1)每个C与相邻4个C以共价键结合,形成正四面体结构(2)键角均为109°28′(3)最小碳环由6个C组成且6个C不在同一平面内(4)每个C参与4个C—C的形成,C原子数与C—C数之比为1∶2(5)密度=8×12 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiO2(1)每个Si与4个O以共价键结合,形成正四面体结构(2)每个正四面体占有1个Si,4个“12O”,因此二氧化硅晶体中Si与O的个数比为1∶2(3)最小环上有12个原子,即6个O,6个Si(4)密度=8×60 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiC、BP、AlN (1)每个原子与另外4个不同种类的原子形成正四面体结构(2)密度:ρ(SiC)=4×40 g·mol-1N A×a3 cm3;ρ(BP)=4×42 g·mol-1N A×a3 cm3;ρ(AlN)=4×41 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)2.常见分子晶体结构的分析晶体晶体结构结构分析干冰(1)每8个CO2构成1个立方体且在6个面的面心又各有1个CO2(2)每个CO2分子周围紧邻的CO2分子有12个(3)密度=4×44 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)白磷密度=4×124 g·mol-1N A×a 3 cm 3(a为晶胞边长,N A为阿伏加德罗常数的值)3.常见离子晶体结构的分析NaCl型CsCl型ZnS型CaF2型晶胞配位数684F-:8;Ca2+:4密度的计算(a为晶胞边长,N A为阿伏加德罗常数的值)4×58.5 g·mol-1N A×a3 cm3168.5 g·mol-1N A×a3 cm34×97 g·mol-1N A×a3 cm34×78 g·mol-1N A×a3 cm31.AB型化合物形成的晶体结构多种多样。
几种典型晶体结构的特点分析(精)

几种典型晶体结构的特点分析徐寿坤有关晶体结构的知识是高中化学中的一个难点,它能很好地考查同学们的观察能力和三维想像能力,而且又很容易与数学、物理特别是立体几何知识相结合,是近年高考的热点之一。
熟练掌握NaCl 、CsCl 、CO 2、SiO 2、金刚石、石墨、C 60等晶体结构特点,理解和掌握一些重要的分析方法与原则,就能顺利地解答此类问题。
通常采用均摊法来分析这些晶体的结构特点。
均摊法的根本原则是:晶胞任意位置上的原子如果是被n 个晶胞所共有,则每个晶胞只能分得这个原子的1/n 。
1. 氯化钠晶体由下图氯化钠晶体结构模型可得:每个Na +紧邻6个-Cl ,每个-Cl 紧邻6个+Na (上、下、左、右、前、后),这6个离子构成一个正八面体。
设紧邻的Na +-a ,每个Na +与12个Na +等距离紧邻(同层4个、上层4个、下层4个),距离为a 2。
由均摊法可得:该晶胞中所拥有的Na +数为4216818=⨯+⨯,-Cl 数为441121=⨯+,晶体中Na +数与Cl -数之比为1:12. 氯化铯晶体每个Cs +紧邻8个-Cl -紧邻8个Cs +,这8个离子构成一个正立方体。
设紧邻的Cs +与Cs +间的距离为a 23,则每个Cs +与6个Cs +等距离紧邻(上、下、左、右、前、后)。
在如下图的晶胞中Cs +数为812164112818=+⨯+⨯+⨯,-Cl 在晶胞内其数目为8,晶体中的+Cs 数与-Cl 数之比为1:1,则此晶胞中含有8个CsCl 结构单元。
3. 干冰每个CO 2分子紧邻12个CO 2分子(同层4个、上层4个、下层4个),则此晶胞中的CO 2分子数为4216818=⨯+⨯。
4. 金刚石晶体每个C 原子与4个C 原子紧邻成键,由5个C 原子形成正四面体结构单元,C-C 键的夹角为'28109︒。
晶体中的最小环为六元环,每个C 原子被12个六元环共有,每个C-C 键被6个六元环共有,每个环所拥有的C 原子数为211216=⨯,拥有的C-C 键数为1616=⨯,则C 原子数与C-C 键数之比为2:11:21=。
高三化学二轮复习 晶胞结构及相关计算

(6) 均摊法
②方法 B. 非长方体晶胞中粒子视具体情况而定:
a.三棱柱
b.六棱柱
1/4 底边
顶点 1/12
1/4 底边
1/2 侧面 1/2 底面
侧棱 1/6 内部 1
1/2 侧面 1/2 底面
顶点 1/6 侧棱 1/3 内部 1
知识梳理
(7) 熟记几种常见的晶胞结构及晶胞含有的粒子数目。当题中信息给出的某种晶胞空间结 构与常见晶胞的空间结构相同时,可以直接套用该种结构。
62
1
5
知识梳理
(6) 均摊法 ②方法 A. 长方体(包括立方体)晶胞中不同位置的微粒数的计算方法如:1/2
棱上:1/4
知识梳理
(6) 均摊法 ②方法 A. 长方体(包括立方体)晶胞中不同位置的微粒数的计算方法如图所示:
面心:1/2
2
1
1
体内:全部 属于该晶胞
1
知识梳理
知识梳理
一、晶胞 (4)晶胞结构的分析 判断某种微粒周围等距且紧邻的微粒数目时,要注意运用三维想象法。
NaCl
Na+周围的Na+数目,每个面上有4个,共计12个。
知识梳理
一、晶胞 (5)晶胞中微粒配位数
概念:在晶体中与离子(或原子)直接相连的离子(或原子 )数目。 理解为:距离某微粒最近且等距的粒子的数目。
A.在晶体学中配位数与晶胞类型有关;
知识梳理
一、晶胞 (5)晶胞中微粒配位数 A.在晶体学中配位数与晶胞类型有关;
复式面心立方 6
复式简单立方 8
六方最密堆积 12
知识梳理
(5)晶胞中微粒配位数 B.离子晶体中指一个离子周围最近的异电性离子的数目;
距Na+最近的Cl-有6个, Na+的上、下、左、右、 前、后。
高中化学第3章晶体结构与性质研究与实践明矾晶体的制备新人教版选择性必修2

3.制备明矾晶体的实验步骤 (1) 在 玻 璃 杯 中 放 入 比 室 温 高 10 ~ 20 ℃ 的 水 , 并 加 入 明 矾 晶 体 [KAl(SO4)2·12H2O],用筷子搅拌,直到有少量晶体不能再溶解。此时得 到的溶液为饱和溶液。 (2)待溶液自然冷却到比室温略高3~5 ℃时,把溶液倒入洁净的碗 中,用硬纸片盖好,静置一夜。 (3)从碗中选取2~3粒形状完整的小晶体作为晶核。将所选的晶核用 细线轻轻系好。
(2) 晶 体 B 的 主 要 成 分 是 _____K_N__O_3______ , 含 有 的 少 量 杂 质 是 ______N_a_C__l_____,要除去晶体B中的少量杂质的方法是__ቤተ መጻሕፍቲ ባይዱ_重__结__晶____。
(3)用少量热水淋洗晶体也是一种除去晶体中少量杂质的方法,这种 方法适用于晶体___A___(填“A”或“B”)。
有关装置如图,回答下列问题:
(1) 通 入 HCl 的 作 用 是 抑 制 AlCl3 水 解 和 ________增__加___c(_C__l-__),__有___利_ _于__A_lC__l3_·_6_H_2_O__结__晶_______。
(2) 步 骤 Ⅰ 中 抽 滤 时 , 用 玻 璃 纤 维 替 代 滤 纸 的 理 由 是 __溶__液___有___强_ _酸__性__,__会__腐__蚀__滤__纸____,洗涤时,合适的洗涤剂是__饱__和__氯__化__铝__溶__液___。
4.试讨论快速制备明矾晶体的条件。 提示:①溶液一定要用饱和溶液,若溶液不饱和,则结晶速度很 慢。 ②溶剂应用蒸馏水,不能用自来水。因自来水里含其他金属离子及 杂质,会影响晶体的生长速度和形状。 ③冷却热饱和溶液时,应自然冷却。快速冷却虽能够得到晶体,但 属于沉底、细小晶体,得不到大晶体。温度下降越快,晶体越小。 ④溶液一定要纯净。里面若含有杂质,就在溶液中形成多个晶核, 这样不利于大晶体的生长。
晶体结构——晶胞计算鲁科版高中化学选修

晶体结构——晶胞计算鲁科版高中化学选修晶体结构是指晶体中原子或离子的排列方式和几何结构。
晶体结构的研究对于理解晶体的性质和物理化学现象至关重要。
在化学选修课程中,晶体结构是一个重要的知识点,通过学习晶体结构的相关理论和计算方法,可以加深对晶体结构和性质的理解。
晶体结构的计算主要基于晶胞的概念。
晶胞是指晶体中最小的周期性结构单元,通过复制和堆积晶胞,构成了整个晶体的结构。
晶胞一般是一个或多个原子或离子所组成的空间集合体,晶胞中包含了晶体中所有原子或离子的信息。
晶胞的计算需要通过晶体学标准符号来描述晶体的结构类型。
晶体学标准符号包括晶胞的晶格参数和晶胞的角度,通过这些参数可以确定晶体的晶胞类型。
晶胞有多种类型,常见的有立方晶系、四方晶系、正交晶系、斜方晶系、单斜晶系和三斜晶系。
每一种晶胞类型都有其特定的晶格参数和角度范围。
晶胞的计算还需要确定晶胞内原子或离子的排列方式和坐标位置。
一般情况下,晶胞内的原子或离子是有序排列的,根据晶格的对称性,可以通过推导和计算确定原子或离子的位置。
晶胞内的原子或离子的位置通常用晶胞坐标或直角坐标表示,以便计算和描述晶体的结构。
在晶体结构的计算中,晶胞的参数和原子或离子的位置可以通过实验方法或计算方法获得。
实验方法包括X射线衍射、电子衍射和中子衍射等,这些方法可以通过分析衍射图案来确定晶体的结构。
计算方法主要包括理论计算和模拟计算,通过建立晶体结构的模型和应用物理化学理论进行计算,可以得到晶胞参数和原子或离子的位置。
晶体结构的计算在理论和实际应用中都有重要的意义。
在理论方面,晶体结构的计算可以帮助研究人员深入理解晶体的基本结构和性质,探索晶体中物质的行为和相互作用。
在应用方面,晶体结构的计算可以用于材料设计和功能材料的开发。
通过计算晶体结构,可以预测材料的物理化学性质,指导材料合成和工艺流程优化。
总之,在高中化学选修课程中学习晶体结构的相关理论和计算方法,可以帮助学生深入理解晶体的基本结构和性质,为进一步学习和研究材料科学奠定基础。
高中化学 几种常见晶体结构分析论文 新人教版选修3

几种常见晶体结构分析一、氯化钠、氯化铯晶体——离子晶体由于离子键无饱和性与方向性,所以离子晶体中无单个分子存在。
阴阳离子在晶体中按一定的规则排列,使整个晶体不显电性且能量最低。
离子的配位数分析如下:离子数目的计算:在每一个结构单元(晶胞)中,处于不同位置的微粒在该单元中所占的份额也有所不同,一般的规律是:顶点上的微粒属于该单元中所占的份额为18,棱上的微粒属于该单元中所占的份额为14,面上的微粒属于该单元中所占的份额为12,中心位置上(嚷里边)的微粒才完全属于该单元,即所占的份额为1。
1.氯化钠晶体中每个Na +周围有6个C l -,每个Cl -周围有6个Na +,与一个Na +距离最近且相等的Cl -围成的空间构型为正八面体。
每个N a +周围与其最近且距离相等的Na +有12个。
见图1。
晶胞中平均Cl -个数:8×18 + 6×12 = 4;晶胞中平均Na +个数:1 + 12×14= 4 因此NaCl 的一个晶胞中含有4个NaCl (4个Na +和4个Cl -)。
2.氯化铯晶体中每个Cs +周围有8个Cl -,每个Cl -周围有8个Cs +,与一个Cs +距离最近且相等的Cs +有6个。
晶胞中平均Cs +个数:1;晶胞中平均Cl -个数:8×18= 1。
因此CsCl 的一个晶胞中含有1个CsCl (1个Cs +和1个Cl -)。
二、金刚石、二氧化硅——原子晶体1.金刚石是一种正四面体的空间网状结构。
每个C 原子以共价键与4个C 原子紧邻,因而整个晶体中无单个分子存在。
由共价键构成的最小环结构中有6个碳原子,不在同一个平面上,每个C 原子被12个六元环共用,每C —C 键共6个环,因此六元环中的平均C 原子数为6×112 = 12 ,平均C —C 键数为6×16 = 1。
C 原子数: C —C 键键数 = 1:2; C 原子数: 六元环数 = 1:2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶体结构的分析与计算1.(2015·全国卷Ⅰ)碳有多种同素异形体,其中石墨烯与金刚石的晶体结构如图所示:(1)在石墨烯晶体中,每个C 原子连接________个六元环,每个六元环占有________个C 原子。
(2)在金刚石晶体中,C 原子所连接的最小环也为六元环,每个C 原子连接______个六元环,六元环中最多有______个C 原子在同一平面。
解析:(1)由石墨烯的结构可知,每个C 原子连接3个六元环,每个六元环占有的C 原子数为13×6=2。
(2)由金刚石的结构可知,每个C 可参与形成4条C —C 键,其中任意两条边(共价键)可以构成2个六元环。
根据组合知识可知四条边(共价键)任选其中两条有6组,6×2=12。
因此每个C 原子连接12个六元环。
六元环中C 原子采取sp 3杂化,为空间六边形结构,最多有4个C 原子位于同一平面。
答案:(1)3 2 (2)12 42.(2016·全国卷Ⅱ)某镍白铜合金的立方晶胞结构如图所示。
(1)晶胞中铜原子与镍原子的数量比为________。
(2)若合金的密度为d g·cm -3,晶胞参数a =________nm 。
解析:(1)由晶胞结构图可知,Ni 原子处于立方晶胞的顶点,Cu 原子处于立方晶胞的面心,根据均摊法,每个晶胞中含有Cu 原子的个数为6×12=3,含有Ni 原子的个数为8×18=1,故晶胞中Cu 原子与Ni 原子的数量比为3∶1。
(2)根据m =ρV 可得, 1 mol 晶胞的质量为(64×3+59)g =a 3×d g·cm -3×N A ,则a =⎝⎛⎭⎫2516.02×1023×d 13cm =⎝⎛⎭⎫2516.02×1023×d 13×107 nm 。
答案:(1)3∶1 (2)⎝⎛⎭⎫2516.02×1023×d 13×107 3.(2017·全国卷Ⅰ)(1)KIO 3晶体是一种性能良好的非线性光学材料,具有钙钛矿型的立方结构,边长为a =0.446 nm ,晶胞中K 、I 、O分别处于顶角、体心、面心位置,如图所示。
K 与O 间的最短距离为______ nm ,与K 紧邻的O 个数为_____。
(2)在KIO 3晶胞结构的另一种表示中,I 处于各顶角位置,则K 处于________位置,O 处于________位置。
解析:(1)二者间的最短距离为晶胞面对角线长的一半,即22×0.446 nm ≈0.315 nm 。
由于K 、O 分别位于晶胞的顶角和面心,所以与钾紧邻的氧原子有12个。
(2)想象4个晶胞紧密堆积,则I 处于顶角,O 处于棱心,K 处于体心。
答案:(1)0.315 12 (2)体心 棱心4.(2016·全国卷Ⅰ)锗(Ge)是典型的半导体元素,在电子、材料等领域应用广泛。
(1)原子坐标参数,表示晶胞内部各原子的相对位置。
如图为Ge 单晶的晶胞,其中原子坐标参数A 为(0,0,0);B 为⎝⎛⎭⎫12,0,12;C 为⎝⎛⎭⎫12,12,0。
则D 原子的坐标参数为________。
(2)晶胞参数,描述晶胞的大小和形状。
已知Ge 单晶的晶胞参数a =565.76 pm ,其密度为________g·cm -3(列出计算式即可)。
解析:(1)根据题给图示可知,D 原子的坐标参数为⎝⎛⎭⎫14,14,14。
(2)每个晶胞中含有锗原子8×1/8+6×1/2+4=8个,每个晶胞的质量为8×73N Ag ,晶胞的体积为(565.76×10-10 cm)3,所以晶胞的密度为8×73N A ×(565.76×10-10)3 g·cm -3。
答案:(1)⎝⎛⎭⎫14,14,14 (2)8×736.02×565.763×107 5.(2017·江苏高考)某Fe x N y 的晶胞如图1所示,Cu 可以完全替代该晶体中a 位置Fe 或者b 位置Fe ,形成Cu 替代型产物Fe (x -n )Cu n N y 。
Fe x N y 转化为两种Cu 替代型产物的能量变化如图2所示,其中更稳定的Cu 替代型产物的化学式为________________。
解析:能量越低越稳定,从图2知,Cu 替代a 位置Fe 型晶胞更稳定,其晶胞中Cu位于8个顶点,N (Cu)=8×18=1,Fe 位于面心,N (Fe)=6×12=3,N 位于体心,N (N)=1,其化学式为Fe 3CuN 。
答案:Fe 3CuN6.(2017·全国卷Ⅲ)MgO 具有NaCl 型结构(如图),其中阴离子采用面心立方最密堆积方式,X 射线衍射实验测得MgO 的晶胞参数为a =0.420 nm ,则r (O 2-)为________ nm 。
MnO 也属于NaCl型结构,晶胞参数为a ′=0.448 nm ,则r (Mn 2+)为________ nm 。
解析:因为O 2-采用面心立方最密堆积方式,所以面对角线长度是O 2-半径的4倍,则有 [4r (O 2-)]2=2a 2,解得r (O 2-)=24×0.420 nm ≈0.148 nm ;MnO 也属于NaCl 型结构,根据晶胞的结构可得2r (Mn 2+)+2r (O 2-)=a ′,代入数据解得r (Mn 2+)=0.076 nm 。
答案:0.148 0.0767.(2016·全国卷Ⅲ)砷化镓(GaAs)是优良的半导体材料,可用于制作微型激光器或太阳能电池的材料等。
GaAs 的熔点为1 238 ℃,密度为ρg·cm -3,其晶胞结构如图所示。
该晶体的类型为________,Ga 与As 以________键键合。
Ga 和As 的摩尔质量分别为M Ga g·mol-1和M As g·mol -1,原子半径分别为r Ga pm 和r As pm ,阿伏加德罗常数值为N A ,则GaAs晶胞中原子的体积占晶胞体积的百分率为________。
解析:GaAs 的熔点为1 238 ℃,其熔点较高,据此推知GaAs 为原子晶体,Ga 与As 原子之间以共价键键合。
分析GaAs 的晶胞结构,4个Ga 原子处于晶胞体内,8个As 原子处于晶胞的顶点、6个As 原子处于晶胞的面心,结合“均摊法”计算可知,每个晶胞中含有4个Ga 原子,含有As 原子个数为8×1/8+6×1/2=4(个),Ga 和As 的原子半径分别为r Ga pm =r Ga ×10-10cm ,r As pm =r As ×10-10 cm ,则原子的总体积为V 原子=4×43π×[(r G a ×10-10cm)3+(r As ×10-10cm)3]=16π3×10-30(r 3Ga +r 3As )cm 3。
又知Ga 和As 的摩尔质量分别为M Ga g·mol -1和M As g·mol -1,晶胞的密度为ρ g·cm -3,则晶胞的体积为V 晶胞=4(M Ga +M As )ρN Acm 3,故GaAs 晶胞中原子的体积占晶胞体积的百分率为V 原子V 晶胞×100%= 16π3×10-30(r 3Ga +r 3As )cm 34(M Ga +M As )ρ N Acm 3×100%= 4π×10-30×N A ρ(r 3Ga +r 3As )3(M Ga +M As )×100%。
答案:原子晶体 共价 4π×10-30×N A ρ(r 3Ga +r 3As )3(M Ga +M As )×100% 8.立方NiO(氧化镍)晶体的结构如图所示,其晶胞边长为a pm ,列式表示NiO 晶体的密度为__________g·cm -3(不必计算出结果,阿伏加德罗常数的值为N A )。
人工制备的NiO晶体中常存在缺陷(如图)。
一个Ni 2+空缺,另有两个Ni 2+被两个Ni 3+所取代,其结果晶体仍呈电中性,但化合物中Ni 和O 的比值却发生了变化。
已知某氧化镍样品组成Ni 0.96O ,该晶体中Ni 3+与Ni 2+的离子个数之比为________。
解析:晶胞中Ni 原子数目为1+12×14=4,O 原子数目为8×18+6×12=4,晶胞质量为4×(16+59)N A g ,晶胞边长为a pm ,晶胞体积为(a ×10-10 cm)3,NiO 晶体的密度为4×(16+59)N A g (a ×10-10 cm )3=4×75N A ×(a ×10-10)3 g·cm -3;设1 mol Ni 0.96O 中含Ni 3+x mol ,Ni 2+为(0.96-x )mol ,根据晶体仍呈电中性可知,3x +2×(0.96-x )=2×1,x =0.08 mol ,Ni 2+为(0.96-x )mol =0.88 mol ,即离子数之比为N (Ni 3+)∶N (Ni 2+)=0.08∶0.88=1∶11。
答案:4×75N A ×(a ×10-10)3 1∶11 9.S 与Zn 所形成化合物晶体的晶胞如图所示。
(1)在该晶胞中,Zn 的配位数为________。
(2)原子坐标参数可表示晶胞内部各原子的相对位置。
如图晶胞中,原子坐标参数a 为(0,0,0);b 为⎝⎛⎭⎫12,0,12;c 为⎝⎛⎭⎫12,12,0。
则d 的坐标参数为________。
(3)已知该晶胞的密度为ρ g·cm -3,则其中两个S 原子之间的距离为________pm 。
(列出计算式即可)解析:(1)该晶胞中Zn 的原子个数为8×18+6×12=4,S 的原子个数为4,故Zn 、S 的配位数相同,根据S 的配位数为4,可知Zn 的配位数为4。
(2)根据d 的位置,可知其坐标参数为⎝⎛⎭⎫1,12,12。
(3)根据S 原子的位置可知,两个S 原子之间的距离为晶胞边长的22,设晶胞边长为a pm ,则该晶胞的质量为65×4+32×4N A g =ρ g·cm -3×(a ×10-10 cm)3,解得a =34×97ρN A×1010,故两个S 原子之间的距离为22× 34×97ρN A ×1010 pm 。
