《线性代数》课程自学进度表
网络11线性代数教学进度表
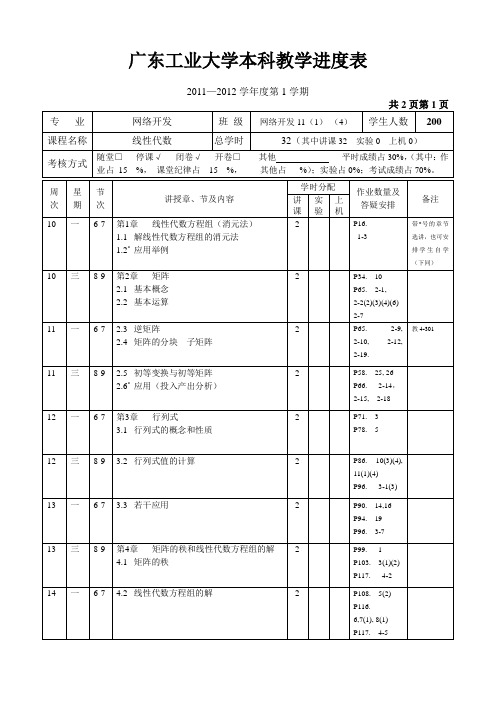
广东工业大学本科教学进度表2011—2012学年度第1学期
说明：
1、本表由主讲教师按《广东工业大学本科教学进度表的编制及管理规定》编写，经基层教学单位教学负责人审核，教师所在学院教学主管审核批准执行；
2、若不在学校安排的地点授课，需在备注栏写明上课地点；
3、本表须在每学期开学后第1周内送交基层教学单位审核，第2周内学院审核，第3周内交学生所在学院2份和发给学生班1份。
主讲教师签名：填写日期：年月日基层教学单位教学负责人签章：审核日期：年月日学院教学主管签章：审核日期：年月日。
《线性代数》课程教学大纲
难点：线性空间的认知与线性变换的计算
课程思政融入点：培养学生精益求精的工匠精神。
16 复习、答疑 2 复习、答疑课堂讲授
合计：32
成绩评定方法及标准
考核形式评价标准权重
出勤状况1. 评价标准：不迟到，请假须有辅导员签字的请假条。
2. 要求：无故旷课1次扣3分，迟到1次扣1分，缺席3
次取消参加期末考试的资格。
10%
课堂表现1. 评价标准：参与课堂程度及随堂测验。
2. 要求：精神饱满，参与课堂程度高。
20%
平时作业1. 评价标准：按照作业完成情况评分。
2. 要求：按时作业，作业工整规范。
20%
期中考试（闭卷考试）1. 评价标准：按照试卷参考解答及评分标准给分。
2. 要求：能灵活运用所学线性代数知识和方法进行求解，独
立、按时完成考试。
若发现任何考试作弊行为，试卷一律按
0分处理。
25%
期末考试（闭卷考试）1. 评价标准：按照试卷参考解答及评分标准给分。
2. 要求：能灵活运用所学线性代数知识和方法进行求解，独
立、按时完成考试。
若发现任何考试作弊行为，试卷一律按
0分处理。
25%
大纲编写时间：2019年9月2日
系（部）审查意见：
系（部）主任签名：日期：年月日。
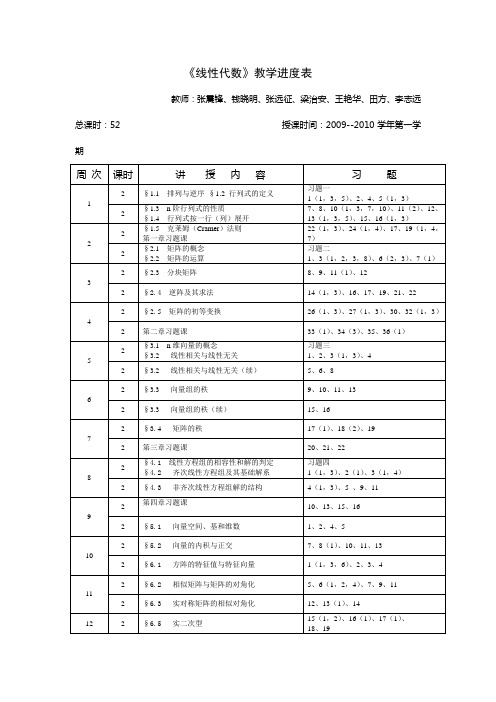
线性代数教学进度表
2
2
§1.5克莱姆（Cramer）法则
第一章习题课
22（1，3）、24（1，4）、17、19（1，4，7）
2
§2.1矩阵的概念
§2.2矩阵的运算
习题二
1、3（1，2，3，8）、6（2，3）、7（1）
3
2
§2.3分块矩阵
8、9、11（1）、12
2
§2.4逆阵及其求法
《线性代数》教学进度表
教师：张震锋、钱晓明、张远征、梁治安、王艳华、田方、李志远
总课时：52授课时间：2009--2010学年第一学期
周次
课时
讲授内容
习题
1
2
§1.1排列与逆序§1.2行列式的定义
习题一
1（1，3，5）、2、4、5（1，3）
2
§1.3 n阶行列式的性质
§1.4行列式按一行（列）展开
7、8、10（1，3，7，10）、11（2）、12、
4（1，3）、5、9、11
9
2
第四章习题课
10、13、15、16
2
§5.1向量空间、基和维数
1、2、4、5
10
2
§5.2向量的内积与正交
7、8（1）、10、11、13
2
§6.1方阵的特征值与特征向量
1（1，3，6）、2、3、4
11
2
§6.2相似矩阵与矩阵的对角化的相似对角化
6
2
§3.3向量组的秩
9、10、11、13
2
§3.3向量组的秩（续）
15、16
7
2
§3.4矩阵的秩
17（1）、18（2）、19
2
第三章习题课
线性代数教学进度表
XXX财经大学
本科课程教学进度计划表2015—2016学年度第二学期
学院XXX学院
教学系
其他院系
（课程组）
主讲教师张三
填表日期：2015年9月10 日
教务处制表
XXX大学本科课程教学进度计划表
2015 —2016学年度第二学期
主讲教师张三职称讲师学历研究生学位_博士_ 主授专业古代文学
课程名称大学语文课程编号00000. 班级A01 学生人数50
总学时48 学时，其中课堂讲授46学时；实验（上机）教学0 学时；其它教学（讨论、见习等） 2 学时；机动0学时实习实训（包括课程实习、课程实训、课程设计等）0 周
教材（名称、主编、出版社、出版时间等）《大学语文》，江西科学技术出版社，2011年7月
成绩考核说明及要求：期末闭卷考试或课程论文
其成绩评定方法：平时成绩占30%，期末考试占70%
考试题型：填空题、选择题、计算题、简答题、应用题、
考试时间：110分钟
系主任（签字）：教学院长（签字）：年月日年月日。
线性代数进程表09—2
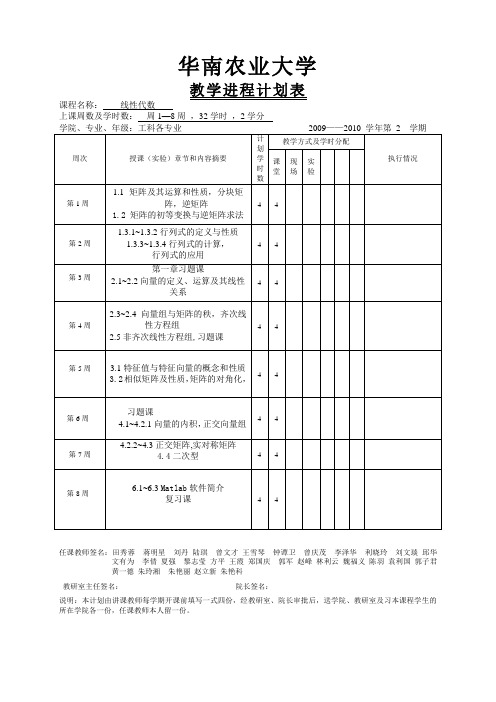
华南农业大学
教学进程计划表
课程名称：线性代数
上课周数及学时数：周1—8周，32学时，2学分
任课教师签名：田秀蓉蒋明星刘丹陆琪曾文才王雪琴钟谭卫曾庆茂李泽华利晓玲刘文琰邱华文有为李倩夏强黎志莹方平王霞郑国庆郭军赵峰林利云魏福义陈羽袁利国郭子君
黄一德朱玲湘朱艳丽赵立新朱艳科
教研室主任签名：院长签名：
说明：本计划由讲课教师每学期开课前填写一式四份，经教研室、院长审批后，送学院、教研室及习本课程学生的所在学院各一份，任课教师本人留一份。
线性代数进度计划表
习题课 P198 习题四
3
3
第 16 周 12 月 16 日--12 月 22 日
周
次
授课内容摘要
周 学 时
教学方式与学时分配 讲 授 实 验 讨 论 自 学
课后安排
执行情况
第 17 周 12 月 23 日--12 月 29 日
第 18 周 12 月 30 日--1 月 5 日
第 19 周 1 月 6 日--1 月 12 日
学
期
教
学
进
线性代数
度 计
划
课程名称 开课单位 教研室 任课教师 专业、年级、班 课程类别 行课周数 总学时
数学与计算机学院 代数几何 杨天标
12 级生物工程非师范本科 1 班 12 级生物工程非师范本科 1 班 12 级旅游管理非师范本科 1 班
公共课 √
专业课□
15 15×3
2013-2014 学年度第 1 学期 教务处制
3
3
第8周 10 月 21 日--10 月 27 日
第三章 线性方程组§3.1 消元法 §3.2 向量与向量组的线性组合
3
3
P157 习题三 §3.1 t1(1)(2) §3.2 t4 课后练习：t3
周
次
授课内容摘要
周 学 时
教学方式与学时分配 讲 授 实 验 讨 论 自 学
课后安排
§3.3 t10 课后练习：t11
t22第1443实对称矩阵的特征值与特征值向量43t23第15日12月15习题课p198习题四知识改变生活精品word文档值得下载值得拥有知识改变生活精品word文档值得下载值得拥有第1612月16日12月22教学方式与学时分配课后安排执行情况12月23日12月2912月30日1知识改变生活精品word文档值得下载值得拥有知识改变生活精品word文档值得下载值得拥有第19日1月12月13日1月19知识改变生活精品word文档值得下载值得拥有知识改变生活精品word文档值得下载值得拥有知识改变生活精品word文档值得下载值得拥有知识改变生活精品word文档值得下载值得拥有
线性代数基础学习计划
线性代数基础学习计划线性代数是数学中的一个重要分支，涉及到了向量、矩阵、线性变换、线性方程组等多个概念。
它是许多学科的基础，如物理学、工程学、计算机科学等。
以下是一个基础学习计划，帮助你系统地学习线性代数。
第一周：了解线性代数的基本概念1.学习什么是向量和矩阵。
了解它们的基本格式和性质，如零向量、单位向量、行矩阵、列矩阵等。
2.掌握向量的基本运算，包括加法、数乘、向量的点乘和叉乘等。
3.掌握矩阵的基本运算，包括加法、减法、数乘、矩阵乘法等。
4.了解什么是矩阵的转置和逆矩阵，并掌握它们的计算方法。
第二周：学习线性变换和矩阵的秩1.学习什么是线性变换，如何将一个向量空间映射到一个向量空间上。
2.了解线性变换的性质和实例，如恒等变换、像和核等。
3.学习矩阵的秩的概念和计算方法，如行秩和列秩等。
4.掌握如何通过初等行变换来求矩阵的秩。
第三周：学习行列式和特征值1.学习行列式的概念和计算方法，了解行列式的性质和在求解线性方程组中的应用。
2.学习特征值的概念和计算方法，了解特征值与矩阵的关系。
3.掌握如何通过特征值和特征向量来研究线性变换的性质。
4.掌握如何求解一个给定矩阵的特征值和特征向量。
第四周：学习向量空间和线性方程组1.学习向量空间的概念和基本性质，如加法和数乘封闭性、加法和数乘的结合律和分配律等。
2.学习如何判定一个给定的集合是否构成一个向量空间。
3.学习线性方程组的概念和分类，如齐次和非齐次、其次和非其次等。
4.掌握如何用高斯消元法求解线性方程组。
5.掌握如何判定一个线性方程组是否有解，以及当有解时如何求解。
6.了解向量空间与线性方程组之间的关系，如解空间和零空间的定义和性质。
第五周：深入理解矩阵和线性变换1.深入学习矩阵的运算和性质，包括矩阵的乘法、转置、逆、行列式、特征值等。
2.深入理解矩阵的应用，包括求解线性方程组、数据分析和可视化、控制系统等。
3.学习如何判定两个矩阵是否相似，以及当两个矩阵相似时它们的特征值和特征向量之间的关系。
线性代数自学指导书
《线性代数》自学指导书一、课程名称：线性代数二、自学学时：72学时三、课件学时：54学时四、教材名称：《线性代数》，张恩众主编，山东大学出版社。
五、参考资料：1、《线性代数》，中国人民大学出版社2、《线性代数》，高等教育出版社六、考核方式：章节同步习题（10%）＋笔试（90％）七、课程简介：本课程是经济管理类各专业的一门主要的数学基础课。
内容包括行列式，矩阵及其运算，矩阵的初等变换与线性方程组，向量组的线性相关性，相似矩阵及二次型。
通过学习本门课程，使学生具备有关线性代数的基础理论知识及用于解决实际问题的能力，从而为学习后续课和进一步扩大数学知识打下必要的数学基础。
八、自学内容指导：第一章行列式1、本章内容概述：行列式的概念和基本性质，行列式按行（列）展开定理，解线性方程组的克莱姆（Cramer）法则。
2、自学课时安排：课件学习12学时，自学16学时3、知识点：A. 了解n阶行列式的概念，掌握行列式的性质．B. 会应用行列式的性质和行列式按行（列）展开定理计算行列式．C. 会用克莱姆法则解线性方程组．4、难点：行列式的概念和基本性质行列式按行（列）展开定理线性方程组的克莱姆（Cramer）法则5、章节同步习题：（单项选择题）（1）行列式0111101111011110＝ （ -3 ）(a) 1; (b) -1; (c) 3; (d) -3 .（2）当a = ( 1 )时，行列式12051336a ---＝0 (a) －1; (b) 1; (c) 2; (d) 0 . （3）如行列式111213212223313233a a a a a a a a a ＝d ，则313233212223111213333222a a a a a a a a a ---＝（ b ） （a ）－6d ； （b ）6d ； （c ） 4d ； （d ）－4d.（4）当a = （ ）时，行列式111111a a a＝0（a ）1； （b ）－1； （c ）2； （d ）0.（5）行列式1256427825169454321111的值为（ ） （a ）12； （b ）－12； （c ）16； （d ）－16. (6)行列式00000000a b c de fg h 中g 元素的代数余子式为（ ）（a ）bcf －bde ； （b ）bde －bcf ； （c ）acf －ade ； （d ）ade －acf.(7)设22112()112211f x x x =-+，则()0f x =的根为（ ）（a ）1, 1, 2, 2； （b ）-1, -1, 2, 2； （c ）1, -1, 2, -2； （d ）-1,-1,-2,-2.（8）行列式12112300 (00)0...0... 000......n n n n nna a a a a a a -＝ （ ）（a ）0； （b ）1211...n n a a a a -（b ）－1211...n n a a a a - （d ）1(1)n +-1211...n n a a a a -（9）行列式00000000a bx yc d uv ＝（ ） （a ）abcd – xyuw ; (b) abxy – cduv ;（c ）(ab – cd)(xy – uv); (d) (ad –bc)(xv – yu).（10）λ不能取（ ）时，方程组12312312302030x x x x x x x x x λ++=⎧⎪++=⎨⎪-+=⎩只有0解.(a) 1； （b ）2； （c ）3； （d ）4.6、课后作业题：A 类练习题：1（1）（2）（3），2，3，4，5，6，7，8（2）（3）（5）（6）（7）（8）14，15，16。
线性代数本学期学习计划
线性代数本学期学习计划一、学习目标线性代数是数学的一门基础课程，是许多高等数学课程的基础，也是计算机科学、物理学和工程学等学科的重要基础。
作为这门课程的学习者，我希望通过本学期的学习，能够达到以下几个目标：1. 理解线性代数的基本概念和原理，包括向量、矩阵、线性方程组、行列式等；2. 掌握线性代数的基本运算和性质，包括向量和矩阵的加减法、乘法、转置、逆矩阵等；3. 学习和掌握线性代数在实际问题中的应用，包括线性方程组的解法、矩阵的应用、特征值和特征向量的计算等；4. 提高解决实际问题的能力，培养分析和抽象问题的能力，为将来的学习和工作打下坚实的数学基础。
二、学习内容和进度安排1. 线性代数的基本概念和原理- 向量的定义和性质- 矩阵的定义和性质- 线性方程组和线性变换的基本概念- 行列式的定义和性质2. 线性代数的基本运算和性质- 向量和矩阵的加减法- 向量和矩阵的标量乘法- 矩阵的乘法和转置- 逆矩阵的定义和计算方法3. 线性代数的应用- 线性方程组的解法和应用- 矩阵的应用，例如在计算机图形学、工程学等领域的应用- 特征值和特征向量的计算和应用4. 解决实际问题的能力- 使用线性代数的知识解决实际问题- 培养分析和抽象问题的能力- 学习如何使用计算机软件（如Matlab、Python等）解决线性代数相关的问题三、学习方法和计划1. 课堂学习- 认真听讲，做好课堂笔记- 听懂老师上课的讲解，及时询问问题2. 自主学习- 阅读教材，理解课程内容- 完成课后习题，加深对知识点的理解- 参考相关资料，了解线性代数在实际问题中的应用3. 实践应用- 在学习过程中，积极参与线性代数的实际应用- 使用计算机软件辅助学习，练习矩阵运算、解线性方程组等四、学习评估1. 定期测试- 每周对所学知识进行复习和巩固，按时完成教师布置的作业- 参加定期测试，检验所学知识的掌握程度2. 课程总结- 每节课后进行知识总结和回顾，检验所学知识的掌握程度- 及时发现并纠正学习中的问题3. 学习反思和调整- 学习过程中，不断总结经验，发现学习中存在的问题并及时调整学习计划- 拓展对线性代数的理解，不仅限于教材中的内容，还要尝试更多的应用和探索总结：线性代数是一门重要的数学基础课程，对于我来说，学习线性代数不仅是为了应付考试，更是为了在数学建模、计算机图形学、工程与物理数学领域更好地应用数学知识。
201411011-线性代数与解析几何A-教学进度表
第5章 向量组的线性相关性 5.1-5.2 n维向量及其线性运算；线性组合
5.3 向量组的线性相关性 5.4 向量组的秩
5.5 线性方程组解的结构 5.6 向量空间与线性变换
习题课 第6章 方阵的对角化 6.1 方阵的特征值与特征向量 6.2-6.3 方阵的相似与对角化； 约当标准形简介
习题课 演示实验二：向量组的线性相关性和方阵的对角化 上机实验二：操作向量组的线性相关性和方阵的对角化
授课 授课 授课 授课 授课 授课
授课 授课 授课 实验 上机
授课 授课 授课 授课
授课 授课 授课
第7章 实对称阵与二次型 7.1 向量的内积
7.2 -7.3 二次型与矩阵的合同；二次型的标准型 7.4 -7.5 惯性定理；正定二次型 习题课 第8章 线性空间与线性映射
8.1-8.2 线性空间的定义与基本性质；线性空间的基、维数与坐标 8.3-8.4 线性子空间与生成子空间；线性映射 习题课 院（系）教学院长（主任）签字：
7～8 9～10 11～12 13～14 15～16 17～18
19～20 21～22 23～24
25～26 27～28 29～30 31～32 33～34 35～36
1.1-1.3 二、三阶行列式；排列；n阶行列式 1.4-1.5 行列式的性质；行列式按行（列）展开
1.6 克莱姆法则；习题课 第2章 空间解析几何与向量代数 2.1-2.2 空间直角坐标系；空间向量及其坐标化 2.3-2.4 向量的数量积、向量积、混合积；平面及其方程
2.5 空间直线及其方程 2.6 曲面及其方程
2.7 空间曲线及其方程 习题课
第3章 线性方程组与矩阵 3.1-3.2 矩阵的概念；矩阵的初等变换与矩阵的秩
赵林《线性代数》
安徽建筑工业学院继续教育学院自学周历及作业安排课程名称：线性代数注：作业面授时交批作业:1、计算下列各行列式:(1)265232112131412-; (2)dc b a 10110011001---.2、证明(1)y x z x z y z y x b a bz ay by ax bx az by ax bx az bz ay bx az bz ay by ax )(33+=+++++++++ (2)0)3()2()1()3()2()1()3()2()1()3()2()1(2222222222222222=++++++++++++d d d d c c c c b b b b a a a a 3. 计算下列各行列式(D k 为k 阶行列式):(1)x a aa x aa a xD n ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅= ; (2)nnnnn d c d c b a b a D ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=111124. 用克莱姆法则解下列方程组:⎪⎩⎪⎨⎧=+++-=----=+-+=+++01123253224254321432143214321x x x x x x x x x x x x x x x x ;5. λ取何值时,齐次线性方程组⎪⎩⎪⎨⎧=-++=+-+=+--0)1(0)3(2042)1(321321321x x x x x x x x x λλλ有非零解？6.设⎪⎪⎭⎫ ⎝⎛--=111111111A , ⎪⎪⎭⎫⎝⎛--=150421321B ,求3AB -2A 及A T B .7. 计算下列乘积:(1)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-127075321134;(2)⎪⎪⎭⎫⎝⎛123)321(;(3))21(312-⎪⎪⎭⎫⎝⎛ 8. 设A , B 为n 阶矩阵,且A 为对称矩阵,证明B T AB 也是对称矩阵. 9．求下列矩阵的逆矩阵:(1)⎪⎭⎫ ⎝⎛5221;(2)⎪⎪⎭⎫⎝⎛---145243121; 10. 解下列矩阵方程:(1)⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛--234311*********X ;(2)⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛021102341010100001100001010X 11. 设方阵A 满足A 2-A -2E =O , 证明A 及A +2E 都可逆, 并求A -1及(A +2E )-1.12. 设A 为3阶矩阵, 21||=A , 求|(2A )-1-5A *|.13.设⎪⎪⎭⎫ ⎝⎛=101020101A ,且AB +E =A 2+B , 求B .14. 设A =diag(1, -2, 1), A *BA =2BA -8E , 求B .15. 设P -1AP =Λ, 其中⎪⎭⎫ ⎝⎛--=1141P , ⎪⎭⎫ ⎝⎛-=Λ2001, 求A 11. 16.已知矩阵A 的伴随阵⎪⎪⎪⎭⎫⎝⎛-=8030010100100001*A 且ABA -1=BA -1+3E ,求B .17. 把下列矩阵化为行最简形矩阵:⎪⎪⎪⎭⎫ ⎝⎛------34732038234202173132.18. 设⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛987654321100010101100001010A , 求A .19. 试利用矩阵的初等变换, 求下列方阵的逆矩阵:⎪⎪⎭⎫⎝⎛323513123;20. 设⎪⎪⎭⎫⎝⎛---=101110011A , AX =2X +A ,求X .21. 求下列矩阵的秩, 并求一个最高阶非零子式:⎪⎪⎭⎫ ⎝⎛-------815073*********; 22.设⎪⎪⎭⎫ ⎝⎛----=32321321k k k A ,问k 为何值, 可使(1)R (A )=1; (2)R (A )=2; (3)R (A )=3. 23. 求解下列齐次线性方程组:(1)⎪⎩⎪⎨⎧=-++=--+=-++05105036302432143214321x x x x x x x x x x x x ;(2)⎪⎩⎪⎨⎧=-+-=+-+=-++=+-+07420634072305324321432143214321x x x x x x x x x x x x x x x x24. 求解下列非齐次线性方程组:(1)⎪⎩⎪⎨⎧-=+-=-+-=+-=++69413283542432z y x z y x z y x z y x(2)⎪⎩⎪⎨⎧-=+-+=-+-=+-+2534432312w z y x w z y x w z y x . 25. λ取何值时, 非齐次线性方程组:⎪⎩⎪⎨⎧=++=++=++23213213211λλλλλx x x x x x x x x .(1)有唯一解; (2)无解; (3)有无穷多个解?26. 设v 1=(1, 1, 0)T , v 2=(0, 1, 1)T , v 3=(3, 4, 0)T , 求v 1-v 2及3v 1+2v 2-v 3.27. 已知向量组：A : a 1=(0, 1, 2, 3)T , a 2=(3, 0, 1, 2)T , a 3=(2, 3, 0, 1)T ; B : b 1=(2, 1, 1, 2)T , b 2=(0, -2, 1, 1)T , b 3=(4, 4, 1, 3)T ,证明：B 组能由A 组线性表示,但A 组不能由B 组线性表示. 28. 已知R (a 1, a 2, a 3)=2, R (a 2, a 3, a 4)=3, 证明 (1) a 1能由a 2, a 3线性表示; (2) a 4不能由a 1, a 2, a 3线性表示.29. 判定下列向量组是线性相关还是线性无关: (-1, 3, 1)T , (2, 1, 0)T , (1, 4, 1)T ; 30. 问a 取什么值时下列向量组线性相关？ a 1=(a , 1, 1)T , a 2=(1, a , -1)T , a 3=(1, -1, a )T . 31. 求下列向量组的秩, 并求一个最大无关组:a 1=(1, 2, -1, 4)T , a 2=(9, 100, 10, 4)T , a 3=(-2, -4, 2, -8)T ; 32. 利用初等行变换求下列矩阵的列向量组的一个最大无关组:⎪⎪⎪⎭⎫ ⎝⎛4820322513454947513253947543173125;33. 设向量组：(a , 3, 1)T , (2, b , 3)T , (1, 2, 1)T , (2, 3, 1)T 的秩为2, 求a ,b .34. 求下列齐次线性方程组的基础解系:⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x ;35. 设有向量组A : a 1=(α, 2, 10)T , a 2=(-2, 1, 5)T , a 3=(-1, 1, 4)T , 及b =(1, β, -1)T , 问α, β为何值时 (1)向量b 不能由向量组A 线性表示;(2)向量b 能由向量组A 线性表示, 且表示式唯一; (3)向量b 能由向量组A 线性表示, 且表示式不唯一, 并求一般表示式.36. 求下列矩阵的特征值和特征向量:(1)⎪⎪⎭⎫ ⎝⎛----201335212;(2)⎪⎪⎭⎫⎝⎛633312321; 37. 设A 为n 阶矩阵, 证明A T 与A 的特征值相同. 38. 设A 2-3A +2E =O , 证明A 的特征值只能取1或2. 39. 已知3阶矩阵A 的特征值为1, 2, 3, 求|A 3-5A 2+7A |. 40. 已知p =(1, 1, -1)T 是矩阵⎪⎪⎭⎫⎝⎛---=2135212b a A 的一个特征向量.(1)求参数a , b 及特征向量p 所对应的特征值;(2)问A 能不能相似对角化？并说明理由. 41.设矩阵⎪⎪⎭⎫⎝⎛------=12422421x A 与⎪⎪⎭⎫ ⎝⎛-=Λy 45相似,求x , y ; 并求一个正交阵P , 使P -1AP =Λ.42. 设3阶方阵A 的特征值为λ1=2, λ2=-2, λ3=1; 对应的特征向量依次为p 1=(0, 1, 1)T , p 2=(1, 1, 1)T , p 3=(1, 1, 0)T , 求A . 43. 设3阶对称矩阵A 的特征值λ1=6, λ2=3, λ3=3, 与特征值λ1=6对应的特征向量为p 1=(1, 1, 1)T , 求A .44.设⎪⎪⎭⎫⎝⎛-=340430241A ,求A 100.45. 求一个正交变换将下列二次型化成标准形: f =2x 12+3x 22+3x 33+4x 2x 3;编者：赵林。
线性代数第I阶段学习计划
2013届钻石卡学员I阶段学习计划——线性代数（数学一）考研产品部公共课教研中心数学教研室2013届钻石卡学员学习计划---数学三线性代数第十五单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第一章行列式第1章第1节二阶与三阶行列式（P1——P4）第1章第2节全排列及其逆序数（P4——P5）第1章第3节n阶行列式的定义（P5——P8）第1章第4节对换（P8——P9）第1章第5节行列式的性质（P9——P15）第1章第6节行列式按行（列）展开（P16——P21）第1章第7节克拉默法则（P21——P25）本单元中我们应当学习——1．行列式的概念和性质，行列式按行（列）展开定理．2．用行列式的性质和行列式按行（列）展开定理计算行列式．3．用克莱姆法则解齐次线性方程组．2013届钻石卡学员学习计划---数学三计划对应课程讲义：线性代数 第一讲 行列式2013届钻石卡学员学习计划---数学三测验对应资料：《考研数学学习进程监控习题汇编》第二篇第一章行列式计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第二章矩阵及其运算第2章第1节矩阵（P29——P32）第2章第2节矩阵的运算（P33——P42）第2章第3节逆矩阵（P42——P47）第2章第4节矩阵分块法（P47——P54）线性代数第三章矩阵的初等变换与线性方程组2013届钻石卡学员学习计划---数学三第3章第1节矩阵的初等变换（P57——P65）本单元中我们应当学习——1．矩阵的概念，单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵和反对称矩阵的概念和性质．2．矩阵的线性运算、乘法运算、转置以及它们的运算规律.3. 方阵的幂与方阵乘积的行列式的性质.4．逆矩阵的概念和性质，矩阵可逆的充分必要条件.5. 伴随矩阵的概念，用伴随矩阵求逆矩阵．6．分块矩阵及其运算．7．矩阵初等变换的概念，初等矩阵的性质，矩阵等价的概念．2013届钻石卡学员学习计划---数学三计划对应课程讲义：2013届钻石卡学员学习计划---数学三第十七单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第三章矩阵的初等变换与线性方程组第3章第2节矩阵的秩（P65——P71）第3章第3节线性方程组的解（P71——P78）线性代数第四章向量组的线性相关性第4章第1节向量组及其线性组合（P81——P86）第4章第2节向量组的线性相关性（P87——P90）第4章第3节向量组的秩（P90——P94）2013届钻石卡学员学习计划---数学三本单元中我们应当学习——1．矩阵的秩的概念，用初等变换求矩阵的秩和逆矩阵．2．n维向量、向量的线性组合与线性表示的概念．3．向量组线性相关、线性无关的概念，向量组线性相关、线性无关的有关性质及判别法．4．向量组的极大线性无关组和向量组的秩的概念和求解．5．向量组等价的概念，矩阵的秩与其行(列)向量组的秩之间的关系.2013届钻石卡学员学习计划---数学三计划对应课程讲义：线性代数 第二讲 矩阵（下）线性代数 第三讲 向量（上）2013届钻石卡学员学习计划---数学三测验对应资料：《考研数学学习进程监控习题汇编》第二篇第二章矩阵第十八单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第四章向量组的线性相关性第4章第4节线性方程组的解的结构（P94——P102）第4章第5节向量空间（P102——P106）本单元中我们应当学习——1．齐次线性方程组有非零解的充分必要条件，非齐次线性方程组有解的充分必要条件．2013届钻石卡学员学习计划---数学三2．齐次线性方程组的基础解系、通解及解空间的概念，齐次线性方程组的基础解系和通解的求法. 3．非齐次线性方程组解的结构及通解． 4．用初等行变换求解线性方程组的方法．5．n 维向量空间、子空间、基底、维数、坐标等概念． 6．基变换和坐标变换公式，过渡矩阵．计划对应课程讲义：线性代数 第三讲 向量（下）2013届钻石卡学员学习计划---数学三第十九单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第五章相似矩阵及二次型第5章第1节向量的内积、长度及正交性（P111——P116）第5章第2节方阵的特征值与特征向量（P117——P121）第5章第3节相似矩阵（P121——P124）2013届钻石卡学员学习计划---数学三本单元中我们应当学习——1．内积的概念，线性无关向量组正交规范化的施密特（Schmidt）方法．2．规范正交基、正交矩阵的概念以及它们的性质．3．矩阵的特征值和特征向量的概念及性质，求矩阵的特征值和特征向量.4．相似矩阵的概念、性质，矩阵可相似对角化的充分必要条件，将矩阵化为相似对角矩阵的方法.2013届钻石卡学员学习计划---数学三计划对应课程讲义：线性代数 第四讲 线性方程组（下）线性代数 第五讲 方阵的特征值和特征向量，矩阵的相似对角化（上）测验对应资料：《考研数学学习进程监控习题汇编》 第二篇 第三章 向量与线性方程组《考研数学客观题能力训练习题集粹》 第二篇 第三章 线性方程组2013届钻石卡学员学习计划---数学三第二十单元（课前或课后学习内容）计划对应教材：工程数学线性代数同济大学数学系编高等教育出版社第五版线性代数第五章相似矩阵及二次型第5章第4节对称矩阵的对角化（P124——P127）第5章第5节二次型及其标准形（P127——P131）第5章第6节用配方法化二次型成标准形（P131——P132）第5章第7节正定二次型（P132——P134）本单元中我们应当学习——1．实对称矩阵的特征值和特征向量的性质．2．二次型及其矩阵表示，二次型秩的概念，合同变换与合同矩阵的概念，二次型的标准形、规范形的概念以及惯性定理．3．正交变换化二次型为标准形，配方法化二次型为标准形．4．正定二次型、正定矩阵的概念和判别法．2013届钻石卡学员学习计划---数学三计划对应课程讲义：2013届钻石卡学员学习计划---数学三测验对应资料：《考研数学学习进程监控习题汇编》第二篇第四章矩阵的特征值与特征向量第二篇第五章二次型《考研数学客观题能力训练习题集粹》第二篇第四章特征值与特征向量第二篇第五章二次型2013届钻石卡学员学习计划---数学三。
对线性代数的学习计划
对线性代数的学习计划在学习线性代数之前，我们应该先了解线性代数究竟是什么以及它是如何应用的。
线性代数是一门研究向量空间和线性映射的数学学科，它是代数学的一个分支，也是现代数学的重要组成部分。
线性代数在许多领域都有广泛的应用，比如计算机图形学、机器学习、控制理论等。
因此，学习线性代数不仅可以增强我们的数学思维能力，还可以更好地了解各种应用领域中的数学原理。
接下来，我将介绍我对线性代数的学习计划。
阶段一：基础知识的学习（1-2周）在线性代数的学习中，我们首先要掌握一些基础概念，比如向量、矩阵、行列式等。
这些基础概念是线性代数的基石，我们需要通过课本、教学视频等方式来学习这些基础知识，并通过大量的例题来加深理解。
阶段二：线性方程组的解法（2-3周）解线性方程组是线性代数中的一个重要内容，我们需要学习如何利用矩阵的方法、高斯消元法等技巧来解线性方程组。
这部分内容通常会涉及到矩阵的运算、方程组的化简和求解等，需要进行大量的练习来掌握这些技巧。
阶段三：线性空间和线性变换（2-3周）线性代数的核心内容之一是线性空间和线性变换。
在这个阶段，我们需要学习向量空间、线性映射、特征值和特征向量等内容。
这部分内容会比较抽象和理论化，需要进行更多的思考和推理来理解。
阶段四：矩阵论和对称性（2-3周）矩阵论是线性代数中的一个重要分支，它涉及到矩阵的运算、特征值分解、奇异值分解等内容。
同时，对称性也是线性代数中的一个重要概念，它在各种应用领域中有广泛的应用。
在这个阶段，我们需要学习矩阵的运算规则、矩阵的分解方法，以及对称矩阵的性质和应用。
阶段五：应用领域的拓展（1-2周）在掌握了线性代数的基础知识之后，我们可以进一步拓展到各种应用领域中，比如计算机图形学、机器学习、信号处理等。
在这个阶段，我们可以通过阅读相关的专业书籍、论文或者参与相关的项目来进一步了解线性代数在实际应用中的作用。
阶段六：实践和综合应用（2-3周）最后，为了更好地巩固所学的知识，我们需要通过大量的练习题和实际应用案例来检验和应用所学的知识。
《线性代数》课程教学大纲(经济管理类)
《线性代数》课程教学大纲一、课程基本信息二、课程教学目标《线性代数》是学生所必备的基础理论知识和重要的数学工具。
它的主要目的和任务是通过本课程的教学，使学生了解和掌握行列式、矩阵、线性方程组、二次型等基本概念，基本原理理论和基本计算方法，并具有熟练的矩阵运算能力和用矩阵方法解决实际问题的能力，同时使学生的抽象思维能力和数学建模能力受到一定的训练。
本课程主要教学内容包括行列式、矩阵、向量的线性相关性，线性方程组，矩阵的特征值，二次型等。
另外，有关的习题课、应用线性代数知识解决实际问题的数学建模课也是教学的重要部分。
1．学好基础知识。
理解和掌握课程中的基本概念和基本理论，知道它的数学思想方法、意义和用途，以及它与其它概念、规律之间的联系。
2．掌握基本技能。
能够根据性质法则、公式正确地进行运算。
能够根据不同问题的情景，寻求和设计合理简捷的运算途径。
3．培养思维能力。
能够对研究的对象进行观察、比较、抽象和概括。
能运用课程中的概念、定理及性质进行合乎逻辑的推理。
能对计算结果进行合乎实际的分析、归纳和类比。
4．提高解决实际问题的能力。
能够将本课程与相关课程有机地联系起来，提出并解决相关学科中与本课程有关的问题。
能够自觉地运用所学的知识方法理念去观察生活，建立简单的数学模型，提出和解决生活中有关的数学问题。
三、教学学时分配《线性代数》课程理论教学学时分配表四、教学内容和教学要求第一章行列式（10）（一）教学要求通过本章相关内容的学习，了解行列式的概念；理解克莱姆法则,并且会用克莱姆法则解相应的方程组；掌握行列式的性质和行列式的展开定理，及正确计算行列式。
（二）教学重点与难点教学重点：n阶行列式的性质，行列式按行（列）展开定理教学难点：n阶行列式的计算（三）教学内容第一节排列与逆序数1．n阶排列及奇（偶）排列的定义2．逆序数第二节 n阶行列式1．二阶、三阶行列式的定义2．n阶行列式的定义3. 一些特殊的n阶行列式计算第三节行列式性质1．行列式的性质2．利用行列式性质计算行列式第四节行列式按行（列）展开1. 余子式2. 行列式按行（列）展开法则3. 范德蒙行列式第五节克莱姆法则本章习题要点：1．n阶行列式的计算2．行列式按行（列）展开3．用克莱姆法则解相应方程组第二章矩阵及其运算（8学时）（一）教学要求通过本章内容的学习，使学生了解单位矩阵、对角矩阵、上（下）三角矩阵、对称矩阵与反对称矩阵的概念以及它们的性质，理解矩阵以及逆矩阵的概念。
《线性代数》课程大纲
《线性代数》课程大纲一、课程简介课程名称：线性代数学时/学分：96/5先修课程：无面向对象：致远学院本科生教学目标：本课程是为致远学院（计算机与生物）开设的系列代数课程的第一部分, 主要包含线性代数的基本内容。
通过本课程的教学，使学生掌握线性代数与多项式的基本理论、思想与方法，使学生的计算能力和抽象思维能力得到系统的训练和提高，为将来进一步学习其它专业课程奠定坚实的代数基础。
在教学过程中既强调一定的抽象性，又特别注意结合具体的应用例子来理解代数学的数学思想和思维方法，注意介绍本课程与其他学科的联系，以及介绍最新的科研成果以开阔同学的视野。
主要内容：多项式理论；行列式的性质与计算技巧；矩阵的性质：等价标准型；解线性方程组；矩阵的相似标准形与特征值、特征向量；二次型与矩阵的合同；Schmidt正交化；线性空间；线性变换。
二、教学内容第一章数环上的矩阵与Gauss消元法主要内容：矩阵的运算与解线性方程组的高斯消元法。
具体重点与难点：矩阵的乘法；初等矩阵第二章行列式主要内容：行列式的定义、性质以及求行列式重点与难点：降阶计算以及升阶计算第三章矩阵的相似对角化主要内容：特征值与特征向量；方阵可相似对角化的判定重点与难点：特征多项式；特征值与特征子空间第四章二次型主要内容：实二次型与实对称矩阵的对应；化二次型为标准型；正定矩阵与正定二次型重点与难点：正定二次型第五章多项式理论主要内容：多项式重点与难点：互素与整除之间的制约关系第六章线性空间主要内容：基与坐标；欧氏空间与Schimidt正交化过程；酉空间重点与难点：欧氏空间与Schimidt正交化过程；酉空间第七章线性变换主要内容：线性变换与矩阵的对应；投影变换与正交变换；正交变换与正交矩阵；不变子空间重点与难点：以上均为重点。
难点很多，不再一一论述三、教学进度安排第一章．数环上的矩阵与Gauss消元法(16课时)1.1．数环与数域（定义及例子）；利用Gauss消元法解一般线性方程组（有解的判断；求解。
《线性代数》课程教学大纲
《线性代数》课程教学大纲课程名称：线性代数课程代码：课程性质: 必修总学分：2 总学时： 32* 其中理论教学学时：32*适用专业和对象：理（非数学类专业）、工、经、管各专业**使用教材：注：（1）大部分高校开设本课程的教学学时数约为32—48学时，为兼顾少学时高校开展教学工作，本大纲以最低学时数32学时（约2学分）进行教学安排，有多余学时的学校或专业可对需要加强的内容适当拓展教学学时。
（2）对线性代数课程而言，理工类与经管类专业的教学基本要求几乎一致，所以这里所列教学内容及要求对这两类专业均适合。
一、课程简介《线性代数》是高等学校理（非数学类专业）、工、经、管各专业的一门公共基础课，其研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。
该课程具有理论上的抽象性、逻辑推理的严密性和工程应用的广泛性。
主要内容是学习科学技术中常用的矩阵方法、线性方程组及其有关的基本计算方法，使学生具有熟练的矩阵运算能力并能用矩阵方法解决一些实际问题。
通过本课程的学习，使学生理解和掌握行列式、矩阵的基本概念、主要性质和基本运算，理解向量空间的概念、向量的线性关系、线性变换、了解欧氏空间的线性结构，掌握线性方程组的求解方法和理论，掌握二次型的标准化和正定性判定。
线性代数的数学思想和数学方法深刻地体现辩证唯物主义的世界观和方法论，线性代数的发展历史也充分展示数学家们开拓创新、追求真理的科学精神，展现古今中外数学家们忠诚爱国、献身事业的高尚情怀。
思想政治教育元素融入线性代数的教学实践之中，可以培养学生用哲学思辨立场、观点和方法分析解决问题，能够提高学生的创新能力和应用意识，培养学生的爱国主义情怀、爱岗敬业精神和开拓创新精神，帮助学生在人生道路上形成良好的人格，树立正确的世界观、人生观、价值观。
线性代数理论不仅渗透到了数学的许多分支中，而且在物理、化学、生物、航天、经济、工程等领域中都有着广泛的应用。
同时，线性代数课程注重培养学生逻辑思维和抽象思维能力、空间直观和想象能力，提高学生分析问题解决问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
教材：《线性代数》教材编者：邱启荣等出版社：中国电力出版社出版时间：2005年5月
周次
学习内容
习题作业
测验作业
学时
自学重点、难点、基本要求
1~3
第一章行列式
第1~4节
习题1-1：3，4，
习题1-1：5，6，7
6
自学重点：
4阶行列式的计算，矩阵运算，矩阵的初等变换，向量组的线性关系、方程组求解、特征值与特征向量、矩阵的对角化、二次型。
习题5-1：1
习题5-1：1（2）
6
第3节
习题5-2：1，4
习题5-2：2，3
6
第4节
习题5-3：1
习题5-3：2
4
注：期中（第10周左右）将前半部分测验作业寄给班主任，期末面授时将后半部分测验作业直接交给任课教师。总成绩中，作业占15分。
参考教材
《线性代数》（第四版），同济大学编，北京，高等教育出版社，2004
难点：
ｎ阶行列式、矩阵的逆、向量组的线性关系、方程组的解。
基本要求：
会计算ｎ阶行列式，利用克莱姆法则求解线性方程组，知道线性变换与矩阵的关系，熟练掌握矩阵线性运算，乘法，转置及其运算规律，熟悉矩阵求逆的方法
理解向量组线性相关，线性无关的含义，会判别向量组相关性，熟悉矩阵秩的概念及其求法，会矩阵的初等变换
习题2-2：6
8
第3节
习题2-3：1
4
第4节
习题2-4：1，3
3,4
习题2-4：2
6
第5节
习题2-5：1，2
习题2-5：4
6
13-16
第三章矩阵及其运算第1节
习题3-1：1，2，3
习题3-1:7，8
6
第2~3节
习题3-2：1，2，3
习题3-2：2二次型第1~2节
会解齐次线性方程组和非齐次线性方程组的解，熟悉基础解系通解等概念及解的结构，会求内积，会将向量组正交化，会求特征值和特征向量，知道实对称阵的相似矩阵，会化二次型为标准形
第5节
习题1-1：8（1）（3）（5）
思考题：1，2，3
6
4~12
第二章线性方程组第1节
习题2-1：1（1）（2）（3）
8
第2节
习题2-2：1，3