初升高数学衔接测试题
初升高衔接数学测试题
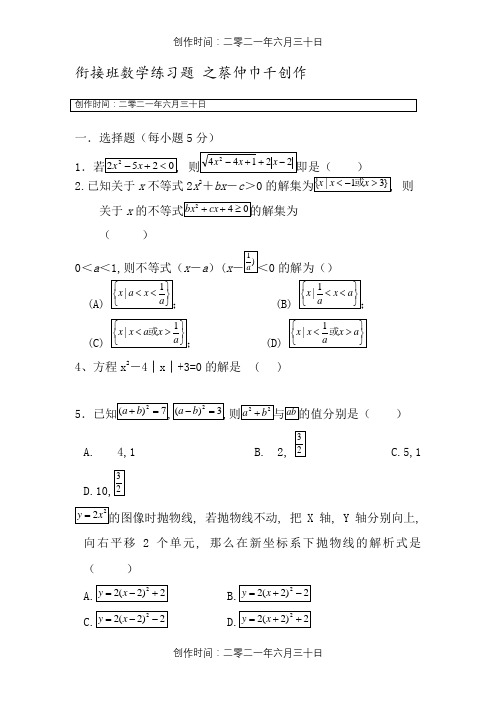
衔接班数学练习题之蔡仲巾千创作一.选择题(每小题5分)1)2.已知关于x不等式2x2+bx-c>0则关于x()0<a<1,则不等式(x-a)(x0的解为()4、方程x2-4│x│+3=0的解是 ( )5)A. 4,1B. 2,C.5,1, 若抛物线不动, 把X轴, Y轴分别向上,向右平移2个单元, 那么在新坐标系下抛物线的解析式是(), 则函数------------------------()(A)但无最年夜值; (B)有最年夜值1;(C) 有最小值1, (D)无最小值, 也无最年夜值.,为()x的二次方程2(k+1)x2+4kx+3k-2=0的两根同号, 则实数k的取值范围为------()(A(C(D,()或11.已知函数y=ax2+bx+c(a≠0)的图象经过点(-1,3)和(1,1)两点,若0<c<1,则a的取值范围是( )A.(1,3) B.(1,2) C.[2,3) D.[1,3], 则a的取值范围是)二、填空题(每小题5分)13.14.不等式|x 2+2x |<3的解为____________.15.1911+⨯.16.(3)ax a ++=, ,, 则实数a 的取值范围是____________. 三.解答题17.(1)作出函数的图象;(2.18.已知关于x 的方程x 2-2(k -1)x+k 2=0有两个实数根x 1, x 2. (I)求k 的取值范围;(II)求k 的值.a 为实数.(1(2)若(1)中的不等式的解包括所有2到5的实数(包括端点), 求a 的取值范围.x 的方程的两根都在[-1, 1]上, 求实数m 的取值范围.2, 求实数a 的值.22.已知当m ∈R 时, 函数y =m (x 2-1)+x -a 的图象和x 轴恒有公共点, 求实数a 的取值范围.。
初升高衔接数学测试(附解答)

初升高衔接数学测试(附解答)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN初升高衔接数学测试(总分100分,时间90分钟)一、选择题(每题3分,共30分)1.一元二次方程x 2+x-2=0的根的情况是( )(A )有两个不相等的实数根 (B )有两个相等的实数根(C )只有一个实数根 (D )没有实数根2.已知0≠xyz ,则z z y y x x ++的值不可能为( ) (A) 1 (B) 0 (C )3 (D) —13.若关于x 的多项式x 2-px -6含有因式x -3,则实数p 的值为( ).A .-5B .5C .-1D .14.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h 随时间t 的变化规律如图所示(图中OABC 为一折线),则这个容器的形状为( ).5.不等式025423≤-+-x x x 的解集是( )A. 2≤xB.2≥xC.21≤≤xD.1≥x6.如图,在边长为2的菱形ABCD 中,∠A=60°,M 是AD 边的中点,N 是AB 边上的一动点,将ΔAMN 沿MN 所在直线翻折得到ΔA ’MN ,则A ’C 长度的最小值是( )A. 7B.17-C. 2D. 73-7.已知某三角形的三边长分别为6,8,6,则该三角形的内接圆半径为( )A.6B.55 C.5 D. 554 8.如图7所示,P 是等腰直角△ABC 外一点,把BP 绕点B 顺时针旋转90°到BP ′,已知∠AP ′B=135°,P ′A :P ′C=1:3,则P ′A :PB=:[ ]。
A .1:21/2;B .1:2;C .31/2:2;D .1:31/2。
9.如果关于x 的不等式组:⎩⎨⎧≤-≥-0203b x a x ,的整数解仅有1,2,那么适合这个不等式组的整数a ,b 组成的有序数对[a ,b]共有( )个。
A.8B.7C.6D.510.设1x ,2x 是一元二次方程2320x x --=的两个实数根,则2211223x x x x ++的值为( ).A. 7B.8C.9D.6二、填空题(每题4分,共20分)图7F E O DB A DC 第12题11.若,x y为实数,且20x +=,则2010()x y +的值为___________.12.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为2cm ,∠A =120°,则EF = cm .13.已知当1x =时,22ax bx +的值为3,则当2x =时,2ax bx +的值为_______.14.已知关于x 的分式方程111=--++x k x k x 的解为负数,则k 的取值范围是 。
初升高衔接数学测试题1

衔接班数学练习题(一)一、选择题(每小题5分)1.设集合{}22,A x x x R =-≤∈,{}2|,B y y x ==-,则()R C A B 等于( )A .(,0]-∞B .{},0x x R x ∈≠C .(0,)+∞D .∅ 2.若112x y -=,则33x xy y x xy y+---的值为( ) A.35 B.35- C.53- D.533.一元二次方程2(1)210k x x ---=有两个不相等的实数根,则k 的取值范围是( )A.2k >B.2,1k k <≠且C.2k <D.2,1k k >≠且4. 已知集合A={直线} B={椭圆},则集合A ∩B 中元素的个数为( )A. 0个B. 1个C. 2 个D. 0个1个或2个 5、要从抛物线y=-2x 2的图象得到y=-2x 2-1的图象,则抛物线y=-2x 2必须 ( )A .向上平移1个单位;B .向下平移1个单位;C .向左平移1个单位;D .向右平移1个单位.6.已知一个直角三角形的两条直角边长恰好是方程2x 2-8x +7=0的两根,则这个直角三角形的斜边长等于 ( ).A .B 3 .C 6 .D 97. 已知()2245f x x x =-+-,若[]3,2x ∈--,则()f x 的最大值( )A. -35B.-21C.-3D.-58、若{}21,,0,,b a a a b a ⎧⎫=+⎨⎬⎩⎭,则20052005a b +的值为( )(A )0 (B )1 (C )1- (D )1或1-9.已知菱形ABCD 的边长为5,两条对角线交于O 点,且OA 、OB 的长分别是关于x 的方程22(21)30x m x m +-++=的根,则m 等于A.3-B.5C.53-或D.53-或10.如图,函数y ax b =+与2y ax bx c =++的图象关系可能正确的是( )二、填空题(每小题5分)11.{}2|60A x x x =+-=,{}|10B x mx =+=,且A B A =,满足条件的m 集合是______12.有意义,则实数x 的取值范围为_________________. 13.若关于x 的不等式2122x x mx -+>的解为{}|02x x <<,则实数m 的值为_______.14.已知集合={||+2|<3}A x R x ∈,集合={|()(2)<0}B x R x m x ∈--,且=(1,)A B n -,则=m __________,=n ___________.15.已知不等式[]22023x x a x -+>∈对任意实数,恒成立,则实数a 的取值范围为 .16.若二次函数c bx ax y ++=2的顶点为)25,21(,与x 轴交于两点,且这两点的横坐标的立方和为19,则这个二次函数的表达式为 .三、解答题17.已知A=11x x ⎧⎫≥⎨⎬⎩⎭,B={}21,y y x x x R =++∈ (1)求A ,B(2)求,R A B A C B ⋃⋂18.不等式(m 2-2m -3)x 2-(m -3)x -1<0的解集为R ,求实数m 的取值范围.19.R t x x x f ∈++= , 34)(2,函数g(t)表示函数f(x)在区间]1,[+t t 上的最小值,求g(t)的表达式.20.(本小题14分)已知关于x 的方程221(1)104x k x k -+++=,根据下列条件,分别求出k 的值.(Ⅰ) 方程两实根的积为5; (Ⅱ) 方程的两实根12,x x 满足12||x x =.21.已知21,x x 是方程01254222=-++m mx x 的两实根,求2221x x +的最大值和最小值。
初升高数学衔接带答案

初升高数学衔接带答案一、选择题1. 已知函数\( f(x) = 2x^2 - 3x + 5 \),求\( f(2) \)的值。
A. 7B. 9C. 11D. 13答案:B2. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
A. 5B. 6C. 7D. 8答案:A3. 一个数列的前三项为1, 2, 3,且每一项都是前一项的两倍加一,求第4项的值。
A. 7B. 8C. 9D. 10答案:A二、填空题1. 计算\( \sqrt{64} \)的值是______。
答案:82. 一个圆的半径为7,求该圆的面积。
面积公式为\( A = \pi r^2 \),所以面积是______。
答案:\( 49\pi \)三、简答题1. 解释什么是二项式定理,并给出一个例子。
答案:二项式定理是代数学中的一个重要定理,它描述了(a+b)^n展开成多项式的形式。
例如,\( (x+y)^2 = x^2 + 2xy + y^2 \)。
2. 给定一个函数\( g(x) = 3x - 4 \),求\( g^{-1}(x) \)。
答案:为了求\( g^{-1}(x) \),我们首先设\( y = g(x) \),即\( y = 3x - 4 \)。
解出x,得到\( x = \frac{y+4}{3} \),所以\( g^{-1}(x) = \frac{x+4}{3} \)。
四、计算题1. 解不等式\( |x - 5| < 2 \)。
答案:解这个绝对值不等式,我们得到两个不等式:\( -2 < x - 5 < 2 \)。
解这两个不等式,我们得到\( 3 < x < 7 \)。
2. 计算\( \int_{0}^{1} (3x^2 + 2x) \, dx \)。
答案:首先找到被积函数的原函数,即\( F(x) = x^3 + x^2 \)。
然后计算定积分:\[ \int_{0}^{1} (3x^2 + 2x) \, dx = F(1) - F(0) = (1^3 + 1^2) - (0^3 + 0^2) = 1 + 1 = 2 \]。
初升高数学衔接测试题(学生版)

初升高数学衔接班测试题(满分:100分,时间:120分钟)姓名成绩一.选择题(每小题3分)1.若02522<+-x x ,则221442-++-x x x 等于()2.已知关于x 不等式2x 2+bx -c >0的解集为{}31|>-<x x x 或,则关于x 的不等式042≥++cx bx 的解集为()3.化简132121++-的结果为()A 、23+B 、23-C 、322+D 、223+4.若0<a <1,则不等式(x -a )(x -)1a<0的解为() A.1|x a x a ⎧⎫<<⎨⎬⎩⎭;B.1|x x a a ⎧⎫<<⎨⎬⎩⎭; C.1|x x a x a ⎧⎫<>⎨⎬⎩⎭或;D.1|x x x a a ⎧⎫<>⎨⎬⎩⎭或 5.方程x 2-4│x│+3=0的解是()A.x=±1或x=±3B.x=1和x=3C.x=-1或x=-3D.无实数根6.已知7)(2=+b a ,3)(2=-b a ,则22b a +与ab 的值分别是()A.4,1B.2,23C.5,1D.10,237.已知22x y =的图像时抛物线,若抛物线不动,把X 轴,Y 轴分别向上,向右平移2个单位,那么在新坐标系下抛物线的解析式是()A.2)2(22+-=x yB.2)2(22-+=x yC.2)2(22--=x yD.2)2(22++=x y 8.已知0322≤-x x ,则函数1)(2++=x x x f ()A.有最小值43,但无最大值;B.有最小值43,有最大值1; C.有最小值1,有最大值419;D.无最小值,也无最大值. 9.设βα、是方程)( 02442R x m mx x ∈=++-的两实根,则22βα+的最小值为().A 1617.B 21.C 2.D 1615 10.若关于x 的二次方程2(k+1)x 2+4kx+3k-2=0的两根同号,则实数k 的取值范围为() A.)1,2(- B.]1,32()1,2[ -- C.),32()1,(+∞--∞ D.)1,32()1,2( -- 11.当11≤≤-x 时,函数a ax x y 21222-+-=有最小值是23-,则a 的值为().A 1.B 3.C 1或3.D 8712.已知函数y=ax 2+bx +c (a ≠0)的图象经过点(-1,3)和(1,1)两点,若0<c <1,则a 的取值范围是()A .(1,3)B .(1,2)C .[2,3)D .[1,3]13.若关于X 的不等式a x x <-+-34为空集,则a 的取值范围是()A.a<1B.a 1≤C.0<a<1D.≤0a 1≤ 二、填空题(每小题3分)14.已知4a b c ++=,4ab bc ac ++=,则222a b c ++_____________.15.不等式|x 2+2x |<3的解为____________.16.计算:1111132435911++++⨯⨯⨯⨯=____________. 17.已知关于x 的方程2(3)0x ax a -++=有两个根,且一个根比3-小,另一个根比3-大,则实数a 的取值范围是____________. 三计算题(第(1)问4分,其余每小题5分)5分) 设函数R x x x y ∈+-+=,1222. (1)作出函数的图象;(2)求函数y 的最小值及y 取最小值时的x 值.19.已知关于x 的方程x 2-2(k -1)x+k 2=0有两个实数根x 1,x 2. (I)求k 的取值范围;(II)若12121x x x x +=-,求k 的值. 20.已知a 为实数。
初升高数学衔接试卷及答案

初升高数学衔接试卷及答案一、选择题(每题3分,共30分)1. 下列哪个数是无理数?A. 0.33333...(无限循环)B. πC. √2D. 1/32. 一个圆的半径为5,那么它的直径是多少?A. 10B. 15C. 20D. 253. 如果一个二次方程 \( ax^2 + bx + c = 0 \) 有两个相等的实根,那么 \( b^2 - 4ac \) 等于多少?A. 0B. 1C. -1D. 44. 函数 \( y = 3x + 2 \) 的斜率是多少?A. 2B. 3C. 5D. 45. 以下哪个表达式是正确的因式分解?A. \( x^2 - 1 = x + 1 \)B. \( x^2 - 1 = x - 1 \)C. \( x^2 - 1 = (x + 1)(x - 1) \)D. \( x^2 - 1 = (x - 1)^2 \)6. 一个三角形的三边长分别是3,4,5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能构成三角形7. 一个数的平方根是2,那么这个数是:A. 4B. -4C. 2D. -28. 如果一个函数 \( f(x) \) 是奇函数,那么 \( f(-x) \) 等于:A. \( f(x) \)B. \( -f(x) \)C. \( x \cdot f(x) \)D. \( x^2 \cdot f(x) \)9. 以下哪个选项是不等式 \( x^2 - 4x + 3 < 0 \) 的解集?A. \( x < 1 \) 或 \( x > 3 \)B. \( x < 3 \) 或 \( x > 1 \)C. \( 1 < x < 3 \)D. \( x < -3 \) 或 \( x > 1 \)10. 一个数列的前5项为1,3,5,7,9,这个数列是:A. 等差数列B. 等比数列C. 既不是等差数列也不是等比数列D. 几何数列二、填空题(每题2分,共20分)11. 一个直角三角形的两条直角边长分别是6和8,那么斜边长是________。
初升高衔接数学题加答案
初升高衔接数学题加答案一、选择题(每题3分,共30分)1. 若a、b、c是三角形的三边长,且满足a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不规则三角形答案:B2. 已知x^2 - 5x + 6 = 0,求x的值。
A. x = 2B. x = 3C. x = -2D. x = -3答案:B3. 一个数列的前三项为1,2,3,若每一项都等于前一项的平方,那么第四项是:A. 4B. 8C. 9D. 16答案:C4. 一个圆的半径为r,圆心到圆上任意一点的距离都等于r,这个圆的面积是:A. πr^2B. 2πrC. r^2D. 2r^2答案:A5. 若函数f(x) = 2x - 3,求f(5)的值。
A. 7B. 4C. 2D. 1答案:A6. 已知集合A = {1, 2, 3},B = {2, 3, 4},求A∪B的结果。
A. {1, 2, 3}B. {1, 2, 3, 4}C. {2, 3}D. {1, 2, 3, 4, 5}答案:B7. 一个数的平方根是4,这个数是:A. 16B. -16C. 8D. -8答案:A8. 一个直角三角形的两条直角边分别为3和4,斜边的长度是:A. 5B. 6C. 7D. 8答案:A9. 一个二次方程x^2 + 2x + 1 = 0的解是:A. x = -1B. x = 1C. x = -2D. x = 2答案:A10. 若a和b互为相反数,且a + b = 0,那么a的值是:A. 0B. 1C. -1D. 无法确定答案:D二、填空题(每题2分,共20分)1. 若一个数的立方等于-27,则这个数是______。
答案:-32. 一个数的绝对值是5,则这个数可以是______或______。
答案:5 或 -53. 一个直角三角形的斜边长为5,若一条直角边长为3,则另一条直角边长为______。
答案:44. 若a = 3b,且b ≠ 0,则a和b的比例是______。
2024年新高一数学初升高衔接《一元二次函数、方程和不等式》含答案解析
第二章:一元二次函数、方程和不等式综合检测卷(试卷满分150分,考试用时120分钟)一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.(23-24高一下·河南开封·期中)不等式220x x +-<的解集为( )A .{21}x x -<<∣B .{12}x x -<<∣C .{2xx <-∣或1}x >D .{1x x <-∣或2}x >2.(23-24高一上·湖南衡阳·月考)若2x >-,则12y x x =++的最小值为( )A .-2B .0C .1D .123.(23-24高一上·广东珠海·期中)已知25P a =+,41Q a =+,则P ,Q 的大小关系是( )A .P Q<B .P Q>C .P Q≤D .P Q≥4.(23-24高一上·江苏盐城·月考)已知实数x ,y 满足41x y -≤-≤-,145x y -≤-≤,则9x y -的取值范围是( )A .[7,26]-B .[1,20]-C .[]4,15D .[]1,155.(23-24高一上·湖南衡阳·月考)已知不等式230ax x b +->的解集为{}12x x -<<,则a 、b 的值等于( )A .3a =,6b =-B .3a =,6b =C .3a =-,6b =-D .3a =-,6b =6.(23-24高一上·贵州黔南·月考)已知,0x y >且41x y +=,则11x y +的最小值为( )A .B .8C .9D .107.(23-24高一下·河南·月考)若命题“x ∃∈R ,20x ax a --≤”为假命题,则实数a 的取值范围是( )A .(,4][0,)-∞-+∞B .(,4)(0,)∞∞--⋃+C .[]4,0-D .()4,0-8.(23-24高一上·广东广州·月考)一家金店使用一架两臂不等长的天平称黄金.一位顾客到店内购买20g 黄金,店员先将10g 的砝码放在天平左盘中,取出一些黄金放在天平右盘中,使天平平衡;再将10g 的砝码放在天平右盘中,再取出一些黄金放在天平左盘中,使得天平平衡;最后将两次称得的黄金交给顾客.记顾客实际购得的黄金为xg ,则x 与20的大小关系为( )A .20x <B .20x >C .20x =D .无法确定二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.(23-24高一上·江苏苏州·月考)若0a b <<,则下列结论正确的是( )A .11a b>B .01a b<<C .2ab b >D .b a a b>10.(22-23高一上·山西大同·月考)下列结论正确的是( )A .当0x >时,2≥B .当2x >时,1x x+的最小值是2C .当0,0x y >>时,2x y y x+≥D .当2x <时,112y x x =-+-的最小值为311.(23-24高一上·湖北武汉·月考)已知01b a <<+,若关于x 的不等式22()()x b ax ->的解集中的整数恰有3个,则a 的值可以为( )A .12-B .12C .32D .52三、填空题:本题共3小题,每小题5分,共15分.12.(23-24高一上·河北沧州·期末)不等式302x x+≥-的解集为 .13.(23-24高一上·江苏连云港·月考)已知方程22240x ax a -+-=的一个实根小于2,另一个实根大于2,求实数a 的取值范围.14.(23-24高一上·山东菏泽·月考)若两个正实数x y ,满足3x y +=,且不等式4161m x y+>+恒成立,则实数m 的取值范围为.四、解答题:本题共5小题,共77分。
初升高衔接数学测试(附解答)
初升高衔接数学测试(附解答)初升高衔接数学测试(附解答)一.填空题。
(每题3分,共30分)1. 已知函数f(x) = x^2 - 4x + 3,则f(1) = ______。
解答:f(1) = 1^2 - 4 × 1 + 3 = 1 - 4 + 3 = 0。
2. 设x = 2,则函数f(x) =x^3 - 3|x|的值为______。
解答:f(2) = 2^3 - 3 × 2 = 8 - 6 = 2。
3. 设一次函数y = kx + 3的图象过点(2, 7),则k的值为______。
解答:代入已知点得7 = k × 2 + 3,整理得k = (7 - 3)/2 = 4/2 = 2。
4. 已知x^2 + k = (x - 2)(x + 3),则k的值为______。
解答:展开右侧得x^2 + k = x^2 + x - 6,比较系数得k = -6。
5. 一个三位数的1/10是5,将这个三位数加上55后得到一个四位数,这个四位数是________。
解答:设三位数为xyz,其中x、y、z表示个位、十位和百位数字。
根据题意得到两个方程:(1)1/10 * 100 * x + 1/10 *10 * y + 1/10 * z = 5;(2)100 * x + 10 * y + z + 55 = 1000 * x+ 100 * y + 10 * z。
计算得x = 4,y = 4,z = 5,所以四位数为4445。
6. 一根绳子长45米,把它剪成3段,第一段比第二段短3米,第二段比第三段短2米,则第一段的长度是________。
解答:设第一段的长度为x,根据题意得到两个方程:(1)x + (x + 3) + (x + 3 + 2) = 45;(2)x + 5 = x + 3。
解得x = 13,所以第一段的长度是13米。
7. 甲、乙两人连续投掷硬币,甲方先开始,投得正面得1分,反面得0分;乙方投得正面得2分,反面得0分。
初升高衔接数学测试题
连接班数学练习题一.选择题(每题5 分)1.若 2x 25 x 2 0 ,则 4x 2 4x 1 2 x 2 等于()2.已知对于 x 不等式 2x 2+ bx -c > 0 的解集为 x | x 1或 x3} ,则对于 x 的不等式 bx 2 cx 40 的解集为( )3.若 0< a < 1,则不等式( x - a ) (x - 1) < 0 的解为()a(A)x | a x1; (B)x | 1x a ;aa(C)x | x a 或 x1; (D)x | x 1 或 x aaa4、方程 x 2-4│x │+3=0的解是 ()A.x= ±1 或 x=±3B.x=1 和 x=3C.x=- 1 或 x= -3D.无实数根5.已知 (a b) 27 , (ab)23, 则 a 2 b 2 与 ab 的值分别是()A. 4,1B. 2,3 C.5,1D. 10,3226. 已知 y2 x 2 的图像时抛物线,若抛物线不动,把X 轴, Y 轴分别向上,向右平移2 个单位,那么在新坐标系下抛物线的分析式是( )A. y 2(x 2) 2 2B. y 2( x 2)2 2C. y2(x2) 2 2 D.y2( x 2)2 27.已知 2 x 23x0 ,则函数 f ( x)x 2x1 ------------------------ ()(A) 有最小值3,但无最大值;(B) 有最小值3,有最大值1;4194(C) 有最小值 ;(D) 无最小值,也无最大值 .1,有最大值48.设 、是方程 4x 2 4mx m2 0 ( x R) 的两实根, 则22的最小值为 ()A.17B.1C. 2D.15162169.若对于 x 的二次方程 2(k+1)x 2+4kx+3k - 2=0的两根同号,则实数 k 的取值范围为 ------ ()(A ) (2,1)(B )[2, 1) (2,1]3(C)(, 1)(2 ,)(D)( 2,1) (2,1)3310.当1x1时,函数 y2x 22ax12a 有最小值是3,则 a 的值为()2A. 1B. 3C.1或3D. 7 811. 已知函数 y=ax2+bx+c(a≠ 0) 的图象经过点 (- 1,3)和 (1,1) 两点 ,若 0<c< 1,则 a 的取值范围是 ()A .(1,3)B . (1,2)C. [2,3) D .[1,3]12.若对于 X 的不等式x43x a 为空集,则 a 的取值范围是()A.a<1B.a1C. 0<a<1D.0a1二、填空题(每题 5 分)13. 已知a b c4, ab bc ac 4,则 a2b2c2_____________.14.不等式 |x2+2x|<3 的解为 ____________.15. 计算:1213191=____________.13451116. 已知对于x的方程x2ax( a3)0 有两个根,且一个根比 3 小,另一个根比 3 大,则实数 a 的取值范围是 _______ _____ .三.解答题17.设函数y x2 2 x21, x R .(1)作出函数的图象 ;(2)求函数y的最小值及y取最小值时的x值 .18. 已知对于x 的方程 x2- 2( k- 1) x+k 2=0 有两个实数根x1,x2.(I)求 k 的取值范围;(II) 若x1x2x1 x2 1 ,求k的值.19.已知 a 为实数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初升高数学衔接班测试题
(满分:100分,时间:120分钟)
姓名 成绩
一.选择题(每小题3分)
1.若02522
<+-x x ,则221442
-++-x x x 等于( )
.A 54-x .B 3- .C 3 .D x 45-
2.已知关于x 不等式2x 2+bx -c >0的解集为{}31|>-<x x x 或,则关于x 的不等式042≥++cx bx 的解集为( )
.A }212|⎩⎨⎧≥-≤x x x 或 .B }221|⎩
⎨⎧
≥-≤x x x 或
.C }221|{≤≤-
x x .D }212|⎩
⎨⎧
≤≤-x x
3.化简
1
321
21++
-的结果为( )
A 、23+
B 、23-
C 、322+
D 、223+
4.若0<a <1,则不等式(x -a )(x -)1
a
<0的解为( ) A. 1|x a x a ⎧⎫
<<
⎨⎬⎩⎭; B. 1|x x a a ⎧⎫<<⎨⎬⎩⎭
; C. 1|x x a x a ⎧
⎫<>
⎨⎬⎩⎭或; D. 1|x x x a a ⎧⎫<>⎨⎬⎩⎭
或 5.方程x 2-4│x│+3=0的解是 ( )
A.x=±1或x=±3
B.x=1和x=3
C.x=-1或x=-3
D.无实数根
6.已知7)(2=+b a ,3)(2
=-b a ,则2
2b a +与ab 的值分别是( )
A. 4,1
B. 2,
23 C. 5,1 D. 10,2
3 7.已知2
2x y =的图像时抛物线,若抛物线不动,把X 轴,Y 轴分别向上,向右平移2个单位,那么在新坐标系下抛物线的解析式是( ) A.2)2(22
+-=x y B.2)2(22
-+=x y
C.2)2(22--=x y
D.2)2(22
++=x y
8.已知0322
≤-x x ,则函数1)(2
++=x x x f ( )
A. 有最小值
43,但无最大值; B. 有最小值4
3
,有最大值1; C. 有最小值1,有最大值
4
19
; D. 无最小值,也无最大值. 9.设βα、是方程)( 02442
R x m mx x ∈=++-的两实根,则2
2βα+的最小值为( )
.
A 16
17
.B 21 .C 2 .D 1615
10.若关于x 的二次方程2(k+1)x 2+4kx+3k -2=0的两根同号,则实数k 的取值范围为( ) A. )1,2(- B. ]1,3
2
()1,2[ --
C. ),32()1,(+∞--∞
D. )1,3
2()1,2( -- 11.当11≤≤-x 时,函数a ax x y 21222
-+-=有最小值是2
3
-
,则a 的值为( ) .A 1 .B 3 .C 1或3 .D 8
7
12. 已知函数y=ax 2+bx +c (a ≠0)的图象经过点(-1,3)和(1,1)两点,若0<c <1,则a 的取值范围是( )
A .(1,3)
B .(1,2)
C .[2,3)
D .[1,3] 13. 若关于X 的不等式a x x <-+-34为空集,则a 的取值范围是 ( ) A.a<1 B.a 1≤ C. 0<a<1 D. ≤0a 1≤
二、填空题(每小题3分)
14.已知4a b c ++=,4ab bc ac ++=,则2
2
2
a b c ++_____________. 15.不等式|x 2+2x |<3的解为_________ ___.
16.计算:
1111
132435
911
++++
⨯⨯⨯⨯=____________. 17. 已知关于x 的方程2(3)0x ax a -++=有两个根,且一个根比3-小,另一个根比3-大,则实数a 的取值范围是_______ _____.
三 计算题(第(1)问4分,其余每小题5分)
四.解答题(每小题5分)
18.设函数R x x x y ∈+-+=,1222
. (1)作出函数的图象;
(2)求函数y 的最小值及y 取最小值时的x 值.
19.已知关于x 的方程x 2-2(k -1)x+k 2=0有两个实数根x 1,x 2. (I)求k 的取值范围;
(II)若12121x x x x +=-,求k 的值.
(1)
(2)
(3)
20.已知a 为实数。
(1)解不等式:()
22321220x a a x a a -++++<;
(2)若(1)中的不等式的解包含所有2到5的实数(包括端点),求a 的取值范围。
21.关于x 的方程22
x -3x+2m=0的两根都在[-1,1]上,求实数m 的取值范围.
22
23. 如图15,在Rt △ABC 中,∠B=90°,∠A 的平分线交BC 于D ,E 为AB 上一点,DE=DC ,以D 为圆心,以DB 的长为半径画圆。
求证:(1)AC 是⊙D 的切线;(2)AB+EB=AC 。
24.已知当m ∈R 时,函数y =m (x 2-1)+x -a 的图象和x 轴恒有公共点,求实数a 的取值范围.
图15 23。
