概率论与数理统计试题6
概率论与数理统计期末考试试题(答案)
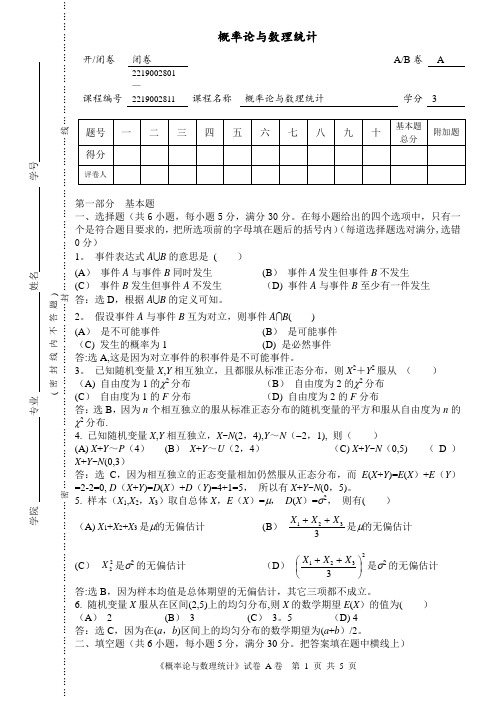
概率论与数理统计开/闭卷闭卷A/B 卷 A课程编号 2219002801—2219002811课程名称 概率论与数理统计学分 3基本题6小题,每小题5分,满分30分。
在每小题给出的四个选项中,只有一把所选项前的字母填在题后的括号内)(每道选择题选对满分,选错分)。
事件表达式A B 的意思是 ( ) ) 事件A 与事件B 同时发生 (B ) 事件A 发生但事件B 不发生) 事件B 发生但事件A 不发生 (D) 事件A 与事件B 至少有一件发生D ,根据A B 的定义可知。
假设事件A 与事件B 互为对立,则事件A B ( )) 是不可能事件 (B ) 是可能事件 C) 发生的概率为1 (D) 是必然事件 :选A,这是因为对立事件的积事件是不可能事件。
已知随机变量X ,Y 相互独立,且都服从标准正态分布,则X 2+Y 2服从 ( ) A) 自由度为1的χ2分布 (B ) 自由度为2的χ2分布 ) 自由度为1的F 分布 (D) 自由度为2的F 分布选B ,因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的2分布.已知随机变量X ,Y 相互独立,X ~N (2,4),Y ~N (-2,1), 则( ) X +Y ~P (4) (B ) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D ) +Y ~N (0,3)C ,因为相互独立的正态变量相加仍然服从正态分布,而E (X +Y )=E (X )+E (Y )D (X +Y )=D (X )+D (Y )=4+1=5, 所以有X +Y ~N (0,5)。
样本(X 1,X 2,X 3)取自总体X ,E (X )=μ, D (X )=σ2, 则有( ) A) X 1+X 2+X 3是μ的无偏估计(B )1233X X X ++是μ的无偏估计) 22X 是σ2的无偏估计(D ) 21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计:选B ,因为样本均值是总体期望的无偏估计,其它三项都不成立。
《概率论与数理统计》6,7,8章测验

样本, 6.设X1, X2, …,Xn是来自总体X样本, 则 , 方差D( X ) = σ 2的无偏估计是( ) n−1 1 n−1 1 2 ( Xi − X )2 ∑ (A) ∑(Xi − X ) (B)
8.. 设总体 X ~ N(µ, σ 2 ) ,其中σ 2 已知, 若样本 已知, 容量n 和置信度 −α 均不变, 则对于不同 1 均不变, 的样本观察值, 的样本观察值, 总体均值 µ 的置信区间的 长度( 长度( )
1 2 s = ∑(Xi −X ) n −1 i=1 1 n 2 2 s3 = ∑(Xi −µ) n −1 i=1
2 1
1 2 s = ∑( Xi −X ) n i=1 1 n 2 2 s4 = ∑( Xi −µ) n i=1
2 2
则服从自由度为n –1的t分布的随机变量 1 是( ) X −µ X −µ (A) t = (B) t =
n −1 i=1 n i=1 n 1 n 2 1 2 (C) ∑(Xi − X ) (D) n −1∑(Xi − X ) i=1 n i=1 2 2 7. 设X 服从正态分布N(µ,σ ), 且 σ 未知, 则µ的置信度为0.95的置信区间 为( ) s σ (A) ( X ± t0.025 ) (B) ( X ± t0.025 ) n n s σ (C) ( X ± z0.025 ) (D) ( X ± z0.025 ) n n
4.设X1, X2, …,Xn是来自正态总体 N(0, 1) 4.设 , 2 简单随机样本, 的简单随机样本,X 和 s 分别为样本均值 和样本方差 本方差, 和样本方差,则( ) (B) nX ~ N(0, 1) (A) X ~ N(0, 1) n X 2 2 ~ t (n −1) (C) ∑Xi ~ χ (n −1) (D) s/ n i=1
概率论与数理统计 自测题6

3
∑ 2.设总体X~N(0,0.09),X1,X2,…,X10为来自X的样本,求
⎧ 10 P⎨
⎩ i=1
X
2 i
>1.44⎫ ⎬源自。(0.10)⎭{ } 3.设X1,X2,…,X17为来自总体X~N(u,δ 2 )的样本,求 P X > u + KSn =0.95 中的K
值。(-0.437)
4.设X1,X2,…,Xn为来自N( μ , δ 2 )的样本,设 X n+1 ~ N ( μ , δ 2 ),且与X1,
5.设R.V.X~N(1,4),X1,X2,…,X100为X的样本,已知 Y = a X + b ~ N (0,1),则
有( A ) A.a=-5,b=5
B.a=5,b=5
C.a= 1 ,b= − 1
5
5
D.a= − 1 ,b= 1 55
1
6.设X1,X2,…,Xn来自正态总体N( μ ,δ 2 ),则下列结论不成立的有( D )
Y
=
a(X1
−
2X 2 )2
+ b(3X 3
−
4X 4 )2
,则a=
1 20
,b= 1 100
时Y
~
χ
2 且自由度为2
5 . 设 X1 , X2 , … , X6 为 来 自 总 体 X~N ( 0 , δ 2 ) 的 样 本 , 设
Y = ( X 1 + X 2 + X 3 )2 + ( X 4 + X 5 + X 6 )2 ,则当C= 3δ 2 时 CY ~ χ 2 (2) 。
独立,
S12
和
S
2 2
分别为两个样本的样本修正方差,则服从F(7,9)的统计量为(
概率论与数理统计教材第六章习题

X σ0 n
~ N(0,1)
对于置信水平1- ,总体均值的置信区间为 对于置信水平 -α,总体均值 的置信区间为
X
σ0
n
uα < < X +
2
σ0
n
uα
2
(2)设总体 ~ N(,σ 2 ), 未知 ,求的置信区间。 设总体X~ 未知σ, 的置信区间。 设总体 的置信区间
σ 0 ,则样本函数 t = X ~ t(n 1) 用 S 代替 S n
i =1
n1
n1
F
1
α ∑ Yj 2
2 j =1
n2
(
)
2
n2
10
2 2 及 (1)设两个总体 ~ N(1,σ1 ) 及Y~ N(2 ,σ 2 ), 未知 1 2, )设两个总体X~ ~
2 σ1 的置信区间。 求 2 的置信区间。 σ2
选取样本函数 选取样本函数
2 2 S1 σ1 F = 2 2 ~ F(n1 1, n2 1) S2 σ2
∑x
i =1
n
i =1
i
n = 0.
1 p
得 p 的极大似然估计值为 p =
n
∑x
i =1
n
1 = x
i
12
1 θ 2. 设总体 服从拉普拉斯分布:f ( x;θ ) = e ,∞< x < +∞, 设总体X 服从拉普拉斯分布: 2θ 求参数 θ 其中 > 0. 如果取得样本观测值为 x1 , x2 ,L, xn , 求参数θ
第六章 参数估计
(一)基本内容
一、参数估计的概念 1 定义:取样本的一个函数θ ( X 1 , X 2 ,L , X n ), 如果以它的观测 定义:
概率论与数理统计考研复习题6

概率论与数理统计考研复习题(6)数理统计的基本概念1.X 与Y 相互独立且都服从)3,0(2N ,而9191,Y Y X X ,和分别是来自总体X 和Y 的简单随机样本,求统计量 292191Y Y X X U ++++= 服从的分布.2.求总体)3,20(N 的容量分别为10,15的两独立样本均值差的绝对值大于0.3的概率.3.设n X X X ,,,21 是来自具有)(2n χ分布的总体样本。
求样本均值X 的数学期望和方差.4.设总体X ~N (0,1),从此总体中取一个容量为6的样本(621,,,X X X ),设Y =(26542321)()X X X X X X +++++,试决定常数C ,使得随机变量CY 服从2χ分布.5.从正态总体)6,4.3(2N 中抽取容量为n 的样本,如果要求其样本均值位于区间 (1.4, 5.4)内的概率不小于0.95,问样本容量n 至少应取多大?6.从装有一个白球,两个黑球的罐子里有放回地取球,令X =0表示取到白球,X =1表示取到黑球,求容量为5的样本(521,,,X X X )的和的分布,并求样本的均值X 和样本的方差2S 的期望值.7.设总体X ~),0(2σN ,(21,X X )为取自这总体的一个样本,求: (1)221221)()(X X X X Y -+=的概率密度;(2)P {Y <4}. 8.设总体服从参数为λ的指数分布,分布密度为⎩⎨⎧≤>=-0,00,);(x x e x F xλλλ,求E (X ),D (X ),E )(2S .9.从正态总体)5.0,(2μN 中抽取样本1021,,,X X X .(1)已知0=μ,求概率P {}41012≥∑=i i X; (2)未知μ,求概率P {85.2)(2101≥-∑=i i X X}.。
概率论与数理统计第六章测试题

第6章 参数估计选择题1.设n X X X ,...,,21是来自正态总体X 的简单随机样本,X 的分布函数F(x;θ)中含未知参数,则(A )用矩估计法和最大似然估计法求出的θ的估计量相同 (B) 用矩估计法和最大似然估计法求出的θ的估计量不同 (C )用矩估计法和最大似然估计法求出的θ的估计量不一定相同 (D) 用最大似然估计法求出的θ的估计量是唯一的2.设n X X X ,...,,21是来自正态总体X 的简单随机样本,EX=μ,DX=σ2,其中μ,σ2均为未知参数,X =1ˆμ,12ˆX =μ,下面结论哪个是错误的。
(A )X =1ˆμ是μ的无偏估计 (B) 12ˆX =μ是μ的无偏估计 (C )X =1ˆμ比12ˆX =μ 有效 (D) ∑=-ni i X n 12)(1μ是σ2的最大似然估计量 3.设n X X X ,...,,21是来自正态分布总体N(μ,σ2)的简单随机样本,其中数学期望μ已知,则总体方差σ2 的最大似然估计量是(A ) ∑=--n i i X X n 12)(11 (B) ∑=-ni i X X n 12)(1 (C ) ∑=--n i i X n 12)(11μ (D) ∑=-n i i X n 12)(1μ 4.已知总体X 在区间[0,θ]上均匀分布,其中θ是未知参数,设n X X X ,...,,21是来自X 的简单随机样本,X 是样本均值,},...,max {1)(n n X X X = 是最大观测值,则下列选项错误的是 (A ))(n X 是θ的最大似然估计量 (B) )(n X 是θ的无偏估计量 (C )X 2是θ的矩估计量 (D) X 2是θ的无偏估计量5. 设总体X~N(μ1,σ2),总体Y~N(μ2,σ2),m X X X ,...,,21和n Y Y Y ,...,,21分别是来自总体X和Y 的简单随机样本,样本方差分别为2X S 与2Y S ,则σ2 的无偏估计量是 (A )22YX S S + (B) 22)1()1(Y X S n S m -+-(C )222-++n m S S YX (D) 2)1()1(22-+-+-n m S n S m Y X6. 设X 是从总体X 中取出的简单随机样本n X X X ,...,,21的样本均值,则X 是μ的矩估计,如果(A )X~N(μ,σ2) (B) X 服从参数为μ的指数分布 (C )P (X=m )=μ(1-μ)m-1,m=1,2,… (D) X 服从[0,μ]上的均匀分布 填空题1.假设总体X 服从参数为λ的泊松分布,n X X X ,...,,21是取自总体X 的简单随机样本,其均值、方差分别为X ,S 2 ,如果2)32(ˆS a X a -+=λ为λ的无偏估计,则a= 。
概率论与数理统计总习题及答案

试题一、填空1、设P(A)=0.4,P(AUB)=0.7,A与B不相容,则P(B)=0.3 解:由公式,P(AUB)= P(A)+ P(B)所以P(B)= 0.7-0.4=0.32、若X~B(n,p),则X的数学期望E(X)= n*p解:定义:二项分布E(X)= n*p D(X)=n*p(1-p)3、甲盒中有红球4个,黑球2个,白球2个;乙盒中有红球5个,黑球3个;丙盒中有黑球2个,白球2个。
从这3个盒子中任取1个盒子,再从中任取1球,他是红球的概率0.375解:设甲为A1,乙为A2,丙为A3,红球为B则P(B)=P(A1)P(B| A1)+P(A2)P(B| A2)+P(A3)P(B| A3)=1/3*1/2+1/3*5/8+1/3*0=0.3754、若随机变量X的分布函数为f(x)={0,x<0√x,0≤x<1 1, x≥1则P{0.25<X≤1}=0.5解:分布函数求其区间概率即右端点函数值减去左端点函数值F (1)-F (0.25) = 1-0.5=0.55、设(X1,X2,…X n)为取自正态分布,总体X~N(μ,σ2),的样本,则X的分布为N(μ,σ2n )解:定义6、设ABC表示三个随机变量事件,ABC至少有一个发生,可表示为AUBUC解:至少;如果是一切发生为A∩B∩C7、设X为连续随机变量,C是一个常数,则P{X=C}=0 解:取常数,取一个点时,恒定为08、一射手对同一目标独立地进行4次射击,若至少命中1次的概率为80/81,则该射击的命中率为2/3解:射击,即伯努利试验。
求P(X=0)=Cn0p0(1−p)4=1−80/81(1−p)4=181,1−p=13,p=239、设X~N(−1,2),Y~N(1,3)且X与Y相互独立,则X+ 2Y~N(1,14)解:因为X与Y相互独立,再由正态分布得E(X)=-1,D(X)=2;E(Y)=1,D(Y)=3;所以E(X+2Y)=E(X)+2E(Y)=-1+2*1=1D(x+2Y)=D(X)+4D(Y)=2+4*3=14所以X+2Y~N(1,14)10、设随机变量X的方差为2.5,利用切比雪夫不等式估计概率得P{|X−E(X)|≥7.5}≤ 2.57.52解:由切比雪夫不等式P{|X−μ|≥ε}≤σ2ε2≤ 2.57.52二、 计算1、 从0,1,2,…9中任意取出3个不同的数字,求下列的概率。
考研数学三(概率论与数理统计)历年真题试卷汇编6(题后含答案及解析)

考研数学三(概率论与数理统计)历年真题试卷汇编6(题后含答案及解析)题型有:1. 选择题 2. 填空题 3. 解答题选择题下列每题给出的四个选项中,只有一个选项符合题目要求。
1.(2000年)在电炉上安装了4个温控器,其显示温度的误差是随机的。
在使用过程中,只要有两个温控器显示的温度不低于临界温度t0,电炉就断电,以E表示事件“电炉断电”,而T(1)≤T(2)≤T(3)≤T(4)为4个温控器显示的按递增顺序排列的温度值,则事件E等于事件( )A.{T(1)≥t0}。
B.{T(2)≥t0}。
C.{T(3)≥t0}。
D.{T(4)≥t0}。
正确答案:C解析:随机变量T(1),T(2),T(3),T(4)为4个温控器显示的按递增顺序排列的温度值,事件E表示事件“电炉断电”,即有两个温控器显示的温度不低于t0,此时必定两个显示较高的温度大于等于t0,即T(4)≥T(3)≥t0。
所以说断电事件就是{T(3)≥t0}。
2.(2009年)设事件A与事件B互不相容,则( )A.B.P(AB)=P(A)P(B)。
C.P(A)=1-P(B)。
D.正确答案:D解析:因为A,B互不相容,所以P(AB)=0。
选项A:=1-P(A∪B),因为P(A ∪B)不一定等于1,所以A不正确;选项B:当P(A),P(B)不为0时,选项B 不成立,故排除B;选项C:只有当A、B互为对立事件的时候才成立,故排除C;选项D:=1-P(AB)-1,故D正确。
3.(2014年)设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=( )A.0.1。
B.0.2。
C.0.3。
D.0.4。
正确答案:B解析:P(A-B)=0.3,则P(A)-P(AB)=0.3,又随机事件A与B相互独立,则有P(AB)=P(A)P(B)。
因此有P(A)-P(A)P(B)=0.3,又P(B)=0.5,故P(A)=0.6,且P(AB)=P(A)P(B)=0.3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广西大学课程考试试卷 ( —— 学年度第 学期) 课程名称:概率论与数理统计 试卷库序号:6 命题教师签名: 教研室主任签名: 院长签名:
———————————————————————————— 一.单项选择题(从下面各题的备选答案A 、B 、C 、D 中选择一个你认为正确的填入括号内。
注意选择两个或两个以上的答案不能得分。
每题2分,共20分) 1.一部4卷的文集随便放在书架上,恰好各卷自左向右卷号为1、2、
3、4的概率是( ). A 0.5 B 0.0417 C 0.125 D 0.25 2. 设A 、B 为两个事件,则()()B A B A ++表示 ( ) A. 必然事件 B.不可能事件 B. C. A 与B 恰有一个发生 D. A 与B 不同时发生 3. 一名射手连续向某个目标射击三次,事件i A 表示第i 次()3,2,1=i 击中目标,用i A ()3,2,1=i 表示三次中至多有一次击中目标是( )。
A 321A A A ++
B
321A A A C 323121A A A A A A ++ D.321A A A
4.设随机变量ξ的密度函数()⎩⎨⎧≤≤><=10 41 0 03x x x x x ϕ 则使()()a p a p ≤=≥ξξ成立的常数a =( ) A.421 B 42 C 21 D 1-42
1 5.假设随机变量ξ服从正态分布N(10,2)2,则有( )成立.
A .()8)8(≥=-≤ξξP P
B ()81)8(≤-=-≤ξξP P
C ()9)9(≥=≤ξξP P
D ()10)10(≥=≤ξξP P
6. 样本()n X X X ,.....,,21取自总体2,,σξμξξ==D E ,则( )可以作为2σ的无偏估计。
A 当μ已知时,统计量()n X n i i /1
2
∑=-μ B 当μ已知时,统计量())1/(1
2
--∑=n X n i i μ C 当μ未知时,统计量()n X n i i /1
2
∑=-μ D 当μ未知时,统计量())1/(1
2
--∑=n X n i i μ 7.若随机变量ξ服从( ),则[]2
ξξE D =。
A 正态分布 B 指数分布 C 二项分布 D 普哇松(poisson)分布8.已知(ξ,η)的联合概率密度函数为()y x ,ϕ:则(ξ,η)关于ξ的边缘密度函数为( ).
A ()dy y x ⎰+∞∞-,ϕ
B ()dx y x ⎰+∞
∞
-,ϕ
C ()dxdy y x ⎰⎰+∞∞-+∞
∞-,ϕ D ()dxdy y x x y ⎰⎰∞-∞-,ϕ
9.甲、乙两人各自投篮的命中率分别是0.8和0.7,假设两人互不影响,则.甲、乙两人都投中篮的概率是( )。
A .0.06
B 0.56
C 0.94 C 0.44
10.设检验问题中,记0H 为待检验假设,则称( )为第一类错误(弃真错误)。
A . 原假设0H 成立,接受0H .
B . 原假设0H 成立,拒绝0H .
C . 原假设0H 不成立,接受0H .
D . 原假设0H 不成立,拒绝0H .
二.填空题(把正确的答案填入_____________.每题3分,共15分)
1. 小样本()n X X X ,.....,,21取自正态总体N (),2σμ,当2σ已知,X 与2S 分别是样本的平均数和方差,则______________服从标准正态分布。
2.设{}15
8≥
<-εξξE p ,1235=ξD 试用切贝谢夫不等式估计ε的最小值是____________。
3. 若随机变量ξ∽N(2,22),η=1-ξa ∽)1,0(N ,则可求a =___________.
4. 随机变量ξ的密度函数为()
010 12⎪⎩
⎪⎨⎧≤≤+=其他x x c x ϕ 则c ___________. 5. 社会上定期发行某种奖券,每券一元,中奖率为0.006,某人每次购买一张奖券,如果没有中奖下次再继续购买一张,直至中奖为止,该人购买次数ξ的概率分布为___________________________________________.
三(13分) 从某厂生产的一批电子元件中,随机抽取9个样品,测得平均寿命x
=1080小时,样本的标准差s=200小时;假设电子元件的寿命服从正态分布,α水平,检验该厂生产的电子元件的平均寿命是否为1000小时?
试以%
5
=
四(12分) 某自动包装机分装糖的重量为随机变量ξ,平均重量Eξ=μ,随机抽取49袋,算得样本的平均数为502,样本的方差为36克,试对平均重量Eξ=μα
进行区间估计()
=
.0
05
五(10分) 一大批种蛋中,其中良种蛋占80%,从中任取500枚,求其中良种蛋率未超过81%的概率?
六(15分) 在一个400人的单位中普查某种疾病,400个人去验血,对这些人的血的化验可以用两种方法进行。
(1)每个人的血分别化验,这时需要化验400次。
(2)把每4个人的血混在一起进行化验,如果结果是阴性,那么对这4个人只作一次化验就够了;如果结果是阳性,那么对这4个人再逐个分别化验,这时对这4个人共需要做5次化验。
假定对所有的人来说,化验是阳性反应的概率是0.1,而这些人的反应是独立的,试说明办法(2)能减少化验的次数。
七(15分) 某商店收进甲厂生产的产品30箱,乙厂生产的同种产品20箱,甲厂每箱装100个,废品率是0.06,甲厂每箱装120个,废品率是0.05,求(1)任取一箱,从中任取一个为废品的概率?(2)若将所有产品开箱混放,求任取一个为废品的概率。
附录:所需的查表的数据:
若标准正态分布的分布函数为:)(0x Φ
T 服从具有1-n 个自由度的t 分布
αα=-≥))1((n t T P
05.0=α, ()31.28=αt ()()201.211 228.2)10( 2.2622 9===αααt t t 本文档部分内容来源于网络,如有内容侵权请告知删除,感谢您的配合!。
