最新文科数学一轮复习考案10.4 回归分析与独立性检验.
高考数学第一轮复习考纲《回归分析与独立性》检验课件39 理

考点 2 独立性检验 例 2:某研究机构随机选取了 60 名高中生,通过问卷调查, 得到以下数据:
作文成绩优秀 作文成绩一般 合计
课外阅读量较大
22
10
32
课外阅读量一般
8
20
28
合计
30
30
60
利用独立性检验的方法判断高中生作文成绩与课外阅读量 之间的关系.
解题思路:根据公式计算 K2 的观测值 k 后与临界值表比较. 解析:假设 H0:高中生作文成绩与课外阅读量无关, 代入公式计算得 k= 60 (22 20 810)2 =9.643.
P(K2 ≥k0)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010 0.005 0.001
0.45 0.70 1.32 2.07 2.70 3.84
10.82
k0
5.024 6.635 7.879
58 3 261
8
例如:当 K2≥3.841 时,则有 95%的把握说 X 和 Y 有关; 当 K2≥6.635 时,则有 99%的把握说 X 和 Y 有关.
5.已知 x 与 y 之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则 y 与 x 的 线 性 回 归 方 程 为 y = bx + a 必 过 点 _(_1_._5_,4_)__
解析: x=1.5, y =4,回归直线必过样本点中心(1.5,4).
考点 1 线性回归的应用
例 1:.某种书每册的成本费 y(元)与印刷册数 x(千册)有关, 经统计得到数据如下:
x 1 2 3 5 10 20 30 50 100 200 y 10.15 5.52 4.08 2.85 2.11 1.62 1.41 1.30 1.21 1.15
2022版高考数学一轮复习第10章第3讲线性回归与独立性检验训练含解析

第十章 第3讲[A 级 基础达标]1.若回归直线方程为y ^=3-2x ,则变量x 增加一个单位,y ( ) A .平均增加3个单位 B .平均增加2个单位 C .平均减少3个单位 D .平均减少2个单位【答案】D2.(2020年南昌模拟)已知一组样本数据点(x 1,y 1),(x 2,y 2),(x 3,y 3),…,(x 6,y 6),用最小二乘法得到其线性回归方程为y ^=-2x +4,若数据x 1,x 2,x 3,…,x 6的平均数为1,则y 1+y 2+y 3+…+y 6等于( )A .10B .12C .13D .14【答案】B3.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为( )A .-1B .0C .12D .1【答案】D4.如果根据是否爱吃零食与性别的列联表得到K 2≈5.852,所以判断是否爱吃零食与性别有关,那么这种判断犯错的可能性不超过( )A .2.5%B .0.5%C .1%D .0.1%P (K 2≥k )0.100 0.050 0.025 0.010 0.001 k2.7063.8415.0246.63510.8285.某考察团对10个城市的职工人均工资x (千元)与居民人均消费y (千元)进行调查统计,得出y 与x 具有线性相关关系,且回归方程为y ^=0.6x +1.2.若某城市职工人均工资为5千元,估计该城市人均消费额占人均工资收入的百分比为( )A .66%B .67%C .79%D .84%【答案】D【解析】因为y 与x 具有线性相关关系,满足回归方程y ^=0.6x +1.2,该城市居民人均工资为x =5,所以可以估计该城市的职工人均消费额y =0.6×5+1.2=4.2(元),所以可以估计该城市人均消费额占人均工资收入的百分比为4.25=84%.6.(2020年成都模拟)某公司一种新产品的销售额y 与宣传费用x 之间的关系如表:已知销售额y 与宣传费用x 具有线性相关关系,并求得其回归直线方程为y ^=b ^x +9,则b ^的值为________.【答案】6.5【解析】由表中数据,得x =0+1+2+3+45=2,y =10+15+20+30+355=1105=22,又回归直线方程y ^=b ^x +9过样本中心点(2,22),得22=2b ^+9,解得b ^=132=6.5.7.(2020年滦南期末)2017年3月15日,某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查,5家商场的售价x (元)和销售量y (件)之间的一组数据如下表所示:y =-3.2x +a ,则a =________.【答案】40 【解析】根据题意:x -=9+9.5+10+10.5+115=10,y -=11+10+8+6+55=8,因为y -=-3.2x +a ,所以a =3.2×10+8=40.8.(2020年六安期末)“埃博拉病毒”在西非的传播速度很快,这已经成为全球性的威胁,为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:附:K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d ).【答案】95%【解析】由题中数据可得:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=100(10×30-40×20)250×50×30×70=10021≈4.762>3.841,根据临界值表可得:犯错误的概率不超过0.05.即有95%的把握认为“小动物是否感染与服用疫苗有关”.故答案为95%.9.(2020年南阳月考)2021年将在日本东京举办第32届夏季奥林匹克运动会,简称为“奥运会”.为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在20~70岁之间的100人进行调查.经统计,“年轻人”与“中老年人”的人数之比为2∶3.(1)的把握认为是否关注“奥运会”与年龄段有关;(2)现采用分层抽样的方法从中老年人中选取6人进行问卷调查.若再从这6人中选取2人进行面对面询问,求事件“选取的2人中至少有1人关注奥运会”的概率.K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .解:(1)“年轻人”共有100×25=40(人),“中老年人”共有100×35=60(人),由此填写列联表如下:根据表中数据,计算K 2=100(30×40-20×10)240×60×50×50=503≈16.67>10.828,所以有99.9%的把握认为是否关注“奥运会”与年龄段有关. (2)用分层抽样法选取6位中老年人中有4人不关注,2人关注, 则所求概率为p =1-C 24C 26=35.10.(2020年湖南雅礼中学月考)近年来,国资委党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某扶贫小组为更好地执行精准扶贫政策,为某扶贫县制定了具体的扶贫政策,并对此贫困县从2015年到2019年的居民家庭人均纯收入(单位:百元)进行统计,数据如下表:(1)求人均纯收入y (2)是否有99.9%的把握认为村民的年龄与对扶贫政策的满意度具有相关性?参考公式:回归直线y ^=a +bx 中斜率和截距的最小二乘估计公式分别为:b ^=∑n =1ix i y i -n x - y-∑n =1ix 2i -n x -2=∑n =1i(x i -x -)(y i -y -)∑n =1i(x i -x -)2,a =y --b x -,K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .临界值表:解:(1)依题意:t =15×(1+2+3+4+5)=3,y =15×(5.8+6.6+7.2+8.8+9.6)=7.6,故∑i =15(t i -t )2=4+1+0+1+4=10,∑i =15(t i -t )(y i -y )=(-2)×(-1.8)+(-1)×(-1)+0×(-0.4)+1×1.2+2×2=9.8,b =∑i =1n(t i -t )(y i -y )∑i =1n(t i -t )2=0.98,所以a =y -b t =7.6-0.98×3=4.66. 所以y ^=0.98t +4.66. (2)依题意,完善表格如下:计算得K 2k 2=300×(150×50-50×50)2200×100×200×100=300×5 000×5 000200×100×200×100=18.75>10.828,故有99.9%的把握认为村民的年龄与扶贫政策的满意度具有相关性.[B 级 能力提升]11.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程y =b ^x +a ,其中b ^=0.76,a =y -b ^x .据此估计,该社区一户年收入为15万元的家庭的年支出为( )A .11.4万元B .11.8万元C .12.0万元D .12.2万元【答案】B【解析】由题意知,x =8.2+8.6+10.0+11.3+11.95=10,y =6.2+7.5+8.0+8.5+9.85=8,所以a ^=8-0.76×10=0.4,所以当x =15时,y ^=0.76×15+0.4=11.8(万元).12.(2020年九江期末)针对“中学生追星问题”,某校团委对“中学生性别和追星是否有关”作了一次调查,其中女生人数是男生人数的12,男生追星的人数占男生人数的13,女生追星的人数占女生人数的23,若有95%的把握认为中学生追星与性别有关,则男生至少有______人.参考数据及公式如下:K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .【答案】30【解析】设男生人数为x ,由题意得列联表如下:计算K 2=32x ·⎝⎛⎭⎫13x ·16x -23x ·13x 2x ·12x ·23x ·56x=320x >3.841,解得x >20×3.8413. 又x =6k ,k ∈N *,所以x min =30,即有95%的把握认为中学生追星与性别有关时,男生至少有30人.13.(一题两空)(2020年吉林模拟)2019年末至2020年初,某在线教育公司为了适应线上教学的快速发展,近5个月加大了对该公司的网上教学使用软件的研发投入,过去5个月资金投入量x (单位:百万元)和收益y (单位:百万元)的数据如下表:若y 与x 的线性回归方程为y =3x +a ,则a =________,资金投入量为16百万元时,该月收益的预报值为________百万元.【答案】8.04 56.04 【解析】由题意得x =2+4+8+10+125=7.2,y -=14.21+20.31+31.18+37.83+44.675=29.64,所以a =y --b ^x =29.64-3×7.2=8.04.所以y 关于x 的回归方程为y ^=3x +8.04.把x =16代入回归方程得y ^=3×16+8.04=56.04,故预报值为56.04百万元.14.新型冠状病毒爆发以来,各地高度重视新型冠状病毒感染的肺炎的防控和卫生健康监督检查工作,务必将督导检查落实到位.某地对8个工厂的生产车间进行了“原料采购加工标准”和“卫生标准”的检查和评分,其评分情况如下表所示:(1)已知x 与y 之间具有线性相关关系,求y 关于x 的线性回归方程;(2)现从8个被检查的工厂中任意抽取两个组成一组,若两个工厂的“原料采购加工标准”和“卫生标准”的评分均超过80分,则组成“对比标兵工厂”,求该组被评为“对比标兵工厂”的概率.参考公式:b ^=∑i =1nx i y i -n x y∑i =1nx 2i -n x2,a ^=y --b ^x ;参考数据:∑i =18x i y i =53 844,∑i =18x 2i =55 656.解:(1)由题意,得x =18×(100+95+93+83+82+75+70+62)=82.5,y =18×(86.5+83.5+83.5+81.5+80.5+79.5+77.5+76.5)=81.125,所以b ^=∑i =1nx i y i -n x y∑i =1nx 2i -n x2=53 844-8×82.5×81.12555 656-8×82.52=14.所以a ^=y -b ^x =81.125-14×82.5=60.5.所以y 关于x 的线性回归方程为y ^=14x +60.5.(2)从8个中任取2个,共有C 28=28个基本事件.“原料采购加工标准”和“卫生标准”的评分均超过80分有C 25=10种情况,故所求的概率为p =1028=514.15.(2020年新课标Ⅱ)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i ,y i )(i =1,2,…,20),其中x i 和y i 分别表示第i 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得∑i =120x i =60,∑i =120y i =1 200,∑i =120(x i -x)2=80,∑i =120 (y i -y -)2=9 000,∑i =120(x i -x )(y i -y -)=800.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i ,y i )(i =1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r =∑i =1n(x i -x )(y i -y -)∑i =1n(x i -x )2∑i =1n(y i -y -)2,2≈1.414.解:(1)已知∑i =120y i =1 200,所以20个样区野生动物数量的平均数为120∑i =120y i =60,所以该地区这种野生动物数量的估计值为60×200=12 000. (2)因为∑i =120(x i -x)2=80,∑i =120(y i -y)2=9 000,∑i =120(x i -x )(y i -y )=800,所以r =∑i =1n(x i -x )(y i -y )∑i =1n(x i -x )2∑i =1n(y i -y )2=80080×9 000=8006002=223≈0.94.(3)更合理的抽样方法是分层抽样,根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.[C 级 创新突破]16.(2020年日照期末)某种疾病可分为Ⅰ、Ⅱ两种类型,为了解该疾病类型与性别的关系,在某地区随机抽取了患该疾病的病人进行调查,其中男性人数为z ,女性人数为2z ,男性患Ⅰ型病的人数占男性病人的56,女性患Ⅰ型病的人数占女性病人的13.与“性别”有关,则男性患者至少有多少人?(2)某药品研发公司欲安排甲、乙两个研发团队来研发此疾病的治疗药物,两个团队各至多安排2个接种周期进行试验.每人每次接种花费m (m >0)元.甲团队研发的药物每次接种后产生抗体的概率为p ,根据以往试验统计,甲团队平均花费为-2mp 2+6m ;乙团队研发的药物每次接种后产生抗体的概率为q ,每个周期必须完成3次接种,若一个周期内至少出现2次抗体,则该周期结束后终止试验,否则进入第二个接种周期.假设两个研发团队每次接种后产生抗体与否均相互独立.若p =2q ,从两个团队试验的平均花费考虑,该公司应选择哪个团队进行药品研发? 附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ).解:(1)根据题意填写列联表如下;则k 2=3z ⎝⎛⎭⎫5z 6·4z 3-z 6·2z 32z ·2z ·3z 2·3z 2=2z 3>7.879,解得z >11.818 5,由z 6∈N *,且z3∈N *,所以z 的最小值为12,即男性患者至少有12人. (2)设甲研发试验品花费为X ,则EX =-2mp 2+6m . 设乙研发试验品花费为Y ,则Y 的可能取值为3m,6m , 所以P (Y =3m )=C 23·q 2(1-q )+q 3=-2q 3+3q 2, P (Y =6m )=1+2q 3-3q 2.11 所以EY =3m ·(-2q 3+3q 2)+6m ·(1+2q 3-3q 2)=6mq 3-9mq 2+6m .因为p =2q ,所以EY -EX =6mq 3-9mq 2+6m +2mp 2-6m =6mq 3-9mq 2+2mp 2=6mq 3-mq 2=mq 2(6q -1).①当0<q <16时,6q -1<0,因为m >0,所以mq 2(6q -1)<0,所以EX >EY ,乙团队试验的平均花费较少,所以选择乙团队进行研发;②当16<q <1时,6q -1>0,因为m >0,所以mq 2(6q -1)>0,所以EX <EY ,甲团队试验的平均花费较少,所以选择甲团队进行研发;③当q =16时,mq 2(6q -1)=0,所以EX =EY ,甲团队试验的平均花费和乙团队试验的平均费用相同,从两个团队试验的平均花费考虑,该公司选择甲团队或乙团队进行研发均可.。
【高考数学总复习】:回归性分析与独立性检验(知识点讲解+真题演练+详细解答)
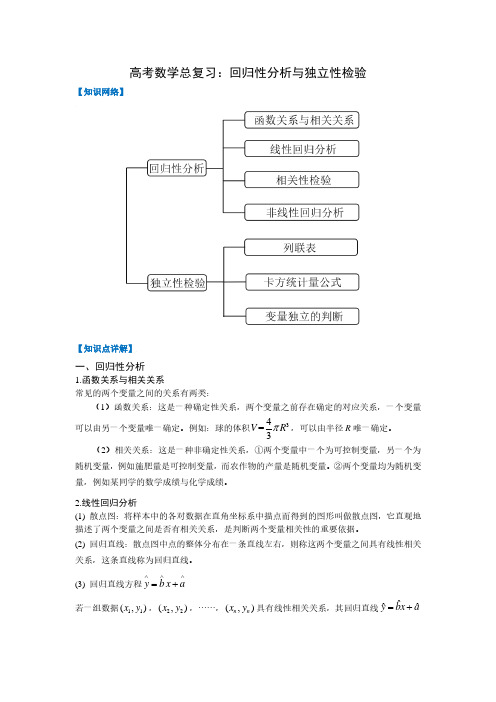
量,例如某同学的数学成绩与化学成绩。
2.线性回归分析 (1) 散点图:将样本中的各对数据在直角坐标系中描点而得到的图形叫做散点图,它直观地 描述了两个变量之间是否有相关关系,是判断两个变量相关性的重要依据。 (2) 回归直线:散点图中点的整体分布在一条直线左右,则称这两个变量之间具有线性相关
(a b)(c d)(a c)(b d )
通过对统计量 K2 的研究,一般情况下认为:
①当 K 2 ≤3.841 时,认为变量 X 与 Y 是无关的。
②当 K 2 >3.841 时,有 95%的把握说变量 X 与 Y 有关;
④ 当 K 2 >6.635 时,有 99%的把握说变量 X 与 Y 有关;
定在多大程度上可以认为“两个分类变量有关系”的方法称为两个分类变量的独立性检验。
2.分类变量的理解: 分类变量是说明事物类别的一个名称,其取值是分类数据。如“性别”就是一个分类变 量,其变量值为“男”或“女”;“行业”也是一个分类变量,其变量值可以为“零售 业”,说明 X 与 Y 无关的把握越小
6. 右表是对与喜欢足球与否的统计列联表依据表中的数据,得到( )
A. K 2 9.564 B. K 2 3.564 C. K 2 2.706 D. K 2 3.841
7. 对两个分类变量 A、B 的下列说法中正确的个数为( ). ①A 与 B 无关,即 A 与 B 互不影响;②A 与 B 关系越密切,则 K2 的值就越大;③K2
x yw
46.6 563 6.8
8
(xi x )2
i 1
高三数学 一轮复习 第10知识块第3讲 变量间的相关关系、回归分析及独立性检验课件 文 新人教A版

解析:①学生的学习态度与学习成绩之间不是因果关系, 是相关关系.②教师的执教水平与学生的学习成绩之间的 关系是关关系.③④都不具备相关关系. 答案:A
2 . (2009· 宁夏、海南 ) 对变量 x , y 有观测数据 (xi , yi)(i = 1,2 ,…, 10) ,得
散 点图(1);对变量u、v有观测数据(ui,vi)(i=1,2,…,10),得散点图 (2).由这两个散点图可以判断( )
对具有相关关系的两个变量进行统计分析时,首先要作出散点图,然后 进行相关性检验,在确认具有线性相关关系后,再求其回归直线. 【例2】 一台机器使用时间较长,但还可以使用.它按不同的转速生产 出来的某机械零件有一些会有缺点,每小时生产有缺点零件的 多少,随机器运转的速度而变化,下表为抽样试验结果:
(1)对变量y与x进行相关性检验; (2)如果y与x有线性相关关系,求回归直线方程; (3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么, 机器的运转速度应控制在什么范围内?
中,
回归系数
(
)
B.小于0 D.只能等于0 能大于0,
A.可能小于0 C.能等于0
解析: =0时,得r=0,这时不具有线性相关关系,但 也能小于0.
答案:A
4.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算 K2=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是 ________的(有关,无关). 解析:∵K2=27.63>6.635, ∴有99%的把握认为“打鼾与患心脏病有关”. 答案:有关
判断两个变量正相关还是负相关,有三种方法: 1.利用散点图;
2.利用相关系数r的符号;当r>0时,正相关;r<0时,负相关;
高三数学一轮(人教A)课件:第10章 第3节 相关关系、回归分析与独立性检验

A.直线 l 过点(-x ,-y ) B.x 和 y 的相关系数为直线 l 的斜率 C.x 和 y 的相关系数在 0 到 1 之间 D.当 n 为偶数时,分布在 l 两侧的样本点的个数一定相同
• [答案] A
[解析] 线性回归直线经过样本点的中心(-x ,-y ),故选 A.
• 3.独立性检验
• (1)若变量的不同“值”表示个体不所同类属别 的 __________,则这些变量称为分类变量.
• (2)两个分类变量X与Y频的数 ________表,称为
2×2列联表.
y1
y2
合计
x1
a
b
a+b
x2
c
d
c+d
合计 a+c b+d a+b+c+d
在 2×2 列联表中,随机变量 K2=a+bcn+add-ab+cc2b+d, 其中 n=a+b+c+d 为样本容量,用 K2 的取值范围可以判断“X 与 Y 有关系”的可信度,临界值如表.(其中频数 a、b、c、d 都不小于 5)
A.-10
B.-8
C.-6
• [答案] C
D.-4
[解析] 由题意可得-x =10,-y =40, 所以a^=-y +2-x =40+2×10=60, 所以^y=-2x+60,当^y=72 时,-2x+60=72, 解得 x=-6,故选 C.
(理)(2013·山东烟台一模)若回归直线方程的斜率的估计值
• 3.了解独立性检验(只要求2×2列联表)的基 本思想、方法及其简单应用.
• 以客观题形式考查回归分析或独立性检验, 在解答题中作为一问呈现,常与概率、统计 知识综合命题.
• 1.两个变量的线性相关
• (1)正相关
• 散点图中各点散布的位置是左从下角_____右_上_角_到
高三一轮复习导学案回归分析和独立性检验

13.2 两变量间的相关性、回归分析和独立性检验(13)考点诠释重点:了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程,了解独立性检验的基本思想、方法及其简单应用.难点:对独立性检验、回归分析的基本思想方法的理解.典例精析题型一 求回归直线方程【例1】(万元)的几组统计数据:(1)若y 对x 呈线性相关关系,求出y 关于x 的线性回归方程y =b ^x +ˆa; (2)估计使用年限为10年时,维修费用为多少?【思路分析】(1)利用回归方程系数公式求出回归方程;(2)利用回归方程进行分析预估. 【解析】(1)【方法归纳】当x 与y 呈线性相关关系时,可直接求出回归直线方程,再利用回归直线方程进行计算和预测.【举一反三】1.某工厂经过技术改造后,生产某种产品的产量(吨)与相应的生产能耗(吨标准煤)有如下几组样本数据.据相关性检验,y 与x 0.7,那么y 关于x 的回归直线方程是_ .【解析】题型二 独立性检验【例2】研究小麦种子经灭菌与否跟发生黑穗病的关系,经试验观察,得到数据如下表所示:试按照原试验目的作统计分析推断.【思路分析】根据K 2公式,计算K 2值后与临界值比较. 【解析】【方法归纳】利用图形来判断两个变量之间是否有关系,可以画出三维柱形图、二维条形图,仅从图形上只可以粗略地估计两个分类变量的关系,也可以结合所求的数值来进行比较,作图时要注意单位统一、图形准确,但图形不能给我们两个分类变量有关或无关的精确的可信程度,只有利用独立性检验的有关计算,才能作出精确的判断.【举一反三】2.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:(1)抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.【解析】体验高考(2011湖南)通过随机询问,得到如下的列联表:由K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )算得,K 2=110×(40×30-20×20)260×50×60×50≈7.8.附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别无关” 【解析】【举一反三】根据上表可得回归方程y ^=b ^x +a ^中的b ^为9.4,据此模型预报广告费用为6万元时销售额为( B )A .63.6万元B .65.5万元C .67.7万元D .72.0万元。
高考数学第一轮复习 10.4 回归分析与独立性检验课件 文
( ).
A.x 和 y 的相关系数为直线 l 的斜率 B.x 和 y 的相关系数在 0 到 1 之间 C.当 n 为偶数时,分布在 l 两侧的样本点的个数一定
相同
D.直线 l 过点(-x ,-y )
A 选项说法错误,相关系数不是直线 l 的斜率.B 选项说 法错误,x 和 y 的相关系数在-1 和 1 之间,当相关系数大
联;
3.当χ2>3.841 时,有 95%的把握判定变量 A,B 有关
联;
4.当χ2>6.635 时,有 99%的把握判定变量 A,B 有关
联.
1.对变量 x,y 有观测数据(xi,yi)(i=1,2,…,10), 得散点图 1;对变量 u,v 有观测数据(ui,vi)(i=1,2,…,
10),得散点图 2. 由这两个散点图可以判断( ).
A.变量 x 与 y 正相关,u 与 v 正相关 B.变量 x 与 y 正相关,u 与 v 负相关 C.变量 x 与 y 负相关,u 与 v 正相关 D.变量 x 与 y 负相关,u 与 v 负相关
由这两个散点图可以判断,变量 x 与 y 负相关,u 与 v 正相关,选 C.
C
2.有下列说法:
①将一组数据中的每个数据都加上或减去同一个常数 后,方差恒不变;
②设有一个回归方程 y=3-5x,变量 x 增加 1 个单位 时,y 平均增加 5 个单位;
③线性回归方程 y=bx+a 必过(-x ,-y );
④在一个 2×2 列联表中,由计算得χ2=13.079,则其
两个变量间有关系的可能性是 90%.
其中错误的个数是( ).
A.1
B.2
C.3
高三数学一轮复习概率回归分析与独立性检验课件_文(精选)共18页PPT
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事,无字句处读书。——周恩来 5、阅读使人充实,会谈使人敏捷,写作使人精确。——培根
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
高三数学一轮复习概率回归 分析与独立性检验课件_文
(精选)
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
高考数学一轮复习第九章概率与统计第11讲回归分析与独立性检验课件理
(xn,yn),通过求偏差的平方和 Q= (yi-b^xi-a^)2 的最小值而 i1
得到回归直线的方法,即求回归直线,使得样本数据的点到它 的距离的平方和最小,这一方法叫做最小二乘法,则回归直线
方程^y=b^x+a^的系数为:
n
n
(xi x)( yi y)
xi yi nx y
(ui u)2
i1
解:(1)由散点图可以判断,y=c+d x适合作为年销售 y
关于年宣传费用 x 的回归方程类型.
(2)令 w= x,先建立 y 关于 w 的线性回归方程.
8
∵d^=
i1
(wi
8
w)( yi
y)
=1018.6.8=68,
(wi w)2
i1
∴^c=-y -d^-w =563-68×6.8=100.6.
系时,用什么方法最有说服力( A.平均数与方差 C.独立性检验
) B.回归直线方程 D.概率
解析:由于参加讨论的公民按性别被分成了两组,而且每 一组又被分成了两种情况:认为有关与无关,故该资料取自完 全随机统计,符合 2×2 列联表的要求.故用独立性检验最有说 服力.
答案:C
2.已知变量 x 与 y 正相关,且由观测数据算得样本平均数 x =3,y =3.5,则由该观测数据算得的线性回归方程可能是( )
i 1
n
n
( xi x)2 ( yi y)2
i 1
i 1
n
xi yi nx y
=
i1
叫做变量 y 与 x 之间的样本相
n
(
i2
n
2
高考数学 一轮 第九章 概率与统计 第10讲 回归分析与独立性检验 理
1.下面是 2×2 列联表:
项目
y1
x1
a
x2
22
合计
b
y2
合计
21
73
25
47
46
120
则表中 a,b 的值分别为( C )
A.94,72
B.52,50
C.52,74
D.74,52
解析:∵a+21=73,∴a=52.又 a+22=b,∴b=74.
3.通过随机询问 110 名性别不同的大学生是否爱好某项运 动,得到如下的列联表:
(xi,yi)(i=1,2,…,n)都在直线
y=
1 2
x+1上,则这组样本数据
的样本相关系数为( D )
A.-1
B.0
C.12
D.1
解析:由题设知,这组样本数据完全正相关,故其相关系 数为 1.故选 D.
考点 1 线性回归分析
例 1:已知 x 与 y 之间的几组数据如下表:
x
1
2
3
4
5
6
y
0
2
1
3
3
4
假设根据上表数据所得线性回归直线方程为^y=b^x+a^.若
某同学根据上表中前两组数据(1,0)和(2,2)求得的线性回归直线
方程为 y=b′x+a′,则以下结论正确的是( )
A.b^>b′,a^>a′
B.b^>b′,a^<a′
C.b^<b′,a^>a′
D.b^<b′,a^<a′
解析:由表格知,-x =261=72,-y =163. 则b^=1×0+2×122++232×+13+2+4×42+3+525+×632+-66××472-2 6×72×163 =57, a^=-y -b^-x =163-57×72=-13.
