第3章 机械零件的强度
合集下载
第三章 机械零件的强度
• 变应力的应力比保持不变，即：r = C
• 变应力的平均应力保持不变，即：sm = C • 变应力的最小应力保持不变，即：smin = C
1.变应力的应力比保持不变，即 r C （如转轴）
s a s max s min 1 r C s m s max s min 1 r
一、疲劳破坏 机械零件在变应力作用下,即使变应力的 smax < sb ，而应
力的每次循环也仍然会对零件造成轻微的损伤。随应力循环次数的 增加，当损伤累积到一定程度时，在零件的表面或内部将出现（萌 生）裂纹。之后，裂纹又逐渐扩展直到发生完全断裂。这种缓慢形 成的破坏称为 “疲劳破坏”。
“疲劳破坏” 是循环应力作用下零件的主 要失效形式。
直线CG方程：
s ae s m e s s
三、单向稳定变应力时机械零件的疲劳强度计算
一般步骤：
1）由外载荷smax 、smin sm 、sa——工作应力；
2）将工作应力sm、sa标在零件极
限应力图上，得工作应力点：
M（ sm，sa ）
M s m e,s ae M s m,s a
在零件极限应力图上表示 为：平行 纵坐标 的一条 直线。
M s m e,s ae M s m,s a
1）如果此线与AG线交于M（ sme ，sae ），则有：
s m e s m
,
s ae
s 1
ss m
Ks
s lim s m ax s ae s m e s 1
M s m e,s ae
s a Cs m
显然，直线OM上任一点的应力
比均相同，M 就是零件的极限
应力点。
M s m,s a
• 变应力的平均应力保持不变，即：sm = C • 变应力的最小应力保持不变，即：smin = C
1.变应力的应力比保持不变，即 r C （如转轴）
s a s max s min 1 r C s m s max s min 1 r
一、疲劳破坏 机械零件在变应力作用下,即使变应力的 smax < sb ，而应
力的每次循环也仍然会对零件造成轻微的损伤。随应力循环次数的 增加，当损伤累积到一定程度时，在零件的表面或内部将出现（萌 生）裂纹。之后，裂纹又逐渐扩展直到发生完全断裂。这种缓慢形 成的破坏称为 “疲劳破坏”。
“疲劳破坏” 是循环应力作用下零件的主 要失效形式。
直线CG方程：
s ae s m e s s
三、单向稳定变应力时机械零件的疲劳强度计算
一般步骤：
1）由外载荷smax 、smin sm 、sa——工作应力；
2）将工作应力sm、sa标在零件极
限应力图上，得工作应力点：
M（ sm，sa ）
M s m e,s ae M s m,s a
在零件极限应力图上表示 为：平行 纵坐标 的一条 直线。
M s m e,s ae M s m,s a
1）如果此线与AG线交于M（ sme ，sae ），则有：
s m e s m
,
s ae
s 1
ss m
Ks
s lim s m ax s ae s m e s 1
M s m e,s ae
s a Cs m
显然，直线OM上任一点的应力
比均相同，M 就是零件的极限
应力点。
M s m,s a
第3章机械零件的强度
a 受拉
对称循环变应力
▴ 变应力参数
σ σmax o 循环变应力 σa
静应力: σ = 常数 变应力: σ 随时间变化
σ
σa
σmin σm t o
σ=常数
t
max min 最大应力： max = m+ a m 平均应力:
2
应力幅:
a
max min 最小应力：min= m－a
§3-2
机械零件的疲劳强度计算
对于切应力的情况，只需用τ代替σ，就可以得到相 应的极限应力曲线方程：
1e
1
K
'ae e ' me
及： 'ae ' me s
k 1 1 K 1 q
或： 1 K 'ae 'me
弯 曲
σb =
32M πd3
D/d 1.30 1.20 1.15 1.10 2.39 2.28 2.14 1.99 1.79 1.69 1.63 1.56 1.59 1.53 1.48 1.44 1.49 1.44 1.40 1.37 1.43 1.37 1.34 1.31 1.39 1.33 1.30 1.28 D/d 2.0 1.50 1.20 1.10 2.33 2.21 2.09 2.00 1.73 1.68 1.62 1.59 1.55 1.52 1.48 1.46 1.44 1.42 1.39 1.38 1.35 1.34 1.33 1.31 1.30 1.29 1.27 1.26
σ e ---零件受弯曲的材料常数；
§3-2
机械零件的疲劳强度计算
综合影响系数Ｋσ 反映了：应力集中、尺寸因素、 表面加工质量及强化等因素的综合影响结果。其计算公 式如下：
第3章 机械零件的强度(用)
变载荷：随时间作周期性或非周期性变化的载荷.如
汽车的齿轮和轴所承受的动载荷。
注意:在设计计算中，载荷又可分为名义载荷和计 算载荷，计算载荷等于载荷系数乘以名义载荷。
名义载荷： 根据机器在稳定和理想工作条件下的工作阻力，
按力学公式求出的载荷称为名义载荷. 计算载荷：
考虑机器在工作中载荷的变化和载荷在零件上
s
m rN
N
C (NC
N
ND)
D点以后(无限寿命区间):
s rN s r （N ND )
用N0及其相对应的疲劳极限σr来近
似代表ND和 σr∞,有：
s
m rN
N
s
m r
N0
C
s－N疲劳曲线
§3-1 材料的疲劳特性 疲劳曲线
２、 s－N疲劳曲线
有限寿命区间内循环次数N与
疲劳极限srN的关系为：
CＧ'直线的方程为：
s a s m s s
σ为试件受循环弯曲 应力时的材料常数，其值 由试验及下式决定：
s
2s 1 s 0 s0
对于碳钢，σ≈0.1~0.2，对于合金钢，σ≈0.2~0.3。
§3-2 机械零件的疲劳强度计算
1、零件的极限应力线图
如设弯曲疲劳极限的综合影响系数 Ｋσ ，且 s 1 ―材料对称循环弯曲疲劳极限
s rN s r
m
N0 N
KNsr
式中， N0为循环基数；
sr为与N0相对应的疲劳极限
s－N疲劳曲线
m为材料常数，值由材料试验确定。
疲劳曲线的意义
s rN
sr m
N0 N
KNsr
汽车的齿轮和轴所承受的动载荷。
注意:在设计计算中，载荷又可分为名义载荷和计 算载荷，计算载荷等于载荷系数乘以名义载荷。
名义载荷： 根据机器在稳定和理想工作条件下的工作阻力，
按力学公式求出的载荷称为名义载荷. 计算载荷：
考虑机器在工作中载荷的变化和载荷在零件上
s
m rN
N
C (NC
N
ND)
D点以后(无限寿命区间):
s rN s r （N ND )
用N0及其相对应的疲劳极限σr来近
似代表ND和 σr∞,有：
s
m rN
N
s
m r
N0
C
s－N疲劳曲线
§3-1 材料的疲劳特性 疲劳曲线
２、 s－N疲劳曲线
有限寿命区间内循环次数N与
疲劳极限srN的关系为：
CＧ'直线的方程为：
s a s m s s
σ为试件受循环弯曲 应力时的材料常数，其值 由试验及下式决定：
s
2s 1 s 0 s0
对于碳钢，σ≈0.1~0.2，对于合金钢，σ≈0.2~0.3。
§3-2 机械零件的疲劳强度计算
1、零件的极限应力线图
如设弯曲疲劳极限的综合影响系数 Ｋσ ，且 s 1 ―材料对称循环弯曲疲劳极限
s rN s r
m
N0 N
KNsr
式中， N0为循环基数；
sr为与N0相对应的疲劳极限
s－N疲劳曲线
m为材料常数，值由材料试验确定。
疲劳曲线的意义
s rN
sr m
N0 N
KNsr
第三章 机械零件的强度
o
每点纵坐标值（应力幅值）
σS
按同一比例缩小（除以一
个大于 1 的系数 K )
A→ A D → D
A( 0 , 1 )
A( o, 1 ) D( 0 , 0 )
K
22
45° C m
D( 0 , 0 )
2 2K
根据A、D 两点的坐标：
A( o, 1 ) D( 0 , 0 )
a
max
max
min
t min
min max a
r=－1 （对称）
3.2.2 材料疲劳的类别 ★依作用在零件上的变应力循环次数的不同，零件材料的疲劳 分为两种。
低周疲劳（应变疲劳） 循环次数低于103次 或104次 ； 高周疲劳 循环次数高于 104次 。
R N 1 F N0
t
或
R
(t)dt
e 0
★浴盆曲线 —描述机械产品典型的失效率λ（t）与时间 t 的关系的曲线。
dN
(t )
(t) dt
N
Ⅰ
Ⅱ
Ⅲ
第Ⅰ阶段：早期失效阶段；
第Ⅱ阶段：正常使用阶段；
第Ⅲ阶段：损坏阶段。
0
t
图1.1 失效率曲线
3.2 机械零件的强度计算
静载荷 不随时间变化或变化缓慢的载荷 变载荷 随时间变化的载荷
名义载荷—根据额定功率用力学公式计算出的
按照计算要求分
载荷。
计算载荷—考虑各种因素综合影响计算的载荷。
2．应力分类
静应力— 不随时间变化或变化缓慢的应力称为静应力；
变应力—随时间变化的应力称为变应力。
Ⅰ
F
《机械设计》第3章_机械零件的强度(正式)
1.最大应力 s max s m s a
2.最小应力 s min s m s a
3.平均应力
sm
s max
s min
2
4.应力幅
sa
s max
s min
2
5.应力循环特性
s min s max
第三章 机械零件的强度
(a)非对称循环变应力
(b)脉动循环变应力
(c)对称循环变应力
疲劳曲线
s max
s min
2
sa
s max
s min
2
r s min
s max
1 r 1 (r 0)
smax
sm
0
t
sm
sa
s max
2
s min 0
r0
sa= smax
0
t
smin
sm 0
s a s max s min
r 1
二、应力的描述
第三章 机械零件的强度
稳定循环变应力的基本参数 共有５个基本参数，知其２就能求其他
应力循环特性 r 一定的条件下，记录出在 不同最大应力σmax下引起试件疲劳破坏所经历 的应力循环次数N，即可得到σ-N疲劳曲线 。
静应力强度（AB段）：N≤103， σmax几乎不 随N变化，可近似看作是静应力强度。
(ND,σr∞)
低周疲劳（BC段）：N↑→ σmax↓。C点对应 的循环次数约为104。
（非周期变化）
循环变应力
（周期变化）
符合统计规律
稳定循环变应力
（等幅变应力）
非稳定循环变应力
（变幅变应力）
非对称循环变应力 对称循环变应力 脉动循环变应力
s
1、非循环变应力 符合统计规律
2.最小应力 s min s m s a
3.平均应力
sm
s max
s min
2
4.应力幅
sa
s max
s min
2
5.应力循环特性
s min s max
第三章 机械零件的强度
(a)非对称循环变应力
(b)脉动循环变应力
(c)对称循环变应力
疲劳曲线
s max
s min
2
sa
s max
s min
2
r s min
s max
1 r 1 (r 0)
smax
sm
0
t
sm
sa
s max
2
s min 0
r0
sa= smax
0
t
smin
sm 0
s a s max s min
r 1
二、应力的描述
第三章 机械零件的强度
稳定循环变应力的基本参数 共有５个基本参数，知其２就能求其他
应力循环特性 r 一定的条件下，记录出在 不同最大应力σmax下引起试件疲劳破坏所经历 的应力循环次数N，即可得到σ-N疲劳曲线 。
静应力强度（AB段）：N≤103， σmax几乎不 随N变化，可近似看作是静应力强度。
(ND,σr∞)
低周疲劳（BC段）：N↑→ σmax↓。C点对应 的循环次数约为104。
（非周期变化）
循环变应力
（周期变化）
符合统计规律
稳定循环变应力
（等幅变应力）
非稳定循环变应力
（变幅变应力）
非对称循环变应力 对称循环变应力 脉动循环变应力
s
1、非循环变应力 符合统计规律
《机械设计》讲义(第八版)濮良贵(第3章)
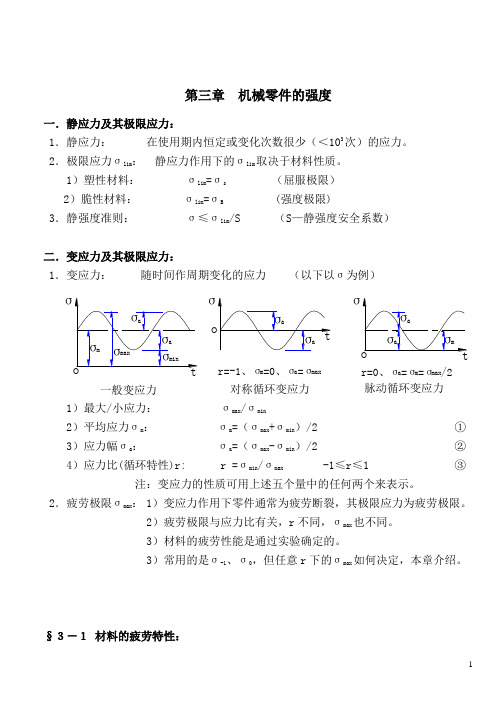
1第三章 机械零件的强度一．静应力及其极限应力：1．静应力： 在使用期内恒定或变化次数很少（＜103次）的应力。
2．极限应力σlim： 静应力作用下的σlim取决于材料性质。
1）塑性材料： σlim =σs （屈服极限）2）脆性材料： σlim=σB (强度极限)3．静强度准则： σ≤σlim/S （S —静强度安全系数）-10max§３－１ 材料的疲劳特性：1．材料的疲劳特性：可用最大应力σmax、应力循环次数N和应力比r表示。
2．材料疲劳特性的确定：用实验测定，实验方法是：1）在材料标准试件上加上一定应力比的等幅变应力，应力比通常为：r=-1或r=02）记录不同最大应力σmax下试件破坏前经历的循环次数N，并绘出疲劳曲线。
3．材料的疲劳特性曲线：有二种1）σ—N疲劳曲线：即一定应力比r下最大应力σmax与应力循环次数N的关系曲线2）等寿命曲线：即一定应力循环次数N下应力幅σa 与平均应力σm的关系曲线2）C点对应的N约为：NC≈1043）这一阶段的疲劳称为应变疲劳或低周疲劳4、CD段：有限寿命疲劳阶段。
试件经历一定的循环次数N后会疲劳破坏实验表明，有限疲劳寿命σrN与相应的循环次数N之间有如下关系：23σm rN ·N = C ( N ≤N D ) （3-1）5、D 点以后： 无限寿命疲劳阶段。
1）无论经历多少次应力循环都不会疲劳破坏。
2）D 点对应的循环次数N 约为：N D =106～25×107 3）D 点对应的应力记为：σr ∞—— 叫持久疲劳极限。
σrN =σr∞( N ＞N D ) （3-2）4）循环基数N O 和疲劳极限σrN D 很大，疲劳试验很费时，为方便起见，常用人为规定一个循环次数N O （称 为循环基数）和与之对应的疲劳极限σrNo（简记为σr ）近似代替N D 和σr ∞6、有限寿命疲劳极限σrN ： 按式（3-1）应有： σm rN·N = σm r ·N O = C （3-1a ）于是：K N ──寿命系数m, N O ──1）钢材（材料）： m = 6～20 ， N O =（1～10）×106 2）中等尺寸零件： m = 9 ， N O = 5×106 3）大尺寸零件： m = 9 ， N O = 107 注： 高周疲劳——曲线CD 及D 点以后的疲劳称作高周疲劳二、等寿命疲劳曲线 图3-2等寿命疲劳曲线——一定循环次数下的疲劳极限的特性。
机械设计第3章机械零件的强度
绝大多数通用零件来说，当其承受变应力作用时，其 应力循环次数总是大于104的。
6
(一) σ—N疲劳曲线
图3—1中曲线CD段代表有限寿命疲劳阶段。在此
范围内，试件经过一定次数的交变应力作用后总会发
生疲劳破坏。曲线CD段上任何一点所代表的疲劳极限，
称为有限寿命疲劳极限，用符号σrN表示。脚标r代表该 变应力的应力比，N代表相应的应力循环次数。曲线 CD段可用式(3—1)来描述：
§3—2 机械零件的疲劳强度计算
由于零件尺寸及几何形状变化、加工质量及强
化因素等的影响，使得零件的疲劳极限要小于
材料试件的疲劳极限。如以弯曲疲劳极限的综
合影响系数Kσ表示材料对称循环弯曲疲劳极限 σ-1与零件对称循环弯曲疲劳极限σ-1e 的比值， 即
Kσ=σ-1 /σ-1 e 当已知Kσ及σ-1时，则
5
在循环次数约为103以前，相应于图3—1中的曲线AB 段，使材料试件发生破坏的最大应力值基本不变，或 者说下降得很小，因此我们可以把在应力循环次数 N≤103时的变应力强度看作是静应力强度的状况。
曲线的BC段，随着循环次数的增加，使材料发生疲 劳破坏的最大应力将不断下降。仔细检查试件在这一 阶段的破坏断口状况，总能见到材料已发生塑性变形 的特征。C点相应的循环次数大约在104左右(也有文 献中认为约在105，现在工程实践中多以104为准)。 这一阶段的疲劳破坏，因为这时已伴随着材料的塑性 变形，所以用应变—循环次数来说明材料的行为更为 符合实际。因此，人们把这一阶段的疲劳现象称为应 变疲劳,亦称低周疲劳。
零件材料(试件)的极限应力曲线即为 折线A＇G＇C。材料中发生的应力如 处于OA＇G＇C区域以内，则表示不 发生破坏；如在此区域以外，则表 示一定要发生破坏；如正好处于折 线上，则表示工作应力状况正好达 到极限状态。
6
(一) σ—N疲劳曲线
图3—1中曲线CD段代表有限寿命疲劳阶段。在此
范围内，试件经过一定次数的交变应力作用后总会发
生疲劳破坏。曲线CD段上任何一点所代表的疲劳极限，
称为有限寿命疲劳极限，用符号σrN表示。脚标r代表该 变应力的应力比，N代表相应的应力循环次数。曲线 CD段可用式(3—1)来描述：
§3—2 机械零件的疲劳强度计算
由于零件尺寸及几何形状变化、加工质量及强
化因素等的影响，使得零件的疲劳极限要小于
材料试件的疲劳极限。如以弯曲疲劳极限的综
合影响系数Kσ表示材料对称循环弯曲疲劳极限 σ-1与零件对称循环弯曲疲劳极限σ-1e 的比值， 即
Kσ=σ-1 /σ-1 e 当已知Kσ及σ-1时，则
5
在循环次数约为103以前，相应于图3—1中的曲线AB 段，使材料试件发生破坏的最大应力值基本不变，或 者说下降得很小，因此我们可以把在应力循环次数 N≤103时的变应力强度看作是静应力强度的状况。
曲线的BC段，随着循环次数的增加，使材料发生疲 劳破坏的最大应力将不断下降。仔细检查试件在这一 阶段的破坏断口状况，总能见到材料已发生塑性变形 的特征。C点相应的循环次数大约在104左右(也有文 献中认为约在105，现在工程实践中多以104为准)。 这一阶段的疲劳破坏，因为这时已伴随着材料的塑性 变形，所以用应变—循环次数来说明材料的行为更为 符合实际。因此，人们把这一阶段的疲劳现象称为应 变疲劳,亦称低周疲劳。
零件材料(试件)的极限应力曲线即为 折线A＇G＇C。材料中发生的应力如 处于OA＇G＇C区域以内，则表示不 发生破坏；如在此区域以外，则表 示一定要发生破坏；如正好处于折 线上，则表示工作应力状况正好达 到极限状态。
第三章 机械零件的强度
应力幅： σ a =
σ max − σ min
2
平均应力： σ m =
σ max + σ min
2
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
强度计算
静应力强度 变应力强度
2、静应力时的机械零件的强度 σ lim σ ≤ [σ ] = S
—— AG 的方程 ′ ′ 2. CG方程：
' ' σ ae + σ me = σ s
σ +σ =σs
' a ' m
—— CG′的方程
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
1. 单向稳定变应力时机械零件的疲劳强度计算 机械零件应力的变化规律： ①变应力的循环特性不变 ②变应力的平均应力不变 ③变应力的最小应力不变
′ ′ AG 的方程：
' ' σ−1 =σa +ϕσσm
其中：
ϕσ =
2 −1 −σ0 σ
σ0
CG′ 的方程：
材料的极限应力线图
' ' σa +σm =σs
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
§3-2 机械零件的疲劳强度计算
机械设计
Design of Machinery
第三章 机械零件的强度
1.载荷和应力的分类 静载荷、变载荷 静应力、变应力
静载荷：大小和方向不随时间变化或变化缓慢的载荷。 变载荷：随时间周期性变化或非周期性变化的载荷。 静应力：不随时间变化或变化缓慢的应力。 （只在静载荷作用下产生） 变应力：随时间变化的应力。 （可由变载荷产生，也可由静载荷产生） σ
σ max − σ min
2
平均应力： σ m =
σ max + σ min
2
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
强度计算
静应力强度 变应力强度
2、静应力时的机械零件的强度 σ lim σ ≤ [σ ] = S
—— AG 的方程 ′ ′ 2. CG方程：
' ' σ ae + σ me = σ s
σ +σ =σs
' a ' m
—— CG′的方程
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
1. 单向稳定变应力时机械零件的疲劳强度计算 机械零件应力的变化规律： ①变应力的循环特性不变 ②变应力的平均应力不变 ③变应力的最小应力不变
′ ′ AG 的方程：
' ' σ−1 =σa +ϕσσm
其中：
ϕσ =
2 −1 −σ0 σ
σ0
CG′ 的方程：
材料的极限应力线图
' ' σa +σm =σs
Well begun is half done. 好的开始等于成功的一半。
机械设计
Design of Machinery
§3-2 机械零件的疲劳强度计算
机械设计
Design of Machinery
第三章 机械零件的强度
1.载荷和应力的分类 静载荷、变载荷 静应力、变应力
静载荷：大小和方向不随时间变化或变化缓慢的载荷。 变载荷：随时间周期性变化或非周期性变化的载荷。 静应力：不随时间变化或变化缓慢的应力。 （只在静载荷作用下产生） 变应力：随时间变化的应力。 （可由变载荷产生，也可由静载荷产生） σ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F
机械与汽车工程学院 school of mechanical and automotive engineering
机械零件的表面挤压强度
当相互接触的零件没有相对运动 时，接触表面在载荷作用下将产生的 挤压应力。 压应力称为挤压应力 挤压应力 挤压强度的计算公式
σP =
F ≤ [σ P ] A
机械设计 Machine design
详细介绍
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
机械零件疲劳强度的计算
二、零件极限应力线图的应用
计算步骤： 计算步骤： 计算出σ （1）求危险截面上的σmax 和 σmin ,计算出σa 和σ m ）求危险截面上的σ 计算出 （2）画零件的极限应力线图 ） （3）判断零件的失效形式 ） （4）用计算法或作图法求 ）
根据弹性力学 Hertz 公式得 : F 1 1 ± L ρ1 ρ 2 = ≤ [σ H ] 2 1 − µ12 1 − µ 2 π + 泊松比 E2 E1
弹性模量 曲率半径
σH
σ
H
L b
式中：正号用于外接触，负号用于内接触。
机械设计 Machine design
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
机械零件的疲劳强度计算
零件弯曲疲劳强度的综合影响系数的计算： 零件弯曲疲劳强度的综合影响系数的计算： 弯曲疲劳强度的综合影响系数的计算
Kσ = kσ
=
σ
lim
s
σlim = ？
疲劳破坏与零件的变应力循环次数有关 N — 应力循环次数 σ
疲劳曲线
σrN — 疲劳极限（对应于 ） 疲劳极限（对应于N） 与材料和应力状 σr N 态有关的指数 ND — 循环基数 σr σr — 持久极限
σ
m rN
N N ND 无限 有限寿命区
N = 常数 = σ
rN
思考题 已知 材料：45 调质处理 求：（1）
σ −1 σ 0 σ S
(r = 0.2; N = 5 ×105 )
（2） σ rN
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
机械零件的疲劳强度计算
机械与汽车工程学院 school of mechanical and automotive engineering
初始裂纹
疲劳破坏的原因：材料内部的缺陷、加工过 疲劳破坏的原因：材料内部的缺陷、 程中的刀痕或零件局部的应力集中等导致 产生了微观裂纹，称为裂纹源，在交变应 产生了微观裂纹，称为裂纹源， 力作用下，随着循环次数的增加，裂纹不 力作用下，随着循环次数的增加， 断扩展，直至零件发生突然断裂。 断扩展，直至零件发生突然断裂。
机械设计 Machine design 机械与汽车工程学院 school of mechanical and automotive engineering
不同 r 下的疲劳曲线
不同r下的疲劳极限σr 不同 下的疲劳极限σ 下的疲劳极限
σrN r=0.5 r=0 r=-1 N
机械设计 Machine design
一、零件的极限应力线图
由于零件几何形状的变化、尺寸大小、加工质量及强化因素等的影响， 使得零件的疲劳极限要小于材料试件的疲劳极限。 以弯曲疲劳极限的综合影响系数Ｋσ表示材料对称循环弯曲疲劳极限σ-1 σ−1 与零件对称循环弯曲疲劳极限σ-1e的比值，即： Kσ =
σ−1e
在不对称循环时，Ｋσ是试件与零件极限应力幅的比值。
a
σ
b
0
t
t
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
单向稳定变应力时零件的疲劳强度计算
M点：疲劳破坏计算安全 系数
' σ max σ −1 S ca = = ≥S σ max K σ σ a + ψ σ σ m
ND
N
AB段 : σ max 基本不变，应力循环次 数N ≤ 10 3， 基本不变， 静应力 BC段 : N ≤ 10 4 带有塑性变形的疲劳， 带有塑性变形的疲劳， 低周疲劳（ 低周疲劳（或应变疲劳 ） C点以后 : N > 10 4 高周疲劳 CD : N在N C～N D 之间，称为有限寿命区 ，曲线形状近似指数曲 线 之间， D : N D点开始疲劳曲线明显趋 于水平， N D = 10 6 ~ 25 × 10 7 或更大 ，σr∞ 持久疲劳极限 于水平，
0 t
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
单向不稳定变应力时的疲劳强度计算
规律性不稳定变应力
若应力每循环一次都对材料的破坏起相同的作用，则应力 σ1 每循环一次对材料 的损伤率即为1/N1，而循环了n1次的σ1对材料的损伤率即为n1/N1。如此类推，循环 了n2次的σ2对材料的损伤率即为n2/N2，……。 当损伤率达到100%时，材料即发生疲劳破坏，故对应于极限状况有：
m r m
N
D
D
σ 由此得： 由此得：
机械设计 Machine design
=σ
r
N
/N
机械与汽车工程学院 school of mechanical and automotive engineering
疲劳曲线（ 曲线） 疲劳曲线（ σ－ N 曲线）
σmax A B C
D
N=
1 4 N ≈ 10 3 N ≈ 104 C B
机械零件的疲劳强度计算
二、零件的极限应力线图
将零件材料的极限应力线图 中的直线A'D'G' 按比例向下移， 成为右图所示的直线ADG，而极 限应力曲线的 CG 部分，由于是 按照静应力的要求来考虑的，故 不须进行修正。这样就得到了零 件的极限应力线图。
强调： 强调：
1. K σ 只影响σ a 不影响σ m 2. CG段按照静应力要求考 段按照静应力要求考 不需修正。 虑，不需修正。 3. AGC为零件 持久 疲劳 为零件 强度曲线。 强度曲线。
机械与汽车工程学院 school of mechanical and automotive engineering
材料的疲劳特性
等寿命疲劳曲线（极限应力线图） 等寿命疲劳曲线（极限应力线图）
不可能通过试验获得所有不同r时的疲劳曲线。 极限应力线图） 不可能通过试验获得所有不同 时的疲劳曲线。等寿命曲线 （极限应力线图） 时的疲劳曲线 是利用试验获得的σ 获得任意r值时的疲劳极限应力近似值的方法 值时的疲劳极限应力近似值的方法。 是利用试验获得的 －1、σ0 及σS ，获得任意 值时的疲劳极限应力近似值的方法。 A'Ｇ'直线的方程为：
第3章 机械零件的强度
3.1 3.2 3.3 3.4
材料的疲劳特性 机械零件的整体强度 机械零件的表面强度 提高机械零件强度的措施
材料的疲劳特性
强度准则是设计机械零件的最基本准则，即 σ ≤ σ lim 。 强度准则是设计机械零件的最基本准则， 是设计机械零件的最基本准则 S 强度问题： 强度问题： 静应力强度： 静应力强度：通常认为在机械零件整个工作寿命期间应力变化次数小 的通用零件，均按静应力强度进行设计。（材料力学范畴） 。（材料力学范畴 于103的通用零件，均按静应力强度进行设计。（材料力学范畴） 变应力强度：在变应力作用下，零件产生疲劳破坏 疲劳破坏。 变应力强度：在变应力作用下，零件产生疲劳破坏。 疲劳破坏定义：金属材料试件在交变应力作用下， 疲劳破坏定义：金属材料试件在交变应力作用下，经过长时间的试验而发生 的破坏。 的破坏。 疲劳破坏的特征： 疲劳破坏的特征： 零件的最大应力在远小于静应力的强度极限时，就可能发生破坏； 1）零件的最大应力在远小于静应力的强度极限时，就可能发生破坏； 即使是塑性材料，在没有明显的塑性变形下就可能发生突然的脆性断裂。 2）即使是塑性材料，在没有明显的塑性变形下就可能发生突然的脆性断裂。
单向不稳定变应力时的疲劳强度计算
不稳定变应力
σ
规律性：机床、 规律性：机床、机械手 非规律性： 非规律性：汽车弹簧
规律性不稳定变应力→疲劳损伤积累假说 （M.A.Miner）转换为稳定变应力
0 T t
σ
非规律性不稳定变应力→统计强度理论→ 转换为规律性不稳定变应力→疲劳损伤积 累假说→转换为稳定变应力
εσ β
式中： 式中：kσ — —有效应力集中系数
kσ = 1 + qσ (α σ − 1)
α σ — —理论应力集中系数
qσ — —敏感系数 敏感系数
ε σ — —尺寸系数
表面状态因数 β ---表面状态因数
注：求Kτ时，将式中σ换成τ
机械设计 Machine design
机械与汽车工程学院 school of mechanical and automotive engineering
机械设计 Machine design
轴 疲劳区 (光滑 光滑) 光滑 粗糙区
机械与汽车工程学院 school of mechanical and automotive engineering
疲劳曲线（ 曲线） 疲劳曲线（ σ－ N 曲线）
变应力作用下零件主要失效形式： 变应力作用下零件主要失效形式：疲劳破坏 强度条件：σ≤ [σ] 强度条件：