扭转习题解答
材料力学第3 章 扭 转习题及答案

第 三 章 扭 转一、判断题1.杆件受扭时,横截面上的最大切应力发生在距截面形心最远处。
( × ) 2.薄壁圆管和空心圆管的扭转切应力公式完全一样。
( × ) 3.圆杆扭转变形实质上是剪切变形。
( √ ) 4.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立。
( √ )5.材料相同的圆杆,它们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等。
( × ) 6.切应力互等定理,仅适用于纯剪切情况。
( × ) 7.受扭杆件的扭矩,仅与杆件受到的转矩(外力偶矩)有关,而与杆件的材料及其横截面的大小、形状无关。
( √ ) 8.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。
( √ ) 9.受扭圆轴的最大切应力只出现在横截面上。
( × ) 10. 因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭矩达到某一极限值时,圆杆将沿轴线方向出现裂纹。
( √ )二、填空题1.一级减速箱中的齿轮直径大小不等,在满足相同的强度条件下,高速齿轮轴的直径要比低速齿轮轴的直径( 小 )。
2. 当实心圆轴的直径增加1培时,其抗扭强度增加到原来的( 8 )倍,抗扭刚度增加到原来的( 16 )倍。
3. 直径D=50mm 的圆轴,受扭矩T=2.15kn.m ,该圆轴横截面上距离圆心10mm 处的剪应力τ=(35.0 MPa ),最大剪应力τmax=(87.6 MPa )。
4. 一根空心轴的内外径分别为d ,D ,当D=2d 时,其抗扭截面模量为(33256153215D d ππ或)。
5. 直径和长度均相等的两根轴,在相同的扭矩作用下,而材料不同,它们的τmax 是( 相 )同的,扭转角φ是( 不 )同的。
6. 等截面圆轴扭转时的单位长度相对扭转角为θ,若圆轴直径增大一倍,则单位长度扭转角将变为(16θ)。
(仅供参考)第3章扭转作业参考解答
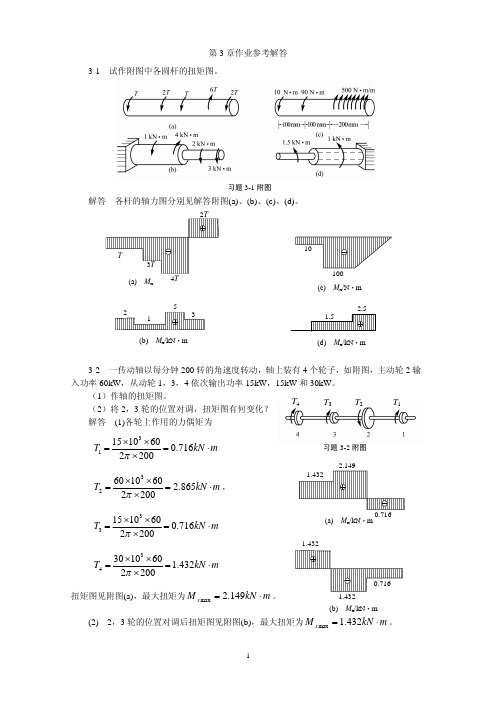
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
4.6 扭转-习题课

第4章扭转4-1 判断题判断下面说法是否正确:切应力互等定理只有材料处于线弹性范围才成立答:错。
推导切应力互等定理时只用到了平衡条件,没有牵涉到材料是否线弹性,因此,只要处于平衡状态,切应力互等定理都是成立的。
4-2 判断题判断下面说法是否正确:低碳钢圆轴扭转破坏是沿横截面剪断。
答:对。
低碳钢是塑性材料,其抗剪能力低于抗拉、抗压能力,因此它的扭转破坏面为最大切应力所在面,即横截面。
4-3 选择题圆轴单位长度扭转角与 无关。
A.扭矩大小B.杆长C. 材料D. 截面几何性质答:B 。
由 可知,表达式中无杆长项。
PGI T =θ4-4 选择题m axτm ax τm ax τ图示由两种不同材料等截面杆连接而成的圆轴,两端受到扭转外力偶作用后,左、右两段 。
A. 相同, 不同B. 不同, 相同C. 与 都不同D. 与都相同 M eM e钢铝l ltm ax WT=τm ax τPGI T=θθ答: A左右两段内力相同, ,与材料无关,所以两段 相同。
而 ,式中G 代表材料不同。
材料不同时G 不同,因此两段 m ax τm ax τθθθθ4-5 选择题图示圆轴表面贴有三片应变片,实测时应变片 的度数几乎为零。
A. 1和2B. 2和3C. 1和3D. 1、2和3M eM e1 2345答: C圆轴在线弹性范围内扭转变形时,轴向尺寸和横截面尺寸没有变化,因此1、3两片应变片不应有度数。
4-6 选择题为提高碳钢圆轴的扭转刚度,下列措施中最有效的是 。
A. 减小轴的长度B. 改用高强度结构钢C. 提高轴表面的粗糙度D. 增加轴的直径P GI PI 答: D圆轴扭转刚度为 ,各种钢材的切变模量G 相差不多,更换钢种无明显效果, 而增加轴的直径可显著提高4-7 计算题Dd ABCM e123M em m 100=D m m 50=d []MPa 60=τ 图示圆轴AB 段为实心,BC 段为空心,它们的外直径都为 ,BC 段的内直径 材料的许用切应力 ,试求此轴能承受的M e 最大值。
扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
扭转习题1
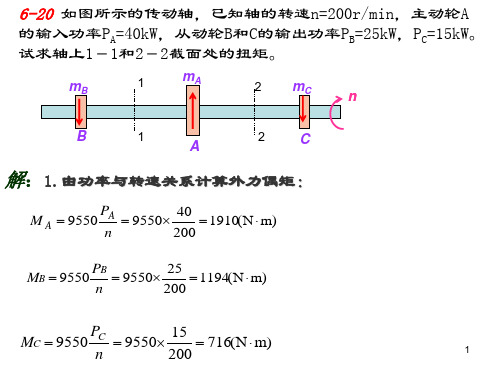
mB
mA
mC
n
(b)
B
A
C
3
解:1.由功率与转速关系计算外力偶矩:
MA
9550 PA n
9550 36 200
1719(N m)
MB 9550 PB 9550 22 1050(N m)
n
200
MC 9550 PC 9550 14 669(N m)
(2)1-1截面的最大剪应力
(3)轴AB的最大剪应力
1 mC=0.2kNm
mB=0.1kNm
φ50 φ40
A
1D
mA=0.3kNm
解:画扭矩图
T
0.3kNm
+
C
B
0.1kNm
+
x
8
(1)在AD段上,D1=50mm,T1=300N.m
Ip1=0.1D14=0.1 ×504 =6.25×105
当ρ=20mm 时 ,
=
T1 I1
300 6.25105
20=0.9610-2(Mpa)
(2)在AD段上,R1=25mm
m ax1
T1 Ip1
R1
300 6.25105
25 1.2102 (Mpa)
(3)在DC段上, T1=300N.m, D2=40mm ,R2=20mm
Ip2=0.1D24=0.1 ×404 =2.56×105
14
6--28实心圆轴如图所示,已知输出扭矩MB=MC=1.64kN.m; MD=2.18kN.m,材料G=80Mpa,【τ】=40Mpa,【θ】=1。/m。 (1)求输入扭矩MA;
(2)试设计轴的直径;
材料力学 扭转2 习题及参考答案

扭转 第二次 作业1. 已知图示实心圆轴的直径d = 100mm 。
材料的剪切弹性模量G = 80GPa 。
(1)求1-1横截面上A 、B 、C 三点的切应力;(2)求1-1横截面上A 点的切应变;(3)整个圆轴上最大的切应力。
2kN·m6kN·m10kN·m2kN·m1-1截面2kN·m4kN·m10kN·m解:由圆轴的扭矩图可知,1-1截面的扭矩T 1 = 4kN·m ,最大扭矩T max = 10kN·m圆截面的极惯性矩 4464π 3.140.19.8110m 3232P d I -⨯===⨯扭矩截面系数 3343π 3.140.1 1.9610m 1616P d W -⨯===⨯(1) 3714410 2.0410Pa 20.4MPa 1.9610A B P T W ττ-⨯====⨯=⨯ 1110.2MPa 2C A P T I ρττ=== (2)由剪切胡克定律 Gτγ=得63920.4100.255108010AA G τγ-⨯===⨯⨯ (3)对于等截面圆轴,最大切应力出现在扭矩最大截面的最外缘37max max41010 5.1010Pa 51.0MPa 1.9610P T W τ-⨯===⨯=⨯ 2. 阶梯状圆轴如图所示,AE 段为空心,外直径D = 140mm ,内直径d = 100mm ;BC 段为实心,直径d = 100mm 。
外力偶矩M A = 18kN·m ,M B = 32kN·m ,M C = 14kN·m 。
已知许用切应力[τ ] = 80MPa 。
试校核该轴的强度。
18kN·m14kN·m解:由扭矩图可知T AB = 18kN·m , |T BC | =14kN·mAE 段()4334431π 3.140.1410011 3.9810m 1616140P D W α-⎛⎫⨯⎛⎫=-=-=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭[]36max41181045.210Pa 45.2MPa<3.9810AB P T W ττ-⨯===⨯=⨯ BC 段33432π 3.140.1 1.9610m 1616P d W -⨯===⨯ []36max 42141071.410Pa 71.4MPa<1.9610BC P T W ττ-⨯===⨯=⨯ 故,该轴安全。
扭转习题解答
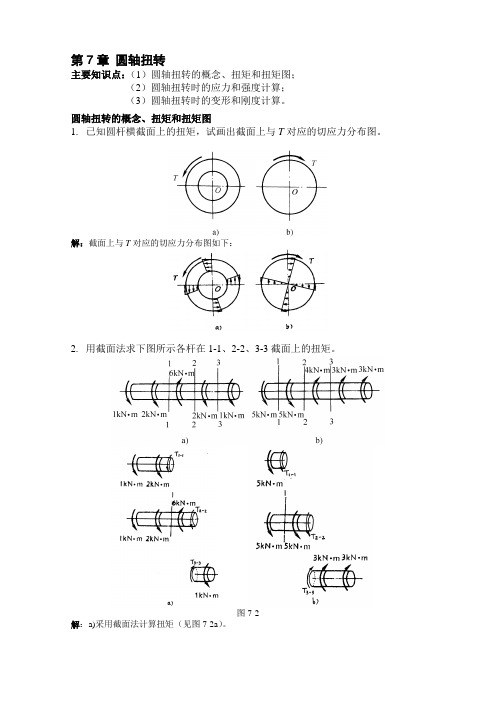
第7章圆轴扭转主要知识点:(1)圆轴扭转的概念、扭矩和扭矩图;(2)圆轴扭转时的应力和强度计算;(3)圆轴扭转时的变形和刚度计算。
圆轴扭转的概念、扭矩和扭矩图1.已知圆杆横截面上的扭矩,试画出截面上与T对应的切应力分布图。
解:截面上与T对应的切应力分布图如下:2.用截面法求下图所示各杆在1-1、2-2、3-3截面上的扭矩。
图7-2解:a)采用截面法计算扭矩(见图7-2a)。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-311。
取2-2截面左侧外力偶矩计算,由平衡方程062122=+⋅-+-T m kN )(,可得m kN T ⋅=-322。
取3-3截面右侧外力偶矩计算,可得m kN T ⋅=-133。
b) 采用截面法计算扭矩(见图7-2b )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-511。
取2-2截面左侧外力偶矩计算,由平衡方程05522=+⋅+-T m kN )(,可得m kN T ⋅-=-1022。
取3-3截面右侧外力偶矩计算,由平衡方程03333=+⋅+-T m kN )(,可得m kN T ⋅-=-633。
3. 作下图各杆的扭矩图。
解:a)采用截面法计算扭矩(见图7-3a )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅=-411。
取2-2截面右侧外力偶矩计算,可得m kN T ⋅-=-222。
作出扭矩图。
a)b) 图7-3 b) 由力矩平衡方程可得e A M M 2-=(负号表示与图中假设方向相反)。
采用截面法计算扭矩(见图7-3b )。
取1-1截面左侧外力偶矩计算,可得e M T 211-=-。
取2-2截面右侧外力偶矩计算,可得e M T -=-22。
作出扭矩图。
圆轴扭转时的应力和强度计算4. 实心圆轴和空心轴通过牙嵌离合器而连接,如图所示。
已知轴的转速n =100r/min ,传递的功率P=7.5kW ,材料的许用应力][τ=40MP a ,试通过计算确定(1) 采用实心轴时,直径d 1和的大小;(2) 采用内外径比值为1/2的空心轴时,外径D 2的大小。
6第六章圆轴的扭转习题+答案

6第六章圆轴的扭转习题+答案⼀、填空题1、圆轴扭转时的受⼒特点是:⼀对外⼒偶的作⽤⾯均_______于轴的轴线,其转向______。
2、圆轴扭转变形的特点是:轴的横截⾯积绕其轴线发⽣________。
3、在受扭转圆轴的横截⾯上,其扭矩的⼤⼩等于该截⾯⼀侧(左侧或右侧)轴段上所有外⼒偶矩的_______。
4、在扭转杆上作⽤集中外⼒偶的地⽅,所对应的扭矩图要发⽣________,_________值的⼤⼩和杆件上集中外⼒偶之矩相同。
5、圆轴扭转时,横截⾯上任意点的剪应变与该点到圆⼼的距离成___________。
6、试观察圆轴的扭转变形,位于同⼀截⾯上不同点的变形⼤⼩与到圆轴轴线的距离有关,显然截⾯边缘上各点的变形为最_______,⽽圆⼼的变形为__________。
7、圆轴扭转时,在横截⾯上距圆⼼等距离的各点其剪应变必然_________。
8、从观察受扭转圆轴横截⾯的⼤⼩、形状及相互之间的轴向间距不改变这⼀现象,可以看出轴的横截⾯上⽆____________⼒。
9、圆轴扭转时,横截⾯上剪应⼒的⼤⼩沿半径呈______规律分布。
11、受扭圆轴横截⾯内同⼀圆周上各点的剪应⼒⼤⼩是_______的。
12、产⽣扭转变形的⼀实⼼轴和空⼼轴的材料相同,当⼆者的扭转强度⼀样时,它们的_________截⾯系数应相等。
13、横截⾯⾯积相等的实⼼轴和空⼼轴相⽐,虽材料相同,但_________轴的抗扭承载能⼒要强些。
16、直径和长度均相等的两根轴,其横截⾯扭矩也相等,⽽材料不同,因此它们的最⼤剪应⼒是________同的,扭转⾓是_______同的。
17、产⽣扭转变形的实⼼圆轴,若使直径增⼤⼀倍,⽽其他条件不改变,则扭转⾓将变为原来的_________。
18、两材料、重量及长度均相同的实⼼轴和空⼼轴,从利于提⾼抗扭刚度的⾓度考虑,以采⽤_________轴更为合理些。
⼆、判断题1、只要在杆件的两端作⽤两个⼤⼩相等、⽅向相反的外⼒偶,杆件就会发⽣扭转变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
扭转习题解答
Company number:【0089WT-8898YT-W8CCB-BUUT-202108】
第7章 圆轴扭转
主要知识点:(1)圆轴扭转的概念、扭矩和扭矩图;
(2)圆轴扭转时的应力和强度计算;
(3)圆轴扭转时的变形和刚度计算。
圆轴扭转的概念、扭矩和扭矩图
1. 已知圆杆横截面上的扭矩,试画出截面上与T 对应的切应力分布图。
解:截面上与T 对应的切应力分布图如下:
2. 用截面法求下图所示各杆在1-1、2-2、3-3截面上的扭矩。
图7-2
解:a)采用截面法计算扭矩(见图7-2a )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-311。
取2-2截面左侧外力偶矩计算,由平衡方程
062122=+⋅-+-T m kN )(,可得m kN T ⋅=-322。
取3-3截面右侧外力偶矩计算,可得m kN T ⋅=-133。
b) 采用截面法计算扭矩(见图7-2b )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅-=-511。
取2-2截面左侧外力偶矩计算,由平衡方程
05522=+⋅+-T m kN )(,可得m kN T ⋅-=-1022。
取3-3截面右侧外力偶矩计算,由平衡方程
03333=+⋅+-T m kN )(,可得m kN T ⋅-=-633。
3. 作下图各杆的扭矩图。
解:a)采用截面法计算扭矩(见图7-3a )。
取1-1截面左侧外力偶矩计算,可得m kN T ⋅=-411。
取2-2截面右侧外力偶矩计算,可得m kN T ⋅-=-222。
作出扭矩图。
a) b)
图7-3
b) 由力矩平衡方程可得e A M M 2-=(负号表示与图中假设方向相反)。
采用截面法计算扭矩(见图7-3b )。
取1-1截面左侧外力偶矩计算,可得e M T 211-=-。
取2-2截面右侧外力偶矩计算,可得e M T -=-22。
作出扭矩图。
圆轴扭转时的应力和强度计算
4. 实心圆轴和空心轴通过牙嵌离合器而连接,如图所示。
已知轴的转速n =100r/min ,传递的功率P=,材料的许用应力][τ=40MP a ,试通过计算确定
(1) 采用实心轴时,直径d 1和的大小;
(2) 采用内外径比值为1/2的空心轴时,外径D 2的大小。
解:计算外力偶矩,作用在轴上的外力偶矩:
(1)采用实心轴时,直径d 1的大小应满足下式:
解得 mm m T d 0.4510
40716][36163161=⨯⨯=⨯≥ππτ (2)采用内外径比值α=1/2的空心轴时,外径D 2的大小应满足下式:
图7-7
解得 mm m T D 0.46)
5.01(1040716)1]([346163
4162=-⨯⨯⨯=-⨯≥ππατ 5. 如图所示为皮带传动轴,轴的直径d =50mm ,轴的转速为n =180r/min ,轴上装有四个皮带轮。
已知A 轮的输入功率为P A =20kW ,轮B 、C 、D 的输出功率分别为P B =3kW ,P C =10kW ,P D =7kW ,轴材料的许用切应力][τ=40MP a 。
(1)画出轴的扭矩图。
(2)校核轴的强度。
图7-5
解:(1)画扭矩图 计算外力偶矩,作用在各轮上的外力偶矩:
用截面法求得1-1截面上的扭矩为m N M T B ⋅-=-=1591;2-2截面的扭矩为
m N M M T B A ⋅=-=9022;3-3截面的扭矩为m N M T D ⋅==3713。
绘出的扭矩图如图7-5所示。
(2)强度校核
由图可见AC 段扭矩最大,由于是等截面圆轴,故危险截面在AC 段内。
由于a a a P W T MP =<MP =P ⨯⨯==-40][7.36105016
902332max τπτ)(,所以轴满足强度条件。
圆轴扭转时的变形和刚度计算
6. 图示圆轴长l =500mm ,直径d =60mm ,受到外力偶矩M 1=4kN ·m 和M 2=7kN ·m 作用,材料的剪切弹性模量G=80GP a
(1)画出轴的扭矩图;
(2)求轴的最大切应力;
(3)求轴的最大单位长度扭转角。
解:(1)绘扭矩图
用截面法求得1-1截面上的扭矩为m kN M M T ⋅=-=3121,
2-2截面的扭矩为m kN M T ⋅-=-=412。
绘出扭矩图如右图。
(2)由扭矩图可见BC 段扭矩最大,由于是等截面圆轴,故危险截面在BC 段内。
得其最大切应力为
(3)BC 段扭矩最大,BC 段内最大单位长度扭转角即轴的最大单位长度扭转角。
7.如图示,在一直径为75mm 的等截面轴上,作用着外力偶矩:M 1=1000N ·m ,M 2=600N ·m ,M 3=M 4=200N ·m ,材料的剪切弹性模量G=80GP a 。
要求:
(1)画出轴的扭矩图;
(2)求出轴的最大切应力; (3)求出轴的总扭转角。
解:(1)画扭矩图
用截面法求得1-1截面上的扭矩为m N M T ⋅==100011;2-2截面的扭矩为
m N M M T ⋅=-=400212;3-3截面的扭矩为m N M T ⋅==20043。
绘出的扭矩图如图7-7所示。
(2)由图7-7可见AB 段扭矩最大,由于是等截面圆轴,故危险截面在AB 段内。
轴的最大切应力
(3)求轴的总扭转角:
D 截面相对A 截面的相对扭转角即为轴的总扭转角
8. 一钢轴的转速n=240r/min ,传递的功率为P=44kW 。
已知][τ=40MP a ,][θ=1/m ,G=80GP a ,试按强度和刚度条件确定轴的直径。
解:钢轴的扭矩
(1)按强度条件确定轴的直径
直径d 1的大小应满足圆轴扭转时的强度条件:
解得 mm m T
d 6.60104016
1751][16363
1=⨯⨯=⨯≥πτπ
(2)按刚度条件确定轴的直径
直径d 2的大小应满足圆轴扭转时的刚度条件:
][18032
18042θπππθ≤⨯⨯=⨯=d G T GI T P (/m) 解得 mm m G T d 8.59180132
10801751180][324942=⨯⨯⨯⨯=⨯⨯⨯≥πππθπ 由于钢轴既要满足强度条件,又要满足刚度条件,所以d 取直径d 1和直径d 2中较大的,确定钢轴直径mm d 6.60=。
