船舶结构力学:第八章杆及板的稳定性
船舶结构力学PPT精品文档

张娟
1
第一章 绪论
2
第一章 绪论
研究船舶结构力学主要是为了保证船体结构具有一定的强度, 保证船舶在正常的使用过程和一定的年限内具有不破坏或不发 生过大变形的能力。
船体强度包括:总纵强度、局部强度、稳定性、扭转、应力集 中、动力响应等。 船舶结构力学只研究静力响应,包括外力计算、结构在外力作 用下的响应、许用应力的确定等。
(2)骨架
船底交叉杆系
大舱口货船悬臂梁结构 11
基本理论和方法;
结合杆及杆系的强度问题讲述力法、位移法、矩阵法和 能量法;
板的强度; 杆和板的稳定性及薄壁杆件的扭转。
12
计算图形根据计算要求会有所改变,并不固定。
6
1.2 船体结构的计算图形
(1)板
7
1.2 船体结构的计算图形
(1)板 一般考虑受骨架支撑的矩形平板问题;此时骨架支撑很重要。
另外还有矩形平板上的开口问题;此时骨架边界不是很重要,主要考虑开 口的形状、大小。
板的边界根据研究问题的不同而不同。 当研究板受垂向力的弯曲与变形时,此时的边界条件刚性固定; 当研究板的稳定性问题时,此时的边界条件为自由支持。
8
1.2 船体结构的计算图形
(2)骨架 骨架大都为细长的型钢或组合型材,称为杆件或杆。 一般分析时,杆的截面形状如下: 骨架带板
9
1.2 船体结构的计算图形
(2)骨架 实际中的杆件系统简化为规则的简单计算图形。
上甲板纵骨(杆件)
中间有支柱的舱口杆系
舱口杆系(交叉杆系)横Fra bibliotek与肋骨组成的刚架 10
1.2 船体结构的计算图形
3
第一章 绪论
船舶结构力学的任务: ① 阐明结构力学的基本原理和方法,包括力法、位移法
船舶结构力学课后题答案(上海交大版)

s目录之马矢奏春创作第1章绪论 (1)第2章单跨梁的弯曲理论 (2)第3章杆件的扭转理论 (7)第4章力法 (9)第5章位移法 (11)第6章能量法 (21)第7章矩阵法 (36)第9章矩形板的弯曲理论 (49)第10章杆和板的稳定性 (55)第1章绪论1.1题1)接受总纵弯曲构件:连续上甲板, 船底板, 甲板及船底纵骨, 连续纵桁,龙骨等远离中和轴的纵向连续构件(舷侧列板等)2)接受横弯曲构件:甲板强横梁, 船底肋板, 肋骨3)接受局部弯曲构件:甲板板, 平台甲板, 船底板, 纵骨等4)接受局部弯曲和总纵弯曲构件:甲板, 船底板, 纵骨, 递纵桁, 龙骨等1.2题甲板板:纵横力(总纵弯曲应力沿纵向, 横向货物或上浪水压力, 横向作用)舷侧外板:横向水压力等骨架限制力沿中面内底板:主要接受横向力货物重量, 骨架限制力沿中面为纵向力舱壁板:主要为横向力如水, 货压力也有中面力第2章 单跨梁的弯曲理论设坐标原点在左跨时与在跨中时的挠曲线分别为v(x)与v(1x ) 1)图2.133323034243()()()424()26666llll l l p x p x p x M x N x v x EI EIEIEIEI---=++++原点在跨中:3230111104()4()266ll p x M x N x v x v EI EIEI-=+++,'11'11()0()022(0)0(0)2l l v v p v N ⎧==⎪⎨⎪==⎩ 2)33203()32.2()266ll p x N x Mx v x x EI EIEIθ-=+++图 3)333002()22.3()666x x x ll p x N x qx dx v x x EI EIEI θ-=++-⎰图a) 33111311131(3)(2)616444641624pp p pl pl v v v EIEI ⎡⎤⎡⎤=+=⨯⨯-+⨯-⨯⎢⎥⎢⎥⎣⎦⎣⎦=3512pl EIb) 2'292(0)(1)3366Ml Ml Pl v EI EI EI-=+++ =2220.157316206327Pl Pl Pl EI EI EI-+=⨯=2220.1410716206327Pl Pl Pl EI EI EI---=⨯=2372430pl EIc) ()44475321927682304ql ql qll v EI EI EI=-=d)2.1图、2.2图和2.3图1)2)32101732418026q l Ml l l Mllq EI EI EIEIθ⎡⎤=-++-⎢⎥⎣⎦ =3311117131824360612080q l q l EI EI⎛⎫-++-=-⎪⨯⎝⎭ 2.4 题2.5图 3000()6N x v x v x EIθ=++, ()00v A p N =-如图2.4, ()()0v l v l '==由得3333()1922pl x x v x EI l l ⎛⎫∴=-+ ⎪⎝⎭2.5题2.5图:(剪力弯矩图如2.5)()132023330222002332396522161848144069186pl Mp pR p ll p pl v AR EI EI v l Mlpl pl pl v EI EI EI EI v Ml pl pl pl v l EI EI EI EIθ-∴==-===⋅=⎛⎫=-=-=⎪⎝⎭-'==--=-=-()16A pa b b M A l K l ⎡⎤=++⎢⎥⎣⎦, 111,0,6632A l a l b A K ====+=将代入得:()16312pl pl M ==2.7图:(剪力弯矩图如2.6)图2.62.8图(剪力弯矩图如2.7)图2.7.[]1max 2max 2113212132142.()()62()()62()()242(0)sN EIv s sss s N dv dx dx dx GGA N EI v dx v C GA GA EI ax bx v v v f x cx d f x ax b C GA EI EIax bx f x f x c a x d GA GA qx qx f x f x EI EIv v τγ'''====-''=−−−→-+⎡⎤''∴=+=++++-+++⎢⎥⎣⎦⎛⎫''=-+++-+ ⎪⎝⎭''==''=⎰式中由于11142323432342(0)00()()00242602,224()241222425()23848s s s s s d b v l v l ql EI ql al EI c a l EI GA EIGA qlal EIql ql c EI EI qx qlx qx qx qlv x x EI EI GA EI GA l ql ql v EI GA ===''==⎧⎛⎫-++-=⎪⎪⎪⎝⎭⎨⎪+=⎪⎩=⎛⎫∴=--++⎪⎝⎭∴=+可得出由得方程组:解出:a=先推广到两端有位移,,,i i j j θθ∆∆情形:212,i j s EI GA l β⎛⎫∆=∆-∆=⎪⎝⎭令 已知:20375225, 1.8,751050kgl cm t cm s cm cm σ=⨯====面积2cm 距参考轴cm面积距3cm惯性矩4cm自惯性矩4cm外板1.845⨯ 81 0 0 0 (21.87)略 球扁钢O N 24a2232 ∑ABC=11662224604.55.04116628610119.8BBe cm I C cm AA ===-=-=275 1.838.75174min ,4555A cm l lI be s cm=⨯+=⎧⎫===⎨⎬⎩⎭计算外力时面积计算时,带板1).计算组合剖面要素:形心至球心概况1240.9 5.0419.862t y h e cm =+-=+-=形心至最外板纤维若不计轴向力影响, 则令u=0重复上述计算:解得:图2.1201)先计算剖面参数:图2.8a2422u u P P l δδδ⎛⎫⋅⎛⎫ ⎪⋅+= ⎪⎝⎭ ⎪⎝⎭p M 图2.8b2.13弥补题剪切对弯曲影响弥补题, 求图示结构剪切影响下的v(x)解:可直接利用 2.14. 弥补题试用静力法及破坏机构法求右图示机构的极限载荷 p, 已知梁的极限弯矩为p M (20分) (1983年华中研究生入学试题) 解: 1)用静力法:(如图2.9)由对称性知首先固端和中间支座到达塑性铰, 再加力u p p →, 当p作用点处也形成塑性铰时结构到达极限状态.即: 2)用机动法: 8282p pu M M p p llδδ⋅=∴=求右图所示结构的极限载荷其中,3l p ql EI α==(1985年哈船工研究生入学试题)解:由对称性只需考虑一半, 用机动法.当此连续梁中任意一个跨度的两端及中间发生三个塑性铰时, 梁将到达极限状态.考虑a) 、b)两种可能:(如图2.10)取小者为极限载荷为28pu M q l =即接受集中载荷p 的跨度是破坏.图2.9 图2.10第3章 杆件的扭转理论a) 由狭长矩形组合断面扭转惯性矩公式:b) 3334170 1.235115 1.260.63J cm ⎡⎤==⨯+⨯+⨯=⎣⎦c) 由环流方程对a)示闭室其扭转惯性矩为()()()4230444a t A J t a t ds a t t t -===--⎰对b)开口断面有()331433i i t J h t a t ==-⎡⎤⎣⎦∑.将剪流对内部任一点取矩 由于I 区与II 区, II 区与III 区扭率相等可得两弥补方程第4章力法由于折曲连续梁足够长且多跨在a, b周期重复.可知各支座断面弯矩且为M对2节点列角变形连续方程4.4题4.4图, 21对,节点角连续方程:4.6题已知:受有对称载荷Q的对称弹性固定端单跨梁(EI l), 证明:相应固定系数χ与α关系为:211EI lαχ⎛⎫=+⎪⎝⎭讨论:1)只要载荷与支撑对称, 上述结论总成立2)当载荷与支撑分歧毛病称时, 重复上述推导可得4.8 题1)如图所示刚架提供的2)01由对称性只需对,节点列出方程组求解4.10题写出下列构件的鸿沟条件:(15分) 1) 2)3) 设x=0,b 时两端刚性固定;y=0,a 时两端自由支持4)已知:x=0,b 为刚性固定边;y=0边也为刚性固定边:y=a 为完全自由边q 主向梁与交叉构件两端简支在刚性支座上, 试分析两向梁的尺寸应坚持何种关系, 才华确保交叉构件对主向梁有支持作用? 解:少节点板架两向梁实际接受载荷如图, 为简单起见都取为均布载荷.由对称性:12R R R ==由节点挠度相等: 当5548115224qlL qlL α→∞=⨯=max 时R=R 这时交叉构件对主向梁的作用相当于一个刚性支座 当3511I 1.3011521944iR lα<<<3时即时L 暗示交叉构件的存在不单不支持主向梁, 反而加重其负担, 使主向梁在接受外载荷以外还要受到向下的节点反作用力这是很晦气的. ∴只有那时33I 1.3L il 〉, 主向梁才受到交叉构件的支持.第5章 位移法10012Ql M -=, 15021Ql M =, 02332==M M200'12)4(2θl I E M =, 200'21)4(4θl I E M = 对节点2, 列平衡方程⎩⎨⎧=+=00212332M M M 即: ⎩⎨⎧=+++=+00212321'23'3232'M M M M M M 代入求解方程组, 有⎪⎪⎩⎪⎪⎨⎧-=++=+154)88(0840*******0300200Ql l EI l EI l EI l EI l EI θθθθ, 解得⎪⎪⎩⎪⎪⎨⎧⨯=⨯-=02302021*******EI Ql EI Ql θθ 所以2'00012121200008410.1242221510330EI Ql Ql M M M Ql Ql l EI ⎡⎤-=+=-=-=-⎢⎥⨯⎣⎦ 图04.5. 由对称性知道:23θθθ=-=-1)10012Ql M -=, 15021Ql M =, 02332==M M2) 200'12)4(2θl I E M =, 200'21)4(4θl I E M = 3) 对2节点列平衡方程23210M M +=即0002200166015EI Ql EI l l θθ++=, 解得20202215Ql EI θ=-⨯ 4)求122123,,M M M (其余按对称求得)2321M M =-, 其余4321M M =-, 3421M M =-, 3223M M =-由对称性只要考虑一半, 如左半边1)固端力(查附表A-4)2120001(2)105M Q l q l =-=-, 2210002(2)1515M Q l q l ==2)转角23,θθ对应弯矩(根据公式5-5)'012202(4)2E I M l θ=, '021204(4)2E I M l θ=, '0023230042EI EI M l l θθ=+, 43'0003434300042442EI EI EI M l l l θθθθθ=-=+=3)对节点2, 3列出平衡方程323421252300M M M M M +=⎧⎨++=⎩ 即()''32343234'''252321232125()M M M M M M M M M M ⎧+=-+⎪⎨++=-++⎪⎩ 则有00023300020000002223000024028422215EI EI EI l l l EI EI EI EI q l l l l l θθθθθθθ⎧++=⎪⎪⎨⎪+++=-⎪⎩, 得30020300301210451631045q l EI q l EI θθ⎧-=⎪⎪⎨⎪=⎪⨯⎩4)其余由对称性可知(各差一负号):6512M M =-, 5621M M =-,5225M M =-, 5423M M =-, 4532M M =-, 433432M M M =-=5.3 题(14250M M ==)128M pl =-, 218M pl =, 其余固端弯矩都为0'4112EI M l θ=, '1414EI M l θ=, '5222EI M l θ=, '2524EI M l θ= '6332EI M l θ=, '3634EI M lθ=图5.1 (单位:200q l )'121242EI EI M l l θθ=+, '211224EI EI M l l θθ=+ '232342EI EI M l l θθ=+, '322324EI EI M l lθθ=+ 由1、2、3节点的平衡条件14122125233236000M M M M M M M +=⎧⎪++=⎨⎪+=⎩ 即()()()''14121412'''252321232125''32363236M M M M M M M M M M M M M M ⎧+=-+⎪⎪++=-++⎨⎪+=-+⎪⎩解得:21272264pl EI θ=⨯, 2252216pl EIθ=-⨯, 2352264pl EI θ=⨯已知1203l l m ==, 2302.2 6.6l l m ==, 24039l l m == 4400.310I cm =⨯, 1202I I =, 2303I I =, 2408I I = 0212001122Q q l q l ==, 404q q =,1)求固端弯矩210010M Q l =, 120015M Q l =-, 02332==M M 2)转角弯矩()0'0121200224(2)E I E I M l l θθ=+, '002323004(3)2(3)2(2)2(2)E I E I M l l θθ=+,'024204(8)(3)E I M l θ=, '042202(8)(3)E I M l θ=3)对1、2、3节点列平衡图5.2(单位:ql )图5.3(单位:00Q l )方程1221242332000M M M M M =⎧⎪++=⎨⎪=⎩即:001200000001230000000230084154796301633115306001111EI EI Q l l l EI EI EI Q l l l l EI EI l l θθθθθθθ⎧+=⎪⎪⎪⎪⎛⎫++=--⎨ ⎪⎝⎭⎪⎪+=⎪⎪⎩解得:22000010022340.0339732880Q l q l EI EI θ=-=-,2200002002090.076281370Q l q l EI EI θ==,4)求出节点弯矩弯矩图如图5.3.5.5 题由对称性只考虑一半;所以:0124341330Ql M M =-=-, 0213455Ql M M =-=, 0233255Ql M M =-=-:令10012100120,, 1.5I I I l l l l ====由表格解出令1003I I =, 012I I =,100l l =, 120l l =0q q =, 1000Q q l =, 00122q l Q =由表格解出:2010.0931M ql =-, 210120.0638M M ql =-=, 2210.0228M ql =若将图5.5中的中间支座去失落, 用位移法解之, 可有: 解得:332770.05149652ql ql EI EIθ==⨯,2120.140M ql =-, 210.040N ql =,5.7题计算如表所示1)不计45杆的轴向变形, 由对称性知, 4、5节点可视为刚性固定端2) ()23000013322Q q l q l ==,()3400000.63 1.8Q q l q l == 223230003(3)/1510M Q l q l ==, 232230009(3)/1020M Q l q l =-=- 3) 计算由下表进行: 21812000.0039M M q l =-=,23234000.518M M q l =-=-,243000.4159M q l =-, 223000.1127M q l =252000.0170M q l =-, 其它均可由对称条件得出.创作时间:二零二一年六月三十日创作时间:二零二一年六月三十日.00005 .00059 .00030.00022 .00043 .00085.00043 .00003 .00005 .00011.00006200/ij M q l创作时间:二零二一年六月三十日5.9 题任一点i 的不服衡力矩为01212i is sql qlM M ==-=∑(i=1, 2, …,h,i,j,…n-1. s=i-1,i+1) 所以任一中间节点的分配弯矩ij m 与传导弯矩'ij ji ji m n m =均为0. 任一杆端力矩:'ij ij ij ij M M m m =++()0ij ij is ji ji js ij s s M M n M M i n λλ⎛⎫=-+-=<< ⎪⎝⎭∑∑对两端0,i n =, 由于只吸收传导弯矩'0ij m = 'ij M ij ij ij M M m =+=两端所以对每个节都有杆端力矩ij M ij M =0iM=∑, 也可以看作两端刚固的单跨梁.第6章 能量法1)方法一 虚位移法考虑b),c)所示单位载荷平衡系统, 分别给予a)示的虚变形 :()M x dx d EIδθ= 外力虚功为 i j 11W θδθ⨯⎧⎫=⎨⎬⨯⎩⎭虚应变能为l001V=M()M ()d EI x x x δ⎰()()()()00011=1li i i l i i i R x M R x dx EI R x M R x dx EI⎧++⎪⎪⎨⎪+⎪⎩⎰⎰j i ij j i j i M M 1M M ..........b)EI 363EI 2=M M 1M M ...........c)EI 363EI 2l l l l ⎧⎛⎫⎛⎫-=-⎪ ⎪ ⎪⎝⎭⎪⎝⎭⎨⎛⎫⎛⎫⎪-=- ⎪ ⎪⎪⎝⎭⎝⎭⎩ 由虚功原理:W V δδ= 得:i i j j 11M 2M 13EI 12l θθ⎡⎤-⎢⎥⎧⎫⎧⎫=⎢⎥⎨⎬⎨⎬⎢⎥⎩⎭⎩⎭-⎢⎥⎣⎦2)方法二 虚力法(单位虚力法)梁弯曲应力:{}()M x y σ=I{}()M x y σε==EEI()()ij iM M x M x M l+=-()1(10)x M x lδ=-+给i M 以虚变动1i M ∂= 虚应力为 {}()M x y δδσ=I虚余功:1W δθ*⨯i =虚余能:*V δΩ⎰=(真实应变)⨯(虚应力)d Ω()()M x M x y ydxdydz EI δ=⎰⎰⎰I()()2201lA M x M x dx y dA EI δ=⎰⎰()()01/1/li i j M M M x l x l dx EI ⎡⎤=-+-⎣⎦⎰ ∴ 132i ij l Q M M EI ⎛⎫=- ⎪⎝⎭同理:给j M 以虚变动1j M δ=, ()0i M δ=可得(将i 换为j )32i j j M l M EI θ⎛⎫=-+ ⎪⎝⎭3)方法三 矩阵法(柔度法)设{}{}i i j j M ,p M θθ⎧⎫⎧⎫∆==⎨⎬⎨⎬⎩⎭⎩⎭, 虚{}{}[]{},i j M p M δδσεδ⎧⎫==⎨⎬⎩⎭力p{}()()[]{}/1i i i j j M M x y y xx y M M M x l c p M I I I ll σσ⎧⎫⎡⎤⎡⎤===-+=--=⎨⎬⎢⎥⎣⎦⎣⎦⎩⎭式中[]1,y x x c I l l ⎡⎤⎛⎫⎛⎫=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦(无妨称为物理矩阵以便与刚度法中几何矩阵[]B 对应)虚应力{}[]{}[]i j M c p c M δδσδδ⎧⎫==⎨⎬⎩⎭实应变{}[]{}[][]{}11D D C p εσ--==虚余功 {}{}{}{}()*TTi i j j W p p M M δδδθδθδ=∆=∆=+虚余能 {}{}{}{}*TTV d d δεδσεσεΩΩ=Ω=Ω⎰⎰{}[][][]{}{}[][][]{}11T T T T p C D C P d p C D C d p δδ--ΩΩ⎡⎤=Ω=Ω⎢⎥⎣⎦⎰⎰ 于虚力原理:**W V δδ=考虑到虚力{}p δ的任意性.得: {}{}[][][][]{}1A Tp C D C d p -Ω∆=Ω=⎰式中 [][][][]1T A C D C d -Ω=Ω⎰——柔度矩阵(以上推导具有普遍意义)对本题:[]220111111l x x x x l l l y y x x l A d dx x I EI l l EI x x x l l l l Ω⎡⎤⎛⎫⎛⎫⎧⎫---⎢⎥- ⎪ ⎪⎪⎪⎡⎤⎪⎪⎝⎭⎝⎭⎛⎫⎢⎥=--Ω=⎨⎬ ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎛⎫⎛⎫⎪⎪-⎢⎥-- ⎪ ⎪⎪⎪⎩⎭⎢⎥⎝⎭⎝⎭⎣⎦⎰⎰ /3/611/21/6/31/213l l ll l EIEI--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦由{}[]{}A p ∆=展开得:11/21/213i i j j M lM EIθθ-⎧⎫⎧⎫⎡⎤=⎨⎬⎨⎬⎢⎥-⎣⎦⎩⎭⎩⎭方法一 单位位移法()/j i u u l ε=- , ()/j i E E u u l σε==- 设 1i u δ=, 则 /1/i u l l δεδ=-=-()()()()2011/l i j i j i i j E EA EAT u u l d u u dx u u l l l Ω-=--Ω=-=-⎰⎰ 同理, 令1j u δ= 可得()()11/j j i ET u u l d l Ω=-Ω⎰()j i EA u u l =- 即:1111i i j j T u EA T u l -⎧⎫⎧⎫⎡⎤=⎨⎬⎨⎬⎢⎥-⎣⎦⎩⎭⎩⎭可记为 {}[]{}ij ij p K =∆ []K 为刚度矩阵.方法二 矩阵虚位移法 设{}Tij i j p T T ⎡⎤=⎣⎦ {}Tij ij u u ⎡⎤∆=⎣⎦(){}[]1{}/11i j i ij j u u u l B u l ε⎧⎫⎧⎫=-=-∆∆⎨⎬⎨⎬⎩⎭⎩⎭式中 []{}111B l=-——几何矩阵 ∴ {}[]{}[][]{}ij D D B σε==∆ 设虚位移{}Tij i j u u δδδ⎡⎤∆=⎣⎦ , 虚应变 {}[]{}ij B δεδ=∆外力虚功 {}{}{}{}TTij ij ij ij W p p δδδ=∆=∆虚应变能 {}{}{}{}TTV d d δσδεδεσΩΩ=Ω=Ω⎰⎰ {}[][][]{}TTij ij B D B d δΩ=∆∆Ω⎰{}[][][]{}TTij ij B D B d δΩ⎡⎤=∆Ω∆⎢⎥⎣⎦⎰{}[]{}ijijK δ∆∆由 W V δδ= 得: {}[]{}ij ij p K =∆ 式中 [][][][]TK B D B d Ω=Ω⎰——刚度矩阵对拉压杆元 []{}1111111111l EA K EA dx l l l --⎧⎫⎡⎤=-=⎨⎬⎢⎥-⎩⎭⎣⎦⎰ 详细见方法一. 方法三 矩阵虚力法设 {}i ij j T p T ⎧⎫=⎨⎬⎩⎭ , {}i ij j u u ⎧⎫∆=⎨⎬⎩⎭ , {}[]{}D δε={}{}[]{}111i j iij j T T T C p T AA σ-⎧⎫==-⎨⎬⎩⎭式中 [][]111C A=-——物理矩阵(指联系杆端力与应力的系数矩阵) ∴ {}[]{}[][]{}11ij D D C p εσ--== 虚应力 {}[]{}ij C p δσδ=设虚力 {}i ij j T p T δδδ⎧⎫=⎨⎬⎩⎭, 则 {}[][]{}1ij D C p δεδ-=虚余功 {}{}{}{}*TTij ij ij ij W p p δδδ=∆=∆虚余能 {}{}{}{}*T TV d d δεδσδσεΩΩ=Ω=Ω⎰⎰{}[][][]{}1TTij ij p C D C p d δ-Ω=Ω⎰{}[][][]{}1T ij ij p C D C d p δ-Ω⎡⎤=Ω⎢⎥⎣⎦⎰{}[]{}ijijp A p δ式中[][][][]1T A C D C d -Ω=Ω⎰ ——柔度矩阵对拉压杆: []{}1111111111l A l K dx E A A EA --⎧⎫⎡⎤=-=⎨⎬⎢⎥-⎩⎭⎣⎦⎰ ∴ {}[]{}ij ij A p ∆=即 1111i i j j u T l u T EA -⎧⎫⎧⎫⎡⎤=⎨⎬⎨⎬⎢⎥-⎣⎦⎩⎭⎩⎭ 讨论: 比力方法二、三.结论: {}[]{}ij ij p K =∆, {}[]{}ij ij A p ∆=若 []K 与[]A 的逆矩阵存在(遗憾的是其实不是总是存在), 则,[]1K -实际上是一个柔度矩阵, []1A -实际上是一个刚度矩阵如图所示设()121cos n n n x v x a l π∞=⎛⎫=- ⎪⎝⎭∑显然满足0,x x l ==处的 变形约束条件()()()()''0000v v l v v l ====变形能 ''20()2l EI V v dx =⎰220122cos 2l n n EI n n x a dx l l ππ∞=⎡⎤⎛⎫=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦∑⎰421222nn EIn l a l π∞=⎛⎫=⎪⎝⎭∑ 力函数()()()2pv c pv l c pv c =+-=(对称)1221cos n n n c p a l π∞=⎛⎫=- ⎪⎝⎭∑由()0nV a ∂-=∂ , 所以 nn Va a ∂∂=∂∂ .即 422()21cos 2n EIl n n c a p l l ππ⎛⎫=- ⎪⎝⎭ 所以, 34421cos 4n n c pl l a EI n ππ⎛⎫- ⎪⎝⎭=⋅()34411221cos 1cos 4n pl n c n x v x EInl l πππ∞=⎛⎫⎛⎫=-- ⎪⎪⎝⎭⎝⎭∑ 0如图所示设()01sinn n n xv x a x a lπ∞==+∑ ()()2222402011sin 22222ln n n n v l a l EI n n x EI n l V a dx a l l A l A πππ∞∞==⎡⎤⎡⎤⎛⎫⎛⎫⎣⎦=-+=+⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦∑∑⎰()01sinn n n cpU c p a a pc lπ∞===+∑ 由()00V a ∂-=∂得 20/a l A pc = , 所以, 20/a Apc l = 由()0nV a ∂-=∂, 得4sin 2n EIl n n ca p l l ππ⎛⎫= ⎪⎝⎭ 所以, ()342sin n pl n c a l EI n ππ= ∴ ()3244121sin sin n Apc pl n c n xv x x l EI n l lπππ∞==+∑如图所示 令()()2v x ax l x =-所以, ''202lEI V v dx =⎰()20232622l EI al ax dx a EIl =-=⎰ ()()/2/22405192l l qU x dx qax l x dx qal ==-=⎰⎰由()0V a∂-=∂ 得 3454192aEIl ql =所以, 5768ql a EI =∴ ()()25768ql v x x l x EI=- 0所示如图,设()2312v x a x a x =+, ()()''1223v x a a x =+''22l EIV v dx =⎰()2120432lEIa a x dx =+⎰()2221122233EIl a a a l a l =++ ()()2312/2/2lll l qv x dx q a xa x dx==+⎰⎰312715838a a l ql ⎛⎫=+ ⎪⎝⎭由()10V a ∂-=∂ 得 ()3122237/24EIla a l ql +=由()20V a ∂-=∂ 得 ()24126215/64EIla l a l ql+=解上述两式得 2216738413192ql a EIql a EI⎧=⎪⎪⎨-⎪=⎪⎩∴ ()2230.17450.0677ql ql v x x x EI EI=-如图所示设 ()1sin xv x a lπ=()/4/2''2''20/42222l l l E I EI V v dx v dx ⎡⎤=+⎢⎥⎣⎦⎰⎰4242/4/222110/4sin 2sin l l l x x EI a dx EI a dx l l l l ππππ⎛⎫⎛⎫⎛⎫⎛⎫=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎰⎰4213142l EIa l ππ⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭()110sin2/l lxqv x dx q a dx qla lππ===⎰⎰由()10V a ∂-=∂ 得 4131222l ql EIa l πππ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭所以, 441540.00718312ql ql a EI EI ππ==⎛⎫+ ⎪⎝⎭()40.00718sin ql x U x EI lπ=如图所示 设 ()()121sin2n n n x v x a lπ∞=-=∑()()222''022l v l EI V v x dx A⎡⎤⎣⎦⎡⎤=+⎣⎦⎰ ()2423112121sin 222n n n n n EI n a a l ππ∞∞==⎡⎤-⎛⎫⎛-⎫⎛⎫⎢⎥=+ ⎪⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦∑∑ 其中, 3l A EI=()4331212121sin sin 222n n n n n V EI n EI n a a a l l πππ∞=-⎡⎤∂-⎛-⎫⎛⎫⎛⎫=+⎢⎥ ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭⎣⎦∑ ()()220121sin2ll n n n x qv x dx q a dx lπ∞=-==∑⎰⎰()()11241cos 212121nn n n a l ql q a n n n πππ∞∞==⎛⎫=--=⎡⎤ ⎪⎣⎦ ⎪--⎝⎭∑∑ 所以,()421n ql a n π∂=∂- 取前两项得 ()41123312V EI EI a a a a l l π∂⎛⎫=+- ⎪∂⎝⎭, ()421233232V EI EIa a a a l l π∂⎛⎫=-- ⎪∂⎝⎭由()10V a ∂-=∂ 得 41233412EI EI qlaa l l ππ⎧⎫⎡⎤⎪⎪⎛⎫+-=⎢⎥⎨⎬ ⎪⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭ 由()20V a ∂-=∂ 得 4213334123EI EI qlaa l l ππ⎧⎫⎡⎤⎪⎪⎛⎫+-=⎢⎥⎨⎬ ⎪⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭即: 41241247.0884494.1333ql a a EI ql a a EI ππ⎧-=⎪⎪⎨⎪-=-⎪⎩解得 41420.17980.00118ql a EI ql a EI⎧=⎪⎪⎨⎪=⎪⎩ ∴()430.180sin 0.0012sin 22x x ql v x l l EI ππ⎛⎫=+ ⎪⎝⎭ ∴中点挠度40.17862l ql v EI ⎛⎫= ⎪⎝⎭6.6题 取12()sin,()sin n n n x n xv x a v x b l lππ==∑∑1'221200222004222422222sin cos 22 222244llsl l s n n s n n s n nGA EI V v dx vdxGA EI n n x n n x a dx b dx l l l l GA EIn l n l a b l l GA l EIl n n a b l l ππππππππ=+⎡⎤⎡⎤⎛⎫⎛⎫=-+⎢⎥ ⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦⎢⎥⎣⎦⎛⎫⎛⎫=+ ⎪⎪⎝⎭⎝⎭⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭⎰⎰∑∑⎰⎰∑∑∑∑42(),()22s n n n n GA l V EIl n V n a b a l b lππ∂∂==∂∂ 120011sinsin (1cos )(1cos )l lll n n n n qv dx qv dxn x n xq a dx q b dxl l n n q a n q b n l l ππππππ--=+=+⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭⎰⎰∑∑⎰⎰∑∑∴(1cos ),(1cos )n n l l a q n b q n n n ππππ⎛⎫⎛⎫∂∂=-∂∂=-⎪⎪⎝⎭⎝⎭由4455()2(1cos )40()()n n n V ql n ql a a n EI n EI πππ∂--==∂=为奇数得 由2233()2(1cos )40()()n n n s s V ql n ql b a n GA n GA πππ∂--==∂=为奇数得 ∴()()12()U x U x U x =+4255334141sin sin (1,3,5, )n n S ql n x ql n xEI n l GA nl N ππππ=+=∑∑1)图6.9 对等断面轴向力沿梁长不变时, 复杂弯曲方程为:''0IV EIV TV q --= 取()sinn nn xv x a lπ=∑ 能满足梁段全部鸿沟条件 ''''''''00,0,0,0,0()0l IV x l v v v v EIV TV q qvdx ==≠=≠∴--=⎰处∴有420()sin ()(sin )sin 0l n n n n x n n x n x EI a T a q dx l l l l l πππππ⎡⎤---=⎢⎥⎣⎦∑∑⎰积分:420cos 022ln n n l n l l n x EIa Ta q l l n l ππππ⎛⎫⎛⎫⎛⎫⎡⎤+--= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ 即:()4425220()1cos 4()()14/()22n l n q n n a ql n EIl n n l EI n u n T l l ππππππ⎛⎫⎧- ⎪⎪⎝⎭==⎨⎛⎫⎛⎫⎪⎡⎤++ ⎪ ⎪⎣⎦⎩⎝⎭⎝⎭为偶数为奇数式中:u =u =1 ∴455222sin4()(1,3,5 )(14/)N n xql l v x n EI n u n πππ==+∑ ∴44522214()0.0093012()(14/)n l ql ql v EI EI n u n ππ===+取一项 准确解为:444055(1)0.7110.0092582384384l ql ql ql v f EI EI EI ⎛⎫⎡⎤==⨯= ⎪⎢⎥⎝⎭⎣⎦误差仅为0.46%结论:1)引进22()cr n EI T lπ=——单跨简支压杆临界力()22554,4384l T u EI π=≈ 2)取一项, 中点挠度表达式可写成如下讨论的形式:445(0)5138423841()()cr cr ql T l ql v EIEI T T T T ⎡⎤⎧⎢⎥=⎪⎛⎫==⎢⎥⎨ ⎪⎝⎭⎢⎥⎪±∞=⎩⎢⎥⎣⎦失稳的压力时 式中:当T 为拉力时取正号(此时相当一缩小系数, 随T ↑而↓)≤1当T 为压力时取负号(此时相当一放年夜系数, 随T ↑而↑)≥1 2)∵弹性基础梁平衡方程为:0IV EIV kv q +-=∴00lIVEIV kv q Vdx δ⎡⎤+-=⎣⎦⎰ 取:()sinn nn xV x a lπ=∑代入上式:40sin sin sin 0ln n n n n n n x n x n x a EI a k a q dx l l l l ππππδ⎡⎤⎛⎫+-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦∑∑⎰由于n a δ的随意性有式中积分为0, 即:()41cos 022n n n l l l EIa ka q n l n πππ⎛⎫⎛⎫+--= ⎪ ⎪⎝⎭⎝⎭∴()44541cos 4()()1/()522n l q n ql n a n n EIl n kl EI n k EI l πππππ⎛⎫- ⎪⎝⎭==⎡⎤⎛⎫++⎢⎥ ⎪⎣⎦⎝⎭为奇数 由442442l u k u k EI EI l ⎛⎫== ⎪⎝⎭得代入得()44542()14n ql a u EI n n ππ=⎡⎤+⎢⎥⎣⎦()4554sin4()(1,3,5 )1nn xql l v x n EI kn EI n l πππ⎛⎫== ⎪⎡⎤⎝⎭+⎢⎥⎢⎥⎣⎦∑今取一项, 且令u=1, 求中点挠度()44454()0.0078882214l ql ql EI EIνππ⎡⎤⎢⎥==⎢⎥⎡⎤⎢⎥+⎢⎥⎢⎥⎣⎦⎣⎦准确值:()4404110.448()10.00862524(21)q ql ql u EI k EI νϕ⎡⎤-=-==⎡⎤⎢⎥⎣⎦⨯⎣⎦误差为8.5%误差较年夜, 若多取几项, 如取二项则误差更年夜, ∴交错级数的和小于首项, 即2l ν⎛⎫⎪⎝⎭按级数法只能收敛到略小于精确解的一个值, 此矛盾是由于0ϕ是近似值.220()()2()1 22lM x dx AREIννν=+=+⎰梁支 020343342()2 ()2222 232162111 (1)6166ll MM x dx AR R EIR R qx x ql x dx AR EI R l ql l ql R EI EI l ql EIEI ν∂∂=+∂∂⎡⎤⎛⎫=---+ ⎪⎢⎥⎝⎭⎣⎦⎡⎤⎛⎫-⎛⎫=-++⎢⎥ ⎪ ⎪⨯⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫=-+++ ⎪⎢⎥⎝⎭⎣⎦⎰⎰由最小功原理:0vR∂=∂解出:528qlR =∴43445(2)(2)384485 0.178528q l R l v EIEIqlql EIEI=-=≈中由对称性可知, 对称断面处剪力为零, 转角00θ=, 静不定内力0T 和0M 可最小功原理求出:2102200()()(/2)2sin (1cos )()qs M OA M s M qr qr T r AB θθ⎧+⎪=⎨⎪+++-⎩—段2—段 001 ()0 ()()() 1 ()(1cos ) ()OA OA M s M s M T AB r AB θ⎧⎧∂∂==⎨⎨∂∂-⎩⎩段—段段—段 最小功原理:()()0022221010000()()11/22sin 1cos 20s rV M s M s ds M EI M qs M ds M qr qr T r rd EI EI πθθθ∂∂=∂∂⎛⎫⎡⎤=+++++- ⎪⎣⎦⎝⎭=⎰⎰⎰()22200012sin (1cos )1cos 02V qr M qr T r r rd T EIπθθθθ∂⎡⎤=+++--=⎢⎥∂⎣⎦⎰分别得:()()()()2002001112226413122424M T r qr M T r qr ππππππ⎧⎛⎫++-=-++ ⎪⎪⎪⎝⎭⎨⎛⎫⎪-+-=+ ⎪⎪⎝⎭⎩解得:2000.5388()2.7452M qrM s T qr⎧=-⎪∴⎨=-⎪⎩表达式正确 由10Ms ∂=∂ 得极值点在0t s =点,该处极值为10M M = 由20Ms ∂=∂ 得020.7285,0.6296qr tg T θθ=-=≈极值为()()2222210.53882sin 0.6296 2.74521cos 20.61M qr qr qr qr θ⎡⎤⎛⎫=-+++-- ⎪⎢⎥⎝⎭⎣⎦=区间端点B 处()222210.53882sin 2.745210.7922B M qr qr qr qr π⎡⎤⎛⎫=-++-=- ⎪⎢⎥⎝⎭⎣⎦{}max 012max max ,,0.79()B B B M M M M M M M qr ∴==∴==-发生在支撑处由左右对称,∴对陈断面01上无剪力. 有垂向静力平衡条件:0sin 2P qr d πθθ=⎰解得:/4q P r =任意断面弯矩为:()()()200020000Pr()sin (1cos )1cos 2Pr(1cos )sin sin 21,1cos M s M T r qr d M T r qr M Mr M T θθθθααθθθθθ=++-+-+-⎡⎤⎣⎦=+-++-+∂∂==-∂∂⎰ 有最小功原理确定T 0和M 0200001Pr (1cos )sin (sin )02V M T r qr rd M EIπθθθθθ∂⎡⎤=+-++-+=⎢⎥∂⎣⎦⎰即:2200Pr (2)02M T r qr πππ+++-+=200001Pr (1cos )sin (sin )(1cos )02V M T r qr r rd T EIπθθθθθθ∂⎡⎤=+-++-+-=⎢⎥∂⎣⎦⎰()(1cos )0()cos 0M s d M s d ππθθθθ-=-=⎰⎰即220000Pr ()cos cos sin (sin cos cos )02M T r T r qr d πθθθθθθθθ⎡⎤∴+-++-+=⎢⎥⎣⎦⎰ 得:2000204/()2T r P qr T qr T πππ--=∴=-=-与图中假设方向相反20Pr(4)8M ππ∴=-2Pr Pr Pr Pr()(4)(1cos )sin 844M s πθθθππ∴=---+- 241cos sin Pr 844πθθθπππ⎡⎤-=-++-⎢⎥⎣⎦第7章 矩阵法322122112x lx l x v θθθθθ+++-= 2221211'32)(x l x l x v θθθθθ+++-=, x ll x v 22121''62)(θθθθ+++-= ∵⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+-==j i l x l l x l y yv θθε22''6264∴[][]E D l x l x l y B =⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=,13232 [][][][]2222222032433213133323221442212312T el x y x x l K B D B d E d x l l l l x x x l l l l l EI EIEI l ll l x ll ΩΩ⎡⎤-⎢⎥⎡⎤⎛⎫⎛⎫⎡⎤=Ω=--Ω⎢⎥ ⎪ ⎪⎢⎥⎣⎦⎝⎭⎝⎭⎣⎦⎢⎥-⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎡⎤--+⎢⎥⎪ ⎪⎢⎥⎡⎤⎝⎭⎝⎭⎢⎥===⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎛⎫⎢⎥- ⎪⎢⎥⎣⎦⎢⎥⎝⎭⎣⎦⎰⎰⎰对称解:如图示离散为3个节点, 2个单位()[]()()()()()()[]()()()()⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=23323222322221221211121112222124262262621226212226426262122621222K K K K K K K K K l l l l l l l l l l l l l I E K形成[]K ()()[]()()()()[]()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+32123323222322212212111211100δδδK K K K K K K K 将各子块代入得:()()()()()()()()()()()()()()()()()()()()()()⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------⨯-00042/622/62/62/242/62/2422/6122/642/122/62/242/62/362/122/2442/12242/62/122/242/62/242/11332211222222222P M R v v v l l l l l l l l l l l l l l l l l x l l l x l l EI R y z z z θθθ 划去1、2行列, (∵011==z v θ)约束处置后得:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--------000412212124812482121212124812144233222222P v vl l l l ll ll l l ll l EI z z θθ图7.3 离散如图∵杆元尺寸图7.2(以2l 代l ), ∴e K ⎡⎤⎣⎦不变, 离散方式一样, 组装成的整体刚度矩一样[]K{}{}11300T TyR yP R M P R ={}{}112233TTz z z v v v δθθθ=约束条件 1130z v v θ===, 划去1、2、5行列得(注意用上题结果时要以2l 代l )222336166612200624z z l l l v P EI l l l θθ⎡⎤⎢⎥⎧⎫⎧⎫⎢⎥-⎪⎪⎪⎪⎢⎥=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎩⎭⎢⎥⎢⎥⎣⎦图7.4, 由对称计算一半, 注意到230,0z v θ=≠[]22(1)(1)(1)1112(1)(1)212222(2)(2)2l l 4I I(2)2223(2)(2)323312612666421261266624l l l l K K EI l l K l K K l l l l l l K K KK K -⎡⎤⎢⎥⎢⎥-⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥---⎣⎦⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤−−−−−→=⎢⎥⎣⎦⎣⎦以代,代[][](1)(1)111211(1)(1)(2)(2)2122222322(2)(2)32333300K K P K K K K P K K P δδδ⎡⎤⎧⎫⎧⎫⎢⎥⎪⎪⎪⎪+=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎩⎭⎣⎦, 将各子块代入得22121112222222233223126126266421212618660326620124666646648y R z z z R ql l l l l R v ql l l M v ql EI l l l l l k v l ql l l v ql l l l l M ll θθθ-⎡⎤⎢⎥⎧⎫+⎢⎥⎪⎪-⎢⎥⎪⎪⎧⎫⎢⎥⎪⎪+⎪⎪⎢⎥⎪⎪---⎪⎪⎢⎥⎪⎪⎪⎪⎪⎪⎢⎥-+=⎨⎬⎨⎬⎢⎥-⎪⎪⎪⎢⎥⎪⎪⎪⎢⎥⎪⎪⎪⎢⎥---⎪⎪⎪⎩⎭⎢⎥⎪⎢⎥⎪-⎢⎥⎩⎢⎥⎣⎦⎪⎪⎪⎪⎪⎪⎪⎪⎭ 由约束条件1132222200,z z EIv R k v lθθ====-=-, 划去1、2、6行列, 将2k 代入[]K 得222223223182060260124666z ql l l v EI ql l l vql l ll θ⎧⎫+-⎡⎤⎪⎪⎢⎥⎪⎪⎧⎫⎢⎥-⎪⎪⎪⎪⎢⎥=⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭--⎪⎪⎢⎥⎪⎪⎢⎥⎣⎦⎩⎭7.3 题a) 写出各杆元对总体坐标之单位刚度矩阵22(1)(3)22000012612600660402E 000012612600660204AA I II I l l l l I I I I l l K K A A l I I I I l l l l I I II l l -⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎡⎤⎡⎤==⎣⎦⎣⎦⎢⎥-⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦(1)(1)(3)(3)(2)(2)(2)222133342l l (2)2223(2)(2)(1)(1)(3)(3)323312114344K K K K K K K K K K K K K K ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤==−−−→==⎢⎥⎣⎦⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦以代[]cos sin 022010sin cos 010022001001t ππππ⎡⎤-⎢⎥-⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦∴[]00t T t ⎡⎤=⎢⎥⎣⎦ [][](1)1(1)(3)K K T K T -⎡⎤⎡⎤⎡⎤==⎣⎦⎣⎦⎢⎥⎣⎦2222000012612600010010100100660402001001010000001010012612610000001001660204AA I II I l l l l I I I I E l l A A l II I I l l l l I I II l l-⎡⎤⎢⎥-⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥-⎢⎥⎣⎦22(3)(3)(1)(1)33342221(3)(3)(1)(1)4344121122126126000000660402126126000000660204I I I I l l l l A A I I I I K K K K E l l I I I I l K K K K l l l l A A I I II ll---⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎢⎥⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦b )集成总刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-------+-----+----+---+-----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡++=I lI Il I A A l I l I lIl I I l I I lI l I I l I A l I A l I l I lI l I l I lI A l I A I l I I lI l I I l Il I l Il I A l I A A l I A l I l I l I Il I I l I A A l I lI l I l IK K K K K K K K K K K K K 40620600006012601220662362300023460234606012602120022306236206234602346000002602126012206406000060126012222222222222)3(44)3(43)3(34)3(33)2(33)2(32)2(23)2(22)1(22)1(21)1(12)1(11c )写出节点位移及外载荷列阵{}{}{}TT z z z z T v u v u v u v u 4321444333222111δδδδθθθθδ==固端力:{}TT Ql Q Ql Q F ⎭⎬⎫⎩⎨⎧-=12201220)1( 局{}{}{}0)3()2(==T T F F 局局{}[]{}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧---=⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡--==12)1()1(1202120212201220100001010100001010T F F Ql Q Ql Q Ql Q Ql Q F F T 局总{}TR yx R y x M R R Ql Q Ql M T Q R P P P P P ⎭⎬⎫⎩⎨⎧-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=44411143210001202122总约束处置⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡++3232)3(33)2(33)2(32)2(23)2(22)1(22P P K K K K K K δδ7.4 题由对称性, 计算图示两个单位即可.但2/12A A =2P 取P/2 045,==⎪⎭⎫⎝⎛∧αx x。
天津大学船舶与海洋工程8结构力学课件第一

天津大学船舶与海洋工程8结构力学课件第一目录•课程介绍与背景•弹性力学基础•杆件结构力学•梁板结构力学•船舶结构力学•海洋工程结构力学•结构优化设计方法•课程总结与展望课程介绍与背景船舶与海洋工程概述船舶工程研究船舶设计、建造、试验和运行的工程领域,涉及船舶总体、船体、轮机、电气等多个方面。
海洋工程以开发利用海洋资源为目标的综合性工程,包括海洋油气开发、海底资源开发、海水淡化、海洋能利用等。
发展趋势随着科技的不断进步,船舶与海洋工程领域正朝着大型化、智能化、绿色环保等方向发展。
结构设计与优化运用结构力学原理进行船舶与海洋工程结构的设计和优化,确保结构的安全性和经济性。
结构强度与稳定性分析通过结构力学方法分析船舶与海洋工程结构在复杂环境中的强度、刚度及稳定性。
结构动力学与振动控制研究结构在动力荷载作用下的响应及振动控制,提高结构的抗振性能。
结构力学在船舶与海洋工程中的应用030201课程内容与教学目标课程内容涵盖结构力学基本概念、静力学、动力学、弹性力学等基础理论及其在船舶与海洋工程中的应用。
教学目标培养学生掌握结构力学基本原理和方法,具备分析和解决船舶与海洋工程结构问题的能力,为从事相关领域的研究和实践打下基础。
弹性力学基础弹性体弹性变形应力应变指在外力作用下能够发生变形,当外力去除后能够完全恢复原来形状的物体。
单位面积上的内力,表示物体内部的受力状态。
弹性体在外力作用下发生的可逆变形。
物体在外力作用下发生的相对变形。
平衡方程表示物体内部各点应力之间必须满足的平衡条件。
几何方程描述物体变形与位移之间的关系。
物理方程表示应力与应变之间的本构关系,即广义胡克定律。
边界条件与圣维南原理边界条件弹性体在边界上必须满足的位移或应力条件。
圣维南原理在弹性力学中,如果外力作用在物体的一小部分边界上,则只在该部分边界附近产生显著的应力集中,而在远离该部分边界的区域,应力分布几乎不受影响。
这一原理为简化复杂弹性力学问题提供了依据。
《船舶结构力学》word版

第一章:绪论1由于船舶经常在航行状态下工作,它所受到的外力是相当复杂的。
这些外力包括船的各种载重〔静载荷〕、水压力、冲击力、以及运动所产生的惯性力〔动载荷〕等。
为了保证船舶在各种受力下都能正常工作,船舶具有一定的强度。
所谓具有一定的强度是指船体构造在正常使用的过程中和一定的年限内具有不破坏或不发生过大变形的才能。
2船体强度包括中拱状态、总纵强度、部分强度、改变强度问题、应力集中问题、低周期疲劳。
3把船舶整体当做空心薄壁梁计算出来的强度就成为船体的总纵强度。
部分强度是指船体的横向构件〔如横梁、肋骨、及肋板等〕一集船体的部分构建〔如船底板、底纵衍等〕在部分载荷作用下的强度。
4船体强度所研究的问题通常包括外力,构造在外力作用下的响应,及内力与变形,以及许用应力确实定等一系列问题。
船舶构造力学只研究船体构造的静力响应,及内力与变形,以及受压构造的稳定性问题,因此,船舶构造力学的首要任务是说明构造力学的根本原理与方法,即说明经典的方法、位移法及能量原理。
5船舶设计与制造是一个综合性很强的行业。
学习本课程不要仅仅满足于会计算船体构造中一些典型构件〔如连续梁、钢架、板架、板〕还应学会解决一般工程构造的计算问题。
6船体构造是由板和骨架等构件组成的空间复杂构造,在进展构造计算之前需要对实际的船体构造加以简化。
简化后的构造图形称为实际构造的理想化图形或计算图形〔又称计算模型或力学模型等〕7构造的计算图形是根据实际构造的受力特征,构建之间的互相影响,计算精度的要求以及所采用的计算方法,计算工具等因素确定的。
因此,对于同一个实际构造,基于不同的考虑就会得出不同的计算图形,对于同一个实际构造,其计算图形不是唯一的,一成不变的。
8首先是船体构造中的板,板是船体的纵、横骨架相连接的,且通常被纵、横骨架划分成许多矩形的板格。
9其次是船体构造中的骨架,船体构造中的骨架无外乎是横向构件—横梁、肋骨、肋板和纵向构件—纵桁、纵骨等,它们大都是细长的型钢或组合型材,故称为“杆件〞或简称为“杆〞。
历年船舶结构力学参考答案及解答

qmn
mx ny sin dxdy a a 16q0 当 m,n=1,3,5„„时 qmn mn 2 4 a2
0
a
b
0
q sin
当 m,n=2,4,6„„时 qm n 0
mx ny sin sin 16q0 Et 3 a a 故 w( x, y ) 2 , D D m1,3,5 n1,3,5 mn[( m ) 2 ( n ) 2 ]2 12(1 2 ) a a
a(sin
2x 2x ) ,满足:v(0)=0,v’(0)=0,v(l)≠0, v’(l)=0 l l
4 l l 1 1 4 4 2 2 16 2 2x 2 sin dx a EI 3 变形能: V EI v dx EI a 0 0 2 2 l4 l l 2 1 l 2 2 3 T v dx a T 2 0 l 4 2
2 EI 6 EI 4 EI l 1 l 2 l 2 v2 0(1处弯矩和为0) m 2 EI 4 EI 6 EI v 4 EI 2 EI 6 EI v ( 0 2处弯矩平衡) 1 2 2 2 3 2 l l l2 l l l2 2 EI 4 EI 6 EI 2 3 2 v2 ( 0 3处弯矩和为0) l l l 6 EI 4 EI 0 4处弯矩和为0) l 4 l 2 v2 ( P 6 EI 6 EI 12 EI v 6 EI 6 EI 12 EI v 2( 6 EI 12 EI v ) ( 0 2处剪力和为0) 1 2 2 2 3 2 4 2 l2 l2 l3 l2 l2 l3 l2 l3
N max I
船舶结构力学习题答案

船舶结构力学习题答案【篇一:船舶结构力学各章思考题】>(摘自习题)(一)绪论1 什么叫做船体总纵弯曲?船体的总纵强度与局部强度有什么区别与联系?2.船体结构中有哪些受压构件?为什么说船在总弯曲时船体受压的构件(主要是中垂状态时的上层甲板)因受压过度而丧生稳定性后,会大大减低船体抵抗总弯曲的能力?3.何谓骨架的带板?带板的宽度(或面积)与什么因素有关,如何确定?试分析带板宽度对骨架断面几何要素的影响。
4.什么叫做船体结构的计算图形,它是用什么原则来确定的?它与真实结构有什么差别?5.一个完整的船体结构计算图形应包含哪些具体内容?为什么对同一船体结构构件,计算图形不是固定的、一成不变的?(二)单跨梁的弯曲理论1 梁弯曲微分方程式是根据什么基本假定导出的,有什么物理意义,适用范围怎样?2 单跨梁初参数法中的四个参数指什么参数?它们与坐标系统的选择有没有关系?3 为什么当单跨梁两端为自由支持与单跨梁两端为弹性支座支持时,在同样外荷重作用下梁梁断面的弯矩和剪力都相等;而当梁两端是刚性固定与梁两端为弹性固定时,在同样外荷重作用下两梁断面的弯矩和剪力都不同?4 梁的边界条件与梁本身的计算长度、剖面几何要素、跨间荷重有没有关系?为什么? 5 当梁的边界点上作用有集中外力p或几种外弯矩m时,一种处理是把该项外力放在梁端,写进边界条件中去。
另一种处理时把该项外力放在梁上,不写进边界条件。
在求解梁的弯曲要素时,两种处理方法的具体过程有哪些不同?最后结果有没有差别?6 梁的弹性支座与弹性固定端各有什么特点?它们与梁本身所受的外荷重(包括大小、方向及分布范围)有没有关系?为什么梁在横弯曲时,横荷重引起的弯曲要素可以用叠加法求出?(三)力法1 什么叫力法?如何建立力法方程式?2 什么是力法的基本结构和基本未知量?基本结构与原结构有什么异同?力法正则方程式的物理意义是什么?3 当连续梁两端为弹性固定时,如何按变形连续条件建立该处的方程?4 力法可否用来计算不可动节点的复杂钢架?如可以,应如何做?5 用力法计算某些支座有限位移的连续梁或平面刚架时应注意什么问题?6 刚架与板架的受力特征和变形特征有何区别?7 何谓梁的固定系数?它与梁端弹性固定端的柔性系数有何不同?(四)位移法1 试举例说明位移法的基本原理。
船舶结构力学

Pre
Next
Exit
11
6、船舶碰撞
★船舶碰撞:船舶之间或船舶与其它海洋结构物
的碰撞,导致船体受损。
Pre
Next
Exit
12
船舶结构力学学习——要掌握在给定的外力作用下如何确定
船体结构中的应力与变形,包括研究受压构件的稳定性问题。
“船舶结构力学”是研究船体结构中板与骨架的强度与 稳定性的科学
★对船体(包括海洋结构物)进行船体结构 设计与强度、稳定性计算。
1 良好的航行性能
船舶 完成
任务 2 良好的工作性能
的 前提
3 具有一定的强度
船舶具有一定的强度,是指船体结构在正常 的使用过程和一定的使用年限中具有不破坏 或不发生过大的变形的能力,以保证船舶能 正常地工作。
Pre
Next Exit
3
传统解船体强度的方法: 静置法
Pre
Next Exit
4
静置法:将船体梁静置于静水和静置于波浪上,然后按静水效应
研究船舶在重力和浮力作用下发生的弯曲变形和应力。
船
第一类载荷为固定载荷,也称常载荷
体
结
包括船体结构自重,主机、辅机、锚机、舵机、救生设备等
构
第二类载荷为变化载荷—随航线及运输任务的不同而变
二、研究内容
阐述问题-《船舶结构力学》研究内容
★研究船舶在外载荷作用下的结构响应(受力与变形)。 ★外载荷:重力、浮力、波浪载荷、冲击力以及惯性力等等。
首要问题
分析船体受力和变形的主要特征
建模: 把船整体当作一根梁
来研究---即船体梁
将“船体梁”’(ship hull girder)静 置于静水中或波浪上,计算在船纵向 (船长方向)分布的重力与浮力作用下 的弯曲变形与应力。
上海交大船舶海洋工程专业历年考研结构力学试题
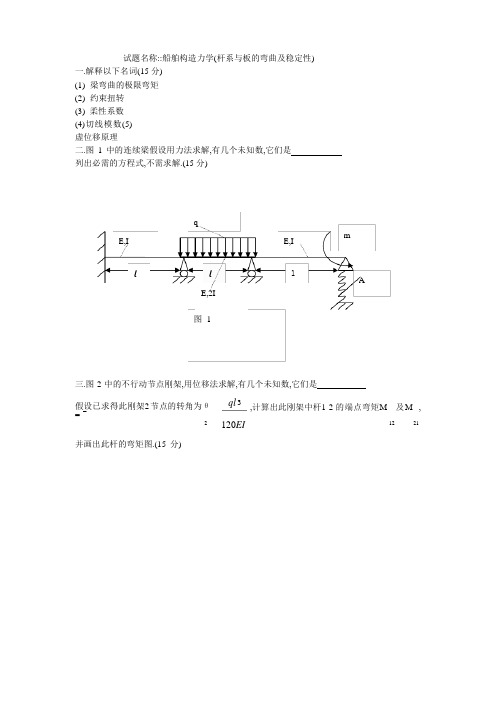
qE,IE,Iml l lAE,2I 图 1试题名称::船舶构造力学(杆系与板的弯曲及稳定性)一.解释以下名词(15 分) (1) 梁弯曲的极限弯矩 (2) 约束扭转 (3) 柔性系数(4)切线模数(5)虚位移原理二.图 1 中的连续梁假设用力法求解,有几个未知数,它们是列出必需的方程式,不需求解.(15 分)三.图 2 中的不行动节点刚架,用位移法求解,有几个未知数,它们是假设已求得此刚架2 节点的转角为θ = -ql 3 ,计算出此刚架中杆1-2 的端点弯矩M 及M ,并画出此杆的弯矩图.(15 分)2120EI12 213 1E,I 2E,I图 2E,I4AEILa E,i图 3 l四.一根穿插构件之板架(图3),在A 点受集中力P 作用,画出此板架的穿插构件作为弹性根底梁的计算图形.求出弹性根底梁的弹性根底刚度及梁上的荷重.(12 分)五.图4 中压杆左端刚性固定,右端的边界状况是:x方向无约束,y方向能移动,但不能发生转动. 试选取适当的基函数后,用里兹法计算此杆的拉力.(12 分)qmO2zxP1b3ay4 EI图 5六.图 5 中之矩形平板,三边自由支持在刚性支座上,第四边支持在一根刚度为 EI 的梁上,板边2 受分布外力矩 m,板厚为 t,材料弹性模数为 E,板中点受一集中力 P 作用,试选择一个满足此板四边位移边界条件的基函数,并写出此板的力函数式子.(11 分)七.图 6 之穿插梁系,l 21= l 23= l 24 = l 25= l ,材料刚度均为 EI,2 处受一集中力 P 作用,且梁1-3 上作用一力矩m=0.1P l ,用位移法求出 2 点挠度,并画出 1-3 弯矩.(4-5 扭转不计)(10 分)T E, Ixl 2ly图 4xaay图 7八.用双三角级数解图 7 中四周自由支持在刚性支座上受均布荷重q 作用的正方形板的中点挠度.板的边长为 a,厚度为 t,材料的弹性模数为 E,板的弯曲微分方程式为 D ▽2▽2ω =q.(D 为弯曲刚度)(10 分)5P13m24图 6试题名称::船舶构造力学(杆系与板的弯曲及稳定性)一. 问答题(15 分)1. 何谓力法,何谓位移法,各有何优劣?2. 何谓应变能,何谓余能,有何区分?3. 表达板弯曲时的根本假定.4. 何谓刚性板,柔性板,正交异性板?5. 为什么在压杆失稳时只能求出失稳时的临界力,而不能确定失稳时的变形值? 二. 画出下面两个单跨梁的弯矩图及剪力图.(16 分) 图 2 中的梁在仅受三角形分布荷重时的最大弯矩值为0.0642q l 2 ,发生在距梁左端0.577 l 处.三.在图 2 中梁的截面为工字钢,尺寸如图 3,试指出此梁的最大正应力和最大剪应力所在截面,并分别算出该截面上的正应力及剪应力分布及数值.(14 分)Al 2Pl 2P = 2kN , q = 1kN / m l = 2m , A = 1cm / kN图 1图 2lMM21qM = 0.8kN ⋅ m , M 12= 0.5kN ⋅ mq = 3kN / m , l = 1.6mq四.试用位移法解图 4 中的简单刚架,列出必需的方程式,不必求解算出结果.:刚架中杆 1-2,2-3,2-4 的长度均为l ,截面惯性矩均为I.(12 分)注(1)两端刚性固定梁,受均布荷重q 时的固端弯矩值为ql 212 .Pl (2)两端刚性固定梁,在跨中受集中力P 时的固端弯矩值为 8.( l 为梁长)五.试用 Ritz 法求解四周自由支持的刚性板的弯曲(图 5),板厚为 t,板的弯曲刚度为 D,板在 C 点处作用一集中力矩m,,计算时级数取一项.(15 分)3qP1l 224图 4图 3100161220016100x六.四周自由支持的刚性板,单向受压(图 6),板厚为t,板的弯曲刚度为D,边长比a/b=3,试求: (1)板失稳时的临界应力.(2)板失稳时的外形,沿x 方向及y 方向的半波数.(15 分)七.图7 中之桁架构造,受集中力P 作用而变形,设材料的应力-应变关系为σ=β ,试求出此构造的应变能及余能.两杆长度均为l,断面积均为A.(13 分)σxbσxa图 6yzOξxηmC by az图 5ε4545P图7θ1θ2EIx1∆2yL 图 1上海交通大学一九九二年争论生入学考试试题试题名称: 船舶构造力学(杆系与板的弯曲及稳定性) 留意:本试卷共有六大题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§8-1 概述
船体结构中有不少受压杆件,除了一些明显受压的 支柱外,还有沿纵向布置的骨架和被纵横骨架支持的 矩形板格。这是因为整个船体在波浪上发生弯曲时, 纵向骨架和矩形板格都会受到拉力或压力,在受压的 情况下都可能发生失稳。现在船舶建造规范都规定: 必须校核船体板格的局部曲曲问题。根据船舶结构实 际情况,甲板骨架和甲板板格失稳的可能性比船底大 的多。因此本章主要研究杆系和板格的稳定性。
c2 coskl c3 sinkl 0
1 0 D 1 0
0 1 kl AEIk 3 0
1 0 0
c oskl
0 1
0 0
s in kl
§8-2 单跨压杆稳定性
展开后,整理得稳定性方程式;
tgkห้องสมุดไป่ตู้ kl AEIk 3 kl 1 kl3
3
40
30
20
Kl=2.2036
10
0
-10
-20
相应于压杆的直线平衡
c1 c3 0
位置,不是具有微弯曲 的中性平衡位置。
我们需要的是齐次方程组的非零解。
§8-2 单跨压杆稳定性
齐次方程组有非零解的充分必要条件是系数矩阵
行列式的值等于零。
kl sinkl
D 0
k2 sinkl 0
展开行列式,得到压杆的稳定性方程。
k3l sinkl 0,sinkl 0
§8-2 单跨压杆稳定性
2.能量法(李慈法)
在比较复杂的情况下,用上述解析法确定压杆的 欧拉力常常遇到困难。在这些情况下,常采用便于 计算的能量法来求欧拉力的近似值
中性平衡状态除了用微分方程来描述外,还可用 位能驻值原理:
V U 0
(8-6)
来描述。不过,此时总位能的驻值不是最小值,而 是中性值(2=0),这将在例题中加以说明。
第八章 杆及板的稳定性
Stability of Column and Plate
§8-1 概述
稳定平衡 中性平衡 失稳或屈曲 临界压力
T
T
(a)
(b)
图8-1
§8-1 概述
稳定平衡 中性平衡 失稳或屈曲 临界压力
§8-1 概述
其它结构也存在稳定性现象
图8-2
§8-1 概述
其它结构也存在稳定性现象
kl n
n 1,2,3,...
代入(8-3)式。
T
n 2
l2
EI
n 1,2,3,...
§8-2 单跨压杆稳定性
最小临界压力: Te
2 EI
l2
kl n
由式(a)
c1 0, c3 0
欧拉力 (8-4)
杆失稳形状为
v
c3
sin
x
l
对于某些杆系结构,如图8-4所示,可将其中某
一杆件取出,而以弹性支座或弹性固定端代替其余部
§8-2 单跨压杆稳定性
由式(8-2)得到CD压杆的相应于Te的失稳形状;
v
c2
1
tg
x l
cos
x
l
1
tg
sin
x
l
式中,α=kl=2.2036。注意,图8-4a中AB杆的 挠曲线不等于CD杆的失稳形状,它是悬臂梁端点受 集中载荷的挠曲线。
由上述两例可知:用解析法确定单跨压杆的欧拉 力时,有以下几个步骤:
图8-2
研究结构的稳定性就是要求出结构的临界压力或临 界载荷。在一般情况下,当载荷达到最小临界值时, 结构已不能正常工作,故从实用的角度来说,最重要 的就是要求出临界载荷。在研究结构的稳定性时,可 先假定所研究的结构处于中性平衡状态,对于压杆来 说,就是具有微小弯曲的平衡状态,满足此条件的最 小载荷即为临界载荷
§8-2 单跨压杆稳定性
(1)确定代求问题的位移边界条件
(2)将式(8-2)代入到边界条件中,得出关于
积分常数的齐次方程组;
(3)令其系数行列式等于零;
(4)展开行列式,得到压杆稳定性方程式;
(5)求解最小正根rmin,得到欧拉力.
rmin l
Te EI
T
rm2in EI l2
(8-5)
对于各种边界条件下的等截面单跨压杆,其欧拉 力都可用上述方法求得,并在有关手册中查到。 表8-1给出几种固定情况的等截面单跨压杆的欧拉 力。
例1:确定两端自由支持压杆(图8-3)的临界压力Te 和相应的失稳形状。
T
T
x
B
l
图8-3
y
§8-2 单跨压杆稳定性
解:在图示坐标系下,边界条件为
x 0, x l, v v 0
将式(8-2)代入这四个边界条件,得:
c0 c2 0
及
c1kl c3 sinkl 0
c3k 2 sinkl 0
A l3 3EI
在图8-5所示坐标系下,边界条件为
x 0,v v 0
x l, v AEIv Tv, v 0
y
图8-5
§8-2 单跨压杆稳定性
将式(8-2)代入上述边界条件,注意式(8-3),
简化后得齐次方程组;
c0 c2 0
c1 c3 0
c0 c1 kl AEIk 3 0
分对它的作用,同时由其余部分求出弹性支座或弹性
固定端柔性系数,然后再按单跨压杆来求临界压力。
§8-2 单跨压杆稳定性
图8-4
例2:试求(图8-4a)所示结构临界压力Te以及相应 的失稳形状。
§8-2 单跨压杆稳定性
解:取出结构中受压杆CD,它是下端刚性固定,上端 弹性支持的压杆(图8-5)。确定弹性支座的柔性系 数时,需在结构的其余部分DBA的B点沿水平方向加 上单位力,求出AB杆端B点的水平位移,其值就是 柔性系数A。查弯曲要素表,得: x
对于单跨压杆的稳定性,将在材料力学的基础上作 更全面的介绍。
§8-1 概述
稳定平衡 中性平衡 失稳或屈曲 临界压力
§8-1 概述
稳定平衡 中性平衡 失稳或屈曲 临界压力
§8-2 单跨压杆稳定性
确定结构临界载荷的方法很多,其中最基本和最重 要的是解析法和能量法。
1.解析法
通过直接求解结构的中性平衡微分方程确定结构临 界载荷。
对于等截面压杆,可以通过等截面直梁的复杂弯曲
微分方程得到:
EIv IV Tv q
(8-1)
通解为:
v A1 A2 x A3chkx A4shkx (8-2)
§8-2 单跨压杆稳定性
k T
(8-3)
EI
对c0、c1、c2、c3—积分常数。将式(8-2)代入压杆两 端的边界条件即可求出压杆的临界压力。
图8-6
-30
-40
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
§8-2 单跨压杆稳定性
由式(8-3)求得临界压力;
Te
4.8559 EI l2
0.492 2 EI
l2
将
tgkl kl AEIk 3 kl 1 kl3
3
代入式(b)
c0 c2, c1 c2 tgkl, c3 c2 tgkl
