条件平差程序
水准网条件平差程序设计毕业论文
本科生毕业设计说明书（毕业论文）题目：水准网条件平差程序设计学生姓名：房新明学号：1072143138专业：测绘工程班级：测绘10-1班指导教师：郭义水准网条件平差程序设计摘要近年来，随着我国经济的快速发展，国家大力于投资各种铁路建设和公路建设，测绘工程的运用也越来越突出。
以水准网布设的高程控制网在各类工程中随处可见。
但观测到的数据存在着各种各样的误差，这就需要我们通过简易平差或严密平差来对数据进行处理，从而使数据能够达到工程的预期精度。
本文主要研究如何解决绘图软件行业标准的网络数据处理问题。
从水准网的结构，平差基本原理、调整模型，基本方程及其解，并对法方程组成，求解，平差值的计算及其精度评定作了介绍。
和Visual studio6.0编程软件的利用，利用C语言是程序设计的相干事情。
在今后的测量工作中，可结合实际平差方案进行平差计算。
关键词：平差模型；精度评定；程序设计Leveling Network Adjustment Program DesignAbstractIn recent years, with China's rapid economic development, the state vigorously investment in all kinds of railway construction and road construction, the use of mapping project is also more and more prominent. In order to control the network level network in various engineering in everywhere. But the observed data exist various error, this needs us through simple adjustment or rigorous adjustment for data processing, so that data to achieve the desired precision engineering.This paper mainly studies how to solve the problem of mapping software industry standard network data processing. From the structure adjustment of leveling network, the basic principle, adjustment model, basic equation and its solution, and the composition of the solution of equations, adjustment calculation and precision evaluation, gross error elimination are introduced as well. And the use of Visual Studio6.0 programming software, using C programming language is related to program design. The measurement work in the future, can be combined with the actual adjustment adjustment calculation.Key words: adjustment model；the accuracy assessment；program design目录摘要 (I)Abstract .......................................................................................................................... I I 第一章绪论 (1)1.1研究背景及意义 (1)1.2国内外研究现状 (2)1.3本文研究的具体内容 (2)第二章条件平差数学模型 (3)2.1条件平差模型 (3)2.1.2测角网条件方程 (6)2.1.3测边网条件方程 (8)2.1.4以坐标为观测值的条件方程 (11)2.2精度评定 (13)2.3条件平差的计算步骤 (17)第三章水准网的设计 (18)3.1水准测量 (18)3.1.1水准网的基本概念 (18)3.2水准网的布设 (19)3.2.1国家水准网的布设 (19)3.2.2水准网的布设要求 (20)第四章C语言介绍 (21)4.1C语言的基本概念 (21)4.2C语言的介绍 (22)4.2.1C语言的特点 (22)第五章程序设计 (24)5.1水准网条件平差和测角网条件平差实例 (24)5.1.1水准网条件平差 (24)5.1.2测角网条件平差 (27)5.2程序代码 (32)参考文献 (57)附录A：外文文献 (58)附录B：中文译文 (70)致谢 (76)第一章绪论1.1研究背景及意义施工测量工作是非常基本的，重要环节。
条件平差原理
§9.1 条件平差原理在条件观测平差中，以n 个观测值的平差值1ˆ⨯n L 作为未知数，列出v 个未知数的条件式，在min =PV V T 情况下，用条件极值的方法求出一组v 值，进而求出平差值。
9.1.1基础方程和它的解设某平差问题，有n 个带有相互独立的正态随机误差的观测值 ，其相应的权阵为 ， 它是对角阵，改正数为 ，平差值为 。
当有r 个多余观测时，则平差值 应满足r 个平差值条件方程为：⎪⎪⎭⎪⎪⎬⎫=++++=++++=++++0ˆˆˆ0ˆˆˆ0ˆˆˆ221122112211οοοr L r L r L r b L b L b L b a L a L a L a n n n n n n （9-1） 式中i a 、i b 、…i r （i =1、2、…n ）——为条件方程的系数；0a 、0b 、…0r ——为条件方程的常项数以ii i v L L +=ˆ（i =1、2、…n ）代入(9-1)得条件方程（9-2）式中a w 、b w 、……r w 为条件方程的闭合差，或称为条件方程的不符值，即（9-3） 令⎪⎪⎪⎪⎪⎭⎫⎝⎛=⨯n n n n r r r r b b b a a a A212121⎪⎪⎭⎪⎪⎬⎫++⋅⋅⋅++=++⋅⋅⋅++=++++=022110221102211r L r L r L r w b L b L b L b w a L a L a L a w n n n n n b n n a ⎪⎪⎭⎪⎪⎬⎫=++⋅⋅⋅++=++⋅⋅⋅++=++⋅⋅⋅++000221122112211r n n b n n a n n w v r v r v r w v b v b v b w v a v a v a ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L 211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯n n L L L L ˆˆˆˆ2111⨯n L nn P ⨯1⨯n V 1ˆ⨯n L 1ˆ⨯n L则(9-1)及（9-2）上两式的矩阵表达式为0ˆ0=+A LA （9-4） 0=+W AV （9-5）上改正数条件方程式中V 的解不是唯一的解，根据最小二乘原理，在V 的无穷多组解中，取PV V T = 最小的一组解是唯一的，V 的这一组解，可用拉格朗日乘数法解出。
1-2条件平差原理--条件平差的计算步骤
得： 3ka 9 0
3.步骤三
依据
K
N
W 1
aa
计算出联系数K。
解法方程得： ka 3
C
L3
L1
A
L2
B
三角形示例图
条件平差的计算步骤
4.步骤四
由式 V P 1 AT K 计算出观测值改正数，并依据式 Lˆ L V
出观测值的平差值。
计算
1 0 0 1
Lˆ3
L3
v3
731234
条件平差的计算步骤
5.步骤五
为了检查平差计算的正确性，将平差值待入平差值条件方程式 ALˆ A0 0 ，
看是否满足方程式关系。
583115 481611 731234 180 0
3
V P1AT K 0 1 0 1 3 3
0 0 1 1
3
Lˆ1 Lˆ2
L1
L2
v1 v2
583115 481611
条件平差的计算步骤
1.步骤一
根据实际问题，确定几何模型的总观测值的个数 n，必要观测值的个数 t 及
多余观测值的个数 r=n-t，进一步列出平差值条件方程 ALˆ A0 0 或改正数条 件方程 AV W 0 。
C
L3
L1
A
L2
B
三角形示例图
以确定三角形的形状为例，对三角形中的三个 内角等精度观测，得观测值如下： L1=58°31′12″，L2=48°16′08″，L3=73°12′31″，试用条 件平差法，计算三角形各内角的平差值。
第3讲(三角网条件平差
第三章 条件平差
第四节
二、条件方程的列立 条件方程的种类：图形条件（内角和条件）、水平条件（圆周条件）、极条件、 条件方程的种类：图形条件（内角和条件）、水平条件（圆周条件）、极条件、 ）、水平条件 ）、极条件 方位角条件、边长条件、坐标条件。 方位角条件、边长条件、坐标条件。 1. 图形条件(n=15 图形条件(n=15 t=8 r=7 哪7个？) 每个三角形内角平差值和等于180 每个三角形内角平差值和等于180
sin L1 sin L4 sin L7 sin L10 sin L13 sin L1 sin L4 sin L7 sin L10 sin L13 v v cot L1 1 − cot L2 2 sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′ sin L2 sin L5 sin L8 sin L11 sin L14 ρ ′′
第三章 条件平差
第四节
三角网平差的目的 求待定点平面坐标平差值， 求待定点平面坐标平差值，并进行精度 评定。 评定。 三角网件方程个数等于多余观测个数。 条件方程个数等于多余观测个数。
r=nr=n-t
测角网、测边网、边角同测网。无 关键在于确定必要观测个数 t 。 测角网、测边网、边角同测网。 论网型多么复杂， 论网型多么复杂，都是由三角形和 大地四边形相互邻接或重叠而组成。 当网中有2个或2 大地四边形相互邻接或重叠而组成。 1.当网中有2个或2个以上已知点时 t=2 t=2倍待定点数 当网中仅具备4个必要起算数据（ 当网中仅具备4个必要起算数据（一点 坐标、一条边的方位、 坐标、一条边的方位、一条边的边 2.当网中少于2个已知点时 当网中少于2 长或已知两点坐标） 称为自由 长或已知两点坐标）时，称为自由 这四个数据成为必要起算数据。 网。这四个数据成为必要起算数据。 （1）测角网 t=2倍总点数t=2倍总点数-4 多余四个必要起算数据时，成为非自由 多余四个必要起算数据时，成为非自由 网。 （2）测边或边角网 t=2倍总点数t=2倍总点数-3
水准网的条件平差
目录目录 (1)观测误差 (2)摘要： (2)关键词： (2)引言 (3)1水准测量 (4)1.1水准测量的原理 .............................................................................. •1.2水准网...................................................................................... •2条件平差 .. (6)2.1 衡量精度的指标 (6)2.2条件平差的原理 .............................................................................. •3水准网的平差 .. (14)3.1必要观测与多余观测 (14)3.2条件方程 (14)3.3条件平差法方程式 (14)3.4条件平差的精度评定 (15)3.5水准网的条件平差 (18)致谢 (20)参考文献 (21)观测误差由观测者、外界环境引起的偶然误差学生：xxx 指导教师：xxx摘要:对一系列带有偶然误差的观测值，采用合理的的方法消除它们间的不符值，得出未知量的最可靠值；以及评定测量成果的精度。
关键词:偶然误差；观测值；精度引言测量工作中，要确定地面点的空间位置，就必须进行高程测量，确定地面点的高程。
几何水准测量是高程测量中最基本、最精密的一种方法。
通过测量仪器，工具等任何手段获得的以数字形式表示的空间信息，即观测量。
然而，测量是一个有变化的过程，受仪器、观测值、外界环境因素的影响，观测的结果与客观上存在的一个能反映其真正大小的数值，即真值（理论值），有一定的差异。
可以说在测量中产生误差是不可避免的。
所以，观测值不能准确得到，在测量上称这种差异为观测误差。
根据其对观测结果影响的性质，可将误差分为系统误差和偶然误差两种。
第三章条件平差
独立三角网
自由三角网
自由测角网
附合三角网（测角）
• 例：
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时，其条件式个数各为多 少？有哪些类型？
图形条件（内角和条件）:
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件（水平条件）:
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
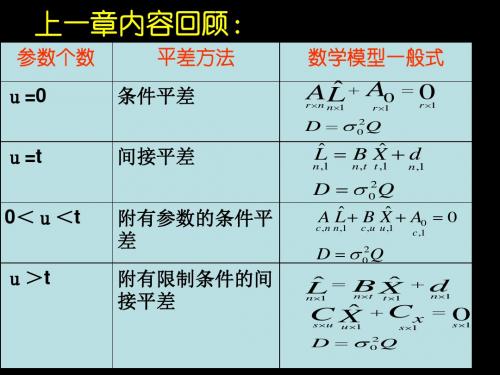
上节内容回顾：
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成：
ˆA 0 AL 0
• 以及改正数条件式：
W AL A0
AV W 0
这样一来，对于一个平差问题，我们能够得到 其数学模型：
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是： 由上述的数学模型来求改正数V。
不难发现，不能求得V的唯一解！！！ 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足：
极条件（边长条件）:
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件（边长条件）就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1） 单三角形 2）大地四边形
3）中点多边形。
第五章条件平差
二、法方程及改正数方程
将V T PV min的原则作用于条件方程 。
组成新函数:
V T PV－2k T AV W
式中
r 1
k k a , kb , k r 条件方程联系数
T
对新函数求导： T T 2V P 2A k ---改正数方程
dSCD ˆ f T dL SCD ˆ SCD T 2 T ˆ f D f f QL ˆL ˆ ˆL ˆ f 0 L S CD
得测边相对中误差为： 3、大地四边形测角网
2
ˆS
CD
SCD
＝
ˆ 0 f T QL ˆL ˆ f
设
F ( f1 , f 2 , f m )
T T
G ( g1 , g 2 , g m ) 有
均为m维向量函数，且 f i、g i 均为x的函数， d F G dG F T dG T dF F G dx dx dx dx
注意：当N为满秩方阵时，才有 N 1唯一存在,法方程才有唯
测方向网
测角网
测角网
三角网
测边网
测边长
测边＋测方向
边角网
（导线网） 测边＋测角
三、三角网的布设－－从高级到低级逐级布设 四、三角网平差的方法 1。严密平差 ----遵守VTPV=min原则 ； 2。近似平差
5.3 测角网条件平差
独立网（经典自由网）－-－只有必要起算数据d。
非独立网（附合网）－-－已知条件超过必要起算数据。
3 图形条件： n=12 t=2×2+4=8 r =4 1 极条件：
v2 v1 v6 v5 v11 v10 W1 0
6 第五章 条件平差
三角网的基本图形构成
单三角形； 大地四边形； 中点多边形
30
§2 条件方程
二.三角网 1.独立测角网条件方程
测角网的观测值
测角网的观测值很简单,全部是角度观测值
测角网的作用
确定待定点的平面坐标
测角网的基准
位置基准2个(任意一点坐标X0Y0) 方位基准1个(任意一边方位角α0) 长度基准1个(任意一边的边长S0)
Av f 0
V PV min
T
在满足 Av f 0 的条件下，
求函数 V PV min 的V值
T
条件 极值 问题
4
§1 条件平差原理 条件平差的步骤
5
§1 条件平差原理
列条件方程 观测值权阵
最小二乘原则
求唯一解
6
§1 条件平差原理 一.基础方程及其解
r个线性条件方程：
3 ka 3 k 2 0 6 b
写成矩阵形式：
(2)定权： 100米量距为单位权：Pi=100/Si
1/Pi=Si/100 1/P1=2， 3=3， 1/P 1/P2=3， 4=5， 1/P
2 0 Q 0 0 0 3 0 0 0 0 3 0 0 0 0 5
AV f 0 PLL diag p1 p2 p4
组、解法方程： AQAT K f 0
由改正数方程求： V P A K
T 1
ˆ 求平差值： L L V
15
§1 条件平差原理 二.条件平差的求解步骤及示例
条件平差计算步骤
16
§1 条件平差原理
例：
r 1
r 1
r个改正数条件式：
a1v1 a2 v2 an vn wa 0 b1v1 b2 v2 bn vn wb 0 r1v1 r2 v2 rn vn wr 0
1-1条件平差原理--求取最或是值
V P 1 AT K
Lˆ L V
理论
感谢聆听，批评指导
公式
思考
平差
算例
转置
PTV AT K
两边左乘权逆阵P–1 V P 1 AT K
条件平差的平差值求取原理（第一任务）
2.基础方程
3.法方程
条件平差的基础方程
AV W 0
令
V P 1 AT K
构法方程
将改正数方程带入条件方程，得
AP 1 AT K W 0
令令
N aa AP 1 AT
1.条件方程
纯量形式
ab11LLˆˆ11 ab22LLˆˆ22 bannLLˆˆnnba0000 r1Lˆ1 r2Lˆ2 rnLˆn r0 0
带入
Lˆi Li vi
令
ALˆ A0 0
平差值条件方程
条件平差是经典平差的重要方法之一，其实质是观测值的改正数在满足一定条 件下，求改正数带权平方和的极值问题，可采用拉格朗日乘任务）
1.条件方程
设在某个测量几何模型中，必要观测数为 t ，观测了 n 个只含偶然误差的独立观测值 ，相应的权为 p1、p2、...、pn ，改正数 v1、v2、...、vn 、平差值 Lˆ1、Lˆ2、、Lˆn 。
将它们用向量（矩阵）表示为：
L1
L
L2
n,1
Ln
v1
V
v2
n,1
vn
p1
P
n,n
0
0
0 0
p2
0
附合导线严密平差算法总结
附合导线严密平差算法总结图1如图的单一附合导线，有4个已知点A、B、C、D，2个未知点TP1、TP2。
设观测边数为n, 则未知点数为n-1, 观测角数为n+1。
以上图为例，n = 3。
观测边为：S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路：由于A、B坐标已知，则可以算出起始方位角，再根据B点坐标和每个观测角（夹角，左角）推算出TP1、TP2、C点的近似坐标值。
如果是用全站仪进行测量，则用盘左盘右重复观测求平均的方式，直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。
再根据c点的已知坐标与近似坐标求坐标闭合差，由CD的已知方位角和近似方位角求角度闭合差，两个闭合差联立求得边长和角度的改正数，最后求得未知点的坐标平差值。
条件平差过程：1.建立条件方程，求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下：1、建立条件方程在单一附合导线中，只需要三个条件方程即：方位角附合条件、纵坐标附合条件和横坐标附合条件方程。
（省略了条件方程的推导过程，详细过程请查看参考资料：《测量平差.pps》）（1）方位角附合条件[Vβi]n+11+ Wβ= 0式中，Wβ= - （T0– T CD+ [βi]n+11 - （n+1）*180°）（角度闭合差）βi ——角度观测值（夹角，左角）Vβi ——各观测角的改正数。
如果是用全站仪观测，则Wβ= - （T CD– T CD）式中，T CD ——CD的方位角观测值，T CD ——CD的已知方位角（2）纵坐标X附合条件方程[Cos TI * VSi]1n - （1/ ρ”）* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值（近似值）Yi——待定点的横坐标Y的观测值Wx = - （Xn+1- XC）XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65（3）横坐标Y附合条件方程[Sin TI * VSi]1n + （1/ ρ”）* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中，TI——各方位角观测值（近似值）VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值（近似值）Xi——待定点的纵坐标X的观测值WX = - （Yn+1- YC）YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组：[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为：（即改正数V的系数，此处以图1为例， n = 3）3、联系数法方程（简称法方程）AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N：N = AP-1A T（权的推导见参考资料：《全站仪观测导线测量平差方法的研究.pdf》）角度权：P βi = 1；（因为角度的标称精度是固定的，各观测角权值相等） 边长权：P Si = (μ0 *μ0 ) / （M D * M D ）（误差比例系数固定，边长的误差与距离有关，因此不一致）式中，μ0 ——先验测角中误差，以秒为单位 M D —— 距离观测中误差若 导线边长为S i （米），e1 为仪器的边长标称固定误差（mm ），e2为仪器的边长比例误差系数（无单位），则M D = ± （e1 + e2 * S i * 0.001）mm 需转化为厘米：M D = M D ** 0.1 （cm ）由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数（P 是对角矩阵，对角矩阵的逆矩阵就是原矩阵元素的倒数） Psi = 1/ Psi ；由上可得，P -1 矩阵如下：4、求改正数由于N 已经在前面的步骤中求出，求N 的逆矩阵。
用MATLAB解决 条件平差和间接平差
C h6 E h3 h5 h7 B h4
disp(‘C是单位权观测高差的线路公里数，S是线路长度’) 是单位权观测高差的线路公里数， 是线路长度 是线路长度’ 是单位权观测高差的线路公里数 C = l*ones(1,6)
S = [1.1, 1.7, 2.3, 2.7, 2.4, 4.0] P = C./S % 定义观测值的权， 定义观测值的权， P = diag(P) % 定义权阵 disp(‘参数的解’) 参数的解’ 参数的解 x = inv(B’*P*B)*B’*P*l disp(‘误差 误差V(mm), 各待定点的高程平差值 （m）’) 各待定点的高程平差值L1（ ） 误差 V = B*x - l % 误差方程 误差方程(mm) L1 = L + V/1000 % 观测值的平差值， 观测值的平差值， disp(‘精度评定’) 精度评定’ 精度评定 n = 6; % 观测值的个数 t = 2; % 必要观测数 delta = sqrt(V’*P*V/(n – t))
H(1,1)+H(2,1)-H(3,1)+HAH(2,1)if H(1,1)+H(2,1)-H(3,1)+HA-HB==0 && H(2,1)H(4,1)==0 disp(‘检核正确 检核正确') disp( 检核正确') else disp(‘检核错误 检核错误') disp( 检核错误') end disp(‘平差后的高程值 平差后的高程值') disp( 平差后的高程值') HC = HA + H(1,1) HD = HA + H(1,1) + H(4,1)
二、间接平差的基本原理
在一个控制网中，设有t个独立参数， 在一个控制网中，设有t个独立参数，将每一个观测值都表达 成所选参数的函数，以此为基础进行平差， 成所选参数的函数，以此为基础进行平差，最终求得参数的估 计值。 计值。 选择参数应做到足数（参数的个数等于必要观测数）和独 选择参数应做到足数（参数的个数等于必要观测数） 参数间不存在函数关系）。 ）。利用参数将观测值表示为 立（参数间不存在函数关系）。利用参数将观测值表示为
第三章 条件平差
返回目录 返回本节
经化简即有
cv t c g v ta c gv t a c g v t a c g v t b c g v tb g b
1 a 1
2 a 2
3 a 3
1 b 1
2 b 1
33
(1
sina1 sinb1
sina2 sinb2
sina3)
sinb3
=0,
圆周条件，即
c ˆ1c ˆ2c ˆ336 o0
或
V V V W 0
c1
c2
c3
4
第三类是极条件或称边长条件。满足上述4个条件方程
的角值还不能使图3-5的几何图形完全闭合，例如，由边
长通过a2、b2、c2计算边长，通过a1、b1、c1由计算边长，
再由通过a3、b3、c3计算边长，计算的结果，其边长不会
(3-21)
这就是极条件（3-20）的线性形式。
三、测边网
和测角同一样，在测边网中也可分解为三角形，大地 四边形和中点多边形三种基本图形。对于测边三角形，决 定其形状和大小的必要观测为三条边长。所以t=3，此时 r=n-t=3-3=0，即测边三角形不存在的条件方程。对于测边 四边形，决定第一个三角形必须观测3条边长，决定第二 个三角形只需要再增加2条边长，所以确定一个四边形的 图形，必须观测5条边长，即t=5，所以r=n-t=6-5=1，存在 一个条件方程。对于中点多边形，例如中点五边形，它由 四个独立三角形组成，此t=3+2×3=9，故有r=n-t=10-9=1。
法，将上式用台劳公式展开取至次项，即可得线性形式的
极条件方程。
将 a ˆ a v,b ˆ b v,c ˆ c v代入（3-20）式，
第五章 条件平差
v1 v V 2 n ,1 vn
W AL A0
则相应方程的矩阵表达式分别为
AV W 0
第五章：条件平差
3. 基础方程
按求函数极值的拉格朗日乘数法，设乘数 联系数向量。组成函数 将 φ 对V 求一阶导数，并令其为零，得
r , n n ,1
A V W 0 ——改正数条件方程 r ,1
W AL A0 —改正数条件方程常数项（闭合差）计算式
第五章：条件平差
例题 ：右图中L1、L2、L3为观测角度， 试列出该图形的条件方程和改正数条件方 程。 解：t=2, r=n-t=3-2=1 条件方程:
ˆ L ˆ L ˆ 180 0 L 1 2 3
试列出条件方程 解：t=2p-q-4=4，r=n-t=9-4=5 条件方程为：
ˆ L ˆ L ˆ 1800 0 L 1 2 3 ˆ L ˆ L ˆ 1800 0 L 4 5 6 ˆ L ˆ L ˆ 1800 0 L
7 8 9
ˆ L ˆ L ˆ 3600 0 L 3 6 9 ˆ sin L ˆ sin L ˆ sinL 1 4 7 1 ˆ ˆ ˆ sinL sin L sin L
第五章：条件平差
4.基础方程的解
将改正数方程代入改正数条件方程，得
AQAT K W 0
令 则有
N aa AQAT AP1 AT
N aa K W 0 ——联系数法方程
秩 RN aa RAQAT RA r ，即 N aa 是个r阶的满秩方阵，由此 可解出
试按条件平差法求C、D点高程的平差值。 解：此例 n=4，t=2，r=n-t=2，可列出两个条件方程。 （1）列条件方程：
5-条件平差.
0 0 s3 0
0 2 0 0 0 0 s4 0
0 1 0 0 0 2 0 0 0 1.5 0 0
§5-1 条件平差原理
二、条件平差步骤及示例
5、组成法方程，求联系数K
2 0 0 1 1 1 0 0 1 0 1 T AP A 0 1 0 1 0 0 2 0 0 0 0 1 0 0 1 1 5 0 1 0 1 1.5 平差步骤及示例
4、确定观测值的权，令C=1，则由定权公式
C 1 pi Si Si
有
p11 0 P 1 0 0
0
1 p2
0 0
1 p3
0 0
0
0 s 0 1 0 0 s2 0 0 0 1 0 0 p4
解：此例n=4，t = 2，r = n-t= 2，可列出两个条件方程。 1、列条件方程：
ˆ h ˆ h ˆ H H 0 h 1 2 3 A B ˆ ˆ h h 0 2 4
h1
C
h4
D
h3
B
h2
A
§5-1 条件平差原理
二、条件平差步骤及示例
2、计算改正数条件方程闭合差
§5-1 条件平差原理
一、基础方程及其解
改正数条件方程
r ,n n ,1
AV W 0
r ,1
改正数条件方程（纯量方程）
a1v1 a2 v 2 ... an vn wa 0 b v b v ... b v w 0 1 1 2 2 n n b ... ... ... r1 v1 r2 v 2 ... rn vn wr 0
课件：第3章第1讲(条件平差原理)
ALˆ A0 0
AV W 0
(2)组成法方程； NK W 0
N AP1AT
(3)计算联系数K； K N 1W
三、解题步骤
(4)计算观测值改正数V ；
V P1 AT K
(5)计算观测值的平差值；
Lˆ L V
(6)检查平差计算的正确性，将平差值代入平差值 条件方程式，检验是否满足方程关系；
法方程的解： K N 1W
平差值： Lˆ L V
aa p
k
a
ab p
k
b
ar p
k
r
wa
0
apbk
a
bb
p
kb
br p
k
r
wb
0
ar
p
ka
br p
k
b
rr
p
kr
wr
0
二、精度评定
1. 单位权中误差的计算
ˆ 0
V T PV r
b0
0
a1v1 a2v2 anvn wa 0 b1v1 b2v2 bnvnwb0 r1v1 r2v2 rnvn wr 0
r1 Lˆ1
r2 Lˆ2
rn Lˆn
r0
0
wa (a1L1 a2 L2 an Ln a0 )
wb (b1L1 b2 L2 bn Ln b0
函数模型
W (AL A0 )
一、条件平差原理
AV W 0 按求函数极值的拉格朗日乘数法组成新函数
V T PV 2K T (AV W) 将Φ对V求导并令一阶导数为零：
K为乘系数（联系数）
K
r ,1
[ka
kb
kr ]T
d (V T PV) 2 (K T AV) 2V T P 2K T A 0
第六章 附有参数的条件平差
问题：如何计算平差值函数的中误差？
X
C
2
§6-2 精度评定
ˆ 设有平差值函数：
对上式全微分得：
ˆ d ˆ ˆ ˆ FxT dX ˆ dL dX F T dL ˆ ˆ L X
权函数式
ˆ, X ˆ) ( L
n ,1 u ,1
0
ˆ L
1 T QAT N 1BN 1 QAT N aa BQXX B aa bb ˆˆ
0
0
Q QVV
( N aa AQAT
1 N bb BT N aa B)
§6-2 精度评定
三、平差值函数的中误差
ˆ L ˆ L ˆ L ˆ ˆ1 180 X 8 6 1 ˆ ˆ2 S BD ˆ L ˆ L ˆ L ˆ) sin(180 X 8 6 1 S AB ˆ L ˆ) sin(L 6 8
c ,1
组成法方程式。
ˆ W 0 N aa K Bx T (式中Naa AQAT） B K 0
Байду номын сангаас
§6-1 附有参数的条件平差原理
解算法方程。
1 T 1 ˆ Nbb x B N aaW 1 ˆ K N aa ( Bx W ) T T 1 ˆ V QA K QA N aa ( Bx W )
L4
C
L3
ˆ W 0 N aa K Bx T B K 0
(式中Naa AQAT）
L1
A
L2
B
§6-1 附有参数的条件平差原理
3 1 1 0 1 1 ka 0 wa 3 k 0 x w 0 ˆ 2 0 1 b b kc 1 wc 0 1 1 ka 0 0 1 kb 0 kc
条件平差
1
线性化，并经整理后得
[ctga1 ctg(a1 b1 )]va1 ctg(a1 b1 )vb1 ctga2va2 ctgb2vb2 ctg(a3 b3 )va3 [ctg(a3 b3 ) ctgb3 ]vb3 w 0
w (1 sin(a1 b1 ) sin b2 sin b3 )
主要内容
第一节 条件平差原理 第二节 条件方程 第三节 精度评定 第四节 水准网平差示例
第1页/共37页
第一节 条件平差原理 （ ） 介绍条件平差原理，给出计算公式
一、基础方程及其解
设有r个观测值平差值线性条件方程：
ALˆ A 0 a1Lˆ1
a2 Lˆ2
...Βιβλιοθήκη an Lˆna00
b1Lˆ1 b2 Lˆ2 ... bn Lˆn b0 0（ 4－1－5），矩阵形式为：
...
sin a1 sin a2 sin b1 sin b2
sin a3 sin b3
ctgb3
vb3
0
ctga1va1
...
ctga3va3
ctgb1vb1
... ctgb3vb3
(1 sin a1 sin a2 sin a3 ) 0
sin b1 sin b2 sin b3 第21页/共37页
..................................
0
r1Lˆ1 r2 Lˆ2 ... rn Lˆn r0
0
注意：第一个条件方程系数到最后一个条件方程系数分别 采用字母a-r,下标与观测值编号对应。r是最后一个条件方 程的编号，表示条件方程个数为r，但是r数目与r在英文字 母中序号无关。
求其一阶偏导数，并令其为0：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
条件平差程序#include <stdio.h>#include <math.h>#include <conio.h>#define N_max 15int n,m,r,p; //n：观测值的个数，m：待定点个数，r：多余观测值个数，p：已知高程的水准点个数float Hd[6]={0};void Choose(){int i;printf("此程序能够解决闭合水准路线、附和水准路线、支水准路线的条件平差。
\n");printf("请问已知高程的水准点个数为：（不要太多喔，~ 。
~）：");scanf("%d",&p);for(i=1;i<=p;i++){printf("已知点%c点的高程为：",64+i);scanf("%f",&Hd[i]);}}void Input(float Hgao[][3]) //输入各测点的高程差以及它们之间的距离{int i;for(i=1;i<=n;i++){printf("请输入h%d的数值：",i);scanf(" %f",&Hgao[i][1]);printf("请输入S%d的数值：",i);scanf("%f",&Hgao[i][2]);}}void Equation(int A[][N_max],char Equa[][50],int asd[][6],float Hgao[][3],float W[],int flag)//输入条件方程或者求某待定点的表达式{int i,j,k,ppt;if(flag==1){ppt=r;printf("请输入%d个条件方程：\n",r);printf("如：h1+h2+h3+Ha-Hb=0.请务必使等号右边等于0，输入的时候中间不要有空格！\n");getchar();for(i=1;i<=r;i++){printf("方程%d\t",i);gets(Equa[i]);}}else{ppt=m;printf("为求得待定点的高程，请分别给出每个待定点的一个与Ha或者Hb\n以及各个高程差h之间的关系式。
\n");printf("比如，Hc=Ha-h1+h2.你只需要输入Ha-h1+h2。
中间不要有空格！\n"); for(i=1;i<=m;i++){printf("待定点%d\t\t",i);gets(Equa[i]);}}for(i=1;i<=ppt;i++){for(j=1;j<=n;j++){for(k=0;Equa[i][k]!='\0';k++){if(k==0){if(Equa[i][1]==j+48){A[i][j]=1;break;}}else{if(Equa[i][k]=='+' && Equa[i][k+2]==j+48){A[i][j]=1;break;}else if(Equa[i][k]=='-' && Equa[i][k+2]==j+48){A[i][j]=-1;break;}}}}}for(i=1;i<=ppt;i++){for(j=1;j<=p;j++){for(k=0;Equa[i][k]!='\0';k++){if(k==0){if(Equa[i][1]==64+j || Equa[i][1]==96+j){asd[i][j]=1;break;}}else{if(Equa[i][k]=='+' && (Equa[i][k+2]==64+j || Equa[i][k+2]==96+j)) {asd[i][j]=1;break;}else if(Equa[i][k]=='-' && (Equa[i][k+2]==64+j || Equa[i][k+2]==96+j)) {asd[i][j]=-1;break;}}}}}if(flag==1){for(i=1;i<=r;i++){for(j=1;j<=n;j++){W[i]+=Hgao[j][1]*A[i][j];}for(k=1;k<=p;k++){W[i]+=asd[i][k]*Hd[k];}}}}void InitialQ(float Q[][N_max],float Hgao[][3]) //初始化协因数阵{int i,j;for(i=1;i<=n;i++){for(j=1;j<=n;j++){if(i==j){Q[i][j]=Hgao[i][2];}}}}void Calculate(float Q[][N_max],float Hgao[][3],float Naa[][10],int A[][N_max]) //计算Naa {int i,j,k;float bs[10][N_max]={0};for(i=1;i<=r;i++){for(j=1;j<=n;j++){for(k=1;k<=n;k++){bs[i][j]=bs[i][j]+A[i][k]*Q[k][j];}}}for(i=1;i<=r;i++){for(j=1;j<=r;j++){for(k=1;k<=n;k++){Naa[i][j]+=bs[i][k]*A[j][k];}}}}void Realv(int A[][N_max],float Q[][N_max],float k123[],float v[]) //计算改正数方程{int i,j,k;float bs[10][N_max]={0};for(i=1;i<=n;i++){for(j=1;j<=r;j++){for(k=1;k<=n;k++){bs[i][j]+=Q[i][k]*A[j][k];}}}for(i=1;i<=n;i++){for(j=1;j<=r;j++){v[i]+=bs[i][j]*k123[j];}}}void getresult(float a[][10],float k123[]) //计算k{int i,j,k,wo;float app,temp;for(i=1;i<r;i++){wo=i;for(j=i+1;j<=r;j++){if(fabs(a[j][i]) > fabs(a[wo][i]))wo=j;}if(wo!=i){for(k=i;k<=r+1;k++){temp=a[i][k];a[i][k]=a[wo][k];a[wo][k]=temp;}}for(j=i+1;j<=r;j++){app=a[j][i]/a[i][i];for(k=i;k<=r+1;k++){a[j][k]-=app*a[i][k];}}}k123[r]=a[r][r+1]/a[r][r];for(i=r-1;i>=1;i--){for(j=i+1;j<=r;j++){a[i][r+1]-=a[i][j]*k123[j];}k123[i]=a[i][r+1]/a[i][i];}}void Solution(float Naa[][10],float W[],float k[],int A[][N_max],float Q[][N_max],float v[]) {int i;if(r==1){k[1]=(-1)*W[1]/Naa[1][1];Realv(A,Q,k,v);}else{for(i=1;i<=r;i++){Naa[i][r+1]=(-1)*W[i];}getresult( Naa, k);Realv(A,Q,k,v);}}void Answer(float Hgao[][3],float v[],float W[],float Point[],int flag) //输出答案{int i,j,k,Asd[N_max][6]={0};int a123[10][N_max]={0};char che[N_max][50];printf("改正数方程的解为：\n");for(i=1;i<=n;i++){printf(" v[%d] ",i);}putchar('\n');for(i=1;i<=n;i++){printf("%f ",v[i]);}putchar('\n');printf("平差后各高差值：\n");for(i=1;i<=n;i++){printf(" h[%d] ",i);}putchar('\n');for(i=1;i<=n;i++){printf("%f ",Hgao[i][1]+v[i]);}putchar('\n');Equation( a123, che, Asd, Hgao, W, flag);printf("\n平差后各待定点的高程如下：\n待定点\t ");for(i=1;i<=m;i++)printf("%d\t ",i);printf("\n ");for(i=1;i<=m;i++){for(j=1;j<=n;j++){if(a123[i][j]!=0){Point[i]+=(Hgao[j][1]+v[j])*a123[i][j];}for(k=1;k<=p;k++){Point[i]+=Asd[i][k]*Hd[k];}printf("%f\t ",Point[i]);}}void main(){int t,flag=1;float k[10],v[N_max]={0},Point[N_max]={0};int A[10][N_max]={0},asd[N_max][6]={0};float Hgao[N_max][3],W[10]={0};float Q[N_max][N_max]={0},Naa[10][10]={0}; char Equa[N_max][50];printf("\t\t");putchar(16);putchar(16);printf(" 欢迎使用"); putchar(17);putchar(17);putchar('\n');Choose();printf("请输入观测值个数n:"); scanf("%d",&n);printf("请输入必要观测值个数t:"); scanf("%d",&t);r=n-t;printf("请输入待定点的个数m:"); scanf("%d",&m);Input(Hgao);InitialQ(Q,Hgao);Equation( A, Equa, asd, Hgao, W, flag);flag=0;Calculate(Q,Hgao,Naa,A);Solution( Naa, W, k, A, Q, v);Answer( Hgao, v, W, Point, flag);printf("\n\n程序已结束。