数学建模课后习题作业
数学建模课后习题答案

方程及方程组的求解路灯照明问题。
在一条20m 宽的道路两侧, 分别安装了一只2kw 和一只3kw 的路灯, 它们离地面的高度分别为5m 和6m 。
在漆黑的夜晚, 当两只路灯开启时 (1)两只路灯连线的路面上最暗的点和最亮的点在哪里? (2)如果3kw 的路灯的高度可以在3m 到9m 之间变化, 如何路面上最暗点的亮度最大? (3)如果两只路灯的高度均可以在3m 到9m 之间变化, 结果又如何?解:根据题意, 建立如图模型P1=2kw P2=3kw S=20m 照度计算公式:2sin r p k I α= (k 为照度系数, 可取为1;P 为路灯的功率)(1)设Q(x,0)点为两盏路灯连线上的任意一点, 则两盏路灯在Q 点的照度分别为21111sin R p k I α= 22222sin R p k I α=22121x h R += 111sin R h =α22222)(x s h R -+= 222sin R h =αQ 点的照度:3232322222322111))20(36(18)25(10))((()(()(x x x s h h P x h h P x I -+++=-+++=要求最暗点和最亮点, 即为求函数I(x)的最大值和最小值, 所以应先求出函数的极值点5252522222522111'))20(36()20(54)25(30))(()(3)(3)(x x x x x s h x s h P x h x h P x I -+-++-=-+-++-=利用MATLAB 求得0)('=x I 时x 的值代码:s=solve('(-30*x)/((25+x^2)^(5/2))+(54*(20-x))/((36+(20-x)^2)^(5/2))'); s1=vpa(s,8); s1运行结果: s1 =19.97669581 9.338299136 8.538304309-11.61579012*i .2848997038e-1综上, x=9.33m 时, 为最暗点;x=19.97m 时, 为最亮点。
数学建模课后作业

数学建模课后作业数学实验与数学建模第四章1、有10个同类企业的⽣产性固定资产年平均价值和⼯业总产值资料如下:(1)说明两变量之间的相关⽅向;(2)建⽴直线回归⽅程;(3)计算估计标准误差;(4)估计⽣产性固定资产(⾃变量)为1100万元时的总资产(因变量)的可能值。
解:由表格易知:⼯业总产值是随着⽣产性固定资产价值的增长⽽增长的,⽽知之间存在正向相关性。
⽤MATLAB 可解:运⾏结果为:b =395.5670 运⾏图为:0.8958stats =1.0e+04 *0.0001 0.0071 0.0000 1.6035 industry =1.0e+03 *1.0220 1.06801.1160 1.16631.2188 1.2736construction =1.0e+03 *1.2190 0.39650.3965 0.39650.3965 0.3965ans = 395.5670 0.89582、设某公司下属10个门市部有关资料如下:(1)、确定适宜(2)、计算有关指标,判断这三种经济现象之间的紧密程度。
(1)设销售利润率(%)为y,流通费⽤⽔平(%)为x2,职⼯平均销售额(万元)为x3 回归模型y=a1+a2*x1+a3*x2利⽤MATLAB:x1=[12.6 10.4 18.5 3.0 8.1 16.3 12.3 6.2 6.6 16.8; 6 5 8 1 4 7 6 33 7; 2.8 3.3 1.8 7.0 3.9 2.1 2.9 4.1 4.2 2.5]';X = [ones(size(x1(:,1))),x1(:,2:3)]; Y = x1(:,1); [b,bint,r,rint,stats] = regress(Y,X,0.05);b,bint,stats运⾏结果为:b =-6.76912.90700.9578bint = -15.7285 2.19022.01383.8003-0.3676 2.2832stats =0.9823 194.2113 0.0000 0.6002所以,相关系数为0.9823 分析可得y=-6.7691+2.9070*x1+0.9578*x2(2)利⽤MATLAB:stepwise(X,Y,[],0.05)运⾏结果为:此时,y与x2线性关系紧密,⽽与x3的线性关系不是很密切,即使没有x3,y=-0.386+2.293*x2,相关系数为:0.975,已经很⾼了。
数学建模课后作业第六章

数学建模课后作业第六章-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第六章.数理统计实验6.2 基本实验1.区间估计解:(1)由点估计与参数估计未知参数和σ^2,可以求出均值与方差;由题目条件可以得出如下的R程序:> x<-c(1067,919,1196,785,1126,936,918,1156,920,948)> n<-length(x)> x.sd<-sd(x)> x.mean<-mean(x); x.mean[1] 997.1> x.var<-sum((x-x.mean)^2)/n; x.var[1] 15574.29即=997.1,σ^2=15574.29令大约95%的灯泡至少使用的时间为x小时,可以得出如下的等式:由标准正态分布表可以得出:Ф()=0.05,可以得出=-1.645可以得出x=791.809小时。
(2)当使用时间至少为1000小时:查阅标准正态分布表可以得出对应的概率为1-Ф()=1-Ф()=1-Ф(0.02324)=1-0.5106=0.4894即由题可以得出使用时间在1000小时以上的概率为48.94%。
2.假设检验I解:对于自然状态下的男子血小板的数目可以假设服从于正态分布,由点估计与参数估计未知参数和σ^2,可以求出均值、均值区间与方差;x<-c(113,126,145,158,160,162,164,175,183,188,188,190,220,224,230,231,2 38,245,247,256)> n<-length(x)> x.sd<-sd(x)> x.mean<-mean(x); x.mean[1] 192.15> x.var<-sum((x-x.mean)^2)/n; x.var[1] 1694.728> tmp<-x.sd/sqrt(n)*qt(1-0.05/2,n-1)> a<-x.mean-tmp;a [1] 172.3827 > b<-x.mean+tmp;b [1] 211.9173可以得出均值为= 192.15,方差σ^2=1694.728;均值区间为(172.3827,211.9173)由此可以得出对于油漆工人而言正常男子血小板数为225单位,油漆工人明显低于正常的数量,则可以得知结论油漆作业对人体血小板数量有严重影响。
数学建模习题及答案

第一部分课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。
(2)2.1节中的Q值方法。
(3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:横线的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
(4)你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。
试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大(如图)。
若知道管道长度,需用多长布条(可考虑两端的影响)。
如果管道是其他形状呢。
数学建模课后习题作业

【陈文滨】1、在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何?【模型假设】(1)椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形.(2)地面高度是连续变化的,沿任何方向都不会出现间断 (没有像台阶那样的情况),即从数学的角度看,地面是连续曲面.这个假设相当于给出了椅子能放稳的必要条件.(3)椅子在任何位置至少有三只脚同时着地.为保证这一点,要求对于椅脚的间距和椅腿的长度而言,地面是相对平坦的.因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使是连续变化的),此时三只脚是无法同时着地的。
【模型建立】在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来.首先,引入合适的变量来表示椅子位置的挪动.生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就是数学上所说的平移与旋转变换.然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法是不能解决问题的.于是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形.注意到椅脚连线呈长方形,长方形是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地.把长方形绕它的对称中心O旋转,这可以表示椅子位置的改变。
于是,旋转角度θ这一变量就表示了椅子的位置.为此,在平面上建立直角坐标系来解决问题.如下图所示,设椅脚连线为长方形ABCD,以对角线AC所在的直线为x轴,对称中心O为原点,建立平面直角坐标系.椅子绕O点沿逆时针方向旋转角度θ后,长方形ABCD转至A1B1C1D1 的位置,这样就可以用旋转角θ(0≤θ≤π)表示出椅子绕点O旋转θ后的位置.其次,把椅脚是否着地用数学形式表示出来.我们知道,当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地.由于椅子在不同的位置是θ的函数,因此,椅脚与地面的竖直距离也是θ的函数.由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都是θ的函数.而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0.因此,只需引入两个距离函数即可.考虑到长方形ABCD是中心对称图形,绕其对称中心 O沿逆时针方向旋转180°后,长方形位置不变,但A,C和B,D对换了.因此,记A、B两脚与地面竖直距离之和为f(θ),C、D两脚与地面竖直距离之和为g(θ),其中θ∈[0,π],从而将原问题数学化。
数学建模课后作业
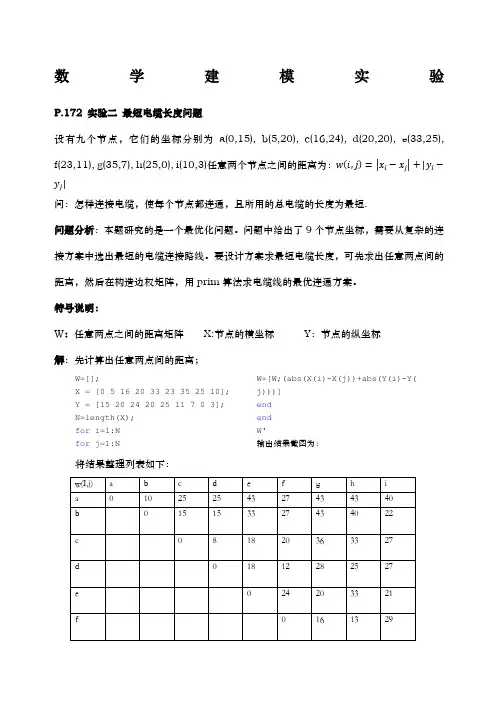
数学建模实验P.172 实验二最短电缆长度问题设有九个节点,它们的坐标分别为a(0,15), b(5,20), c(16,24), d(20,20), e(33,25), f(23,11), g(35,7), h(25,0), i(10,3)任意两个节点之间的距离为:问:怎样连接电缆,使每个节点都连通,且所用的总电缆的长度为最短.问题分析:本题研究的是一个最优化问题。
问题中给出了9个节点坐标,需要从复杂的连接方案中选出最短的电缆连接路线。
要设计方案求最短电缆长度,可先求出任意两点间的距离,然后在构造边权矩阵,用prim算法求电缆线的最优连通方案。
符号说明:W:任意两点之间的距离矩阵X:节点的横坐标Y:节点的纵坐标解:先计算出任意两点间的距离;W=[];X = [0 5 16 20 33 23 35 25 10]; Y = [15 20 24 20 25 11 7 0 3]; N=length(X);for i=1:Nfor j=1:N W=[W;(abs(X(i)-X(j))+abs(Y(i)-Y( j)))]endendW'输出结果截图为:将结果整理列表如下:用prim算法求电缆线的最优连通方案;运行结果截图为:分析结果可知:最小生成树的边集合为{(1,2),(2,3),(3,4),(4,6),(6,8),(6,7),(3,5),(8,9)}即用prime算法求出的最优电缆连接方案为:{(a,b),(b,c),(c,d),(d,f),(f,h),(f,g),(c,e),(h,i)}。
P186实验一求最短路问题求图14.9所示有向网络中自点1到点6的最短有向路问题分析:用floyde 算法算出任意两点之间的最短的距离。
符号说明:D:任意两个点之间的最短距离n:迭代次数解:function [D,path]=floyd(a)n=size(a,1);%设置D和Path的初值D=a;path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j; %j是i的后继点endendend%做n次迭代,每次迭代均更新D(i,j)和path(i,j) for k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendend在MATLAB命令窗口键入:a=[0 5 inf 3 inf inf;inf 0 4 2 inf inf;inf inf 0 2 4 3;inf inf inf 0 5 inf;inf inf inf inf 0 2;inf inf inf inf inf 0];[D,path]=floyd(a)运行结果截图为:D =0 5 9 3 8 10 Inf 0 4 2 7 7 Inf Inf 0 2 4 3 Inf Inf Inf 0 5 7 Inf Inf Inf Inf 0 2 Inf Inf Inf Inf Inf 0 path =1 2 2 4 4 4 0 2 3 4 4 3 0 0 3 4 5 6 0 0 0 4 5 5 0 0 0 0 5 6 0 0 0 0 0 6由运行结果得:因为path(1,6)=4,意味着顶点1的后继点为4, path(4,6)=5,从而顶点4的后继点为5,同理,因path(5,6)=6,从而顶点5的后继点为6,故1→4→5→6便是顶点1到顶点6的最短路径。
数学建模课后作业第三章
线性规划和整数规划实验3.2.基本实验1.生产计划安排解:(1)设A、B、C三种产品的生产量为x、y、z,则可以得出生产利润:f=3*x+y+4*z;约束条件为:6*x+3*y+5*z≤45;3*x+4*y+5*z≤30;x、y、z均大于0;只要f取得最大值即为最大利润则可以得出以下lingo程序;model:max=3*x+y+4*z;6*x+3*y+5*z<=45;3*x+4*y+5*z<=30;end运行程序后可得;Global optimal solution found.Objective value: 27.00000Infeasibilities: 0.000000Total solver iterations: 2Model Class: LPTotal variables: 3Nonlinear variables: 0Integer variables: 0Total constraints: 3Nonlinear constraints: 0Total nonzeros: 9Nonlinear nonzeros: 0Variable Value Reduced Cost X 5.000000 0.000000Y 0.000000 2.000000Z 3.000000 0.000000Row Slack or Surplus Dual Price1 27.00000 1.0000002 0.000000 0.20000003 0.000000 0.6000000则可得当x=5、y=0、z=3时fmax=27为获利最大的生产方案;(2)由(1)中的程序Objective Coefficient Ranges:Current Allowable AllowableVariable Coefficient Increase DecreaseX 3.000000 1.800000 0.6000000Y 1.000000 2.000000 INFINITYZ 4.000000 1.000000 1.500000Righthand Side Ranges:Current Allowable AllowableRow RHS Increase Decrease2 45.00000 15.00000 15.000003 30.00000 15.00000 7.500000可以得出A的利润范围[4,4.8],B的利润范围[1,3],C的利润范围为[2.5,5](3)假设购买材料的数量为d,生产利润:f=3*x+y+4*z-0.4d;约束条件为:6*x+3*y+5*z≤45;3*x+4*y+5*z-d≤30;x、y、z、d均大于0;则可以得到下面新的lingo程序;model:max=3*x+y+4*z-0.4*d;6*x+3*y+5*z<=45;3*x+4*y+5*z-d<=30;end运行程序后可以得出:Global optimal solution found.Objective value: 30.00000Infeasibilities: 0.000000Total solver iterations: 2Model Class: LPTotal variables: 4Nonlinear variables: 0Integer variables: 0Total constraints: 3Nonlinear constraints: 0Total nonzeros: 11Variable Value Reduced Cost X 0.000000 0.6000000 Y 0.000000 1.800000Z 9.000000 0.000000D 15.00000 0.000000Row Slack or Surplus Dual Price1 30.00000 1.0000002 0.000000 0.40000003 0.000000 0.4000000由以上程序可以得出当z=9,d=15时,利润可以达到30,(4)假设新产品的数量为D,可以得出如下的生产利润:f=3*x+y+4*z+3D;约束条件为:6*x+3*y+5*z+8*D≤45;3*x+4*y+5*z+2*D≤30;x、y、z、D均大于0;则可以得到下面新的lingo程序;model:max=3*x+y+4*z+3*D;6*x+3*y+5*z+8*D<=45;3*x+4*y+5*z+2*D<=30;End运行程序可以得出:Global optimal solution found.Objective value: 27.50000Infeasibilities: 0.000000Total solver iterations: 2Model Class: LPTotal variables: 4Nonlinear variables: 0Total constraints: 3Nonlinear constraints: 0Total nonzeros: 12Nonlinear nonzeros: 0Variable Value Reduced Cost X 0.000000 0.1000000 Y 0.000000 1.966667Z 5.000000 0.000000D 2.500000 0.000000Row Slack or Surplus Dual Price1 27.50000 1.0000002 0.000000 0.23333333 0.000000 0.5666667利润为27.5>27但是z=5,D=2.5,由于D只能取整数,故当D=3时则不满足约束条件,当D=2是,利润为26<27,所以如果其他条件不变化的话,这种产品不值得生产。
数学建模课后习题
数学建模课后习题第⼀章课后习题6、利⽤1、5节药物中毒施救模型确定对于孩⼦及成⼈服⽤氨茶碱能引起严重中毒与致命得最⼩剂量。
解:假设病⼈服⽤氨茶碱得总剂量为a ,由书中已建⽴得模型与假设得出肠胃中得药量为:由于肠胃中药物向⾎液系统得转移率与药量成正⽐,⽐例系数,得到微分⽅程(1)原模型已假设时⾎液中药量⽆药物,则,得增长速度为。
由于治疗⽽减少得速度与本⾝成正⽐,⽐例系数,所以得到⽅程:(2)⽅程(1)可转换为:? 带⼊⽅程(2)可得:将与带⼊以上两⽅程,得:针对孩⼦求解,得:严重中毒时间及服⽤最⼩剂量:,; 致命中毒时间及服⽤最⼩剂量:, 针对成⼈求解:严重中毒时间及服⽤最⼩剂量:, 致命时间及服⽤最⼩剂量:,课后习题7、对于1、5节得模型,如果采⽤得就是体外⾎液透析得办法,求解药物中毒施救模型得⾎液⽤药量得变化并作图。
解:已知⾎液透析法就是⾃⾝排除率得6倍,所以 ,x 为胃肠道中得药量,1386.0,639.0,5.236)2(,1100,2,====≥-=-λλλu z e x t uz x dtdzt 解得:⽤matla b画图:图中绿⾊线条代表采⽤体外⾎液透析⾎液中药物浓度得变化情况。
从图中可以瞧出,采取⾎液透析时⾎液中药物浓度就开始下降。
T=2时,⾎液中药物浓度最⾼,为236、5;当z=200时,t=2、8731,⾎液透析0、8731⼩时后就开始解毒。
第⼆章1、⽤2、4节实物交换模型中介绍得⽆差别曲线得概念,讨论以下得雇员与雇主之间得关系:1)以雇员⼀天得⼯作时间与⼯资分别为横坐标与纵坐标,画出雇员⽆差别曲线族得⽰意图,解释曲线为什么就是那种形状;2)如果雇主付计时费,对不同得⼯资率画出计时⼯资线族,根据雇员得⽆差别曲线族与雇主得计时⼯资线族,讨论双⽅将在怎样得⼀条曲线上达成协议;3)雇员与雇主已经达成了协议,如果雇主想使⽤雇员得⼯作时间增加到t2,她有两种办法:⼀就是提⾼计时⼯资率,在协议线得另⼀点达成新得协议;⼆就是实⾏超时⼯资制,即对⼯时仍付原计时⼯资,对⼯时付给更⾼得超时⼯资,试⽤作图⽅法分析那种办法对雇主更有利,指出这个结果得条件。
数学建模习题集及答案解析课后习题集
第一局部课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用以下方法分配各宿舍的委员数:〔1〕按比例分配取整数的名额后,剩下的名额按惯例分给小数局部较大者。
〔2〕2.1节中的Q值方法。
〔3〕d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
〔4〕你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品廉价这种现象了吗。
比方洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。
试用比例方法构造模型解释这个现象。
〔1〕分析商品价格C与商品重量w的关系。
价格由生产本钱、包装本钱和其他本钱等决定,这些本钱中有的与重量w成正比,有的与外表积成正比,还有与w无关的因素。
〔2〕给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w 的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大〔如图〕。
假设知道管道长度,需用多长布条〔可考虑两端的影响〕。
如果管道是其他形状呢。
5.用尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘。
6.动物园里的成年热血动物靠饲养的食物维持体温根本不变,在一些合理、简化的假设下建立动物的饲养食物量与动物的某个尺寸之间的关系。
7.举重比赛按照运发动的体重分组,你能在一些合理、简化的假设下建立比赛成绩与体重之间的关系吗。
数学建模习题及答案课后习题
第一部分课后习题1.学校共1000名学生,235人住在A宿舍,333人住在B宿舍,432人住在C宿舍。
学生们要组织一个10人的委员会,试用下列办法分配各宿舍的委员数:(1)按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者。
(2)2.1节中的Q值方法。
(3)d’Hondt方法:将A,B,C各宿舍的人数用正整数n=1,2,3,…相除,其商数如下表:将所得商数从大到小取前10个(10为席位数),在数字下标以横线,表中A,B,C行有横线的数分别为2,3,5,这就是3个宿舍分配的席位。
你能解释这种方法的道理吗。
如果委员会从10人增至15人,用以上3种方法再分配名额。
将3种方法两次分配的结果列表比较。
(4)你能提出其他的方法吗。
用你的方法分配上面的名额。
2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。
比如洁银牙膏50g装的每支1.50元,120g装的3.00元,二者单位重量的价格比是1.2:1。
试用比例方法构造模型解释这个现象。
(1)分析商品价格C与商品重量w的关系。
价格由生产成本、包装成本和其他成本等决定,这些成本中有的与重量w成正比,有的与表面积成正比,还有与w无关的因素。
(2)给出单位重量价格c与w的关系,画出它的简图,说明w越大c越小,但是随着w 的增加c减少的程度变小。
解释实际意义是什么。
3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数4.用宽w的布条缠绕直径d的圆形管道,要求布条不重叠,问布条与管道轴线的夹角 应多大(如图)。
若知道管道长度,需用多长布条(可考虑两端的影响)。
如果管道是其他形状呢。
5.用已知尺寸的矩形板材加工半径一定的圆盘,给出几种简便、有效的排列方法,使加工出尽可能多的圆盘。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选修课——数学建模部分习题详细解答【陈文滨】1、在稳定的椅子问题中,如设椅子的四脚连线呈长方形,结论如何?【模型假设】(1)椅子四条腿一样长,椅脚与地面接触处视为一点,四脚的连线呈长方形.(2)地面高度是连续变化的,沿任何方向都不会出现间断 (没有像台阶那样的情况),即从数学的角度看,地面是连续曲面.这个假设相当于给出了椅子能放稳的必要条件.(3)椅子在任何位置至少有三只脚同时着地.为保证这一点,要求对于椅脚的间距和椅腿的长度而言,地面是相对平坦的.因为在地面上与椅脚间距和椅腿长度的尺寸大小相当的范围内,如果出现深沟或凸峰(即使是连续变化的),此时三只脚是无法同时着地的。
【模型建立】在上述假设下,解决问题的关键在于选择合适的变量,把椅子四只脚同时着地表示出来.首先,引入合适的变量来表示椅子位置的挪动.生活经验告诉我们,要把椅子通过挪动放稳,通常有拖动或转动椅子两种办法,也就是数学上所说的平移与旋转变换.然而,平移椅子后问题的条件没有发生本质变化,所以用平移的办法是不能解决问题的.于是可尝试将椅子就地旋转,并试图在旋转过程中找到一种椅子能放稳的情形.注意到椅脚连线呈长方形,长方形是中心对称图形,绕它的对称中心旋转180度后,椅子仍在原地.把长方形绕它的对称中心O旋转,这可以表示椅子位置的改变。
于是,旋转角度θ这一变量就表示了椅子的位置.为此,在平面上建立直角坐标系来解决问题.如下图所示,设椅脚连线为长方形ABCD,以对角线AC所在的直线为x轴,对称中心O为原点,建立平面直角坐标系.椅子绕O点沿逆时针方向旋转角度θ后,长方形ABCD转至A1B1C1D1 的位置,这样就可以用旋转角θ(0≤θ≤π)表示出椅子绕点O旋转θ后的位置.其次,把椅脚是否着地用数学形式表示出来.我们知道,当椅脚与地面的竖直距离为零时,椅脚就着地了,而当这个距离大于零时,椅脚不着地.由于椅子在不同的位置是θ的函数,因此,椅脚与地面的竖直距离也是θ的函数.由于椅子有四只脚,因而椅脚与地面的竖直距离有四个,它们都是θ的函数.而由假设(3)可知,椅子在任何位置至少有三只脚同时着地,即这四个函数对于任意的θ,其函数值至少有三个同时为0.因此,只需引入两个距离函数即可.考虑到长方形ABCD是中心对称图形,绕其对称中心 O沿逆时针方向旋转180°后,长方形位置不变,但A,C和B,D对换了.因此,记A、B两脚与地面竖直距离之和为f(θ),C、D两脚与地面竖直距离之和为g(θ),其中θ∈[0,π],从而将原问题数学化。
数学模型:已知f(θ)和g(θ)是θ的非负连续函数,对任意θ,f(θ)•g(θ)=0,证明:存在θ0∈[0,π],使得f(θ0)=g(θ0)=0成立。
【模型求解】如果f(0)=g(0)=0,那么结论成立。
如果f(0)与g(0)不同时为零,不妨设f(0)>0,g(0)=0。
这时,将长方形ABCD 绕点O逆时针旋转角度π后,点A,B分别与C,D互换,但长方形ABCD在地面上所处的位置不变,由此可知,f(π)=g(0),g(π)=f(0).而由f(0)>0,g(0)=0,得g(π)>0, f(π)=0。
令h(θ)=f(θ)-g(θ),由f(θ)和g(θ)的连续性知h(θ)也是连续函数。
又h(0)=f(0)-g(0)>0,h(π)=f(π)-g(π)<0,,根据连续函数介值定理,必存在θ0∈(0,π)使得h(θ0)=0,即f(θ0)=g(θ0);又因为f(θ0)•g(θ0)=0,所以f(θ0)=g(θ0)=0。
于是,椅子的四只脚同时着地,放稳了。
【模型讨论】用函数的观点来解决问题,引入合适的函数是关键.本模型的巧妙之处就在于用变量θ表示椅子的位置,用θ的两个函数表示椅子四只脚与地面的竖直距离.运用这个模型,不但可以确信椅子能在不平的地面上放稳,而且可以指导我们如何通过旋转将地面上放不稳的椅子放稳.2、人、狗、鸡、米均要过河,船需要人划,另外至多还能载一物,而当人不在时,狗要吃鸡,鸡要吃米。
问人、狗、鸡、米怎样过河 【模型假设】人带着猫、鸡、米过河,从左岸到右岸,船除了需要人划之外,只能载猫、鸡、米三者之一,人不在场时猫要吃鸡、鸡要吃米。
试设计一个安全过河方案,使渡河次数尽量地少。
【符号说明】1X :代表人的状态,人在该左岸或船上取值为1,否则为0; 2X :代表猫的状态,猫在该左岸或船上取值为1,否则为0; 3X :代表鸡的状态,鸡在该左岸或船上取值为1,否则为0; 4X :代表米的状态,米在该左岸或船上取值为1,否则为0; 1234(,,,)K S X X X X =:状态向量,代表时刻K 左岸的状态; 1234(,,,)K D X X X X =:决策向量,代表时刻K 船上的状态;【模型建立】限制条件:23134202X X X X X +≠⎧=⇒⎨+≠⎩ 初始状态:00(1,1,1,1),(0,0,0,0)S D ==目标:确定有效状态集合,使得在有限步内左岸状态由(1,1,1,1)(0,0,0,0)→ 【模型求解】根据乘法原理,四维向量1234(,,,)X X X X 共有4216=种情况,根据限制条件可以排除(0,1,1,1),(0,1,0,1),(0,0,1,1)三种情况,其余13种情况可以归入两个集合进行匹配,易知可行决策集仅有五个元素:{}(1,1,1,0),(1,0,1,0),(1,0,0,1),(1,0,0,0),(0,0,0,0)D =,状态集有8个元素,将其进行匹配,共有两种运送方案:方案一:人先带鸡过河,然后人再回左岸,把米带过右岸,人再把鸡运回左岸,人再把猫带过右岸,最后人回来把鸡带去右岸(状态见表1);方案二:人先带鸡过河,然后人再回左岸,把猫带过右岸,人再把鸡运回左岸,人再把米带过右岸,最后人回来把鸡带去右岸(状态见表2)。
表1:方案一的状态与决策表2:方案二的状态与决策3、报童每天清晨从报社购进报纸零售,晚上将没有卖完的报纸退回。
设每份报纸的购进价为,零售价为,退回价为,应该自然地假设。
这就是说,报童售出一份报纸赚,退回一份报纸赔。
报童如果每天购进的报纸太少,不够卖的,会少赚钱;如果购进太多,卖不完,将要赔钱。
请你为报童筹划一下,他应该如何确定每天购进报纸的数量,以获得最大的收入。
【符号说明】报纸具有时效性每份报纸进价b元,卖出价a元,卖不完退回份报纸c元。
设每日的订购量为n,如果订购的多了,报纸剩下会造成浪费,甚至陪钱。
订的少了,报纸不够卖,又会少赚钱。
为了获得最大效益,现在要确定最优订购量n。
n的意义。
n是每天购进报纸的数量,确定n一方面可以使报童长期以内拥有一个稳定的收入,另一方面也可以让报社确定每日的印刷量,避免纸张浪费。
所以,笔者认为n的意义是双重的。
本题就是让我们根据a、b、c及r来确定每日进购数n。
【模型假设】1、假设报童现在要与报社签定一个长期的订购合同,所以要确定每日的订购量n。
2、假设报纸每日的需求量是r,但报童是一个初次涉足卖报行业的菜鸟,毫无经验,无法掌握需求量r的分布函数,只知道每份报纸的进价b、售价a及退回价c。
3、假设每日的定购量是n。
4、报童的目的是尽可能的多赚钱。
【模型建立】应该根据需求量r确定需求量n,而需求量r是随机的,所以这是一个风险决策问题。
而报童却因为自身的局限,无法掌握每日需求量的分布规律,已确定优化模型的目标函数。
但是要得到n值,我们可以从卖报纸的结果入手,结合r与n的量化关系,从实际出发最终确定n值。
由常识可以知道卖报纸只有赚钱、不赚钱不赔钱、赔钱会有三种结果。
现在用简单的数学式表示这三种结果。
1、赚钱。
赚钱又可分为两种情况:①r>n,则最终收益为(a-b)n (1)②r<n,则最终收益为(a-b)r-(b-c)(n-r)>0整理得:r/n>(b-c)/(a-c) (2)2、由(2)式容易得出不赚钱不赔钱。
r/n=(b-c)/(a-c) (3)3、赔钱。
r/n<(b-c)/(a-c) (4)【模型求解】首先由(1)式可以看出n与最终的收益呈正相关。
收益越多,n的取值越大。
但同时订购量n 又由需求量r约束,不可能无限的增大。
所以求n问题就转化成研究r与n的之间的约束关系。
然后分析(3)、(4)两式。
因为(3)、(4)分别代表不赚钱不赔钱及赔钱两种情况,而我们确定n值是为了获得最大收益,所以可以预见由(3)、(4)两式确立出的n值不是我们需要的结果,所以在这里可以排除,不予以讨论。
最后重点分析(2)式。
显然式中r表需求量,n表订购量,(b-c)表示退回一份儿报纸赔的钱。
因为(a-c)无法表示一个显而易见的意义,所以现在把它放入不等式中做研究。
由a>b>c,可得a-c>a-b,而(a-b)恰好是卖一份报纸赚得的钱。
然后采用放缩法,把(2)式中的(a-c)换成(a-b),得到r/n<(b-c)/(a-b) (5)不等式依然成立。
由(5)式再结合(1)式可知收益与n正相关,所以要想使订购数n的份数越多,报童每份报纸赔钱(b-c)与赚钱(a-b)的比值就应越小。
当报社与报童签订的合同使报童每份报纸赔钱与赚钱之比越小,订购数就应越多。
5、赛艇是一种靠桨手划桨前进的小船,分单人艇、双人艇、四人艇、八人艇四种。
各种艇虽大小不同,但形状相似。
现在考虑八人艇分重量级组(桨手体重不超过86kg)和轻量级组(桨手体重不超过73kg),建立模型说明重量级组的成绩比轻量级组大约好5%。
【符号说明】【模型假设】1./l b 为常数,赛艇净重0W 与浆手数目成正比,即08W ∝;2.赛艇前进时收到阻力与2sv 成正比;3.每个浆手比赛时划桨功率保持不变,且功率与体重成正比。
【模型建立】克服阻力做功功率为Fst ,因此总功率满足P Fv ∝,且2,F sv P W ∝∝,我们用量纲法进行建模:对于重量级八人赛艇:111P FV ∝ (1) 211F sV ∝ (2)11P W ∝ (3)由上述各式有:311W sV ∝,因此1311W V s ⎛⎫∝ ⎪⎝⎭ (4) 且已知 23s A ∝ (5) 又赛艇总重018W W W =+;由于假设2可知:08W w =(w 为常数),因此有1()W W w ∝+。
我们如下定义λ:111W wW λ+=(6)从而11W W λ∝ (7)根据阿基米德定律A W ∝,根据(7)式: 11A W λ∝ (8)将(8)式代入(5)式中有: ()2311s W λ∝ (9)将(9)式代入(4)式中有: ()()2193111V W λ--∝ (10)因为V 与t 成反比,有:()()2193111t W λ∝ (11)同理,对于轻量级快艇,我们有:()()2193222t W λ∝ (12)结合(11)与(12)式,我们可以知道两种快艇成绩比值的关系:2193111222t W t W λλ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(13)【模型求解】根据(13)式,我们有重量级八人赛艇比轻量级八人赛艇的成绩领先率为:219311122211t W t W λλ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭ 259911122211t W w W t W w W ⎛⎫⎛⎫+⇒-=- ⎪ ⎪+⎝⎭⎝⎭我们令W1=86kg ,W2=73kg在12λλ十分接近1时,12110.561 5.61%t t -==;在12,w W w W <<<<的情况下,791286110.13613.6%73t t ⎛⎫-≈-== ⎪⎝⎭。
