九年级数学《圆》经典试题集锦

合集下载

人教版九年级数学上册《24.1.1圆》同步测试题带答案

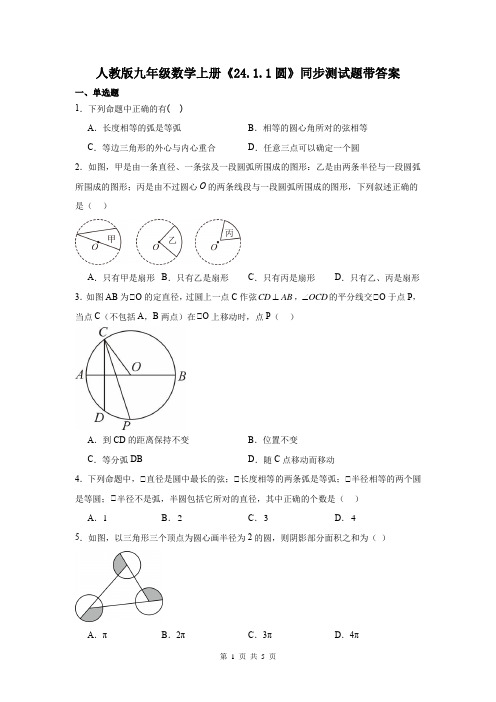
人教版九年级数学上册《24.1.1圆》同步测试题带答案一、单选题1．下列命题中正确的有( ) A ．长度相等的弧是等弧 B ．相等的圆心角所对的弦相等 C ．等边三角形的外心与内心重合D ．任意三点可以确定一个圆2．如图，甲是由一条直径、一条弦及一段圆弧所围成的图形：乙是由两条半径与一段圆弧所围成的图形；丙是由不过圆心O 的两条线段与一段圆弧所围成的图形，下列叙述正确的是（）A ．只有甲是扇形B ．只有乙是扇形C ．只有丙是扇形D ．只有乙、丙是扇形3．如图AB 为⊙O 的定直径，过圆上一点C 作弦CD AB ⊥，OCD ∠的平分线交⊙O 于点P ，当点C （不包括A ，B 两点）在⊙O 上移动时，点P （）A ．到CD 的距离保持不变B ．位置不变C ．等分弧DBD ．随C 点移动而移动4．下列命题中，⊙直径是圆中最长的弦；⊙长度相等的两条弧是等弧；⊙半径相等的两个圆是等圆；⊙半径不是弧，半圆包括它所对的直径，其中正确的个数是（） A ．1B ．2C ．3D ．45．如图，以三角形三个顶点为圆心画半径为2的圆，则阴影部分面积之和为（）A ．πB ．2πC ．3πD ．4π6．如图，在Rt ⊙ABC 中，⊙ACB =90°， AC =3，以点C 为圆心、CA 为半径的圆与AB 交于点D ，若点D 巧好为线段AB 的中点，则AB 的长度为（）A ．32B ．3C ． 6D ．9二、填空题7．到点O 的距离等于7cm 的点的集合是．8．下图中，点O 是( )，线段OA 是圆的( )，线段BC 是圆的( )．9．已知，如图AB ，AD 是O 的弦 30B ∠=︒，点C 在弦AB 上，连结CO 并延长交O 于点D ，35D ∠=︒则BAD ∠的度数是．10．如图，半径为r 的O 沿着边长为a 的正方形ABCD 的边作无滑动地滚动一周回到原来的位置，O 自身转动的圈数是．（用含a r ，的代数式表示）11．下列说法：⊙直径是弦；⊙弦是直径；⊙大于半圆的弧是优弧；⊙长度相等的弧是等弧，其中正确的是．12．顶点在圆外，并且两边都和圆相交的角叫做圆外角．圆外角的两边所夹的两条弧的度数与该角的度数之间的数量关系是：圆外角的度数等于．三、解答题13．如图，O 的弦,AB CD 的延长线交于点P ，连接OP ，且OP 平分APC ∠．求证：PA PC =．14．如图，点O 是同心圆的圆心，大圆半径OA ，OB 分别交小圆于点C ，D ，求证：AB CD ∥．15．如图所示，AB 为O 的直径，CD 是O 的弦，AB CD ，的延长线交于点E ，已知220AB DE AEC =∠=︒，．求AOC ∠的度数．16．如图，O 的半径5cm OA =，AB 是弦，C 是AB 上一点，且OC OA ⊥，OC BC =求A ∠的度数．17．如图,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于C,交弦AB 于D ．（1）求作此残片所在的圆的圆心（不写作法,保留作图痕迹）；（2）若AB=8cm,CD=2cm,求（1）中所作圆的半径．18．如图，在O 中，AB 是直径，CD 是弦，延长AB ，CD 相交于点P ，且2AB DP = 18P ∠=︒ 求AOC ∠的度数．题号 1 2 3 4 5 6 答案CBBCD C7．以点O 为圆心，7cm 为半径的圆 8．圆心半径直径 9．65︒ 10．21a r π+/21arπ+ 11．①③/③①12．两条弧度数差值的绝对值的一半 15．60AOC ∠=︒ 16．30︒17．(2) 圆的半径为5cm. 18．54。

人教版九年级数学上册第24章《圆》单元练习题(含答案)

人教版九年级数学上册第24章《圆》单元练习题（含答案）一、单选题1．如图，一个油桶靠在直立的墙边，量得0.8m,BC =并且,AB BC ⊥则这个油桶的底面半径是（）A ．1.6mB ．1.2mC ．0.8mD ．0.4m 2．在O 中，AB ，CD 为两条弦，下列说法：①若AB CD =，则AB CD =；②若AB CD =，则2AB CD =；③若2AB CD =，则弧AB=2弧CD ；④若2AOB COD ∠=∠，则2AB CD =.其中正确的有（）A ．1个B ．2个C ．3个D ．4个3．如图，点A 、B 、C 在⊙O 上，且∠ACB=100o ，则∠α度数为（）A ．160oB ．120oC ．100oD ．80o4．如图，在⊙O 中，CD 是直径，AB 是弦，AB ⊥CD 于E ，AB ＝8，OD ＝5，则CE 的长为（）A ．4B ．2C 2D ．15．如图，ABC 内接于O ，CD 是O 的直径，40ACD ∠=︒，则B ∠=（）A ．70°B ．60°C ．50°D ．40°6．如图，AB 为⊙O 的直径，点 D 是弧 AC 的中点，过点 D 作 DE ⊥AB 于点 E ，延长 DE 交⊙O 于点 F ，若 AC ＝12，AE ＝3，则⊙O 的直径长为（）A ．7.5B ．15C ．16D ．187．如图，已知AB 、AD 是O 的弦，30B ∠=︒，点C 在弦AB 上，连接CO 并延长CO 交于O 于点D ，20D ∠=︒，则BAD ∠的度数是（）A ．30°B ．40°C ．50°D ．60°8．将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上．点A ，B 的读数分别为86°，30°，则∠ACB 的度数是（）A ．28°B ．30°C ．36°D ．56°9．如图，⊙O 是△ABC 的外接圆，将△ABC 绕点C 顺时针旋转至△EDC ，使点E 在⊙O 上，再将△EDC 沿CD 翻折，点E 恰好与点A 重合，已知∠BAC =36°，则∠DCE 的度数是（）A．24 B．27 C．30 D．3310．下列说法正确的是（）①近似数2⨯精确到十分位；32.610--中，最小的是38-；②在2，2，38-，2③如图所示，在数轴上点P所表示的数为15-+；④用反证法证明命题“一个三角形最多有一个钝角”时，首先应假设“这个三角形中有两个钝角”；⑤如图，在ABC内一点P到这三条边的距离相等，则点P是三个角平分线的交点．A．1 B．2 C．3 D．4二、填空题11．某圆的周长是12.56米，那么它的半径是______________，面积是__________．OA=，12．如图，A、B、C是O上的点，OC AB⊥，垂足为点D，且D为OC的中点，若7则BC的长为___________．13．如图，AB 、AC 是O 的弦，过点A 的切线交CB 的延长线于点D ，若35BAD ∠=︒，则C ∠=___________°．14．如图，在正五边形ABCDE 中，连结AC ，以点A 为圆心，AB 为半径画圆弧交AC 于点F ，连接DF ．则∠FDC 的度数是 _____．15．如图，A 、B 是⊙O 上的两点，AC 是过A 点的一条直线，如果∠AOB =120°，那么当∠CAB 的度数等于________度时，AC 才能成为⊙O 的切线．16．如图，ABC 是O 的内接三角形．若=45ABC ∠︒，2AC =，则O 的半径是______．三、解答题17．如图，在菱形ABCD 中，90BAD ∠>︒，P 为AC ，BD 的交点，O 经过A ，B ，P 三点．(1)求证：AB 为O 的直径．(2)请用无刻度的直尺在圆上找一点Q ，使得BP =PQ （不写作法，保留作图痕迹）．18．请用圆规、直尺作图，不写作法，但要保留作图痕迹．已知：如图，Rt △ABC 中，∠C ＝90°．求作：一个⊙O ，使⊙O 与AB 、BC 所在直线都相切，且圆心O 在边AC 上．19．如图所示，AB 为⊙O 的直径，在△ABC 中，AB =BC ，AC 交⊙O 于点D ，过点D 作DE ⊥BC ，垂足为点E ．(1)证明DE 是⊙O 的切线；(2)AD =8，P 为⊙O 上一点，P 到弦AD 的最大距离为8．①尺规作图作出此时的P 点，保留作图痕迹；②求DE 的长．20．如图，在Rt ABC △中，90ACB ∠=︒，延长CA 到点D ，以AD 为直径作O ，交BA 的延长线于点E ，延长BC 到点F ，使BF EF =．(1)求证：EF 是O 的切线；(2)若9OC =，4AC =，8AE =，求BE 的长．21．如图，点A ，B ，C ，D 在⊙O 上，AB ＝CD ．求证：AC ＝BD ；<），点E是线段OP的中点．在22．如图，点P是O的直径AB延长线上的一点（PB OB=．求证：PC是O的切线．直径AB上方的圆上作一点C，使得EC EP23．如图，四边形ABCD内接于120，，，求证：ABC是等边三角形．O AB AC ADC=∠=︒24．如图，四边形ABCD是菱形，以AB为直径作⊙O，交CB于点F，点E在CD上，且CE＝CF，连接AE．(1)求证：AE是⊙O的切线；(2)连接AC交⊙O于点P，若3AP ，BF＝1，求⊙O的半径．25．如图，⊙O是以△ABC的边AC为直径的外接圆，∠ACB＝54°，如图所示，D为⊙O上与点B关于AC的对称点，F为劣弧BC上的一点，DF交AC于N点，BD交AC于M点．(1)求∠DBC的度数；(2)若F为弧BC的中点，求MN ON．26．已知P为⊙O上一点，过点P作不过圆心的弦PQ，在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合)，连接AP、BP，若∠APQ=∠BPQ（1）如图1，当∠APQ=45°，AP=1，2⊙O的半径。

(常考题)人教版初中数学九年级数学上册第四单元《圆》测试题(答案解析)

一、选择题1．如图，AB 、AC 是⊙O 的切线，B 、C 为切点，∠A ＝50°，点P 是圆上异于B 、C 的点，则∠BPC 的度数是（）A ．65°B ．115°C ．115°或65°D ．130°或65° 2．如图，点A 、B 、C 在⊙O 上，∠ACB ＝54°，则∠ABO 的度数是（）A ．54°B ．30°C ．36°D ．60°3．如图，AB 是半圆O 的直径，20BAC =︒∠，则D ∠的度数是（）A ．70°B ．100°C ．110°D ．120° 4．已知O 的直径10CD cm ，AB 是O 的弦，AB CD ⊥，垂足为M ，且8AB cm =，则AC 的长为（） A ．25 B ．43 C ．25或45 D ．23或43 5．如图，在ABC 中，90C ∠=︒，7AB =，4AC =，以点C 为圆心、CA 为半径的圆交AB 于点D ，求弦AD 的长为（）A 433B ．327C 233D ．1676．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（）A ．13cmB ．12cmC ．11cmD ．10cm 7．中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花，图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到12AC BD cm ==，C ，D 两点之间的距离为3cm ，圆心角为60︒，则图中摆盘的面积是（）A ．212cm πB ．224cm πC ．236cm πD ．248cm π 8．如图，在⊙O 中，AB 是直径，弦AC=5，∠BAC=∠D ．则AB 的长为（）A ．5B ．10C ．52D ．102 9．已知O 的半径为4，点P 在O 外，OP 的长可能是（）A ．2B ．3C ．4D ．5 10．如图，PA 、PB 、CD 是O 的切线，切点分别是A 、B 、E ，CD 分别交PA 、PB 于C 、D 两点，若60APB ∠=︒，则COD ∠的度数（）A ．50°B ．60°C ．70°D ．75° 11．如图，AB 是⊙的直径，DB 、DE 分别切⊙O 于点B 、C ，若∠ACE ＝35°，则∠D 的度数是（）A ．65°B ．55°C ．60°D ．70° 12．如图，AB 为圆O 的直径，点C 在圆O 上，若∠OCA =50°，OB =2，则弧BC 的长为（）A ．103πB ．59π C ．109π D ．518π 二、填空题13．已知ABC 的周长为30，面积为20，其内角平分线交于点O ，则点O 到边BC 的距离为________．14．如图，AB 、AC 、BD 是O 的切线，P 、C 、D 为切点，如果8AB =，5AC =，则BD 的长为_______．15．如图，点A ，B ，C 在O 上，顺次连接A ，B ，C ，O ．若四边形ABCO 为平行四边形，则AOC ∠=________︒．16．如图，⊙O 是ABC 的外接圆，64A ∠=︒，则OBC ∠=______°．17．如图，点C ，D 是半圈O 的三等分点，直径43AB =．连结AC 交半径OD 于E ，则阴影部分的面积是_______．18．如图，△ABC 中，∠A=60°，若O 为△ABC 的内心，则∠BOC 的度数为______度．19．如图，已知AD 为半圆形O 的直径，点B ，C 在半圆形上，AB BC =，30BAC ∠=︒，8AD =，则AC 的长为________．20．如图，AB 是O 的直径，CD AB ⊥于E ，24CD =，8BE =，则AB =__________．三、解答题21．如图，在矩形ABCD 中，4AB =，6BC =．E 为CD 边上的一个动点（不与C 、D 重合），⊙O 是BCE 的外接圆．（1）若2CE =，⊙O 交AD 于点F 、G ．求FG 的长度；（2）若CE 的长度为m ，⊙O 与AD 的位置关系随着m 的值变化而变化，试探索⊙O 与AD 的位置关系及对应的m 的取值范围．22．如图，已知圆内接四边形ABDC 中，∠BAC ＝60°，AB ＝AC ，AD 为它的对角线．求证：AD ＝BD+CD ．23．如图，已知在△ABC 中，∠A ＝90°．（1）作∠ABC 的角平分线交AC 于点P ，以点P 为圆心，PA 长为半径作⊙P ，则⊙P 与BC 的位置关系是．（2）在（1）的条件下，若AB=3，BC=5，求⊙P 的面积．24．如图，四边形ABCD 为菱形，且120BAD ∠=，以AD 为直径作O ，与CD 交于点P ．请仅用无刻度的直尺按下列要求画图．（保留作图痕迹）（1）在图1中，过点O 作AB 边的平行线OE ；（2）在图2中，过点C 作AB 边上的高CF ．25．如图，在ABC 中，45C ∠=︒，以AB 为直径的O 经过BC 的中点D ．（1）求证：AC 是O 的切线；（2）取AD 的中点E ，连接OE ，延长OE 交AC 于点F ，若2EF =，求O 的半径．26．图①、图②均为 4×4 的正方形网格，线段 AB 、BC 的端点均在格点上，按要求在图①、图②中作图并计算其面积．（1）在图①中画一个四边形 ABCD ，点D 在格点上，使四边形 ABCD 有一组对角相等，并求=四边形ABCD S ．（2）在图②中画一个四边形 ABCE ，点E 在格点上，使四边形 ABCE 有一组对角互补，并求ABCE S =四边形．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据切线的性质得到OB ⊥AB ，OC ⊥AC ，求出∠BOC ，分点P 在优弧BC 上、点P 在劣弧BC 上两种情况，根据圆周角定理、圆内接四边形的性质计算即可．【详解】解：∵AB 、AC 是⊙O 的切线，∴OB ⊥AB ，OC ⊥AC ，∴∠OBA ＝90°，∠OCA ＝90°∵∠A ＝50°，∴∠BOC ＝360°﹣90°﹣90°﹣50°＝130°，如图，当点P 在优弧BPC 上时，∠BPC ＝12∠BOC ＝65°，当点P ′在劣弧BC 上时，∠BP ′C ＝180°﹣65°＝115°，故选：C ．【点睛】本题考查的是切线的性质、圆周角定理、圆内接四边形的性质，掌握圆的切线垂直于经过切点的半径及圆周角定理是解题的关键．2．C解析：C【分析】根据圆周角定理求出∠AOB ，根据等腰三角形的性质求出∠ABO=∠BAO ，根据三角形内角和定理求出即可．【详解】解：∵∠ACB ＝54°，∴圆心角∠AOB ＝2∠ACB ＝108°，∵OB ＝OA ，∴∠ABO ＝∠BAO ＝12（180°﹣∠AOB ）＝36°，故选：C ．【点睛】本题考查了圆周角定理，圆心角、弧、弦之间的关系，等腰三角形的性质和三角形的内角和定理等知识点，能求出圆心角∠AOB 的度数是解此题的关键． 3．C解析：C【分析】先根据圆周角定理可得90ACB ∠=︒，再根据直角三角形的性质可得70B ∠=︒，然后根据圆内接四边形的性质即可得．【详解】AB 是半圆O 的直径，90ACB ∴∠=︒，20BAC ∠=︒，9070B BAC ∴∠=︒-∠=︒，又四边形ABCD 是圆O 内接四边形，180110D B ∴∠=︒-∠=︒，故选：C ．【点睛】本题考查了圆周角定理、直角三角形的性质、圆内接四边形的性质，熟练掌握圆周角定理是解题关键．4．C解析：C【分析】连结OA ，由AB CD ⊥，根据垂径定理可以得到4AM =,结合勾股定理可以得到3OM =．在分类讨论，如图，当8CM =和2CM =时，再结合勾股定理即可求出AC ．【详解】连结OA ，∵AB CD ⊥， ∴118422AM BM AB ===⨯=，在Rt OAM 中，5OA =，∴223OA OM AM -==，当如图时，538CM OC OM =+=+=，在Rt ACM △中，2245AC AM CM =+=，当如图时，532CM OC OM =-=-=，在Rt ACM △中，2225AC AM CM +=故选C ．【点睛】本题考查垂径定理“垂直于弦的直径平分弦且平分这条弦所对的两条弧”．分类讨论思想也是解决本题的关键．5．B解析：B【分析】过C 作CF ⊥AB 于F ，根据垂径定理得出AD=2AF ，根据勾股定理求BC ，根据三角形面积公式求出CF ，根据勾股定理求出AF 即可．【详解】过C 作CF ⊥AB 于F ，∵CF⊥AB，CF过圆心C，∴AD=2AF．∵△ABC中，∠ACB是直角，AC=4，AB=7，∴由勾股定理得：22227433AB AC-=-=由三角形的面积公式得：AC×BC=AB×CF，即33=7CF，∴433在△AFC中，由勾股定理得：222243316477 AC CF⎛⎫-=-=⎪⎪⎝⎭，∴AD=2AF=327．故选：B．【点睛】本题考查了勾股定理，垂径定理，三角形的面积等知识点的应用，关键是求出AF的长．6．B解析：B【分析】先根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到12•2π•5•OA=65π，可求出OA=13，然后利用勾股定理计算圆锥的高．【详解】解：根据题意得12•2π•5•OA=65π，解得：OA=13，所以圆锥的高2213512．故选：B．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．7．C解析：C【分析】首先证明△OCD 是等边三角形，求出OC=OD=CO=3cm ，再根据S 阴影=S 扇形OAB -S 扇形OCD ，求解即可．【详解】解：如图，连结CD ．∵OC=OD ，∠O=60°，∴△OCD 是等边三角形，∴OC=OD=CO=3cm ，∴OA=OC+AC=15cm ，∴OB=OA=15cm ，∴S 阴影=S 扇形OAB -S 扇形OCD =226015603360360ππ⋅⋅⋅⋅-=236cm π．故选C ．【点睛】本题考查了扇形的面积，等边三角形的性质与判定等知识．扇形的面积=2360n r π︒． 8．C解析：C【分析】根据圆周角定理得出∠D=∠B ，得出△ABC 是等腰直角三角形，进而解答即可．【详解】∵AC=AC ，∴∠D=∠B ，∵∠BAC=∠D ，∴∠B=∠BAC ，∴△ABC 是等腰三角形，∵AB 是直径，∴△ABC 是等腰直角三角形，∵AC=5，∴AB=52故选：C ．【点睛】本题考查了圆周角定理，等腰直角三角形的判定和性质，勾股定理的应用，关键是根据圆周角定理得出∠D=∠B ．9．D解析：D【分析】根据题意可以求得OP 的取值范围，从而可以解答本题．【详解】解：∵O 的半径为4，点P 在⊙O 外，∴OP ＞4，故选：D ．【点睛】本题考查点和圆的位置关系，解答本题的关键是明确题意，求出OP 的取值范围． 10．B解析：B【分析】连接AO ，BO ，OE 由切线的性质可得90PAO PBO ︒∠=∠=，结合已知条件和四边形的内角和为360°可求出AOB 的度数，再由切线长定理即可求出COD 的度数.【详解】如图，连接AO ，BO ，OE ，∵PA 、PB 是O 的切线，∴∠PAO =∠PBO =90∘，∵60APB ∠=︒，∴36029060120AOB ∠=︒-⨯︒-︒=︒，∵PA 、PB 、CD 是⊙O 的切线，∴∠ACO =∠ECO ，∠DBO =∠DEO ，∴∠AOC =∠EOC ，∠EOD =∠BOD ， ∴1602COD COE EOD AOB ∠=∠+∠=∠=︒，故选B.【点睛】本题考查了切线的性质及切线长定理，解答本题的关键是熟练掌握：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线，平分两条切线的夹角.11．D解析：D【分析】连结BC ，则由已知可以求得∠BCD 与∠CBD 的度数，最后由三角形的内角和定理可以得到∠D 的度数．【详解】解：如图，连结BC ，则由弦切角定理可知：∠ABC=∠ACE=35°，∵DB 与⊙O 相切，∴∠CBD=90°-∠ABC=90°-35°=55°，∵AB 是⊙的直径，∴∠ACB=90°，∴∠BCD=180°-∠ACE-∠90°=55°，∴∠D=180°-∠BCD-∠CBD=70°，故选D ．【点睛】本题考查圆的应用，灵活运用直线与圆相切的性质求解是解题关键．12．C解析：C【分析】先根据等腰三角形的性质求出∠A ，再利用圆周角定理求得∠BOC ，最后根据弧长公式求求解即可．【详解】解：∵∠OCA =50°，OA =OC ，∴∠A =50°，∴∠BOC =100°∵BO =2， ∴1002101809BC l ππ⨯==．故答案为C ．【点睛】本题主要考查了弧长公式应用以及圆周角定理，根据题意求得∠BOC 是解答本题的关键．二、填空题13．【分析】过O 作OD ⊥BC 于DOE ⊥AB 于EOF ⊥AC 于F 连接OAOBOC 根据三角形的内心和角平分线的性质得出OE=OD=OF 再根据三角形的面积公式求出即可【详解】如图过O 作OD ⊥BC 于DOE ⊥AB 于解析：4 3【分析】过O作OD⊥BC于D，OE⊥AB于E，OF⊥AC于F，连接OA、OB、OC，根据三角形的内心和角平分线的性质得出OE=OD=OF，再根据三角形的面积公式求出即可．【详解】如图，过O作OD⊥BC于D，OE⊥AB于E，OF⊥AC于F，连接OA、OB、OC，∵O是△ABC内角平分线的交点，∴OE=OF=OD，∵△ABC的面积是20，∴S△AOB+S△BOC+S△AOC=20，∴111AB OE BC OD222⨯⨯+⨯⨯+×AC×OF=20，∴(AB+BC+AC)×OD=40，∵△ABC的周长为30，∴AB+BC+AC=30，∴OD=404303=，∴即O到BC的距离是43，故答案为：43．【点睛】本题考查了三角形的内心，角平分线的性质和三角形的面积等知识点，能求出OD=OE=OF 是解此题的关键．14．【分析】由于ABACBD是⊙O的切线则AC=APBP=BD求出BP的长即可求出BD的长【详解】解：∵ACAP为⊙O的切线∴AC=AP∵BPBD为⊙O的切线∴BP=BD∴BD=PB=AB-AP=8-5解析：3【分析】由于AB、AC、BD是⊙O的切线，则AC=AP，BP=BD，求出BP的长即可求出BD的长．【详解】解：∵AC、AP为⊙O的切线，∴AC=AP，∵BP、BD为⊙O的切线，∴BP=BD，∴BD=PB=AB-AP=8-5=3．故答案为：3．【点睛】本题考查了切线长定理，两次运用切线长定理并利用等式的性质是解题的关键．15．120【分析】连接OB先证明四边形ABCD是菱形然后再说明△AOB△OBC 为等边三角形最后根据等边三角形的性质即可解答【详解】解：如图：连接OB∵点在上∴OA=OC=OB∵四边形为平行四边形∴四边形解析：120【分析】连接OB，先证明四边形ABCD是菱形，然后再说明△AOB、△OBC为等边三角形，最后根据等边三角形的性质即可解答．【详解】解：如图：连接OB∵点A，B，C在O上∴OA=OC=OB∵四边形ABCO为平行四边形∴四边形ABCO是菱形∴OA=OC=OB=AB=BC∴△AOB、△OBC为等边三角形∴∠AOB=∠BOC=60°∴∠AOC=120°．故答案为120．【点睛】本题主要考查了圆的性质和等边三角形的性质，根据题意证得△AOB、△OBC为等边三角形是解答本题的关键．16．26【分析】先利用圆周角定理得到∠BOC=2∠A=128°然后根据等腰三角形的性质和三角形内角和定理计算∠OBC的度数【详解】解：∵∠A=64°∴∠BOC=2∠A=128°∵OB=OC∴∠OBC=∠解析：26【分析】先利用圆周角定理得到∠BOC=2∠A=128°，然后根据等腰三角形的性质和三角形内角和定理计算∠OBC的度数．【详解】解：∵∠A=64°，∴∠BOC=2∠A=128°，∵OB=OC，∴∠OBC=∠OCB，∴∠OBC=12（180°-128°）=26°．故答案为26．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．17．【分析】连接OC由点CD是半圆O的三等分点得到根据垂径定理得到OD⊥AC∠DOC=60°求得OE=CE=3根据扇形和三角形的面积公式即可得到结论【详解】解：连接OC∵点CD是半圆O的三等分点∴∴OD解析：33 2π-【分析】连接OC，由点C，D是半圆O的三等分点，得到AD CD CB==，根据垂径定理得到OD⊥AC，∠DOC=60°，求得OE=3，CE=3，根据扇形和三角形的面积公式即可得到结论．【详解】解：连接OC，∵点C，D是半圆O的三等分点，∴AD CD CB ==，∴OD ⊥AC ，∠DOC=60°，∴∠OCE=30°， ∵AB =∴∴CE=3，∴S阴影=S 扇形COD -S △OCE =2601236022ππ⋅⋅-⨯=-．故答案为：22π-．【点睛】本题考查了扇形的面积的计算，垂径定理，含30°角的直角三角形的性质，正确的识别图形是解题的关键． 18．120【分析】根据三角形的内心是三角形角平分线的交点结合公式求出即可【详解】解：为的内心故答案是：120【点睛】注意此题中的结论：若是内心则熟记公式可简化计算解析：120【分析】根据三角形的内心是三角形角平分线的交点，结合公式1902BOC A ∠=+∠︒求出即可．【详解】解：60A ∠=︒，O 为ABC ∆的内心， 1190906012022BOC A ，故答案是：120．【点睛】注意此题中的结论：若O 是内心，则1902BOC A ∠=+∠︒．熟记公式可简化计算． 19．【分析】连接CD 由已知可以得到∠B=120°所以∠D=60°然后在Rt △ACD 中计算AC 即可【详解】解：如图所示连接CD ∵∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4∴AC解析：【分析】连接CD ，由已知可以得到∠B=120°，所以∠D=60°，然后在Rt △ACD 中计算AC 即可．【详解】解：如图所示，连接CD∵AB BC =，30BAC ∠=︒∴∠B=120°∴∠D=60°∵AD 为直径∴∠ACD=90°∴CD=4 ∴AC=43【点睛】本题主要考查圆的内接四边形对角性质，掌握直径所对的圆周角是90°和圆的内接四边形对角互补是解题的关键．20．【分析】连接OD 设的半径为r 则OE=r-8再根据勾股定理求出r 最后根据直径和半径的关系即可解答【详解】解：如图：设的半径为r 则OE=r-8∵AB ⊥CD 于E 且CD=24∴DE=CD=12在Rt △ODE解析：26【分析】连接OD ，设O 的半径为r ，则OE=r-8，再根据勾股定理求出r ，最后根据直径和半径的关系即可解答．【详解】解：如图：设O 的半径为r ，则OE=r-8，∵AB ⊥CD 于E ，且CD=24，∴DE=12CD=12，在Rt △ODE 中，OD=r ，OE=r-8，DE=12，∴OE 2+DE 2=OD 2，∴（r-8）2+122=r 2，解得r=13∴AB=2r=26．故答案为26．【点睛】本题主要考查了垂径定理，正确作出辅助线、构造出直角三角形是解答本题的关键．三、解答题21．（1）2FG =；（2）当704m <<时，⊙O 与AD 相离；当74m =时，⊙O 与AD 相切；当744m <<时，⊙O 与AD 相交【分析】（1）过点O 作OM FG ⊥于点M ，延长MO 交BC 于点N ，连接OG ．在Rt BCE ∆中，利用勾股定理求出BE ，再在Rt OMG ∆中求出MG 即可解决问题．（2）如图1中，当O 与AD 相切于点M 时，连接OM 并反向延长交BC 于点N ．求出相切时，m 的值即可判断．【详解】解：（1）解：过点O 作OM FG ⊥于点M ，延长MO 交BC 于点N ，连接OG ，四边形ABCD 是矩形，90C D ∴∠=∠=︒，BE ∴是O 的直径．90C D DMN ∠=∠=∠=︒，∴四边形MNCD 是矩形，MN BC ∴⊥，4MN CD AB ===，BN CN ∴=．OB OE =，ON ∴是BCE ∆的中位线，112ON CE ∴==， 413OM ∴=-=，在Rt BCE ∆中，22210+=BE BC CE1102OG BE ∴==，在Rt OMG ∆中，221-=MG OG OM ，22FG MG ∴==．（2）解：如图1中，当O 与AD 相切于点M 时，连接OM 并反向延长交BC 于点N ．由（1）易得1122==ON CE m ，142==-OB OM m ，3BN =，在Rt BON ∆中，222+=ON BN OB ，即22211()3(4)22m m +=-，解得74m =， ∴当704m <<时，O 与AD 相离，当74m =时，O 与AD 相切，当744m <<时，O 与AD 相交．【点睛】本题考查直线与圆的位置关系，矩形的性质，垂径定理，三角形的外心等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．22．见解析．【分析】连接BC ，证明∠ADB ＝∠ADC ＝60°，在AD 上取点E 、F ，使DE ＝DB 、DF ＝DC ，连接BE 、CF ，证明△BDE 、△CDF 为正三角形，再证明∠AEB ＝∠CFA ＝120°，∠EAB ＝∠FCA ，证明△ABE ≌△CAF ，可得AE ＝CF ，从而可得结论．【详解】解：连接BC ， ∠BAC ＝60°，AB ＝AC ，∴ △ABC 为等边三角形，∴ ∠ABC ＝∠ACB ＝60°，,,AC AC AB AB ==∴ ∠ADC ＝∠ABC 60,=︒ ∠ADB ＝∠ACB 60,=︒在AD 上取点E 、F ，使DE ＝DB 、DF ＝DC ，连接BE 、CF ，∴△BDE 、△CDF 为等边三角形，∴∠DEB ＝∠DFC ＝60°，,,DE BD CF DC ==∴∠AEB ＝∠CFA ＝120°，又∠FAC+∠FCA ＝∠DFC ＝60°、∠FAC+∠EAB ＝∠BAC ＝60°，∴∠EAB ＝∠FCA ，在△ABE 和△CAF 中，∵EAB FCA AEB CFA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CAF （AAS ），∴AE ＝CF ，∴AD ＝DE+AE ＝BD+FC ＝BD+CD ．【点睛】本题考查的是等边三角形的性质与判定，全等三角形的判定与性质，圆周角定理，掌握以上知识是解题的关键．23．（1）相切；（2）94π 【分析】（1）先利用角平分线的性质得到点P 到BC 的距离等于PA ，然后根据直线与圆的位置关系进行判断．（2）由全等三角形的性质，先求出CD=2，由勾股定理求出AC=4，再利用勾股定理求出PD 的长度即可．【详解】解：（1）作PD ⊥BC ，交BC 于点D ，如图：∵PB 平分∠ABC ，∴点P 到BC 的距离等于PA ，∴PA=PD ，∴BC 为⊙P 的切线．故答案为：相切．（2）由（1）可知，易得△ABP ≌△DBP ，∴BD=AB=3，∴CD=5-3=2，∵在直角△ABC 中，由勾股定理，得 22534AC =-=，设PA PD r ==，∴4PC r =-，在直角△PDC 中，由勾股定理，则()22242r r -=+，解得：32r =， ∴圆的面积为：223924S r πππ==•=()．【点睛】本题考查了圆的定义，勾股定理，角平分线的性质，全等三角形的判定和性质，解题的关键是熟练掌握所学的知识，正确的进行解题．24．（1）见解析；（2）见解析【分析】（1）连接BD 、AC 交于点E ，连接OE ；（2）连接BD ，则点P 和BD 与O 的交点的延长线与AB 的交点即为F 点．【详解】（1）如图所示，∵四边形ABCD 是菱形，∴E 是BD 中点，∵O 是DA 中点，∴//OE AB ；（2）如图所示，∵120BAD ∠=，∴60ADC ∠=︒，∵AD CD =，∴ACD △是等边三角形，∵AD 是直径，∴90APD ∠=︒，即AP DC ⊥，∴P 是CD 中点，通过如图所示找到的点F 是AB 的中点，∵ABC 也是等边三角形，∴CF AB ⊥．【点睛】本题考查作图，解题的关键是要熟悉各种几何的性质，比如：等边三角形的性质，中位线的性质，菱形的性质，圆的性质．25．（1）见解析；（2）22+ 【分析】（1）连接AD ，先由圆周角定理得∠ADB ＝90°，则AD ⊥BC ，再由线段垂直平分线的性质得AB ＝AC ，则∠B ＝∠C ＝45°，求得∠BAC ＝90°，即可得出结论；（2）作EH ⊥OF 交AF 于H ，则EH 是⊙O 的切线，先由垂径定理得OE ⊥AD ，AG ＝DG ，再证出△EFH 是等腰直角三角形，得EH ＝EF ＝2，则FH ＝2EF ＝2，然后由切线长定理得AH ＝EH ＝2，则AF ＝AH ＋FH ＝2＋2，最后由等腰直角三角形的性质得OA ＝AF ＝2＋2即可．【详解】（1）证明：连接AD ，如图所示：∵AB 是⊙O 的直径，∴∠ADB ＝90°，OA 是⊙O 的半径，∴AD ⊥BC ，∵D 是BC 的中点，∴AB ＝AC ，∴∠B ＝∠C ＝45°，∴∠BAC ＝180°−45°−45°＝90°，∴AC ⊥OA ，∴AC 是⊙O 的切线；（2）解：作EH ⊥OF 交AF 于H ，如图所示：则EH 是⊙O 的切线，∵E是AD的中点，∴OE⊥AD，AG＝DG，∵AD⊥BC，∴OF∥BC，∴∠EFH＝∠C＝45°，∵EH⊥OF，∴△EFH是等腰直角三角形，∴EH＝EF2FH2EF＝2，∵AC是⊙O的切线，∴AH＝EH2∴AF＝AH＋FH2＋2，由（1）得：∠BAC＝90°，∴△AOF是等腰直角三角形，∴OA＝AF2＋2，即⊙O2＋2．【点睛】本题考查了切线的判定与性质、圆周角定理、垂径定理、线段垂直平分线的性质、等腰三角形的判定与性质等知识；熟练掌握切线的判定与性质、垂径定理和圆周角定理是解题的关键．26．（1）图见详解，6 ；（2）图见详解，4.5【分析】（1）过C画AB的平行线，过A画BC的平行线，两线交于一点D，根据平行四边形的判定定理可得四边形ABCD是平行四边形，由平行四边形的性质可知∠CBA=∠CDA，然后用用割补法求出面积即可；（2）根据图中正方形网格和∠B的特点，作出∠E与∠B互补，然后用割补法求面积即可．【详解】解：（1）如图，S四边形ABCD=3×4-122⨯×2-222⨯-112⨯=6；（2）如图，S四边形ABCE=3×3-122⨯×2-222⨯-112⨯=92．【点睛】此题主要考查了应用设计作图，首先要理解题意，弄清问题中对所作图形的要求，然后利用割补法求面积．。

初中九年级数学圆测试题及答案

初中九年级数学圆测试题及答案与圆有关的位置关系圆与点的位置关系有三种：点在圆外、点在圆上、点在圆内。

对应的点到圆心的距离d和半径r之间的数量关系分别为：d。

r、d = r、d < r。

直线与圆的位置关系有三种：相交、相切、相离。

对应的圆心到直线的距离d和圆的半径r之间的数量关系分别为：d。

r。

圆与圆的位置关系有五种：内含、相内切、相交、相外切、外离。

两圆的圆心距d和两圆的半径R、r（R≥r）之间的数量关系分别为：d。

R+r。

圆的切线垂直于过切点的半径；经过直径的一端，并且垂直于这条直径的直线是圆的切线。

从圆外一点可以向圆引两条切线，切线长相等，这点与圆心之间的连线平分这两条切线的夹角。

与圆有关的计算圆的周长为2πr，1°的圆心角所对的弧长为πr/180，n°的圆心角所对的弧长为nπr/180，弧长公式为l=nπr。

圆的面积为πr^2，1°的圆心角所在的扇形面积为πr^2/360，n°的圆心角所在的扇形面积为S=nπr^2/360（n为圆心角的度数，R为圆的半径）。

圆锥的侧面积公式：S=πrl（其中r为底面的半径，l为母线的长）。

圆锥的侧面积与底面积之和称为圆锥的全面积。

圆柱的侧面积公式：S=2πrl（其中r为底面圆的半径，l为圆柱的高）。

4．已知∠BOC为130°，O是△XXX的内心，求∠A的度数。

解析：由内心的性质可知，∠BOC=2∠A，所以∠A=65°，选项B。

5．已知∠A=100°，∠C=30°，求∠DFE的度数。

解析：由内切圆的性质可知，∠DFE=90°-1/2(∠A+∠C)=55°，选项A。

6．将羊拴在使草地上活动区域面积最大的位置，即正方形的对角线中点处，选项B。

7．两圆心距离等于半径之差的情况为内含，等于半径之和的情况为外切，大于半径之和小于半径之差的情况为相交，两圆心距离为3，所以为相交，选项C。

中考数学-圆经典必考题型中考试题集锦(附答案)解答题

中考数学圆经典必考题型中考试题（附答案）解答题1.（已知：如图，△ ABC 内接于O O 过点B 作的切线，交 CA 的延长线于点 E / EB & 2① 求证：AB= AC1AB ② 若tan / ABE=丄，（i ）求的值；（ii ）求当 AC= 2时，AE 的长. 2BC=4cm 求O o 的半径.2.如图,PA 为O O 的切线, A 为切点，O 0的割线PBC 过点0与O O 分别交于B 、C, PA= 8cm PB3.已知：如图，BC 是O 0的直径，AC 切O 0于点C AB 交O 0于点D,若AD ： DB= 2 : 3, AC= 10,求 sin B 的值.4.如图，PC 为O 0的切线，C 为切点，PAB 是过0的割线,1若tan B= _ , PC= 10cm 求三角形BCD的面积.25•如图，在两个半圆中，大圆的弦MNW小圆相切，D为切点，且MN AB MN a, ON CD分别为两圆的半径，求阴影部分的面积.6.已知，如图，以△ ABC的边AB作直径的O O分别并AC BC于点D E,弦FG// AB S A CDE S△ ABC= 1 : 4, DE= 5cm FG= 8cm,求梯形AFG啲面积.7.如图所示：PA为O O的切线，A为切点，PBC是过点O的割线,PA= 10, PB= 5，求：(1)O O的面积(注：用含n的式子表示)；(2)cos / BAP的值.参考答案1.( 1)v BE 切O O 于点 B ,「. / ABE=Z C./ EBC= 2/ C,即 / ABH / ABC= 2/C,/ C +Z ABO 2 / C,/ ABC=Z C, ••• AB= AC.(2)①连结AO 交BC 于点F ,AB- AC, AOL BC 且 BF = FC.AF 在 Rt A ABF 中， =tan / ABF BF1 又 tan / ABF= tan C = tan / ABE=2 AF = 1 BF.AB AB .5BC 2BF4 ②在△ EBA M^ ECB 中 ,^EA 2- EA- (EA^ AC ),又 EA M 0 , 5 11EA= AC EA= — x 2 = 10 .5 11 11 22 •设O 的半径为r ,由切割线定理，得 PA = PB- PCAC 切O O 于点C,线段ADB 为O O 的割线,2AC = AD- ABAB= AM DB= 2k + 3k = 5k ,2 210 = 2k X 5k,••• k = 10,AB= AF 2 * * * BF 2BF 2 AF = 1BF 2/ E =Z E , / EBA=Z ECB△ EBA^A ECBEAEBBE 2 AB BC ,解之，得 EA ECk> 0,「. k= 10 .AB= 5k= 10 .AC切O O于C, BC为O O的直径,ACL BC在Rt A ACB中, sin B=虫10 10 .AB 5 屁5CD L AB于点D,/ADC=Z BD= 90°,/ 2= 90°—/ BAC=Z B.1tan B=2tan / 2=—.2AD CD 1 ACCD DB 2 CB .设AD= x (x > 0), CD= 2x, DB= 4x, AB= 5x .•/ PC切O O于点C,点B在O O上，• / 1 = / B./ P=/ P,「. △ PAC^ PCBPA AC 1PC CB 2 .PC= 10,「. PA= 5,PC 切O O 于点C, PAB 是O 0的割线,2PC = PA- PB210 = 5 (5 + 5 x ).解得 x = 3.AD= 3, CD= 6, DB= 12.1 1S ^BCD = CD" DB= — x 6X 12 = 36.2 22即三角形BCD 的面积36cm .PA= 10,二 PB= 20.2由切割线定理，得 PC = PA- PBA 內 DB= x + 4x = 15,解得 x = 3,CD= 2x = 6, DB= 4x = 12.S A BCD = ^CD- DB= 1 x 6X 12= 36.2 22即三角形BCD 的面积36cm .5.解：如图取 MN 的中点E 连结OE解法二：同解法一，由△ PAC^A PCB 得 PA PC AC CBPB 101220 AB= PB- PA= 15,2 2 2 a在 Rt A NOE 中 NO- OE = EN =2 6.解：T / CDE=/ CBA / DCE=/ BCA /• △ CDE^A ABC2S CDEDE S ABC AB DE = S CDE =任=1AB S ABC ' 42 ' 51 即，解得 AB= 10 (cm ,AB 2作OML FG 垂足为M11 则 FM= ^FG=丄^ 8= 4 (cm),22连结OF 11 OA= AB= — x 10= 5 (cm ).2 2OF= OA= 5 (cm ).在Rt A OMF 中由勾股定理，得 OM = . OF 2 FM 2 = -52 42 = 3 (cm ).A B FG10 Q 2 ••• 梯形 AFG 啲面积= -------------- • OM= -------- x 3 = 27 (cm ).2 27. 2 1 a n2 n ・ — =—a 2 2 8 2 2 1n( NO — OE ) 2 （平方单位）. (2) CBAP AC PA △ ACP^A BAP —— P P AB PBAC 2AB 1S阴影 ⑴PA 是。

人教版九年级数学上册第24章《圆》选择专项练习题(含答案)

人教版九年级数学上册第24章《圆》选择专项练习题 1．若⊙A 的半径为5，圆心A 与点P 的距离是25，则点P 与⊙A 的位置关系是（） A ．P 在⊙A 上 B ．P 在⊙A 外 C ．P 在⊙A 内 D ．不确定 2．扇形的半径为20cm ，扇形的面积2100cm π，则该扇形的圆心角为（） A ．120︒ B ．100︒ C ．90︒ D ．60︒ 3．在下列命题中，正确的是（）A ．长度相等的弧是等弧B ．直径所对的圆周角是直角C ．三点确定一个圆D ．三角形的外心到三角形各边的距离相等 4．如图，点A 、B 、C 是⊙O 上的三个点，若∠AOB ＝82°，则∠C 的度数为（）A ．82°B ．38°C ．24°D ．41° 5．如图，AB 是O 的直径，点E ，C 在O 上，点A 是EC 的中点，过点A 画O 的切线，交BC 的延长线于点D ，连接EC ．若58.5ADB ∠=︒，则ACE ∠的度数为（）A ．29.5︒B ．31.5︒C ． 58.5︒D ．63︒ 6．如图，在⊙O 中，半径r ＝5，弦AB ＝8，P 是弦AB 上的动点（不含端点A ，B ），若线段OP 长为正整数，则点P 的个数有（）A ．2个B ．5个C ．4个D ．3个 7．已知⊙O 的直径为12，直线l 上有一点P ，OP ＝6，则直线l 与⊙O 的位置关系是（）A．相交B．相切C．相离D．相切或相交8．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16cm，则球的半径为（）A．103cm B．10cm C．102cm D．83cm9．一个圆锥体底面半径为3cm，高为4cm，则这个圆锥体的侧面积为（）A．12πcm²B．28πcm²C．15πcm²D．20πcm²10．如图，A，B，C是⊙O上的三个点，若∠B＝32°，则∠AOC＝（）A．64°B．58°C．68°D．55°11．如图，BD是⊙O的直径，点A、C在圆上，且CD＝OB，则∠BAC＝（）A．120°B．90°C．60°D．30°12．下列命题：①平⾏四边形是中⾏对称图形，也是轴对称图形；②直径是最长的弦，半径是最短的弦；③过切点的直线是圆的切线；④三角形的外⾏是三条边垂直平分线的交点；⑤三角形的内⾏是三条内角平分线的交点；其中正确的有（）A．1个B．2个C．3个D．4个13．如图，PA、PB切⊙O于点A、B，PA＝10，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是（）A．10 B．18 C．20 D．2214．下列关于圆的说法，正确的是（）A．在同圆或等圆中，相等的弦所对的圆周角相等B．平分弦的直径垂直于弦C．圆的每一条直径所在的直线都是它的对称轴D．过三点可以作一个圆15．一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合，且与边AB、CD相交于G、H（如图）.图中阴影部分的面积记为S，三条线段GB、BC、CH的长度之和记为l，大正六边形在绕点O旋转过程中，下列说法正确的是（）A．S变化，l不变B．S不变，l变化C．S变化，l变化D．S与l均不变16．下列四个命题：①直角三角形斜边上的中线等于斜边的一半；②对角线相等的平行四边形是菱形；③一组邻边相等的矩形是正方形；④三角形三条角平分线的交点是三角形的外心．其中真命题共有（）A．1个B．2个C．3个D．4个17．下列说法正确的是（）A．三角形三条中线的交点是三角形重心B．等弦所对的圆周角相等C．长度相等的两条弧是等弧D．三角形的外心到三边的距离相等18．如图，四边形ABCD内接于⊙O，若∠C＝100°，则∠A的度数是（）A ．80°B ．100°C ．110°D ．120°19．下列说法正确的是（）A ．等弧所对的圆心角相等B ．同弦所对的圆周角相等C ．经过三点可以作一个圆D ．相等的圆心角所对的弧相等20．如图，P 是O 外一点，PA 、PB 切O 于点A 、B ，点C 在优弧AB 上，若68P ∠=︒，则ACB ∠等于( )A ．22︒B ．34︒C ．56︒D ．68︒21．有四个命题：①直径相等的两个圆是等圆 ②长度相等的两条弧是等弧；③圆中最大的弦是过圆心的弦；④圆周角是圆心角的一半．其中真命题是（）A ．①③B ．①③④C ．①④D ．④22．⊙O 的直径是10，两平行弦的长度分别是6和8，那么这两弦的距离是（） A ．1 B ．7 C ．8 D ．1或723．△ABC 的顶点都在⊙O 上，若∠BOC ＝120°，则∠BAC 等于（）A ．60°B ．90°C ．120°D ．60°或120° 24．如图，OA 为⊙O 的半径，弦BC ⊥OA 于点P ．若BC =8，AP =2，则⊙O 的半径长为（）A ．5B ．6C ．10D 1725．如图，两个同心圆的半径分别是3cm 和5cm ，大圆的一条弦AB 与小圆相切，则弦ABA ．3cmB ．4cmC ．6cmD ．8cm26．如图，已知O 的半径为2，AC 与O 相切，连接AO 并延长，交O 于点B ，过点C 作CD AB ⊥，交O 于点D ，连接BD ，若30A ∠=︒，则弦BD 的长为（）A ．3B ．5C ．23D ．3227．下列说法正确的是（）A ．在同一平面内，三点确定一个圆B ．等弧所对的圆心角相等C ．旋转会改变图形的形状和大小D ．平分弦的直径垂直于弦28．如图，⊙O 内切于ABC ，切点分别为D ，E ，F ．已知50B ∠=︒，60C ∠=°，连接OE ，OF ，DE ，DF ，那么EDF ∠等于（）A ．40︒B ．55︒C ．65︒D ．70︒29．下列语句中：①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤圆内接四边形的对角互补；⑥在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等，不正确的有（）A ．5个B ．4个C ．3个D ．2个30．用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应该假设这个三角A ．有一个内角小于60°B ．每一个内角都小于60°C ．有一个内角大于60°D ．每一个内角都大于60°31．AB ＝12cm ，过A 、B 两点画半径为6cm 的圆，能画的圆的个数为（） A ．0个 B ．1个 C ．2个 D ．无数个 32．“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”用现在的几何语言表达即：如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长度是（）A ．12寸B ．24寸C ．13寸D ．26寸33．如图，将边长为a 的正六边形123456A A A A A A 在直线l 上由图1的位置按顺时针方向向右作无滑动滚动，当正六边形旋转一周滚动到图2位置时，顶点1A 所经过的路径（）A 843a +B 423a +C 43a +D 423a + 34．已知⊙O 的半径为1，点P 在⊙O 外，则OP 的长（）A ．大于1B ．小于1C ．大于2D ．小于235．如图，在Rt △ABC 中，∠ACB =90°， AC =3，以点C 为圆心、CA 为半径的圆与AB 交于点D ，若点D 巧好为线段AB 的中点，则AB 的长度为（）A．32B．3 C．6 D．936．如图所示，在⊙O中，AB AC=，∠A＝30°，则∠B＝（）A．150°B．75°C．60°D．15°37．如图，F为正方形ABCD的边CD上一动点，AB＝2．连接BF，过A作AH⊥BF交BC于H，交BF于G，连接CG，当CG为最小值时，CH的长为（）A．2B．225C．3﹣5D．3+538．如图，ABC内接与O，50A∠=，E是边BC的重点，连接OE并延长，交O于点D，连接BD，则DBC∠的大小为（）A．55°B．6 C．25°D．75°39．已知圆心角为120°的扇形的面积为12π，则扇形的半径为（）A ．4B ．6C ．43D ．6240．如图O 的直径AB 垂直于弦CD ，垂足是E ，225A ∠=︒．，4OC =，CD 的长为（）A ．22B ．4C ．42D ．841．如图，AB 是⊙O 的直径，点C 在⊙O 上，∠ABC ＝30°，AC ＝1，则⊙O 的半径为（）A ．1B ．2C ．3D ．2342．如图，点A 、B 、C 是⊙O 上的三个点，若∠AOB ＝66°，则∠C 的度数为（）A ．33°B ．34°C ．44°D ．46°43．已知⊙O 的直径是10，圆心O 到直线l 的距离是5，则直线l 和⊙O 的位置关系是（） A ．相离 B ．相交 C ．相切 D ．无法确定 44．下列说法中一定正确的是（）A ．相等的圆心角所对的弧相等B ．圆上任意两点间的部分叫做圆弧C ．平分弦的直径垂直于弦D ．圆周角等于圆心角的一半45．已知O 的半径为2，点P 为O 内一定点，且1PO =，过点P 作O 的弦，其中最短的弦的长度是（）A．4 B．3C．23D．246．如图，AB是☉O的直径，∠CAB=40°，则∠D=（）A．60°B．30°C．40°D．50°47．下列说法：①优弧比劣弧长；②三点可以确定一个圆；③长度相等的弧是等弧；④经过圆内的一个定点可以作无数条弦；其中不正确的个数是（）A．1个B．2个C．3个D．4个48．将一个底面半径为6cm，母线长为15cm的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是( )A．54︒B．126︒C．136︒D．144︒49．如图，⊙O的直径CD垂直弦AB于点E，且CE＝4，OB＝8，则AB的长为（）A．3B．4 C．6 D．350．已知⊙O半径为6，圆心O在坐标原点上，点P的坐标为（3，4），则点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O上C．点P在⊙O外D．不能确定51．⊙O的半径为5，点P到圆心O的距离为5，点P与⊙O的位置关系是（）A．点P在⊙O内B．点P在⊙O外C．点P在⊙O上D．无法确定52．如图．在⊙O中，直径AB⊥CD，下列说法不正确的是（）A．AB是最长的弦B．∠ADB＝90°C．PC=PD D．∠ABD＝2∠ADC53．如图，在Rt ABC中，∠ACB＝90°，∠A＝54°，以BC为直径的⊙O交AB于点D．E是⊙O上一点，且CE＝CD，连接OE．过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为（）A．92°B．108°C．112°D．124°54．如图，Rt△ABC的直角顶点C在⊙O上滑动，且各边与⊙O分别交于点D，E，F，G，若EF，DG，DE的度数比为2：3：5，BE＝BF，则∠A的度数为（）A．30°B．32°C．34°D．36°55．如图，MN是⊙O的直径，MN=2，点A在⊙O上，∠AMN=40°，B为弧AN的中点，P 是直径MN上一动点，则PA+PB的最小值为（）A．5B．3C．5D．356．如图，正方形ABCD的四个顶点分别在⊙O上，点P是弧CD上不同于点C的任意一点，则∠BPC＝（）A．45°B．60°C．75°D．90°57．如图，点A、B、P在⊙O上，且∠APB＝50°．若点M是⊙O上的动点，要使△ABM为等腰三角形，则所有符合条件的点M有（）A．1个B．2个C．3个D．4个58．O的半径为6cm，圆心O到直线l的距离为7cm，则直线l与O的位置关系是（）A．相交B．相切C．相离D．不能确定59．如图，已知直线334y x=-与x轴、y轴分别交于A、B两点，P在以C（0，1）为圆心，1为半径的圆上一动点，连结PA、PB，则△PAB面积的最小值为（）A．5.5 B．10.5 C．8 D．1260．如图，⊙O的半径为2，定点P在⊙O上，动点A，B也在⊙O上，且满足∠APB＝30°，C为PB的中点，则点A，B在圆上运动的过程中，线段AC的最大值为（）A．3B3C．3 2 D．3参考答案1．C2．C3．B4．D5．B6．D7．D8．B9．C10．A11．C12．B13．C14．C15．D16．B 17．A18．A19．A20．C21．A22．D23．D24．A25．D26．C27．B28．B29．A30．D 31．B32．D33．B34．A35．C36．B37．C38．C39．B40．C41．A42．A43．C44．B 45．C46．D47．C48．D49．D50．A51．C52．D53．B54．D55．B56．A57．D58．C 59．A60．A。

九年级上数学圆的测试题

九年级上数学圆的测试题一、选择题（每题3分，共15分）1. 已知⊙O的半径为5cm，点A到圆心O的距离OA = 3cm，则点A与⊙O的位置关系为（）A. 点A在圆上。

B. 点A在圆内。

C. 点A在圆外。

D. 无法确定。

解析：当点到圆心的距离d＜r（r为圆半径）时，点在圆内。

已知圆O半径r = 5cm，OA=3cm，因为3＜5，所以点A在圆内，答案为B。

2. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB = 10，AE = 2，则弦CD的长为（）A. 4.B. 6.C. 8.D. 10.解析：连接OC，因为AB = 10，所以OC=OB = 5，AE = 2，则OE=OA - AE=5 - 2 = 3。

在Rt△OCE中，根据勾股定理CE=√(OC^2)-OE^{2}=√(5^2)-3^{2}=√(16) = 4。

因为CD⊥AB，所以CD = 2CE = 8，答案为C。

3. 圆锥的底面半径为3cm，母线长为5cm，则它的侧面积为（）A. 15πcm².B. 30πcm².C. 45πcm².D. 60πcm².解析：圆锥侧面积公式为S=π rl（r为底面半径，l为母线长）。

已知r = 3cm，l = 5cm，则侧面积S=π×3×5 = 15πcm²，答案为A。

4. 如图，在⊙O中，弧AB = 弧AC，∠AOB = 40°，则∠ADC的度数是（）A. 40°.B. 30°.C. 20°.D. 15°.解析：因为弧AB = 弧AC，所以∠AOB=∠AOC = 40°，圆周角∠ADC所对的弧为弧AC，根据圆周角定理，同弧所对圆周角是圆心角的一半，所以∠ADC=(1)/(2)∠AOC=(1)/(2)×40° = 20°，答案为C。

5. 已知⊙O的半径为4，圆心O到直线l的距离为3，则直线l与⊙O的位置关系是（）A. 相交。

(常考题)人教版初中数学九年级数学上册第四单元《圆》测试题(含答案解析)(1)

一、选择题1．在ABC 中，90,4,3C AC BC ∠=︒==，把它绕AC 旋转一周得一几何体，该几何体的表面积为（）A ．24πB ．21πC ．16.8πD ．36π2．如图，,AB AC 分别是O 的直径和弦，OD AC ⊥于点,D 连接,BD BC ．若10,8AB AC ==，则BD 的长是（）A ．25B ．4C ．213D ．2453．如图，AB 是⊙O 的弦，AO 的延长线交过点B 的⊙O 的切线于点C ，如果∠ABO =30°，则∠C 的度数是（）A ．70°B ．45°C ．30°D ．20°4．如图，AB 是半圆O 的直径，20BAC =︒∠，则D ∠的度数是（）A ．70°B ．100°C ．110°D ．120° 5．点P 到圆上各点的最大距离为10cm ，最小距离为6cm ，则此圆的半径为（）A ．8cmB ．5cm 或3cmC ．8cm 或2cmD ．3cm 6．已知⊙O ，如图，（1）作⊙O 的直径AB ；（2）以点A 为圆心，AO 长为半径画弧，交⊙O 于C ，D 两点；（3）连接CD 交AB 于点E ，连接AC ，BC ．根据以上作图过程及所作图形，有下面三个推断：①CE DE =；②3BE AE =；③2BC CE =．其中正确的推断的个数是（）A ．0个B ．1个C ．2个D ．3个 7．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（） A ．13cmB ．12cmC ．11cmD ．10cm 8．如图，⊙O 的半径为2，四边形ADBC 为⊙O 的内接四边形，AB ＝AC ，∠D ＝112.5°，则弦BC 的长为（）A ．2B ．2C ．22D ．23 9．如图，AB 为⊙O 的直径，,C D 为⊙O 上的两点，若7OB BC ==．则BDC ∠的度数是（）A ．15︒B ．30C ．45︒D ．60︒10．如图，⊙P 与y 轴相切于点C （0，3），与x 轴相交于点A （1，0），B （7，0），直线y=kx-1恰好平分⊙P 的面积，那么k 的值是（）A ．12B ．45C ．1D ．4311．如图，在△ABC 中，（1）作AB 和BC 的垂直平分线交于点O ；（2）以点O 为圆心，OA 长为半径作圆；（3）⊙O 分别与AB 和BC 的垂直平分线交于点M ，N ；（4）连接AM ，AN ，CM ，其中AN 与CM 交于点P ．根据以上作图过程及所作图形，下列四个结论：①BC ＝2NC ；②AB ＝2AM ；③点P 是△ABC 的内心；④∠MON ＋2∠MPN ＝360°．其中正确结论的个数是（）A ．1B ．2C ．3D ．4 12．一个圆锥的底面直径为4 cm ，其侧面展开后是圆心角为90°的扇形，则这个圆锥的侧面积等于（）A ．4πcm 2B ．8πcm 2C ．12πcm 2D ．16πcm 2第II 卷（非选择题）请点击修改第II 卷的文字说明参考答案二、填空题13．如图，点A ，B ，C 在圆O 上，54ACB ∠=︒，则ABO ∠的度数是______．14．如图，PA ，PB 是O 的切线，A ，B 为切点，AC 是O 的直径，35BAC ∠=︒，则P ∠的度数为________.15．已知扇形的圆心角为120︒，面积为π，则扇形的半径是___________．16．ABC 是边长为5的等边三角形，点D 在ABC 的外部且30BDC ∠=︒，则AD 的最大值是______．17．已知O 的直径10AB =cm ，CD 是O 的弦，AE CD ⊥，垂足为点E ，BF CD ⊥，垂足为点F ，且8CD =cm ，则BF AE -的长为________cm ．18．如图，已知AB 是O 的直径，点C ，D 在O 上，2BC =，30CDB ∠=︒，则O 的半径为_____．19．如图，在Rt △ABC 中，∠C ＝90°，AC ＝3cm ，BC ＝4cm ，若以C 为圆心，r 为半径所作的圆与斜边AB 相切，则r 的值是________20．湖州南浔镇河流密如蛛网，民间有“千步一桥”之说．如图，某圆弧形桥拱的跨度AB =12米，拱高CD =4米，则该拱桥的半径为____米．三、解答题21．如图，在平面直角坐标系中有一矩形ABCD （每一小格为一个单位长度），将矩形ABCD 绕着点A 逆时针旋转90°后得到新的图形．（1）请画出旋转后的图形，旋转后C 点对应点的坐标为______．（2）请计算点C 在旋转过程中的路径长．22．如图，四边形ABCD 为菱形，且120BAD ∠=，以AD 为直径作O ，与CD 交于点P ．请仅用无刻度的直尺按下列要求画图．（保留作图痕迹）（1）在图1中，过点O 作AB 边的平行线OE ；（2）在图2中，过点C 作AB 边上的高CF ．23．如图，以点O 为圆心的两个同心圆中，大圆的弦AB 是小圆的切线，点P 为切点．求证：AP=BP ．24．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm 2，求大正方形的面积．25．如图，O 中，AB CD =，A C ∠=∠，AB 与CD 交于点P ．求证=DP BP ．26．如图，长方形的长为a ，宽为2a ，用整式表示图中阴影部分的面积，并计算当2a =时阴影部分的面积（π取3.14）．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】以直线AC 为轴旋转一周所得到的几何体的表面积是圆锥的侧面积加底面积，根据圆锥的侧面积公式计算即可．【详解】解：根据题意得：圆锥的底面周长6π=，所以圆锥的侧面积165152ππ=⨯⨯=，圆锥的底面积239ππ=⨯=，所以以直线AC 为轴旋转一周所得到的几何体的表面积15924πππ=+=．故选：A ．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了扇形的面积公式．2．C解析：C【分析】先根据圆周角定理得∠ACB=90°，则利用勾股定理计算出BC=6，再根据垂径定理得到CD=AD=12AC=4，然后利用勾股定理计算BD 的长．【详解】解：∵AB 为直径，∴∠ACB=90°，∴22221086BC AB AC =-=-=，∵OD ⊥AC ，∴CD=AD=12AC=4，在Rt △CBD 中，BD ==故选：C ．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．也考查了垂径定理．3．C解析：C【分析】由BC 是⊙O 的切线，OB 是⊙O 的半径，得到∠OBC =90°，根据等腰三角形的性质得到∠A =∠ABO =30°，由外角的性质得到∠BOC =60°，即可求得∠C =30°．【详解】∵BC 是⊙O 的切线，OB 是⊙O 的半径，∴∠OBC =90°，∵OA =OB ，∴∠A =∠ABO =30°，∴∠BOC =60°，∴∠C =30°．故选：C ．【点睛】本题考查了切线的性质，等腰三角形的性质，三角形的外角性质，解题的关键是灵活运用所学知识解决问题．4．C解析：C【分析】先根据圆周角定理可得90ACB ∠=︒，再根据直角三角形的性质可得70B ∠=︒，然后根据圆内接四边形的性质即可得．【详解】AB 是半圆O 的直径，90ACB ∴∠=︒，20BAC ∠=︒，9070B BAC ∴∠=︒-∠=︒，又四边形ABCD 是圆O 内接四边形，180110D B ∴∠=︒-∠=︒，故选：C ．【点睛】本题考查了圆周角定理、直角三角形的性质、圆内接四边形的性质，熟练掌握圆周角定理是解题关键．5．C解析：C【分析】分析题意，本题应分两种情况讨论：（1）点P在圆内；（2）点P在圆外；根据“一个点到圆的最大距离和最短距离都在过圆心的直线上”可知，点P到圆的最大距离与最小距离的和或差即是圆的直径，进而即可得出半径的长．【详解】当点P在圆内时，圆的直径是10+6=16cm，所以半径是8cm．当点P在圆外时，圆的直径是10-6=4cm，所以半径是2cm．故选C．【点睛】本题考查了圆的有关性质，熟知一个点到圆的最大距离和最短距离都在过圆心的直线上是解题的关键．6．D解析：D【分析】①根据作图过程可得AC AD=，根据垂径定理可判断；②连接OC，根据作图过程可证得△AOC为等边三角形，由等边三角形的性质即可判断；③根据直角三角形中30°角所对的直角边等于斜边的一半即可判断．【详解】解：①∵以点A为圆心，AO长为半径画弧，交⊙O于C，D两点，∴AC AD=，根据垂径定理可知，AB⊥CE，CE=DE，∴①正确；②连接OC，∵AC=OA=OC，∴△AOC为直角三角形，∵AB⊥CE，∴AE=OE，∴BE=BO+OE=3AE，∴②正确；③∵AB为直径，∴∠ACB=90°，∵∠CAB=60°，∴∠ABC=30°，∴BC=2CE，∴③正确，故选：D．【点睛】本题考查了垂径定理、圆周角定理、等边三角形的判定与性质、含30°角的直角三角形的性质，理解基本作图知识，熟练掌握各基本性质和综合运用是解答的关键．7．B解析：B【分析】先根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形面积公式得到12•2π•5•OA=65π，可求出OA=13，然后利用勾股定理计算圆锥的高．【详解】解：根据题意得12•2π•5•OA=65π，解得：OA=13，所以圆锥的高2213512．故选：B．【点睛】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．8．C解析：C【分析】如图：连接OB、O C,先根据圆的内接四边形对角互补得到∠C=67.5°，再利用等腰三角形的性质和三角形内角和计算出∠BAC=45°，再根据圆周角定理可得∠BOC=90°，最后根据勾股定理求解即可．【详解】解：∵四边形ADBC为⊙O的内接四边形，∠D＝112.5°∴∠C=180°-∠D＝180°-112.5°=67.5°∵AC=AB∴∠BAC=180°-2∠C=45°∴∠BOC=90°∴BC=22222222OB OC+=+=．故答案为C．【点睛】本题考查了圆内接四边形的性质、等腰直角三角形的性质和圆周角定理，掌握圆内接四边形的对角互补是解答本题的突破口．9．B解析：B【分析】如图（见解析），先根据圆的性质可得OC OB=，再根据等边三角形的判定与性质可得60BOC∠=︒，然后根据圆周角定理即可得．【详解】如图，连接OC，由同圆半径相等得：OC OB=，7OB BC==，OC OB BC∴==，BOC∴是等边三角形，60BOC∴∠=︒，由圆周角定理得：1230BOCBDC∠=︒=∠，故选：B．【点睛】本题考查了等边三角形的判定与性质、同圆半径相等、圆周角定理，熟练掌握等边三角形的判定与性质是解题关键．10．C解析：C【分析】连接PC，PA，过点P作PD⊥AB于点D，根据切线的性质可知PC⊥y轴，故可得出四边形PDOC是矩形，所以PD=OC=3，再求出AB的长，由垂径定理可得出AD的长，故可得出OD 的长，进而得出P点坐标，再把P点坐标代入直线y=kx-1即可得出结论．【详解】解：连接PC，PA，过点P作PD⊥AB于点D，∵⊙P与y轴相切于点C（0，3），∴PC⊥y轴，∴四边形PDOC是矩形，∴PD=OC=3，∵A（1，0），B（7，0），∴AB=7-1=6，∴AD=12AB=12×6=3，∴OD=AD+OA=3+1=4，∴P（4，3），∵直线y=kx-1恰好平分⊙P的面积，∴3=4k-1，解得k=1．故选：C．【点睛】本题考查的是圆的综合题，根据题意作出辅助线，构造出直角三角形求出P点坐标即可得出结论．11．C解析：C【分析】利用垂径定理可对①②进行判断；利用圆周角定理可得到CM、AN为角平分线，则利用三角形内心的定义可对③进行判断；根据P是△ABC的内心得出∠APC=90°+12∠B，进而得出∠MON+∠B=180°，再代入求解即可．【详解】解：作BC的垂直平分线，则ON平分BC，则BC＝2NC，所以①正确；作AB的垂直平分线，则OM平分AB，则AB＝2AM，2AM＞AB，所以②错误；∵M点为AB的中点，∴∠ACM=∠BCM，∵点N 为BC 的中点，∴∠BAN=∠CAN ，故P 点为△ABC 的内心，所以③正确；∵∠APC=180°-∠PAC-∠PCA=180°-12∠BAC-12∠BCA=180°-12(∠BAC+∠BCA)=180°-12(180°-∠B)=90°+12∠B ， ∴2∠MPN=2∠APC=180°+∠B ，又OM ⊥AB ，ON ⊥BC ，∴∠MON+∠B=180°，∴∠MON+2∠MPN=∠MON+180°+∠B=180°+180°=360°，故④正确，∴正确的结论有3个，故选：C ．【点睛】本题考查了垂径定理、圆周角定理、三角形内心及外心的性质、线段的垂直平分线的尺规作图等，熟练掌握各图形的性质及尺规作图步骤是解决本题的关键．12．D解析：D【分析】设展开后的圆半径为r ，根据圆锥性质可知底面周长就等于展开后扇形的弧长，然后算出展开后扇形的半径，进而计算出扇形的面积．【详解】解：设展开后的扇形半径为r ，由题可得：4π=2r π解得r =8∴S 扇形=14π×82 =16π故选：D【点睛】此题主要考查了圆锥的计算，正确理解圆锥侧面展开图与各部分对应情况是解题关键．二、填空题13．36°【分析】根据圆周角定理可得再利用等腰三角形的性质即可求解【详解】解：∵∴∵∴故答案为：36°【点睛】本题考查圆周角定理掌握圆周角定理是解题的关键解析：36°【分析】根据圆周角定理可得2108AOB ACB ∠=∠=︒，再利用等腰三角形的性质即可求解．【详解】解：∵54ACB ∠=︒，∴2108AOB ACB ∠=∠=︒，∵OA OB =， ∴()1180362ABO BAO AOB ∠=∠=︒-∠=︒，故答案为：36°．【点睛】本题考查圆周角定理，掌握圆周角定理是解题的关键． 14．70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数然后根据∠BAC ＝35°即可求得∠P 的度数【详解】解：连接OB ：∵PAPB 是⊙O 的两条切线AB 是切点AC 是⊙O 的直径∴∠OAP ＝∠OBP ＝90°解析：70°【分析】根据题意可以求得∠OAP 和∠OBP 的度数，然后根据∠BAC ＝35°，即可求得∠P 的度数．【详解】解：连接OB ：∵PA 、PB 是⊙O 的两条切线，A 、B 是切点，AC 是⊙O 的直径，∴∠OAP ＝∠OBP ＝90°，∵∠BAC ＝35°，OA ＝OB ，∴∠BAC ＝∠OBA ＝35°，∴∠PAB ＝∠PBA ＝55°，∴∠P ＝180°−∠PAB−∠PBA ＝70°，即∠P 的度数是70°，故答案为：70°．【点睛】本题考查切线的性质，解答此类问题的关键是明确题意，找出所求问题需要的条件，利用切线的性质解答问题．15．【分析】根据扇形的面积公式S 扇形=即可求得【详解】解：∵S 扇形=∴r2==3∴r=（负值舍去）故答案为：【点睛】本题主要考查扇形面积的计算解题的关键是掌握扇形面积的计算公式：S 扇形=3【分析】根据扇形的面积公式S 扇形=2360n r π 即可求得．【详解】解：∵S 扇形=2360n r π， ∴r 2=360360 120S n πππ==3， ∴（负值舍去），【点睛】本题主要考查扇形面积的计算，解题的关键是掌握扇形面积的计算公式：S 扇形=2360n r π． 16．【分析】作A 点关于BC 的对称点A 以A 点为圆心以BC 的长为半径作圆连接AA 交BC 于E 点延长AA 交⊙A 与点D 连接BDCD 则∠BDC ＝∠BAC ＝×60°＝30°此时AD 为最大值根据等边三角形的性质可求解A解析：5【分析】作A 点关于BC 的对称点A'，以A'点为圆心，以BC 的长为半径作圆，连接AA'交BC 于E 点，延长AA'交⊙A'与点D ，连接BD ，CD ，则∠BDC ＝12∠BA'C ＝12×60°＝30°，此时AD为最大值，根据等边三角形的性质可求解A'E ＝AE ，A'D ＝A'B ＝AB ＝5，进而可求解．【详解】作A 点关于BC 的对称点A'，以A'点为圆心，以BC 的长为半径作圆，连接AA'交BC 于E 点，延长AA'交⊙A'与点D ，连接BD ，CD ，则∠BDC ＝12∠BA'C ＝12×60°＝30°，此时AD 为最大值，∵△ABC 是边长为5的等边三角形，∴BC ＝AB ＝5，∴BE=12BC=52∴A'E ＝AE A'D ＝A'B ＝AB ＝5， ∴AD ＝AE ＋A'E ＋A'D ＝5．故答案为5．【点睛】本题主要考查等边三角形的性质，轴对称的性质，圆周角定理等知识的综合运用，解题的关键是根据题意作出示意图进行求解．17．6【分析】如图作OH⊥CD于H连接AH延长AH交BF于K连接OC证明AE=FK利用勾股定理求出OH再利用三角形的中位线定理求出BK即可解决问题【详解】解：如图作OH⊥CD于H连接AH延长AH交BF于解析：6【分析】如图，作OH⊥CD于H，连接AH，延长AH交BF于K，连接OC．证明AE=FK，利用勾股定理求出OH，再利用三角形的中位线定理求出BK即可解决问题．【详解】解：如图，作OH⊥CD于H，连接AH，延长AH交BF于K，连接OC．∵OH⊥CD，∴CH=DH=4（cm），∠CHO=90°，∴2222-=-=3（cm），OC CH54∵AE⊥CD，BF⊥CD，∴AE∥OH∥BF，∵OA=OB，∴EH=FH，∵∠AEH=∠KFH=90°，∠AHE=∠FHK，∴△AEH≌△KFH（AAS），∴AH=HK，AE=FK，∵AO=OB，∴OH=12BK，∴BK=6（cm），∴BF-AE=BF-FK=BK=6（cm）．故答案为6．【点睛】本题考查了垂径定理，勾股定理，三角形的中位线定理，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．18．2【分析】根据圆周角定理得出∠A=∠CDB∠ACB=90°根据含30°角的直角三角形的性质得出AB=2BC求出AB再求出半径即可【详解】解：∵∴∠A=∠CDB∵∠CDB=30°∴∠A=30°∵AB为解析：2【分析】根据圆周角定理得出∠A=∠CDB，∠ACB=90°，根据含30°角的直角三角形的性质得出AB=2BC，求出AB，再求出半径即可．【详解】解：∵=BC BC∴∠A=∠CDB，∵∠CDB=30°，∴∠A=30°，∵AB为⊙O的直径，∴∠ACB=90°，∵BC=2，∴AB=2BC=4，∴⊙O的半径是1422⨯=，故答案为：2．【点睛】本题考查了圆周角定理，含30°角的直角三角形的性质等知识点，能根据圆周角定理得出∠A=∠CDB和∠ACB=90°是解此题的关键．19．【分析】根据相切的定义可得利用等面积法即可求解【详解】解：∵∠C＝90°AC＝3cmBC＝4cm∴由题意可得∴即故答案为：【点睛】本题考查直线与圆的位置关系勾股定理掌握相切的定义是解题的关键解析：12 5【分析】根据相切的定义可得CD AB ⊥，利用等面积法即可求解．【详解】解：∵∠C ＝90°，AC ＝3cm ，BC ＝4cm ， ∴225cm AB AC BC =+=，由题意可得CD AB ⊥，∴1122AC BC AB CD ⋅=⋅，即125CD =，故答案为：125．【点睛】本题考查直线与圆的位置关系、勾股定理，掌握相切的定义是解题的关键．20．65【分析】根据垂径定理的推论此圆的圆心在CD 所在的直线上设圆心是O 连接OA 根据垂径定理和勾股定理求解【详解】根据垂径定理的推论知此圆的圆心在CD 所在的直线上设圆心是O 连接OA 拱桥的跨度AB=12m解析：6.5【分析】根据垂径定理的推论，此圆的圆心在CD 所在的直线上，设圆心是O ．连接OA ．根据垂径定理和勾股定理求解．【详解】根据垂径定理的推论，知此圆的圆心在CD 所在的直线上，设圆心是O ，连接OA ．拱桥的跨度AB =12m ，拱高CD =4m ，根据垂径定理，得AD=6 m ，利用勾股定理可得：()22264AO AO =--，解得：AO =6.5m ．即圆弧半径为6.5米，故答案为：6.5．【点睛】本题综合运用了勾股定理以及垂径定理．注意由半径、半弦、弦心距构造的直角三角形进行有关的计算．三、解答题21．（1）图见解析，(2,3)-；（2）52π．【分析】（1）先根据旋转的性质分别画出点,,B C D 旋转后的对应点,,B C D '''，再顺次连接点,,,A B C D '''可得旋转后的图形，然后根据旋转的性质可得四边形AB C D '''是矩形，,AD AD C D CD '''==，由此即可得；（2）先利用矩形的性质、勾股定理求出AC 的长，再利用弧长公式即可得．【详解】（1）先根据旋转的性质分别画出点,,B C D 旋转后的对应点,,B C D '''，再顺次连接点,,,A B C D '''可得旋转后的图形，如图所示：由题意得：(2,0),(5,0),(5,4),(2,4)A B C D ，2,3,4OA AB CD BC AD ∴=====，由旋转的性质得：4,3AD AD C D CD '''====，四边形AB C D '''是矩形， 2,OD AD OA C D AD '''''∴=-=⊥，∴点C '的坐标为(2,3)C '-，即旋转后C 点对应点的坐标为(2,3)-；（2）由题意得：点C 在旋转过程中的路径长为CC '的长，如图所示：四边形ABCD 是矩形，3,4AB BC ==，∴对角线225AC AB +BC ，由旋转的性质得：90CAC '∠=︒，则CC '的长为90551802ππ⨯=，即点C 在旋转过程中的路径长为52π．【点睛】本题考查了画旋转图形、旋转的性质、弧长公式等知识点，熟练掌握旋转的性质是解题关键．22．（1）见解析；（2）见解析【分析】（1）连接BD 、AC 交于点E ，连接OE ；（2）连接BD ，则点P 和BD 与O 的交点的延长线与AB 的交点即为F 点．【详解】（1）如图所示，∵四边形ABCD 是菱形，∴E 是BD 中点，∵O 是DA 中点，∴//OE AB ；（2）如图所示，∵120BAD ∠=，∴60ADC ∠=︒，∵AD CD =，∴ACD △是等边三角形，∵AD 是直径，∴90APD ∠=︒，即AP DC ⊥，∴P 是CD 中点，通过如图所示找到的点F 是AB 的中点，∵ABC 也是等边三角形，∴CF AB ⊥．【点睛】本题考查作图，解题的关键是要熟悉各种几何的性质，比如：等边三角形的性质，中位线的性质，菱形的性质，圆的性质．23．见解析【分析】根据切线的性质得出OP ⊥AB ，根据垂径定理得出即可．【详解】证明：如图，连接OP ，∵大圆的弦AB是小圆的切线，点P为切点，∴OP⊥AB，∵OP过O，∴AP=BP．【点睛】本题考查了切线的性质和垂径定理的应用，主要考查学生的推理能力，题目比较好，难度适中．24．64cm2【分析】连接OA、OB、OE，证Rt△ADO≌Rt△BCO，推出OD=OC，设AD=a，则OD=12a，由勾股定理求出OA=OB=OE=5a，求出EF=FC=4cm，在△OFE中由勾股定理求出a，即可求出答案．【详解】解：连接OA、OB、OE，∵四边形ABCD是正方形，∴AD=BC，∠ADO=∠BCO=90°，∵在Rt△ADO和Rt△BCO中∵OA OB AD BC=⎧⎨=⎩，∴Rt△ADO≌Rt△BCO，∴OD=OC，∵四边形ABCD是正方形，∴AD=DC，设AD=acm，则OD=OC=12DC=12AD=12acm，在△AOD中，由勾股定理得：5acm，∵小正方形EFCG的面积为16cm2，∴EF=FC=4cm ，在△OFE 中，由勾股定理得：a)2=42+(12a+4)2，解得：a=-4（舍去），a=8，∴正方形面积为264cm故答案为：64cm²．【点睛】本题考查了全等三角形的性质和判定，勾股定理的应用，主要考查学生运用定理进行计算的能力，用的数学思想是方程思想．25．见解析．【分析】根据已知条件和圆周角定理证明△APD ≌△CPB 即可得到DP=BP ．【详解】证明：∵AB CD =，∴CD = AB ，∴ CD- CA= AB - AC ，∴ AD = BC.又∵∠A=∠C ，∠APD=∠CPB ，∴△APD ≌△CPB.∴DP=BP .【点睛】本题考查了全等三角形的判定以及圆心角定理：在同圆或等圆中圆心角相等，弧相等，弦相等，弦心距相等，在这几组相等关系中，只要有一组成立，则另外几组一定成立． 26．2(2)4a π-，1.14 【分析】根据对称性用a 表示出阴影的面积，再将a=2代入求解即可．【详解】解：由题意可知：S 阴=211442222a a a π⎡⎤⎛⎫-⋅⋅⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 2(2)4a π-= 当2a =时，S 阴=(3.142)4 1.144-⨯=．【点睛】本题考查列代数式、代数式求值、圆的面积公式、三角形的面积公式，解答的关键是找出面积之间的关系，利用基本图形的面积公式解决问题．。

【九年级数学《圆》同步练习题含答案

九年级数学上册《圆》同步练习一、选择题1．圆的直径为13cm，如果圆心与直线的距离是d，则（）A.当d=8 cm，时，直线与圆相交B.当d=4.5 cm时，直线与圆相离C.当d=6.5 cm时，直线与圆相切D.当d=13 cm时，直线与圆相切2．如图，在⊙O中，AB为直径，点C为圆上一点，将劣弧AC沿弦AC翻折交AB于点D，连接CD．如果∠BAC=20°，则∠BDC=（）A.80°B.70°C.60°D.50°3．如图是一个正八边形，图中空白部分的面积等于20，则阴影部分的面积等于（）A．102 B．20 C．18 D．202 4．如图，△ABC内接于⊙O，且∠ABC=700，则∠AOC为（）（A）1400 （B）1200（C）900 （D）3505．⊙O的半径为5cm，点A到圆心O的距离OA=3cm，则点A与圆O 的位置关系为（）A．点A在圆上 B．点A在圆内 C．点A在圆外 D．无法确定6．（3分）在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（）A．30° B．45° C．60° D．90°7．（3分）（2015•牡丹江）如图，△ABD的三个顶点在⊙O上，AB是直径，点C在⊙O上，且∠ABD=52°，则∠BCD等于（）．A．32° B．38° C．52° D．66°8．已知一块圆心角为300°的扇形铁皮，用它做一个圆锥形的烟囱帽（接缝忽略不计），圆锥的底面圆的直径是80cm，则这块扇形铁皮的半径是（）A．24cm B．48cm C．96cm D．192cm二、填空题9．用半径为6cm的半圆围成一个圆锥的侧面，则圆锥的底面半径等于 cm．10．一个几何体的三视图如图，根据图示的数据计算该几何体的表面积为．（结果保留π）11．如果一个扇形的圆心角为120°，半径为6，那么该扇形的弧长是．12．如图，在⊙O中，∠OAB=45°，圆心O到弦AB的距离OE=2cm，则弦AB的长为 cm．13．（3分）用一个圆心角为90°，半径为4的扇形围成一个圆锥的侧面，该圆锥底面圆的半径．14．（3分）边长为1的正三角形的内切圆半径为．15．（3分）（2015•郴州）已知圆锥的底面半径是1cm，母线长为3cm，则该圆锥的侧面积为 cm2．16．（4分）如图，AD是⊙O的直径，弦BC⊥AD于E，AB=BC=12，则OC= ．三、解答题17．如图，已知AB 是⊙O 的直径，AP 是⊙O 的切线，A 是切点，BP 与⊙O 交于点C ，若AB=2，∠P=30°，求AP 的长（结果保留根号）．已知：如图，AB 为⊙O 的直径，AD 为弦，∠DBC =∠A.18．求证： BC 是⊙O 的切线；19．若OC ∥AD ，OC 交BD 于E ，BD=6，CE=4，求AD 的长. O EDA20．如图，已知⊙O 与BC 相切，点C 不是切点，AO ⊥OC ，∠OAC=∠ABO ，且AC=BO ，判断直线AB 与⊙O 的位置关系，并说明理由．21．已知，如图，直线MN交⊙O于A，B两点，AC是⊙O的直径，DE 切⊙O于点D，且DE⊥MN于点E．（1）求证：AD平分∠CAM．（2）若DE=6，AE=3，求⊙O的半径．22．（10分）如图，已知AB是⊙O的直径，点C，D在⊙O上，点E 在⊙O外，∠EAC=∠B．（1）求证：直线AE是⊙O的切线；（2）若∠D=60°，AB=6时，求劣弧AC的长（结果保留π）．参考答案1．C2．B．3．B．4．A5．B．6．D．7．B．8．B．9．310．24π．11．4π．12．4．13．1．．14．3615．3π．16．43．17．23．18．证明：（1）∵AB为⊙O的直径∴D=90°, A+ABD=90°∵∠DBC =∠A∴∠DBC+∠ABD=90°∴BC⊥AB∴BC是⊙O的切线19．∵OC∥AD，D=90°，BD=6∴OC⊥BDBD=3∴BE=12∵O是AB的中点∴AD=2EO -∵BC⊥AB ，OC⊥BD∴△CEB∽△BEO，∴2=•BE CE OE∵CE=4，∴9OE=4∴AD=9220．直线AB与⊙O的位置关系是相离．理由见解析．21．（1）证明见解析；（2）⊙O的半径为7.5．22．（1）证明见试题解析；（2）2π．《圆》的练习一、选择题（共10小题，每小题3分，共30分）1．下列说法正确的是（）A．三点确定一个圆B．一个三角形只有一个外接圆C．和半径垂直的直线是圆的切线D．三角形的内心到三角形三个顶点距离相等2．如图，⊙O的直径AB与弦CD的延长线交于点E，若DE=OB，∠AOC=84°，则∠E等于（）A．42°B．28°C．21°D．20°3．已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD=6，AE=1，则⊙O的直径为（）A．6 B．8 C．10 D．124．如图，DC是以AB为直径的半圆上的弦，DM⊥CD交AB于点M，CN ⊥CD交AB于点N．AB=10，CD=6．则四边形DMNC的面积（）A．等于24 B．最小为24 C．等于48 D．最大为485．如图，在半径为5的⊙O中，弦AB=6，OP⊥AB，垂足为点P，则OP的长为（）A．3 B．2.5 C．4 D．3.56．如图表示一圆柱形输水管的横截面，阴影部分为有水部分，如果输水管的半径为5cm，水面宽AB为8cm，则水的最大深度CD为（）A．4cm B．3cm C．2cm D．1cm7．图中的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行，乙虫沿ACB路线爬行，则下列结论正确的是（）A．甲先到B点B．乙先到B点C．甲、乙同时到B D．无法确定8．在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm9．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，若BC=CD=DA=4cm，则⊙O的周长为（）A．5πcm B．6πcm C．9πcm D．8πcm10．如图，AB是⊙O的弦，点C在圆上，已知∠OBA=40°，则∠C=（）A．40°B．50°C．60°D．80°二、填空题（共6小题，每小题3分，共18分）11．如图，在⊙O中，弦AB∥CD，若∠ABC=40°，则∠BOD= ．12．如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是．13．如图，已知∠BOA=30°，M为OB边上一点，以M为圆心、2cm 为半径作⊙M．点M在射线OB上运动，当OM=5cm时，⊙M与直线OA 的位置关系是．14．如图，正方形ABCD内接于⊙O，其边长为4，则⊙O的内接正三角形EFG的边长为．15．已知扇形的半径为6cm，圆心角的度数为120°，则此扇形的弧长为cm．16．如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．三、解答题（共8题，共72分）17．圆锥底面圆的半径为3m，其侧面展开图是半圆，求圆锥母线长．18．在一个底面直径为5cm，高为18cm的圆柱形瓶内装满水，再将瓶内的水倒入一个底面直径是6cm，高是10cm的圆柱形玻璃杯中，能否完全装下？若未能装满，求杯内水面离杯口的距离．19．如图，AB和CD分别是⊙O上的两条弦，过点O分别作ON⊥CD 于点N，OM⊥AB于点M，若ON=AB，证明：OM=CD．20．如图为桥洞的形状，其正视图是由和矩形ABCD构成．O点为所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F ）EF为2米．求所在⊙O的半径DO．21．△ABC是⊙O的内接三角形，BC=．如图，若AC是⊙O的直径，∠BAC=60°，延长BA到点D，使得DA=BA，过点D作直线l⊥BD，垂足为点D，请将图形补充完整，判断直线l和⊙O的位置关系并说明理由．22．如图直角坐标系中，已知A（﹣8，0），B（0，6），点M在线段AB上．（1）如图1，如果点M是线段AB的中点，且⊙M的半径为4，试判断直线OB与⊙M的位置关系，并说明理由；（2）如图2，⊙M与x轴、y轴都相切，切点分别是点E、F，试求出点M的坐标．23．已知等边三角形ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连接GD，（1）求证：DF与⊙O的位置关系并证明；（2）求FG的长．24．如图，等边△ABC的边长为2，E是边BC上的动点，EF∥AC交边AB于点F，在边AC上取一点P，使PE=EB，连接FP．（1）请直接写出图中与线段EF相等的两条线段；（不再另外添加辅助线）（2）探究：当点E在什么位置时，四边形EFPC是平行四边形？并判断四边形EFPC是什么特殊的平行四边形，请说明理由；（3）在（2）的条件下，以点E为圆心，r为半径作圆，根据⊙E与平行四边形EFPC四条边交点的总个数，求相应的r的取值范围．参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）1．下列说法正确的是（）A．三点确定一个圆B．一个三角形只有一个外接圆C．和半径垂直的直线是圆的切线D．三角形的内心到三角形三个顶点距离相等【考点】圆的认识．【分析】根据确定圆的条件对A、B进行判断；根据切线的判定定理对C进行判断；根据三角形内心的性质对D进行判断．【解答】解：A、不共线的三点确定一个圆，所以A选项错误；B、一个三角形只有一个外接圆，所以B选项正确；C、过半径的外端与半径垂直的直线是圆的切线，所以C选项错误；D、三角形的内心到三角形三边的距离相等，所以D选项错误．故选B．【点评】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了确定圆的条件和切线的判定．2．如图，⊙O的直径AB与弦CD的延长线交于点E，若DE=OB，∠AOC=84°，则∠E等于（）A．42°B．28°C．21°D．20°【考点】圆的认识；等腰三角形的性质．【专题】计算题．【分析】利用半径相等得到DO=DE，则∠E=∠DOE，根据三角形外角性质得∠1=∠DOE+∠E，所以∠1=2∠E，同理得到∠AOC=∠C+∠E=3∠E，然后利用∠E=∠AOC进行计算即可．【解答】解：连结OD，如图，∵OB=DE，OB=OD，∴DO=DE，∴∠E=∠DOE，∵∠1=∠DOE+∠E，∴∠1=2∠E，而OC=OD，∴∠C=∠1，∴∠C=2∠E，∴∠AOC=∠C+∠E=3∠E，∴∠E=∠AOC=×84°=28°．故选B．【点评】本题考查了圆的认识：掌握与圆有关的概念（弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等）．也考查了等腰三角形的性质．3．已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD=6，AE=1，则⊙O的直径为（）A．6 B．8 C．10 D．12【考点】垂径定理；勾股定理．【分析】连接OC，根据题意OE=OC﹣1，CE=3，结合勾股定理，可求出OC的长度，即可求出直径的长度．【解答】解：连接OC，∵弦CD⊥AB于E，CD=6，AE=1，∴OE=OC﹣1，CE=3，∴OC2=（OC﹣1）2+32，∴OC=5，∴AB=10．故选C．【点评】本题主要考查了垂径定理、勾股定理，解题的关键在于连接OC，构建直角三角形，根据勾股定理求半径OC的长度．4．如图，DC是以AB为直径的半圆上的弦，DM⊥CD交AB于点M，CN ⊥CD交AB于点N．AB=10，CD=6．则四边形DMNC的面积（）A．等于24 B．最小为24 C．等于48 D．最大为48【考点】垂径定理；勾股定理；梯形中位线定理．【分析】过圆心O作OE⊥CD于点E，则OE平分CD，在直角△ODE中利用勾股定理即可求得OE的长，即梯形DMNC的中位线，根据梯形的面积等于OE?CD即可求得．【解答】解：过圆心O作OE⊥CD于点E，连接OD．则DE=CD=×6=3．在直角△ODE中，OD=AB=×10=5，OE===4．则S四边形DMNC=OE?CD=4×6=24．故选A．【点评】本题考查了梯形的中位线以及垂径定理，正确作出辅助线是关键．5．如图，在半径为5的⊙O中，弦AB=6，OP⊥AB，垂足为点P，则OP的长为（）A．3 B．2.5 C．4 D．3.5【考点】垂径定理；勾股定理．【分析】连接OA，根据垂径定理得到AP=AB，利用勾股定理得到答案．【解答】解：连接OA，∵AB⊥OP，∴AP==3，∠APO=90°，又OA=5，∴OP===4，故选C．【点评】本题考查的是垂径定理的应用，掌握垂直于弦的直径平分这条弦是解题的关键．6．如图表示一圆柱形输水管的横截面，阴影部分为有水部分，如果输水管的半径为5cm，水面宽AB为8cm，则水的最大深度CD为（）A．4cm B．3cm C．2cm D．1cm【考点】垂径定理的应用；勾股定理．【分析】根据题意可得出AO=5cm，AC=4cm，进而得出CO的长，即可得出答案．【解答】解：如图所示：∵输水管的半径为5cm，水面宽AB为8cm，水的最大深度为CD，∴DO⊥AB，∴AO=5cm，AC=4cm，∴CO==3（cm），∴水的最大深度CD为：2cm．故选：C．【点评】本题考查的是垂径定理的应用及勾股定理，根据构造出直角三角形是解答此题的关键．7．图中的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行，乙虫沿ACB路线爬行，则下列结论正确的是（）A．甲先到B点B．乙先到B点C．甲、乙同时到B D．无法确定【考点】圆的认识．【专题】应用题．【分析】甲虫走的路线应该是4段半圆的弧长，那么应该是π（AA1+A1A2+A2A3+A3B）=π×AB，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B点．【解答】解：π（AA1+A1A2+A2A3+A3B）=π×AB，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B点．故选C．【点评】本题考查了圆的认识，主要掌握弧长的计算公式．8．在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm【考点】垂径定理的应用；勾股定理．【分析】连接OA，过点O作OE⊥AB，交AB于点M，由垂径定理求出AM的长，再根据勾股定理求出OM的长，进而可得出ME的长．【解答】解：连接OA，过点O作OE⊥AB，交AB于点M，∵直径为200cm，AB=160cm，∴OA=OE=100cm，AM=80cm，∴OM===60cm，∴ME=OE﹣OM=100﹣60=40cm．故选：A．【点评】本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．9．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，若BC=CD=DA=4cm，则⊙O的周长为（）A．5πcm B．6πcm C．9πcm D．8πcm【考点】圆心角、弧、弦的关系；等边三角形的判定与性质．【分析】如图，连接OD、OC．根据圆心角、弧、弦的关系证得△AOD 是等边三角形，则⊙O的半径长为BC=4cm；然后由圆的周长公式进行计算．【解答】解：如图，连接OD、OC．∵AB是⊙O的直径，四边形ABCD内接于⊙O，若BC=CD=DA=4cm，∴==，∴∠AOD=∠DOC=∠BOC=60°．又OA=OD，∴△AOD是等边三角形，∴OA=AD=4cm，∴⊙O的周长=2×4π=8π（cm）．故选：D．【点评】本题考查了圆心角、弧、弦的关系，等边三角形的判定．该题利用“有一内角是60度的等腰三角形为等边三角形”证得△AOD 是等边三角形．10．如图，AB是⊙O的弦，点C在圆上，已知∠OBA=40°，则∠C=（）A．40°B．50°C．60°D．80°【考点】圆周角定理．【分析】首先根据等边对等角即可求得∠OAB的度数，然后根据三角形的内角和定理求得∠AOB的度数，再根据圆周角定理即可求解．【解答】解：∵OA=OB，∴∠OAB=∠OBA=40°，∴∠AOB=180°﹣40°﹣40°=100°．∴∠C=∠AOB=×100°=50°．故选B．【点评】本题考查了等腰三角形的性质定理以及圆周角定理，正确理解定理是关键．二、填空题（共6小题，每小题3分，共18分）11．如图，在⊙O中，弦AB∥CD，若∠ABC=40°，则∠BOD= 80°．【考点】圆周角定理；平行线的性质．【分析】根据平行线的性质由AB∥CD得到∠C=∠ABC=40°，然后根据圆周角定理求解．【解答】解：∵AB∥CD，∴∠C=∠ABC=40°，∴∠BOD=2∠C=80°．故答案为80°．【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．也考查了平行线的性质．12．如图，在矩形ABCD中，AB=4，AD=3，以顶点D为圆心作半径为r的圆，若要求另外三个顶点A、B、C中至少有一个点在圆内，且至少有一个点在圆外，则r的取值范围是3＜r＜5 ．【考点】点与圆的位置关系．【分析】要确定点与圆的位置关系，主要根据点与圆心的距离与半径的大小关系来进行判断．当d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内．【解答】解：在直角△ABD中，CD=AB=4，AD=3，则BD==5．由图可知3＜r＜5．故答案为：3＜r＜5．【点评】此题主要考查了点与圆的位置关系，解决本题要注意点与圆的位置关系，要熟悉勾股定理，及点与圆的位置关系．13．如图，已知∠BOA=30°，M为OB边上一点，以M为圆心、2cm 为半径作⊙M．点M在射线OB上运动，当OM=5cm时，⊙M与直线OA 的位置关系是相离．【考点】直线与圆的位置关系．【专题】常规题型．【分析】作MH⊥OA于H，如图，根据含30度的直角三角形三边的关系得到MH=OM=，则MH大于⊙M的半径，然后根据直线与圆的位置关系的判定方法求解．【解答】解：作MH⊥OA于H，如图，在Rt△OMH中，∵∠HOM=30°，∴MH=OM=，∵⊙M的半径为2，∴MH＞2，∴⊙M与直线OA的位置关系是相离．故答案为相离．【点评】本题考查了直线与圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d，直线l和⊙O相交?d＜r；直线l和⊙O相切?d=r；直线l和⊙O相离?d＞r．14．如图，正方形ABCD内接于⊙O，其边长为4，则⊙O的内接正三角形EFG的边长为 2 ．【考点】正多边形和圆．【分析】连接AC、OE、OF，作OM⊥EF于M，先求出圆的半径，在RT △OEM中利用30度角的性质即可解决问题．【解答】解；连接AC、OE、OF，作OM⊥EF于M，∵四边形ABCD是正方形，∴AB=BC=4，∠ABC=90°，∴AC是直径，AC=4，∴OE=OF=2，∵OM⊥EF，∴EM=MF，∵△EFG是等边三角形，∴∠GEF=60°，在RT△OME中，∵OE=2，∠OEM=∠GEF=30°，∴OM=，EM=OM=，∴EF=2．故答案为2．【点评】本题考查正多边形与圆、等腰直角三角形的性质、等边三角形的性质等知识，解题的关键是熟练应用这些知识解决问题，属于中考常考题型．15．已知扇形的半径为6cm，圆心角的度数为120°，则此扇形的弧长为4πcm．【考点】弧长的计算．【分析】在半径是R的圆中，因为360°的圆心角所对的弧长就等于圆周长C=2πR，所以n°圆心角所对的弧长为l=nπR÷180．【解答】解：∵扇形的半径为6cm，圆心角的度数为120°，∴扇形的弧长为： =4πcm；故答案为：4π．【点评】本题考查了弧长的计算．解答该题需熟记弧长的公式l=．16．如图，半圆O的直径AB=2，弦CD∥AB，∠COD=90°，则图中阴影部分的面积为．【考点】扇形面积的计算．【分析】由CD∥AB可知，点A、O到直线CD的距离相等，结合同底等高的三角形面积相等即可得出S△ACD=S△OCD，进而得出S阴影=S 扇形COD，根据扇形的面积公式即可得出结论．【解答】解：∵弦CD∥AB，∴S△ACD=S△OCD，∴S阴影=S扇形COD=?π?=×π×=．故答案为：．【点评】本题考查了扇形面积的计算以及平行线的性质，解题的关键是找出S阴影=S扇形COD．本题属于基础题，难度不大，解决该题型题目时，通过分割图形找出面积之间的关系是关键．三、解答题（共8题，共72分）17．圆锥底面圆的半径为3m，其侧面展开图是半圆，求圆锥母线长．【考点】圆锥的计算．【分析】侧面展开后得到一个半圆就是底面圆的周长．依此列出方程即可．【解答】解：设母线长为x，根据题意得2πx÷2=2π×3，解得x=6．故圆锥的母线长为6m．【点评】本题考查圆锥的母线长的求法，注意利用圆锥的弧长等于底面周长这个知识点．18．在一个底面直径为5cm，高为18cm的圆柱形瓶内装满水，再将瓶内的水倒入一个底面直径是6cm，高是10cm的圆柱形玻璃杯中，能否完全装下？若未能装满，求杯内水面离杯口的距离．【考点】圆柱的计算．【专题】计算题．【分析】设将瓶内的水倒入一个底面直径是6cm，高是10cm的圆柱形玻璃杯中时，水面高为xcm，根据水的体积不变和圆柱的条件公式得到π?（）2?x=π?（）2?18，解得x=12.5，然后把12.5与10进行大小比较即可判断能否完全装下．【解答】解：设将瓶内的水倒入一个底面直径是6cm，高是10cm的圆柱形玻璃杯中时，水面高为xcm，根据题意得π?（）2?x=π?（）2?18，解得x=12.5，∵12.5＞10，∴不能完全装下．【点评】本题考查了圆柱：圆柱的母线（高）等于展开后所得矩形的宽，圆柱的底面周长等于矩形的长；圆柱的侧面积=底面圆的周长×高；圆柱的表面积=上下底面面积+侧面积；圆柱的体积=底面积×高．19．如图，AB和CD分别是⊙O上的两条弦，过点O分别作ON⊥CD 于点N，OM⊥AB于点M，若ON=AB，证明：OM=CD．【考点】垂径定理；全等三角形的判定与性质．【专题】证明题．【分析】设圆的半径是r，ON=x，则AB=2x，在直角△CON中利用勾股定理即可求得CN的长，然后根据垂径定理求得CD的长，然后在直角△OAM中，利用勾股定理求得OM的长，即可证得．【解答】证明：设圆的半径是r，ON=x，则AB=2x，在直角△CON中，CN==，∵ON⊥CD，∴CD=2CN=2，∵OM⊥AB，∴AM=AB=x，在△AOM中，OM==，∴OM=CD．【点评】此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解．20．如图为桥洞的形状，其正视图是由和矩形ABCD构成．O点为所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F ）EF为2米．求所在⊙O的半径DO．【考点】垂径定理的应用；矩形的性质．【分析】先根据垂径定理求出DF的长，再由勾股定理即可得出结论．【解答】解：∵OE⊥弦CD于点F，CD为8米，EF为2米，∴EO垂直平分CD，DF=4m，FO=DO﹣2，在Rt△DFO中，DO2=FO2+DF2，则DO2=（DO﹣2）2+42，解得：DO=5；答：所在⊙O的半径DO为5m．【点评】本题考查的是垂径定理的应用，此类题中一般使用列方程的方法，这种用代数方法解决几何问题即几何代数解的数学思想方法一定要掌握．21．△ABC是⊙O的内接三角形，BC=．如图，若AC是⊙O的直径，∠BAC=60°，延长BA到点D，使得DA=BA，过点D作直线l⊥BD，垂足为点D，请将图形补充完整，判断直线l和⊙O的位置关系并说明理由．【考点】直线与圆的位置关系．【分析】作OF⊥l于F，CE⊥l于E，设AD=a，则AB=2AD=2a，只要证明OF是梯形ADEC的中位线即可解决问题．【解答】解：图形如图所示，直线l与⊙O相切．理由：作OF⊥l于F，CE⊥l于E，∵AC是直径，∴∠ABC=90°，∵l⊥BD，∴∠BDE=90°，∵OF⊥l，CE⊥l，∴AD∥OF∥CE，∵AO=OC，∴DF=FE，∴OF=（AD+CE），设AD=a，则AB=2AD=2a，∵∠ABC=∠BDE=∠CED=90°，∴四边形BDEC是矩形，∴CE=BD=3a，∴OF=2a，∵在Rt△ABC中，∠ABC=90°，∠ACB=30°，AB=2a，∴AC=4a，∴OF=OA=2a，∴直线l是⊙O切线．【点评】本题考查直线与圆的位置关系、图形中位线的性质等知识，解题的关键是添加辅助线，要证明切线的方法有两种，一是连半径，证垂直，二是作垂直，正半径，此题则是运用第二种方法．22．如图直角坐标系中，已知A（﹣8，0），B（0，6），点M在线段AB上．（1）如图1，如果点M是线段AB的中点，且⊙M的半径为4，试判断直线OB与⊙M的位置关系，并说明理由；（2）如图2，⊙M与x轴、y轴都相切，切点分别是点E、F，试求出点M的坐标．【考点】直线与圆的位置关系；坐标与图形性质．【分析】（1）设线段OB的中点为D，连结MD，根据三角形的中位线求出MD，根据直线和圆的位置关系得出即可；（2）求出过点A、B的一次函数关系式是y=x+6，设M（a，﹣a），把x=a，y=﹣a代入y=x+6得出关于a的方程，求出即可．【解答】解：（1）直线OB与⊙M相切，理由：设线段OB的中点为D，连结MD，如图1，∵点M是线段AB的中点，所以MD∥AO，MD=4．∴∠AOB=∠MDB=90°，∴MD⊥OB，点D在⊙M上，又∵点D在直线OB上，∴直线OB与⊙M相切；，（2）解：连接ME，MF，如图2，∵A（﹣8，0），B（0，6），∴设直线AB的解析式是y=kx+b，∴，解得：k=，b=6，即直线AB的函数关系式是y=x+6，∵⊙M与x轴、y轴都相切，∴点M到x轴、y轴的距离都相等，即ME=MF，设M（a，﹣a）（﹣8＜a＜0），把x=a，y=﹣a代入y=x+6，得﹣a=a+6，得a=﹣，∴点M的坐标为（﹣，）．【点评】本题考查了直线和圆的位置关系，用待定系数法求一次函数的解析式的应用，能综合运用知识点进行推理和计算是解此题的关键，注意：直线和圆有三种位置关系：已知⊙O的半径为r，圆心O 到直线l的距离是，当d=r时，直线l和⊙O相切．23．已知等边三角形ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连接GD，（1）求证：DF与⊙O的位置关系并证明；（2）求FG的长．【考点】直线与圆的位置关系；等边三角形的性质；勾股定理；垂径定理．【分析】（1）连接OD，证∠ODF=90°即可．（2）利用△ADF是30°的直角三角形可求得AF长，同理可利用△FHC 中的60°的三角函数值可求得FG长．【解答】（1）证明：连接OD，∵以等边三角形ABC的边AB为直径的半圆与BC边交于点D，∴∠B=∠C=∠ODB=60°，∴OD∥AC，∵DF⊥AC，∴∠CFD=∠ODF=90°，即OD⊥DF，∵OD是以边AB为直径的半圆的半径，∴DF是圆O的切线；（2）∵OB=OD=AB=6，且∠B=60°，∴BD=OB=OD=6，∴CD=BC﹣BD=AB﹣BD=12﹣6=6，∵在Rt△CFD中，∠C=60°，∴∠CDF=30°，∴CF=CD=×6=3，∴AF=AC﹣CF=12﹣3=9，∵FG⊥AB，∴∠FGA=90°，∵∠FAG=60°，∴FG=AFsin60°=．【点评】本题主要考查了直线与圆的位置关系、等边三角形的性质、垂径定理等知识，判断直线和圆的位置关系，一般要猜想是相切，那么证直线和半径的夹角为90°即可；注意利用特殊的三角形和三角函数来求得相应的线段长．24．如图，等边△ABC的边长为2，E是边BC上的动点，EF∥AC交边AB于点F，在边AC上取一点P，使PE=EB，连接FP．（1）请直接写出图中与线段EF相等的两条线段；（不再另外添加辅助线）（2）探究：当点E在什么位置时，四边形EFPC是平行四边形？并判断四边形EFPC是什么特殊的平行四边形，请说明理由；（3）在（2）的条件下，以点E为圆心，r为半径作圆，根据⊙E与平行四边形EFPC四条边交点的总个数，求相应的r的取值范围．【考点】点与圆的位置关系；等边三角形的性质；平行四边形的判定；菱形的判定．【专题】探究型．【分析】（1）由平行易得△BFE是等边三角形，那么各边是相等的；（2）当点E是BC的中点时，△PEC为等边三角形，可得到PC=EC=BE=EF，也就得到了四边形EFPC是平行四边形，再有EF=EC 可证为菱形；（3）根据各点到圆心的距离作答即可．【解答】解：（1）如图，∵△ABC是等边三角形，∴∠B=∠A=∠C=60°．又∵EF∥AC，∴∠BFE=∠A=60°，∠BEF=∠C=60°，∴△BFE是等边三角形，PE=EB，∴EF=BE=PE=BF；（2）当点E是BC的中点时，四边形是菱形；∵E是BC的中点，∴EC=BE，∵PE=BE，∴PE=EC，∵∠C=60°，∴△PEC是等边三角形，∴PC=EC=PE，∵EF=BE，∴EF=PC，又∵EF∥CP，∴四边形EFPC是平行四边形，∵EC=PC=EF，∴平行四边形EFPC是菱形；（3）如图所示：当点E是BC的中点时，EC=1，则NE=ECcos30°=，当0＜r＜时，有两个交点；当r=时，有四个交点；当＜r＜1时，有六个交点；当r=1时，有三个交点；当r＞1时，有0个交点．【点评】本题综合考查了等边三角形的性质和判定，菱形的判定及点和圆的位置关系等知识点．注意圆和线段有交点，应根据半径作答．。

中考数学-圆经典必考题型中考试题集锦(附答案)解答题

中考数学圆经典必考题型中考试题(附答案) 解答题1．（已知：如图，△ABC 内接于⊙O ，过点B 作⊙O 的切线，交CA 的延长线于点E ，∠EBC ＝2∠C ．①求证：AB ＝AC ；②若tan ∠ABE ＝21，（ⅰ）求BCAB 的值；（ⅱ）求当AC ＝2时，AE 的长．2．如图，PA 为⊙O 的切线，A 为切点，⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ，PA ＝8cm ，PB ＝4cm ，求⊙O 的半径．3．已知：如图，BC 是⊙O 的直径，AC 切⊙O 于点C ，AB 交⊙O 于点D ，若AD ︰DB ＝2︰3，AC ＝10，求sin B 的值．4．如图，PC 为⊙O 的切线，C 为切点，PAB 是过O 的割线，CD ⊥AB 于点D ，若tan B ＝21，PC ＝10cm ，求三角形BCD 的面积． 5．如图，在两个半圆中，大圆的弦MN 与小圆相切，D 为切点，且MN ∥AB ，MN ＝a ，ON 、CD 分别为两圆的半径，求阴影部分的面积．6．已知，如图，以△ABC 的边AB 作直径的⊙O ，分别并AC 、BC 于点D 、E ，弦FG ∥AB ，S △CDE ︰S △ABC ＝1︰4，DE ＝5cm ，FG ＝8cm ，求梯形AFGB 的面积．7．如图所示：PA 为⊙O 的切线，A 为切点，PBC 是过点O 的割线，PA ＝10，PB ＝5，求：（1）⊙O 的面积（注：用含π的式子表示）；（2）cos ∠BAP 的值．参考答案1．（1）∵ BE 切⊙O 于点B ，∴ ∠ABE ＝∠C ．∵ ∠EBC ＝2∠C ，即 ∠ABE ＋∠ABC ＝2∠C ，∴ ∠C ＋∠ABC ＝2∠C ，∴ ∠ABC ＝∠C ，∴ AB ＝AC ．（2）①连结AO ，交BC 于点F ，∵ AB ＝AC ，∴ ＝，∴ AO ⊥BC 且BF ＝FC ．在Rt △ABF 中，BFAF ＝tan ∠ABF ，又 tan ∠ABF ＝tan C ＝tan ∠ABE ＝21，∴ BF AF ＝21， ∴ AF ＝21BF ． ∴ AB ＝22BF AF +＝2221BF BF +⎪⎭⎫ ⎝⎛＝25BF ． ∴ 452==BF AB BC AB ． ②在△EBA 与△ECB 中，∵ ∠E ＝∠E ，∠EBA ＝∠ECB ，∴ △EBA ∽△ECB ．∴ ⎪⎩⎪⎨⎧⋅==EC EA BE BC AB EB EA 2，解之，得516EA 2＝EA ·（EA ＋AC ），又EA ≠0， ∴ 511EA ＝AC ，EA ＝115×2＝1110． 2．设⊙的半径为r ，由切割线定理，得PA 2＝PB ·PC ，∴ 82＝4（4＋2r ），解得r ＝6（cm ）．即⊙O 的半径为6cm ．3．由已知AD ︰DB ＝2︰3，可设AD ＝2k ，DB ＝3k （k ＞0）．∵ AC 切⊙O 于点C ，线段ADB 为⊙O 的割线，∴ AC 2＝AD ·AB ，∵ AB ＝AD ＋DB ＝2k ＋3k ＝5k ，∴ 102＝2k ×5k ，∴ k 2＝10，∵ k ＞0，∴ k ＝10． ∴ AB ＝5k ＝510．∵ AC 切⊙O 于C ，BC 为⊙O 的直径，∴ AC ⊥BC ．在Rt △ACB 中，sin B ＝51010510==AB AC ．4．解法一：连结AC ．∵ AB 是⊙O 的直径，点C 在⊙O 上，∴ ∠ACB ＝90°．CD ⊥AB 于点D ，∴ ∠ADC ＝∠BDC ＝90°，∠2＝90°－∠BAC ＝∠B ．∵ tan B ＝21，∴ tan ∠2＝21．∴ CB ACDB CD CD AD ===21．设AD ＝x （x ＞0），CD ＝2x ，DB ＝4x ，AB ＝5x ．∵ PC 切⊙O 于点C ，点B 在⊙O 上，∴ ∠1＝∠B ．∵ ∠P ＝∠P ，∴ △PAC ∽△PCB ，∴ 21==CB ACPC PA．∵ PC ＝10，∴ PA ＝5，∵ PC 切⊙O 于点C ，PAB 是⊙O 的割线，∵ PC 2＝PA ·PB ，∴ 102＝5（5＋5 x ）．解得x ＝3．∴ AD ＝3，CD ＝6，DB ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．解法二：同解法一，由△PAC ∽△PCB ，得21==CB ACPC PA．∵ PA ＝10，∴ PB ＝20．由切割线定理，得PC 2＝PA ·PB ．∴ PA ＝201022-PB PC ＝5，∴ AB ＝PB －PA ＝15，∵ AD ＋DB ＝x ＋4x ＝15，解得x ＝3，∴ CD ＝2x ＝6，DB ＝4x ＝12．∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．5．解：如图取MN 的中点E ，连结OE ，∴ OE ⊥MN ，EN ＝21MN ＝21a ．在四边形EOCD 中，∵ CO ⊥DE ，OE ⊥DE ，DE ∥CO ，∴ 四边形EOCD 为矩形．∴ OE ＝CD ，在Rt △NOE 中，NO 2－OE 2＝EN 2＝22⎪⎭⎫ ⎝⎛a ． ∴ S 阴影＝21π（NO 2－OE 2）＝21π·22⎪⎭⎫ ⎝⎛a ＝28πa ．6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ．∴ 2⎪⎭⎫ ⎝⎛=∆∆AB DE S S ABC CDE ∴ AB DE ＝ABC CDE S S ∆∆＝41＝21，即215=AB ，解得 AB ＝10（cm ），作OM ⊥FG ，垂足为M ，则FM ＝21FG ＝21×8＝4（cm ），连结OF ， ∵ OA ＝21AB ＝21×10＝5（cm ）． ∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）．∴ 梯形AFGB 的面积＝2FG AB +·OM ＝2810⨯×3＝27（cm 2）． 7． ⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2＝PB ·PC ⇒PC ＝20⇒半径为7.5⇒圆面积为π4225（或56.25π）（平方单位）．⎭⎬⎫∠=∠∠=∠P P BAP C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC ．解法一：设AB ＝x ，AC ＝2x ， BC 为⊙O 的直径⇒∠CAB ＝90°，则 BC ＝5x ． ∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==xx BC AC 解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65， ∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC。

(必考题)初中九年级数学上册第二十四章《圆》经典练习卷(含答案解析)

一、选择题1．在ABC 中，90,4,3C AC BC ∠=︒==，把它绕AC 旋转一周得一几何体，该几何体的表面积为（）A ．24πB ．21πC ．16.8πD ．36π 2．如图，在平行四边形ABCO 中，45C ∠=︒，点A ，B 在⊙O 上，点D 在优弧ADB 上，DA DB =，则AOD ∠的度数为（）A ．165°B ．155°C ．145°D ．135° 3．如图在ABC 中，∠B=90°，AC=10，作ABC 的内切圆圆O ，分别与AB 、BC 、AC 相切于点D 、E 、F ，设AD=x ，ABC 的面积为S ，则S 关于x 的函数图像大致为（）A ．B ．C ．D ．4．如图，一条公路的拐弯处是一段圆弧AB ，点O 是这段弧所在的圆的圆心，20cm AB =，点C 是AB 的中点，点D 是AB 的中点，且5cm CD =，则这段弯路所在圆的半径为（）A ．10cmB ．12.5cmC ．15cmD ．17cm 5．如图，AB 为O 的直径，C 为O 上一点，其中6AB =，120AOC ∠=︒，P 为O 上的动点，连AP ，取AP 中点Q ，连CQ ，则线段CQ 的最大值为（）A ．37B ．3272+C ．237+D ．33722+ 6．给出下列说法：①圆是轴对称图形，对称轴是圆的每一条直径；②三角形的外心到三角形各顶点的距离相等；③经过三个点一定可以画一个圆；④平分弦的直径垂直于弦；⑤垂直于弦的直径平分弦，并且平分弦所对的两条弧．正确的有（）A ．4B ．3C ．2D ．17．以O 为中心点的量角器与直角三角板ABC 如图所示摆放，直角顶点B 在零刻度线所在直线DE 上，且量角器与三角板只有一个公共点P ，∠POB ＝40°，则∠CBD 的度数是（）A ．50°B ．45°C ．35°D ．40° 8．若圆锥的底面半径为5cm ，侧面积为265cm π，则该圆锥的高是（） A ．13cm B ．12cm C ．11cm D ．10cm 9．如图，ABC 的三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将ABC 绕点B 顺时针旋转到A B C '''的位置，且点A '、C '仍落在格点上，则线段AB 扫过的图形的面积是（）平方单位（结果保留）A ．254πB ．134π C ．132π D ．136π 10．如图，A ，B ，C 三点在O 上，若120ACB ∠=︒，则AOB ∠的度数是（）A ．60︒B ．90︒C ．100︒D ．120︒ 11．如图，在等边ABC 中，点O 在边AB 上，O 过点B 且分别与边AB BC 、相交于点D 、E ，F 是AC 上的点，判断下列说法错误的是（）A ．若EF AC ⊥，则EF 是O 的切线 B ．若EF 是O 的切线，则EF AC ⊥ C ．若32BE EC =，则AC 是O 的切线 D ．若BE EC =，则AC 是O 的切线 12．如图，AB 为O 的弦，半径OC 交AB 于点D ，AD DB =，5OC =，3OD =，则AB 的长为（）A ．8B ．6C ．4D ．213．如图，⊙O 的半径为1，点 O 到直线 a 的距离为2，点 P 是直线a 上的一个动点，PA 切⊙O 于点 A ，则 PA 的最小值是（）A ．1B ．3C ．2D ．5 14．如图，点M 是矩形ABCD 的边BC 、CD 上的点，过点B 作BN ⊥AM 于点P ，交矩形ABCD 的边于点N ，连接DP ，若AB=6，AD=4，则DP 的长的最小值为（）A ．2B ．121313C ．4D ．515．如图，在平行四边形ABCO 中，45C ∠=︒，点A ，B 在O 上，点D 在ADB 上，DA DB =，则AOD ∠的度数为（）A ．112.5°B ．120°C ．135°D ．150°二、填空题16．如图，等腰直角△ABC 中，∠BAC=90°，AB=AC=4．平面内的直线l 经过点A ，作CE ⊥l 于点E ，连接BE.则当直线l 绕着点A 转动时，线段BE 长度的最大值是________．17．如图，有一半径为6cm 的圆形纸片，要从中剪出一个圆心角为60︒的扇形ABC ，AB ，AC 为⊙O 的弦，那么剪下的扇形ABC （阴影部分）的面积为 ___________．18．如图，PA ，PB 分别与O 相切于A 、B 两点，点C 为劣弧AB 上任意一点，过点C 的切线分别交AP ，BP 于D ，E 两点．若8AP =，则PDE △的周长为______．19．如图，,PA PB 切⊙O 于,A B ，点C 在AB 上，DE 切⊙O 于C ，10cm,PO =⊙O 的半径为6cm ，则PDE △的周长是_________cm ．20．如图，A 是半径为1的O 外一点，2OA =，AB 是O 的切线，点B 是切点，弦//BC OA ，连接AC ，则图中阴影部分的面积为________．21．如图，已知点,,A B C 在O 上，若50ACB ∠=，则AOB ∠=_____________________度．22．在矩形ABCD 中，43AB =，6BC =，若点P 是矩形ABCD 上一动点，要使得60APB ∠=︒，则AP 的长为__________．23．如图，ABC 内接于半径为10的半圆，AB 为直径，点M 是弧AC 的中点，连结BM 交AC 于点E ，AD 平分∠CAB 交BM 于点D ，∠ADB ＝_____°，当点D 恰好为BM 的中点时，BM 的长为____．24．如图，在⊙O 中，弦AC 、BD 相交于点E ，且AB BC CD ==，若∠BEC=130°，则∠ACD 的度数为_____25．小红在手工制作课上，用面积为215cm π，半径为15cm 的扇形卡纸，围成一个圆锥侧面，则这个圆锥的底面半径为_______cm ．26．如图，MN 是O 的直径，2MN =，点A 在O 上，30AMN ∠=︒，B 为弧AN 的中点，点P 是直径MN 上的一个动点，则PA PB +的最小值为_______．三、解答题27．如图，AB是⊙O的一条弦，OD⊥AB，垂足为C，OD交⊙O于点D，点E在⊙O上，若∠AOD＝50°．（1）求∠DEB的度数；（2）若OC＝3，OA＝5，①求弦AB的长；②求劣弧AB的长．28．如图，在⊙O中，C是AB的中点，∠ACB=∠AOB．求证：四边形OACB是菱形．=，点F是29．如图，AB、CD是O中两条互相垂直的弦，垂足为点E，且AE CEBC的中点，延长FE交AD于点G，已知1,3,2AE BE OE===．≌；（1）求证：AED CEB⊥；（2）求证：FG AD（3）求O的半径．30．如图，长方形ABCD的长是a，宽是b，分别以A、C为圆心作扇形，用代数式表示阴影部分的周长L和面积S（结果中保留π）．。

(好题)初中数学九年级数学下册第三单元《圆》测试题(答案解析)(3)

一、选择题1．如图，PA PB 、分别与О相切于A B 、两点，点C 为О上一点，连接AC 、,BC 若50P ∠=，则ACB ∠的度数为（）A ．115B ．130C ．65D ．752．下列命题：①任意三点确定一个圆；②平分弦（不是直径）的直径垂直于弦；③相等的圆心角所对的弦相等；④长度相等的弧是等弧．其中真命题的有（）A ．0个B ．1个C ．2个D ．3个3．如图，已知E 是ABC 的外心，P ，Q 分别是AB ，AC 的中点，连接EP ，EQ ，分别交BC 于点F ，D ．若10BF =，6DF =，8CD =，则ABC 的面积为（）A ．72B ．96C ．120D ．1444．如图，AB 是⊙O 的直径，C 是⊙O 上一点，BD 平分∠ABC 交⊙O 于点D ，交AC 于点E ，已知DE =2，DB =6，则阴影部分的面积为（）A ．2π3B ．4π3C ．4π3D ．π3 5．如图，O 的半径为5，3OP =，则经过点P 的弦长可能是（）A ．3B ．5C ．9D ．126．如图一个扇形纸片的圆心角为90°，半径为6，将这张扇形纸片折叠，使点A 和点O 恰好重合，折痕为CD ，则阴影部分的面积为（）A ．933π-B ．693π-C ．393π-D ．936π- 7．下列关于正多边形的叙述，正确的是（）A ．正七边形既是轴对称图形又是中心对称图形B ．存在一个正多边形，它的外角和为720︒C ．任何正多边形都有一个外接圆D ．不存在每个外角都是对应每个内角两倍的正多边形8．已知：O 的半径为2，3OA =，则正确的图形可能为（）A ．B ．C ．D ．9．如图，四边形ABCD 中，对角线AC ，BD 交于点E ．若BAC BDC ∠=∠，则下列结论中正确的是（）①AE BE DE CE = ②ABE △与DCE 的周长比为BE CE③ADE ABC =∠∠ ④ABE DCE ADE BCE S S S S ⋅=⋅ A ．③④B ．①②③C ．①②④D ．①②③④ 10．下列事件是随机事件的是（）A ．一个图形平移后所得的图形与原来的图形全等B ．直径是圆中最长的弦C ．方程2210ax x ++=是一元二次方程D ．任意画一个三角形，其内角和是360︒11．如图，半径为10的扇形AOB 中，90AOB ∠=︒，C 为弧AB 上一点，CD OA ⊥，CE OB ⊥，垂足分别为D ，E ．若图中阴影部分的面积为10π，则CDE ∠=（）A ．30B ．36︒C ．54︒D ．45︒12．如图，正方形ABCD 的四个顶点都在⊙O 上，在AD 上取一点E （点E 不与D 重合），连接EC ，ED ，则∠CED 的度数为（）A ．30°B ．45°C ．60°D ．75°二、填空题13．如图，一次函数3233y x =-+的图象与x 轴交于点A ，与y 轴交于点B ，若向ABO 的外接圆C 内随机抛掷一枚小针，则针尖落在阴影部分的概率是_____________．14．已知O 的半径为1，AB 是O 的弦，2AB =，P 为O 外一点，且PA 切O 于点A ，1PA =，则线段PB 的长为________．15．圆锥的表面展开图由一个扇形和一个圆组成，已知扇形的半径为9，圆心角为120°，则圆锥的底面圆的半径为__________．16．如图，O 是ABC 的内切圆，切点分别为D 、E 、F ，80A ∠=︒，点P 为O 上任意一点（不与E 、F 重合），则EPF ∠=______．17．如图，BAC 是O 的内接三角形，BC 为直径，AD 平分BAC ∠，连接BD 、CD ，若65ACB ∠=︒，则ABD ∠的度数为_________．18．如图，从一块直径为2m 的圆形铁皮上画出一个圆心角为90的扇形．若随机在圆及其内部投针，则针孔扎在扇形（阴影部分）的概率为____．19．如图，已知O 的半径为2，ABC 内接于O ，135ACB ∠=︒，则弓形ACB （阴影部分）的面积为_____________．20．如图，ABC 内接于O ，70B ∠=︒，50OCB ∠=︒，点P 是O 上一个动点（不与图中已知点重合），若ACP △时等腰三角形，则ACP ∠的度数为___．三、解答题21．如图，已知ABC ∆．（1）用无刻度的直尺、圆规作ABC ∆的外接圆（只需作出图形，并保留作图痕迹)．（2）若110BAC ︒∠=，在ABC ∆的外接圆中，仅用无刻度的直尺能画出的不同度数的圆周角有 (写度数)．22．如图，台风中心位于点P ，并沿东北方向PQ 移动，已知台风移动的速度为40千米时，受影响区域的半径为260千米，B 市位于点P 的北偏东75︒方向上，距离P 点480千米．问：本次台风是否会影响B 市．若这次台风会影响B 市，求B 市受台风影响的时间．23．如图，直线AB 经过⊙O 上一点C ，且OA ＝OB ，CA ＝CB ．（1）求证：AB 是⊙O 的切线；（2）若AB ＝6，△AOB 的面积为9，求图中阴影部分的面积．24．如图，在10×10的网格图内，建立如图所示的平面直角坐标系，△ABC 的顶点坐标分别为A （﹣1，2）、B （2，3）、C （3，1）．（1）以原点O 为位似中心，将△ABC 按相似比2：1放大，得△A 1B 1C 1，请画出△A 1B 1C 1；（2）以原点O 为旋转中心，将△ABC 按顺时针方向旋转90°，画出旋转后的△A 2B 2C 2．直接写出点B 到B 2所经过的路径长．25．学校花园边墙上有一宽（BC ）为23m 的矩形门ABCD ，量的门框对角线AC 长为4cm ，为美化校园，现准备打掉地面BC 上方的部分墙体，使其变为以AC 为直径的圆弧形门，问要打掉墙体（阴影部分）的面积是多少？（结果中保留π，3）26．如图，ABC 中，D 为AB 边上一点，连接CD ，BD CD =．以AC 为直径作O ，过点O 作OE AC ⊥ 交BC 于点E ，连接DE ，BDE CDE ∠=∠．（1）求证：AB 为O 的切线；（2）若16AB =，8AC =，求BD 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】由切线的性质得出∠OAP=∠OBP=90°，利用四边形内角和可求∠AOB=130°，再利用圆周角定理可求∠ADB=65°，再根据圆的内接四边形对角互补可求∠ACB ．【详解】解：如图所示，连接OA 、OB ，在优弧AB 上取点D ，连接AD 、BD ，∵ AP 、BP 是切线，∠P=50°，∴ ∠OAP=∠OBP=90°，∴∠AOB=360°-90°-90°-50°=130°，∴∠ADB=65°，又∵圆的内接四边形对角互补，∴∠ACB=180°-∠ADB=180°-65°=115°．故选：A ．【点睛】本题考查了切线的性质、圆周角定理、圆内接四边形的性质、解题的关键是连接OA 、OB ，求出∠AOB ．2．B解析：B【分析】依次判断真假命题即可，可以通过找到相应的反例，去论证命题的正确性．【详解】解：①假命题，当三点在同一条直线上时，就不能确定一个圆了，故此项错误； ②真命题，平分弦（不是直径）的直径垂直于弦，故此项正确；③假命题，在同圆或等圆中，相等的圆心角所对的弦相等，故此项错误；④假命题，在同圆或等圆中，长度相等的弧是等弧，故此项错误；综上所述，②正确．故选：B ．【点睛】本题主要考查了确定圆的条件，垂径定理及圆周角定理等圆的一些基本的知识，解答此题的关键掌握理解圆的定义及性质．3．B解析：B【分析】连接AF ，AD ，AE ，BE ，CE ，根据三角形外心的定义，可得PE 垂直平分AB ，QE 垂直平分AC ，进而求得AF ，DF ，AD 的长度，可知△ADF 是直角三角形，即可求出△ABC 的面积．【详解】如图，连接AF ，AD ，AE ，BE ，CE ，∵点E 是△ABC 的外心，∴AE=BE=CE ，∴△ABE ，△ACE 是等腰三角形，∵点P 、Q 分别是AB 、AC 的中点，∴PE ⊥AB ，QE ⊥AC ，∴PE 垂直平分AB ，QE 垂直平分AC ，∴AF=BF=10， AD=CD=8，在△ADF 中，∵2222286=100=AD DF AF +=+，∴△ADF 是直角三角形，∠ADF=90°，∴S △ABC = ()()1122=1068896BF DF CD AD ⨯++⨯++=，故选：B ．【点睛】本题考查三角形外心的定义，勾股定理逆定理等知识点，解题的关键是得到△ADF 是直角三角形． 4．A解析：A【分析】证明△DAE ~△DBA ，求得DA 23=，由AB 是⊙O 的直径，利用勾股定理求得⊙O 的直径，求得∠ABD=30︒，∠COD=60︒，再利用OCD OCD S S S=-阴影扇形即可求解．【详解】连接OC 、OD 、AD ，∵BD 平分∠ABC ，∴AD CD =，∴∠DAC=∠DBA ，∴△DAE ~△DBA ，∴DA DE DB DA =，即26DA DA=， ∴212DA =，∴DA 23=，∵AB 是⊙O 的直径，∴∠ADB=90︒，∴222AD BD AB +=，∴AB=43∴⊙O 的半径为3∵DA=OA=OD 23=，∴△DOA 是等边三角形，∴∠COD=∠AOD=60︒，∴OCD OCD S S S =-阴影扇形(2601603602π⨯=-⨯︒2π=-故选：A ．【点睛】本题考查了相似三角形的判定与性质、等边三角形的判定与性质、勾股定理、扇形与等边三角形的面积等知识点，熟练掌握相关性质及定理是解题的关键．5．C解析：C【分析】当经过点O 、P 的弦是直径时，弦最长为10；当弦与OP 是垂直时，弦最短为8；判断即可.【详解】当经过点O 、P 的弦是直径时，弦最长为10；当弦与OP 垂直时，根据垂径定理，得半弦长，所以最短弦为8；所以符合题意的弦长为8到10，故选C.【点睛】本题考查了直径是最长的弦，垂径定理，熟练运用分类思想，垂径定理，勾股定理是解题的关键.6．A解析：A【分析】连接OD ，AD ，由题意得1122AC CO AO OD ===，30CDO ∠=︒，60COD ∠=︒，进而可得=AOD OAD AOD S S S S+-空白扇形扇形，然后可得=AOB S S S -阴影空白扇形，进而问题可求解．【详解】解：连接OD ，AD ， ∴1122AC CO AO OD ===， ∵DC ⊥AO ，∴30CDO ∠=︒，60COD ∠=︒，∴=AOD OAD AOD S S S S +-空白扇形扇形，22260603=666360360ππ⨯+⨯-⨯， 1293π=-，∴=AOB S S S -阴影空白扇形，()290=61293360ππ⨯--， 933π=-；故选A ．【点睛】本题主要考查扇形面积，熟练掌握求不规则面积的方法及扇形面积计算公式是解题的关键．7．C解析：C【分析】根据中心对称图形、轴对称图形的定义、多边形外角和定理、正多边形的性质对各选项逐一判断即可得答案．【详解】A.正七边形是轴对称图形，不是中心对称图形，故该选项错误，B.任意多边形的外角和都等于360°，故该选项错误，C.任何正多边形都有一个外接圆，故该选项正确，D.∵正三角形的每个外角为120°，对应的每个内角为60°，∴存在每个外角都是对应每个内角两倍的正多边形，故该选项错误，故选：C ．【点睛】本题考查正多边形的性质、中心对称图形、轴对称图形的定义及多边形外角和定理，熟练掌握相关性质及定理是解题关键．8．C解析：C【分析】根据圆的半径和OA 的大小确定点A 与圆的位置关系，从而作出判断即可．【详解】∵根据图的意义，得OA=2，与OA=3矛盾，∴A 选项错误；∵根据图的意义，得OA ＜2，与OA=3矛盾，∴B 选项错误；∵根据图的意义，得OA ＞2，且离圆较近，与OA=3相符，∴C 选项正确；∵根据图的意义，得OA ＞2，且离圆较远，与OA=3不符合，∴D 选项错误；故选C ．【点睛】本题考查了点与圆的位置关系，熟练掌握圆心到点的距离与圆的半径的大小比较是解题的关键．9．C解析：C【分析】根据相似三角形可得①②正确，由四点共圆可知③不符合题意，面积比转化成边长比可得④正确．【详解】解：∵BAC BDC ∠=∠，AEB DEC ∠=∠∴ABE DCE ∴AE BE DE CE = ∴①正确；相似三角形周长比等于相似比，②正确∵BAC BDC ∠=∠，且△BDC 和△BAC 共有底BC∴得到A ，B ，C ，D 四点共圆；若ADE ABC =∠∠，则=ADE ABC ACB =∠∠∠，则AB=AC ，但题目中并没有告诉这个条件，所以③不一定正确；∵△ABE 和△ADE 共有高，∴ABE ADE S BE S DE =， ∵△CBE 和△CDE 共有高，∴BCE DCE BE S DE S = ∴ABEBCEADE DCE S BE S S DE S ==即，ABE DCE ADE BCE S S S S ⋅=⋅，故 ④正确；∴①②④正确，选C.【点睛】此题主要考查了相似三角形的判断及其性质，解决本题的关键是合理作辅助圆，熟练掌握相似三角的性质定理．10．C解析：C【分析】根据随机事件是可能发生也可能不发生的事件判断即可．【详解】解：A 、是必然事件，选项不符合题意；B 、是必然事件，选项不符合题意；C 、是随机事件，选项符合题意；D 、是不可能事件，选项不符合题意．故选：C ．【点睛】本题考查了必然事件的定义，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件． 11．B解析：B【分析】连接OC ，易得四边形CDOE 是矩形，△DOE ≌△CEO ，根据扇形的面积公式得∠COE=36°，进而即可求解．【详解】解：连接OC ，∵∠AOB ＝90°，CD ⊥OA ，CE ⊥OB ，∴四边形CDOE 是矩形，∴CD ∥OE ，∴∠DEO ＝∠CDE ，由矩形CDOE 易得到△DOE ≌△CEO ，∴图中阴影部分的面积＝扇形OBC 的面积，∵S 扇形OBC ＝210360n π⨯＝10π，解得：n=36， ∴CDE ∠=∠DEO=∠COE=36°．故选B ．【点睛】本题考查了扇形面积的计算，矩形的判定与性质，全等三角形的判定和性质，利用扇形OBC 的面积等于阴影的面积是解题的关键．12．B解析：B【分析】连接DO 、CO ，利用正方形的性质可求得圆心角的度数为90°，再根据圆周角定理求解即可得出结论．【详解】解：如图，连接DO 、CO ，∵四边形ABCD 为正方形，∴∠COD ＝90°，∴∠CED ＝12∠COD ＝45°．故选：B ．【点睛】考查了正方形和圆的性质，掌握正方形的性质及圆周角定理并能正确的作出辅助线是解答此题的关键．二、填空题13．【分析】利用一次函数解析式求出点AB 的坐标即可得由勾股定理求出求出则可得是等边三角形可得根据圆周角定理求出扇形圆心角的度数并由三角形中线将三角形可分为面积相等的两个三角形得可求出阴影部分的面积及圆的解析：13【分析】利用一次函数解析式求出点A 、B 的坐标，即可得6OA =，OB =AB =，求出BC OC AC ===OBC 是等边三角形，可得60OBA ∠=︒，根据圆周角定理求出扇形圆心角的度数，并由三角形中线将三角形可分为面积相等的两个三角形得OBC OAC SS =，可求出阴影部分的面积及圆的面积，利用面积比即可求出结论．【详解】解：∵一次函数y x =-+的图象与x 轴交于点A ，与y 轴交于点B ，令0y =，则6x =，∴()6,0A -，令0x =，则y =∴(0,B ，∴6OA =，OB =在Rt AOB 中，由勾股定理得：AB ==， ∴BC OC AC ===，∴BC OC OB ==， ∴OBC 是等边三角形，∴60OBA ∠=︒， ∴120ACO ∠=︒，∵OC 是AB 边上的中线，∴OBC OAC S S =，∴(2120=4360ACO S S ππ==阴影扇形，(212C S ππ==,∴针尖落在阴影部分的概率41123P ππ==．故答案为：13．【点睛】此题考查了几何概率，掌握几何概率的计算方法及求出阴影部分的面积是解题的关键． 14．1或【分析】先利用勾股定理逆定理求出∠AOB 是直角再利用一组对边平行且相等得到四边形APBO 是平行四边形从而PB 的长等于半径OA 另当B 在右侧时还需讨论【详解】解：①如图所示：连接OAOB ∵OA=OB解析：1或5【分析】先利用勾股定理逆定理求出∠AOB 是直角，再利用一组对边平行且相等得到四边形APBO 是平行四边形，从而PB 的长等于半径OA ．另当B 在右侧时，还需讨论．【详解】解：①如图所示：连接OA 、OB ．∵OA=OB=1，AB=2，∴根据勾股定理的逆定理，得∠AOB=90°，根据切线的性质定理，得∠OAP=90°，则AP ∥OB ，又AP=OB=1，所以四边形PAOB 是平行四边形，所以PB=OA=1；②当B 在右侧时，如图所示：与①同理可证四边形APOB 是平行四边形，且∠AOB=90°，∴11,222OC AC BP BC ===，在Rt △OBC 中，根据勾股定理 222215()122BC OC OB =+=+=， ∴PB=25BC =故答案为：15【点睛】考查了圆的性质、平行四边形判定和性质以及勾股定理，解题关键是能够根据勾股定理的逆定理发现直角三角形，进一步发现特殊四边形平行四边形．15．3【分析】根据弧长公式求出扇形的弧长圆锥侧面展开扇形的弧长等于圆锥底面圆的周长再利用圆周长的公式求解即可【详解】扇形的半径为9圆心角为120°扇形的弧长圆锥侧面展开扇形的弧长等于圆锥底面圆的周长设圆解析：3【分析】根据弧长公式求出扇形的弧长，圆锥侧面展开扇形的弧长等于圆锥底面圆的周长，再利用圆周长的公式求解即可【详解】扇形的半径为9，圆心角为120°∴扇形的弧长12096 180180n rlπππ⨯===圆锥侧面展开扇形的弧长等于圆锥底面圆的周长设圆锥底面圆的半径为r26rππ∴=3r∴=故答案为：3．【点睛】本题考查了圆锥侧面展开图与底面圆之间的关系，弧长的计算，解题关键是熟知圆锥侧面展开扇形的弧长等于圆锥底面圆的周长．16．50°或130°【分析】有两种情况：①当P在优弧EF上时连接OEOF求出∠EOF根据圆周角定理求出即可；②当P在劣弧EF上时根据圆内接四边形的性质得到∠EP1F+∠EP2F=180°代入求出即可【详解析：50°或130°【分析】有两种情况：①当P在优弧EF上时，连接OE、OF，求出∠EOF，根据圆周角定理求出即可；②当P在劣弧EF上时，根据圆内接四边形的性质得到∠EP1F+∠EP2F=180°，代入求出即可．【详解】解：有两种情况：①当P在优弧EF上时，连接OE、OF，∵圆O是△ABC的内切圆，∴OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，∵∠A=80°，∴∠EOF=360°-∠AEO-∠AFO-∠A=100°，∴∠EP 1F =12∠EOF=50°， ②当P 在劣弧EF 上时，∠FP 2E =180°-50°=130°，故答案为：50°或130°．．【点睛】本题考查了垂线的定义，多边形的内角和定理，三角形的内切圆与内心，圆周角定理等知识点的理解和掌握，能综合运用性质进行推理是解题的关键．17．【分析】由为直径可得∠BAC=∠BDC=90°由平分可证BD=DC 可得∠DBC=∠DCB=45°可求∠ABC=90°-∠ACB=25°可求∠ABD=∠ABC+∠DBC=70°即可【详解】解：∵是的内解析：70︒【分析】由BC 为直径，可得∠BAC=∠BDC=90°由AD 平分BAC ∠，可证BD=DC ，可得∠DBC=∠DCB=45°，65ACB ∠=︒，可求∠ABC=90°-∠ACB=25°，可求∠ABD=∠ABC+∠DBC=70°即可．【详解】解：∵BAC 是O 的内接三角形，BC 为直径，∴∠BAC=∠BDC=90°∵AD 平分BAC ∠，∴∠BAD=∠CAD ， ∴BD DC =，∴BD=DC ，∴∠DBC=∠DCB=45°，∵65ACB ∠=︒，∴∠ABC=90°-∠ACB=90°-65°=25°，∴∠ABD=∠ABC+∠DBC=25°+45°=70°．故答案为：70°．【点睛】本题考查圆的性质，直径所对圆周角性质，角平分线性质，直角三角形性质，掌握圆的性质，直径所对圆周角性质，角平分线性质，直角三角形性质是解题关键．18．【分析】连接AC根据圆周角定理得出AC为圆的直径解直角三角形求出AB求出扇形面积和面积两者的面积比即是针孔扎在扇形（阴影部分）的概率【详解】解：连接AC∵从一块直径为2m的圆形铁皮上剪出一个圆心角为解析：12【分析】连接AC，根据圆周角定理得出AC为圆的直径，解直角三角形求出AB，求出扇形面积和O面积，两者的面积比，即是针孔扎在扇形（阴影部分）的概率．【详解】解：连接AC，∵从一块直径为2m的圆形铁皮上剪出一个圆心角为90︒的扇形，即∠ABC=90︒，∴AC为直径，即AC=2m，AB=BC（扇形的半径相等），∵AB2+BC2=22，∴2m，∴S阴影部分=29023602ππ︒⨯=︒（m2），则：P针孔扎在扇形（阴影部分）=212==2OSS OA=阴影部分ππ故答案为：12．【点睛】本题考查了几何概率：求概率时，已知和未知与几何有关的就是几何概率．计算方法是长度比，面积比，体积比等．19．【分析】根据圆内接四边形对角互补和同弧所对的圆心角是圆周角的二倍可以求得∠AOB的度数然后根据弓形ACB的面积=S扇形OAB-S△OAB得出结果即可【详解】解：设点D为优弧AB上一点连接ADBDOA解析：2π-【分析】根据圆内接四边形对角互补和同弧所对的圆心角是圆周角的二倍，可以求得∠AOB的度数，然后根据弓形ACB的面积=S扇形OAB-S△OAB得出结果即可．【详解】解：设点D 为优弧AB 上一点，连接AD 、BD 、OA 、OB ，如图所示，∵⊙O 的半径为2，△ABC 内接于⊙O ，∠ACB=135°，∴∠ADB=45°，∴∠AOB=90°，∵OA=OB=2，∴弓形ACB 的面积=S 扇形OAB -S △OAB =29021223602π⨯⨯-⨯⨯=2π-，故答案为：2π-．【点睛】本题主要考查求弓形的面积，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．20．或或【分析】根据题意分三种情况讨论即可得∠ACP 的度数【详解】解：如图连接OAOB ∵∠OCB=50°∴∠OBC=50°∴∠BOC=180°-50°-50°=80°∵∠B=70°∴∠OBA=∠OAB=解析：35︒或40︒或55︒【分析】根据题意分三种情况讨论即可得∠ACP 的度数．【详解】解：如图，连接OA ，OB ，∵∠OCB=50°，∴∠OBC=50°，∴∠BOC=180°-50°-50°=80°．∵∠B=70°，∴∠OBA=∠OAB=20°，∴∠AOB=140°，∴∠AOC=360°-80°-140°=140°，∴∠OAC=∠OCA=20°，∴∠ACB=50°+20°=70°，∴AB=AC．当AP′=AC时，此时点P′与点B重合，不符合题意；当AP=PC时，∵∠B=70°，∴∠APC=180°-70°=110°，∴∠ACP=∠CAP=1(180°-110°)=35°；2当AP′=P′C时，∠P′AC=∠P′CA=1(180°-70)=55°；2当AC=P′C时，∠ACP′=180°-70°-70°=40°．故答案为：35°或40°或55°．【点评】本题考查了三角形的外接圆与外心、圆周角定理、等腰三角形的性质，解决本题的关键是综合运用以上知识进行分类讨论．三、解答题21．（1）见解析；（2）70︒、110︒【分析】（1）利用三角形外接圆的做法作出任意两边的垂直平分线进而得出圆心的位置即可得出答案．（2）根据同弧所对的圆周角相等求解即可．【详解】解：(1) 如图的圆为所求作(2) 若110BAC ∠=︒，则优弧BC 所对的圆周角大小为110°，劣弧BC 对应的圆周角的大小为180°-110°=70°，故有两个不同度数的圆周角，其度数分别为：70°和110°．故答案为：70°和110°．【点睛】此题主要考查了三角形外接圆的作法以及圆周角与弧的关系，熟练掌握三角形外接圆作法是解答此题的关键．22．本次台风会影响B 市，影响时间为5小时【分析】作BH ⊥PQ 于点H ，在Rt BHP 中，利用含30°角的直角三角形的性质求出BH 的长与260千米相比较即可．以B 为圆心，以260为半径作圆交PQ 于P 1、P 2两点，根据垂径定理即可求出P 1P 2的长，进而求出台风影响B 市的时间．【详解】如图，作BH ⊥PQ 于点H在Rt BHP 中，由条件知，PB ＝480，∠BPQ ＝75°﹣45°＝30°，∴BH=14802⨯=240＜260， ∴本次台风会影响B 市．如图，以B 为圆心，以260为半径作圆交PQ 于P 1、P 2两点，若台风中心移动到P 1时，台风开始影响B 市，台风中心移动到P 2时，台风影响结束．根据BH=240，由条件得BP 1=BP 2=260，∴P1P2=222260240-=200，∴台风影响的时间t=20040=5（小时）．故B市受台风影响的时间为5小时．【点睛】本题考查了含30°角的直角三角形的性质，勾股定理及垂径定理在实际生活中的运用，解答此题的关键是构造出直角三角形及圆．23．（1）见解析；（2）994π-．【分析】（1）连接OC，结合已知条件利用SSS易证△AOC≌△BOC，再利用全等三角形的性质可得∠OCA＝∠OCB＝90°，然后利用切线的判定可得直线AB与⊙O相切；（2）根据AB＝6和（1）中三角形的全等，可得AC＝BC＝3，根据△AOB的面积为9，可得OC，并推出∠AOB＝90°，则可利用扇形面积公式与△AOB的面积计算阴影部分的面积．【详解】（1）证明：如图，连接OC，∵OA＝OB，CA＝CB，OC＝OC，∴△AOC≌△BOC（SSS），∴∠OCA＝∠OCB＝90°，∴直线AB与⊙O相切；（2）解：∵△AOC≌△BOC，∴AC＝BC＝12AB＝3，∵△AOB的面积为9，∴12×AB•OC＝9，∴12×6•OC＝9，∴OC＝3，∴OC ＝AC ，∴△OAC 是等腰直角三角形，∴∠AOC ＝∠BOC ＝45°，∴∠AOB ＝90°，∴S 阴影＝S △AOB −S 扇形＝29039993604ππ⋅-=-．【点睛】本题考查了切线的判定和性质、全等三角形的判定和性质、扇形面积的计算等知识，解题的关键是掌握切线的判定与性质．24．（1）答案见详解；（2）13π．【分析】（1）把A 、B 、C 的横纵坐标都乘以2得到A 1、B 1、C 1的坐标，然后描点连线即可；（2）利用网格特点和旋转性质画出A 、B 、C 的对应点A 2、B 2、C 2即可，然后利用弧长公式计算点B 到B 2所经过的路径长．【详解】解：（1）如图，△A 1B 1C 1为所作；（2）如图，△A 2B 2C 2为所作；OB 222313=+=所以点B 到B 2所经过的路径长901313π⨯⨯==． 13．【点睛】本题考查了作图﹣位似变换：在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k ，那么位似图形对应点的坐标的比等于k 或﹣k ．也考查了旋转变换． 25．8-333π【分析】利用整个圆的面积减矩形的面积减扇形OBC 的面积加上三角形OBC 的面积，即可解答．【详解】由题可得：在Rt ABC 中4,2sin 26030120AB BC AB BC BAC AC BAC BCO BOC ==∴===∴∠==∴∠=︒∴∠=︒∴∠=︒要打掉的墙体面积OBC O ABCD OBC S S S S =--+△圆矩形扇形 ∴要打掉的墙体面积223238=-2234343O ABCD S S ππ=⋅⋅-⨯=-圆矩形【点睛】本题考查了矩形的性质，直角三角形的性质，矩形、圆的面积公式及勾股定理，解题关键是结合图形通过面积转换得到规则的几何图形面积进而求解．26．（1）见解析；（2）10【分析】（1）根据等腰三角形的性质可证点E 为BC 的中点，在结合三角形中位线定理，证明//OE AB ，即可得到结论（2）设BD=CD=x ，在Rt ACD △中利用勾股定理，列出关于x 的方程即可求解【详解】（1）BD CD =BDC ∴是等腰三角形又BDE CDE ∠=∠．BE EC ∴=，AO OC =OE ∴为ABC 的中位线//OE AB ∴，BAC EOC ∴∠=∠OE AC ⊥，90BAC EOC ∴∠=∠=︒AB AC ∴⊥， AC 为O 的直径，AB ∴是O 的切线（2）设BD x =，CD BD x ∴==，16AB=，∴=-16AD xAC=在Rt ADC中，222+=，8AD AC DC()222∴-+=，168x xx=，解得：10∴=BD10【点睛】本题考查了圆切线的判定，等腰三角形的性质，以及勾股定理，解题关键是熟练掌握圆切线的判定定理，和等腰三角形性质的应用．。

人教版九年级上册数学圆专题卷(有答案)

人教版九年级上册数学圆专题卷（有答案）一、单选题（共12题；共24分）1.如图，AB是半圆的直径，AB＝2r，C、D为半圆的三等分点，则图中阴影部分的面积是（）.A. πr2B. πr2C. πr2D. πr22.若⊙O的半径为6，点P在⊙O内，则OP的长可能是（）A. 5B. 6C. 7D. 83.如图，A、B、C三点在⊙O上，∠AOB＝80º，则∠ACB的大小（）`A. 40ºB. 60ºC. 80ºD. 100º4.已知AB、CD是两个不同圆的弦，如AB=CD，那么与的关系是（）A. =B. ＞C. ＜D. 不能确定5.已知⊙O中最长的弦为8cm，则⊙O的半径为（）cm．A. 2B. 4C. 8D. 166.已知⊙O1与⊙O2的半径分别为3和4，若圆心距O1O2=1，则两圆的位置关系是（）:A. 相交B. 相离C. 内切D. 外切7.两圆的半径分别是5cm和4cm,圆心距为7cm,则两圆的位置关系是( )A. 相交B. 内切C. 外切D. 外离8.如图，某公园的一座石拱桥是圆弧形（劣弧），拱的半径为13米，拱高CD为8米，则拱桥的跨度AB 的长为（）)A. 20米B. 24米C. 28米D. 24米9.如图，PA、PB、DE分别切⊙O于A、B、C点，若圆O的半径为6，OP=10，则△PDE的周长为（）A. 10B. 12C. 16D. 2010.如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（）A. B. 2 C. 2 D. 311.（2017•葫芦岛）如图，点A,B,C是⊙O上的点，∠AOB=70°，则∠ACB的度数是（））A. 30°B. 35°C. 45°D. 70°12.如图是由7个形状、大小完全相同的正六边形组成的网格，正六边形的各顶点称为格点，直角△ABC的顶点均在格点上，则满足条件的点C有（）A. 6个B. 8个C. 10个D. 12个二、填空题（共6题；共20分）13.如图，AB是⊙O的弦，点C在过点B的切线上，且OC⊥OA，OC交AB于点P，已知∠OAB＝22°，则∠OCB ＝________°．14.（2011•南通）比较正五边形与正六边形，可以发现它们的相同点和不同点．例如：它们的一个相同点：正五边形的各边相等，正六边形的各边也相等．它们的一个不同点：正五边形不是中心对称图形，正六边形是中心对称图形．请你再写出它们的两个相同点和不同点：相同点：①________；②________．不同点：①________；②________．!15.如图，在⊙O中，点A、O、D和点B、O、C分别在一条直线上，图中共有 ________条弦，它们分别是 ________16.如图，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为________．17.如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D （4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是________．18.一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘，如图所示，AB与CD是水平的，BC与水平面的夹角为60°，其中AB=60cm，CD=40cm，BC=40cm，那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为________cm．三、综合题（共5题；共56分）19.如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．》（1）求证：AE=ED；（2）若AB=10，∠CBD=36°，求的长．20.如图，在半径为2的⊙O中，弦AB长为2．、（1）求点O到AB的距离．（2）若点C为⊙O上一点（不与点A，B重合），求∠BCA的度数．21.（2015•北海）如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD 的延长线交于点P，使∠PED=∠C．^（1）求证：PE是⊙O的切线；（2）求证：ED平分∠BEP；（3）若⊙O的半径为5，CF=2EF，求PD的长．;22.（2017•安顺）如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．（1）求证：BE与⊙O相切；（2）设OE交⊙O于点F，若DF=1，BC=2 ，求阴影部分的面积．23.如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．（1）∠ACB=________°，理由是：________；（2）猜想△EAD的形状，并证明你的猜想；（3）若AB=8，AD=6，求BD．`答案一、单选题1.B2. A3. A4.D5. B6. C7. A8. B9. C 10.C 11.B 12. C二、填空题13.4414.都是轴对称图形；都有外接圆和内切圆；内角和不同；对角线的条数不同15.三；AE，DC，AD.16.17.618.三、综合题19. （1）证明：∵AB是⊙O的直径，∴∠ADB=90°，∵OC∥BD，∴∠AEO=∠ADB=90°，即OC⊥AD，∴AE=ED；（2）解：∵OC⊥AD，∴，∴∠ABC=∠CBD=36°，∴∠AOC=2∠ABC=2×36°=72°，∴．20.（1）解：过点O作OD⊥AB于点D，连接AO，BO．如图1所示：∵OD⊥AB且过圆心，AB=2，∴AD= AB=1，∠ADO=90°，在Rt△ADO中，∠ADO=90°，AO=2，AD=1，∴OD= = ．即点O到AB的距离为．（2）解：如图2所示：∵AO=BO=2，AB=2，∴△ABO是等边三角形，∴∠AOB=60°．若点C在优弧上，则∠BCA=30°；若点C在劣弧上，则∠BCA= （360°﹣∠AOB）=150°；综上所述：∠BCA的度数为30°或150°．21.（1）证明：如图，连接OE．∵CD是圆O的直径，∴∠CED=90°．∵OC=OE，∴∠1=∠2．又∵∠PED=∠C，即∠PED=∠1，∴∠PED=∠2，∴∠PED+∠OED=∠2+∠OED=90°，即∠OEP=90°，∴OE⊥EP，又∵点E在圆上，∴PE是⊙O的切线；（2）证明：∵AB、CD为⊙O的直径，∴∠AEB=∠CED=90°，∴∠3=∠4（同角的余角相等）．又∵∠PED=∠1，∴∠PED=∠4，即ED平分∠BEP；（3）解：设EF=x，则CF=2x，∵⊙O的半径为5，∴OF=2x﹣5，在RT△OEF中，OE2=OF2+EF2，即52=x2+（2x﹣5）2，解得x=4，∴EF=4，∴BE=2EF=8，CF=2EF=8，∴DF=CD﹣CF=10﹣8=2，∵AB为⊙O的直径，∴∠AEB=90°，∵AB=10，BE=8，∴AE=6，∵∠BEP=∠A，∠EFP=∠AEB=90°，∴△AEB∽△EFP，∴，即，∴PF=，∴PD=PF﹣DF=﹣2=．22.（1）证明：连接OC，如图，∵CE为切线，∴OC⊥CE，∴∠OCE=90°，∵OD⊥BC，∴CD=BD，即OD垂中平分BC，∴EC=EB，在△OCE和△OBE中，∴△OCE≌△OBE，∴∠OBE=∠OCE=90°，∴OB⊥BE，∴BE与⊙O相切（2）解：设⊙O的半径为r，则OD=r﹣1，在Rt△OBD中，BD=CD= BC= ，∴（r﹣1）2+（）2=r2，解得r=2，∵tan∠BOD= = ，∴∠BOD=60°，∴∠BOC=2∠BOD=120°，在Rt△OBE中，BE= OB=2 ，∴阴影部分的面积=S四边形OBEC﹣S扇形BOC=2S△OBE﹣S扇形BOC=2× ×2×2 ﹣=4 ﹣π23.（1）90；直径所对的圆周角是直角（2）解：△EAD是等腰三角形．证明：∵∠ABC的平分线与AC相交于点D，∴∠CBD=∠ABE∵AE是⊙O的切线，∴∠EAB=90°∴∠AEB+∠EBA=90°，∵∠EDA=∠CDB，∠CDB+∠CBD=90°，∵∠CBE=∠ABE，∴∠AED=∠EDA，∴AE=AD∴△EAD是等腰三角形（3）解：∵AE=AD，AD=6，∴AE=AD=6，∵AB=8，∴在直角三角形AEB中，EB=10∵∠CDB=∠E，∠CBD=∠ABE∴△CDB∽△AEB，∴= = =∴设CB=4x，CD=3x则BD=5x，∴CA=CD+DA=3x+6，在直角三角形ACB中，AC2+BC2=AB2即：（3x+6）2+（4x）2=82，解得：x=﹣2（舍去）或x=∴BD=5x=。

九年级数学上册《圆》章节复习经典习题荟萃人教新课标版

九年级数学上册《圆》章节复习经典习题荟萃人教新课标版一、选择题1.如图， A 、B 、C 是⊙O 上的三点，且A 是优弧BAC 上与点B 、点C 不同的一点，若BOC ∆是直角三角形，则BAC ∆必是( ) .A.等腰三角形B.锐角三角形C.有一个角是︒30的三角形D.有一个角是︒45的三角形 2.有下列四个命题：①在同圆或等圆中，相等的圆周角所对的弦相等②经过三个点一定可以作圆；③三角形的外心到三角形各边的距离都相等；④三角形的内心到三角形各顶点的距离相等．其中正确的有( )A ．4个B ．3个C ． 2个D ． 1个3.如图,AB 是⊙O 的直径，CD 是弦，若AB=10 cm,CD=8 cm ，则A 、B 两点到直线CD 的距离之和为( )A ．12 cmB ．10 cmC ．8 cmD ．6 cm4.如图：四边形ABCD 为⊙O 的内接四边形，点E 在CD 的延长线上，如果∠BOD=120°，那么∠BCE 等于（）A ：30°B ：60°C ：90°D ：120° 5.如图，弦AB ∥CD,E 为»CD 上一点，AE 平分CEB ∠，则图中与AEC ∠相等（不包括AEC ∠）的角共有（）A ．3个B ．4个C ．5个D ．6个6.若正三角形、正方形、正六边形的周长相等，它们的面积分别是S 1、S 2、S 3，则下列关系成立的是（）A ．S 1=S 2=S 3B ．S 1>S 2>S 3C ．S 1<S 2<S 3D ．S 2>S 3>S 17.如图，等腰梯形ABCD 中，AD ∥BC ，以A 为圆心，AD 为半径的圆与BC 切于点M ，与AB 交于点E ，若AD ＝2，BC ＝6，则⌒DE 的长为（） A ．23π B ． 43π C ． 83πD ．π3 8.如图中的正方形的边长都相等，其中阴影部分面积相等的图形的个数是（）A ．1个B ．2个C ．3个D ．4个9.一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B 点从开始至结束所走过的路径长度为（）A O BC第1题图B （第4题）A CDEO A M DEB CA.23π B.34π C.4 D.2＋23π 10.如图10，两个半径都是4cm 的圆外切于点C ，一只蚂蚁由点A 开始依A 、B 、C 、D 、E 、F 、C 、G 、A 的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm 后才停下来，则蚂蚁停的那一个点为（） A ．D 点 B ．E 点 C ．F 点 D ．G 点二．填空题11.半径为1，圆心角是300º的弧长为 ,在半径为12cm 的圆中，一条弧长为π6cm ，此弧所对的圆周角是．12.一条弦把圆分成2:3两部分，那么这条弦所对的圆周角的度数为______________． 13．如图⊙O 1与⊙O 2的半径分别是方程27110x x -+=的两根，如果两圆相切，那么圆心距d 的值是14.△ABC 内接于⊙O ，若∠A0B=110°，则∠C= ； 15. ⊙O2 和⊙O1 相交于点A 、B ，它们的半径分别为2 和2 ，公共弦AB 长为2，则∠21AO O =____.16.已知⊙O 的半径5=r ，O 到直线l 的距离OA=3，点B 在直线l 上，如果线段AB=2，则点B 在⊙O ．17.如图所示，⊙O 的半径OA=6，以A 为圆心，OA 为半径的弧交⊙O 于B ，则BC=18.如图所示，两圆轮叠靠在墙边，已知两圆轮半径分别为4和1，则它们与墙的切点A 、B 之间的距离为19.如图，⊙1o 、⊙2o 相内切于点A ，其半径分别是8和4，将⊙2o 沿直线1o 2o 平移至两圆相外切时，则点2o 移动的长度是__________20.如图：⊙I 是直角△ABC 的内切圆，切点为D 、E 、F ，若AF ，BE 的长是方程213300x x -+=的两根，则△ABC 的面积为；21.如图所示，∠ABC=90°，O 为射线BC 上一点，以点O 为圆心，1/2BO 长为半径作⊙O ，当射线BA 绕点B 按顺时针方向旋转 __________时与⊙O 相切22.如图，在边长为3cm 的正方形中，⊙P 与⊙Q 相外切，且⊙P 分别与DA 、DC 边相切，⊙Q 分别与BA 、BC 边相切，则圆心距PQ 为______________．9题 A C B B C A B 8题I FB（第13题）ACDE 10题23.如图，⊙O 的半径为3cm ，B 为⊙O 外一点，OB 交⊙O 于点A ，AB=OA ，动点P 从点A 出发，以πcm/s 的速度在⊙O 上按逆时针方向运动一周回到点A 立即停止．当点P 运动的时间为_________s 时，BP 与⊙O 相切．24.如图，90的直径AB 和弦CD 相交于点E ，已知AE ＝1 cm ，EB ＝5 cm ，∠DEB ＝60°，则CD 的长为___________．25．如图， ⊙1O 与⊙2O 相交于点A 、B ，且A O 1是⊙2O 的切线， A O 2是⊙1O 的切线，A 是切点．若⊙1O 与⊙2O 的半径分别为3和4，则公共弦AB 的长为 cm ．三、解答题26.如图，在△ABC 中，AB =AC ，D 是BC 中点，AE 平分∠BAD 交BC 于点E ，点O 是AB 上一点，⊙O 过A 、E 两点,交AD 于点G ，交AB 于点F ．（1）求证：BC 与⊙O 相切（2）当∠BAC =120°时，求∠EFG 的度数．27.如图，AB 是⊙O 的直径，AM 和BN 是它的两条切线，DE 切⊙O 于点E ，交AM 于点D ，交BN 于点C ，F 是CD 的中点，连接OF ，（1）求证：OD ∥BE ；（2）猜想：OF 与CD 有何数量关系？并说明理由．MNFEODCB A27题 C B A D Q PB A O P2，⊙A的半径为1，如图所示．若点O在BC边上28.△ABC中，∠BAC=90°，AB=AC=2运动（与点B、C不重合），设BO=x，△AOC的面积为y．（1）求⊙A与△ABC重叠部分图形的面积（结果用π的式子表示）；（2）求y关于x的函数解析式，并写出函数自变量x的取值范围；（3）以点O为圆心，BO长为半径作圆，求当⊙O与⊙A相切时，求△AOC的面积．29.在某张航海图上，标明了三个观测点的坐标为O（0，0）、B（12，0）、C（12，16），由三个观测点确定的圆形区域是海洋生物保护区，如图所示．（1）求圆形区域的面积；（2）某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，求观测点B到渔船A的距离（结果保留三个有效数字）；（3）当渔船A由（2）中的位置向正西方向航行时，是否会进入海洋生物保护区？请通过计算解释．30．如图，在平面直角坐标系中，M为x轴上一点，⊙M交x轴于A,B两点，交y轴于C,D 两点，P为弧BC 上的一个动点，CQ平分∠PCD．A(-1,0),M(1,0)(1)求C点的坐标，（2）当当P点运动时，线段AQ的长度是否改变？若不变，请求其值；若改变，请求出其变化范围；。

九年级数学圆试题及答案

九年级数学圆试题及答案一、选择题（每题3分，共30分）1. 下列说法正确的是（）A. 圆的半径是圆心到圆上任意一点的距离B. 圆的直径是圆心到圆上任意一点的线段C. 圆的周长是圆的直径与π的积D. 圆的面积是圆的半径的平方与π的积答案：A2. 已知圆的半径为5cm，那么圆的周长是（）A. 10π cmB. 15π cmC. 20π cmD. 25π cm答案：C3. 圆的面积公式为（）A. πr²B. 2πrC. πdD. 2πr²答案：A4. 圆心角为60°的弧长是圆的周长的（）A. 1/6B. 1/3C. 1/2D. 2/3答案：A5. 圆的直径是半径的（）A. 2倍B. 1/2倍C. 1/4倍D. 1/3倍答案：A6. 圆的半径增加1倍，圆的面积增加（）A. 1倍B. 2倍C. 3倍D. 4倍答案：D7. 圆的周长与直径的比值是（）A. πB. 2πC. 4πD. 6π答案：A8. 一个圆的半径是2cm，那么它的直径是（）A. 4cmB. 6cmC. 8cmD. 10cm答案：A9. 圆的周长公式为（）A. πr²B. 2πrC. πdD. 2πr²答案：B10. 圆的半径为3cm，圆心角为90°的弧长是（）A. 3π cmB. 4.5π cmC. 6π cmD. 9π cm答案：B二、填空题（每题4分，共20分）1. 圆的周长公式为C=____，面积公式为S=____。

答案：2πr；πr²2. 圆的直径是半径的____倍。

答案：23. 圆心角为120°的弧长是圆的周长的____。

答案：1/34. 已知圆的半径为4cm，那么圆的周长为____cm。

答案：8π5. 圆的面积是半径的平方与π的____。

答案：积三、解答题（每题10分，共50分）1. 已知圆的半径为7cm，求圆的周长和面积。

答案：周长为14π cm，面积为49π cm²。

第24章《圆》单元复习测试题(含答案)

九年级数学第二十四章《圆》单元复习测试题（含答案）一、选择题(本大题10小题，每小题3分，共30分)1．已知AB是半径为6的圆的一条弦，则AB的长不可能是()A．8 B．10 C．12 D．142．已知⊙O的半径为4，点O到直线l的距离为2，则直线l与⊙O的位置关系是()A．相交B．相切C．相离D．无法判断3．在圆内接四边形ABCD中，∠A＝80°，则∠A的对角∠C＝()A．20°B．40°C．80°D．100°4．如题4图，在⊙O中，AB＝AC.若∠B＝75°，则∠A的度数为()题4图A．15°B．30°C．75°D．60°5．如题5图，AB为⊙O的直径，点C，D在⊙O上．若∠CAB＝36°，则∠D的度数为()题5图A．72°B．54°C．45°D．36°6．已知半径为9的扇形的弧长为6π，该扇形的面积为()A．18πB．27πC．36πD．54π7．如题7图，点I为△ABC的外心，且∠BIC＝150°，则∠A的度数为()题7图A．70°B．75°C．140°D．150°8．如题8图，AB是⊙O的直径，P A切⊙O于点A，连接PO并延长，交⊙O于点C，连接AC.若AB ＝8，∠P＝30°，则AC＝()A ．43B ．42C ．4D ．39．小英家的圆形镜子被打碎了，她拿了如题9图(网格中的每个小正方形边长为1)所示的一块碎片到玻璃店，配制成形状、大小与原来一致的镜面，则这个镜面的半径是( )A ．2B ．5C ．22D ．310．如题10图，将矩形ABCD 绕点A 逆时针旋转90°得到矩形AEFG ，点D 的旋转路径为DG .若AB ＝2，BC ＝4，则阴影部分的面积为( )A ．π2B ．8π3C ．4π3＋43D ．4π3＋23二、填空题(本大题7小题，每小题4分，共28分)11．已知⊙O 的半径为5cm ，点P 在⊙O 内，则OP ________5cm.(填“＞”“＜”或“＝”) 12．如题12图，⊙O 的半径为6，OA 与弦AB 的夹角是30°，则弦AB 的长是__________．13．如题13图，从⊙O 外一点P 引⊙O 的两条切线P A ，PB ，切点分别是A ，B ，若P A ＝6cm ，C 是AB 上一动点(点C 与A ，B 两点不重合)，过点C 作⊙O 的切线，分别交P A ，PB 于点D ，E ，则△PED 的周长是________cm.14．如题14图，正五边形ABCDE 内接于⊙O ，点F 在DE 上，则∠CFD ＝________．题14图15．用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝处忽略不计)，则这个圆锥的底面圆的半径为________．16．如题16图，AB 是⊙O 的弦，AB ＝8，C 是⊙O 上一动点，且∠ACB ＝45°.若点M ，N 分别是AB ，AC 的中点，则MN 长的最大值是________．题16图17．如题17图，直线l 1∥l 2，⊙O 与l 1和l 2分别相切于点A 和点B ，直线MN 与l 1相交于点M ，与l 2相交于点N ，⊙O 的半径为1，∠1＝60°，直线MN 从图中位置向右平移．下列结论：①l 1和l 2的距离为2；②MN ＝433 ；③当直线MN 与⊙O 相切时，∠MON ＝90°；④当AM ＋BN ＝433 时，直线MN 与⊙O 相切．其中正确的结论是____________．(填序号)题17图三、解答题(一)(本大题3小题，每小题6分，共18分)18．如题18图，点A ，B ，C ，D 在⊙O 上，BD ＝AC .求证：AB ＝CD .题18图19．用铁皮制作如题19图所示的圆锥形容器盖，求这个容器盖所需铁皮的面积(结果保留π)，并求制作容器盖的扇形的圆心角．题19图20．如题20图，在△ABC 中，AB ＝AC .(1)求作一点P ，使得点P 为△ABC 外接圆的圆心；(保留作图痕迹，不要求写作法) (2)在(1)的条件下，连接AP ，BP ，延长AP 交BC 于点D ，若∠BAC ＝50°，求∠PBC 的度数．题20图四、解答题(二)(本大题3小题，每小题8分，共24分)21．如题21图，隧道的截面由半圆和矩形构成，矩形的长BC为12m，宽AB为3m，若该隧道内设双行道，现有一辆货运卡车高8m，宽2.3m，则这辆货运卡车能否通过该隧道？请说明理由．题21图22．如题22图，已知△ABC内接于⊙O，AD为⊙O的直径，点C在劣弧AB上(不与点A，B重合)，设∠DAB＝α，∠ACB＝β，小明同学通过画图和测量得到以下近似数据：α30°35°40°50°60°80°β120°125°130°140°150°170°试判断α与β之间的关系，并给出证明．题22图23．在如题23图所示的网格中，每个小正方形的顶点叫格点，且边长均为1，△ABC的三个顶点均在格点上，以点A为圆心的EF与BC相切于点D，分别交AB，AC于点E，F.(1)求△ABC三边的长；(2)求图中由线段EB，BC，CF及EF所围成的阴影部分的面积．题23图五、解答题(三)(本大题2小题，每小题10分，共20分)24．如题24图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E，D，OB与⊙O交于点F，连接DF，DC.已知OA＝OB，CA＝CB，DE＝10，DF＝6.(1)求证：①AB是⊙O的切线；②∠EDC＝∠FDC.(2)求CD的长．题24图25．阅读以下材料，并回答问题：若一个三角形两边平方的和等于第三边平方的两倍，我们称这样的三角形为奇异三角形．(1)命题“等边三角形一定是奇异三角形”是________命题；(填“真”或“假”)(2)在△ABC中，∠C＝90°，△ABC的内角∠A，∠B，∠C所对边的长分别为a，b，c，且b＞a，若Rt △ABC 是奇异三角形，求a ∶b ∶c 的值；(3)如题25图，已知AB 是⊙O 的直径，C 是⊙O 上一点(点C 与点A ，B 不重合)，D 是ADB 的中点，点C ，D 在直径AB 的两侧，若存在点E ，使得AE ＝AD ，CB ＝CE .求证：△ACE 是奇异三角形．题25图参考答案1．D 2.A 3.D 4.B 5.B 6.B 7.B 8.A 9.B 10.D 11．< 12.63 13.12 14.36° 15.1 16.42 17.①②③④ 18．证明：∵BD ＝AC ，∴BD ＝AC .∴BD －AD ＝AC －AD ，即AB ＝CD .∴AB ＝CD .19．解：由图可知圆锥的底面圆的直径为80 cm ，母线长为50 cm ， ∴圆锥的底面圆的周长为80π cm.∴圆锥形容器盖的侧面展开图的弧长为80π cm. ∴面积为 12 ×80π×50＝2 000π(cm 2).设制作容器盖的扇形的圆心角为n °. ∴n π×50180＝80π.解得n ＝288.答：这个容器盖所需铁皮的面积为2 000π cm 2，制作容器盖的扇形的圆心角为288°. 20．解：(1)如答题20图，点P 即为△ABC 外接圆的圆心．答题20图(2)∵点P 为△ABC 外接圆的圆心，AB ＝AC ，∠BAC ＝50°， ∴AD ⊥BC ，∠BAP ＝∠CAP ＝25°，P A ＝PB . ∴∠BPD ＝2∠BAP ＝50°，∠BDP ＝90°. ∴∠PBD ＝90°－50°＝40°，即∠PBC ＝40°.21．解：这辆货运卡车能通过该隧道．理由如下：如答题21图，设点O 为AD 的中点，在AD 上取点G ，使得OG ＝2.3，过点G 作GF ⊥BC 于点F ，延长FG 交半圆于点E ，则GF ＝AB ＝3，半圆的半径OE ＝12 AD ＝12BC ＝6.答题21图∴EG ＝OE 2－OG 2 ＝62－2.32 ≈5.54.∴EF ＝EG ＋GF ≈5.54＋3＝8.54＞8. ∴这辆货运卡车能通过该隧道． 22.解：β－α＝90°.证明：如答题22图，连接BD .答题22图∵AD 为⊙O 的直径，∴∠DBA ＝90°. ∵∠DAB ＝α，∴∠D ＝90°－α. ∵B ，D ，A ，C 四点共圆， ∴∠ACB ＋∠D ＝180°. ∵∠ACB ＝β，∴β＋90°－α＝180°.∴β－α＝90°.23．解：(1)由图可得AB ＝22＋62 ＝210 ，AC ＝62＋22 ＝210 ， BC ＝42＋82 ＝45 .(2)由(1)得AB 2＋AC 2＝(210 )2＋(210 )2＝(45 )2＝BC 2. ∴∠BAC ＝90°. 如答题23图，连接AD ，则AD ⊥BC ，BD ＝DC ＝12BC ＝25 .答题23图∴AD ＝AB 2－BD 2 ＝（210）2－（25）2 ＝25 . ∴S 阴＝S △ABC －S 扇形AEF ＝12 AB ·AC －90π360 ·AD 2＝20－5π.24．(1)证明：①如答题24图，连接OC .∵OA ＝OB ，CA ＝CB ，∴OC ⊥AB . ∵OC 为⊙O 的半径， ∴AB 是⊙O 的切线．②∵OA ＝OB ，CA ＝CB ，∴∠AOC ＝∠BOC . ∴EC ＝FC .∴∠EDC ＝∠FDC .答题24图(2)解：如答题24图，过点O 作ON ⊥DF 于点N ，延长DF 交AB 于点M . ∵ON ⊥DF ，OD ＝OF ，DF ＝6， ∴DN ＝NF ＝12 DF ＝3，∠DON ＝∠FON .在Rt △ODN 中，OD ＝12 DE ＝5，DN ＝3，∴ON ＝OD 2－DN 2 ＝4.∵∠AOC ＝∠BOC ，∠DON ＝∠FON ， ∴∠BOC ＋∠FON ＝12 ×180°＝90°.∴∠OCM ＝∠CON ＝∠MNO ＝90°. ∴四边形OCMN 是矩形．∴CM ＝ON ＝4，MN ＝OC ＝12DE ＝5.在Rt △CDM 中，CM ＝4，DM ＝DN ＋MN ＝8， ∴CD ＝DM 2＋CM 2 ＝82＋42 ＝45 . 25．(1)解：真． (2)解：∵∠C ＝90°，∴a 2＋b 2＝c 2.①∵Rt △ABC 是奇异三角形，且b ＞a ，∴a 2＋c 2＝2b 2.② 由①②，得b ＝2 a ，c ＝3 a .∴a ∶b ∶c ＝1∶2 ∶3 . (3)证明：如答题25图，连接BD .答题25图∵AB是⊙O的直径，∴∠ACB＝∠ADB＝90°.在Rt△ACB中，AC2＋CB2＝AB2，在Rt△ADB中，AD2＋BD2＝AB2.∵点D是ADB的中点，∴AD＝BD.∴AD＝BD.∴AB2＝AD2＋BD2＝2AD2.∴AC2＋CB2＝2AD2.又CB＝CE，AE＝AD，∴AC2＋CE2＝2AE2.∴△ACE是奇异三角形。

人教版九年级数学上册《圆》真题精选(含答案解析)

拓视线·真题备选1.(20XX ·无锡中考 ) 如图 ,A,B,C 是☉ O上的三点 , 且∠ ABC=70° , 则∠ AOC的度数是 ()A.35°B.140°C.70°D.70°或 140°【分析】选 B. 依据圆周角定理 , 同弧所对的圆周角等于它所对的圆心角的一半, ∠ ABC=∠AOC,∵∠ ABC=70° , ∴∠ AOC=140°.2.(20XX ·济南中考 ) 如图 ,AB 是☉ O的直径 ,C 是☉ O上一点 ,AB=10,AC=6,OD⊥BC,垂足为 D,则BD的长为 ()A.2B.3C.4D.6【分析】选 C.∵AB是直径 , 所以∠ C是直角 ,∴BC==8,∵OD⊥ BC,依据垂径定理 ,BD= BC,所以 BD=4.3.(20XX ·临沂中考 ) 如图 , ☉O中, ∠CBO=45° , ∠CAO=15° , 则∠ AOB的度数是()A.75°B.60°C.45°D.30°【分析】选 B. 连结 OC,延伸 AO与☉ O交于点 D, ∴△ BOC为等腰三角形 ,∴∠ BOC=180°-2 ∠ CBO=180° -2 ×45°=90°, ∵∠ CAO=15° , ∴∠ COD=30°,∴∠ AOB=60°.4.(20XX·乐山中考 ) 如图 , 圆心在 y 轴的负半轴上 , 半径为 5 的☉ B 与 y 轴的正半轴交于点A(0,1),过点 P(0,-7) 的直线 l 与☉ B订交于 C,D两点 , 则弦 CD的长全部可能的整数值有 ()A.1 个B.2 个C.3 个D.4 个【分析】选 C.半径为 5 的☉ B 与 y 轴的正半轴交于点A(0,1),可知OB=4,所以点B(0,-4).因为 P(0,-7),BP=3. 当弦 CD⊥AB 时, 弦 CD最短. 连结 BC,由勾股定理得CP===4, 由垂径定理可知CD=2CP=8;当弦 CD是☉ B 的直径时 ,CD=10.所以 8≤ CD≤10, 所以 CD的整数值为 :8,9,10共三个.5.(20XX ·枣庄中考 ) 如图 , 已知线段 OA交☉ O于点 B, 且 OB=AB,点 P 是☉ O上的一个动点 , 那么∠OAP的最大值是 ()A.30°B.45 °C.60 °D.90 °【分析】选 A. 依据题意知 , 当∠ OAP取最大值时 ,OP⊥AP;在 Rt △AOP中, ∵OP=OB,OB=AB,∴OA=2OP,∴∠ OAP=30°.6.(20XX ·舟山中考 ) 如图 , 某厂生产横截面直径为7cm的圆柱形罐头 , 需将“蘑菇罐头”字样贴在罐头侧面 , 为了获取较佳视觉成效, 字样在罐头侧面所形成的弧的度数为90°, 则“蘑菇罐头”字样的长度为 ()A. cmB. cmC. cmD.7πcm【分析】选B. ∵字样在罐头侧面所形成的弧的度数为90°,∴此弧所对的圆心角为90° , 由题意可得 ,r=cm,则“蘑菇罐头”字样的长7.(20XX ·泰安中考) 如图 ,AB,CD 是☉ O 的两条相互垂直的直径, 点OA,OB,OC,OD的中点 , 若☉ O的半径是 2, 则暗影部分的面积为 ()==O1 ,O2,O3,O4cm.分别是A.8B.4C.4 π +4D.4π-4【分析】选 A. 连结 AD,DB,BC,CA,S暗影面积 =S 四边形ADBC=42÷2=8.8.(20XX ·恩施中考 ) 如图 , 在直角坐标系中搁置一个边长为 1 的正方形ABCD,将正方形 ABCD 沿 x 轴的正方向无滑动地在x 轴上转动 , 当点 A 走开原点后第一次落在x 轴上时 , 点 A 运动的路径线与 x 轴围成图形的面积为 ()A. +B.+1C.π+1D.π +【分析】选 C.依据条件看出 : 点 A 到 A1, 是以点 B 为圆心、 AB 为半径所得 ; 点 A1到 A2, 是以点C1为圆心、 A1C1为半径所得 ; 点 A2到 A3 , 是以点 D2为圆心、 A2D2为半径所得 . 即由 2 个半径为 1、圆心角为 90°的扇形和半径为、圆心角为90°的扇形以及2个直角边长为1 的等腰直角三角形构成的图形 , 其面积为π +1.9.(20XX ·赤峰中考 ) 如图 ,ABCD是平行四边形 ,AB 是☉ O 的直径 , 点 D 在☉ O 上,AD = OA =1,则图中阴影部分的面积为 ()A. B. + C. - D.【分析】选 A.DC交☉ O于 E, 连结 OE,过 D 作形. ∴AF= , 在 Rt△ ADF中 , 依据勾股定理得DF⊥ AB于 DF=F, ∵ OA=OD=AD=1,∴△ ADO是等边三角= . 在平行四边形ABCD中,AB∥CD.∴∠ EDO=60° . ∵ OD=OE,∴△ ODE是等边三角形 .∴∠ EOB=∠DEO=60°. ∵S? ABCD=AB×DF=2×= ,S△AOD=S△DOE= ×1× = ,S 扇形OEB=S扇形ODE== . ∴暗影部分的面积 =S? ABCD-S △AOD-S△DOE-S 扇形OEB+S 扇形ODE-S△DOE= - ×2- + -= .10.(20XX ·邵阳中考 ) 如下图 , 弦 AB,CD订交于点 O,连结 AD,BC.在不增添协助线的状况下 ,请在图中找出一对相等的角 , 它们是.【分析】对顶角有 : ∠AOC=∠BOD,和∠ AOD=∠BOC.同弧所对的圆周角有:∠A=∠C,∠B=∠D.故填∠ A=∠C(或∠ B=∠ D 或∠ AOC=∠BOD,或∠ AOD=∠BOC).答案 : 答案不独一 , ∠A=∠C, 或∠ B=∠ D,或∠ AOC=∠ BOD,或∠ AOD=∠ BOC11.(20XX ·兰州中考 ) 如图 , 量角器的直径与直角三角板ABC的斜边 AB重合 , 此中量角器 0 刻度线的端点N与点A重合, 射线CP从CA处出发沿顺时针方向以每秒 3 度的速度旋转,CP 与量角器的半圆弧交于点E, 第24秒时, 点E 在量角器上对应的度数是度 .【分析】连结 OE,∵∠ ACB=90° ,∴点 C在以 AB为直径的圆上 , 即点 C 在☉ O上 , ∴∠ EOA=2∠ECA,∵∠ ECA=3°× 24=72° ,∴∠ AOE=2∠ECA=2×72°=144°.答案 : 14412.(20XX ·烟台中考 ) 如图 , 正方形 ABCD的边长为 4, 点 E 在 BC边上 , 四边形 EFGB也是正方形 ,以 B 为圆心 ,BA 长为半径画, 连结 AF,CF,则图中暗影部分的面积为.a, 则暗影部分的面积=+a2+-=4π.【分析】设正方形EFGB的边长为答案 : 4π13.(20XX ·衢州中考 ) 如图 , 将一块三角板和半圆形量角器按图中方式叠放, 三角板一边与量角器的零刻度线所在直线重合, 重叠部分的量角器弧() 对应的圆心角( ∠AOB)为120XXOC的长为2cm,则三角板和量角器重叠部分的面积为.【分析】∵∠ AOB=120XX∴∠ BOC=60° , 在 Rt △ BOC中 ,OC=2,∴ OB=4,BC=2 , ∴ S 重叠部分=+ ×2×2 = π+2 .答案 :2π+2 cm14.(20XX ·六水中考) 把 1 的正方形片OABC放在直m上,OA 在直m上, 而后将正方形片着点 A 按方向旋90°, 此 , 点 O运到了点 O1( 即点 B ), 点 C 运到了C1, 点 B 运到了点B1, 又将正方形片AO1C1 B1B1点按方向旋90°⋯⋯ , 按上述方法 4 次旋后 , 点 O 的行程.61 次旋后 ,点 O的行程.【分析】依据形的旋性可知 , 正方形第一次旋点 O的路 l1 =×π× 1;第二次旋点 O的路 l2=×π×; 第三次旋点 O的路 l3 =×π× 1; 第四次旋点 O 的路 0, 所以 4 次旋后 , 点 O 的行程l 1+l2 +l 3+0=×π× 1+×π×+×π× 1+0=π .由于 61=4× 15+1, 所以61次旋后, 点O的行程π ×15+ =π .答案 :ππ15.(20XX ·巴中中考 ) 底面半径 1, 母 2 的的面等于.【分析】因的面就等于母乘底面周的一半, 所以的面 =2×2π÷ 2=2π.答案 : 2π( 接缝处16.(20XX ·大连中考 ) 用一个圆心角为 90°, 半径为 32cm的扇形作为一个圆锥的侧面不重叠 ), 则这个圆锥的底面圆的半径为cm.【分析】扇形的弧长 l==16π,16 π÷ 2π =8.答案: 817.(20XX ·黄石中考 ) 如图 ,AB 是☉ O的直径 ,AM 和 BN是☉ O的两条切线 ,E 是☉ O上一点 ,D 是AM上一点 , 连结 DE并延伸交 BN于点 C,且 OD∥BE,OF∥ BN.(1)求证 :DE 是☉ O的切线 .(2)求证 :OF= CD.【证明】 (1) 连结 OE,AM是☉ O的切线 ,OA 是☉ O的半径 , ∴∠ DAO=90°,∵OD∥ BE,∴∠ AOD=∠OBE,∠DOE=∠OEB,∵OB=OE,∴∠ OEB=∠OBE.∴∠ AOD=∠DOE.在△ AOD和△ DOE中∴△ AOD≌△ EOD,∴∠ DAO=∠DEO=90°,∴DE与☉ O相切 .(2)∵AM和 BN是☉ O的两切线 ,∴MA⊥ AB,NB⊥AB,∴AD∥BC,∵O是 AB的中点 ,OF∥BN,∴OF∥ AD且 OF= (AD+BC).∵DE切☉ O于点 E, ∴ DA=DE,CB=CE,∴DC=AD+CB,∴OF= CD.。

九年级数学《圆》经典试题集锦

九年级数学《圆》经典试题集锦九年级数学《圆》经典试题集锦一、选择题1．如图，BC是⊙O的直径，P是CB延长线上一点，PA切⊙O 于点A，如果PA＝，PB＝1，那么∠APC等于2．如果圆柱的高为20厘米，底面半径是高的，那么这个圆柱的侧面积是100π平方厘米200π平方厘米500π平方厘米200平方厘米3．“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，CE＝1寸，AB＝寸，求直径CD的长”．依题意，CD长为寸13寸25寸26寸4．已知：如图，⊙O半径为5，PC切⊙O于点C，PO交⊙O于点A，PA＝4，那么PC的长等于 6 2 2 2 5．如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于2厘米2厘米4厘米8厘米6．相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘米和17厘米，则这两圆的圆心距为7厘米16厘米21厘米27厘米7．如图，⊙O为△ABC的内切圆，∠C＝，AO 的延长线交BC于点D，AC＝4，DC＝1，，则⊙O的半径等于8．一居民小区有一正多边形的活动场．为迎接“AAPP”会议在重庆市的召开，小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台，花台都以多边形的顶点为圆心，比多边形的内角为圆心角，花台占地面积共为12π平方米．若每个花台的造价为400元，则建造这些花台共需资金2400元2800元3200元3600元9．如图，AB是⊙O直径，CD是弦．若AB＝10厘米，CD＝8厘米，那么A、B两点到直线CD的距离之和为12厘米10厘米8厘米6厘米10．某工件形状如图所示，圆弧BC 的度数为，AB＝6厘米，点B到点C的距离等于AB，∠BAC ＝，则工件的面积等于4π6π8π10π 11．如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA＝4，PB＝2，则⊙O的半径等于 3 4 6 8 12．已知⊙O的半径为3厘米，⊙的半径为5厘米．⊙O与⊙相交于点D、E．若两圆的公共弦DE 的长是6厘米，则两圆的圆心距O的长为2厘米10厘米2厘米或10厘米4厘米13．如图，两个等圆⊙O和⊙的两条切线OA、OB，A、B是切点，则∠AOB等于14．如图，AB是⊙O的直径，∠C＝，则∠ABD＝15．弧长为6π的弧所对的圆心角为，则弧所在的圆的半径为 6 6 12 18 16．如图，在△ABC中，∠BAC＝，AB＝AC＝2，以AB为直径的圆交BC于D，则图中阴影部分的面积为 1 2 1+ 2－17．已知圆的内接正六边形的周长为18，那么圆的面积为18π9π6π3π 18．如图，点P是半径为5的⊙O内一点，且OP＝3，在过点P的所有弦中，长度为整数的弦一共有2条3条4条5条19．如图，正六边形ABCDEF的边长的上a，分别以C、F为圆心，a为半径画弧，则图中阴影部分的面积是20．过⊙O内一点M的最长的弦长为6厘米，最短的弦长为4厘米，则OM的长为厘米厘米2厘米5厘米21．已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是12π15π30π24π22．已知⊙O的直径AB与弦AC的夹角为，过C点的切线PC与AB延长线交P．PC＝5，则⊙O的半径为10 5 23．如图：PA 切⊙O于点A，PBC是⊙O的一条割线，有PA＝3，PB＝BC，那么BC的长是3 3 24．如图，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE，则图中五个扇形的面积之和是π 1.5π2π 2.5π 25．正六边形的半径为2厘米，那么它的周长为6厘米12厘米24厘米12厘米26．一个圆柱形油桶的底面直径为0.6米，高为1米，那么这个油桶的侧面积为0.09π平方米0.3π平方米0.6平方米0.6π平方米27．一个形如圆锥的冰淇淋纸筒，其底面直径为6厘米，母线长为5厘米，围成这样的冰淇淋纸筒所需纸片的面积是66π平方厘米30π平方厘米28π平方厘米15π平方厘米28．在半径为2的⊙O中，圆心O到弦AB的距离为1，则弦AB所对的圆心角的度数可以是29．将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面，，则桶底的面积为平方厘米1600π平方厘米平方厘米6400π平方厘米30．如图，已知AB是⊙O的直径，弦CD⊥AB于点P，CD＝10厘米，AP∶PB＝1∶5，那么⊙O的半径是6厘米厘米8厘米厘米31．在Rt△ABC中，已知AB＝6，AC＝8，∠A＝．如果把Rt△ABC 绕直线AC旋转一周得到一个圆锥，其表面积为S；把Rt△ABC绕直线AB旋转一周得到另一个圆锥，其表面积为S，那么S∶S等于2∶3 3∶4 4∶9 5∶12 32．如图，⊙O的弦AB＝8厘米，弦CD平分AB于点E．若CE＝2厘米．ED长为8厘米6厘米4厘米2厘米33．如图，四边形ABCD 内接于⊙O，若∠BOD＝，则∠BCD＝34．如图，正方形ABCD内接于⊙O，E为DC的中点，直线BE交⊙O于点F．若⊙O的半径为，则BF的长为35．如图，AB是⊙O的直径，∠ACD＝，则∠BAD的度数为36．已知：点P直线l 的距离为3，以点P为圆心，r为半径画圆，如果圆上有且只有两点到直线l的距离均为2，则半径r的取值范围是r ＞1 r＞2 2＜r＜3 1＜r＜5 37．边长为a的正方边形的边心距为 a a a 2a 38．如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为30ππ20ππ 39．如图，扇形的半径OA＝20厘米，∠AOB＝，用它做成一个圆锥的侧面，则此圆锥底面的半径为3.75厘米7.5厘米15厘米30厘米40．如图，正六边形ABCDEF中．阴影部分面积为12平方厘米，则此正六边形的边长为2厘米4厘米6厘米8厘米41．已知扇形的弧长是2π厘米，半径为12厘米，则这个扇形的圆心角是42．圆锥的高线长是厘米，底面直径为12厘米，则这个圆锥的侧面积是48π厘米24平方厘米48平方厘米60π平方厘米43．如图，AB是⊙O的直径，点P在BA的延长线上，PC 是⊙O的切线，C为切点，PC＝2，PA＝4，则⊙O的半径等于1 2 44．已知圆柱的母线长为5厘米，表面积为28π平方厘米，则这个圆柱的底面半径是5厘米4厘米2厘米3厘米45．半径相等的圆内接正三角形、正方形、正六边形的边长之比为1∶∶∶∶13∶2∶1 1∶2∶3 46．如图，若四边形ABCD是半径为1和⊙O的内接正方形，则图中四个弓形的面积和为厘米厘米厘米厘米47．如图，已知圆心角∠BOC＝，则圆周角∠BAC 的度数是48．半径为5厘米的圆中，有一条长为6厘米的弦，则圆心到此弦的距离为3厘米4厘米5厘米6厘米49．已知：Rt△ABC中，∠C＝，O为斜边AB上的一点，以O为圆心的圆与边AC、BC分别相切于点E、F，若AC＝1，BC＝3，则⊙O的半径为50．已知：如图，E是相交两圆⊙M和⊙O 的一个交点，且ME⊥NE，AB为外公切线，切点分别为A、B，连结AE、BE．则∠AEB的度数为145°140°135°130°二、填空题1．如图，AB、AC是⊙O的两条切线，切点分别为B、C，D是优弧上的一点，已知∠BAC＝，那么∠BDC＝__________度．2．在Rt△ABC中，∠C＝，AＢ＝3，BC＝1，以AC 所在直线为轴旋转一周，所得圆锥的侧面展开图的面积是__________．3．如果圆锥母线长为6厘米，那么这个圆锥的侧面积是_______平方厘米4．一种圆状包装的保鲜膜，如图所示，其规格为“20厘米×60米”，经测量这筒保鲜膜的内径、外径的长分别为3.2厘米、4.0厘米，则该种保鲜膜的厚度约为_________厘米．5．两个点O为圆心的同心圆中，大圆的弦AB与小圆相切，如果AB的长为24，大圆的半径OA为13，那么小圆的半径为___________．6．已知⊙O中，两弦AB与CD相交于点E，若E为AB的中点，CE∶ED＝1∶4，AB ＝4，则CD的长等于___________．7．如图，AB是⊙O的直径，四边形ABCD内接于⊙O，，，的度数比为3∶2∶4，MN是⊙O的切线，C是切点，则∠BCM的度数为___________．8．如图，P是⊙O的直径AB延长线上一点，PC切⊙O于点C，PC＝6，BC∶AC＝1∶2，则AB的长为___________．9．如图，四边形ABCD内接于⊙O，AD∥BC，＝，若AD＝4，BC＝6，则四边形ABCD的面积为__________．10．(山西省)若一个圆柱的侧面积等于两底面积的和，则它的高h与底面半径r的大小关系是__________．11．要用圆形铁片截出边长为4厘米的正方形铁片，则选用的圆形铁片的直径最小要___________厘米．12．圆内两条弦AB和CD相交于P点，AB长为7，AB把CD分成两部分的线段长分别为2和6，那么＝__________．13．△ABC是半径为2厘米的圆内接三角形，若BC＝2厘米，则∠A的度数为________．14．如图，已知OA、OB是⊙O的半径，且OA＝5，∠AOB＝15，AC⊥OB于C，则图中阴影部分的面积S＝_________．15．如图，圆内接正六边形ABCDEF中，AC、BF交于点M．则∶＝_________．16．(哈尔滨市)两圆外离，圆心距为25厘米，两圆周长分别为15π厘米和10π厘米．则其内公切线和连心线所夹的锐角等于__________度．17．将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周，所得圆柱体的表面积为_________平方厘米．18．如图，在⊙O的内接四边形ABCD中，∠BCD＝130，则∠BOD的度数是________．19．已知⊙O的半径为4厘米，以O为圆心的小圆与⊙O组成的圆环的面积等于小圆的面积，则这个小圆的半径是______厘米．20．如图，⊙O的半径OA是⊙O的直径，C是⊙O上的一点，OC交⊙O于点B．若⊙O的半径等于5厘米，的长等于⊙O周长的，则的长是_________．21．正三角形的内切圆与外接圆面积之比为_________．22．如图，AB＝8，AC＝6，以AC和BC为直径作半圆，两圆的公切线MN与AB的延长线交于D，则BD的长为_________．23．圆锥的母线长为5厘米，高为3厘米，在它的侧面展开图中，扇形的圆心角是_________度．24．如图，AB是⊙O的直径，弦CD⊥AB，垂足是G，F是CG的中点，延长AF交⊙O于E，CF＝2，AF＝3，则EF的长是_________．25．在⊙O中，直径AB＝4厘米，弦CD⊥AB于E，OE＝，则弦CD的长为__________厘米．26．若圆锥底面的直径为厘米，线线长为5厘米，则它的侧面积为__________平方厘米．27．如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于M点．若OA＝a，PM ＝a，那么△PMB的周长的__________．28．在半径9厘米的圆中，的圆心角所对的弧长为__________厘米．29．扇形的圆心角为120，弧长为6π厘米，那么这个扇形的面积为_________．30．如果圆O的直径为10厘米，弦AB的长为6厘米，那么弦AB的弦心距等于________厘米．31．某种商品的商标图案如图所求，已知菱形ABCD的边长为4，∠A＝，是以A为圆心，AB 长为半径的弧，是以B为圆心，BC长为半径的弧，则该商标图案的面积为_________．32．已知，一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周，所得圆锥的表面积是__________．33．正六边形的边心距与半径的比值为_________．34．如图，已知扇形AOB的半径为12，OA⊥OB，C为OA上一点，以AC为直径的半圆和以OB 为直径的半圆相切，则半圆的半径为__________．35．如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D．已知∠APB＝，AC＝2，那么CD的长为________．36．底面半径为2厘米，高为3厘米的圆柱的体积为_________立方厘米．37．边长为2厘米的正六边形的外接圆半径是________厘米，内切圆半径是________厘米．38．如图，PT是⊙O的切线，T为切点，PB是⊙O的割线交⊙O于A、B两点，交弦CD 于点M，已知：CM＝10，MD＝2，PA＝MB＝4，则PT的长等于__________．39．如图，扇形OAB中，∠AOB ＝，半径OA＝1，C是线段AB的中点，CD∥OA，交于点D，则CD＝________．40．已知扇形的圆心角为150，它所对的弧长为20π厘米，则扇形的半径是________厘米，扇形的面积是__________平方厘米．41．如图，AB是⊙O直径，CE切⊙O于点C，CD⊥AB，D为垂足，AB＝12厘米，∠B＝30，则∠ECB＝__________；CD＝_________厘米．42．如图，DE是⊙O直径，弦AB⊥DE，垂足为C，若AB＝6，CE＝1，则CD＝________，OC＝_________．43．如果把人的头顶和脚底分别看作一个点，把地球赤道作一个圆，那么身高压2米的汤姆沿着地球赤道环道环行一周，他的头顶比脚底多行________米．44．已知：⊙O的半径为1，M为⊙O外的一点，MA切⊙O于点A，MA＝1．若AB是⊙O的弦，且AB＝，则MB的长度为_________．45．如果圆的半径为4厘米，那么它的周长为__________厘米．三、解答题： 1．已知：如图，△ABC内接于⊙O，过点B作⊙O的切线，交CA的延长线于点E，∠EBC＝2∠C．①求证：AB ＝AC；②若tan∠ABE＝，求的值；求当AC＝2时，AE的长．2．如图，PA为⊙O的切线，A为切点，⊙O的割线PBC 过点O与⊙O分别交于B、C，PA＝8cm，PB＝4cm，求⊙O 的半径．3．已知：如图，BC是⊙O的直径，AC切⊙O于点C，AB 交⊙O于点D，若AD︰DB＝2︰3，AC＝10，求sinB的值． 4．如图，PC为⊙O的切线，C为切点，PAB是过O的割线，CD⊥AB于点D，若tanB＝，PC＝10cm，求三角形BCD 的面积．5．如图，在两个半圆中，大圆的弦MN与小圆相切，D为切点，且MN∥AB，MN＝a，ON、CD分别为两圆的半径，求阴影部分的面积．6．已知，如图，以△ABC的边AB作直径的⊙O，分别并AC、BC于点D、E，弦FG∥AB，S△CDE︰S△ABC＝1︰4，DE＝5cm，FG＝8cm，求梯形AFGB的面积．7．如图所示：PA为⊙O的切线，A为切点，PBC是过点O 的割线，PA＝10，PB＝5，求：⊙O的面积；cos∠BAP的值．参考答案一、选择题1．B 2．B 3．D 4．D 5．C 6．C 7．A 8．C 9．D 10．B 11．A 12．B 13．C 14．D 15．D 16．A 17．B 18．C 19．C 20．B 21．C 22．A 23．A 24．B 25．B 26．D 27．D 28．C 29．A 30．B 31．A 32．A 33．B 34．C 35．A 36．D 37．B 38．B 39．B 40．B 41．C 42．D 43．A 44．C 45．B 46．C 47．A 48．B 49．C 50．C 二、填空题1．50 2．2π3．18π4．5．5 6．5 7．30°8．9 9．25 10．h＝r 11．4 12．3或4 13．60°或120°14．15．1:2 16．30 17．80π或120π18．100°19．20．π21．1:4 22．1 23．288 24．4 25．2 26．15π27．28．3π29．27π平方厘米30．4 31．32．24π平方厘米或36π平方厘米33．34．4 35．36．12π37．2，38．39．40．24，240π41．60°，42．9，4 43．4π44．1或45．8π 三、解答题：1．∵BE切⊙O于点B，∴∠ABE＝∠C．∵∠EBC＝2∠C，即∠ABE＋∠ABC＝2∠C，∴∠C ＋∠ABC＝2∠C，∴∠ABC＝∠C，∴AB＝AC．①连结AO，交BC于点F，∵AB＝AC，∴＝，∴AO⊥BC且BF＝FC．在Rt△ABF 中，＝tan∠ABF，又tan∠ABF＝tanC＝tan∠ABE＝，∴＝，∴AF＝BF．∴AB＝＝＝BF．∴．②在△EBA与△ECB中，∵∠E＝∠E，∠EBA＝∠ECB，∴△EBA∽△ECB．∴，解之，得EA2＝EA·，又E A≠0，∴EA＝AC，EA＝×2＝．2．设⊙的半径为r，由切割线定理，得PA2＝PB·PC，∴82＝4，解得r＝6．即⊙O的半径为6cm．3．由已知AD︰DB＝2︰3，可设AD＝2k，DB ＝3k．∵AC切⊙O于点C，线段ADB为⊙O的割线，∴AC2＝AD·AB，∵AB＝AD＋DB＝2k ＋3k＝5k，∴102＝2k×5k，∴k2＝10，∵k ＞0，∴k＝．∴AB＝5k＝5．∵AC切⊙O 于C，BC为⊙O的直径，∴AC⊥BC．在Rt△ACB中，sinB＝．4．解法一：连结AC．∵AB是⊙O的直径，点C在⊙O上，∴∠ACB ＝90°．CD⊥AB于点D，∴∠ADC＝∠BDC ＝90°，∠2＝90°－∠BAC＝∠B．∵tanB＝，∴tan∠2＝．∴．设AD＝x，CD＝2x，DB＝4x，AB＝5x．∵PC切⊙O于点C，点B在⊙O上，∴∠1＝∠B．∵∠P＝∠P，∴△PAC∽△PCB，∴．∵PC＝10，∴PA＝5，∵PC切⊙O 于点C，PAB是⊙O的割线，∵PC2＝PA·PB，∴102＝5．解得x＝3．∴AD＝3，CD＝6，DB＝12．∴S△BCD＝CD·DB＝×6×12＝36．即三角形BCD的面积36cm2．解法二：同解法一，由△PAC ∽△PCB，得．∵PA＝10，∴PB＝20．由切割线定理，得PC2＝PA·PB．∴PA＝＝5，∴AB ＝PB－PA＝15，∵AD＋DB＝x＋4x＝15，解得x＝3，∴CD＝2x＝6，DB＝4x＝12．∴S△BCD ＝CD·DB＝×6×12＝36．即三角形BCD的面积36cm2．5．解：如图取MN的中点E，连结OE，∴OE⊥MN，EN＝MN＝a．在四边形EOCD中，∵CO⊥DE，OE⊥DE，DE∥CO，∴四边形EOCD 为矩形．∴OE＝CD，在Rt△NOE中，NO2－OE2＝EN2＝．∴S阴影＝π＝π·＝．6．解：∵∠CDE＝∠CBA，∠DCE＝∠BCA，∴△CDE ∽△ABC．∴∴＝＝＝，即，解得AB ＝10，作OM⊥FG，垂足为M，则FM＝FG＝×8＝4，连结OF，∵OA＝AB＝×10＝5．∴OF＝OA＝5．在Rt△OMF中，由勾股定理，得OM ＝＝＝3．∴梯形AFGB的面积＝·OM＝×3＝27．7．ÞPA2＝PB·PCÞPC＝20Þ半径为7.5Þ圆面积为．Þ△ACP∽△BAPÞÞ．解法一：设AB＝x，AC＝2x，BC为⊙O的直径Þ∠CAB＝90°，则BC＝x．∵∠BAP＝∠C，∴cos∠BAP＝cos∠C＝解法二：设AB＝x，在Rt△ABC中，AC2＋AB2＝BC2，即x2＋2＝152，解之得x＝3，∴AC＝6，∵∠BAP＝∠C，∴∴cos∠BAP＝cos∠C＝。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九年级数学《圆》经典试题集锦一、选择题1．如图，BC 是⊙O 的直径，P 是CB 延长线上一点，PA 切⊙O 于点A ，如果PA ＝3，PB ＝1，那么∠APC 等于（）（A ） 15 （B ） 30 （C ） 45 （D ） 602．如果圆柱的高为20厘米，底面半径是高的41，那么这个圆柱的侧面积是（）（A ）100π平方厘米（B ）200π平方厘米（C ）500π平方厘米（D ）200平方厘米3．“圆材埋壁”是我国古代著名的数学菱《九章算术》中的一个问题，“今在圆材，埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图，CD 为⊙O 的直径，弦AB ⊥CD ，垂足为E ，CE ＝1寸，AB ＝寸，求直径CD 的长”．依题意，CD 长为（）（A ）225寸（B ）13寸（C ）25寸（D ）26寸 4．（北京市朝阳区）已知：如图，⊙O 半径为5，PC 切⊙O 于点C ，PO 交⊙O 于点A ，PA ＝4，那么PC 的长等于（）（A ）6 （B ）25 （C ）210 （D ）2145．如果圆锥的侧面积为20π平方厘米，它的母线长为5厘米，那么此圆锥的底面半径的长等于（）（A ）2厘米（B ）22厘米（C ）4厘米（D ）8厘米6．相交两圆的公共弦长为16厘米，若两圆的半径长分别为10厘米和17厘米，则这两圆的圆心距为（）（A ）7厘米（B ）16厘米（C ）21厘米（D ）27厘米7．如图，⊙O 为△ABC 的内切圆，∠C ＝90，AO 的延长线交BC 于点D ，AC ＝4，DC ＝1，，则⊙O 的半径等于（）（A ）54 （B ）45 （C ）43 （D ）65 8．一居民小区有一正多边形的活动场．为迎接“AAPP ”会议在重庆市的召开，小区管委会决定在这个多边形的每个顶点处修建一个半径为2米的扇形花台，花台都以多边形的顶点为圆心，比多边形的内角为圆心角，花台占地面积共为12π平方米．若每个花台的造价为400元，则建造这些花台共需资金（）（A ）2400元（B ）2800元（C ）3200元（D ）3600元9．如图，AB 是⊙O 直径，CD 是弦．若AB ＝10厘米，CD ＝8厘米，那么A 、B 两点到直线CD 的距离之和为（）（A ）12厘米（B ）10厘米（C ）8厘米（D ）6厘米10．某工件形状如图所示，圆弧BC 的度数为60，AB ＝6厘米，点B到点C 的距离等于AB ，∠BAC ＝ 30，则工件的面积等于（）（A ）4π （B ）6π （C ）8π （D ）10π11．如图，PA 切⊙O 于点A ，PBC 是⊙O 的割线且过圆心，PA ＝4，PB ＝2，则⊙O 的半径等于（）（A ）3 （B ）4 （C ）6 （D ）812．已知⊙O 的半径为35厘米，⊙O '的半径为5厘米．⊙O 与⊙O '相交于点D 、E ．若两圆的公共弦DE 的长是6厘米（圆心O 、O '在公共弦DE 的两侧），则两圆的圆心距O O '的长为（）（A ）2厘米（B ）10厘米（C ）2厘米或10厘米（D ）4厘米13．如图，两个等圆⊙O 和⊙O '的两条切线OA 、OB ，A 、B 是切点，则∠AOB 等于（）（A ） 30 （B ） 45 （C ） 60 （D ）9014．如图，AB 是⊙O 的直径，∠C ＝ 30，则∠ABD ＝（）（A ） 30 （B ） 40 （C ） 50 （D ） 6015．弧长为6π的弧所对的圆心角为 60，则弧所在的圆的半径为（）（A ）6 （B ）62 （C ）12 （D ）18 16．（甘肃省）如图，在△ABC 中，∠BAC ＝ 90，AB ＝AC ＝2，以AB 为直径的圆交BC 于D ，则图中阴影部分的面积为（）（A ）1 （B ）2 （C ）1+4π （D ）2－4π 17．（宁夏回族自治区）已知圆的内接正六边形的周长为18，那么圆的面积为（）（A ）18π （B ）9π （C ）6π （D ）3π18．（山东省）如图，点P 是半径为5的⊙O 内一点，且OP ＝3，在过点P的所有弦中，长度为整数的弦一共有（）（A ）2条（B ）3条（C ）4条（D ）5条19．（南京市）如图，正六边形ABCDEF 的边长的上a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是（）（A ）261a π （B ）231a π （C ）232a π （D ）234a π20．（杭州市）过⊙O 内一点M 的最长的弦长为6厘米，最短的弦长为4厘米，则OM 的长为（）（A ）3厘米（B ）5厘米（C ）2厘米（D ）5厘米21．（安徽省）已知圆锥的底面半径是3，高是4，则这个圆锥侧面展开图的面积是（）（A ）12π （B ）15π （C ）30π （D ）24π22．（安微省）已知⊙O 的直径AB 与弦AC 的夹角为 30，过C 点的切线PC 与AB 延长线交P ．PC ＝5，则⊙O 的半径为（）（A ）335 （B ）635 （C ）10 （D ）5 23．（福州市）如图：PA 切⊙O 于点A ，PBC 是⊙O 的一条割线，有PA＝32，PB ＝BC ，那么BC 的长是（）（A ）3 （B ）32 （C ）3 （D ）3224．（河南省）如图，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）（A ）π （B ）1.5π （C ）2π （D ）2.5π25．（四川省）正六边形的半径为2厘米，那么它的周长为（）（A ）6厘米（B ）12厘米（C ）24厘米（D ）122厘米26．（四川省）一个圆柱形油桶的底面直径为0.6米，高为1米，那么这个油桶的侧面积为（）（A ）0.09π平方米（B ）0.3π平方米（C ）0.6平方米（D ）0.6π平方米27．（贵阳市）一个形如圆锥的冰淇淋纸筒，其底面直径为6厘米，母线长为5厘米，围成这样的冰淇淋纸筒所需纸片的面积是（）（A ）66π平方厘米（B ）30π平方厘米（C ）28π平方厘米（D ）15π平方厘米28．（新疆乌鲁木齐）在半径为2的⊙O 中，圆心O 到弦AB 的距离为1，则弦AB 所对的圆心角的度数可以是（）（A ） 60 （B ） 90 （C ） 120 （D ） 15029．（新疆乌鲁木齐）将一张长80厘米、宽40厘米的矩形铁皮卷成一个高为40厘米的圆柱形水桶的侧面，（接口损耗不计），则桶底的面积为（）（A ）π1600平方厘米（B ）1600π平方厘米（C ）π6400平方厘米（D ）6400π平方厘米 30．（成都市）如图，已知AB 是⊙O 的直径，弦CD ⊥AB 于点P ，CD ＝10厘米，AP ∶PB ＝1∶5，那么⊙O 的半径是（）（A ）6厘米（B ）53厘米（C ）8厘米（D ）35厘米31．（成都市）在Rt △ABC 中，已知AB ＝6，AC ＝8，∠A ＝90．如果把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1；把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，那么S 1∶S 2等于（）（A ）2∶3 （B ）3∶4 （C ）4∶9 （D ）5∶1232．（苏州市）如图，⊙O 的弦AB ＝8厘米，弦CD 平分AB 于点E ．若CE ＝2厘米．ED 长为（）（A ）8厘米（B ）6厘米（C ）4厘米（D ）2厘米33．（苏州市）如图，四边形ABCD 内接于⊙O ，若∠BOD ＝160，则∠BCD ＝（）（A ） 160 （B ） 100 （C ） 80 （D ） 2034．（镇江市）如图，正方形ABCD 内接于⊙O ，E 为DC 的中点，直线BE交⊙O 于点F ．若⊙O 的半径为2，则BF 的长为（）（A ）23 （B ）22 （C ）556 （D ）554 35．（扬州市）如图，AB 是⊙O 的直径，∠ACD ＝ 15，则∠BAD 的度数为（）（A ） 75 （B ） 72 （C ） 70 （D ） 6536．（扬州市）已知：点P 直线l 的距离为3，以点P 为圆心，r 为半径画圆，如果圆上有且只有两点到直线l 的距离均为2，则半径r 的取值范围是（）（A ）r ＞1 （B ）r ＞2 （C ）2＜r ＜3 （D ）1＜r ＜537．（绍兴市）边长为a 的正方边形的边心距为（）（A ）a （B ）23a （C ）3a （D ）2a 38．（绍兴市）如图，以圆柱的下底面为底面，上底面圆心为顶点的圆锥的母线长为4，高线长为3，则圆柱的侧面积为（）（A ）30π （B ）76π （C ）20π （D ）74π39．（昆明市）如图，扇形的半径OA ＝20厘米，∠AOB ＝ 135，用它做成一个圆锥的侧面，则此圆锥底面的半径为（）（A ）3.75厘米（B ）7.5厘米（C ）15厘米（D ）30厘米40．（昆明市）如图，正六边形ABCDEF 中．阴影部分面积为123平方厘米，则此正六边形的边长为（）（A ）2厘米（B ）4厘米（C ）6厘米（D ）8厘米41．（温州市）已知扇形的弧长是2π厘米，半径为12厘米，则这个扇形的圆心角是（）（A ） 60 （B ） 45 （C ） 30 （D ） 2042．（温州市）圆锥的高线长是厘米，底面直径为12厘米，则这个圆锥的侧面积是（）（A ）48π厘米（B ）24π13平方厘米（C ）48π13平方厘米（D ）60π平方厘米43．（温州市）如图，AB 是⊙O 的直径，点P 在BA 的延长线上，PC是⊙O 的切线，C 为切点，PC ＝26，PA ＝4，则⊙O 的半径等于（）（A ）1 （B ）2 （C ）23 （D ）26 44．（常州市）已知圆柱的母线长为5厘米，表面积为28π平方厘米，则这个圆柱的底面半径是（）（A ）5厘米（B ）4厘米（C ）2厘米（D ）3厘米45．（常州市）半径相等的圆内接正三角形、正方形、正六边形的边长之比为（）（A ）1∶2∶3 （B ）3∶2∶1（C ）3∶2∶1 （D ）1∶2∶346．（广东省）如图，若四边形ABCD 是半径为1和⊙O 的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为（）（A ）（2π－2）厘米（B ）（2π－1）厘米（C ）（π－2）厘米（D ）（π－1）厘米47．（武汉市）如图，已知圆心角∠BOC ＝100，则圆周角∠BAC 的度数是（）（A ） 50 （B ） 100 （C ） 130 （D ） 20048．（武汉市）半径为5厘米的圆中，有一条长为6厘米的弦，则圆心到此弦的距离为（）（A ）3厘米（B ）4厘米（C ）5厘米（D ）6厘米49．已知：Rt △ABC 中，∠C ＝ 90，O 为斜边AB 上的一点，以O 为圆心的圆与边AC 、BC 分别相切于点E 、F ，若AC ＝1，BC ＝3，则⊙O 的半径为（）（A ）21 （B ）32 （C ）43 （D ）54 50．（武汉市）已知：如图，E 是相交两圆⊙M 和⊙O 的一个交点，且ME ⊥NE ，AB 为外公切线，切点分别为A 、B ，连结AE 、BE ．则∠AEB 的度数为（）（A ）145° （B ）140° （C ）135° （D ）130°二、填空题1．（北京市东城区）如图，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D 是优弧上的一点，已知∠BAC ＝80，那么∠BDC ＝__________度．2．（北京市东城区）在Rt △ABC 中，∠C ＝ 90，A Ｂ＝3，BC ＝1，以AC 所在直线为轴旋转一周，所得圆锥的侧面展开图的面积是__________．3．（北京市海淀区）如果圆锥母线长为6厘米，那么这个圆锥的侧面积是_______平方厘米4．（北京市海淀区）一种圆状包装的保鲜膜，如图所示，其规格为“20厘米×60米”，经测量这筒保鲜膜的内径1ϕ、外径2ϕ的长分别为3.2厘米、4.0厘米，则该种保鲜膜的厚度约为_________厘米（π取3.14，结果保留两位有效数字）．5．（上海市）两个点O 为圆心的同心圆中，大圆的弦AB 与小圆相切，如果AB 的长为24，大圆的半径OA 为13，那么小圆的半径为___________．6．（天津市）已知⊙O 中，两弦AB 与CD 相交于点E ，若E 为AB 的中点，CE ∶ED ＝1∶4，AB ＝4，则CD 的长等于___________．7．（重庆市）如图，AB 是⊙O 的直径，四边形ABCD 内接于⊙O ，，，的度数比为3∶2∶4，MN 是⊙O 的切线，C 是切点，则∠BCM 的度数为___________．8．（重庆市）如图，P 是⊙O 的直径AB 延长线上一点，PC 切⊙O于点C ，PC ＝6，BC ∶AC ＝1∶2，则AB 的长为___________．9．（重庆市）如图，四边形ABCD 内接于⊙O ，AD ∥BC ，＝，若AD ＝4，BC ＝6，则四边形ABCD 的面积为__________．10．(山西省)若一个圆柱的侧面积等于两底面积的和，则它的高h 与底面半径r 的大小关系是__________．11．（沈阳市）要用圆形铁片截出边长为4厘米的正方形铁片，则选用的圆形铁片的直径最小要___________厘米．12．（沈阳市）圆内两条弦AB 和CD 相交于P 点，AB 长为7，AB 把CD 分成两部分的线段长分别为2和6，那么＝__________．13．（沈阳市）△ABC 是半径为2厘米的圆内接三角形，若BC ＝23厘米，则∠A 的度数为________．14．（沈阳市）如图，已知OA 、OB 是⊙O 的半径，且OA ＝5，∠AOB ＝15，AC ⊥OB 于C ，则图中阴影部分的面积（结果保留π）S ＝_________．15．（哈尔滨市）如图，圆内接正六边形ABCDEF 中，AC 、BF 交于点M ．则ABM S △∶AFM S △＝_________．16．(哈尔滨市)两圆外离，圆心距为25厘米，两圆周长分别为15π厘米和10π厘米．则其内公切线和连心线所夹的锐角等于__________度．17．（哈尔滨市）将两边长分别为4厘米和6厘米的矩形以其一边所在直线为轴旋转一周，所得圆柱体的表面积为_________平方厘米．18．（陕西省）如图，在⊙O 的内接四边形ABCD 中，∠BCD ＝130 ，则∠BOD的度数是________．19．（陕西省）已知⊙O 的半径为4厘米，以O 为圆心的小圆与⊙O 组成的圆环的面积等于小圆的面积，则这个小圆的半径是______厘米．20．（陕西省）如图，⊙O 1的半径O 1A 是⊙O 2的直径，C 是⊙O 1上的一点，O 1C 交⊙O 2于点B ．若⊙O 1的半径等于5厘米，的长等于⊙O 1周长的101，则的长是_________． 21．（甘肃省）正三角形的内切圆与外接圆面积之比为_________．22．（甘肃省）如图，AB ＝8，AC ＝6，以AC 和BC 为直径作半圆，两圆的公切线MN 与AB 的延长线交于D ，则BD 的长为_________．23．（宁夏回族自治区）圆锥的母线长为5厘米，高为3厘米，在它的侧面展开图中，扇形的圆心角是_________度．24．（南京市）如图，AB 是⊙O 的直径，弦CD ⊥AB ，垂足是G ，F 是CG 的中点，延长AF 交⊙O 于E ，CF ＝2，AF ＝3，则EF 的长是_________．25．（福州市）在⊙O 中，直径AB ＝4厘米，弦CD ⊥AB 于E ，OE ＝3，则弦CD 的长为__________厘米．26．（福州市）若圆锥底面的直径为厘米，线线长为5厘米，则它的侧面积为__________平方厘米（结果保留π）．27．（河南省）如图，AB 为⊙O 的直径，P 点在AB 的延长线上，PM 切⊙O 于M 点．若OA ＝a ，PM ＝3a ，那么△PMB 的周长的__________．28．（长沙市）在半径9厘米的圆中， 60的圆心角所对的弧长为__________厘米． 29．（四川省）扇形的圆心角为120 ，弧长为6π厘米，那么这个扇形的面积为_________．30．（贵阳市）如果圆O 的直径为10厘米，弦AB 的长为6厘米，那么弦AB 的弦心距等于________厘米．31．（贵阳市）某种商品的商标图案如图所求（阴影部分），已知菱形ABCD的边长为4，∠A ＝ 60，是以A 为圆心，AB 长为半径的弧，是以B 为圆心，BC 长为半径的弧，则该商标图案的面积为_________．32．（云南省）已知，一个直角三角形的两条直角边的长分别为3厘米、4厘米、以它的直角边所在直角线为轴旋转一周，所得圆锥的表面积是__________．33．（新疆乌鲁木齐）正六边形的边心距与半径的比值为_________．34．（新疆乌鲁木齐）如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OA 上一点，以AC 为直径的半圆1O 和以OB 为直径的半圆2O 相切，则半圆1O 的半径为__________．35．（成都市）如图，PA 、PB 与⊙O 分别相切于点A 、点B ，AC 是⊙O的直径，PC 交⊙O 于点D ．已知∠APB ＝ 60，AC ＝2，那么CD 的长为________．36．（苏州市）底面半径为2厘米，高为3厘米的圆柱的体积为_________立方厘米（结果保留π）．37．（扬州市）边长为2厘米的正六边形的外接圆半径是________厘米，内切圆半径是________厘米（结果保留根号）．38．（绍兴市）如图，PT 是⊙O 的切线，T 为切点，PB 是⊙O 的割线交⊙O 于A 、B 两点，交弦CD 于点M ，已知：CM ＝10，MD ＝2，PA ＝MB ＝4，则PT 的长等于__________．39．（温州市）如图，扇形OAB 中，∠AOB ＝90，半径OA ＝1，C 是线段AB 的中点，CD ∥OA ，交于点D ，则CD ＝________．40．（常州市）已知扇形的圆心角为150 ，它所对的弧长为20π厘米，则扇形的半径是________厘米，扇形的面积是__________平方厘米．41．（常州市）如图，AB 是⊙O 直径，CE 切⊙O 于点C ，CD ⊥AB ，D 为垂足，AB ＝12厘米，∠B ＝30 ，则∠ECB ＝__________ ；CD ＝_________厘米．42．（常州市）如图，DE 是⊙O 直径，弦AB ⊥DE ，垂足为C ，若AB ＝6，CE ＝1，则CD ＝________，OC ＝_________．43．（常州市）如果把人的头顶和脚底分别看作一个点，把地球赤道作一个圆，那么身高压2米的汤姆沿着地球赤道环道环行一周，他的头顶比脚底多行________米． 44．（海南省）已知：⊙O 的半径为1，M 为⊙O 外的一点，MA 切⊙O 于点A ，MA ＝1．若AB 是⊙O 的弦，且AB ＝2，则MB 的长度为_________．45．（武汉市）如果圆的半径为4厘米，那么它的周长为__________厘米．三、解答题：1．（苏州市）已知：如图，△ABC 内接于⊙O ，过点B 作⊙O 的切线，交CA 的延长线于点E ，∠EBC ＝2∠C ． ①求证：AB ＝AC ； ②若tan ∠ABE ＝21，（ⅰ）求BC AB 的值；（ⅱ）求当AC ＝2时，AE 的长．2．（广州市）如图，PA 为⊙O 的切线，A 为切点，⊙O 的割线PBC 过点O 与⊙O 分别交于B 、C ，PA ＝8cm ，PB ＝4cm ，求⊙O 的半径．3．（河北省）已知：如图，BC 是⊙O 的直径，AC 切⊙O 于点C ，AB 交⊙O 于点D ，若AD ︰DB ＝2︰3，AC ＝10，求sin B 的值．4．（北京市海淀区）如图，PC 为⊙O 的切线，C 为切点，PAB 是过O 的割线，CD ⊥AB 于点D ，若tan B ＝21，PC ＝10cm ，求三角形BCD 的面积．5．（宁夏回族自治区）如图，在两个半圆中，大圆的弦MN 与小圆相切，D 为切点，且MN ∥AB ，MN ＝a ，ON 、CD 分别为两圆的半径，求阴影部分的面积．6．（四川省）已知，如图，以△ABC 的边AB 作直径的⊙O ，分别并AC 、BC 于点D 、E ，弦FG ∥AB ，S △CDE ︰S △ABC ＝1︰4，DE ＝5cm ，FG ＝8cm ，求梯形AFGB 的面积．7．（贵阳市）如图所示：PA 为⊙O 的切线，A 为切点，PBC 是过点O 的割线，PA ＝10，PB ＝5，求：（1）⊙O 的面积（注：用含π的式子表示）；（2）cos ∠BAP 的值．参考答案一、选择题1．B 2．B 3．D 4．D 5．C 6．C 7．A 8．C 9．D 10．B 11．A 12．B 13．C 14．D 15．D 16．A 17．B 18．C 19．C 20．B 21．C 22．A 23．A 24．B 25．B 26．D 27．D 28．C 29．A 30．B 31．A 32．A 33．B 34．C 35．A 36．D 37．B 38．B 39．B 40．B 41．C 42．D 43．A 44．C 45．B 46．C 47．A 48．B 49．C50．C 二、填空题1．50 2．2π 3．18π 4．4105.7-⨯ 5．5 6．5 7．30° 8．9 9．25 10．h ＝r 11．42 12．3或4 13．60°或120° 14．8252425-π 15．1:2 16．30 17．80π或120π 18．100° 19．22 20．π 21．1:4 22．1 23．288 24．4 25．2 26．15π 27．()a 23+ 28．3π 29．27π平方厘米 30．4 31．34 32．24π平方厘米或36π平方厘米 33．23 34．4 35．774 36．12π 37．2，3 38．13239．213- 40．24，240π 41．60°，33 42．9，4 43．4π 44．1或5 45．8π三、解答题：1．（1）∵ BE 切⊙O 于点B ，∴ ∠ABE ＝∠C ． ∵ ∠EBC ＝2∠C ，即 ∠ABE ＋∠ABC ＝2∠C ， ∴ ∠C ＋∠ABC ＝2∠C ， ∴ ∠ABC ＝∠C ，∴ AB ＝AC ．（2）①连结AO ，交BC 于点F ， ∵ AB ＝AC ，∴＝，∴ AO ⊥BC 且BF ＝FC ．在Rt △ABF 中，BFAF＝tan ∠ABF ，又 tan ∠ABF ＝tan C ＝tan ∠ABE ＝21，∴ BF AF ＝21，∴ AF ＝21BF ．∴ AB ＝22BF AF +＝2221BF BF +⎪⎭⎫ ⎝⎛＝25BF ．∴452==BF AB BC AB ． ②在△EBA 与△ECB 中，∵ ∠E ＝∠E ，∠EBA ＝∠ECB ，∴ △EBA ∽△ECB ．∴ ⎪⎩⎪⎨⎧⋅==ECEA BE BC ABEB EA 2，解之，得516EA 2＝EA ·（EA ＋AC ），又EA ≠0，∴511EA ＝AC ，EA ＝115×2＝1110． 2．设⊙的半径为r ，由切割线定理，得PA 2＝PB ·PC ， ∴ 82＝4（4＋2r ），解得r ＝6（cm ）．即⊙O 的半径为6cm ．3．由已知AD ︰DB ＝2︰3，可设AD ＝2k ，DB ＝3k （k ＞0）．∵ AC 切⊙O 于点C ，线段ADB 为⊙O 的割线， ∴ AC 2＝AD ·AB ，∵ AB ＝AD ＋DB ＝2k ＋3k ＝5k ， ∴ 102＝2k ×5k ，∴ k 2＝10， ∵ k ＞0，∴ k ＝10． ∴ AB ＝5k ＝510．∵ AC 切⊙O 于C ，BC 为⊙O 的直径， ∴ AC ⊥BC ．在Rt △ACB 中，sin B ＝51010510==AB AC ． 4．解法一：连结AC ．∵ AB 是⊙O 的直径，点C 在⊙O 上， ∴ ∠ACB ＝90°． CD ⊥AB 于点D ，∴ ∠ADC ＝∠BDC ＝90°，∠2＝90°－∠BAC ＝∠B ．∵ tan B ＝21， ∴ tan ∠2＝21．∴ CBACDB CD CD AD ===21．设AD ＝x （x ＞0），CD ＝2x ，DB ＝4x ，AB ＝5x ． ∵ PC 切⊙O 于点C ，点B 在⊙O 上，∴ ∠1＝∠B ． ∵ ∠P ＝∠P ，∴ △PAC ∽△PCB ， ∴21==CB AC PC PA ． ∵ PC ＝10，∴ PA ＝5，∵ PC 切⊙O 于点C ，PAB 是⊙O 的割线， ∵ PC 2＝PA ·PB ，∴ 102＝5（5＋5 x ）．解得x ＝3． ∴ AD ＝3，CD ＝6，DB ＝12． ∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．解法二：同解法一，由△PAC ∽△PCB ，得21==CB AC PC PA ． ∵ PA ＝10，∴ PB ＝20．由切割线定理，得PC 2＝PA ·PB ．∴ PA ＝201022-PB PC ＝5，∴ AB ＝PB －PA ＝15， ∵ AD ＋DB ＝x ＋4x ＝15，解得x ＝3， ∴ CD ＝2x ＝6，DB ＝4x ＝12． ∴ S △BCD ＝21CD ·DB ＝21×6×12＝36．即三角形BCD 的面积36cm 2．5．解：如图取MN 的中点E ，连结OE ，∴ OE ⊥MN ，EN ＝21MN ＝21a ．在四边形EOCD 中，∵ CO ⊥DE ，OE ⊥DE ，DE ∥CO ， ∴ 四边形EOCD 为矩形． ∴ OE ＝CD ，在Rt △NOE 中，NO 2－OE 2＝EN 2＝22⎪⎭⎫⎝⎛a ．∴ S 阴影＝21π（NO 2－OE 2）＝21π·22⎪⎭⎫⎝⎛a ＝28πa ．6．解：∵ ∠CDE ＝∠CBA ，∠DCE ＝∠BCA ，∴ △CDE ∽△ABC ．∴ 2⎪⎭⎫⎝⎛=∆∆AB DE S S ABC CDE∴AB DE ＝ABC CDE S S ∆∆＝41＝21，即215=AB ，解得 AB ＝10（cm ），作OM ⊥FG ，垂足为M ，则FM ＝21FG ＝21×8＝4（cm ），连结OF ， ∵ OA ＝21AB ＝21×10＝5（cm ）． ∴ OF ＝OA ＝5（cm ）．在Rt △OMF 中，由勾股定理，得OM ＝22FM OF -＝2245-＝3（cm ）．∴ 梯形AFGB 的面积＝2FG AB +·OM ＝2810⨯×3＝27（cm 2）．7．⎭⎬⎫的割线⊙是的切线⊙是O PBC O PA )1(⇒PA 2＝PB ·PC ⇒PC ＝20⇒半径为7.5⇒圆面积为π4225（或56.25π）（平方单位）．⎭⎬⎫∠=∠∠=∠P P BAP C )2(⇒△ACP ∽△BAP ⇒PB PA AB AC =⇒12=AB AC ．解法一：设AB ＝x ，AC ＝2x ，BC 为⊙O 的直径⇒∠CAB ＝90°，则 BC ＝5x ． ∵ ∠BAP ＝∠C ，∴ cos ∠BAP ＝cos ∠C ＝55252==x x BC AC 解法二：设AB ＝x ，在Rt △ABC 中，AC 2＋AB 2＝BC 2，即 x 2＋（2x ）2＝152，解之得 x ＝35，∴ AC ＝65，∵ ∠BAP ＝∠C ，∴ ∴ cos ∠BAP ＝cos ∠C ＝5521556==BC AC。