工程力学--材料力学(第五、六章)经典例题及讲解
工程力学--材料力学(北京科大、东北大学版)第4版第五章习题答案
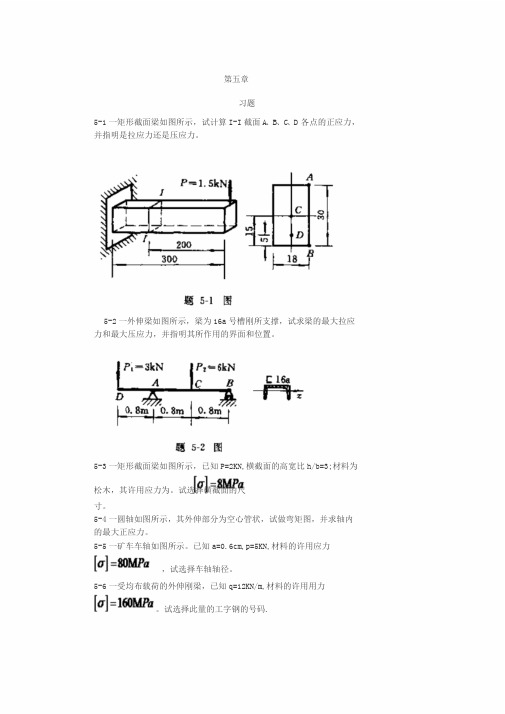
第五章习题5-1一矩形截面梁如图所示,试计算I-I截面A、B、C、D各点的正应力,并指明是拉应力还是压应力。
5-2一外伸梁如图所示,梁为16a号槽刚所支撑,试求梁的最大拉应力和最大压应力,并指明其所作用的界面和位置。
5-3一矩形截面梁如图所示,已知P=2KN,横截面的高宽比h/b=3;材料为松木,其许用应力为。
试选择横截面的尺寸。
5-4一圆轴如图所示,其外伸部分为空心管状,试做弯矩图,并求轴内的最大正应力。
5-5一矿车车轴如图所示。
已知a=0.6cm,p=5KN,材料的许用应力,试选择车轴轴径。
5-6一受均布载荷的外伸刚梁,已知q=12KN/m,材料的许用用力。
试选择此量的工字钢的号码.5-7图示的空气泵的操纵杆右端受力为8.5KN,截面I-I和II-II位矩形,其高宽比为h/b=3,材料的许用应力。
试求此二截面的尺寸。
5-8图示为以铸造用的钢水包。
试按其耳轴的正应力强度确定充满钢水所允许的总重量,已知材料的许用应力,d=200mm.5-9求以下各图形对形心轴的z的惯性矩。
5-10横梁受力如图所试。
已知P=97KN,许用应力。
校核其强度。
5-11铸铁抽承架尺寸如图所示,受力P=16KN。
材料的许用拉应力。
许用压应力。
校核截面A-A的强度,并化出其正应力分布图。
5-12铸铁T形截面如图所示。
设材料的许用应力与许用压应力之比为,试确定翼缘的合理跨度b.5-13试求题5-1中截面I-I上A、B、C、D各点处的切应力。
5-14制动装置的杠杆,在B处用直径d=30mm的销钉支承。
若杠杆的许用应力,销钉的,试求许可载荷和。
5-15有工字钢制成的外伸梁如图所示。
设材料的弯曲许用应力,许用且应力,试选择工字钢的型号。
5-16一单梁吊车由40a号工字钢制成,在梁中段的上下翼缘上各加焊一块的盖板,如图所示。
已知梁跨长=8m,=5.2m,材料的弯曲许用应力,许用且应力。
试按正应力强度条件确定梁的许可载荷,并校核梁的切应力。
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
第五章 习题解答(材料力学课件)-PPT文档资料

换后最大扭矩将由1.5kN m减小为1kN m
4. 解 :
AC
AB
3
BC
T1 l 1 T 2 l 2 G Ip G Ip
3
1.5 1 0 1.2 0 .5 1 0 0 .8 9 4 80 10 0 .0 5 32 0 .0 4 4 8 4 ra d A、 B两 轮 互 换 位 置 后 , 轴 两 端 的 相 对 扭 转 角 为 1.0 1 0 1.2 0 .5 1 0 0 .8 9 80 10 0 .0 5 4 32 0 .0 1 6 3 ra d
m
x
l
XT5TU1
1 0 .解 : 轴 的 扭 矩 图 如 下 图 , 最 大 扭 矩 T . k N m m a x 05 T m a x 由 强 度 条 件 m [] 得 轴 的 直 径 a x 3 d 1 6 1 6 T m a x 3 d 5 03 . m m []
m
A
B
m
C
D
mD
即
1 2m 解 得 m 05 . 5 7 m D 4 4 A 端 的 反 力 偶 m m .4 3m A m D 04
4
(m ) 4m D m D 2
m D 2 0
内、外层横截面上剪应力的计算公式分别为 T1 m T2 2m 1 , 2 I p1 I p1 2 I p 2 I p2 I p1 2 I p 2
1 9 .解 : 此 为 一 次 静 不 定 问 题 。 解 除端 D 约 束 , 代 之 以 反 力 偶 m D 由 变 形 协 调 条 件 A A 0 , 得 D B B C C D ( m ml )A m m D B Dl B C Dl C D 0 G IpA G IpB IpC B C G D
工程力学第六章答案 梁的变形

第五章 梁的变形测试练习1. 判断改错题5—1—1 梁上弯矩最大的截面,挠度也最大,弯矩为零的截面,转角亦为零。
( )5-1—2 两根几何尺寸、支承条件完全相同的静定梁,只要所受荷栽相同,则两梁所对应的截面的挠度及转角相同,而与梁的材料是否相同无关. ( ) 5—1-3 悬臂梁受力如图所示,若A 点上作用的集中力P 在A B 段上作等效平移,则A 截面的转角及挠度都不变。
( )5-1-4 图示均质等直杆(总重量为W ),放置在水平刚性平面上,若A 端有一集中力P 作用,使A C 部分被提起,C B 部分仍与刚性平面贴合,则在截面C 上剪力和弯矩均为零.( )5—1-5 挠曲线近似微分方程不能用于求截面直梁的位移. ( ) 5—1—6 等截面直梁在弯曲变形时,挠度曲线的曲率最大值发生在转角等于零的截面处。
( ) 5-1—7两简支梁的抗刚度E I 及跨长2a 均相同,受力如图所示,则两梁跨中截面的挠度不等而转角是相等的. ( ) 5-1—8 简支梁在图示任意荷载作用下,截面C 产生挠度和转角,若在跨中截面C 又加上一个集中力偶M 0作用,则梁的截面C 的挠度要改变,而转角不变. ( )5—1-9 一铸铁简支梁,在均布载荷作用下,当其横截面相同且分别按图示两种情况放置时,梁同一截面的应力及变形均相同。
( ) 5—1-10 图示变截面梁,当用积分法求挠曲线方程时,因弯矩方程有三个,则通常有6个积分常量。
( )题5-1-3图题5-1-4图题5-1-8图题5-1-7图题5-1-9图2.填空题5-2—1 挠曲线近似微分方程EIx M x y )()("-= 的近似性表现在和。
5—2-2 已知图示二梁的抗弯度E I 相同,若使二者自由端的挠度相等,则=21P P 。
5-2-3 应用叠加原理求梁的变形时应满足的条件是:。
5-2—4 在梁的变形中挠度和转角之间的关系是。
5—2-5 用积分法求图示的外伸梁(B D 为拉杆)的挠曲线方程时,求解积分常量所用到的边界条件是,连续条件是.5—2-6 用积分法求图示外伸梁的挠曲线方程时,求解积分常量所用到边界条件是,连续条件是。
《工程力学》第五章拉伸和压缩试卷

《工程力学》第五章拉伸和压缩试卷一、单项选择题1.由于常发生在应力集中处,须尽力减缓应力集中对构件的影响。
(2 分)A.变形B.失稳C.噪声D.破坏2.按照强度条件,构件危险截面上的工作应力不应超过材料的。
(2 分)A.许用应力B.极限应力C.破坏应力3.下图中,真正符合拉杆受力特点的是。
(2 分)A.aB.bC.cD.a、b、c4."截面法"是材料力学中常用的的方法。
(2 分)A.假想切断杆件并研究截面上内力B.实际切断杆件并研究截面上内力C.实际切断杆件后,画出外力代表内力5.拉(压)杆的危险截面必为全杆中的横截面。
(2 分)A.正应力最大B.面积最大C.轴力最大6.如图所示AB杆两端受大小为F的力的作用,则杆内截面上的内力大小为。
(2 分)A.FB.F/2C.07.安全系数n取值大于1,在建立材料的许用应力时可。
(2 分)A.将极限应力折减B.将极限应力增大C.方便计算8.低碳钢等塑性材料的极限应力是材料的。
(2 分)A.许用应力B.屈服极限C.抗拉强度R mD.比例极限9.铸铁,适宜制造承压零件。
(多选)(2 分)A.抗压性能优良B.价格低廉、易浇铸成形C.材料坚硬耐磨10.采用过渡圆角等避免截面尺寸突变的措施,可应力集中现象。
(2 分)A.消除B.降低C.增大二、判断题11.( )两根材料不同、长度和横截面积相同的杆件,受相同轴向力作用,则两杆的相对变形相同。
(2 分)12.( )两根材料不同、长度和横截面积相同的杆件,受相同轴向力作用,则材料的许用应力相同。
(2 分)13.( )下图的σ- ε曲线上,对应a点的应力称为比例极限。
(2 分)14.( )受力构件的内力是指构件材料内部颗粒间的相互作用力。
(2 分)15.( )两根材料不同、长度和横截面积相同的杆件,受相同轴向力作用,则两杆的绝对变形相同。
(2 分)16.( )塑性材料许用应力[σ]为材料断裂时的应力除以安全系数。
05工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩

eBook工程力学(静力学与材料力学)习题详细解答(教师用书)(第5章)范钦珊 唐静静2006-12-18第5章轴向拉伸与压缩5-1试用截面法计算图示杆件各段的轴力,并画轴力图。
解:(a)题(b)题(c)题(d)题习题5-1图F NxF N(kN)x-3F Nx A5-2 图示之等截面直杆由钢杆ABC 与铜杆CD 在C 处粘接而成。
直杆各部分的直径均为d =36 mm ,受力如图所示。
若不考虑杆的自重,试求AC 段和AD 段杆的轴向变形量AC l Δ和AD l Δ解:()()N N 22ssππ44BCAB BC AB ACF l F l l d dE E Δ=+33321501020001001030004294720010π36.××+××=×=××mm ()3N 232c100102500429475286mm π10510π364..CDCD AD AC F l l l d E ΔΔ×××=+=+=×××5-3 长度l =1.2 m 、横截面面积为1.10×l0-3 m 2的铝制圆筒放置在固定的刚性块上;-10F N x习题5-2图刚性板固定刚性板A E mkN习题5-4解图直径d =15.0mm 的钢杆BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。
若在钢杆的C 端施加轴向拉力F P ,且已知钢和铝的弹性模量分别为E s =200GPa ,E a =70GPa ;轴向载荷F P =60kN ,试求钢杆C 端向下移动的距离。
解: a a P A E l F u u ABB A −=−(其中u A = 0)∴ 935.0101010.11070102.1106063333=×××××××=−B u mm钢杆C 端的位移为33P 32s s601021100935450mm π20010154...BC C B F l u u E A ×××=+=+=×××5-4 螺旋压紧装置如图所示。
材料力学习题第六章应力状态分析答案详解

材料⼒学习题第六章应⼒状态分析答案详解第6章应⼒状态分析⼀、选择题1、对于图⽰各点应⼒状态,属于单向应⼒状态的是(A )。
20(MPa )20d20(A )a 点;(B )b 点;(C )c 点;(D )d 点。
2、在平⾯应⼒状态下,对于任意两斜截⾯上的正应⼒αβσσ=成⽴的充分必要条件,有下列四种答案,正确答案是( B )。
(A ),0x y xy σστ=≠;(B ),0x y xy σστ==;(C ),0x y xy σστ≠=;(D )x y xy σστ==。
3、已知单元体AB 、BC ⾯上只作⽤有切应⼒τ,现关于AC ⾯上应⼒有下列四种答案,正确答案是( C )。
(A )AC AC /2,0ττσ==;(B )AC AC /2,/2ττσ==;(C )AC AC /2,/2ττσ==;(D )AC AC /2,/2ττσ=-=。
4、矩形截⾯简⽀梁受⼒如图(a )所⽰,横截⾯上各点的应⼒状态如图(b )所⽰。
关于它们的正确性,现有四种答案,正确答案是( D )。
(b)(a)(A)点1、2的应⼒状态是正确的;(B)点2、3的应⼒状态是正确的;(C)点3、4的应⼒状态是正确的;(D)点1、5的应⼒状态是正确的。
5、对于图⽰三种应⼒状态(a)、(b)、(c)之间的关系,有下列四种答案,正确答案是( D )。
τ(a) (b)(c)(A)三种应⼒状态均相同;(B)三种应⼒状态均不同;(C)(b)和(c)相同;(D)(a)和(c)相同;6、关于图⽰主应⼒单元体的最⼤切应⼒作⽤⾯有下列四种答案,正确答案是( B )。
(A) (B) (D)(C)解答:maxτ发⽣在1σ成45o的斜截⾯上7、⼴义胡克定律适⽤范围,有下列四种答案,正确答案是( C )。
(A)脆性材料;(B)塑性材料;(C)材料为各向同性,且处于线弹性范围内;(D)任何材料;8、三个弹性常数之间的关系:/[2(1)]G E v =+ 适⽤于( C )。
材料力学第五章习题选及其解答

5-1. 矩形截面悬臂梁如图所示,已知l =4m ,h/b=2/3,q=10kN/m ,[σ]=10MPa ,试确定此梁横截面的尺寸。
解:(1)画梁的弯矩图由弯矩图知:22max ql M =(2)计算抗弯截面模量96326332h hbh W ===(3)强度计算mmb mm ql h h ql h ql W M 277416][29][12992323232max max ≥=≥∴≤⋅===σσσ5-2. 20a 工字钢梁的支承和受力情况如图所示,若[σ]=160MPa ,试求许可载荷。
解:(1)画梁的弯矩图qNo20aql 2x由弯矩图知:32max P M =(2)查表得抗弯截面模量3610237m W -⨯=(3)强度计算kNW P P WW PW M 88.562][3][3232max max =≤∴≤⋅===σσσ 取许可载荷kN P 57][=5-3. 图示圆轴的外伸部分系空心轴。
试作轴弯矩图,并求轴最大正应力。
解:(1)画梁的弯矩图由弯矩图知:可能危险截面是C 和B 截面 (2)计算危险截面上的最大正应力值x1.34kNmxC 截面:MPa d MW M CC C C C 2.63323max ===πσ B 截面:MPa D d D M W M BB BBB B B 1.62)1(32443max =-==πσ (3)轴的最大正应力值MPaC 2.63max max ==σσ5-8. 压板的尺寸和载荷如图所示。
材料为45钢,σs =380MPa ,取安全系数n=1.5。
试校核压板的强度。
解:(1)画梁的弯矩图由弯矩图知:危险截面是A 截面,截面弯矩是Nm M A 308=(2)计算抗弯截面模量3633210568.1)1(6m Hh bH W -⨯=-=(3)强度计算许用应力A-AxMPa nS253][==σσ强度校核][196max σσ MPa WM A==压板强度足够。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
15kN 解:由弯矩图可见 M max = 20 kN ⋅ m
20 M ( kN ⋅ m)
15 σ + = M max = 20 × 10 max 2 Wz . 01 × 0.2 11.25 6 = 30MPa < [σ ]
A
C
a 2 l 2
P a
2
l 2
D
B
解:
主梁AB 主梁AB
A
P 2
P 2
B
M
L−a 2
M max AB =
P (l − a ) 4
L−a 2
P
副梁CD 副梁CD
C a M
D
M max CD =
Pa 4
P 主梁AB的最大弯矩 主梁AB的最大弯矩 M max AB = (l − a ) 4 Pa 副梁CD的最大弯矩 副梁CD的最大弯矩 M max CD = 4
ql MC = = 45kN ⋅ m 8
2
A
C
15 m .
15 m .
例10:图示木梁,已知下边缘纵向总伸长 10:图示木梁,
为 10 mm,E=10GPa,求载荷 P 的大小。 mm,E=10GPa 的大小。
P A
300 B 200
C
2m
2m
l /2
l /2
解:
∆ AC =
l /2
∫ ε ( x) ⋅ d x
F ≤ 24.6kN
+ σ B max
F ≤ 19.2kN = [ F ]
F × 2m × 0.086m = 2 ≤ 30 ×106 Pa 5493 ×10−8 m4
2、工字形截面梁的剪应力
在腹板上:
翼缘
b
腹板
y
h H
B
3、圆截面梁的剪应力
FS
z
最大剪应力:
τ max
y
4 FS = 3 A
例15:圆形截面梁受力如图所示。已知材料的 :圆形截面梁受力如图所示。
第六章
圆环:
y
复 习
I y = I z = I z 大 − I z小 =
π D4
64 64 4 πD = (1 − α 4 ) 64
其中
−
πd4
d D
z
α
=
d D
bh IZ = 12
IZ =
3
bh WZ = 6
2
h
Z
b
πd
4
64
4
WZ =
4
πd
3பைடு நூலகம்
d
32
4
Z
IZ =
π (D − d )
64
=
4
πD
64
σ max
M y max M = = IZ WZ
Wz: 抗弯截面模量 Wz:
例1:图示工字形截面外伸梁受均布荷载作用,试 图示工字形截面外伸梁受均布荷载作用,
求当最大正应力为最小时的支座位置。 求当最大正应力为最小时的支座位置。
q
解:作弯矩图
a
支座位置α 支座位置α直接影响支座截面和跨 中截面上的弯矩值。当中性轴为截 面的对称轴,最大拉、压应力相等 时,只有支座处截面与跨中截面之 弯矩的绝对值相等,才能使该梁的 最大弯矩的绝对值为最小,从而使 其最大正应力为最小。
F A C b b B b D 180 134
q=F
120
b
40 86
z
解:求出中性轴位置 作弯矩图
Fb/4 Fb/4 20
y
20
⊕
+ σ C max
分析可知,不论截面B或截面C 分析可知,不论截面B或截面C,梁的强度 均由最大拉应力控制
Fb/2 Fb/2 F × 2m × 0.134m = 4 ≤ 30 ×106 Pa 5493 ×10−8 m 4
许用应力[ ] MPa,[ ,[τ] MPa, 许用应力[σ]=160MPa,[ ]=100MPa, 试求最小直径 dmin。
q = 20 kN / m
A
解:
跨中截面弯矩最大,支座附近截面剪力最大
4m
B
d
FS max = 40kN,
σ m ax =
M m ax ≤ [σ ] Wz
M max
即
A1 = 72cm 2
A2 ≈ 100cm 2
(2)圆形 (2)圆形 (3)工字形 (3)工字形
π d3
查型钢表,取16号工字钢 查型钢表,取16号工字钢
Wz = 141cm3 A3 = 26.1cm2
例14:一槽形截面铸铁梁,试求梁的许可荷载 14:一槽形截面铸铁梁, [F ] 已知b=2m 已知b=2m , [σ + ] = 30MPa [σ − ] = 90MPa I z = 5493 ×104 mm4
y2 = 210m m
P=80kN A 1m 2m B
y2
y1
δ
220
z
60 220
24 × 2203 220 × 603 2 Iz = + 24 × 220 × (210 − 110) + + 220 × 60 × (70 − 30) 2 12 12 Pl 80 × 2 6 4 −6 4 M max = = = 40kN ⋅ m ≈ 99.3 ×10 mm = 99.3 ×10 m 4 4
9 kN
C
z
4 kN 52 B A C D 88 1m 1m 1m 2.5kN 10.5kN M ( kN ⋅ m) + σ C m ax C截面: 截面: 2.5
σ
− C m ax
9 kN
C
z
2 .5 × 8 8 = = 2 8 .8 M P a Iz
4
满足强度要求
本题
− σ C max
2 .5 × 5 2 = = 1 7 .0 M P a Iz
Wz ≥
M max = P ⋅ l = 20kN ⋅ m
σ max
由强度条件
l = 1m
(1)矩形 (1)矩形
M max
[σ ]
20 ×103 3 = m ≈ 143cm3 140 × 106
b=6cm h=12cm d≈11.3cm
M max = ≤ [σ ] Wz
P ⋅l
bh 2 Wz = 6
Wz = 32
3
20
该梁满足强度条件,安全
例7:图示铸铁梁,许用拉应力[σ+ ]=30MPa, 图示铸铁梁,许用拉应力[σ ]=30MPa
许用压应力[σ ]=60MPa 许用压应力[σ- ]=60MPa,Iz=7.63×10-6m4, 7.63× 试校核此梁的强度。 试校核此梁的强度。
A
4 kN 52 B C D 88 1m 1m 1m
4 × 52 = = 27 .3 M P a Iz
σ B截面: 截面:
+ B m ax
可不必计算
σ
− B m ax
为什么?
4 × 88 = = 4 6 .1 M P a Iz
例8:简支梁AB,在C截面下边缘贴一应 简支梁AB,
变片,测得其应变ε= 6×10-4,材料的弹性 变片,测得其应变ε= 200GPa 求载荷P的大小。 模量 E=200GPa,求载荷P的大小。
220 220 ⋅ δ ⋅ (60 + ) + 60 ⋅ 220 ⋅ 30 2 y1 = = 70mm 220 ⋅ δ + 60 ⋅ 220
δ =24mm
σ
+ max
还需校核最大工作压应力吗? 梁满足强度要求
M max ⋅ y1 = ≈ 28.3MPa Iz
<
[σ + ] = 30MPa
例13:图示悬臂梁在自由端受集中力作用,P 13:图示悬臂梁在自由端受集中力作用,
压应力分别为
[σ + ] = 30MPa 和 [σ − ] = 90MPa
