2016年五年级数学6.2 不规则图形的面积练习题及答案
五年级数学下册典型例题系列之期中专项练习:求不规则立体图形的表面积及体积(含答案)人教版

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好! 经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!1五年级数学下册典型例题系列之期中专项练习:求不规则立体图形的表面积与体积(解析版)1.计算下面图形的表面积和体积。
【解析】(1)(10×6+10×4+6×4)×2=(60+40+24)×2=124×2=248(cm2)10×4×6=40×6=240(cm3)(2)556⨯⨯=25×6=150(dm2)⨯⨯555=25×5=125(dm3)2.求下面图形的表面积和体积。
五年级上册数学一课一练-第6单元第4课时《组合图形的面积及不规则图形的面积》

第6单元第4课时《组合图形的面积及不规则图形的面积》同步练习一、选择题。
1、如图是一个直角梯形,图中阴影部分面积是100平方厘米,空白部分面积是()平方厘米.A.140 B.120 C.100 D.702、下面三个完全一样的直角梯形中,阴影部分的面积().A.甲最大B.乙最大 C.丙最大 D.一样大3、如图的长方形的面积是96,空白部分的面积().A.24 B.32 C.484、如图,平行四边形的面积是24cm2,则阴影部分的面积是().A.2cm2B.4cm2C.10cm2D.12cm25、如图所示,正方形的边长6厘米,计算阴影部分的面积,方法正确的是().A.6×6﹣×3×3 B.6×6﹣×6×6÷2C.×3×3×2 D.3×3×÷46、图中阴影部分的面积是()平方厘米.A.24 B.28 C.327、如图阴影部分的面积是().A.36cm2B.42cm2C.48cm2D.56cm28、如图中,阴影部分的面积是()平方厘米.A.400 B.200 C.314 D.1579、估算方格纸中不规则图形的面积时,下列说法不正确的是().A、可以采用数方格的方法。
B、可以把它看成近似规则图形进行估算。
C、方格纸中每个方格的边长表示的长度越长,估算的结果也就越准确。
10、如图A、B分别是长方形长和宽的中点,阴影部分面积是长方形的().A. B. C. D.二、填一填。
1、如图,四边形ABCD是一个梯形,由三个直角三角形拼成,它的面积是平方厘米.2、如图,边长相等的两个正方形中,画了甲、乙两个三角形(用阴影表示),它们的面积相比 .3、如图中阴影部分的面积是60平方厘米,空白部分的面积是平方厘米.4、(1)亮亮刚出生时脚印的面积约 cm²(假设每个小方格的面积是1cm²)(2)亮亮5岁时脚印的面积约是 cm²。
人教版数学五年级上册 第六单元 三角形的面积 练习卷(含答案)

人教版五年级上册6.2 三角形的面积练习卷一、选择题1.下面图形的周长都是16厘米,()的面积最大.(单位:厘米)A.B.C.D.2.下列说法正确的是()A.三角形的面积是平行四边形面积的一半B.一个自然数不是质数就是合数C.已知a能整除23,那么a是1或者233.一个三角形的面积是30平方厘米,底扩大到原来的3倍,高扩大到原来的2倍,则面积是()。
A.30平方厘米B.90平方厘米C.180平方厘米4.如图中,阴影部分面积与三角形()的面积相等.A.BCD B.BFC C.BCE5.下图中,阴影部分的面积和空白部分的面积相比,S阴()S空。
A.大于B.小于C.等于D.以上都有可能二、其他计算6.根据已知条件求出三角形的面积。
(单位:厘米)a=8h=2S=a=2.8h=0.2S=a=2.4h=0.5S=a=20h=0.8S=a=1.8h=1.8S=a=15h=10S=三、填空题7.以4dm长的线段为公共边,在两侧分别画出高是6dm和8dm的两个三角形,这个组合图形的面积是_____dm2。
8.三角形的高越长,面积越大..9.一个平行四边形的面积是212cm,底是6cm,这条底边上的高是( )cm,与这个平行四边形同底等高的三角形的面积是( )2cm。
10.有3人携带会议材料乘坐电梯,这3人的体重共210千克,每捆材料重25千克,电梯最大负荷为1050千克,则该电梯在此3人乘坐的情况下最多还能搭载______捆材料。
11.三角形的面积是15平方厘米,底5厘米,高是_____.四、判断题12.平行四边形的底扩大到原来的2倍,高扩大到原来的2倍,它的面积也扩大到原来的2倍.( )13.两个长方形一定能拼成一个正方形,一个正方形能剪成2个一样的长方形.( )14.判断对错.一个平行四边形面积是36平方米,如果底边缩小一半,高不变,面积是18平方米.( )15.周长相等的两个三角形,它们的面积也相等。
( )五、解答题16.现在有一块长6m,宽2.5m的黄布,要做成底0.2米,高0.15米的小三角形旗,可以做多少面?17.一张边长8厘米的正方形纸(如下图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?18.等底等高的三角形和平行四边形的面积是什么关系?等底等面积的三角形和平行四边形,高有什么关系?19.下图中有三角形ABC。
五年级数学上册不规则图形的面积巩固练习(无答案)西师大版
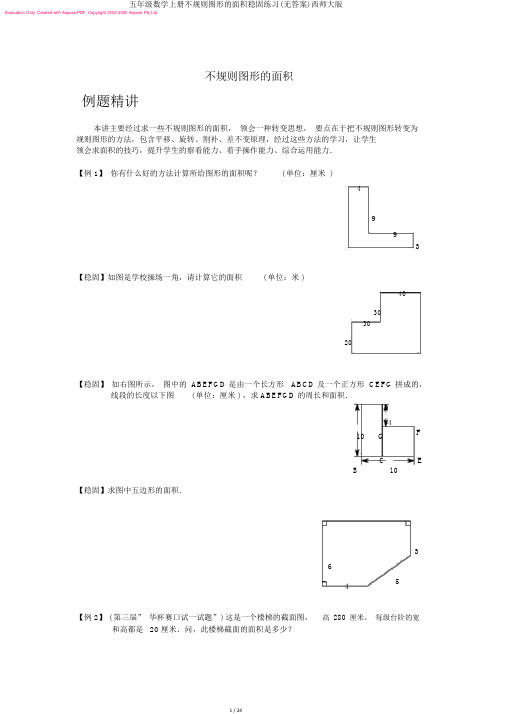
Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.不规则图形的面积例题精讲本讲主要经过求一些不规则图形的面积,领会一种转变思想,要点在于把不规则图形转变为规则图形的方法,包含平移、旋转、割补、差不变原理,经过这些方法的学习,让学生领会求面积的技巧,提升学生的察看能力、着手操作能力、综合运用能力.【例 1】你有什么好的方法计算所给图形的面积呢?( 单位:厘米 )4993【稳固】如图是学校操场一角,请计算它的面积( 单位:米 )40303020【稳固】如右图所示,图中的 ABEFGD 是由一个长方形ABCD 及一个正方形 CEFG 拼成的,线段的长度以下图( 单位:厘米 ) ,求ABEFGD的周长和面积.A D4F10 GB C E10【稳固】求图中五边形的面积.643 5【例 2】 ( 第三届” 华杯赛口试一试题”)这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【稳固】如图是一个楼梯的截面图,每级台阶的宽和高都是20 厘米.这楼梯的截面积是多少平方厘米?【例 3】有一块菜地长16米,宽 8米,菜地中间留了宽 2 米的路,把菜地均匀分红四块,每一块地的面积是多少?2米2米8米16米【例 4】有 10 张长 3 厘米,宽2 厘米的纸片,将它们依据下列图的样子摆放在桌面上,那么这 10 张纸片所遮住的桌面的面积是多少平方厘米?【例 5】下列图 ( 单位:厘米 ) 是两个相同的直角梯形重叠在一同,求暗影部分的面积.5820【稳固】两个相同的直角三角形以下列图所示( 单位:厘米 ) 重叠在一同,求暗影部分的面积.ADBO C32E F【例 6】如图,李大伯给一块长方形田地喷药,喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长 2 米的正方形地区,他从图中的 A 点出发,沿最短路线( 图中虚线 )走,走过88 米抵达B点,恰巧把这块田地所有喷完,这块田地的面积是多少平方米?A1米1米B【例 7】 ( 第六届”走进美好的数学花园”中国青少年数学论坛兴趣数学解题技术展现大赛初赛 ) 右图中甲的面积比乙的面积大 __________平方厘米.4厘米乙甲6厘米8厘米【例 8】右图中,矩形ABCD的边AB为4厘米,BC为6厘米,三角形ABF比三角形EDF的面积大 9 平方厘米,求 ED 的长.EFA DB C 【稳固】以下图,CA AB 4 厘米,△ ABE 比△CDE 的面积小 2 平方厘米,求CD 的长Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.为多少厘米?CDEBA【稳固】如图,平行四边形ABCD种, BC 10cm ,直角三角形 ECB的边 EC 8cm ,已知暗影部分的总面积比三角形 EFG的面积大10cm2,求平行四边形 ABCD的面积.EA F G DB C【例9】如图,ABCD是 74 的长方形,DEFG是 102 的长方形,求VBCO 与 VEFO 的面积差.A BD C O EG F【例 10】有一个长方形菜园,假如把宽改成50米,长不变,那么它的面积减少680平方米,假如使宽为 60 米,长不变,那么它的面积比本来增添 2720 平方米,本来的长和宽各是多少米?5060680平方米2720平方米【稳固】有一个长方形,假如宽减少 2 米,或长减少 3 米,则面积均减少24 平方米,求这个长方形的面积?32【例 11】一块长方形铁板,长15 分米,宽 12 分米,假如长和宽各减少 2 分米,面积比本来减少多少平方分米?212 2215【例 12】一个长方形,假如长减少 5 厘米,宽减少 2 厘米,那么面积就减少66 平方厘米,这时剩下的部分恰巧成为一个正方形,求本来长方形的面积?5 22 ×5【稳固】一块长方形纸片,在长边剪去5cm ,宽边剪去 2cm 后(如图),获得的正方形面积比原长方形面积少 31cm2.求原长方形纸片的面积.52【稳固】一个正方形,假如把它的相邻两边都增添6 厘米,就能够获得一个新正方形,新正方形的面积比原正方形大 120 平方厘米.求原正方形的面积?6厘米120平方厘米6厘米【例 13】一块正方形的钢板,先截去一个宽 5 分米的长方形,又截去一个宽8 分米的长方形 ( 如图 ) ,面积就比本来正方形减少 181 平方分米.原正方形的边长是多少分米?58【稳固】一张长方形纸片,先把长剪去5 厘米,这时面积又减少了8 厘米,这时面积减少了72 平方厘米,又把宽剪去60 平方厘米,本来这张长方形纸片的面积是多少平方厘米?长5宽8【稳固】 ( 希望杯培训题) 如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽 7 分米的长方形,所得图形的面积比原正方形减少 301平方分米.原正方形的边长是______分米.711【例14】如图长方形被分红两部分,已知暗影面积比空白部分面积大暗影部分的面积.34 平方厘米,求10cm18cm【例15】一张长方形纸片,把它的右上角往下折叠( 如图甲) ,暗影部分面积占原纸片面2 ;再把左下角往上折叠( 如图乙) ,乙图中暗影部分面积占原纸片面积的积的7________( 答案用分数表示) .甲乙【稳固】折叠后,原平行四边形面积是折叠后图形面积的1.5 倍.已知暗影部分面积之和为 1 ,则重叠部分 ( 即空白部分 ) 的面积是多少?【稳固】如图,一张长方形纸片,长7 厘米,宽 5 厘米.把它的右上角往下折叠,再把左下角往上折叠,未遮住的暗影部分的面积是多少平方厘米?75【例16】如图,大正方形的边长为10 厘米.连结大正方形的各边中点得小正方形,将小正方形每边三平分,再将三平分点与大正方形的中心和一个极点相连,那么图中暗影部分的面积总和等于多少平方厘米?【例 17】以下图,直角三角形中有一个长方形,求长方形的面积?46【例 18】一个边长为20 厘米的正方形,挨次连结四边中点获得第二个正方形,这样继续下去可获得第三个、第四个、第五个正方形.求第五个正方形的面积??【稳固】(2008年第七届”小灵巧杯”数学比赛决赛而成的,假如最小的正方形( 暗影部分是.) 如图是由5个大小不一样的正方形叠放) 的周长是8 ,那么最大的正方形的边长第 6题【稳固】图中有 6 个正方形,较小的正方形都由较大的正方形的 4 边中点连结而成.已知最大的正方形的边长为16 厘米,那么最小的正方形的面积等于多少平方厘米?【例 19】已知图中大正方形的面积是22 平方厘米,小正方形面积是多少平方厘米?【稳固】以下图,外侧大正方形的边长是10cm ,在里面画两条对角线、一个圆、两个正方形,暗影的总面积为 26cm2,最小的正方形的边长为多少厘米?【例 20】有一个边长为16 厘米的正方形,连结每边的中点构成第二个正方形,再连结每边的中点构成第三个正方形,第四个正方形.求图中暗影部分的面积?【例 21】(2008 年全国小学生” 我爱数学夏令营”数学比赛)如图,边长为10 的正方形中有一等宽的十字,其面积( 暗影部分) 为36,则十字中央的小正方形面积为.第 2题【例 22】下列图大小两个正方形有一部分重合,两块没有重合的暗影部分面积相差是多少? ( 单位:厘米 )663【稳固】( 2008 年武汉明心奥数挑战赛)以下图,四个相叠的正方形,边长分别是5、7、9、 11. 问灰色区与黑色区的面积的差是多少?11975【例 23】甲、乙、丙三个正方形,它们的边长分别是6、8、10 厘米,乙的一个极点在甲的中心上,丙的一个极点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?甲6乙8丙10【稳固】将 20 张边长为10 厘米的正方形纸片,按次序一张一张地摆放在地板上,摆的时候,要求后摆的纸片一定有一个极点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分 ( 右图表示已经摆好的 5 张 ) .地板被这 20 张纸片所覆盖部分的面积是多少?【例 24】有2个大小不一样的正方形A 和 B .以下左图所示的那样,在将B正方形的对角Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.线的交点与 A 正方形的一个极点相重叠时,相重叠部分的面积为 A 正方形面积的1.求 A 与 B 的边长之比.假如当按下右图那样,将 A 和 B 反向重叠的话,所重9叠部分的面积是 B 的几分之几?BAA B左图右图【例 25】有一个正方形水池 ( 图中暗影部分 ) ,在它的四周修一个宽是8 米的草地,草地的面积为 480 平方米,求水池的边长?88 88【稳固】一块长方形草坪( 图中暗影部分 ) 长是宽的2倍,它的四周围的总面积是34平方米的 1 米宽的小道.求草坪的面积是多少平方米?【例 26】(2008年北京”数学解题能力展现”读者评比活动复赛) 以下图,一个长方形广场的正中央有一个长方形的水池.水池长 8 米、宽 3 米.水池四周用边长为 1 米的方砖一圈一圈地向外铺.恰巧铺了若干圈,共用了152 块方砖,那么共铺了圈.水池Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【例 27】用四个相同的长方形拼成一个面积为100cm2的大正方形,每个长方形的周长是多少平方厘米?【稳固】以下图, 4 个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是 100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例 28】四个完整相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6 平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?16【稳固】 (2008 年”陈省身杯”国际青少年数学邀请赛) 如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知此中小正方形的面积为 4 平方厘米,大正方形的面积为400平方厘米,则此中长方形的长为厘米,宽厘米.第19题【例 29】街心花园里有一个正方形花坛,四周有一条宽 1 米的甬道 ( 如图 ) ,假如甬道的面积是 12 平方米,那么中间花坛的面积是多少平方米?1米【稳固】在一个正方形的小花园四周,围绕着宽 5 米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?5 【稳固】有大、小两个长方形( 如图 ) ,对应边的距离均为1cm,已知两个长方形之间部分的2面积是 16cm ,且小长方形的长是宽的 2 倍,求大长方形的面积.【例 30】已知大正方形比小正方形边长多 4厘米,大正方形面积比小正方形面积大96 平方厘米.问大、小正方形面积各是多少?496平方厘米4【稳固】两个正方形的面积相差9cm2,边长相差1cm.求两个正方形的面积和.C BA【稳固】(第四届《小数报》数学比赛决赛试题)有一大一小两个正方形,它们的周长相差20 厘米,面积相差55 平方厘米.小正方形的面积是多少平方厘米?【例 31】在一个正方形中放入一个四个极点与大正方形相接的一个小正方形( 如图 ) ,如果两个正方形的周长相差16厘米,面积相差96 平方厘米,求小正方形的面积是多少平方厘米?( 1)【例 32】用两块长方形纸片和一块正方形纸片拼成一个大正方形,长方形纸片面积分别为44平方厘米与28 平方厘米,原正方形纸片面积是多少平方厘米?【例 33】计划修筑一个正方形的花坛,并在花坛四周种上3米宽的草坪,草坪的面积为300平方米,那么修筑这个花坛需要占地多少平方米?【稳固】有大、小两个长方形( 右图 ) ,对应边的距离均为1厘米,已知两个长方形之间部分的面积是 16 平方厘米,且小长方形的长是宽的 2 倍,求大长方形的面积.【稳固】一块长方形的草坪 ( 见图中暗影部分 ) ,长是宽的2倍,它的四周围的总面积是34 平方米的 1米宽的小道,求草坪的总面积是多少平方米?A BCA B【例 34】一块正方形的苗圃( 如右图实线所示) ,若将它的边长各增添30米(如图虚线所示 ) ,则面积增添9900平方米,问本来这块正方形苗圃的面积是多少平方米?Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【例 35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为 5 平方米,请问锯下的长方形玻璃条的面积等于多少?【稳固】从一个正方形的木板上锯下宽1m 的一个长方形木条后,剩下的长方形面积为 6m2,问锯下的长方形木条面积是多少?1 米的一个木条此后,剩下的面积是65 平方米.问锯【稳固】从一块正方形木板锯下宽为2 18下的木条面积是多少平方米?【例 36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大 40 平方厘米.求乙正方形的面积.Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【例37】有一大一小两块正方形试验田,他们的周长相差么小正方形试验田的面积是多少平方米?40米,面积相差220 平方米,那【例 38】(第十二届“迎春杯” 刊赛试题)如图,边长是整数的四边形AFED 的面积是48 平方厘米,FB为 8 厘米.那么,正方形ABCD 的面积是平方厘米.B 8 FA48C DE【例 39】如图,一个正方形被分红 4 个小长方形,它们的面积分别是1 平方米、1平10 5方米、3 平方米和2 平方米.已知图中的暗影部分是正方形,那么它的面积是多10 5少平方米?【例 40】长方形 ABCD的周长是 30 厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290 平方厘米,那么长方形 ABCD 的面积是多少平方厘米?E 1 D 1 C 1ED CA 1 A BEvaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【稳固】 ( 第四届华杯复赛试题) 如图,长方形ABCD的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68 平方厘米,求长方形 ABCD 的面积?A DB C【例 41】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是 2 厘米,这条手帕白色部分的面积是多少?【例 42】用相同大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其余地方铺白色的,以下图.假如铺满这块地面共用 101 块黑色瓷砖,那么白色瓷砖用了多少块?【例 43】7 个完整相同的长方形拼成了图中暗影部分,图中空白部分的面积是多少平方厘米?24Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【稳固】以下图, 7 个完整相同的长方形拼成了图中的暗影部分,图中空白部分的面积是多少平方厘米?【例44】( 第五届”祖冲之杯”数学邀请赛) 如右图所示,在长方形ABCD 中,放入六个形状大小相同的长方形( 尺寸如图 ) ,图中暗影部分的面积是__________ .D C6AB 14【例 45】若干相同大小的长方形小纸片摆成了以下图的图形.已知小纸片的宽是12 厘米,问暗影部分的总面积是多少平方厘米?【例46】一个大长方形若能切割成若干个大小不一样的小正方形,则称为完满长方形.下边一个长方形是由 9 个小正方形构成的完满长方形.图中正方形A和B的边长分别是 7 厘米和 4 厘米,那么这个完满长方形的面积分别是多少平方厘米?AB【稳固】 (2008 年中国台湾小学数学比赛选拔赛) 如图:有一个矩形能够被切割为个正方11形,此中最小的正方形( 暗影部分 ) 面积为 81cm 2 ,请问这个矩形之面积为多少平方厘米?Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.ijgfeh ac b d第2题【稳固】图中的长方形被切割成 6 个正方形,已知中央小正方形的面积是 1平方厘米,求本来长方形的面积.【稳固】 9 个边长分别为1、 4、7、 8、 9、10、 14、 15、 18 的正方形拼成一个长方形,问这个长方形的长和宽是多少?并请画出这个长方形的拼接图.1518874114 910【例 47】图中数字分别表示两个长方形和一个直角三角形的面积,另一个三角形的面积是.?1215 5【例 48】如图,一个矩形被分红八个小矩形,此中有五个矩形的面积如图中所示( 单位:平方厘米 ) ,问大矩形的面积是多少平方厘米?五年级数学上册不规则图形的面积稳固练习(无答案)西师大版Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.G36AD16C 20B 30E12F【稳固】 阳阳用四块小长方形恰巧拼成了一个大的长方形, 以下图. 此刻知道此中三块长方形的面积分别为 48平方厘米、 24 平方厘米、 30 平方厘米,那么,暗影部分的面积是多少?48 2430【稳固】 ( 南京市第三届”兴趣杯”少年数学邀请赛决赛试题) 如图,矩形 ABCD 被切割成 9 个小矩形.此中有 5 个小矩形的面积以下图.矩形ABCD 的面积为 . A 2 D12 416BC【例 49】 有红、 黄、绿三块大小相同的正方形纸片,放在一个底面为正方形的盒内, 它们之间互相叠合 ( 见下列图 ) .已知露在外面的部分中,红色面积是 20 ,黄色面积是14,绿色面积是 10 .求正方形盒底的面积.黄红绿【例 50】以下图,在正方形ABCD 内,红色、绿色正方形的面积分别是48 和 12,且红、绿两个正方形有一个极点重合. 黄色正方形的一个极点位于红色正方形两条对 角线的交点, 另一个极点位于绿色正方形两条对角线的交点. 那么黄色正方形的面积是 .黄红Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.A D红黄绿B C【稳固】以下图,在正方形ABCD 中,红色,绿色正方形的面积分别是 52 和 13 ,且红、绿两个正方形有一个极点重合 . 黄色正方形的一个极点位于红色正方形两条对角线的交点,另一个极点位于绿色正方形两条对角线的交点,求黄色正方形面积.A B红黄绿D C【例51】如图,三个相同大小的正方形放在一个长方形的盒内, A 和 B 是两个正方形的重叠部分, C、D、E 是空出的部分,每一部分都是矩形,它们的面积比是A:B: C:D: E=1:2:3:4:5,那么这个长方形的长与宽之比是________.【例52】(2005米,且 MD边形 MNPQ 全国华罗庚金杯少年数学邀请赛2厘米、QC 3 厘米、CP的面积是多少厘米?) 如图假如长方形的面积为56 平方厘5 厘米、 BN6 厘米,那么请你求出四21 / 24Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.D Q 3 C2M 5PA N 6 B【稳固】( 南京市第三届”兴趣杯”少年数学邀请赛初赛8 米,A,B,C,D分别在四条边上,而且四边形 ABCD 的面积是平方米.) 长方形的广告牌长为10 米,宽为C比 A低5米, D在B的左侧2米,DA CB【例 53】(2004 全国华罗庚金杯少年数学邀请赛) 直角三角形 PQR 的直角边为5 厘米,9 厘米,问:图中三个正方形的面积之和比 4 个三角形的面积之和大多少?B AC P5R9 FD QE【例 54】以下图,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间暗影为正方形.已知甲、乙、丙、丁四个长方形面积的和是32cm 2,四边形 ABCD 的面积是 20cm 2.⑴求正方形EFGH的边长?⑵求甲、乙、丙、丁四个长方形周长的总和?EAH 甲B丁乙 D丙F C G22 / 24Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.【例 55】如图,平面上CDEF是正方形,ABCD是等腰梯形,它的上底AD 23厘米,下底 BC 35 厘米.求三角形ADE 的面积.EADFB C【例 56】右图是由9 个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例 57】把正三角形的每条边三平分,以各边的中间一段为边向外作小正三角形,获得一个六角形.再将这个六角形的六个”角”(即小正三角形)的两边三平分,又以它的中间段为边向外作更小的小正三角形,这样就获得如右图所示的图形.假如所作的最小的小正三角形的面积为 1 平方厘米,求如图中整个图形的面积.中中大中图 a【例 58】(1992 年小学数学奥林匹克初赛 ) 如图,长方形的面积是小于100 的数.它的5 ,正方形①的内部有三个边长是整数的正方形.正方形②的边长是长方形长的1 .那么,图中暗影部分的面积是12边长是长方形宽的8(2)(1)23 / 24Evaluation Only. Created with Aspose.PDF. Copyright 2002-2020 Aspose Pty Ltd.24 / 24。
【分层作业】6.2探索活动:成长的脚印(同步练习)五年级上册数学同步课时练(北师大版,含答案)

第六单元组合图形的面积6.2 探索活动:成长的脚印【基础巩固】一、选择题1.右图中每个方格的边长是1cm,树叶的面积大约()。
A.20cm2B.29cm2C.42cm2D.50cm22.如图,阴影部分的面积大约是()平方厘米。
A.30 B.20 C.163.图中每个小方格的面积表示1平方厘米,估计这个米老鼠图片的面积是()平方厘米。
A.10 B.20 C.35 D.504.下图每个小方格的边长表示1cm,估算小猫的面积最接近实际结果的是()。
A.10m2B.18cm2C.30cm2D.40cm25.估一估,下图中圆的面积约是()cm2。
(每个小方格的面积表示1cm2)A.9 B.18 C.25二、填空题6.下图中每个小方格的面积都是21cm,估一估方格中图形的面积大约是( )2cm。
7.估计下列图形的面积。
(每个小方格的边长表示1cm)面积约为( )cm2面积约为( )cm28.求下列图形面积。
(每个方格表示1cm2)( )cm2约( )cm29.估一估。
(每个小方格表示12cm)“泉州老君岩”图片的面积约是( )2cm。
10.用数方格的方法估算下面两个图形的面积.(每个小方格的边长表示1 cm)( )2cm( )2cm三、图形计算题11.求出下面图形的面积。
【能力提升】四、解答题12.科技小组收集玉兰树的树叶,每片树叶如图所示。
(每个小方格的边长表示1cm)每平方米树叶每天能吸收约5g二氧化碳进行光合作用。
如果一棵玉兰树有10000片这样的树叶,这棵玉兰树一年大约能吸收多少千克二氧化碳?(按一年365天计算)【拓展实践】13.下面方格纸市的每个口是1平方厘米。
(1)上面是小明设计的作品,你知道这些作品的面积分别是多少吗?请填写在下面的括号里。
电风扇的面积是()平方厘米;花瓶的面积是()平方厘米(2)请在方格纸上的右边画出一个面积为12平方厘米的图形。
14.市政公司准备给新玛特商场门口的广场(如图所示)重新铺地砖,每个方格表示1平方米。
人教版五年级数学上册不规则图形面积的计算测试卷附答案

人教版五年级数学上册不规则图形面积的计算测试卷附答案一、每个小方格的面积是1 cm2,估算下面图形的面积。
(每小题4分,共24分)1.2.()cm2()cm23.4.()cm2()cm25.6.()cm2()cm2二、计算下面各图形的面积。
(单位:cm)(每小题6分,共24分) 1.2.3.4.三、求阴影部分的面积。
(每小题6分,共12分)1.2.四、聪明的你,答一答。
(共40分)1.美术手工剪纸课中,乐乐剪了一个大写英文字母“E”,它的面积是多少?(单位:cm)(7分)2.几位“环保大使”用铁板给学校的草地做了一个标语牌(如图),请算出用了多少铁板?(7分)3.下图是一个占地6240平方米的花坛。
花坛两条平行的边分别是88米和42米。
请你算出这两条边的距离。
(6分)4.聪聪将一张长方形纸的一角如图折叠。
聪聪考大家:请求出阴影部分的面积。
(单位:dm)(6分)5.下图是一面墙,中间有一个长2 m,宽1.5 m的窗户,如果砌这面墙平均每平方米用160块砖,一共需要用多少块砖?(7分)6.雯雯家装修需要用下面的木板,木板形状如下图,一共需要多少平方米的木板?(7分)答案一、1.242.333.154.105.136.26二、1.(8+18)×20÷2-15×8÷2=260-60=200(cm2)2.20-9=11(cm)18×9+(18+30)×11÷2=162+264=426(cm2)【点拨】分割成一个长方形和一个梯形较简单。
3.6-2×2=2(cm)6×4-(2+1.5)×2÷2=24-3.5=20.5(cm2)4.11×8÷2+(11+22)×10÷2=209(cm2)三、1.15×10=150(平方厘米)5×(10-5)=25(平方厘米)5×(10-5)÷2=12.5(平方厘米)(15-5-5)×(10-5)÷2=12.5(平方厘米)150-(25+12.5+12.5)=100(平方厘米)2.8×8=64(dm2)6×6=36(dm2)(8+6)×6÷2=42(dm2)64+36-42=58(dm2)四、1.20-15=5(cm)15×5×3+25×5=75×3+125=350(cm2)答:它的面积是350 cm2。
【思维拓展】数学五年级思维拓展之不规则图形面积的计算1(附答案) 必考知识点

五年级奥数不规则图形面积的计算(一)我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
解:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
练习题1.如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积.2.两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
C3如右图,A 为△CDE 的DE 边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米.求△ABD 及△ACE 的面积.4如右图,在正方形ABCD 中,三角形ABE 的面积是8平方厘米,它是三角形DEC 的面积的45,求正方形ABCD 的面积。
5如右图,已知:S△ABC=1,AE=ED,BD=23BC.求阴影部分的面积。
6如右图,正方形ABCD 的边长是4厘米,CG=3厘米,矩形DEFG 的长DG 为5厘米,求它的宽DE 等于多少厘米?D7如右图,梯形ABCD的面积是45平方米,高6米,△AED的面积是5平方米,BC=10米,求阴影部分面积.8如右图,四边形ABCD和DEFG都是平行四边形,证明它们的面积相等.参考答案1解:∵△ABE、△ADF与四边形AECF的面积彼此相等,∴四边形AECF的面积与△ABE、△ADF的面积都等于正方形ABCD的1 3。
五年级不规则图形面积计算

五年级不规那么图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为根本图形或规那么图形.我们的面积及周长都有相应的公式直接计算.如下表:实际问题中,有些图形不是以根本图形的形状出现,而是由一些根本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规那么图形。
那么,不规那么图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为根本图形的和、差关系,问题就能解决了。
一、例题与方法指导例1 如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影局部的面积。
思路导航:阴影局部的面积等于甲、乙两个正方形面积之和减去三个“空白〞三角形〔△ABG、△BDE、△EFG〕的面积之和。
例2 如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积. 思路导航:∵△ABE 、△ADF 与四边形AECF 的面积彼此相等,∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。
在△ABE 中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2, ∴△ECF 的面积为2×2÷2=2。
所以S △AEF=S 四边形AECF-S △ECF=12-2=10〔平方厘米〕。
例3 两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合局部〔阴影局部〕的面积。
思路导航:在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4,∴阴影局部面积=S △ABG-S △BEF=25-8=17〔平方厘米〕。
例4 如右图,A 为△CDE 的DE 边上中点,BC=CD ,假设△ABC 〔阴影局部〕面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航:取BD中点F,连结AF.因为△ADF、△ABF和△ABC等底、等高,所以它们的面积相等,都等于5平方厘米.∴△ACD的面积等于15平方厘米,△ABD的面积等于10平方厘米。
